七年级下册数学证明题练习

苏科版七年级下册数学第12章证明含答案一、单选题(共15题，共计45分)1、已知，如图，△ABC是等边三角形，AE=CD，BQ⊥AD于Q，BE交AD于点P，下列说法：①∠APE=∠C，② AQ=BQ，③BP=2PQ, ④AE+BD=AB，其正确的个数有（）个．A.1B.2C.3D.42、下列定理有逆定理的是（）A.直角都相等B.同旁内角互补，两直线平行C.对顶角相等D.全等三角形的对应角相等3、下列语句中，属于定义的是( )A.两点确定一条直线B.同角或等角的余角相等C.两直线平行，内错角相等D.点到直线的距离是该点到这条直线的垂线段的长度4、下列命题中真命题的是（）A.同旁内角互补B.三角形的一个外角等于两个内角的和C.若，则 D.同角的余角相等5、下列命题中的假命题是（）A.一组邻边相等的平行四边形是菱形B.一组邻边相等的矩形是正方形 C.一组对边平行且相等的四边形是平行四边形 D.一组对边相等且有一个角是直角的四边形是矩形6、如图是一个长为2m，宽为2n（m＞n）的长方形，用剪刀剪成四个一样的小长方形拼成一个正方形，则正方形中空白的面积为（）A.（m﹣n）2B.（m+n）2C.m 2﹣n 2D.2mn7、下列命题是真命题的是（）A.相等的角是对顶角B.在同一平面内，如果，，则C.内错角相等D.如果，，则8、下列各运算中，计算正确的是（）A. B. C. D.9、如图，直线a、b被直线c所截，给出的下列条件中不能得出结论a∥b的是（）A.∠1=∠3B.∠1=∠4C.∠1=∠2D.∠1+∠2=180°10、等腰三角形的一外角是130°，则其底角是 ( )A.65°B.50°C.80°D.50°或65°11、已知x+y=7，xy=﹣8，则x2+y2=（）A.49B.65C.33D.57为12、已知Rt△ABC中，∠C＝90°，若cm，cm，则S△ABC （）．A.24cm 2B.36cm 2C.48cm 2D.60cm 213、多项式4x2+mxy+25y2是完全平方式，则m的值是（）A.20B.10C.10或﹣10D.20或﹣2014、下列命题中是真命题的是（）A.“面积相等的两个三角形全等”是必然事件B.“任意画一个等边三角形，它是轴对称图形”是随机事件C.“同位角相等”这一事件是不可能事件D.“三角形三条高所在直线的交点在三角形的外部”这一事件是随机事件15、如图，∠1=∠2，∠B=∠D，下列四个结论中，错误的是（）A.∠DCA=∠DACB.AD∥BCC.AB∥CDD.∠DAC=∠BCA二、填空题(共10题，共计30分)16、三角形中三个角的度数之比为3：2：5，那么最大的角是________度，这个三角形是________三角形．17、一大门的栏杆如图所示，BA垂直地面AE于A，CD平行于地面AE，则________度．18、如图，线段AB，BC的垂直平分线l1， l2相交于点O，若∠B＝50°，则∠AOC＝________.19、等边三角形ABC的边长为6，在AC，BC边上各取一点E、F，连接AF，BE 相交于点P，若AE=CF，则∠APB= ________ ．20、如图所示，△ABC中，点D，E分别是AC，BD上的点，且∠A＝65°，∠ABD＝∠DCE＝30°，则∠BEC的度数是________．21、如图，一条公路修到湖边时，需拐弯绕湖而过；如果第一次拐角∠A是120°，第二次拐角∠B是150°，第三次拐角是∠C，这时的道路恰好和第一次拐弯之前的道路平行，则∠C是________22、如图，⊙O与AC相切于点A，BC过圆心O，圆周角∠B＝25°，则∠C的度数为________．23、若 x2+y2=3，xy=1，则 x−y=________.24、命题“对角线相等”的逆命题是________.25、如图，在中，点是边上一点，，，，则的度数为________.三、解答题(共5题，共计25分)26、简便运算：20142﹣2018×2010．27、问题再现：数形结合是解决数学问题的一种重要的思想方法，借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性，从而可以帮助我们快速解题．初中数学里的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释．例如：利用图形的几何意义证明完全平方公式．证明：将一个边长为a的正方形的边长增加b，形成两个矩形和两个正方形，如图1：这个图形的面积可以表示成：（a+b）2或 a2+2ab+b2∴（a+b）2 =a2+2ab+b2这就验证了两数和的完全平方公式．类比解决：①请你类比上述方法，利用图形的几何意义证明平方差公式．（要求画出图形并写出推理过程）问题提出：如何利用图形几何意义的方法证明：13+23=32？如图2，A表示1个1×1的正方形，即：1×1×1=13B表示1个2×2的正方形，C与D恰好可以拼成1个2×2的正方形，因此：B、C、D就可以表示2个2×2的正方形，即：2×2×2=23而A、B、C、D恰好可以拼成一个（1+2）×（1+2）的大正方形．由此可得：13+23=（1+2）2=32尝试解决：②请你类比上述推导过程，利用图形的几何意义确定：13+23+33= ▲．（要求写出结论并构造图形写出推证过程）．问题拓广：③请用上面的表示几何图形面积的方法探究：13+23+33+…+n3= ▲．（直接写出结论即可，不必写出解题过程）28、如图，AD为△ABC的高，BE为△ABC 的角平分线，若∠EBA=35°，∠AEB=80°，求∠CAD的度数.29、20152﹣2014×2016（利用整式的乘法公式计算）30、如图，在△ABC中，∠B=46°，∠C=54°，AD平分∠BAC，交BC于D，DE ∥AB，交AC于E，则∠ADE的大小是多少？参考答案一、单选题(共15题，共计45分)1、C2、B3、D4、D5、D7、D8、D9、C10、D11、B12、A13、D14、D15、A二、填空题(共10题，共计30分)16、17、18、19、20、22、23、24、25、三、解答题(共5题，共计25分)26、28、29、30、。

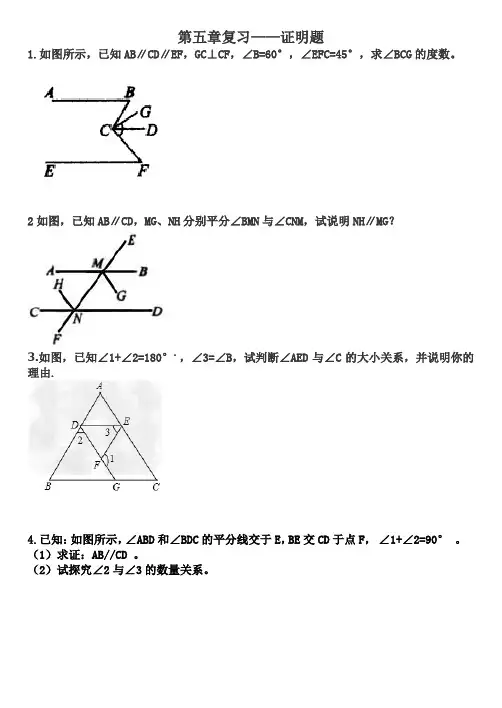
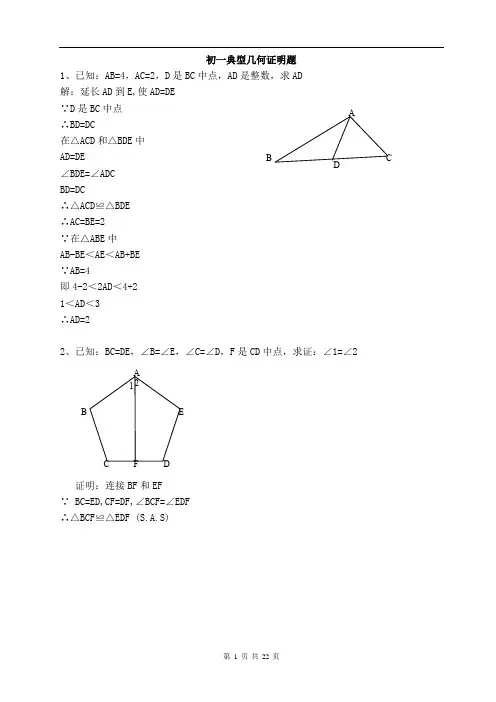
初一典型几何证明题1、已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD 解：延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=22、已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)ADBCA BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。

∴ ∠BAF=∠EAF (∠1=∠2)。

3、已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF，可得，∠EFD＝CGD DE ＝DC∠FDE＝∠GDC（对顶角） ∴△EFD≌△CGD EF ＝CG ∠CGD＝∠EFD 又，EF∥AB ∴，∠EFD＝∠1 ∠1=∠2 ∴∠CGD＝∠2∴△AGC 为等腰三角形， AC ＝CG 又 EF ＝CG ∴EF ＝AC4、已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CBA CDF2 1 EA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C5、已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC平分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE6、如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。

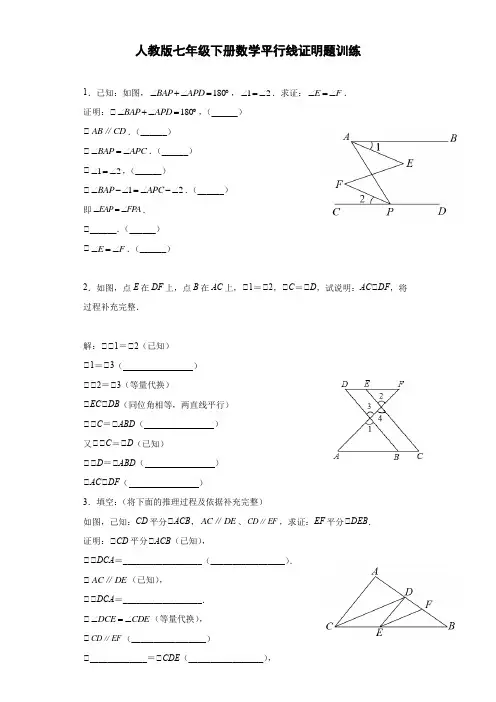
人教版七年级下册数学平行线证明题训练1．已知：如图，180BAP APD ∠+∠=︒，12∠=∠．求证：E F ∠=∠． 证明：∵180BAP APD ∠+∠=︒，（______）∵AB CD ∥．（______）∵BAP APC ∠=∠．（______）∵12∠=∠，（______）∵12BAP APC ∠-∠=∠-∠．（______）即EAP FPA ∠=∠．∵______．（______）∵E F ∠=∠．（______）2．如图，点E 在DF 上，点B 在AC 上，∵1＝∵2，∵C ＝∵D ，试说明：AC ∵DF ，将过程补充完整．解：∵∵1＝∵2（已知）∵1＝∵3（ ）∵∵2＝∵3（等量代换）∵EC ∵DB （同位角相等，两直线平行）∵∵C ＝∵ABD （ ）又∵∵C ＝∵D （已知）∵∵D ＝∵ABD （ ）∵AC ∵DF （ ）3．填空：（将下面的推理过程及依据补充完整）如图，己知：CD 平分∵ACB ，AC DE ∥、CD EF ∥，求证：EF 平分∵DEB ． 证明：∵CD 平分∵ACB （已知），∵∵DCA ＝__________________（_________________）．∵AC DE ∥（已知），∵∵DCA ＝__________________．∵DCE CDE ∠=∠（等量代换），DCE BEF ∠=∠（_________________），∵_____________＝_____________（等量代换）．∵EF 平分∵DEB （_________________）4．完成下面推理过程．在括号内的横线上填上推理依据．如图，已知：AB EF ∥，EP EQ ⊥，90EQC APE ∠+∠=︒，求证：AB CD ∥． 证明：∵AB EF ∥，∵APE PEF ∠=∠（_________）．∵EP EQ ⊥，∵90PEQ ∠=︒（__________）．即90QEF PEF ∠+∠=︒．∵90APE QEF ∠+∠=︒∵90EQC APE ∠+∠=︒，∵EQC ∠=_________（_______）．∵EF CD ∥（___________）．∵AB CD ∥（_________）．5．在横线上填上适当的内容，完成下面的证明．如图，∵E =∵1，∵3+∵ABC =180°，BE 是∵ABC 的角平分线，求证：DF∥AB ．证明：∵BE 是∵ABC 的角平分线∵∵1=∵2（________________）又∵∵E =∵1∵∵E =∵2（___________）∵____∥____（____________________）∵∵A +∵ABC =180°（____________________）又∵∵3+∵ABC =180°∵____=____（________________）∵DF∥AB （____________________）．6．在下面解答中填空.如图，,,12AB BF CD BF ⊥⊥∠=∠，试说明3E ∠=∠．解：∵,AB BF CD BF ⊥⊥（已知），∵∵ABF=∵________________=90°（垂直的定义）.∵12∠=∠（已知），∵AB//EF（__________________________________）.∵CD//EF（平行于同一条直线的两条直线互相平行）.∠=∠（___________________________________）．∵3E7．如图，已知直线AB∵CD，∵B=50°，∵BEC＝25°，EC平分∵BEF.(1)请说明AB∵EF的理由；(2)求∵DCE的度数．8．如图，EF∵BC，∵1＝∵C，∵2+∵3＝180°，试说明∵ADC＝90°．请完善解答过程，并在括号内填写相应的理论依据．解：∵∵1＝∵C，（已知）∵GD∵ ．（）∵∵2＝∵DAC．（）∵∵2+∵3＝180°，（已知）∵∵DAC+∵3＝180°．（等量代换）∵AD∵EF．（）∵∵ADC＝∵．（）∵EF∵BC，（已知）∵∵EFC＝90°．（）∵∵ADC＝90°．（等量代换）60°．请问：(1)GD 与CB 有怎样的位置关系？为什么？(2)求∵ACB 的度数．10．如图，已知,12,34AB CD ∠=∠∠=∠∥，求证：D DCE ∠=∠．11．如图，在∵ABC 中，CD ∵AB ，垂足为D ，点E 在BC 上，EF ∵AB ，垂足为F ．(1)CD 与EF 平行吗？请说明理由；(2)如果∵1＝∵2，且∵3＝110°，求∵ACB 的度数．12．如图，在∵ABC中，E、G分别是AB、AC上的点，F、D是BC上的点，连接EF、AD、DG，AD∥EF，∵1+∵2=180°．(1)说明：AB∥DG；(2)若∵2=145°，∵B=35°，说明：DG是∵ADC的平分线．13．如图，已知AB∵CD，∵2+∵3＝180°，DA平分∵BDC，CE∵FE于点E，∵1＝70°．(1)求证：AD∵CE；(2)求∵F AB的度数．14．如图，已知F是四边形BCDE的边BE上一点，CB与DF的延长线相交于点A，其中∵A=∵ADE．(1)若∵EDC=3∵C，求∵C的度数；(2)若∵C=∵E，求证：BE∥CD．15．如图，已知点D、E、F分别在ABC的边AB、AC、BC上，∵1+∵2=180°，∵3=∵B，请说明∵DEC+∵C= 180°的理由16．如图，在∵ABC中，点D、E分别在AB、BC上，且DE∵AC，∵1=∵2．(1)求证：AF∵BC；(2)若AC平分∵BAF，∵B=50°，求∵1的度数．17．如图，已知∵1=52°，∵2=128°，∵C=∵D．求证：∵A=∵F．18．如图，B ，E 分别是AC ，DF 上的点，180A ABF ∠+∠=︒，A F ∠=∠，求证：AC DF ∥．19．请根据条件进行推理，得出结论，并在括号内注明理由．已知，如图，AB DC ∥，直线EF 分别交AB 、CD 于点G 、H ，GM 、HN 分别平分∵BGH 与∵DHF ．求证：GM HN ∥；证明：∵AB DC ∥（已知），∵∵BGH=∵DHF （__________________），∵GM 、HN 分别平分∵BGH 与∵DHF ， ∵∵_____=12∵BGH ，∵_____=12∵DHF （__________________），∵∵_____=∵_____（__________________），∵GM //HN （__________________________）．20．（1）（问题）如图1，若AB CD ∥，40AEP ∠=︒，50PFC ∠=︒，求EPF ∠的度数．（3）（联想拓展）如图3所示，在（2）的条件下，已知60EPF ∠=︒，120PFC ∠=︒，PEA ∠的平分线和PFC ∠的平分线交于点G ，直接写出G ∠的度数．。

初一典型几何证明题1、已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD 解：延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE ＜AE ＜AB+BE ∵AB=4即4-2＜2AD ＜4+2 1＜AD ＜3 ∴AD=22、已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)ADBCA BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。

∵ ∠ABC=∠AED 。

∴ ∠ABE=∠AEB 。

∴ AB=AE 。

在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。

∴ ∠BAF=∠EAF (∠1=∠2)。

3、已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF，可得，∠EFD＝CGD DE ＝DC∠FDE＝∠GDC（对顶角） ∴△EFD≌△CGD EF ＝CG ∠CGD＝∠EFD 又，EF∥AB ∴，∠EFD＝∠1 ∠1=∠2 ∴∠CGD＝∠2∴△AGC 为等腰三角形， AC ＝CG 又 EF ＝CG ∴EF ＝AC4、已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠CBA CDF2 1 EA证明：延长AB取点E，使AE＝AC，连接DE∵AD平分∠BAC∴∠EAD＝∠CAD∵AE＝AC，AD＝AD∴△AED≌△ACD （SAS）∴∠E＝∠C∵AC＝AB+BD∴AE＝AB+BD∵AE＝AB+BE∴BD＝BE∴∠BDE＝∠E∵∠ABC＝∠E+∠BDE∴∠ABC＝2∠E∴∠ABC＝2∠C5、已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE证明：在AE上取F，使EF＝EB，连接CF∵CE⊥AB∴∠CEB＝∠CEF＝90°∵EB＝EF，CE＝CE，∴△CEB≌△CEF∴∠B＝∠CFE∵∠B＋∠D＝180°，∠CFE＋∠CFA＝180°∴∠D＝∠CFA∵AC平分∠BAD∴∠DAC＝∠FAC∵AC＝AC∴△ADC≌△AFC（SAS）∴AD＝AF∴AE＝AF＋FE＝AD＋BE6、如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。

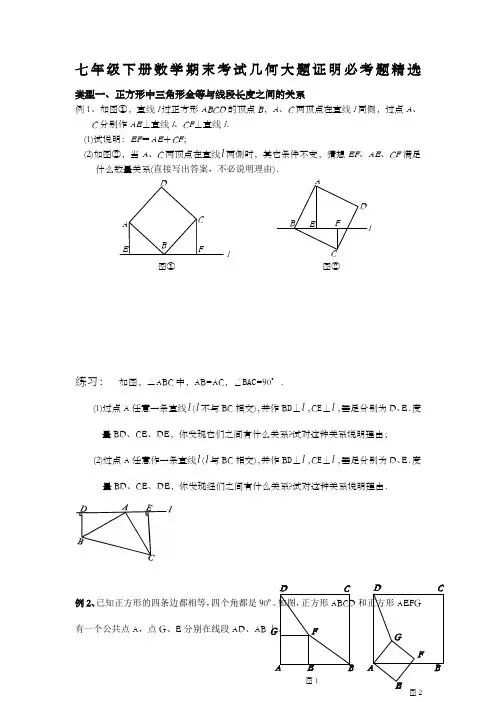
图①DA EC BFl图②ABE F ClD七年级下册数学期末考试几何大题证明必考题精选类型一、正方形中三角形全等与线段长度之间的关系例1、如图①，直线l 过正方形ABCD 的顶点B ，A 、C 两顶点在直线l 同侧，过点A 、C 分别作AE ⊥直线l 、CF ⊥直线l ． (1)试说明：EF ＝AE ＋CF ；(2)如图②，当A 、C 两顶点在直线l 两侧时，其它条件不变，猜想EF 、AE 、CF 满足什么数量关系(直接写出答案，不必说明理由)．练习： 如图，△ABC 中，AB=AC ，∠BAC =90°．(1)过点A 任意一条直线l (l 不与BC 相交)，并作B D ⊥l ，C E ⊥l ，垂足分别为D 、E ．度量BD 、CE 、DE ，你发现它们之间有什么关系?试对这种关系说明理由； (2)过点A 任意作一条直线l (l 与BC 相交)，并作B D ⊥l ，C E ⊥l ，垂足分别为D 、E ．度量BD 、CE 、DE ，你发现经们之间有什么关系?试对这种关系说明理由．例2、已知正方形的四条边都相等，四个角都是90º。

如图，正方形ABCD 和正方形AEFG 有一个公共点A ，点G 、E 分别在线段AD 、AB 上。

A E B 图1D CG FA BD CG FE图2（1）如图1， 连结DF 、BF ，说明：DF ＝BF ； （2）若将正方形AEFG 绕点A 按顺时针方向旋转，连结DG ，在旋转的过程中，你能否找到一条长度与线段DG 的长始终相等的线段？并以图2为例说明理由。

练习：如图，正方形ABCD 的边CD 在正方形ECGF 的边CE 上，B 、C 、G 三点在一条直线上，且边长分别为2和3，在BG 上截取GP ＝2，连结AP 、PF. （1）观察猜想AP 与PF 之间的大小关系，并说明理由.（2）图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形？若存在，请说明变换过程；若不存在，请说明理由.（3）若把这个图形沿着PA 、PF 剪成三块，请你把它们拼成一个大正方形，在原图上画出示意图，并请求出这个大正方形的面积.附加：如图，△ABC 与△ADE 都是等边三角形，连结BD 、CE（1）BD 与CE 相等吗？请说明理由．A BCFDE GP32B（2）你能求出BD与CE的夹角∠BFC的度数吗？（3）若将已知条件改为：四边形ABCD与四边形AEFG都是正方形，连结BE、DG交点记为点M（如图）．请直接写出线段BE和DGF例3、正方形四边条边都相等，四个角都是90o．如图，已知正方形ABCD在直线MN 的上方，BC在直线MN上，点E是直线MN上一点，以AE为边在直线MN的上方作正方形AEFG．（1）如图1，当点E在线段BC上（不与点B、C重合）时：①判断△ADG与△ABE是否全等，并说明理由；②过点F作FH⊥MN，垂足为点H，观察并猜测线段BE与线段CH的数量关系，并说明理由；（2）如图2，当点E在射线CN上（不与点C重合）时：①判断△ADG与△ABE是否全等，不需说明理由；②过点F 作FH ⊥MN ，垂足为点H ，已知GD ＝4，求△CFH 的面积．练习：如图1，四边形ABCD 是正方形，G 是CD 边上的一个点(点G 与C 、D 不重合)，以CG 为一边作正方形CEFG ，连结BG ，DE ．（1）如图1，说明BG= DE 的理由（2）将图1中的正方形CEFG 绕着点C 按顺时针方向旋转任意角度 ，得到如图2．请你猜想①BG= DE 是否仍然成立？②BG 与DE 位置关系？并选取图2验证你的猜想．图 2FG DA图 1FDA类型二、探究题例1、如图，已知等边△A B C 和点P ，设点P 到△A B C 三边A B 、A C 、B C （或其延长线）的距离分别为h 1、h 2、h 3，△A B C 的高为h ．在图（1）中，点P 是边B C 的中点，此时h 3=0，可得结论：h h h h =++321． 在图（2）--（5）中，点P 分别在线段M C 上、M C 延长线上、△A B C 内、△A B C 外．（1）请探究：图（2）--（5）中， h 1、h 2、h 3、h 之间的关系；（直接写出结论）（2）证明图（2）所得结论； （3）证明图（4）所得结论．（4）（附加题2分）在图（6）中，若四边形R B C S 是等腰梯形，∠B =∠C =60o ，R S =n ，B C =m ，点P 在梯形内，且点P 到四边B R 、R S 、S C 、C B 的距离分别是h 1、h 2、h 3、h 4，桥形的高为h ，则h 1、h 2、h 3、h 4、h 之间的关系为： ；图（4）与图（6）中的等式有何关系？ABC DEPM(3)ABCDE (2)ABCD EM (P )(1)练习：1、如图，在△ABC 中，AB=AC ，P 为底边上任意一点，PE ⊥AB ，PF ⊥AC ，BD ⊥AC.（1）求证：PE+PF=BD ；（2）若点P 是底边BC 的延长线上一点，其余条件不变，（1）中的结论还成立吗？如果成立，请说明理由；如果不成立，请画出图形，并探究它们的关系.CBAPDE2、如图，已知△ABC 三边长相等，和点P ，设点P 到△ABC 三边AB 、AC 、BC （或其延长线）的距离分别为h 1、h 2、h 3，△ABC 的高为h ．在图（1）中， 点P 是边BC 的中点，由S △ABP+S △ACP=S △ABC 得，h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21又因为h 3=0，所以：h h h h =++321．图（2）~（5）中，点P 分别在线段MC 上、MC 延长线上、△ABC 内、△ABC 外．（1）请探究：图（2）~（5）中， h 1、h 2、h 3、h 之间的关系；（直接写出结论）⑵ ⑶ ⑷ ⑸ （2）说明图（2）所得结论为什么是正确的； （3）说明图（5）所得结论为什么是正确的．ABC DEP ABCDEPM(3)ABCDE P M (2)ABCDEM (P )(1)ABCDEP M(5)FC B E 例2、已知△ABC 是等边三角形，将一块含30o 角的直角三角板DEF 如图1放置，当点E 与点B 重合时，点A 恰好落在三角板的斜边DF 上. （1）AC=CF 吗? 为什么?（2）让三角板在BC 上向右平行移动，在三角板平行移动的过程中，(如图2)是否存在与线段EB 始终相等的线段（设AB ，AC 与三角板斜边的交点分别为G ，H ）？如果存练习：1、如图1，一等腰直角三角尺GEF （∠EGF=90°,∠GEF=∠GFE=45°,GE=GF ）的两条直角边与正方形ABCD 的两条边分别重合在一起．现正方形ABCD 保持不动，将三角尺GEF 绕斜边EF 的中点O （点O 也是BD 中点）按顺时针方向旋转．（1）如图2，当EF 与AB 相交于点M ，GF 与BD 相交于点N 时，通过观察或测量BM ，FN 的长度，猜想BM ，FN 相等吗？并说明理由；（2）若三角尺GEF 旋转到如图3所示的位置时，线段FE 的延长线与AB 的延长线相交于点M ，线段BD 的延长线与GF 的延长线相交于点N ，此时，（1）中的猜想还成立C图1吗？请说明理由．2、已知：△ABC 为等边三角形，M 是BC 延长线上一点，直角三角尺的一条直角边经过点A ，且60º角的顶点E 在BC 上滑动，（点E 不与点B 、C 重合），斜边∠ACM 的平分线CF 交于点F（1）如图（1）当点B 在BC 边得中点位置时（6分） ○1猜想AE 与BF 满足的数量关系是 。

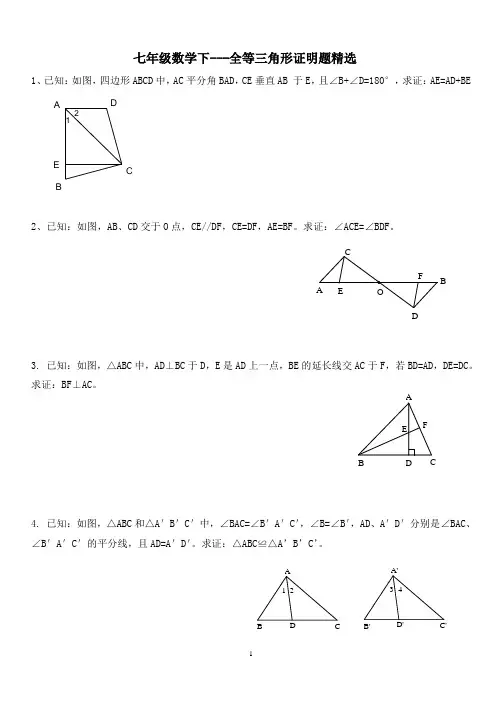
七年级数学下---全等三角形证明题精选1、已知：如图，四边形ABCD 中，AC 平分角BAD ，CE 垂直AB 于E ，且∠B+∠D=180°，求证：AE=AD+BEABDCE 122、已知：如图，AB 、CD 交于O 点，CE//DF ，CE=DF ，AE=BF 。

求证：∠ACE=∠BDF 。

3. 已知：如图，△ABC 中，AD ⊥BC 于D ，E 是AD 上一点，BE 的延长线交AC 于F ，若BD=AD ，DE=DC 。

求证：BF ⊥AC 。

4. 已知：如图，△ABC 和△A ＇B ＇C ＇中，∠BAC=∠B ＇A ＇C ＇，∠B=∠B ＇，AD 、A ＇D ＇分别是∠BAC 、∠B ＇A ＇C ＇的平分线，且AD=A ＇D ＇。

求证：△ABC ≌△A ’B ’C ’。

ABCDEFOAB CDEFAB C D A' B'C'D' 1 23 45、已知：如图，AB=CD ，AD=BC ，O 是AC 中点，OE ⊥AB 于E ，OF ⊥D 于F 。

求证：OE=OF 。

A BCDE F O6.已知：如图，AC ⊥OB ，BD ⊥OA ，AC 与BD 交于E 点，若OA=OB ，求证：AE=BE 。

OB ACDE7.已知：如图，AB//DE ，AE//BD ，AF=DC ，EF=BC 。

求证：△AEF ≌△DBC 。

A BDEF8.如图，B ，E 分别是CD 、AC 的中点，AB ⊥CD ，DE ⊥AC 求证：AC=CD （连接AD ）9.已知：如图，PA 、PC 分别是△ABC 外角∠MAC 和∠NCA 的平分线，•它们交于点P ，PD ⊥BM 于D ，PF ⊥BN 于F ．求证：BP 为∠MBN 的平分线．10、如图，已知AD 是∠BAC 的平分线， DE ⊥AB 于E ， DF ⊥AC 于F ， 且BE=CF ， 求证： (1)AD 是△ABC 的中线；(2)AB=AC ．11.在△ABC 中，∠ACB =90°，AC =BC ，直线MN 经过点C ，且AD ⊥MN 于D ，BE ⊥MN 于E ． （1）当直线MN 绕点C 旋转到图1的位置时，求证：①△ADC ≌△CEB ；②DE =AD ＋BE ； （2）当直线MN 绕点C 旋转到图2的位置时，求证：DE =AD －BE ；（3）当直线MN 绕点C 旋转到图3的位置时，试问DE ，AD ，BE 具有怎样的等量关系？请写出这个等量关系，并加以证明．CBAE D图1NMABCDEMN图2ACBEDN M 图3 A1 2 EF CDB12、如图，等腰直角三角形ABC 中，∠ACB ＝90°，AD 为腰CB 上的中线，CE ⊥AD 交AB 于E ． 求证∠CDA ＝∠EDB ．（作CF ⊥AB ）13、在Rt △ABC 中，∠B AC ＝90°，CE 是角平分线，和高AD 相交于F ，作FG ∥BC 交AB 于G ， 求证：AE ＝BG （平行四边形对边相等）．14、如图，已知△ABC 是等边三角形，∠BDC ＝120º，说明AD=BD+CD 的理由15、如图，在△ABC 中，AD 是中线，BE 交AD 于F,且AE=EF,说明AC=BF 的理由。

___版七年级下数学平行四边形全等证明典型习题一、题目一题目描述给定平行四边形ABCD和EFGH，证明四边形ABCD全等于四边形EFGH。

解答首先，根据平行四边形的定义，我们知道对于平行四边形ABCD和EFGH，有AB∥CD且AB = CD，而且AD∥BC且AD = BC。

其次，我们可以通过以下步骤来证明四边形ABCD全等于四边形EFGH：1.连接AC和BD，得到交点O。

2.因为平行四边形ABCD和平行四边形EFGH的对边平行且相等，所以AC∥EG且AC = EG，BD∥FH且BD = FH。

3.因为AC和BD的交点O同时在平行四边形ABCD和平行四边形EFGH的对角线上，所以O是平行四边形ABCD和平行四边形EFGH的一个共同顶点。

4.因为AO和CO是平行四边形ABCD的对角线，所以AO = CO，同理，EO = GO。

因此，AO = EO。

5.同理可证，BO = FO，DO = HO。

6.根据SSS全等条件（边-边-边全等条件），我们可以得出四边形ABCD全等于四边形EFGH。

综上所述，我们证明了四边形ABCD全等于四边形EFGH。

二、题目二题目描述给定平行四边形PQRS和TUVW，证明四边形PQRS全等于四边形TUVW。

解答同样地，我们可以通过以下步骤来证明四边形PQRS全等于四边形TUVW：1.连接PT，得到交点X。

2.根据平行四边形的性质，我们知道对于平行四边形PQRS和平行四边形TUVW，有PQ∥TS且PQ = TS，RS∥UW且RS = UW。

3.因为PQ∥TS且SR∥UW，而且PT是两个平行线PQ和SR的交线，所以PT是平行四边形PQRS和平行四边形___的一个共同边。

4.因为PT是平行四边形PQRS的对角线，所以PT平分了对角线PS。

同理，PT平分了对角线TU。

5.因此，PX = XT。

6.同理可证，RX = WT。

7.根据SAS全等条件（边-角-边全等条件），我们可以得出四边形PQRS全等于四边形TUVW。

初一下数学证明题(精选多篇)第一篇：初一下数学证明题初一下数学证明题6、如图，ce平分∠acb且ce⊥bd，∠dab=∠dba，ac=18，△cdb 的周长是28。

求bd的长大家看我的步骤，我的步骤只做到这里就坐不下去了解：因为∠dab=∠dba(已知)所以ad=bd(等角对等边)因为ce平分∠acb，ce⊥bd(已知)所以∠dce=∠bce(角平分线的意义)∠bec=∠dec=90度(垂直意义)在△ace与△bce中因为{∠dce=∠bce(已求){ce=ec(公共边){∠bec=∠dec(已求)所以△ace≌△bce(a.s.a)所以bc=cd(全等三角形对应边相等)因为ac=18,即cd+ad=18所以cd+bd=18因为△cdb的周长是28，即cd+bd+bc=28所以bc=28-18=10所以cd=10所以bd=18-10=82在△abc中，已知∠cab=60°，d，e分别是边ab，ac上的点，且∠aed=60°，ed+db=ce，∠cdb=2∠cde，则∠dcb=a.15°b.20°c.25°d.30°这题实际上是一传统题的翻版，原题中条件为△ade为等边三角形，c，b分别是ae，ad延长线的点，且ec=ab，求证;cd=cb，结论明确，本题增加了一个条件∠cdb=2∠cde，把结论改为求值题，其它改动没有多大变化，很快就会知道△ade为等边三角形，ec=ab，∠edc=∠cdb/2=40°，但结论为求值题后使结论没有目标，实际上是故弄玄虚，习难学生，使分析没有方向，要是学生没做过原题要得出正确结论是不大可能的!但学生可做一下投机;地图作得尽量正确，用量角器测一下也可得正确的结论。

但我觉得不会是供题者的本意吧。

故我认为对本题的改动看起来是改革，实为一败笔!不可取!但本题的原题我认为是一个能提高学生学习数学的兴趣与陪养学生创造性思维的好题题，现就原题给出若干分析请于指正。

人教版七年级下册数学平行线的判定及性质证明题训练（含答案）1．如图，三角形ABC 中，点D 在AB 上，点E 在BC 上，点F ，G 在AG 上，连接,,DG BG EF ．己知12∠=∠，3180ABC ∠+∠=︒，求证：∥BG EF ．将证明过程补充完整，并在括号内填写推理依据．证明：∵_____________（已知）∴∥DG BC （_______________________）∴．CBG ∠=________（____________________）∵12∠=∠（已知）∴2∠=________（等量代换）∴∥BG EF （___________________）2．如图，已知12∠=∠，A F ∠=∠，试说明C D ∠=∠的理由．解：把1∠的对顶角记作3∠，所以13∠=∠（对顶角相等）．因为12∠=∠（已知），所以23∠∠=（ ），所以 ∥ （ ）．（请继续完成接下去的说理过程）3．如图，CD ∥AB ，点O 在直线AB 上，OE 平分∠BOD ，OF ⊥OE ，∠D ＝110°，求∠DOF 的度数．4．如图，DH 交BF 于点E ，CH 交BF 于点G ，12∠=∠，34∠=∠，5B ∠=∠．试判断CH 和DF 的位置关系并说明理由．5．已知：如图，直线DE//AB．求证：∠B+∠D=∠BCD．6．如图，已知AB CD∥，BE平分ABC∠，CE平分BCD∠，求证1290∠+∠=︒．证明：∵BE平分ABC∠（已知），∴2∠=（），同理1∠=，∴1122∠+∠=，又∵AB CD∥（已知）∴ABC BCD∠+∠=（），∴1290∠+∠=︒．7．请把下列证明过程及理由补充完整（填在横线上）：已知：如图，BC，AF是直线，AD∥BC，∠1＝∠2，∠3＝∠4．求证：AB∥CD．证明：∵AD∥BC（已知），∴∠3＝（）．∵∠3＝∠4（已知），∴∠4＝（）．∵∠1＝∠2（已知），∴∠1+∠CAF＝∠2+∠CAF（）．即∠BAF＝．∴∠4＝∠BAF．（）．∴AB∥CD（）．8．如图，已知∠A＝120°，∠FEC＝120°，∠1＝∠2，试说明∠FDG＝∠EFD．请补全证明过程，即在下列括号内填上结论或理由．解：∵∠A＝120°，∠FEC＝120°（已知），∴∠A＝（）．∴AB∥（）．又∵∠1＝∠2（已知），∴EF ∥ （ ）．∴∠FDG ＝∠EFD （ ）．9．在三角形ABC 中，CD AB ⊥于D ，F 是BC 上一点，FH AB ⊥于H ，E 在AC 上，EDC BFH ∠=∠．(1)如图1，求证：∥DE BC ；(2)如图2，若90ACB ∠=︒，请直接写出图中与ECD ∠互余的角，不需要证明．10．已知：如图，直线MN HQ ∥，直线MN 交EF ，PO 于点A ，B ，直线HQ 交EF ，PO 于点D ，C ，DG 与OP 交于点G ，若1103∠=︒，277∠=︒，396∠=︒．（1）求证：EF OP ∥；（2）请直接写出CDG ∠的度数．11．如图直线a b ∥，直线EF 与,a b 分别和交于点,,A B AC AB AC ⊥、交直线b 于点C ．（1）若160∠=︒，直接写出2∠= ；（2）若3,4,5AC AB BC ===，则点B 到直线AC 的距离是 ；（3）在图中直接画出并求出点A 到直线BC 的距离．12．如图，已知AB CD ，BE 平分∠ABC ，∠CDE = 150°，求∠C 的度数．13．如图，在ABC 中，CD 平分ACB ∠交AB 于D ，EF 平分AED ∠交AB 于F ，已知ADE B ∠=∠，求证：EF CD ∥．14．已知：如图，AB ∥CD ∥EF ，点G 、H 、M 分别在AB 、CD 、EF 上．求证：GHM AGH EMH ∠∠∠=+．15．如图所示，点B 、E 分别在AC 、DF 上，BD 、CE 均与AF 相交，A F ∠=∠，C D ∠=∠，求证：12∠=∠．16．如图，在ABC 中，DE ∥AC ，DF ∥AB ．（1）判断∠A 与∠EDF 之间的大小关系，并说明理由．（2）求∠A +∠B +∠C 的度数．17．已知：如图，ABC 中，点D 、E 分别在AB 、AC 上，EF 交DC 于点F ，32180∠+∠=︒ ，1B ∠=∠．（1）求证：∥DE BC ；（2）若DE 平分ADC ∠，33B ∠=∠，求2∠的度数．18．如图，AB ∥DG ，∠1+∠2＝180°．（1）试说明：AD ∥EF ；（2）若DG 是∠ADC 的平分线，∠2＝142°，求∠B 的度数．19．问题情境：如图1，AB CD ∥，130PAB ∠=︒，120PCD ∠=︒，求APC ∠的度数．小明的思路是：如图2，过P 作PE AB ∥，通过平行线性质，可得APC ∠=______．问题迁移：如图3，AD BC ∥，点P 在射线OM 上运动，ADP α∠=∠，BCP β∠=∠．（1）当点P 在A 、B 两点之间运动时，CPD ∠、α∠、β∠之间有何数量关系？请说明理由．（2）如果点P 在A 、B 两点外侧运动时（点P 与点A 、B 、O 三点不重合），请你直接写出CPD ∠、α∠、β∠之间有何数量关系．20．直线AB CD∠．∥，直线EF分别交AB、CD于点M、N，NP平分MND（1）如图1，若MR平分EMB∠，则MR与NP的位置关系是．∠，则MR与NP有怎样的位置关系？请说明理由．（2）如图2，若MR平分AMN（3）如图3，若MR平分BMN∠，则MR与NP有怎样的位置关系？请说明理由．参考答案：1．解：证明：∵3180ABC ∠+∠=︒（已知）∴∥DG BC （同旁内角互补，两直线平行）∴．1CBG ∠=∠（两直线平行，内错角相等）∵12∠=∠（已知）∴2CBG ∠=∠（等量代换）∴∥BG EF （同位角相等，两直线平行）2．解：把1∠的对顶角记作3∠，所以13∠=∠（对顶角相等）．因为12∠=∠（已知），所以23∠∠=（等量代换），所以//BD CE （同位角相等，两直线平行），所以4C ∠=∠（两直线平行，同位角相等），又因为A F ∠=∠，所以//DF AC （同位角相等，两直线平行），所以4D ∠=∠（两直线平行，内错角相等），所以C D ∠=∠（等量代换）．故答案为：等量代换；BD ；CE ；同位角相等，两直线平行．3．解：∵CD AB ∥∴110DOB D ∠=∠=︒∵OE 平分∠BOD ∴1552DOE DOB ∠=∠=︒ 又∵OF ⊥OE∴90EOF ∠=︒∴905535DOF EOF DOE ∠=∠-∠=︒-︒=︒故答案为：35︒4．解：CH DF，理由如下：∵34∠=∠，∴CD BF，∴5180BED∠+∠=︒，∵5B∠=∠，∴180B BED∠+∠=︒，∴BC DH，∴2H∠=∠，∵12∠=∠，∴1H∠=∠，∴CH DF．5．证明：过点C作CF∥AB，∴∠B=∠BCF，∵DE//AB．CF∥AB，∴CF∥DE，∴∠D=∠DCF，∴∠BCD=∠BCF+∠DCF=∠B+∠D．6．证明：∵BE平分∠ABC（已知），∴∠2=12∠ABC（角平分线的定义），同理∠1=12∠BCD，∴∠1+∠2=12(∠ABC+∠BCD)，又∵AB∥CD（已知）∴∠ABC +∠BCD =180°（两直线平行，同旁内角互补 ），∴∠1+∠2=90°． 故答案为：12∠ABC ；角平分线的定义；12∠BCD ；(∠ABC +∠BCD )；180°；两直线平行，同旁内角互补．7．证明：∵AD ∥BC （已知），∴∠3＝∠CAD （两直线平行，内错角相等）．∵∠3＝∠4（已知），∴∠4＝∠CAD （等量代换）．∵∠1＝∠2（已知），∴∠1+∠CAF ＝∠2+∠CAF （等式的性质）．即∠BAF ＝∠CAD ．∴∠4＝∠BAF ．（等量代换）．∴AB ∥CD （同位角相等，两直线平行）．8．解：∵∠A =120°，∠FEC =120°（已知），∴∠A =∠FEC （等量代换），∴AB ∥EF （同位角相等，两直线平行），又∵∠1=∠2（已知），∴AB ∥CD （内错角相等，两直线平行），∴EF ∥CD （平行于同一条直线的两直线互相平行），∴∠FDG =∠EFD （两直线平行，内错角相等），故答案为：∠FEC ；等量代换；EF ；同位角相等，两直线平行；内错角相等，两直线平行；CD ；平行于同一条直线的两直线互相平行；两直线平行，内错角相等．9．证明：∵CD AB ⊥，FH AB ⊥，∴//CD FH ，∴BCD BFH ∠=∠．∵EDC BFH ∠=∠，∴BCD EDC ∠=∠，∴//ED BC ．(2)与ECD ∠互余的角有：EDC BCD BFH A ∠∠∠∠，，，．证明：∵//ED BC ，∴90DEC ACB ∠=∠=︒，EDC BCD ∠=∠，∴90ECD EDC ∠+∠=︒，90ECD BCD ∠+∠=︒．∵//CD FH ，∴BCD BFH ∠=∠，∴90ECD BFH ∠+∠=︒．∵CD AB ⊥，∴90ACD A ∠+∠=︒，即90ECD A ∠+∠=︒．综上，可知与ECD ∠互余的角有：EDC BCD BFH A ∠∠∠∠，，，．10．解：（1）∵1103∠=︒，∴77∠=︒ABC ，∵277∠=︒，∴2ABC ∠=∠，∴EF OP ∥；（2）∵MN HQ ∥，EF OP ∥，∴1103∠=∠=∠=︒FDC FAB ，3180∠+∠=︒FDG ，∵396∠=︒，∴180********∠=︒-∠=︒-︒=︒FDG ，∴1038419∠=∠-∠=︒-︒=︒CDG FDC FDG ．11．解：（1）∵a b ∥，∴12180BAC ∠+∠+∠=︒，∵AC AB ⊥，160∠=︒，∴230∠=︒，故答案为：30︒；（2）∵AC AB⊥，∴点B到直线AC的距离为线段4AB=，故答案为：4；（3）如图所示：过点A作AD BC⊥，点A到直线BC的距离为线段AD的长度，∵AC AB⊥，∴ABC∆为直角三角形，∴1122ABCS AC AB BC AD∆=⨯⨯=⨯⨯，即1134522AD ⨯⨯=⨯⨯，解得：125 AD=，∴点A到直线BC的距离为125．12．解：∵∠CDE=150°，∴∠CDB=180°-∠CDE=30°，又∵AB CD，∴∠ABD=∠CDB=30°，∵BE平分∠ABC，∴∠ABC=2∠ABD=60°，∵AB CD，∴∠C=180°-∠ABC=120°．13．证明：ADE B∠=∠（已知），DE//BC∴（同位角相等，两直线平行），ACB AED∴∠=∠（两直线平行，同位角相等），CD 平分ACB ∠，EF 平分AED ∠（已知），12ACD ACB ∴∠=∠，12AEF AED ∠=∠（角平分线的定义）， ACD AEF ∴∠=∠（等量代换）.EF //CD ∴（同位角相等，两直线平行）.14．证明：∵AB ∥CD （已知）∴1AGH ∠=∠（两直线平行，内错角相等） 又 ∵CD ∥EF （已知）∴2EMH ∠=∠，（两直线平行，内错角相等） ∵12GHM ∠∠∠=+（已知）∴GHM AGH EMH ∠∠∠=+（等式性质）15．证明：∵A F ∠=∠，∴AC DF ∥，∴ABD D ∠=∠，又∵C D ∠=∠，∴ABD C ∠=∠，∴DB CE ∥，∴13∠=∠，∵23∠∠=，∴12∠=∠．16．（1）两角相等，理由如下：∵DE ∥AC ，∴∠A =∠BED (两直线平行，同位角相等).∵DF ∥AB ，∴∠EDF =∠BED (两直线平行，内错角相等)， ∴∠A =∠EDF (等量代换).（2）∵DE ∥AC ，∴∠C =∠EDB (两直线平行，同位角相等).∵DF ∥AB ，∴∠B =∠FDC (两直线平行，同位角相等).∵∠EDB +∠EDF +∠FDC =180°，∴∠A +∠B +∠C =180°(等量代换).17．解：（1）∵32180∠+∠=︒，∠2+∠DFE ＝180°， ∴∠3＝∠DFE ，∴EF //AB ，∴∠ADE ＝∠1，又∵1B ∠=∠，∴∠ADE ＝∠B ，∴DE //BC ，（2）∵DE 平分ADC ∠，∴∠ADE ＝∠EDC ，∵DE //BC ，∴∠ADE ＝∠B ，∵33B ∠=∠∴∠5+∠ADE +∠EDC ＝3B B B ∠+∠+∠＝180°， 解得：36B ∠=︒，∴∠ADC ＝2∠B ＝72°，∵EF //AB ，∴∠2＝∠ADC ＝180°－108°＝72°，18．（1）∵AB ∥DG ，∴∠BAD ＝∠1，∵∠1+∠2＝180°，∴∠BAD +∠2＝180°.∵AD ∥EF .（2）∵∠1+∠2＝180°且∠2＝142°，∴∠1＝38°，∵DG 是∠ADC 的平分线，∴∠CDG ＝∠1＝38°，∵AB ∥DG ，∴∠B ＝∠CDG ＝38°．19．解：问题情境：∵AB ∥CD ，PE ∥AB ，∴PE ∥AB ∥CD ，∴∠A +∠APE =180°，∠C +∠CPE =180°，∵∠P AB =130°，∠PCD =120°，∴∠APE =50°，∠CPE =60°，∴∠APC =∠APE +∠CPE =50°+60°=110°；（1）CPD αβ∠=∠+∠；过点P 作PQ AD ∥，又因为AD BC ∥，所以PQ AD BC ∥∥，则ADP DPE ∠=∠，BCP CPE ∠=∠，所以CPD DPE CPE ADP BCP ∠=∠+∠=∠+∠；（2）情况1：如图所示，当点P 在B 、O 两点之间时，过P 作PE ∥AD ，交ON 于E ，∵AD ∥BC ，∴AD ∥BC ∥PE ，∴∠DPE =∠ADP =∠α，∠CPE =∠BCP =∠β， ∴∠CPD =∠DPE -∠CPE =∠α-∠β，情况2：如图所示，点P 在射线AM 上时，过P 作PE ∥AD ，交ON 于E ，∵AD ∥BC ，∴AD ∥BC ∥PE ，∴∠DPE =∠ADP =∠α，∠CPE =∠BCP =∠β， ∴∠CPD =∠CPE -∠DPE =∠β-∠α20．（1）如题图1，AB CD ∥EMB END ∴∠=∠MR 平分EMB ∠，NP 平分MND ∠．11,22EMR EMB ENP END ∴∠=∠∠=∠ EMR ENP ∴∠=∠∴MR ∥NP ；（2）如题图2，AB CD ∥AMN END ∴∠=∠MR 平分AMN ∠，NP 平分MND ∠．11,22RMN AMN ENP END ∴∠=∠∠=∠ RMN ENP ∴∠=∠∴MR ∥NP ；（3）如图，设,MR PN 交于点Q ，过点Q 作QG AB ∥AB CD ∥180BMN END ∴∠+∠=︒，QG CD ∥ ,MQG BMR GQN PND ∴∠=∠∠=∠ MR 平分BMN ∠，NP 平分MND ∠．11,22BMR BMN PND END ∴∠=∠∠=∠ 90BMR PND ∴∠+∠=︒90MQN MQG NQG ∴∠=∠+∠=︒ ∴MR ⊥NP ；。

人教版七年级下册数学平行线证明题专题训练 1．如图，已知∠1＋∠2＝180°，且∠3＝∠B ．(1)求证：∠AFE ＝∠ACB ；(2)若CE 平分∠ACB ，且∠2＝110°，∠3＝50°，求∠ACB 的度数．2．如图，点D 、F 在线段AB 上，点E 、G 分别在线段BC 和AC 上，CD EF ∥，12∠=∠．(1)求证： DG BC ∥；(2)若DG 是角ADC ∠的平分线，385∠=︒，且:9:10DCE DCG ∠∠=，请说明AB 和CD 怎样的位置关系？3．如图，已知BE AO ∥，12∠=∠，OE OA ⊥于点O ，那么4∠与5∠有什么数量关系？为什么？4．如图所示，已知CD 平分ACB ∠，12∠=∠，那么B 与4∠相等吗？完成下面的填空．CD 平分ACB ∠（已知）2∴∠=∠______（______）， 12∠=∠（已知）， ∴∠______1=∠（______），∴______∥______（______），4B ∴∠=∠（______）． 5．如图，在四边形ABCD 中，AD BC ∥，连接BD ，点E 在BC 边上，点F 在DC 边上，且12∠=∠．(1)求证：EF BD ∥．(2)若DB 平分ABC ∠，130A ∠=︒，70C ∠=︒，求CFE ∠的度数．6．如图，D ，E ，G 分别是AB ，AC ，BC 边上的点，12180∠+∠=︒，3B ∠=∠．(1)请说明∥DE BC 的理由；7．已知如图，已知∠1＝∠2，∠C ＝∠D ．(1)判断BD 与CE 是否平行，并说明理由；(2)当∠A =30°时，求∠F 的大小．8．如图所示，已知BE FG ∥，12∠=∠．求证∥DE BC ．9．推理填空：如图，CF 交BE 于点H ，AE 交CF 于点D ，∠1＝∠2，∠3＝∠C ，∠ABH ＝∠DHE ，求证：BE ∠AF ．证明：∠∠ABH ＝∠DHE （已知），∠_______（_____________），∠∠3+______＝180°（_______）．∠∠3＝∠C （已知），∠∠C +________＝180°（_________），∠AD ∠BC （___________），∠∠2＝∠E （___________）．∠∠1＝∠2（已知），∠∠1＝∠E （等量代换）．∠BE ∠AF （内错角相等，两直线平行）．10．如图，AB 、CD 是两条直线，BMN CNM ∠=∠，12∠=∠．请说明E F ∠=∠的理由．11．如图，MN BC ∥，BD DC ⊥，1260∠=∠=︒，DC 是NDE ∠的平分线(1)AB 与DE 平行吗？请说明理由；(2)试说明ABC C ∠=∠；(3)求ABD ∠的度数．12．如图，AD 与BE 相交于F ，∠A =∠C ，∠1与∠2互补．(1)试说明：AB CE ∥；(2)若∠1=85°，∠E =26°，求∠A 的度数．13．已知，点A ，B 在直线EF 上，∠1+∠2＝180°，DB 平分∠CDA ，CD ∠AB ．(1)求证：AD ∠BC ；(2)若∠DAB ＝52°，求∠BDC 的度数．14．如图，已知180BAD ADC ∠+∠=︒，AE 平分BAD ∠，交CD 于点F ，交BC 的延长线于点E ，DG 交BC 的延长线于点G ，CFE AEB ∠=∠．(1)若87B ∠=︒，求DCG ∠的度数；(2)AD 与BC 是什么位置关系？请说明理由；(3)若DAB α∠=，DGC β∠=，直接写出α，β满足什么数量关系时AE DG ∥．15．已知：如图，D ，E ，F 分别是AB ，AC ，BC 上的点，DE ∠BC ，∠ADE =∠EFC ，求证：∠1=∠2．16．如图，直线EF分别与直线AB，CD相交于点A，C，AD平分∠BAC，交CD于点D，若∠1＝∠2，且∠ADC＝54°．(1)直线AB、CD平行吗？为什么？(2)求∠1的度数．17．如图，AE∠BC，FG∠BC，∠1＝∠2，求证：AB∠CD．18．如图，已知DG∠BC，AC∠BC，EF∠AB，∠1=∠2，求证：CD∠AB19．如图，已知AD∠BC，FG∠BC，垂足分别为D，G.且∠1＝∠2，猜想：DE与AC 有怎样的关系？说明理由．20．（1）如图1，AB∠CD，∠A=38°，∠C=50°，求∠APC的度数．（提示：作PE∠AB）．（2）如图2，AB∠DC，当点P在线段BD上运动时，∠BAP=∠α，∠DCP=∠β，求∠CPA与∠α，∠β之间的数量关系，并说明理由．（3）在（2）的条件下，如果点P在段线OB上运动，请你直接写出∠CPA与∠α，∠β之间的数量关系______．参考答案：1．证明：∠∠1＋∠2＝180°，∠1＋∠FDE ＝180°，∠∠FDE ＝∠2，∠∠3＋∠FEC ＋∠FDE ＝180°，∠2＋∠B ＋∠ECB ＝180°，∠B ＝∠3， ∠∠FEC ＝∠ECB ，∠EF ∥ BC ，∠∠AFE ＝∠ACB ；(2)解：∠∠3＝∠B ，∠3＝50°，∠∠B ＝50°，∠∠2＋∠B ＋∠ECB ＝180°，∠2＝110°，∠∠ECB ＝20°，∠CE 平分∠ACB ，∠∠ACB ＝2∠ECB ＝40°．2．(1)证明∠CD EF ∥，∠2DCB =∠∠，又∠12∠=∠，∠1DCB ∠=∠，∠DG BC ∥；(2)CD AB ⊥，理由如下：由（1 ）知DG BC ∥，∠385∠=︒，∠180395BCG ∠=︒-∠=︒，∠:9:10DCE DCG ∠∠=， ∠9954519DCE ∠=︒⨯=︒， ∠DG BC ∥，∠45CDG ∠=︒，∠DG 是ADC ∠的平分线， ∠290ADC CDG ∠=∠=︒， ∠CD AB ⊥．3．解：∠4与∠5互余，理由：∠OE ∠OA ，∠∠AOE ＝90°，即∠2＋∠3＝90°， ∠∠1＋∠2＋∠3＋∠4＝180°， ∠∠1＋∠4＝90°∠∠1＝∠2，∠∠2＋∠4＝90°，∠BE AO ∥，∠∠2＝∠5， ∠∠5＋∠4＝90°，即∠4与∠5互余． 4．【详解】 CD 平分ACB ∠（已知）23∴∠=∠（角平分线的定义），12∠=∠（已知）， 31∴∠=∠（等量代换），DE BC ∴∥（内错角相等，两直线平行），4B ∴∠=∠（两直线平行，同位角相等）． 5．(1)证明：AD BC （已知）， 1∴∠=∠DBC （两直线平行，内错角相等）， 12∠=∠，2DBC ∴∠=∠（等量代换），EF BD ∴∥（同位角相等，两直线平行）． (2)AD BC （已知），180ABC A ∴∠+∠=（两直线平行，同旁内角互补）， 130A ∠=（已知）， 50ABC ∴∠=， DB 平分 ABC ∠（已知）， 1252DBC ABC ∴∠=∠=， 225DBC ∴∠=∠=，在 CFE 中，2180CFE C ∠+∠+∠=（三角形内角和定理），70C ∠=，85CFE ∴∠=．6．(1)解：∠12180∠+∠=︒，1DFG ∠=∠， ∠2180DFG ∠+∠=︒，∠AB EG ∥，∠B EGC ∠=∠．又∠3B ∠=∠，∠3EGC ∠=∠，∠∥DE BC ；(2)∠DE 平分ADC ∠，∠ADE EDC ∠=∠．∠∥DE BC ，∠B ADE EDC ∠=∠=∠，∠22B ∠=∠，2180ADE EDC ∠+∠+∠=︒， ∠2180B B B ∠+∠+∠=︒， ∠45B ∠=︒，∠2290B ∠=∠=︒，∠CD AB ⊥，∠AB EG∥，⊥．∠CD EG7．(1)BD∠CE，理由如下：∠∠1＝∠2，∠2＝∠3，∠∠1＝∠3，∠BD∠CE；(2)∠BD∠CE，∠∠C＝∠4,∠∠C＝∠D，∠∠D＝∠4，∠AC∠DF，∠∠A＝∠F=30°．8．∥证明：∠BE FG∠2CBE∠=∠（两直线平行，同位角相等）又∠12∠=∠∠1CBE∠=∠DE BC（内错角相等，两直线平行）-∠∥9．证明：∠∠ABH＝∠DHE（已知），∠AB∠CF（同位角相等，两直线平行），∠∠3+∠ADC＝180°（两直线平行，同旁内角互补），∠∠3＝∠C（已知），∠∠C+∠ADC＝180°（等量代换），∠AD∠BC（同旁内角互补，两直线平行），∠∠2＝∠E（两直线平行，内错角相等）．∠∠1＝∠2（已知），∠∠1＝∠E（等量代换），∠BE∠AF（内错角相等，两直线平行）．故答案为：AB∠CF，同位角相等，两直线平行；∠ADC，两直线平行，同旁内角互补；∠ADC，等量代换；同旁内角互补，两直线平行；两直线平行，内错角相等．10．∵∠BMN＝∠CNM（已知），∠AB CD（内错角相等，两直线平行）．∠∠AMN＝∠MND（两直线平行，内错角相等）．∠∠1＝∠2（已知），∠∠EMN＝∠MNF（等式性质）．∥（内错角相等，两直线平行）．∠ME NF∠∠E＝∠F（两直线平行，内错角相等），11．(1)解：AB DE∥，理由如下：∥，∠MN BC∠∠ABC=∠1=60°.又∠∠1=∠2，∠∠ABC=∠2，∠AB∠DE.(2)解：∠MN∠BC，∠∠NDE+∠2=180°，∠∠NDE=180°-∠2=180°-60°=120°.∠DC是∠NDE的平分线，∠1602∠=∠=∠=︒EDC NDC NDE.∠MN∠BC，∠∠C=∠NDC=60°，∠∠ABC=∠C.(3)解：∠ADC=180°-∠NDC=180°-60°=120°，∠BD∠DC，∠∠BDC=90°，∠∠ADB=∠ADC-∠BDC=120°-90°=30°.∠MN∠BC，∠∠DBC=∠ADB=30°，∠∠ABC=∠C=60°，∠∠ABD=30°12．(1)证明：∠∠1与∠2互补，∠AD BC∥，∠∠ADE=∠C，∠∠A=∠C，∠∠A=∠ADE，∠AB CE∥；(2)解：∠∠1与∠2互补，∠1=85°，∠∠2=180º－85º=95º，∠AB CE∥，∠E=26º，∠∠ABE=∠E=26º，∠∠ABC=∠ABE+∠2=26º+95º=121º，∠AD BC ∥，∠∠A =180º－∠ABC =180º－121º=59º．13．(1)∠∠1+∠2＝180°，点A ，B 在直线EF 上， ∠∠1+∠DAB ＝180°，∠∠2＝∠DAB ，∠AD ∠BC ；(2)∠CD ∠AB ，∠DAB ＝52°，∠∠CDA ＝180°﹣∠DAB ＝180°﹣52°＝128°， ∠DB 平分∠CDA ，∠∠BDC 12=∠CDA ＝64°． 14．(1)解：∠180BAD ADC ∠+∠=︒，∠AB CD ∥，∠87B DCG ∠=∠=︒．(2)解：AD 与BC 是的位置关系为：AD BC ∥，理由如下： ∠AE 平分BAD ∠，∠BAE DAE ∠=∠，∠180BAD ADC ∠+∠=︒，∠AB CD ∥，∠BAE CFE ∠=∠，∠AEB CFE ∠=∠，∠∠AEB =∠BAE =∠DAE ，∠AD BC ∥．(3)解：α与β的数量关系为：12αβ=，理由如下：当AE DG∥时，AEB DGCβ∠=∠=，由(2)中推导可知，1122 AEB EAD BADα∠=∠=∠=，∠12αβ=．15．证明：∠DE∠BC，∠∠ADE＝∠ABC．∠∠ADE＝∠EFC，∠∠ABC＝∠EFC．∠AB∠EF．∠∠1＝∠2．16．(1)解：AB CD∥，理由：∠∠1=∠2，∠1=∠DCA，∠∠2=∠DCA，∠AB CD∥(2)解：∠∠ADC＝54°，AB CD∥，∠∠DAB=∠ADC＝54°，∠AD平分∠BAC，∠∠BAC=2∠DAB=108°，∠∠2=180°-∠BAC=72°，∠∠1=72°．17．直线平行可得AB∠CD．【详解】证明：如图，设BC与AE、GF分别交于点M、N.∠AE∠BC，FG∠BC，∠∠AMB=∠GNB=90°，∠AE∠FG，∠∠A=∠1；又∠∠2=∠1，∠∠A=∠2，∠AB∠CD．18．证明：∠ DG∠BC，AC∠BC（已知），∠ ∠DGB=∠ACB=90°（垂直的定义），∠ DG∠AC（同位角相等，两直线平行）.∠ ∠2=∠ACD（两直线平行，内错角相等）.∠ ∠1=∠2（已知），∠ ∠1=∠ACD（等量代换），∠ EF∠CD（同位角相等，两直线平行）.∠ ∠AEF=∠ADC（两直线平行，同位角相等）.∠ EF∠AB（已知），∠ ∠AEF=90°（垂直的定义），∠ ∠ADC=90°（等量代换）.∠ CD∠AB（垂直的定义）．19．DE∠AC．理由如下：∠AD∠BC，FG∠BC，∠∠ADG=∠FGC=90°，∠AD∠FG，∠∠1=∠CAD，∠∠1=∠2，∠∠CAD=∠2，∠DE∠AC．20．（1）如图1，过P作PE∠AB，∠AB∠CD，∠PE∠AB∠CD，∠∠A＝∠APE，∠C＝∠CPE，∠∠A=38°，∠C=50°，∠∠APE＝38°，∠CPE＝50°，∠∠APC＝∠APE＋∠CPE＝38°＋50°＝88°；（2）∠APC＝∠α＋∠β，理由是：如图2，过P作PE∠AB，交AC于E，∠AB∠CD，∠AB∠PE∠CD，∠∠APE＝∠PAB＝∠α，∠CPE＝∠PCD＝∠β，∠∠APC＝∠APE＋∠CPE＝∠α＋∠β；（3）如图3，过P作PE∠AB，交AC于E，∠AB∠CD，∠AB∠PE∠CD，∠∠PAB＝∠APE＝∠α，∠PCD＝∠CPE＝∠β，∠∠APC＝∠CPE-∠APE，∠∠APC＝∠β-∠α．故答案为：∠APC＝∠β-∠α．。

2023年人教版七年级下册数学第五章平行线证明题专项训练1．推理填空如图，已知∠BCD+∠B=180˚，AE平分∠BAD，CD与AE相交于点F，∠CFE=∠E．求证：AD∥BC．证明∵AE平分∠BAD（已知），∴∠1=∠2（），∵∠BCD+∠B=180˚∴AB∥CD（），∴∠1= （），∵∠CFE=∠E（已知），∴∠1=∠E（），∴∠2= ，∴AD∥BC（）．2．已知：如图，点AA，BB，CC，DD在一条直线上，CCCC与BBBB交于点H，1∠=∠，ACM∥DN．求证：M N∠=∠．3．如图，已知AB∥CD，CF为∠ACD的平分线，∠A＝110°，∠EFC＝35°．求证：EF∥CD．请将下面的证明过程补充完整．证明：∵AB∥CD，(已知)∴∠＋∠ACD＝180°．( )∵∠A＝110°，（已知）∴∠ACD＝ °．(等量代换)∵CF为∠ACD的平分线，(已知)∴∠FCD＝12∠＝35°．(角平分线定义)∵∠EFC＝35°，(已知)∴∠FCD＝∠EFC，(等量代换)∴EF∥CD．( )4．已知：如图，∠1=∠2，∠3=∠BB ，∠4=∠5．试说明：AADD ∥EEEE ．请完成下列填空．解：因为∠1=∠2，所以______∥AABB ．所以∠3=______（____________）．又因为∠3=∠BB ，所以B ∠=______． 所以______∥BBCC （_____________）．所以∠5=∠DDDDEE ，又因为∠4=∠5，所以∠4=∠DDDDEE ，所以AADD ∥EEEE ．5．在下面的括号内，填上推理的根据．如图，已知3A ∠=∠，DE BC ⊥，AABB ⊥BBCC ．求证DDEE 平分CDB ∠．证明：∵DE BC ⊥，AABB ⊥BBCC （已知）∴∠DDEECC =∠AABBCC =90°（垂直的定义）∴DDEE ∥AABB （________________________）∴∠2=∠3（________________________）∠1=________________________（两直线平行，同位角相等）又∵3A ∠=∠（已知） ∴∠_______=∠__________（________________________）∴DDEE 平分CDB ∠6．完成推理填空．如图，AB ⊥BF ，CD ⊥BF ，∠1＝∠2，试说明∠3＝∠E ．证明：∵AB ⊥BF ，CD ⊥BF （已知），∴∠ABD ＝∠CDF ＝90°（垂直定义），∴AABB ∥CCDD （同位角相等，两直线平行）．∵∠1＝∠2（已知），∴______∥______（______），∴CCDD ∥EEEE （______），∴∠3＝∠E （______）．7．如图，∠B+∠BAD=180°，∠1=∠2．求证：AB∥C D．请将下面的证明过程补充完整．证明：∵∠B+∠BAD=180°（已知），∠1+∠BAD=180°（），∴∠1=∠B（）．∵∠1=∠2（已知），∴∠2＝（）．∴AB∥CD（）．8．如图，已知：在△ABC中，点D是AC边上一点，过点D作DF∥AB交BC于点F，点E为AB边上一点，连接DE、若∠FDE＝∠B，∠C＝90°，求证：DE⊥A C．证明：∵DF∥AB（已知），∴∠FDE＝∠（两直线平行，内错角相等）．∠FDE＝∠B（已知），∴∠＝∠（等量代换）．∴∥（同位角相等，两直线平行）．∴∠＝∠C（两直线平行，同位角相等）．又∵∠C＝90°（已知），∴∠ADE＝90°（等量代换）．∴DE⊥AC（）．9．如图，已知CCDD∥EEFF,∠EEDDCC=∠BBEEFF，试说明DE BC∥的理由．10．如图，已知AB∥CD，EG平分∠BEF，FH平分∠CFE，求证：EG∥HF．请将过程补充完整．证明：AB∥CD（已知）∴∠BEF＝______，（____________）又∵EG平分∠BEF，FH平分∠CFE（已知）∴∠1=12∠BBEEEE，∠2＝______，（____________）∴∠1＝∠2，（____________）∴EG∥HF．（____________）11．如图，直线AABB、CCDD交于点O，OOEE为∠BBOODD的平分线，OOEE⊥OOEE，CG//OOEE，且∠CC=30°．∠的度数；(1)求AOE(2)判断∠AAOOEE与∠DDOOEE的大小关系，并说明理由．12．如图，E，G是分别是AB，AC上的点，F，D是BC上的点，连接EF，AD，DG，如果AB∥DG，∠1+∠2＝180°．(1)判断AD与EF的位置关系，并说明理由；(2)若DG是∠ADC的平分线，∠2＝145°，求∠B的度数．13．如图，已知AB ∥CD ，∠B ＝∠D ．(1)求证：AD ∥BE(2)若∠1＝∠2＝60°，∠BAC ＝3∠EAC ，求∠DAF 的度数．14．如图，在三角形ABC 中，∠AABBCC =90°，将△AABBCC 沿射线BC 方向 平移，得到△DDEEEE ，A ，B ，C 的对应点分别是D ，E ，F ，AD ∥BF ．(1)请说明∠DDAACC =∠EE ；(2)若BBCC =6cccc ，当AADD =2EECC 时，求AD 的长．15．如图，AABB ∥CCDD ，AE 平分∠BBAADD ，CD 与AE 相交于点F ，CFE E ∠=∠．求证：∠AADDCC =∠DDCCEE ．完成下列证明，并在括号填上理由：证明：∵AABB ∥CCDD （已知）∴∠BBAAEE =∠CCEEEE （______）又∵AE 平分∠BBAADD （______）∴∠BBAAEE =∠______∴∠CCEEEE =∠DDAAEE （______）又∵CFE E ∠=∠， ∴∠DDAAEE =∠EE （______）∴______∥BBEE （______）∴∠AADDCC =∠DDCCEE （______）16．已知：如图，AABB∥CCDD，∠1=∠2．试说明：BBEE∥CCEE．请按照下列说明过程填空．解：∵AABB∥CCDD，根据________________________________∴∠AABBCC=________．∵∠1=∠2，∴∠AABBCC−∠1=________−∠2，即∠EEBBCC=________．根据________________________________∴BBEE∥CCEE．17．如图，已知∠1+∠BBDDEE=180°，∠2+∠4=180°．(1)证明：AADD∥EEEE；∠=°，求∠BBAACC的度数．(2)若∠3=90°，414018．如图，AABB//CCDD，∠AA=∠CC，BE平分∠AABBCC交AADD的延长线于点EE，(1)证明：AADD//BBCC；(2)若∠AADDCC=118°，求∠EE的度数．19．如图，已知∠1+∠2=180°，CCDD∥AABB．求证：3∠=∠A20．如图，在三角形AABBCC中，点DD，EE在BBCC边上，点EE在AABB边上，点FF在AACC边上，EEEE与FFDD的延长线交于点H，∠1=∠BB，∠2+∠3=180°．(1)请写出EEDD与AADD的位置关系，并说明理由；(2)若∠DDFFCC=58°，且∠DD=∠4+10°，求∠DD的度数。

人教版七年级下册数学第5章 相交线与平行线 证明题专题训练1．如图，直线AB 与直线CD 相交于点O ，OE ⊥OF ，且OA 平分⊥COE ． (1)若⊥DOE ＝50°，求⊥AOE ，⊥BOF 的度数．(2)设⊥DOE =α，⊥BOF =β，请探究α与β的数量关系（要求写出过程）．2．如图，直线AB 和CD 相交于点O ，OE 把⊥AOC 分成两部分，且⊥AOE ⊥⊥EOC ＝2⊥3，OF 平分⊥BOE ． (1)若⊥BOD ＝65°，求⊥BOE ．(2)若⊥AOE ＝12⊥BOF ﹣10°，求⊥COE ．3．已知如图，直线AB 、直线CD 相交于点O ，OE 是AOD ∠内的一条射线，且OE CD ⊥，:1:2AOE AOC ∠∠=． (1)求BOD ∠的度数；(2)如图2，射线OM 平分AOD ∠，射线ON 在BON ∠内部，且23BON BOM ∠=∠，求DON ∠的度数．4．如图，⊥1+⊥2＝180°，⊥C ＝⊥D ．求证：AD ⊥BC ．5．如图，FCG B ∠=∠，180DEF D +=︒∠∠，则AB 与EF 平行吗？为什么？6．已知，如图，ABC ADC ∠=∠，BF 、DE 分别平分ABC ∠与ADC ∠，且13∠=∠．求证：//AB DC ．7．如图，点A 在CF 上，46BAF ∠=︒，136ACE ∠=︒，CE DG ⊥于点C ．问 //DG AB 吗？为什么？8．如图，//AB CD ，//CD EF ，//BC ED ，70B ∠=︒，求C ∠，D ∠和E ∠的度数．9．将一副直角三角板按如图所示的方式放置，60B ∠=︒，45E ∠=︒，75AFD ∠=︒．求证：//AE BC ．10．如图，已知180BAD ADC ∠+∠=︒，AE 平分BAD ∠，交CD 于点F ，交BC 的延长线于点E ，DG 交BC 的延长线于点G ，CFE AEB ∠=∠． (1)若87B ∠=︒，求DCG ∠的度数；(2)AD 与BC 是什么位置关系？请说明理由；(3)若DAB α∠=，DGC β∠=，直接写出α，β满足什么数量关系时AE DG ∥．11．如图，已知射线AM ⊥BN ，连结AB ，点C 是射线BN 上的一个动点（与点B 不重合），AD ，AE 分别平分⊥BAC 和⊥CAM ，交射线BN 于点D ，E ． (1)试说明：⊥ACB ＝2⊥AEB ；(2)若⊥ADB ﹣⊥BAD ＝45°，求⊥AEB 的度数．12．如图所示，点B 、E 分别在AC 、DF 上，BD 、CE 均与AF 相交，A F ∠=∠，C D ∠=∠，求证：12∠=∠．13．如图，⊥ENC +⊥CMG =180°，AB ⊥CD ． （1）求证：⊥2=⊥3．（2）若⊥A =⊥1+70°，⊥ACB =42°，则⊥B 的大小为______．14．已知：如图，ABC 中，点D 、E 分别在AB 、AC 上，EF 交DC 于点F ，32180∠+∠=︒ ，1B ∠=∠． （1）求证：∥DE BC ；（2）若DE 平分ADC ∠，33B ∠=∠，求2∠的度数．15．如图，点D ，E 分别在AB 和AC 上，DE BC ∥，30DBE ∠=︒，25EBC ∠=︒，求BDE ∠的度数．16．如图，已知,A ADE C E ∠=∠∠=∠． （1）若3,EDC C ∠=∠求C ∠的度数； （2）求证：//BE CD ．17．已知：如图，CDG B ∠=∠，AD BC ⊥于点D ，EF BC ⊥于点F ，试判断1∠与2∠的关系，并说明理由．(写出推理依据)18．已知：如图，⊥BAP+⊥APD =180°，⊥1 =⊥2.求证：AE⊥PF．19．如图，AE⊥BC，FG⊥BC，⊥1＝⊥2，求证：AB⊥CD．20．如图，AB⊥DE，C为BD上一点，⊥A＝⊥BCA，⊥E＝⊥ECD，求证：CE⊥CA．21．如图，AB⊥BC于点B，DC⊥BC于点C，DE平分⊥ADC交BC于点E，点F为线段CD延长线上一点，⊥BAF＝⊥EDF(1)求证：⊥DAF＝⊥F；(2)在不添加任何辅助线的情况下，请直接写出所有与⊥CED互余的角．22．已知AB⊥CD，点E为AB，CD之外任意一点．(1)如图1，探究⊥BED与⊥B，⊥D的数量关系，并说明理由；(2)如图2，探究⊥CDE与⊥B，⊥E的数量关系，并说明理由．参考答案：1．解：⊥⊥DOE=50°，⊥⊥COE=180°-⊥DOE=180°-50°=130°，⊥OA平分⊥COE，⊥⊥AOE=12⊥COE=12×130°=65°，⊥OE⊥OF，⊥⊥EOF=90°，⊥⊥BOF=180°-⊥AOE-⊥EOF=180°-65°-90°=25°；(2)解：⊥⊥DOE=α，⊥⊥COE=180°-⊥DOE=180°-α，⊥OA平分⊥COE，⊥⊥AOE=12⊥COE=12（180°-α）=90°-12α，⊥OE⊥OF，⊥⊥EOF=90°，⊥⊥BOF=β=180°-⊥AOE-⊥EOF=180°-（90°-12α）-90°=12α，即α=2β．2．解：⊥⊥AOC与⊥BOD是对顶角，⊥⊥AOC=⊥BOD=65°．⊥⊥AOE：⊥EOC=2：3，⊥⊥AOE=25⊥AOC=26°．⊥⊥BOE=180°-⊥AOE=180°-26°=154°；(2)解：设⊥AOE=2x，⊥EOC=3x．⊥⊥AOE=12⊥BOF-10°，⊥⊥BOF=4x+20°．⊥OF平分⊥BOE，⊥⊥BOE=2⊥BOF=8x+40°．⊥⊥AOE +⊥BOE =2x +8x +40°=180°． ⊥x =14°． ⊥⊥COE =3x =42°． 3．解：⊥OE ⊥CD ， ⊥⊥COE =90°， ⊥⊥AOE :⊥AOC =1:2， ⊥⊥AOC =90°×23=60°，⊥⊥BOD =⊥AOC =60°； (2)由（1）可知：⊥BOD =60°，⊥⊥AOD =180°-⊥BOD =180°-60°=120°， ⊥OM 平分⊥AOD ， ⊥⊥AOM =12 ×120°=60°，⊥⊥BOM =180°-⊥AOM =180°-60°=120°， ⊥⊥BON =23 ⊥BOM =23×120°=80°，⊥⊥DON =⊥BON -⊥BOD =80°-60°=20°． 4．证明：⊥⊥1+⊥2＝180°，⊥2+⊥AED ＝180°， ⊥⊥1＝⊥AED ， ⊥DE ⊥AC ， ⊥⊥D ＝⊥DAF ， ⊥⊥C ＝⊥D ， ⊥⊥DAF ＝⊥C ， ⊥AD ⊥BC ． 5．解：AB 与EF 平行， 理由：⊥FCG B ∠=∠， ⊥//AB DC ，⊥180DEF D +=︒∠∠， ⊥//EF DC ，6．证明：BF ，DE 分别平分ABC ∠与ADC ∠21ABC ∴∠=∠，22ADC ∠=∠ ABC ADC ∠=∠ 12∠∠∴=13∠=∠23∴∠=∠//AB CD ∴．7．解：//DG AB ，理由如下． ⊥CE CD ⊥， ⊥90DCE ∠=︒， ⊥136ACE ∠=︒，⊥36013690134ACD ∠=︒-︒-︒=︒， ⊥46BAF ∠=︒，⊥180********BAC BAF ∠=︒-∠=︒-︒=︒， ⊥ACD BAC ∠=∠， ⊥//DG AB ． 8．//AB CD ，//CD EF ，////AB CD EF ∴，70C B ∴∠=∠=︒，E D ∠=∠，又//BC DE ， 180C D ∴∠+∠=︒，⊥⊥D =110°，110E ∴∠=︒．答：C ∠，D ∠和E ∠的度数分别是70︒、110︒、110︒． 9．解：由直角三角板的性质可得： ⊥C=30°，⊥⊥AFD=⊥C+⊥CDF=75°，⊥⊥CDF=⊥E ， ⊥AE⊥BC ． 10．解：⊥180BAD ADC ∠+∠=︒， ⊥AB CD ∥， ⊥87B DCG ∠=∠=︒． (2)解：AD 与BC 是的位置关系为：AD BC ∥，理由如下： ⊥AE 平分BAD ∠， ⊥BAE DAE ∠=∠， ⊥180BAD ADC ∠+∠=︒， ⊥AB CD ∥， ⊥BAE CFE ∠=∠， ⊥AEB CFE ∠=∠， ⊥⊥AEB =⊥BAE =⊥DAE ， ⊥AD BC ∥． (3)解：α与β的数量关系为：12αβ=，理由如下：当AE DG ∥时，AEB DGC β∠=∠=，由(2)中推导可知，1122AEB EAD BAD α∠=∠=∠=，⊥12αβ=． 11．解：⊥AE 平分⊥CAM2.CAM EAM ∴∠=∠,AM BN ∥,.CAM ACB EAM AEB ∴∠=∠∠=∠2.ACB AEB ∴∠=∠(2) 解：,AM BN ∥,.CAM ACB ADB DAM ∴∠=∠∠=∠⊥AD 平分⊥BAC.BAD CAD ∴∠=∠45,ADB BAD ︒∠-∠=45.DAM CAD ︒∴∠-∠= 45.CAM ACB ︒∴∠=∠= 由（1）知，2,ACB AEB ∠=∠22.5.AEB ︒∴∠= 12．证明：⊥A F ∠=∠， ⊥AC DF ∥， ⊥ABD D ∠=∠， 又⊥C D ∠=∠， ⊥ABD C ∠=∠， ⊥DB CE ∥， ⊥13∠=∠， ⊥23∠∠=， ⊥12∠=∠． 13．（1）证明：⊥⊥ENC +⊥CMG =180°，⊥CMG =⊥FMN ， ⊥⊥ENC +⊥FMN =180°， ⊥FG ⊥ED ， ⊥⊥2=⊥D ， ⊥AB ⊥CD ， ⊥⊥3=⊥D ， ⊥⊥2=⊥3；（2）解：⊥AB ⊥CD ，⊥⊥A +⊥ACD =180°，⊥⊥A =⊥1+70°，⊥ACB =42°，⊥⊥1+70°+⊥1+42°=180°，⊥⊥1=34°，⊥AB ⊥CD ，⊥⊥B =⊥1=34°．故答案为：34°．14．解：（1）⊥32180∠+∠=︒，⊥2+⊥DFE ＝180°， ⊥⊥3＝⊥DFE ，⊥EF //AB ，⊥⊥ADE ＝⊥1，又⊥1B ∠=∠，⊥⊥ADE ＝⊥B ，⊥DE //BC ，（2）⊥DE 平分ADC ∠，⊥⊥ADE ＝⊥EDC ，⊥DE //BC ，⊥⊥ADE ＝⊥B ，⊥33B ∠=∠⊥⊥5+⊥ADE +⊥EDC ＝3B B B ∠+∠+∠＝180°， 解得：36B ∠=︒，⊥⊥ADC ＝2⊥B ＝72°，⊥EF //AB ，⊥⊥2＝⊥ADC ＝180°－108°＝72°，15．解：⊥30DBE ∠=︒，25EBC ∠=︒，⊥⊥ABC =⊥DBE +⊥EBC =55°，⊥DE ⊥BC ，⊥⊥BDE +⊥ABC =180°，⊥⊥BDE =180°-⊥ABC =125°．16．（1）A ADE ∠=∠，//ED AC ∴，180EDC C ∴∠+∠=︒．3EDC C ∠=∠ ，3180C C ∴∠+∠=︒，45C ∴∠=︒ ；（2）A ADE ∠=∠，//ED AC ∴，ABE E ∴∠=∠．C E ∠=∠，ABE C ∴∠=∠，//BE CD ∴ ．17．CDG B ∠=∠DG AB ∴1DAB ∴∠=∠ 又AD BC ⊥于点D ，EF BC ⊥于点FAD EF ∴2DAB ∴∠=∠12∠∠∴=18．证明：⊥⊥BAP +⊥APD =180°⊥AB⊥CD⊥⊥BAP=⊥CPA⊥⊥1 =⊥2⊥⊥BAP-⊥1=⊥CPA-⊥2，即⊥EAP=⊥FPA ⊥AE⊥PF19．证明：如图，设BC 与AE 、GF 分别交于点M 、N.⊥AE⊥BC，FG⊥BC，⊥⊥AMB=⊥GNB=90°，⊥AE⊥FG，⊥⊥A=⊥1；又⊥⊥2=⊥1，⊥⊥A=⊥2，⊥AB⊥CD．20．证明⊥AB⊥DE，⊥⊥B＋⊥D＝180°，⊥⊥A＝⊥BCA，⊥E＝⊥ECD，⊥⊥B＝180°－2⊥BCA，⊥D＝180°－2⊥ECD，⊥(180°－2⊥BCA)＋(180°－2⊥ECD)＝180°，⊥⊥BCA＋⊥ECD＝90°，⊥⊥ACE＝90°，⊥CE⊥CA.21．解：（1）⊥AB⊥BC于点B，DC⊥BC于点C，⊥⊥B+⊥C＝180°，⊥AB⊥CF，⊥⊥BAF+⊥F＝180°，又⊥⊥BAF＝⊥EDF，⊥⊥EDF+⊥F＝180°，⊥ED⊥AF，⊥⊥ADE＝⊥DAF，⊥EDC＝⊥F，⊥DE平分⊥ADC，⊥⊥ADE＝⊥CDE，⊥⊥DAF＝⊥F；（2）⊥⊥C＝90°，⊥⊥CED+⊥CDE＝90°，⊥⊥CED与⊥CDE互余，又⊥⊥ADE＝⊥DAF＝⊥EDC＝⊥F，⊥与⊥CED互余的角有⊥ADE，⊥CDE，⊥F，⊥FAD．22．解：(1)⊥B＝⊥BED＋⊥D.理由如下：过点E作EF⊥AB.又⊥AB⊥CD，⊥EF⊥AB⊥CD.⊥⊥BEF＝⊥B，⊥D＝⊥DEF.⊥⊥BEF＝⊥BED＋⊥DEF，⊥⊥B＝⊥BED＋⊥D.(2)⊥CDE＝⊥B＋⊥BED.理由如下：过点E作EF⊥AB.又⊥AB⊥CD，⊥EF⊥AB⊥CD.⊥⊥B＋⊥BEF＝180°，⊥CDE＋⊥DEF＝180°.又⊥⊥DEF＝⊥BEF－⊥BED，⊥⊥CDE＋⊥BEF－⊥BED＝⊥B＋⊥BEF，即⊥CDE＝⊥B＋⊥BED.。

人教版七年级下册数学平行线证明题专项练习1．已知：如图A ADE ∠=∠，（）若3EDC C ∠=∠，求的度数．（）求证：BE CD ∥2、如图，已知，，，求的度数．3.如图，已知直线BC 、DE 交于O 点，OA 、OF 为射线，OA ⊥BC ，OF 平分∠COE ，∠COF =17°．求∠AOD 的度数．4．如图，AB∥CD，直线EF分别与AB、CD交于点G，H，GM⊥EF，HN⊥EF，交AB于点N，∠1＝50°．（1）求∠2的度数；（2）试说明HN∥GM；（3）∠HNG＝°．5．如图，∠EFC+∠BDC＝180°，∠DEF＝∠B．（1）求证：∠ADE＝∠DEF；（2）判定DE与BC的位置关系，并说明理由．6.如图,已知AB∥CD,∠B＝40°,CN是∠BCE的平分线,CM⊥CN.求∠BCM的度数．7.如图，已知∠BAP+∠APD=180°，∠1 =∠2.求证:∠E =∠F．8．如图，、分别在和上，，与互余，于，求证：//AB CD．9．填空，完成下列证明过程，并在括号中注明理由．如图，已知，，求证：．10．如图，已知，，，//AE BC，求的度数．11．已知//AD BC，//AB CD，在线段延长线上，平分．连接，若，．（1）求证：；（2）求的度数．12、如图所示，直线AB、CD、EF交于点O，OG平分∠BOF，且CD⊥EF，∠AOE=70°，求∠DOG的度数．13、已知如图，过点做DAE BAC∠=∠，且//AD BC，．第12题（1）求证//AB DE；（2）若已知平分，，求的度数．14．如图，已知CD∥AB，OE平分∠BOD，OE⊥OF，∠CDO=62°，求∠DOF的度数．15．如图所示，AD与BE相交于点F，∠A=∠C，∠1与∠2互补．（1）试说明AB∥CE；（2）若∠2=95°，∠C=59°，求∠E的度数．16．如图①，△ABC中，AD平分∠BAC交BC于点D，AE⊥BC，垂足为E，CF∥AD．（1）如图①，∠B=30°，∠ACB=70°，则∠CFE的度数；（2）若（1）中的∠B=α，∠ACB=β，则∠CFE的度数；（用α、β表示）（3）如图②，（2）中的结论还成立么？请说明理由．17．如图1，//⊥，垂足为．⊥于，过作BD CNAM CN，点为平面内一点，AB BC（1）求证：BAM CBD∠=∠；（2）如图2，分别作、的平分线交于、，连接，若，①求的度数；②求证：CBF CFB∠=∠．18．（2020春•新洲区期中）已知：//AB CD，点在直线上，点在直线上．（1）如图（1），，．①若，求的度数；②试判断与的位置关系，并说明理由；（2）如图（2），平分，平分，试探究与的数量关系，并说明理由．19．探究题：（1）如图1，若AB∥CD，则∠B+∠D＝∠E，你能说明理由吗？（2）反之，若∠B+∠D＝∠E，直线AB与直线CD有什么位置关系？简要说明理由；（3）若将点E移至图2的位置，此时∠B、∠D、∠E之间有什么关系？直接写出结论；（4）若将点E移至图3的位置，此时∠B、∠D、∠E之间有什么关系？直接写出结论．。

如图，已知AB ∥CD ，EF 交AB,CD 于G ， H, GM ， HN 分别平分EHD AGF ∠∠,，试说明GM ∥HN 。

2. 已知：如图,AD ∥BC ，∠BAD = ∠BCD ，求证：AB ∥CD 。

3。

如图，AB ∥CD,P 为AB ，CD 之间的一点，已知︒=∠321,︒=∠252,求BPC ∠的度数。

4.已知AB ∥CD ，BC ∥DE 。

试说明D B ∠=∠.5.已知：,21,,,∠=∠⊥⊥⊥G AB FG AC BC E AC DE 于于求证:AB CD ⊥.6.在ABC ∆中，,D AB CD 于⊥AB FG ⊥于G ，ED ∥BC ，试说明21∠=∠。

7.已知：在△ABC 中,∠BAC=80°，∠B=60°，AD ⊥BC 于D,AE 平分∠DAC ，求∠AEC8。

如图，已知∠A=∠F ，AB ∥EF ，BC=DE ，请说明AD ∥CF. 解：∵ BC=DE （已知） ∴ 在△ABD 与△FEC 中， ∴ BC+CD=DE+CD( ) ∠A=∠F （已知） 即:_________＝_________ _______＝______（已证) 又∵AB ∥EF （已知) _______＝______(已证） ∴ ________＝_________ ∴ △ABD ≌△FEC （________）∴ ∠ADB =∠FCE （______________________________）∴ AD ∥CF(______________________________）9。

如图，AB=AD ，AC=AE ，∠BAE=∠DAC ，试说明∠C=∠E10.如图，已知OC=OE ，OD=OB,试说明△ADE ≌△ABC 。

BACDECBEADFOEC已知AO 是△ABC 中BC 边上的高，点D 、点E 是三角形外的两个点，且满足AD=AE,DB ＝EC ，∠D ＝∠E, 试说明AO 平分∠BAC12．如图，在△ABC 中，BC=10，边BC 的垂直平分线分别交AB ，BC 于点E 和D,BE=6, 求△BCE 的周长．1．如图，已知在AB=AC,DB=DC,则AD ⊥BC ，为什么?14、在Rt △ABC 中，BD 是∠B 的平分线，DE ⊥AB 于E, 则DE = DC 吗?说明你的理由。

七年级数学下---全等三角形证明题精选9.已知：如图，PA 、PC 分别是△ABC 外角∠MAC 和∠NCA 的平分线，•它们交于点P ，PD ⊥BM 于D ，PF ⊥BN 于F ．求证：BP 为∠MBN 的平分线．10、如图，已知AD 是∠BAC 的平分线， DE ⊥AB 于E ， DF ⊥AC 于F ， 且BE=CF ， 求证： (1)AD 是△ABC 的中线；(2)AB=AC ．11.在△ABC 中，∠ACB =90°，AC =BC ，直线MN 经过点C ，且AD ⊥MN 于D ，BE ⊥MN 于E ． （1）当直线MN 绕点C 旋转到图1的位置时，求证：①△ADC ≌△CEB ；②DE =AD ＋BE ； （2）当直线MN 绕点C 旋转到图2的位置时，求证：DE =AD －BE ；（3）当直线MN 绕点C 旋转到图3的位置时，试问DE ，AD ，BE 具有怎样的等量关系？请写出这个等量关系，并加以证明．C BAE D 图N M ABCDEM N图AC BE D N M图A 1 2E CD B12、如图，等腰直角三角形ABC 中，∠ACB ＝90°，AD 为腰CB 上的中线，CE ⊥AD 交AB 于E ． 求证∠CDA ＝∠EDB ．（作CF ⊥AB ）13、在Rt △ABC 中，∠B AC ＝90°，CE 是角平分线，和高AD 相交于F ，作FG ∥BC 交AB 于G ， 求证：AE ＝BG （平行四边形对边相等）．14、如图，已知△ABC 是等边三角形，∠BDC ＝120º，说明AD=BD+CD 的理由15、如图，在△ABC 中，AD 是中线，BE 交AD 于F,且AE=EF,说明AC=BF 的理由。

C12ABCDEGF EDCB A注意：（等腰三角形两底角相等）16、如图，在△ABC 中，∠ABC=100º，AM=AN,CN=CP,求∠MNP 的度数。

人教版七年级下册数学第5章相交线与平行线证明题专题训练1．如图，直线CD ，AB 相交于点O ，∠BOM ＝90°，∠DON ＝90°.(1)若∠COM ＝∠AOC ，求∠AOD 的度数；(2)若∠COM ＝14∠BOC ，求∠BOD 的度数．2．已知：如图，∠1＝∠2，∠3＝∠4，∠5＝∠C ．DE 与BF 平行吗？请说明理由．3．如图，已知：12∠=∠，50D ︒∠=，求B 的度数4．如图，已知AB//CD ，AE//CF ，求证：∠BAE=∠DCF.5．如图//AB CD ，AE 平分BAD ∠，CD 与AE 相交于F ，CFE E ∠=∠，求证：//AD BC ．6．如图，已知//AB CD ，40B ∠=，CN 是BCE ∠的平分线，CM CN ⊥，求BCM ∠的度数．7．如图，已知EA∠AB 于A ，CD∠DF 于D ，AB∠CD ，请判断：EA 与DF 平行吗？为什么？8．如图，AB∠CD ，BN ，DN 分别平分∠ABM ，∠MDC ，试问∠M 与∠N 之间的数量关系如何？请说明理由．9．如图，已知∠B=∠C ．（1）若AD∠BC ，则AD 平分∠EAC 吗？请说明理由．（2）若∠B+∠C+∠BAC=180°，AD 平分∠EAC ，则AD∠BC 吗？请说明理由．10．如图，AB∠DE ，C 为BD 上一点，∠A ＝∠BCA ，∠E ＝∠ECD ，求证：CE∠CA ．11．如图所示，已知∠1＝∠2，AC 平分∠DAB ，试说明DC∠AB ．12．如图，AB∠DE∠GF ，∠1：∠D ：∠B ＝2：3：4，求∠1的度数．13．如图，四边形ABCD中，∠A＝∠C＝90°，BE，DF分别是∠ABC，∠ADC的平分线．(1)∠1与∠2有什么关系，为什么？(2)BE与DF有什么关系？请说明理由．14．如图，AD是∠EAC的平分线，AD∠BC，∠B=30o，∠EAD、∠DAC、∠C的度数．15．已知：如图，∠BAP+∠APD =180°，∠1 =∠2.求证：AE∠PF．16．如图，∠1＝∠2，∠3＝∠4，∠5＝∠6，求证：CE//BF．17．如图，AD∠BC，垂足为D，∠ADE=∠CFG，∠C+∠CFG=90°.试说明DE∠AC18．如图，AD∠BC，BE平分∠ABC交AD于点E，BD平分∠EBC．(1)若∠DBC＝30°，求∠A的度数；(2)若点F在线段AE上，且7∠DBC－2∠ABF＝180°，请问图中是否存在与∠DFB相等的角？若存在，请写出这个角，并说明理由；若不存在，请说明理由．19．如图，已知∠BEF+∠EFD=180°，EM平分∠BEF，FN平分∠EFC，求证：∠M=∠N.20．已知：如图，AB∠CD，∠1=∠2，∠3=∠4．（1）求证：AD∠BE；（2）若∠B=∠3=2∠2，求∠D的度数．。