高考数学课时达标42

课时作业42 空间几何体的表面积与体积时间：45分钟 分值：100分一、选择题(每小题5分，共30分)1．圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面的半径为( )A ．7B ．6C ．5D ．3解析：设圆台较小底面半径为r ，则另一底面半径为3r .由S ＝π(r ＋3r )·3＝84π，解得r ＝7.答案：A2．一个空间几何体的正视图和侧视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的全面积为( )A.32π B ．2π C ．3πD ．4π解析：依题意知，该几何体是一个底面半径为12、高为1的圆柱，则其全面积为2π×⎝ ⎛⎭⎪⎫122＋2π×12×1＝32π. 答案：A3．某几何体的三视图如图所示，它的体积为( )A．72π B．48πC．30π D．24π解析：此几何体由半个球体与一个圆锥组成，其体积V＝12×43π×33＋13π×32×52－32＝30π.答案：C4．(2013·重庆卷)某几何体的三视图如图所示，则该几何体的表面积为()A．180 B．200C．220 D．240解析：该几何体为水平放置的底面为梯形的直四棱柱．S 表＝S 侧＋S 底＝(32＋42×2＋2＋8)×10＋12×(2＋8)×4×2＝240，选D.答案：D5．(2013·山东卷)一个四棱锥的侧棱长都相等，底面是正方形，其正(主)视图如图所示，则该四棱锥侧面积和体积分别是( )A ．45，8B ．45，83 C ．4(5＋1)，83D ．8,8解析：由三视图知该四棱锥为正四棱锥，且底面边长为2，高为2，斜高为22＋12＝5，所以S 侧＝12×2×5×4＝45，V ＝13×2×2×2＝83，故选B.答案：B6．(2013·辽宁卷)已知直三棱柱ABC －A 1B 1C 1的6个顶点都在球O 的球面上．若AB ＝3，AC ＝4，AB ⊥AC ，AA 1＝12，则球O 的半径为( )A.3172 B ．210 C.132D ．310解析：O 在面ABC 内的射影为△ABC 的外心，即BC 的中点，设球的半径为r ，则有r 2＝(12|BC |)2＋(12|AA 1|)2＝(52)2＋(122)2＝1694，∴r＝132.答案：C二、填空题(每小题5分，共15分)7．四棱锥P —ABCD 的顶点P 在底面ABCD 中的投影恰好是A ，其三视图如下图所示，则四棱锥P —ABCD 的表面积为________．解析：依题意得知，在该四棱锥中，P A ⊥底面ABCD ，P A ＝a ，底面四边形ABCD 是边长为a 的正方形，因此有PD ⊥CD ，PB ⊥BC ，PB ＝PD ＝2a ，所以该四棱锥的表面积等于a 2＋2×12a 2＋2×12×2a ×a ＝(2＋2)a 2.答案：(2＋2)a 28．(2013·新课标全国卷Ⅰ)已知H 是球O 的直径AB 上一点，AH :HB ＝1:2，AB ⊥平面α，H 为垂足，α截球O 所得截面的面积为π，则球O 的表面积为________．解析：由题知，∠ACB ＝90°，设球O 的半径为R ，则AH ＝23R ，BH ＝43R .设CH ＝r ，则πr 2＝π，∴r ＝1.由射影定理知，CH 2＝BH ·AH .∴1＝43R ·23R ，∴R ＝324，∴球O 的表面积为S ＝4πR 2＝92π.答案：9π29．(2013·湖北卷)我国古代数学名著《数书九章》中有“天池盆测雨”题：在下雨时，用一个圆台形的天池盆接雨水．天池盆盆口直径为二尺八寸，盆底直径为一尺二寸，盆深一尺八寸．若盆中积水深九寸，则平地降雨量是________寸．(注：①平地降雨量等于盆中积水体积除以盆口面积；②一尺等于十寸)解析：由题知，当盆中积水深九寸时，积水表面圆直径为二十寸，其半径为r 1＝10，又盆底半径r 2＝6，水深h ＝9，∴圆台盆中积水体积为V ＝13π(r 21＋r 1r 2＋r 22)h ＝13π(102＋10×6＋62)×9＝588π，∴平均降雨量为V π·142＝588ππ×142＝3. 答案：3三、解答题(共55分，解答应写出必要的文字说明、演算步骤或证明过程)10．(15分)如图，在四边形ABCD 中，∠DAB ＝90°，∠ADC ＝135°，AB ＝5，CD ＝22，AD ＝2，求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积．解：由已知得：CE ＝2，DE ＝2，CB ＝5，S表面＝S圆台侧＋S圆台下底＋S 圆锥侧＝π(2＋5)×5＋π×25＋π×2×22＝(60＋42)π，V ＝V 圆台－V 圆锥＝13(π·22＋π·52＋22·52π2)×4－13π×22×2＝1483π.11．(20分)一个几何体的三视图如图所示．已知正视图是底边长为1的平行四边形，侧视图是一个长为3，宽为1的矩形，俯视图为两个边长为1的正方形拼成的矩形．(1)求该几何体的体积V ； (2)求该几何体的表面积S .解：(1)由三视图可知，该几何体是一个平行六面体(如图)，其底面是边长为1的正方形，高为 3.所以V＝1×1×3＝ 3.(2)由三视图可知，该平行六面体中，A1D⊥平面ABCD，CD⊥平面BCC1B1，所以AA1＝2，侧面ABB1A1，CDD1C1均为矩形，所以S ＝2×(1×1＋1×3＋1×2)＝6＋2 3.——创新应用——12．(20分)(2013·安徽卷)如图，四棱锥P－ABCD的底面ABCD 是边长为2的菱形，∠BAD＝60°，已知PB＝PD＝2，P A＝ 6.(1)证明：PC⊥BD；(2)若E为P A的中点，求三棱锥P－BCE的体积．解：(1)连接AC，交BD于O点，连接PO.因为底面ABCD是菱形，所以AC⊥BD，BO＝DO.由PB＝PD知，PO⊥BD.再由PO∩AC＝O知，BD⊥面APC，因此BD ⊥PC .(2)因为E 是P A 的中点，所以V P －BCE ＝V C －PEB ＝12V C －P AB ＝12V B －APC . 由PB ＝PD ＝AB ＝AD ＝2知，△ABD ≌△PBD .因为∠BAD ＝60°，所以PO ＝AO ＝3，AC ＝23，BO ＝1.又P A ＝6，PO 2＋AO 2＝P A 2，即PO ⊥AC ，故S △APC ＝12PO ·AC ＝3.由(1)知，BO ⊥面APC ，因此 V P －BCE ＝12V B －APC ＝12·13·BO ·S △APC ＝12.。

课时规范练42　椭圆基础巩固组1.(2021山东济南十一校联考)“2<m<6”是“方程x 2m -2+y 26-m=1表示椭圆”的( )A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件2.(2021福建厦门集美中学月考)已知点M (3,√15)是椭圆x 2a 2+y 2b2=1(a>b>0)上的一点,椭圆的长轴长是焦距的32倍,则该椭圆的方程为( )A.x 225+y 220=1 B.x 227+2y 245=1C.x 218+y 210=1 D.x 236+y 220=13.已知F 1,F 2分别为椭圆E :y 2a 2+x 2b 2=1(a>b>0)的两个焦点,点P 是椭圆E 上的点,PF 1⊥PF 2,且sin∠PF 2F 1=3sin∠PF 1F 2,则椭圆E 的离心率为( )A.√102B.√104C.√52D.√544.(2021新高考Ⅰ,5)已知F 1,F 2是椭圆C :x 29+y 24=1的两个焦点,点M 在椭圆C 上,则|MF 1||MF 2|的最大值为( )A.13B.12C.9D.65.关于椭圆3x 2+4y 2=12有以下结论,其中正确的是( )A.离心率为15B.长轴长是2√3C.焦点在y 轴上D.焦点坐标为(-1,0),(1,0)6.椭圆E 的焦点在x 轴上,其短轴的两个端点和两个焦点恰为边长为2的正方形的顶点,则( )A.椭圆E 的长轴长为4√2B.椭圆E 的焦点坐标为(-2,0),(2,0)C.椭圆E 的离心率为12D.椭圆E 的标准方程为x 24+y 22=17.若圆C 以椭圆x 216+y 212=1的右焦点为圆心,长半轴长为半径,则圆C 的方程为 . 8.(2021湖南浏阳一中模拟)椭圆x 29+y 23=1的左、右焦点分别为F 1,F 2,点P 在椭圆上,如果线段PF 1的中点在y 轴上,那么|PF 1|是|PF 2|的 倍.综合提升组9.(2021江西南昌三中月考)已知椭圆x 2a 2+y 2b2=1(a>b>0)的左、右焦点分别为F 1,F 2,|F 1F 2|=√10,点P 是y 轴正半轴上一点,线段PF 1交椭圆于点A ,若AF 2⊥PF 1,且△APF 2的内切圆半径为√22,则椭圆的离心率是( )A.√54 B.√510 C.√53 D.√15410.如图所示,某月球探测器飞行到月球附近时,首先在以月球球心F 为圆心的圆形轨道Ⅰ上绕月飞行,然后在点P 处变轨进入以点F 为一个焦点的椭圆轨道Ⅱ上绕月飞行,最后在点Q 处变轨进入以点F 为圆心的圆形轨道Ⅲ绕月飞行,设圆形轨道Ⅰ的半径为R,圆形轨道Ⅲ的半径为r,则以下说法正确的是(　)A.椭圆轨道Ⅱ上任意两点距离最大为2RB.椭圆轨道Ⅱ的焦距为R-rC.若r不变,则R越大,椭圆轨道Ⅱ的短轴越短D.若R不变,则r越小椭圆轨道Ⅱ的离心率越小11.已知点P是椭圆x249+y245=1上一动点,点M,点N分别是圆(x+2)2+y2=116与圆(x-2)2+y2=116上的动点,则( )A.|PM|+|PN|的最小值为272B.|PM|+|PN|的最小值为252C.|PM|+|PN|的最大值为252D.|PM|+|PN|的最大值为272创新应用组12.“蒙日圆”涉及几何学中的一个著名定理,该定理的内容为:椭圆上任意两条互相垂直的切线的交点,必在一个与椭圆同心的圆上,该圆称为椭圆的“蒙日圆”.若椭圆C:x 24+y2m=1(m>0,m≠4)的离心率为√32,则椭圆C的“蒙日圆”方程为( )A.x2+y2=5或x2+y2=7B.x2+y2=7或x2+y2=20C.x2+y2=5或x2+y2=20D.x2+y2=7或x2+y2=2813.(2021河北保定三中月考)椭圆C :x 2a 2+y 2b 2=1(a>b>0)的右焦点为F (c ,0),已知定点M (14a 29c,0),若椭圆C 上存在点N ,使得△FMN 为等腰钝角三角形,则椭圆C 的离心率的取值范围是　.课时规范练42　椭圆1.B 解析:若方程x 2m -2+y 26-m =1为椭圆方程,则{m -2>0,6-m >0,m -2≠6-m ,解得2<m<6且m ≠4,故“2<m<6”是“方程x 2m -2+y 26-m =1表示椭圆方程”的必要不充分条件.故选B .2.D 解析:由题意{a 2=b 2+c 2,a =32c ,9a 2+15b 2=1,解得{a =6,b =2√5,所以椭圆方程为x 236+y 220=1.故选D .3.B 解析:因为F 1,F 2分别为椭圆E :y 2a 2+x 2b 2=1(a>b>0)的两个焦点,点P 是椭圆E 上的点,PF 1⊥PF 2,且sin∠PF 2F 1=3sin∠PF 1F 2,所以由正弦定理可得|PF 1|=3|PF 2|,且|PF 1|+|PF 2|=2a ,|PF 1|2+|PF 2|2=4c 2,所以52a 2=4c 2,所以椭圆的离心率e=c a =√524=√104.故选B .4.C 解析:由题意知|MF 1|+|MF 2|=2a=6,则√|M F 1||M F 2|❑≤|M F 1|+|M F 2|2=3,则|MF 1||MF 2|≤9,当且仅当|MF 1|=|MF 2|=3时,等号成立,故|MF 1||MF 2|的最大值为9.故选C .5.D 解析:将椭圆方程化为标准方程为x 24+y 23=1.该椭圆的焦点在x 轴上,故C 错误;焦点坐标为(-1,0),(1,0),故D 正确;a=2,长轴长是4,故B 错误;离心率e=c a =12,故A 错误.故选D .6.D 解析:设椭圆E 的方程为x 2a 2+y 2b 2=1(a>b>0).由题可知b=c=√2,所以a 2=b 2+c 2=4,所以a=2,所以椭圆E 的长轴长2a=4,焦点坐标为(-√2,0),(√2,0),离心率为√22,标准方程为x 24+y 22=1.故选D .7.(x-2)2+y 2=16　解析:由椭圆方程可知a 2=16,b 2=12,则c 2=4,所以椭圆右焦点为(2,0),长半轴长为4.由题可知,圆C 以(2,0)为圆心,4为半径,所以圆的方程为(x-2)2+y 2=16.8.5　解析:由题可知a=3,c=√6,PF 2⊥x 轴.当x=√6时,69+y 23=1,解得y=±1,所以|PF 2|=1,所以|PF1|=2×3-|PF2|=6-1=5,所以|PF1|是|PF2|的5倍.9.C　解析:由题可知2c=√10,所以c=√102.因为直角三角形APF2的内切圆半径为√2 2,所以|AP|+|AF2|-|PF2|=2×√22=√2.又由椭圆的对称性可知|PF2|=|PF1|,所以|AP|+|AF2|-|PF2|=√2=|AP|+|AF2|-|PF1|=|AF2|-|AF1|.在直角三角形AF1F2中,由{|A F2|-|A F1|=√2,|A F1|2+|A F2|2=|F1F2|2=10,解得{|A F1|=2-√2,|A F2|=√2,所以|PF1|+|PF2|=3√2,即2a=3√2,a=3√22,所以椭圆的离心率e=ca √103√22√53.故选C.10.B　解析:设椭圆轨道Ⅱ的长轴长为2a,短轴长为2b,焦距为2c,依题意得{a+c=R,a-c=r,解得a=R+r2,c=R-r2.椭圆轨道Ⅱ上任意两点距离的最大值为2a=R+r,故A错误;椭圆轨道Ⅱ的焦距为2c=R-r,故B正确;椭圆轨道Ⅱ的短轴长2b=2√a2-c2=2√Rr,若r不变,R越大,则2b越大,椭圆轨道Ⅱ的短轴越长,故C 错误;椭圆轨道Ⅱ的离心率e=ca =R-rR+r=1-2rR+r=1-2Rr+1,若R不变,r越小,则e越大,故D错误.故选B.11.A　解析:由题可知,圆(x+2)2+y2=116与圆(x-2)2+y2=116的圆心分别为A(-2,0),B(2,0),且A,B是椭圆x 249+y245=1的两个焦点,两圆的半径均为14,所以|PM|+|PN|的最大值为|PA|+|PB|+2×14=2a+12=2×√49+12=292,|PM|+|PN|的最小值为|PA|+|PB|-2×14=2a-12=2×√49−12=272.故选A.12.C　解析:若m>4,√m-4√=√32,即m=16,所以C:x24+y216=1.因为椭圆上任意两条互相垂直的切线的交点,必在一个与椭圆同心的圆上,不妨取两点(2,0),(0,4),则两条切线为x=2和y=4,所以两条切线的交点为(2,4),所以点(2,4)在蒙日圆上,所以半径为√22+42=√20,所以蒙日圆为x2+y2=20.若0<m<4,则√4-m2=√32,即m=1,所以C:x24+y2=1.因为椭圆上任意两条互相垂直的切线的交点,必在一个与椭圆同心的圆上,不妨取两点(2,0),(0,1),则两条切线为x=2和y=1,所以两条切线的交点为(2,1),所以点(2,1)在蒙日圆上,所以半径为√22+12=√5,所以蒙日圆为x2+y2=5.综上,椭圆C的“蒙日圆”方程为x2+y2=5或x2+y2=20.故选C.13.(23,1)　解析:因为|OM|-|OF|=14a29c-c=14a2-9c29c =5a2+9b29c,且a,b,c均为正数,所以|OM|-|OF|>0,所以M在F点右侧.又14a29c -a=14a2-9ac9c=a(14a-9c)9c>0,所以M在椭圆外部,所以∠NMF不可能为钝角.若∠FNM为钝角,设MF的中点为E,N的横坐标为x0,则c≤x0≤a,应有NE垂直平分FM,即x0=|OE|.因为|OE|=|OF|+12|FM|=c+12(14a29c-c)=12(14a29c+c),而1 2(14a29c+c)-a=14a2+9c2-18ac18c=5a2+9(c-a)218c>0,所以∠FNM不可能为钝角.故∠NFM为钝角,且|FM|=|FN|,此时|FM|=14a 29c-c,|FN|∈(c,a+c).当NF垂直x轴时,N(c,y0),所以c2a2+y02b2=1,解得|y0|=b2a,所以b2a<14a29c-c<a+c,所以{18e2+9e-14>0, 9e3-9e2-9e+14>0,0<e<1,解得23<e<1.。

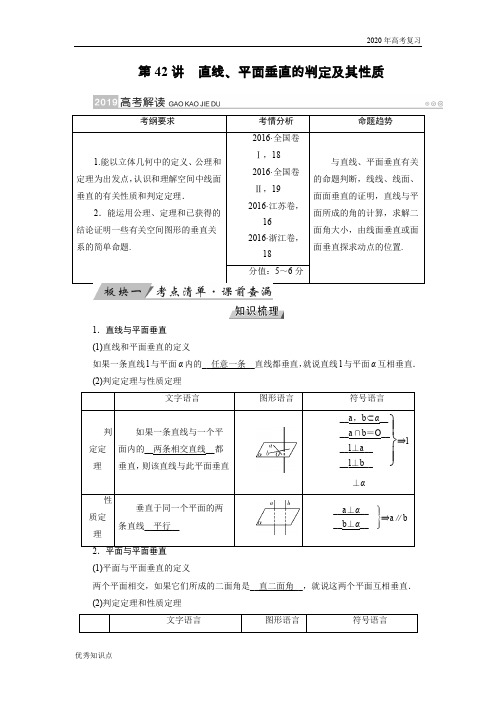
第42讲 直线、平面垂直的判定及其性质1．直线与平面垂直 (1)直线和平面垂直的定义如果一条直线l 与平面α内的__任意一条__直线都垂直，就说直线l 与平面α互相垂直． (2)判定定理与性质定理则该直线与此平面垂直⎭⎪⎬⎪⎫__a ，b ⊂α____a ∩b ＝O ____l ⊥a ____l ⊥b __⇒l ⊥α⎭⎪⎬⎪⎫__a ⊥α____b ⊥α__⇒a ∥b (1)平面与平面垂直的定义两个平面相交，如果它们所成的二面角是__直二面角__，就说这两个平面互相垂直． (2)判定定理和性质定理一个平面过另一个平面的一，则这两个平面互相⎭⎪⎬⎪⎫__l⊂β____l⊥α__⇒α⊥β两个平面互相垂直，则一个的直线与⎭⎪⎬⎪⎫__α⊥β____l⊂β____α∩β＝a____l⊥a__⇒l⊥α1．思维辨析(在括号内打“√”或“×”)．(1)直线l与平面α内无数条直线都垂直，则l⊥α.(×)(2)过一点作已知直线的垂面有且只有一个．(√)(3)若两条直线垂直，则这两条直线相交．(×)(4)若两平面垂直，则其中一个平面内的任意一条直线垂直于另一平面．(×)(5)若平面α内的一条直线垂直于平面β内的无数条直线，则α⊥β.(×)解析(1)错误．直线l与α内两条相交直线都垂直才有l⊥α.(2)正确．过一点可以作两条相交直线都垂直于已知直线，而这两条相交直线可确定一个平面，此平面与直线垂直．(3)错误．两条直线垂直，这两条直线可能相交，也可能异面．(4)错误．两个平面垂直，有一条交线，一个平面内垂直于交线的直线垂直于另一个平面，而不是任意一条直线．(5)错误．α内的一条直线如果与β内的两条相交直线都垂直才能线面垂直，从而面面垂直．2．设平面α与平面β相交于直线m，直线a在平面α内，直线b在平面β内，且b⊥m，则“α⊥β”是“a⊥b”的(A)A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件解析由面面垂直的性质定理可知，当α⊥β时，b⊥α.又因为a⊂α，则a⊥b;如果a∥m，a⊥b，不能得到α⊥β，故“α⊥β”是“a⊥b”的充分不必要条件．故选A．3．已知m和n是两条不同的直线，α和β是两个不重合的平面，下面给出的条件中一定能推出m⊥β的是(C)A．α⊥β且m⊂αB．α⊥β且m∥αC．m∥n且n⊥βD．m⊥n，n⊂α且α∥β解析α⊥β，且m⊂α⇒m⊂β或m∥β或m与β相交，故A项不成立；α⊥β，且m∥α⇒m⊂β或m∥β或m与β相交，故B项不成立；m∥n，且n⊥β⇒m⊥β.故C项成立；m⊥n，n⊂α，且α∥β，知m⊥β不成立，故D项不成立，故选C．4．PD垂直于正方形ABCD所在的平面，连接PB，PC，P A，AC，BD，则一定互相垂直的平面有__7__对．解析平面P AD、平面PBD、平面PCD都垂直于平面ABCD，平面P AD⊥平面PCD，平面PCD⊥平面PBC，平面P AD⊥平面P AB，平面P AC⊥平面PBD，共有7对．5．在三棱锥P－ABC中，点P在平面ABC内的射影为点O.(1)若P A＝PB＝PC，则点O是△ABC的__外__心；(2)若P A⊥PB，PB⊥PC, PC⊥P A，则点O是△ABC的__垂__心．解析(1)若P A＝PB＝PC，由勾股定理易得OA＝OB＝OC，故O是△ABC的外心；(2)由P A⊥PB，PC⊥P A，得P A⊥平面PBC，则P A⊥BC．又由PO⊥平面ABC知PO⊥BC，所以BC⊥平面P AO，则AO⊥BC，同理得BO⊥AC，CO⊥AB，故O是△ABC的垂心．一直线与平面垂直的判定与性质(1)证明直线和平面垂直的常用方法：①判定定理；②垂直于平面的传递性(a∥b，a⊥α⇒b⊥α)；③面面平行的性质(a⊥α，α∥β⇒a⊥β)；④面面垂直的性质．(2)证明线面垂直的核心是证线线垂直，而证明线线垂直则需借助线面垂直的性质．因此，判定定理与性质定理的合理转化是证明线面垂直的基本思想．(3)线面垂直的性质常用来证明线线垂直．【例1】如图，在正方体ABCD－A1B1C1D1中，E为棱C1D1的中点，F为棱BC的中点．(1)求证：直线AE⊥直线DA1；(2)在线段AA1上求一点G，使得直线AE⊥平面DFG.解析(1)证明：由正方体的性质可知，DA1⊥AD1，DA1⊥AB，又AB∩AD1＝A，∴DA1⊥平面ABC1D1，又AE⊂平面ABC1D1，∴DA1⊥AE.(2)所求G点即为A1点，证明如下：由(1)可知AE⊥DA1，取CD的中点H，连接AH，EH，由DF⊥AH，DF⊥EH，AH∩EH＝H，可证DF⊥平面AHE，∵AE⊂平面AHE，∴DF⊥AE.又DF∩A1D＝D，∴AE⊥平面DF A1，即AE⊥平面DFG.二平面与平面垂直的判定与性质(1)判定面面垂直的方法：①面面垂直的定义；②面面垂直的判定定理(a⊥β，a⊂α⇒α⊥β)．(2)在已知平面垂直时，一般要用性质定理进行转化．在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直．【例2】已知三棱柱A1B1C1－ABC的侧棱与底面成60°角，底面是等边三角形，侧面B1C1CB是菱形且与底面垂直，求证：AC1⊥BC．证明过C1作C1H⊥BC于H，连接AH，又∵侧面B1C1CB⊥底面ABC，侧面B1C1CB∩底面ABC＝BC，∴C1H⊥底面ABC．∴侧棱CC1与底面ABC所成角，即为∠C1CH＝60°，在Rt △C 1CH 中，CH ＝12CC 1，又∵CC 1＝BC ，∴CH ＝12BC ，即H 为BC 的中点，∴在等边△ABC 中，AH ⊥BC ，又∵C 1H ⊥BC ，AH ∩C 1H ＝H ，∴BC ⊥平面AC 1H ， 又∵AC 1⊂平面AC 1H ，∴AC 1⊥BC ．三 垂直关系中的探索性问题解决垂直关系中的探索性问题的方法同“平行关系中的探索性问题”的规律方法一样，一般是先探求点的位置，多为线段的中点或某个等分点，然后给出符合要求的证明．【例3】 如图，在三棱台ABC －DEF 中，CF ⊥平面DEF ，AB ⊥BC ．(1)设平面ACE ∩平面DEF ＝a ，求证：DF ∥a ；(2)若EF ＝CF ＝2BC ，试问在线段BE 上是否存在点G ，使得平面DFG ⊥平面CDE ？若存在，请确定G 点的位置；若不存在，请说明理由．解析 (1)证明：在三棱台ABC －DEF 中，AC ∥DF ，AC ⊂平面ACE ，DF ⊄平面ACE ，∴DF ∥平面ACE .又∵DF ⊂平面DEF ，平面ACE ∩平面DEF ＝a ，∴DF ∥a . (2)线段BE 上存在点G ，且BG ＝13BE ，使得平面DFG ⊥平面CDE .证明如下：取CE 的中点O ，连接FO 并延长交BE 于点G .连接GD ， ∴CF ＝EF ，∴GF ⊥CE .在三棱台ABC －DEF 中， 由AB ⊥BC 得DE ⊥EF . 由CF ⊥平面DEF ，得CF ⊥DE .又CF ∩EF ＝F ，∴DE ⊥平面CBEF ，∴DE ⊥GF . 又CE ∩DE ＝E ，∴GF ⊥平面CDE .又GF ⊂平面DFG ，∴平面DFG ⊥平面CDE . 此时，如平面图所示，∵O 为CE 的中点，EF ＝CF ＝2BC ，易证△HOC ≌△FOE ， ∴HB ＝BC ＝12EF .由△HGB ∽△FGE 可知BG GE ＝12，即BG ＝13BE .1．(2018·山东青岛模拟)设a ，b 是两条不同的直线，α，β是两个不同的平面，则能得出a ⊥b 的是( C )A ．a ⊥α，b ∥β，α⊥βB ．a ⊥α，b ⊥β，α∥βC ．a ⊂α，b ⊥β，α∥βD ．a ⊂α，b ∥β，α⊥β解析 对于C 项，由α∥β，a ⊂α可得a ∥β，又b ⊥β，得a ⊥b ，故选C ．2．(2016·浙江卷)已知互相垂直的平面α，β交于直线l ，若直线m ，n 满足m ∥α，n ⊥β，则( C )A ．m ∥lB ．m ∥nC ．n ⊥lD ．m ⊥n解析 ∵α∩β＝l ，∴l ⊂β，∵n ⊥β，∴n ⊥l .3．如图，在四棱锥P －ABCD 中，P A ⊥底面ABCD ，AB ⊥AD, AC ⊥CD ，∠ABC ＝60°， P A ＝AB ＝BC ，E 是PC 的中点．证明：(1) CD ⊥AE ； (2)PD ⊥平面ABE .证明 (1)在四棱锥P －ABCD 中，∵P A ⊥底面ABCD ，CD ⊂平面ABCD ，∴P A ⊥CD ．∵AC ⊥CD ，P A ∩AC ＝A ，∴CD ⊥平面P AC ，而AE ⊂平面P AC ，∴CD ⊥AE .(2)由P A ＝AB ＝BC ，∠ABC ＝60°，可得AC ＝P A ．∵E 是PC 的中点，∴AE ⊥PC ．由(1)知AE ⊥CD ，且PC ∩CD ＝C ，∴AE ⊥平面PCD ．而PD ⊂平面PCD ，∴AE ⊥PD ．∵P A ⊥底面ABCD ，∴P A ⊥AB ．又∵AB ⊥AD 且P A ∩AD ＝A ， ∴AB ⊥平面P AD ，而PD ⊂平面P AD ，∴AB ⊥PD ． 又∵AB ∩AE ＝A ，∴PD ⊥平面ABE .4．如图，在四棱锥S －ABCD 中，平面SAD ⊥平面ABCD ，四边形ABCD 为正方形，且P 为AD 的中点，Q 为SB 的中点．(1)求证：CD ⊥平面SAD ； (2)求证：PQ ∥平面SCD ；(3)若SA ＝SD ，M 为BC 的中点，在棱SC 上是否存在点N ，使得平面DMN ⊥平面ABCD ？并证明你的结论．解析 (1)证明：因为四边形ABCD 为正方形，所以CD ⊥AD ． 又平面SAD ⊥平面ABCD ，且平面SAD ∩平面ABCD ＝AD ， 所以CD ⊥平面SAD ．(2)证明：取SC 的中点R ，连接QR ，DR .由题意知，PD ∥BC 且PD ＝12BC ．在△SBC 中，Q 为SB 的中点，R 为SC 的中点， 所以QR ∥BC 且QR ＝12BC ．所以QR ∥PD 且QR ＝PD ， 则四边形PDRQ 为平行四边形， 所以PQ ∥DR .又PQ ⊄平面SCD ，DR ⊂平面SCD ，所以PQ ∥平面SCD ． (3)存在点N 为SC 的中点，使得平面DMN ⊥平面ABCD ． 连接PC ，DM 交于点O ，连接PM ，SP ，NM ，ND ，NO ，因为PD ∥CM ，且PD ＝CM ， 所以四边形PMCD 为平行四边形，所以PO＝CO.又因为N为SC的中点，所以NO∥SP.易知SP⊥AD，平面SAD⊥平面ABCD，平面SAD∩平面ABCD＝AD，所以SP⊥平面ABCD，所以NO⊥平面ABCD．因为NO⊂平面DMN，所以平面DMN⊥平面ABCD．易错点联想不到已学定理错因分析：已知条件中给出了线面垂直，求证的是线线平行，若忽略线面垂直的性质定理，则觉得论证无从下手，从而造成解题困难．【例1】在正方体ABCD－A1B1C1D1中，点M，N分别在BD，B1C上，且MN⊥BD, MN ⊥B1C，求证：MN∥AC1.证明连接A1D，A1B，AC，∵MN⊥B1C，B1C∥A1D，∴MN⊥A1D．又∵MN⊥BD，BD∩A1D＝D，∴MN⊥平面A1BD．∵CC1⊥底面ABCD，∴CC1⊥BD．又∵BD⊥AC，AC∩CC1＝C，∴BD⊥平面ACC1.∴BD⊥AC1.同理AC1⊥A1B．又A1B∩BD＝B，∴AC1⊥平面A1BD．又∵MN⊥平面A1BD，∴MN∥AC1.【跟踪训练1】如图，P A垂直于圆O所在的平面，AB是圆O的直径，C是圆O上的一点，E, F分别是点A在PB, PC上的射影，给出下列结论：①AF⊥PB；②EF⊥PB；③AF⊥BC；④AE⊥BC．正确结论的个数为(C)A．1B．2C．3D．4解析∵AB是圆O的直径，∴AC⊥BC，又P A⊥面ABC，故P A⊥BC，且P A∩AC＝A，∴BC⊥面P AC，∴BC⊥AF.又AF⊥PC，且PC∩BC＝C，∴AF⊥面PBC，故AF⊥PB．又AE⊥PB，且AF∩AE＝A，∴PB⊥面AEF，从而EF⊥PB，故①②③正确．若AE⊥BC，则可证AE⊥面PBC，则AE∥AF，这是不可能的，选C．课时达标第42讲[解密考纲]对直线、平面垂直的判定与性质定理的初步考查一般以选择题、填空题的形式出现，难度不大；综合应用直线、平面垂直的判定与性质常以解答题为主，难度中等．一、选择题1．已知平面α⊥平面β，α∩β＝l，点A∈α，A∉l，直线AB∥l，直线AC⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是(D)A．AB∥m B．AC⊥mC．AB∥βD．AC⊥β解析如图所示，AB∥l∥m；AC⊥l，m∥l⇒AC⊥m；AB∥l⇒AB∥β，只有D项不一定成立，故选D．2．在空间中，l，m，n，a，b表示直线，α表示平面，则下列命题正确的是(D) A．若l∥α，m⊥l，则m⊥αB．若l⊥m，m⊥n，则l∥nC．若a⊥α，a⊥b，则b∥αD．若l⊥α，l∥a，则a⊥α解析对于A项，m与α位置关系不确定，故A项错；对于B项，当l与m，m与n为异面垂直时，l与n可能异面或相交，故B项错；对于C项，也可能b⊂α，故C项错；对于D项，由线面垂直的定义可知正确．3．(2018·江西南昌模拟)已知m，n为异面直线，m⊥平面α，n⊥平面β.直线l满足l⊥m，l⊥n，l⊄α，l⊄β，则(D)A．α∥β且l∥αB．α⊥β且l⊥βC．α与β相交，且交线垂直于lD．α与β相交，且交线平行于l解析由于m，n为异面直线，m⊥平面α，n⊥平面β，则平面α与平面β必相交，但不一定垂直，且交线垂直于直线m，n，又直线l满足l⊥m，l⊥n，则交线平行于l.4．设a，b是夹角为30°的异面直线，则满足条件“a⊂α，b⊂β，且α⊥β”的平面α，β(D)A．不存在B．有且只有一对C．有且只有两对D．有无数对解析过直线a的平面α有无数个，当平面α与直线b平行时，两直线的公垂线与b确定的平面β⊥α，当平面α与b相交时，过交点作平面α的垂线与b确定的平面β⊥α.故选D．5．(2018·宁夏银川一模)如图，在正方形ABCD中，E，F分别是BC，CD的中点，G 是EF的中点，现沿AE，AF及EF把这个正方形折成一个空间图形，使B，C，D三点重合，重合后的点记为H，那么，在这个空间图形中必有(A)A．AH⊥平面EFH B．AG⊥平面EFHC．HF⊥平面AEF D．HG⊥平面AEF解析由平面图形得AH⊥HE，AH⊥HF，又HE∩HF＝H，∴AH⊥平面HEF，故选A．6．(2018·陕西宝鸡质检)对于四面体ABCD，给出下列四个命题：①若AB＝AC，BD＝CD，则BC⊥AD；②若AB＝CD，AC＝BD，则BC⊥AD；③若AB⊥AC，BD⊥CD，则BC⊥AD；④若AB⊥CD，AC⊥BD，则BC⊥AD．其中为真命题的是(D)A．①②B．②③C．②④D．①④解析①如图，取BC的中点M，连接AM，DM，由AB＝AC⇒AM⊥BC，同理DM⊥BC ⇒BC⊥平面AMD，而AD⊂平面AMD，故BC⊥AD．④设A在平面BCD内的射影为O，连接BO，CO，DO，由AB⊥CD⇒BO⊥CD，由AC⊥BD⇒CO⊥BD⇒O为△BCD的垂心⇒DO⊥BC⇒AD⊥BC．二、填空题7．若α，β是两个相交平面，m为一条直线，则下列命题中，所有真命题的序号为__②④__.①若m ⊥α，则在β内一定不存在与m 平行的直线；②若m ⊥α，则在β内一定存在无数条直线与m 垂直；③若m ⊂α，则在β内不一定存在与m 垂直的直线；④若m ⊂α，则在β内一定存在与m 垂直的直线．解析 对于①，若m ⊥α，如果α，β互相垂直，则在平面β内存在与m 平行的直线，故①错误；对于②，若m ⊥α，则m 垂直于平面α内的所有直线，故在平面β内一定存在无数条直线与m 垂直，故②正确；对于③④，若m ⊂α，则在平面β内一定存在与m 垂直的直线，故③错误，④正确．8．(2018·吉林长春模拟)如图所示，在直角梯形ABCD 中，BC ⊥DC ，AE ⊥DC ，N ，M 分别是AD ，BE 的中点， 将三角形ADE 沿AE 折起，下列说法正确的是__①②__(填上所有正确的序号)．①不论D 折至何位置(不在平面ABC 内)都有MN ∥平面DEC ；②不论D 折至何位置都有MN ⊥AE ；③不论D 折至何位置(不在平面ABC 内)都有MN ∥AB ．解析 ①如图，分别取EC ，DE 的中点P ，Q ，由已知易知四边形MNQP 为平行四边形，则MN ∥PQ ，又PQ ⊂平面DEC ，故MN ∥平面DEC ，①正确；②取AE 的中点O ，易证NO ⊥AE ，MO ⊥AE .故AE ⊥平面MNO ，又MN ⊂平面MNO ，则AE ⊥MN ，②正确；③∵D ∉平面ABC ，∴N ∉平面ABC ，又A ，B ，M ∈平面ABC ，∴MN 与AB 异面，③错误．9．如图，在直三棱柱ABC －A 1B 1C 1中，侧棱长为2，AC ＝BC ＝1，∠ACB ＝90°，D 是A 1B 1的中点，F 是BB 1上的动点，AB 1，DF 交于点E ，要使AB 1⊥平面C 1DF ，则线段B 1F的长为__12__.解析 设B 1F ＝x ，因为AB 1⊥平面C 1DF ，DF ⊂平面C 1DF ，所以AB 1⊥DF .由已知可以得A 1B 1＝ 2.设Rt △AA 1B 斜边AB 1上的高为h ，则DE ＝12h . 又2×22＝h 22＋(2)2，所以h ＝233，DE ＝33. 在Rt △DB 1E 中，B 1E ＝⎝⎛⎭⎫222－⎝⎛⎭⎫332＝66. 由面积相等得66×x 2＋⎝⎛⎭⎫222＝22x ，得x ＝12. 即线段B 1F 的长为12. 三、解答题10．如图，在△ABC 中，∠ABC ＝90°，D 是AC 的中点，S 是△ABC 所在平面外一点，且SA ＝SB ＝SC ．(1)求证：SD ⊥平面ABC ；(2)若AB ＝BC ，求证：BD ⊥平面SAC ．证明 (1)因为SA ＝SC ，D 是AC 的中点，所以SD ⊥AC ．在Rt △ABC 中，AD ＝BD ，又SA ＝SB ，SD ＝SD ，所以△ADS ≌△BDS ，所以SD ⊥BD ．又AC ∩BD ＝D ，所以SD ⊥平面ABC ．(2)因为AB ＝BC ，D 为AC 的中点，所以BD ⊥AC ．由(1)知SD ⊥BD ，又SD ∩AC ＝D ，所以BD ⊥平面SAC ．11．(2018·河南郑州模拟)如图，已知三棱柱ABC －A ′B ′C ′的侧棱垂直于底面，AB ＝AC ，∠BAC ＝90°，点M ，N 分别为A ′B 和B ′C ′的中点．(1)证明：MN ∥平面AA ′C ′C ；(2)设AB ＝λAA ′，当λ为何值时，CN ⊥平面A ′MN ，试证明你的结论．解析 (1)证明：如图，取A ′B ′的中点E ，连接ME ，NE .因为E ，N 分别为A ′B ′和B ′C ′的中点，所以NE ∥A ′C ′，ME ∥BB ′∥AA ′. 又A ′C ′⊂平面AA ′C ′C ，NE ⊄平面AA ′C ′C ，所以NE ∥平面AA ′C ′C ，同理ME ∥平面AA ′C ′C ，又EM ∩EN ＝E ，所以平面MNE ∥平面AA ′C ′C ，因为MN ⊂平面MNE ，所以MN ∥平面AA ′C ′C ．(2)当λ＝2时，CN ⊥平面A ′MN ，证明如下：连接BN ，设AA ′＝a ，则AB ＝λAA ′＝λa ，由题意知BC ＝2λa ，CN ＝BN ＝a 2＋12λ2a 2， 因为三棱柱ABC －A ′B ′C ′的侧棱垂直于底面，所以平面A ′B ′C ′⊥平面BB ′C ′C ，因为AB ＝AC ，点N 是B ′C ′的中点，所以A ′N ⊥平面BB ′C ′C ，所以CN ⊥A ′N ，要使CN ⊥平面A ′MN ，只需CN ⊥BN 即可，所以CN 2＋BN 2＝BC 2，即2⎝⎛⎭⎫a 2＋12λ2a 2＝2λ2a 2， 解得λ＝2，故当λ＝2时，CN ⊥平面A ′MN .12．如图，在△ABC 中，∠B ＝90°，AB ＝2，BC ＝1，D ，E 两点分别是边AB ，AC 的中点，现将△ABC 沿DE 折成直二面角A －DE －B ．(1)求证：平面ADC ⊥平面ABE ；(2)求直线AD 与平面ABE 所成角的正切值．解析 (1)证明：∵D ，E 两点分别是边AB ，AC 的中点， ∴DE ∥BC ．∵∠B ＝90°，∠ADE ＝90°，∴DE ⊥AD ，DE ⊥BD ，∴∠ADB 为二面角A －DE －B 的平面角，∵∠ADB ＝90°， ∴AD ⊥平面BCD ．又∵BE ⊂平面BCD ，∴AD ⊥BE . 又∵BD ＝22，DE ＝12，BC ＝1，即BD DE ＝BC BD， ∴△BDE ∽△CBD ，∴∠EBD ＝∠DCB ，∴∠EBD ＋∠BDC ＝90°，∴BE ⊥DC ．又∵DC ∩AD ＝D ，∴BE ⊥平面ADC ． 又∵BE ⊂平面ABE ，∴平面ABE ⊥平面ADC ．(2)设BE 交CD 于H ，连接AH ，过点D 作DO ⊥AH 于O .∵AD ⊥BE ，BE ⊥DH ，又∵AD ∩DH ＝D ，∴BE ⊥平面ADH .∵DO ⊂平面ADH ，∴BE ⊥DO .又∵DO ⊥AH ，BE ∩AH ＝H ，∴DO ⊥平面ABE ， ∴∠DAO 为AD 与平面ABE 所成的角．在Rt △BDE 中，BD ＝22，DE ＝12，∴DH ＝BD ·DE BE ＝66. 在Rt △ADH 中，tan ∠DAO ＝DH DA ＝66×2＝33， ∴直线AD 与平面ABE 所成角的正切值为33.。

课时作业(四十二)A 级 基础达标1．设A (2，－1)，B (4,1)，则以线段AB 为直径的圆的方程为( )A ．(x －3)2＋y 2＝2B ．(x －3)2＋y 2＝8C ．(x －3)2＋y 2＝2D ．(x ＋3)2＋y 2＝8A [设P (x ，y )是圆上任意一点，则AP →·BP →＝0.AP →＝(x －2，y ＋1)，BP →＝(x －4，y －1)，所以(x －2)(x －4)＋(y ＋1)(y －1)＝0，整理得x 2＋y 2－6x ＋7＝0，即(x －3)2＋y 2＝2，故选A.]2．若圆x 2＋y 2＋2ax －b 2＝0的半径为2，则点(a ，b )到原点的距离为( )A ．1B ．2 C. 2 D ．4B [由r ＝12D 2＋E 2－4F ＝124a 2＋4b 2＝2，得a 2＋b 2＝2. ∴点(a ，b )到原点的距离d ＝a 2＋b 2＝2，故选B.]3．已知点M 是直线3x ＋4y －2＝0上的动点，点N 为圆(x ＋1)2＋(y ＋1)2＝1上的动点，则|MN |的最小值是( )A.95 B ．1 C.45 D.135C [圆心(－1，－1)到点M 的距离的最小值为点(－1，－1)到直线的距离d ＝|－3－4－2|5＝95，故点N 到点M 的距离的最小值为d －1＝45.] 4．圆心在直线2x －y －7＝0上的圆C 与y 轴交于A (0，－4)，B (0，－2)两点，则圆C 的标准方程为( )A ．(x ＋2)2＋(y ＋3)2＝5B ．(x －2)2＋(y －3)2＝5C ．(x ＋2)2＋(y －3)2＝5D ．(x －2)2＋(y ＋3)2＝5D [通解：设圆的标准方程为(x －a )2＋(y －b )2＝r 2，故⎩⎪⎨⎪⎧ 2a －b －7＝0a 2＋(4＋b )2＝r 2a 2＋(2＋b )2＝r 2，解得⎩⎪⎨⎪⎧a ＝2b ＝－3，半径r ＝22＋12＝5，故圆C 的标准方程为(x －2)2＋(y ＋3)2＝5.故选D. 优解：利用圆心在直线2x －y －7＝0上来检验，只有D 符合，即(x －2)2＋(y ＋3)2＝5的圆心为(2，－3)，2×2＋3－7＝0，其他三个圆心(－2，－3)，(2,3)，(－2,3)均不符合题意．]5．(2021·江西南昌二中月考)若坐标原点在圆(x －m )2＋(y ＋m )2＝4的内部，则实数m 的取值范围是( )A ．(－1,1)B ．(－3，3)C ．(－2，2) D.⎝⎛⎭⎫－22，22 C [∵原点(0,0)在圆(x －m )2＋(y ＋m )2＝4的内部，∴(0－m )2＋(0＋m )2＜4，解得－2＜m ＜2，故选C.]6．(2021·江西新余一中)若圆C 与y 轴相切于点P (0,1)，与x 轴的正半轴交于A ，B 两点，且|AB |＝2，则圆C 的标准方程是( )A ．(x ＋2)2＋(y ＋1)2＝2B ．(x ＋1)2＋(y ＋2)2＝2C ．(x －2)2＋(y －1)2＝2D ．(x －1)2＋(y －2)2＝2C [设线段AB 的中点为D ，则|AD |＝|CD |＝1，∴r ＝|AC |＝2＝|CP |，故C (2，1)，故圆C 的标准方程是(x －2)2＋(y －1)2＝2，故选C.]7．(2021·湖北名校联考)圆(x －3)2＋(y －1)2＝5关于直线y ＝－x 对称的圆的方程为( )A ．(x ＋3)2＋(y －1)2＝5B ．(x －1)2＋(y －3)2＝5C ．(x ＋1)2＋(y ＋3)2＝5D ．(x －1)2＋(y ＋3)2＝5C [由题意知，所求圆的圆心坐标为(－1，－3)，所以所求圆的方程为(x ＋1)2＋(y ＋3)2＝5，故选C.]8．(2019·北京卷)设抛物线y 2＝4x 的焦点为F ，准线为l ，则以F 为圆心，且与l 相切的圆的方程为________．[解析] ∵抛物线y ＝4x 的焦点F 的坐标为(1,0)，准线l 为直线x ＝－1，∴圆的圆心坐标为(1,0)．又∵圆与l 相线，∴圆心到l 的距离为圆的半径，∴r ＝2.∴圆的方程为(x －1)2＋y 2＝4.[答案] (x －1)2＋y 2＝49.若圆C 经过坐标原点和点(4,0)，且与直线y ＝1相切，则圆C 的方程是 ________ .[解析] 由已知可设圆心为(2，b )，由22＋b 2＝(1－b )2＝r 2，得b ＝－32，r 2＝254. 故圆C 的方程为(x －2)2＋⎝⎛⎭⎫y ＋322＝254. [答案] (x －2)2＋⎝⎛⎭⎫y ＋322＝25410．已知点P 是圆(x ＋3)2＋(y －1)2＝2上的动点，点Q (2,2)，O 为坐标原点，则△OPQ 面积的最小值是 ________ .[解析] 因为|OQ |＝22，直线OQ 的方程为y ＝x ，圆心(－3,1)到直线OQ 的距离为d ＝|－3－1|2＝22，所以圆上的动点P 到直线OQ 的距离的最小值为22－2＝2，所以△OPQ 面积的最小值为12×22×2＝2. [答案] 211．已知点P (－2，－3)，圆C ：(x －4)2＋(y －2)2＝9，过点P 作圆C 的两条切线，切点为A ，B ，则过P 、A 、B 三点的圆的方程为________．[解析] 易知圆C 的圆心为C (4,2)，连接AC 、BC ，由题意知P A ⊥AC ，PB ⊥BC ， 所以P ，A ，B ，C 四点共圆，连接PC ，则所求圆的圆心O ′为PC 的中点，所以O ′⎝⎛⎭⎫1，－12， 所以所求圆的半径r ′＝(1＋2)2＋⎝⎛⎭⎫－12＋32＝614. 所以过P ，A ，B 三点的圆的方程为(x －1)2＋⎝⎛⎭⎫y ＋122＝614. [答案] (x －1)2＋⎝⎛⎭⎫y ＋12＝61412．已知以点P 为圆心的圆经过点A (－1,0)和B (3,4)，线段AB 的垂直平分线交圆P 于点C 和D ，且|CD |＝410.(1)求直线CD 的方程；(2)求圆P 的方程．[解] (1)直线AB 的斜率k ＝1，AB 的中点坐标为(1,2)，∴直线CD 的方程为y －2＝－(x －1)，即x ＋y －3＝0.(2)设圆心P (a ，b )，则由P 在CD 上得a ＋b －3＝0.①又直径|CD |＝410，∴|P A |＝210.∴(a ＋1)2＋b 2＝40.②由①②解得⎩⎪⎨⎪⎧ a ＝－3b ＝6或⎩⎪⎨⎪⎧a ＝5b ＝－2， ∴圆心P (－3,6)或P (5，－2)，∴圆P 的方程为(x ＋3)2＋(y －6)2＝40或(x －5)2＋(y ＋2)2＝40.B 级 能力提升13．(2021·海南联考)抛物线y ＝x 2－2x －3与坐标轴的交点在同一圆上，则由交点确定的圆的方程为( )A ．x 2＋(y －1)2＝4B ．(x －1)2＋(y －1)2＝4C ．(x －1)2＋y 2＝4D ．(x －1)2＋(y ＋1)2＝5D [抛物线y ＝x 2－2x －3关于直线x ＝1对称，与坐标轴的交点为A (－1,0)，B (3,0)，C (0，－3)，设圆心为M (1，b )，半径为r ，则|MA |2＝|MC |2＝r 2，即4＋b 2＝1＋(b ＋3)2＝r 2，解得b ＝－1，r ＝5，∴由交点确定的圆的方程为(x －1)2＋(y ＋1)2＝5，故选D.]14．(2021·江西赣州模拟)已知动点A (x A ，y A )在直线l ：y ＝6－x 上，动点B 在圆C ：x 2＋y 2－2x －2y －2＝0上，若∠CAB ＝30°，则x A 的最大值为( )A ．2B ．4C ．5D ．6C [由题意可知，当AB 是圆的切线时，∠CAB 最大，此时|CA |＝4，点A 的坐标满足(x －1)2＋(y －1)2＝16，与y ＝6－x 联立，解得x ＝5或x ＝1，∴点A 的横坐标的最大值为5.故选C.]15．(2019·浙江卷)已知圆C 的圆心坐标是(0，m )，半径长是r .若直线2x －y ＋3＝0与圆C 相切于点A (－2，－1)，则m ＝ ________ ，r ＝ ________ .[解析] 根据题意画出图形，可知 A (－2，－1)，C (0，m )，B (0,3)，则|AB |＝(－2－0)2＋(－1－3)2＝25，|AC |＝(－2－0)2＋(－1－m )2＝4＋(m ＋1)2，|BC |＝|m －3|.∵直线2x －y ＋3＝0与圆C 相切于点A ，∴∠BAC ＝90°，∴|AB |2＋|AC |2＝|BC |2. 即20＋4＋(m ＋1)2＝(m －3)2，解得m ＝－2.因此r ＝|AC |＝4＋(－2＋1)2＝ 5.[答案] －2 516．在平面直角坐标系xOy 中，曲线Γ：y ＝x 2－mx ＋2m (m ∈R )与x 轴交于不同的两点A ，B ，曲线Γ与y 轴交于点C .(1)是否存在以AB 为直径的圆过点C ？若存在，求出该圆的方程；若不存在，请说明理由．(2)求证：过A ，B ，C 三点的圆过定点．[解] 由曲线Γ：y ＝x 2－mx ＋2m (m ∈R )，令y ＝0，得x 2－mx ＋2m ＝0.设A (x 1,0)，B (x 2,0)，则可得Δ＝m 2－8m ＞0，x 1＋x 2＝m ，x 1x 2＝2m .令x ＝0，得y ＝2m ，即C (0,2m )．(1)若存在以AB 为直径的圆过点C ，则AC →·BC →＝0，得x 1x 2＋4m 2＝0，即2m ＋4m 2＝0，所以m ＝0或m ＝－12. 由Δ＞0得m ＜0或m ＞8，所以m ＝－12， 此时C (0，－1)，AB 的中点M ⎝⎛⎭⎫－14，0即圆心，半径r ＝|CM |＝174，故所求圆的方程为⎝⎛⎭⎫x ＋142＋y 2＝1716. (2)证明：设过A ，B 两点的圆的方程为x 2＋y 2－mx ＋Ey ＋2m ＝0，将点C (0,2m )代入可得E ＝－1－2m ，所以过A ，B ，C 三点的圆的方程为x 2＋y 2－mx －(1＋2m )y ＋2m ＝0，整理得x 2＋y 2－y －m (x ＋2y －2)＝0.令⎩⎪⎨⎪⎧ x 2＋y 2－y ＝0，x ＋2y －2＝0，可得⎩⎪⎨⎪⎧ x ＝0，y ＝1或⎩⎨⎧ x ＝25，y ＝45， 故过A ，B ，C 三点的圆过定点(0,1)和⎝⎛⎭⎫25，45.。

第4章第2讲一、选择题1．函数f(x)＝1－xe x的单调递增区间是( )A．(－∞，－1) B．(－1,0)C．(0,1) D．(－1，＋∞)[解析] f′(x)＝－e x－xe x＝－e x(1＋x)>0，得x<－1，选A.[答案] A2．函数f(x)＝x3＋ax－3在区间(1，＋∞)内是增函数，则实数a的取值范围是( ) A．[3，＋∞) B．[－3，＋∞)C．(－3，＋∞) D．(－∞，－3)[解析] f′(x)＝3x2＋a，令f′(x)≥0,3x2＋a≥0a≥－3x2(x∈(1，＋∞))∴a≥－3 选B.[答案] B3．函数y＝f(x)的图象过原点且它的导函数y＝f′(x)的图象如图所示的一条直线，则y ＝f(x)图象的顶点在( )A．第Ⅰ象限B．第Ⅱ象限C．第Ⅲ象限D．第Ⅳ象限[解析] y＝f′(x)的图象是与坐标轴不平行的直线，所以y＝f(x)是二次函数，直线与x轴正半轴相交，它在交点左边的函数值大于0(f′(x)>0)在交点右边，f′(x)<0，函数y＝f(x)图象过原点．所以y＝f(x)图象顶点在第Ⅰ象限，开口向下，选A.[答案] A4．已知f(x)＝x3－ax在[1，＋∞)上是单调增函数，则a的最大值是( )A．0 B．1C．2 D．3[解析] f ′(x )＝3x 2－a ，由已知可得f ′(x )＝3x 2－a ≥0在[1，＋∞)上恒成立，即a ≤3x 2恒成立，故选D.[答案] D5．(·广东高考题)设a ∈R ，若函数y ＝e ax＋3x ，x ∈R 有大于零的极值点，则( ) A ．a ＞－3 B ．a ＜－3 C ．a ＞－13D ．a ＜－13[解析] f ′(x )＝3＋ae ax，若函数在x ∈R 上有大于零的极值点，即f ′(x )＝3＋ae ax＝0有正根．当有f ′(x )＝3＋ae ax＝0成立时，显然有a ＜0，此时x ＝1a ln(－3a)，由x ＞0我们马上就能得到参数a 的范围为a ＜－3.[答案] B6．(·湖北高考题)若f (x )＝－12x 2＋b ln(x ＋2)在(－1，＋∞)上是减函数，则b 的取值范围是( )A ．[－1，＋∞)B ．(－1，＋∞)C ．(－∞，－1]D ．(－∞，－1)[解析] f ′(x )＝－x ＋b x ＋2，又由题意可知，当x ＞－1时恒有f ′(x )＜0，即－x ＋bx ＋2＜0，即b ＜x (x ＋2)．而当x ＞－1时，y ＝x (x ＋2)递增，∴y ＞－1，故b ≤－1.[答案] C 二、填空题7．f ′(x )是f (x )＝13x 3＋2x ＋1的导函数，则f ′(－1)的值是________．[答案] 38．函数f (x )＝x ln x (x ＞0)的单调递增区间是________． [答案] [1e，＋∞)9．若函数f (x )＝x 3＋bx 2＋cx ＋d 的单调递减区间为[－1,2]，则b ＝________，c ＝________.[解析] 因为f ′(x )＝3x 2＋2bx ＋c ，由题设知－1<x <2是不等式3x 2＋2bx ＋c <0的解集，所以－1,2是方程3x 2＋2bx ＋c ＝0的两个根，由根与系数的关系得b ＝－32，c ＝－6.[答案] b ＝－32，c ＝－610．已知函数f (x )是R 上的偶函数，且在(0，＋∞)上有f ′(x )＞0，若f (－1)＝0，那么关于x的不等式xf(x)＜0的解集是________．[解析] 由题意知，f(x)在(0，＋∞)上单调递增，又f(－1)＝0，f(x)为偶函数，所发当－1＜x＜0或0＜x＜1时，f(x)＜0；当x＜－1或x＞1时，f(x)＞0.故不等式xf(x)＜0的解集为(－∞，－1)∪(0,1)．[答案] (－∞，－1)∪(0,1)三、解答题11．(·陕西卷)已知函数f(x)＝x3－3ax－1，a≠0(1)求f(x)的单调区间；(2)若f(x)在x＝－1处取得极值，直线y＝my与y＝f(x)的图象有三个不同的交点，求m 的取值范围．[解] (1)f′(x)＝3x2－3a＝3(x2－a)，当a＜0时，对x∈R，有f′(x)＞0，当a＜0时，f(x)的单调增区间为(－∞，＋∞)当a＞0时，由f′(x)＞0解得x＜－a或x＞a；由f′(x)＜0解得－a＜x＜a，当a＞0时，f(x)的单调增区间为(－∞，－a)，(a，＋∞)；f(x)的单调减区间为(－a，a)．(2)因为f(x)在x＝－1处取得极大值，所以f′(－1)＝3×(－1)2－3a＝0，∴a＝1.所以f(x)＝x3－3x－1，f′(x)＝3x2－3，由f′(x)＝0解得x1＝－1，x2＝1.由(1)中f(x)的单调性可知，f(x)在x＝－1处取得极大值f(－1)＝1，在x＝1处取得极小值f(1)＝－3.因为直线y＝m与函数y＝f(x)的图象有三个不同的交点，又f(－3)＝－19＜－3，f(3)＝17＞1，结合f(x)的单调性可知，m的取值范围是(－3,1)．12．(·北京)已知函数f(x)＝x3＋ax2＋3bx＋c(b≠0)，且g(x)＝f(x)－2是奇函数．(1)求a，c的值；(2)求函数f(x)的单调区间．[解] (1)因为函数g(x)＝f(x)－2为奇函数，所以，对任意的x∈R，g(－x)＝－g(x)，即f(－x)－2＝－f(x)＋2.又f(x)＝x3＋ax2＋3bx＋c所以－x3＋ax2－3bx＋c－2＝－x3－ax2－3bx－c＋2.所以⎩⎪⎨⎪⎧a ＝－a ，c －2＝－c ＋2.解得a ＝0，c ＝2.(2)由(1)得f (x )＝x 3＋3bx ＋2. 所以f ′(x )＝3x 2＋3b (b ≠0)．当b ＜0时，由f ′(x )＝0得x ＝±－b .x 变化时，f ′(x )的变化情况如下表：递减，在(－b ，＋∞)上单调递增．当b ＞0时，f ′(x )＞0，所以函数f (x )在(－∞，＋∞)上单调递增．亲爱的同学请写上你的学习心得。

高考数学一轮复习 42课时作业一、选择题1．(2010·重庆卷，文)在等差数列{a n }中，a 1＋a 9＝10，则a 5的值为( ) A ．5 B ．6 C ．8 D ．10答案 A解析 依题意得a 1＋a 9＝2a 5＝10，a 5＝5，选A.2．在等差数列{a n }中，a 2＋a 6＝3π2，则sin(2a 4－π3)＝( )A.32 B.12 C ．－32D ．－12答案 D解析 ∵a 2＋a 6＝3π2，∴2a 4＝3π2，∴sin(2a 4－π3)＝sin(3π2－π3)＝－cos π3＝－12，选D.3．(2011·合肥质检)设S n 是等差数列{a n }的前n 项和，若a 4＝9，S 3＝15，则数列{a n }的通项a n ＝( )A ．2n －3B ．2n －1C ．2n ＋1D ．2n ＋3答案 C解析 由⎩⎪⎨⎪⎧a 4＝9S 3＝15⇒⎩⎪⎨⎪⎧a 1＋3d ＝93a 1＋3d ＝15⇒⎩⎪⎨⎪⎧a 1＝3d ＝2，所以通项a n ＝2n ＋1.4．等差数列{a n }的前n 项和为S n ，已知a m －1＋a m ＋1－2a 2m ＝0，S 2m －1＝39，则m ＝( ) A ．38 B ．39 C ．20 D ．19答案 C解析 ∵a m －1＋a m ＋1＝2a 2m 又∵a m －1＋a m ＋1＝2a m ∴a m ＝1或0(舍去) ∵S 2m －1＝2m －1a 1＋a 2m －12＝(2m －1)a m∴(2m －1)a m ＝39，∴2m －1＝39 ∴m ＝20.5．设{a n }是公差为正数的等差数列，若a 1＋a 2＋a 3＝15，a 1a 2a 3＝80，则a 11＋a 12＋a 13＝( ) A ．120 B ．105 C ．90 D ．75答案 B解析 设公差为d 且d >0.由已知⎩⎪⎨⎪⎧a 1＋a 2＋a 3＝15a 1a 2a 3＝80，得⎩⎪⎨⎪⎧a 1＋d ＝5a 1a 1＋d a 1＋2d ＝80.解得a 1＝2，d ＝3(∵d >0)．∴a 11＋a 12＋a 13＝3a 12＝3(a 1＋11d )＝1056．若两个等差数列{a n }和{b n }的前n 项和分别是S n ，T n ，已知S n T n ＝7n n ＋3，则a 5b 5等于( )A ．7 B.23 C.278D.214答案 D解析 a 5b 5＝2a 52b 5＝a 1＋a 9b 1＋b 9＝92a 1＋a 992b 1＋b 9＝S 9T 9＝214. 7．等差数列{a n }的前n 项和为S n ，且S 3＝6，a 3＝4，则公差d 等于( ) A ．1 B.53 C ．2 D ．3答案 C解析 由⎩⎪⎨⎪⎧3a 1＋42＝6a 1＋2d ＝4，解得d ＝2.二、填空题8．已知S n 是等差数列{a n }的前n 项和，且a 4＝15，S 5＝55，则过点P (3，a 3)、Q (4，a 4)的直线的斜率是________．解析 设数列{a n }的公差为d ，则依题意，得⎩⎪⎨⎪⎧a 4＝a 1＋3d ＝15S 5＝5a 1＋10d ＝55⇒⎩⎪⎨⎪⎧a 1＝3d ＝4，故直线PQ 的斜率为a 4－a 34－3＝d1＝4.9．已知数列{a n }中，a 3＝2，a 5＝1，若{11＋a n}是等差数列，则a 11＝________. 答案 0解析 记b n ＝11＋a n ，则b 3＝13，b 5＝12，数列{b n }的公差为12×(12－13)＝112，b 1＝16，∴b n ＝n ＋112，即11＋a n ＝n ＋112，∴a n ＝11－nn ＋1，故a 11＝0. 10．等差数列{a n }中，S n 是其前n 项和，a 1＝－2010，S 20092009－S 20072007＝2，则S 2010的值为________．答案 －2010解析 在等差数列{a n }中，设公差为d ，则S n n＝na 1＋n2n －1dn＝a 1＋d 2(n －1)，∴S 20092009－S 20072007＝a 1＋d 2×2008－a 1－d2×2006＝d ＝2，∴S 2010＝－2010×2010＋2010×20092×2＝－2010×2010＋2010×2009＝－2010.11．方程(x 2－x ＋m )(x 2－x ＋n )＝0有四个不等实根，且组成一个公差为12的等差数列，则mn 的值为________．答案 －15256解析 设四个根组成的等差数列为x 1，x 2，x 3，x 4，根据等差数列的性质，则有x 1＋x 4＝x 2＋x 3＝1∴2x 1＋3d ＝1，又d ＝12，∴x 1＝－14∴x 2＝14，x 3＝34，x 4＝54∴mn ＝(x 1x 4)(x 2x 3)＝－1525612．(2010·浙江卷，文)在如下数表中，已知每行、每列中的数都成等差数列，那么位于表中的第n 行第n ＋1列的数是________． 答案 n 2＋n解析 第n 行的第一个数是n ，第n 行的数构成以n 为公差的等差数列，则其第n ＋1项为n ＋n ·n ＝n 2＋n .13．(2010·苏北四市调研)已知数列{a n }共有m 项，记{a n }的所有项和为S (1)，第二项及以后所有项和为S (2)，第三项及以后所有项和为S (3)，…，第n 项及以后所有项和为S (n )，若S (n )是首项为1，公差为2的等差数列的前n 项和，则当n <m 时，a n ＝________.答案 －2n －1解析 由题意得S (n )＝a n ＋…＋a m ＝n ×1＋n n －12×2＝n 2，当n <m 时，S (n ＋1)＝a n ＋1＋…＋a m ＝(n ＋1)2.故a n ＝S (n )－S (n ＋1)＝n 2－(n ＋1)2＝－2n －1.三、解答题14．在编号为1～9的九个盒子中，共放有351粒米，已知每个盒子都比前一号盒子多放同样粒数的米．(1)如果1号盒子内放了11粒米，那么后面的盒子比它前一号的盒子多放几粒米？ (2)如果3号盒子内放了23粒米，那么后面的盒子比它前一号的盒子多放几米粒？ 答案 (1)7 (2)8解析 1～9号的九个盒子中米的粒数依次组成等差数列{a n } (1)a 1＝11，S 9＝351，求得：d ＝7 (2)a 3＝23，S 9＝351，求得：d ＝815．(2010·浙江卷，文)设a 1，d 为实数，首项为a 1，公差为d 的等差数列{a n }的前n 项和为S n ，满足S 5S 6＋15＝0.(1)若S 5＝5，求S 6及a 1； (2)求d 的取值范围．解析 (1)由题意知S 6＝－15S 5＝－3，a 6＝S 6－S 5＝－8，所以⎩⎪⎨⎪⎧5a 1＋10d ＝5，a 1＋5d ＝－8.解得a 1＝7，所以S 6＝－3，a 1＝7.(2)因为S 5S 6＋15＝0，所以(5a 1＋10d )(6a 1＋15d )＋15＝0， 即2a 21＋9da 1＋10d 2＋1＝0， 故(4a 1＋9d )2＝d 2－8，所以d 2≥8. 故d 的取值范围为d ≤－22或d ≥2 2.16．设等差数列{a n }的首项a 1及公差d 都为整数，前n 项和为S n . (1)若a 11＝0，S 14＝98，求数列{a n }的通项公式；(2)若a 1≥6，a 11>0，S 14≤77，求所有可能的数列{a n }的通项公式．答案 (1)a n ＝22－2n (2)a n ＝12－n 和a n ＝13－n解 (1)由S 14＝98得2a 1＋13d ＝14， 又a 11＝a 1＋10d ＝0，故解得d ＝－2，a 1＝20. 因此{a n }的通项公式是a n ＝22－2n ，n ＝1,2,3，….(2)由⎩⎪⎨⎪⎧S 14≤77a 11>0a 1≥6，得⎩⎪⎨⎪⎧2a 1＋13d ≤11a 1＋10d >0a 1≥6，即⎩⎪⎨⎪⎧2a 1＋13d ≤11 ①－2a 1－20d <0， ②－2a 1≤－12 ③由①＋②得－7d <11，即d >－117.由①＋③得13d ≤－1， 即d ≤－113.于是－117<d ≤－113.又d ∈Z ，故d ＝－1.④ 将④代入①②得10<a 1≤12. 又a 1∈Z ，故a 1＝11或a 1＝12. 所以所有可能的数列{a n }的通项公式是a n ＝12－n 和a n ＝13－n ，n ＝1,2,3，….。

课时作业(四十二) 一元二次不等式及其解法A 级1．不等式x －1x ＋2＜0的解集为( ) A ．(1，＋∞) B ．(－∞，－2)C ．(－2,1)D ．(－∞，－2)∪(1，＋∞)2．不等式(x －1)x ＋2≥0的解集是( ) A ．{x |x ＞1}B ．{x |x ≥1}C ．{x |x ≥1或x ＝－2}D ．{x |x ≥－2且x ≠－1}3．(2012·济宁模拟)设函数f (x )＝x m＋ax 的导函数f ′(x )＝2x ＋1，则不等式f (－x )＜6的解集是( )A ．{x |－2＜x ＜3}B ．{x |－3＜x ＜2}C ．{x |x ＞3或x ＜－2}D ．{x |x ＞2或x ＜－3}4．(2012·长春模拟)不等式组⎩⎪⎨⎪⎧x －1＞a2x －4＜2a 有解，则实数a 的取值范围是( )A ．(－1,3)B ．(－∞，－1)∪(3，＋∞)C ．(－3,1)D ．(－∞，－3)∪(1，＋∞)5．(2012·长沙模拟)已知二次函数f (x )＝ax 2－(a ＋2)x ＋1(a ∈Z )，且函数f (x )在(－2，－1)上恰有一个零点，则不等式f (x )＞1的解集为( )A ．(－∞，－1)∪(0，＋∞)B ．(－∞，0)∪(1，＋∞)C ．(－1,0)D ．(0,1)6．(2012·长春模拟)已知不等式x 2＋ax ＋4＜0的解集不是空集，则实数a 的取值范围是________．7．不等式|x －2|－|x －1|＞0的解集为________．8．若关于x 的不等式ax 2－6x ＋a 2＜0的解集为(1，m )，则实数m ＝________. 9．某商家一月份至五月份累计销售额达3 860万元，预测六月份销售额为500万元，七月份销售额比六月份递增x %，八月份销售额比七月份递增x %，九、十月份销售总额与七、八月份销售总额相等，若一月至十月份销售总额至少达7 000万元，则x 的最小值是________．10．已知二次函数y ＝x 2＋px ＋q ，当y ＜0时，有－12＜x ＜13，解不等式qx 2＋px ＋1＞0.11．行驶中的汽车，在刹车时由于惯性作用，要继续往前滑行一段距离才能停下，这段距离叫做刹车距离．在某种路面上，某种型号汽车的刹车距离s (m)与汽车的车速v (km/h)满足下列关系：s ＝nv 100＋v 2400(n 为常数，且n ∈N )，做了两次刹车试验，有关试验数据如图所示，其中⎩⎪⎨⎪⎧6＜s 1＜814＜s 2＜17，(1)求n 的值；(2)要使刹车距离不超过12.6 m ，则行驶的最大速度是多少？B 级1．已知函数f(x)＝－x2＋ax＋b2－b＋1(a∈R，b∈R)，对任意实数x都有f(1－x)＝f(1＋x)成立，若当x∈[－1，1]时，f(x)＞0恒成立，则b的取值范围是( ) A．－1＜b＜0 B．b＞2C．b＜－1或b＞2 D．不能确定2．若关于x的不等式x2＋12x－⎝⎛⎭⎪⎫12n≥0对任意n∈N*在x∈(－∞，λ]上恒成立，则实常数λ的取值范围是________．3．已知函数f(x)＝mx2－mx－1.(1)若对于x∈R，f(x)＜0恒成立，求实数m的取值范围；(2)若对于x∈[1,3]，f(x)＜5－m恒成立，求实数m的取值范围．详解答案课时作业(四十二)A 级1．C 原不等式化为(x－1)(x＋2)＜0，解得－2＜x＜1，∴原不等式的解集为(－2,1)．2．C 由(x －1)x ＋2≥0，可知⎩⎪⎨⎪⎧x ＋2＞0，x －1≥0或x ＋2＝0，解得x ≥1或x ＝－2.3．A ∵f ′(x )＝2x ＋1，∴f (x )＝x 2＋x .又∵f (－x )＜6，∴(－x )2－x ＜6，即x 2－x －6＜0，解得－2＜x ＜3.4．A ∵⎩⎪⎨⎪⎧x －1＞a2x －4＜2a⇔⎩⎪⎨⎪⎧x ＞a 2＋1x ＜2a ＋4，由题意得a 2＋1＜2a ＋4，即a 2－2a －3＜0，解得－1＜a ＜3. 5．C ∵f (x )＝ax 2－(a ＋2)x ＋1，Δ＝(a ＋2)2－4a ＝a 2＋4＞0， ∴函数f (x )＝ax 2－(a ＋2)x ＋1必有两个不同的零点， 又f (x )在(－2，－1)上有一个零点，则f (－2)f (－1)＜0， ∴(6a ＋5)(2a ＋3)＜0，∴－32＜a ＜－56，又a ∈Z ，∴a ＝－1，不等式f (x )＞1即为－x 2－x ＞0，解得－1＜x ＜0. 6．解析： 由题意可得Δ＝a 2－16＞0，即a ＞4或a ＜－4. 答案： {a |a ＞4或a ＜－4}7．解析： 原不等式等价于|x －2|＞|x －1|，则(x －2)2＞(x －1)2，解得x ＜32.答案： ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＜32 8．解析： 由已知得1，m 是ax 2－6x ＋a 2＝0的两根，且a ＞0， ∴a 2＋a －6＝0，解得a ＝2或a ＝－3(舍)． 又1＋m ＝6a，∴m ＝2.答案： 29．解析： 由题意得，3 860＋500＋[500(1＋x %)＋500(1＋x %)2]×2≥7 000， 化简得(x %)2＋3·x %－0.64≥0， 解得x %≥0.2或x %≤－3.2(舍去)． ∴x ≥20，即x 的最小值为20. 答案： 2010．解析： 因为当y ＜0时，有－12＜x ＜13，所以x 1＝－12与x 2＝13是方程x 2＋px ＋q ＝0的两个实数根．由根与系数的关系得⎩⎪⎨⎪⎧13－12＝－p ，13×⎝ ⎛⎭⎪⎫－12＝q ，解得⎩⎪⎨⎪⎧p ＝16，q ＝－16，所以不等式qx 2＋px ＋1＞0⇔－16x 2＋16x ＋1＞0⇔x 2－x －6＜0，解得－2＜x ＜3，即不等式qx 2＋px ＋1＞0的解集为{x |－2＜x ＜3}． 11．解析： (1)依题意得⎩⎪⎨⎪⎧6＜40n 100＋1 600400＜814＜70n 100＋4 900400＜17，解得⎩⎪⎨⎪⎧5＜n ＜1052＜n ＜9514，又n ∈N ，所以n ＝6.(2)s ＝3v 50＋v 2400≤12.6⇒v 2＋24v －5 040≤0⇒－84≤v ≤60，因为v ≥0，所以0≤v ≤60，即行驶的最大速度为60 km/h.B 级1．C 由f (1－x )＝f (1＋x )知f (x )图象关于直线x ＝1对称，即a2＝1得a ＝2.又f (x )开口向下，所以当x ∈[－1,1]时，f (x )为增函数，∴f (x )min ＝f (－1)＝－1－2＋b 2－b ＋1＝b 2－b －2，f (x )＞0恒成立，即b 2－b －2＞0恒成立，解得b ＜－1或b ＞2.2．解析： 由题意得x 2＋12x ≥⎝ ⎛⎭⎪⎫12n max ＝12，∴x ≥12或x ≤－1.又x ∈(－∞，λ]，∴λ∈(－∞，－1]． 答案： (－∞，－1]3．解析： (1)由题意可得m ＝0或⎩⎪⎨⎪⎧m ＜0，Δ＝m 2＋4m ＜0⇔m ＝0或－4＜m ＜0⇔－4＜m ≤0. 故m 的取值范围为(－4,0]．(2)∵f (x )＜－m ＋5⇔m (x 2－x ＋1)＜6， ∵x 2－x ＋1＞0，∴m ＜6x 2－x ＋1对于x ∈[1,3]恒成立，记g (x )＝6x 2－x ＋1，x ∈[1,3]，记h (x )＝x 2－x ＋1，h (x )在x ∈[1,3]上为增函数．则g (x )在[1,3]上为减函数，∴[g (x )]min ＝g (3)＝67，∴m ＜67.所以m 的取值范围为⎝ ⎛⎭⎪⎫－∞，67.。

课时规范练42 椭圆及几何性质基础巩固组1.已知焦点坐标为(0，-4)，(0，4)，且过点(0，-6)的椭圆方程为()A.x236+y220=1 B.x220+y236=1C.x236+y216=1 D.x216+y236=12.(2020广东深圳外国语学校高三考试)已知椭圆x2a2+y2b2=1(a>b>0)的离心率为√53，椭圆上一点P到两焦点的距离之和为12，则椭圆的短轴长为()A.8B.6C.5D.43.(2020湖南长沙一中高三段考)已知P是椭圆上一点，F是椭圆的一个焦点，则以线段PF为直径的圆和以椭圆长轴为直径的圆的位置关系是()A.相离B.内切C.内含D.相交4.已知F1，F2为椭圆x2a2+y2b2=1(a>b>0)的两个焦点，B为椭圆短轴的一个端点，BF1⃗⃗⃗⃗⃗⃗⃗ ·BF2⃗⃗⃗⃗⃗⃗⃗ ≥14F1F2⃗⃗⃗⃗⃗⃗⃗⃗ 2，则椭圆的离心率的取值范围为()A.0，12B.0，√22C.0，√33D.(12,1)5.(多选)如图所示，“嫦娥一号”探月卫星沿地月转移轨道飞向月球，在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行，最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行，若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距，用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长，下列式子中正确的是()A.a1+c1=a2+c2B.a1-c1=a2-c2C.c1a2>a1c2D.c1a1<c2a26.已知椭圆C:x2a2+y2b2=1(a>b>0)的右焦点为F(1，0)，点F关于直线y=bx的对称点Q在椭圆C上，则离心率e=，S△FOQ=.7.(2019全国3，理15)设F1，F2为椭圆C:x236+y220=1的两个焦点，M为C上一点且在第一象限.若△MF1F2为等腰三角形，则M的坐标为.综合提升组8.(2019全国1，理10)已知椭圆C的焦点为F1(-1，0)，F2(1，0)，过F2的直线与C交于A，B两点.若|AF2|=2|F2B|，|AB|=|BF1|，则C的方程为()A.x22+y2=1 B.x23+y22=1C.x24+y23=1 D.x25+y24=19.已知椭圆x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1，F2，P是椭圆上一点，△PF1F2是以F2P为底边的等腰三角形，且60°<∠PF1F2<120°，则该椭圆的离心率的取值范围是()A.(√3-12,1) B.(√3-12,12)C.(12,1) D.(0,12)10.(2020福建福州模拟)已知F1，F2为椭圆x24+y2=1的左、右焦点，P为椭圆上异于顶点的任意一点，K为△F1PF2内切圆的圆心，过点F1作F1M⊥PK于点M，O为坐标原点，则|OM|的取值范围为.创新应用组11.(2020江西八校联考)已知椭圆E:x2a2+y2b2=1(a>b>0)，F1，F2为其左、右焦点，B1，B2为其上、下顶点，四边形F1B1F2B2的面积为2，P为椭圆E上任意一点，以P为圆心的圆(记为圆P)总经过坐标原点O.(1)求椭圆E的长轴A1A2的长的最小值，并确定此时椭圆E的方程.(2)对于(1)中确定的椭圆E，若给定圆F1:(x+1)2+y2=3，则圆P和圆F1的公共弦MN的长是否为定值?若是，求|MN|的值;若不是，请说明理由.参考答案课时规范练42 椭圆及几何性质1.B 由题意，椭圆焦点坐标为(0，-4)，(0，4)，可得椭圆的焦点在y 轴，且c=4，又由过点(0，-6)，则a=6，所以b 2=a 2-c 2=62-42=20，所以椭圆的标准方程为x 220+y 236=1.故选B . 2.A 椭圆x 2a2+y 2b 2=1(a>b>0)的离心率e=ca=√53，椭圆上一点P 到两焦点距离之和为12，即2a=12，则a=6，c=2√5，所以b=√a 2-c 2=√36-20=4，则椭圆短轴长为2b=8.故选A . 3.B 不妨设椭圆的方程为x 2a2+y 2b 2=1(a>b>0)，F ，F'分别是椭圆的左右焦点，作出以线段PF 为直径的圆和以长轴为直径的圆x 2+y 2=a 2，如图所示.设PF 中点为M ，连接PF'，∴OM 是△PFF'的中位线，∴|OM|=12|PF'|，即两圆的圆心距为12|PF'|，根据椭圆定义，可得|PF|+|PF'|=2a ，∴圆心距|OM|=12|PF'|=12(2a-|PF|)=a-12|PF|，即两圆的圆心距等于它们半径之差，∴以PF 为直径的圆与以椭圆长轴为直径的圆的位置关系是内切.故选B . 4.C 由椭圆定义可知|BF 1|=|BF 2|=a ，|OF 1|=|OF 2|=c ，则sin ∠OBF 1=ca =e ，所以cos ∠F 1BF 2=1-2sin 2∠OBF 1=1-2e 2，因为BF 1⃗⃗⃗⃗⃗⃗⃗ ·BF 2⃗⃗⃗⃗⃗⃗⃗ ≥14F 1F 2⃗⃗⃗⃗⃗⃗⃗⃗ 2，即(1-2e 2)a 2≥c 2，(1-2e 2)≥e 2， 即e 2≤13.所以0<e ≤√33.故选C .5.BC 由题图可知a 1>a 2，c 1>c 2，∴a 1+c 1>a 2+c 2，∴A 不正确;∵a 1-c 1=|PF|，a 2-c 2=|PF|， ∴a 1-c 1=a 2-c 2，B 正确;由a 1+c 2=a 2+c 1，可得(a 1+c 2)2=(a 2+c 1)2，a 12−c 12+2a 1c 2=a 22−c 22+2a 2c 1， 即b 12+2a 1c 2=b 22+2a 2c 1，∵b 1>b 2，∴a 2c 1>a 1c 2，C 正确; 可得c 1a 1>c 2a 2，D 不正确.故选BC .6.√22 12 设点Q (x ，y )，则由点Q 与椭圆的右焦点F (1，0)关于直线y=bx 对称得{yx -1=-1b ,y 2=b ·x+12,解得{x =1-b 21+b 2,y =2b 1+b 2,代入椭圆C 的方程得(1-b 2)2a 2(1+b 2)2+4b 2b 2(1+b 2)2=1，结合a 2=b 2+1解得{a =√2,b =1,则椭圆的离心率e=ca =√22，S △FOQ =12|OF|·|2b 1+b 2|=12×1×21+12=12.7.(3，√15) ∵a 2=36，b 2=20，∴c 2=a 2-b 2=16，∴c=4. 由题意得，|MF 1|=|F 1F 2|=2c=8. ∵|MF 1|+|MF 2|=2a=12， ∴|MF 2|=4.设点M 的坐标为(x 0，y 0)(x 0>0，y 0>0)，则S △MF 1F 2=12×|F 1F 2|×y 0=4y 0.又S △MF 1F 2=12×4×√82-22=4√15，∴4y 0=4√15，解得y 0=√15.又点M 在椭圆C 上， ∴x 0236+(√15)220=1，解得x 0=3或x 0=-3(舍去). ∴点M 的坐标为(3，√15). 8.B 如图，由已知可设|F 2B|=n ，|BF 1|=m.由|AB|=|BF 1|，则|AF 2|=m-n ，|AB|=m.又|AF 1|+|AF 2|=|BF 1|+|BF 2|，故|AF 1|=2n. 由椭圆的定义及|AF 2|=2|F 2B|，得{m -n =2n ,m +n =2a ,解得{m =3a2,n =a 2.∴|AF 1|=a ，|AF 2|=a.∴点A 为(0，-b ).∴k AF 2=b1=b.过点B 作x 轴的垂线，垂足为点P. 由题意可知△OAF 2∽△PBF 2. 又|AF 2|=2|F 2B|，∴|OF 2|=2|F 2P|. ∴|F 2P|=12. 又k AF 2=|BP ||F 2P |=|BP |12=b ，∴|BP|=12b.∴点B (32,12b).把点B 坐标代入椭圆方程x 2a 2+y 2b 2=1中，得a 2=3.又c=1，故b 2=2. 所以椭圆方程为x 23+y 22=1.9.B 由题意可得，|PF 2|2=|F 1F 2|2+|PF 1|2-2|F 1F 2|·|PF 1|cos ∠PF 1F 2=4c 2+4c 2-2·2c·2c·cos ∠PF 1F 2，即|PF 2|=2√2c ·√1F 2所以a=|PF 1|+|PF 2|2=c+√2c ·√1-cos∠PF 1F 2，又60°<∠PF 1F 2<120°，所以-12<cos ∠PF 1F 2<12，所以2c<a<(√3+1)c ，则√3+1<ca <12，即√3-12<e<12. 10.(0，√3) 如图，延长PF 2，F 1M 相交于点N ，∵K 是△F 1PF 2内切圆的圆心， ∴PK 平分∠F 1PF 2， ∵F 1M ⊥PK ，∴|PN|=|PF 1|，M 为F 1N 中点， ∵O 为F 1F 2中点，M 为F 1N 中点，∴|OM|=12|F 2N|=12||PN|-|PF 2||=12||PF 1|-|PF 2||<12|F 1F 2|=c=√3，∴|OM|的取值范围为(0，√3). 11.解(1)依题意四边形F 1B 1F 2B 2的面积为2bc ，所以2bc=2.因为|A 1A 2|=2a=2√b 2+c 2≥2√2bc =2√2，当且仅当b=c=1时，等号成立，此时a=√2， 所以长轴A 1A 2的长的最小值为2√2，此时椭圆E 的方程为x 22+y 2=1.(2)是定值.设点P (x 0，y 0)，则x 022+y 02=1，所以y 02=1-x 022. 圆P 的方程为(x-x 0)2+(y-y 0)2=x 02+y 02，即x 2+y 2-2x 0x-2y 0y=0，① 圆F 1的方程为(x+1)2+y 2=3，即x 2+y 2+2x-2=0， ②①-②得公共弦MN 所在直线的方程为(x 0+1)x+y 0y-1=0，所以点F 1到公共弦MN 所在直线的距离d=0√(x 0+1)+y 0=0√(x 0+1)+1-12x 0=0√12x 0+2x 0+2=√2，则|MN|=2√3-d 2=2，所以圆P 和圆F 1的公共弦MN 的长为定值2.。

课时规范练42空间向量及其运算一、基础巩固组1.已知空间四边形OABC中,=a,=b,=c,点M在OA上,且OM=2MA,N为BC中点,则=()A.a-b+cB.-a+b+cC.a+b-cD.a+b-c2.设一地球仪的球心为空间直角坐标系的原点O,球面上的两个点A,B的坐标分别为A(1,2,2),B(2,-2,1),则|AB|等于()A.18B.12C.3D.23.已知正方体ABCD-A1B1C1D1中,点E为上底面A1C1的中心,若+x+y,则x,y的值分别为()A.x=1,y=1B.x=1,y=C.x=,y=D.x=,y=14.向量a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),下列结论正确的是()A.a∥b,a∥cB.a∥b,a⊥cC.a∥c,a⊥bD.以上都不对5.A,B,C,D是空间不共面的四点,且满足=0,=0,=0,M为BC中点,则△AMD是()A.钝角三角形B.锐角三角形C.直角三角形D.不确定6.(2017浙江舟山模拟)平行六面体ABCD-A1B1C1D1中,向量两两的夹角均为60°,且||=1,||=2,||=3,则||等于()A.5B.6C.4D.87.已知空间向量a,b,满足|a|=|b|=1,且a,b的夹角为,O为空间直角坐标系的原点,点A,B满足=2a+b,=3a-b,则△OAB的面积为.8.在空间直角坐标系中,以点A(4,1,9),B(10,-1,6),C(x,4,3)为顶点的△ABC是以BC为斜边的等腰直角三角形,则实数x的值为.9.(2017宁夏银川模拟)已知点A(1,2,1),B(-1,3,4),D(1,1,1),若=2,则||的值是.10.如图,在棱长为a的正方体ABCD-A1B1C1D1中,G为△BC1D的重心,求证:(1)A1,G,C三点共线;(2)A1C⊥平面BC1D.〚导学号21500751〛二、综合提升组11.已知=(2,2,-2),=(1,y,z),若=(x-1,y,1),且BP⊥AB,则实数x,y,z分别为()A.5,-1,1B.1,1,-1C.-3,1,1D.4,1,-212.(2017安徽合肥质检)在长方体ABCD-A1B1C1D1中,AB=1,BC=2,AA1=3,点M是BC的中点,点P∈AC1,Q∈MD,则PQ长度的最小值为()A.1B.C.D.213.(2017内蒙古包头模拟)如图所示,PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos<>=,若以DA,DC,DP所在直线分别为x,y,z轴建立空间直角坐标系,则点E的坐标为.〚导学号21500752〛14.在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E,F分别是AB,PB的中点.(1)求证:EF⊥CD.(2)在平面PAD内是否存在一点G,使GF⊥平面PCB.若存在,求出点G坐标;若不存在,试说明理由.三、创新应用组15.如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E,F分别为AB,BC的中点.设异面直线EM与AF所成的角为θ,则cos θ的最大值为.16.如图所示的直三棱柱ABC-A1B1C1,在其底面三角形ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N 分别是A1B1,A1A的中点.(1)求的模;(2)求cos<>的值;(3)求证:A1B⊥C1M.〚导学号21500753〛课时规范练42空间向量及其运算1.B)-=-a+b+c.2.C|AB|=--=33.C如图,)=4.C因为c=(-4,-6,2)=2(-2,-3,1)=2a,所以a∥c.又a·b=(-2)×2+(-3)×0+1×4=0,所以a⊥b.5.C∵M为BC中点,).)=0.∴AM⊥AD,△AMD为直角三角形.6.A设=a,=b,=c,则=a+b+c,||2=a2+b2+c2+2a·b+2b·c+2c·a=25,因此||=5.7由=2a+b,=3a-b,得||=,||=-=(2a+b)·(3a-b)=∴cos∠BOA=,∴sin∠BOA=∴S△OAB=|||sin∠BOA=8.2由题意知=0,||=||=(6,-2,-3),=(x-4,3,-6),--解得x=2.-9设P(x,y,z),则=(x-1,y-2,z-1),=(-1-x,3-y,4-z).由=2,得点P坐标为-又D(1,1,1),∴||=10.证明(1))=)=)=,,即A1,G,C三点共线.(2)设=a,=b,=c,则|a|=|b|=|c|=a,且a·b=b·c=c·a=0.=a+b+c,=c-a,=(a+b+c)·(c-a)=c2-a2=0.因此,即CA1⊥BC1.同理CA1⊥BD.又BD与BC1是平面BC1D内的两条相交直线,故A1C⊥平面BC1D.11.B,=-,解得y=1,z=-1.∵BP⊥AB,∴2(x-1)+2y-2=0,解得x=1.12.C根据题意建立如图所示的空间直角坐标系,设P(x0,2x0,3-3x0),Q(x1,2-x1,3),x0∈[0,1],x1∈[0,1],所以PQ=------,当且仅当x 0= ,x 1= 时,PQ 取得最小值,即PQ min =13.(1,1,1)由已知得D (0,0,0),A (2,0,0),B (2,2,0),设P (0,0,a )(a>0),则E,所以 =(0,0,a ),-,||=a ,| |= -又cos <>= ,所以 -,解得a 2=4,即a=2,所以E (1,1,1).14.(1)证明如图,以DA ,DC ,DP 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,设AD=a ,则D (0,0,0),A (a ,0,0),B (a ,a ,0),C (0,a ,0),E,P (0,0,a ),F-=(0,a ,0). =0,, 即EF ⊥CD.(2)解假设存在满足条件的点G ,设G (x ,0,z ),则---,若使GF ⊥平面PCB , 则由 x-,- ,z- (a ,0,0)=a - =0,得x=由x- ,- ,z- (0,-a ,a )= +a -=0,得z=0. ∴点G 坐标为,即存在满足条件的点G ,且点G 为AD 的中点.15以A 为坐标原点,射线AB ,AD ,AQ 分别为x ,y ,z 轴的正半轴,建立如图所示的空间直角坐标系.设正方形ABCD 和ADPQ 的边长为2,则E (1,0,0),F (2,1,0),M (0,y ,2)(0≤y ≤2).所以=(2,1,0), =(-1,y ,2). 所以=-2+y ,| |= ,| |= 所以cos θ==令2-y=t,则y=2-t,且t∈[0,2].所以cosθ=-=-当t=0时,cosθ=0.当t≠0时,cosθ=-,=-由t∈(0,2],得,所以-所以0<cos,即cosθ的最大值为16.(1)解如图,建立空间直角坐标系.依题意得B(0,1,0),N(1,0,1),∴||=---=(2)解依题意得A1(1,0,2),B(0,1,0),C(0,0,0),B1(0,1,2),=(1,-1,2),=(0,1,2),=3,||=,||=∴cos<>==(3)证明依题意,得C1(0,0,2),M=(-1,1,-2),,=-+0=0.,∴A1B⊥C1M.。

温馨提示：此套题为Word版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，答案解析附后。

关闭Word文档返回原板块。

课时素养评价四十二事件的相互独立性(15分钟30分)1.若P(AB)=,P()=,P(B)=,则事件A与B的关系是( )A.事件A与B互斥B.事件A与B对立C.事件A与B相互独立D.事件A与B既互斥又独立【解析】选C.因为P()=,所以P(A)=,又P(B)=,P(AB)=,所以有P(AB)=P(A)P(B),所以事件A与B相互独立但不一定互斥.2.如图,在两个圆盘中,指针落在圆盘每个数所在区域的机会均等,那么两个指针同时落在奇数所在区域的概率是( )A. B. C. D.【解析】选A.题图中左边圆盘指针落在奇数区域的概率为=,题图中右边圆盘指针落在奇数区域的概率也为,所以两个指针同时落在奇数区域的概率为×=.【补偿训练】甲、乙两班各有36名同学,甲班有9名三好学生,乙班有6名三好学生,两班各派1名同学参加演讲活动,派出的恰好都是三好学生的概率是( ) A. B. C. D.【解析】选C.两班各自派出代表是相互独立事件,设事件A,B分别为甲班、乙班派出的是三好学生,则事件AB为两班派出的都是三好学生,则P(AB)=P(A)P(B)=×=.3.已知A,B是相互独立事件,若P(A)=0.2,P(AB+B+A)=0.44,则P(B)等于( )A.0.3B.0.4C.0.5D.0.6【解析】选A.因为A,B是相互独立事件,所以,B和A,均相互独立.因为P(A)=0.2,P(AB+B+A)=0.44,所以P(A)P(B)+P()P(B)+P(A)P()=0.44,所以0.2P(B)+0.8P(B)+0.2[1-P(B)]=0.44,解得P(B)=0.3.【补偿训练】已知A,B是两个相互独立事件,P(A),P(B)分别表示它们发生的概率,则1-P(A)P(B)是下列哪个事件的概率( ) A.事件A,B同时发生B.事件A,B至少有一个发生C.事件A,B至多有一个发生D.事件A,B都不发生【解析】选C.P(A)P(B)是指A,B同时发生的概率,1-P(A)P(B)是A,B不同时发生的概率,即至多有一个发生的概率.4.已知P(A)=0.3,P(B)=0.5,当事件A,B相互独立时,P(A∪B)=.【解析】因为A,B相互独立,所以P(AB)=P(A)·P(B),所以P(A∪B)=P(A)+P(B)-P(A)·P(B)=0.3+0.5-0.3×0.5=0.65.答案:0.655.甲袋中有8个白球、4个红球,乙袋中有6个白球、6个红球,从每袋中任取一球,则取到相同颜色的球的概率是.【解析】由题意知P=×+×=.答案:【补偿训练】荷花池中,有只青蛙在成“品”字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是.【解析】青蛙跳三次要回到A叶只有两条途径.第一条:按A→B→C→A,P1=××=;第二条:按A→C→B→A,P2=××=,所以跳三次之后停在A叶上的概率为P=P1+P2=+=.答案:6.一个家庭中有若干个小孩,假定生男孩和生女孩是等可能的,令A={一个家庭中既有男孩又有女孩},B={一个家庭中最多有一个女孩}.对下述两种情形,讨论A与B的独立性:(1)家庭中有两个小孩.(2)家庭中有三个小孩.【解析】(1)有两个小孩的家庭,男孩、女孩的可能情形为Ω={(男,男),(男,女),(女,男),(女,女)},它有4个基本事件,由等可能性知概率都为.这时A={(男,女),(女,男)},B={(男,男),(男,女),(女,男)},AB={(男,女),(女,男)},于是P(A)=,P(B)=,P(AB)=.由此可知,P(AB)≠P(A)P(B),所以事件A,B不相互独立.(2)有三个小孩的家庭,小孩为男孩、女孩的所有可能情形为Ω={(男,男,男),(男,男,女),(男,女,男),(男,女,女),(女,男,男),(女,男,女),(女,女,男),(女,女,女)}.由等可能性知这8个基本事件的概率均为,这时A中含有6个基本事件,B中含有4个基本事件,AB中含有3个基本事件.于是P(A)==,P(B)==,P(AB)=,显然有P(AB)==P(A)P(B)成立.从而事件A与B是相互独立的.(30分钟60分)一、单选题(每小题5分,共20分)1.设两个独立事件A和B都不发生的概率为,A发生B不发生的概率与B发生A不发生的概率相同,则事件A发生的概率P(A)是( ) A. B. C. D.【解析】选D.由P(A)=P(B),得P(A)P()=P(B)P(),即P(A)=P(B),又P()=,则P()=P()=.所以P(A)=.2.从甲袋中摸出一个红球的概率是,从乙袋中摸出一个红球的概率是,从两袋各摸出一个球,则等于( )A.2个球不都是红球的概率B.2个球都是红球的概率C.至少有1个红球的概率D.2个球中恰有1个红球的概率【解析】选C.分别记从甲、乙袋中摸出一个红球为事件A,B,则P(A)=,P(B)=,由于A,B相互独立,所以1-P()P()=1-×=.根据互斥事件可知C正确.3.甲、乙两队进行排球决赛,现在的情形是甲队只要再赢一局就获得冠军,乙队需要再赢两局才能得到冠军,若两队胜每局的概率相同,则甲队获得冠军的概率为( ) A. B. C. D.【解析】选D.设A i(i=1,2)表示继续比赛时,甲在第i局获胜,B事件表示甲队获得冠军.方法一:B=A1+A2,故P(B)=P(A1)+P()P(A2)=+×=.方法二:P(B)=1-P()=1-P()P()=1-×=.4.一个电路如图所示,A,B,C,D,E,F为6个开关,其闭合的概率都是,且是相互独立的,则灯亮的概率是( )A. B. C. D.【解析】选B.设A与B中至少有一个不闭合的事件为T,E与F中至少有一个不闭合的事件为R,则P(T)=P(R)=1-×=,所以灯亮的概率P=1-P(T)P(R)P(C)P(D)=.【补偿训练】某种开关在电路中闭合的概率为p,现将4只这种开关并联在某电路中(如图所示),若该电路为通路的概率为,则p= ( )A. B. C. D.【解析】选B.因为该电路为通路的概率为,所以该电路为不通路的概率为1-,只有当并联的4只开关同时不闭合时该电路不通路,所以1-=(1-p)4,解得p=或p=(舍去).二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错的得0分)5.分别抛掷两枚质地均匀的硬币,设事件A是“第一枚为正面”,事件B是“第二枚为正面”,事件C是“两枚结果相同”,则下列事件具有相互独立性的是( ) A.A与B B.A与CC.B与CD.都不具有独立性【解题指南】根据事件相互独立的定义判断,只要P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C)成立即可.【解析】选ABC.易知P(A)=0.5,P(B)=0.5,P(C)=0.5,P(AB)=0.25,P(AC)=0.25,P(BC)=0.25.可以验证P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C).所以根据事件相互独立的定义,事件A与B相互独立,事件B与C相互独立,事件A与C相互独立.6.某商场推出二次开奖活动,凡购买一定价值的商品可以获得一张奖券.奖券上有一个兑奖号码,可以分别参加两次抽奖方式相同的兑奖活动.如果两次兑奖活动的中奖概率都是0.05,则两次抽奖中( )A.都抽到某一指定号码的概率为0.05B.都没有抽到某一指定号码的概率为0.95C.恰有一次抽到某一指定号码的概率为0.095D.至少有一次抽到某一指定号码的概率为0.097 5【解析】选CD.记“第一次抽奖抽到某一指定号码”为事件A,“第二次抽奖抽到某一指定号码”为事件B,则“两次抽奖都抽到某一指定号码”就是事件AB.由于两次抽奖结果互不影响,因此A与B相互独立.于是由独立性可得,两次抽奖都抽到某一指定号码的概率P(AB)=P(A)P(B)=0.05×0.05=0.002 5.同理“两次抽奖都没有抽到某一指定号码”的概率P()=P()P()=0.95×0.95=0.902 5; “两次抽奖恰有一次抽到某一指定号码”可以用(A)∪(B)表示.由于事件A与B互斥,根据概率加法公式和相互独立事件的定义,所求的概率为P(A)+P(B)=P(A)P()+P()P(B)=0.05×(1-0.05)+(1-0.05)×0.05=0.095;“两次抽奖至少有一次抽到某一指定号码”可用(AB)∪(A)∪(B)表示.由于事件AB,A和B两两互斥,据概率加法公式和相互独立事件的定义,所求的概率为P(AB)+P(A)+P(B)=0.002 5+0.095=0.097 5.三、填空题(每小题5分,共10分)7.事件A,B,C相互独立,如果P(AB)=,P(C)=,P(AB)=,则P(B)= ,P(B)= .【解析】由题意可得解得P(A)=,P(B)=,P(C)=,所以P(B)=P()P(B)=×=.答案:8.水平相当的四人打麻将,彼此之间互不影响,也不受上局胜败的影响,甲连和4局的概率为,乙4局均不和的概率为.【解析】由题意,每局每人和牌的概率为,且相互独立,故甲连和4局的概率为=;每局每人不和牌的概率都是,且相互独立,故乙4局均不和的概率为=.答案:四、解答题(每小题10分,共20分)9.据大地保险公司统计,某地车主购买车损险的概率为0.5,购买第三者人身安全险的概率为0.6,购买两种保险相互独立,各车主间相互独立.(1)求一位车主同时购买车损险与第三者人身安全险保险的概率.(2)求一位车主购买第三者人身安全险但不购买车损险的概率.【解析】记A表示事件“购买车损险”,B表示事件“购买第三者人身安全险”,则由题意,得A与B,A与,与B,与都是相互独立事件,且P(A)=0.5,P(B)=0.6.(1)记C表示事件“同时购买两种保险”,则C=AB,所以P(C)=P(AB)=P(A)P(B)=0.5×0.6=0.3.(2)记D表示事件“购买第三者人身安全险但不购买车损险”,则D=B,所以P(D)=P(B)=P()P(B)=(1-0.5)×0.6=0.3.10.A,B是治疗同一种疾病的两种药,用若干试验组进行对比试验,每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效,若在一个试验组中,服用A有效的白鼠的只数比服用B有效的多,就称该试验组为甲类组.设每只小白鼠服用A有效的概率为,服用B有效的概率为.(1)求一个试验组为甲类组的概率.(2)观察3个试验组,求这3个试验组中至少有一个甲类组的概率.【解析】(1)设A i表示事件“一个试验组中,服用A有效的小白鼠有i只”,i=0,1,2.B i表示事件“一个试验组中,服用B有效的小白鼠有i只”,i=0,1,2.据题意有:P(A0)=×=,P(A1)=2××=,P(A2)=×=,P(B0)=×=,P(B1)=2××=.所求概率为P=P(B0A1)+P(B0A2)+P(B1A2)=×+×+×=.(2)所求概率P′=1-=.1.同学甲参加某科普知识竞赛,需回答三个问题,竞赛规则规定:答对第一、二、三个问题分别得100分、100分、200分,答错或不答均得零分.假设同学甲答对第一、二、三个问题的概率分别为0.8,0.6,0.5,且各题答对与否相互之间没有影响,则同学甲得分不低于300分的概率是.【解析】设“同学甲答对第i个题”为事件A i(i=1,2,3),则P(A1)=0.8,P(A2)=0.6,P(A3)=0.5,且A1,A2,A3相互独立,同学甲得分不低于300分对应于事件(A1A2A3)∪(A1A3)∪(A2A3)发生,故所求概率为P=P[(A1A2A3)∪(A1A3)∪(A2A3)]=P(A1A2A3)+P(A1A3)+P(A2A3)=P(A1)P(A2)P(A3)+P(A1)P()P(A3)+P()P(A2)P(A3)=0.8×0.6×0.5+0.8×0.4×0.5+0.2×0.6×0.5=0.46.答案:0.462.四人打麻将,老张最后手中牌除了一张6筒和一张一万外,其他都已成牌,他下一张牌会摸到是4筒或5筒.如果听坎5筒和牌的概率是20%,听4,7筒和牌的概率是40%.请计算老张这手牌和牌的概率.(手牌中已有6筒,如果再摸到4筒,此时听牌叫听坎5筒.手牌中有6筒,如果再摸到5筒,此时听牌叫听4,7筒.“筒”即“饼”,“坎”即顺子牌中间的一张.)【解析】有两种情况:(1)手中的牌有50%的概率摸到4筒,则打出一万,听坎5筒,有20%的概率和牌.摸到4筒与听坎5筒和牌相互独立,故和牌概率为:0.5×0.2=0.1.(2)手中牌有50%的概率摸到5筒,则打出一万,听4,7筒,有40%的概率和牌.摸到5筒与听4,7筒和牌相互独立,故和牌概率为:0.5×0.4=0.2.以上两种情况互斥,故老张这手牌和牌的概率为0.1+0.2=0.3.关闭Word文档返回原板块- 11 -。