高考数学一轮复习课时作业(四) 新人教版

2021年高考数学总复习高效课时作业X4-5-2 文新人教版制卷人：歐陽文化、歐陽理複；制卷時間：二O二二年二月七日一、选择题1．M＝a2＋b2，N＝ab＋a＋b－1，那么M、N的大小关系为( )A．M＞N B．M＜NC．M≥N D．M≤N解析：∵(a2＋b2)－(ab＋a＋b－1)＝a2＋b2－ab－a－b＋1＝12(2a2＋2b2－2ab－2a－2b＋2)＝12[(a2－2ab＋b2)＋(a2－2a＋1)＋(b2－2b＋1)]＝12[(a－b)2＋(a－1)2＋(b－1)2]≥0，∴a2＋b2≥ab＋a＋b－1，∴M≥N. 故应选C.答案：C2．假设a，b∈R＋，且a≠b，M＝ab＋ba，N＝a＋b，那么M与N的大小关系是( )A．M＞N B．M＜N C．M≥N D．M≤N解析：∵a≠b，∴ab＋b＞2a，ba＋a＞2b.∴ab＋b＋ba＋a＞2a＋2b，∴a b ＋b a ＞b ＋a . ∴M ＞N .故应选A.答案：A二、填空题3．设两个不相等的正数a 、b 满足a 3－b 3＝a 2－b 2，那么a ＋b 的取值范围是________． 解析：∵a 3－b 3＝a 2－b 2(a ≠b )，∴a 2＋ab ＋b 2＝a ＋b ，∴(a ＋b )2－ab ＝a ＋b ，∴ab ＝(a ＋b )2－(a ＋b )，又∵0＜ab ＜(a ＋b2)2， ∴0＜(a ＋b )2－(a ＋b )＜(a ＋b 2)2， 解之得1＜a ＋b ＜43. 答案：⎝ ⎛⎭⎪⎫1，43 4．假设log x y ＝－2，那么x ＋y 的最小值是________．解析：∵log x y ＝－2，∴y ＝1x2， ∴x ＋y ＝x ＋1x 2＝x 2＋x 2＋1x2 ≥3314＝3232. 答案：32325．设不等式x ＋y ≤a x ＋y 对一切x ＞0，y ＞0恒成立，务实数a 的最小值为________． 解析：原题即a ≥x ＋y x ＋y对一切x ＞0，y ＞0恒成立． 设A ＝x ＋y x ＋y， A 2＝x ＋y ＋2xy x ＋y ＝1＋2xy x ＋y≤2， 当x ＝y 时等号成立，∵A ＞0， ∴0＜A ≤ 2.即A 有最大值 2. ∴当a ≥2时，x ＋y ≤a x ＋y 对一切x ＞0，y ＞0成立．∴a 的最小值为 2.答案： 26．有以下四个不等式：①(x ＋1)(x ＋3)＞(x ＋2)2； ②ab －b 2＜a 2；③1|a |＋1＞0； ④a 2＋b 2≥2|ab |. 其中恒成立的为________(写出序号即可)．解析：∵(x ＋1)(x ＋3)－(x ＋2)2＝－1＜0，∴(x ＋1)(x ＋3)＜(x ＋2)2，①错．∵a 2－(ab －b 2)＝(a －b 2)2＋3b 24≥0， ∴ab －b 2≤a 2，②错．③显然成立．④由均值不等式，|a |2＋|b |2≥2|ab |，即a 2＋b 2≥2|ab |成立．答案：③④7．假设1a ＜1b＜0，那么以下四个结论 ①|a |＞|b |；②a ＋b ＜ab ；③b a ＋a b ＞2；④a 2b＜2a －b . 其中正确的选项是________．解析：∵1a ＜1b＜0，∴b ＜a ＜0， ∴－b ＞－a ＞0，∴|b |＞|a |，故①错误．∵b ＜a ＜0，显然②正确．又∵b a ＞0，a b ＞0，且b a ≠a b，∴③正确． 又∵a 2b －(2a －b )＝a 2b－2a ＋b ＝a 2－2ab ＋b 2b ＝〔a －b 〕2b＜0， ∴a 2b＜2a －b ，∴④正确． 答案：②③④8．设a ＞0，b ＞0，M ＝a ＋b a ＋b ＋2，N ＝a a ＋2＋b b ＋2，那么M 与N 的大小关系是________． 解析：∵a ＞0，b ＞0，∴N ＝a a ＋2＋b b ＋2＞a a ＋b ＋2＋ba ＋b ＋2 ＝a ＋b a ＋b ＋2＝M . ∴M ＜N .答案：M ＜N9．设x ，y ，z ∈R，假设x 2＋y 2＋z 2＝4，那么x －2y ＋2z 的最小值为________时，(x ，y ，z )＝________．解析：∵(x －2y ＋2z )2≤(x 2＋y 2＋z 2)[12＋(－2)2＋22]＝4×9＝36，∴x －2y ＋2z 最小值为－6，此时x 1＝y －2＝z 2. 又∵x 2＋y 2＋z 2＝4，∴x ＝－23，y ＝43，z ＝－43. 答案：－6 ⎝ ⎛⎭⎪⎫－23，43，－43 三、解答题10．求证：112＋122＋…＋1n 2<2(n ∈R *)． 证明：∵1k 2<1k 〔k －1〕＝1k －1－1k ， ∴112＋122＋…＋1 n 2<1＋(1－12)＋(12－13)＋…＋(1n －1－1n )＝1＋(1－1n )＝2－1n<2. 11．(2021年)函数f (x )＝|x －2|－|x －5|.(1)证明：－3≤f (x )≤3；(2)求不等式f (x )≥x 2－8x ＋15的解集．解析：(1)证明：f (x )＝|x －2|－|x －5|＝⎩⎪⎨⎪⎧－3，x ≤2，2x －7，2<x <5，3，x ≥5.当2<x <5时，－3<2x －7<3，所以－3≤f (x )≤3.(2)由(1)可知，当x ≤2时，f (x )≥x 2－8x ＋15的解集为空集；当2<x <5时，f (x )≥x 2－8x ＋15的解集为{x |5－3≤x <5}；当x ≥5时，f (x )≥x 2－8x ＋15的解集为{x |5≤x ≤6}．综上，不等式f (x )≥x 2－8x ＋15的解集为{x |5－3≤x ≤6}． 12．a ，b ，c 均为正数，证明：a 2＋b 2＋c 2＋⎝ ⎛⎭⎪⎫1a ＋1b ＋1c 2≥63，并确定a ，b ，c 为何值时，等号成立．证明：法一：因为a ，b ，c 均为正数，由均值不等式得a 2＋b 2＋c 2≥3(abc )23， ①1a ＋1b ＋1c ≥3(abc )－13， 所以⎝ ⎛⎭⎪⎫1a ＋1b ＋1c 2≥9(abc )－23. ② 故a 2＋b 2＋c 2＋⎝ ⎛⎭⎪⎫1a ＋1b ＋1c 2≥3(abc )23＋9(abc )－23. 又3(abc )23＋9(abc )－23≥227＝63， ③所以原不等式成立． 当且仅当a ＝b ＝c 时，①和②式等号成立．当且仅当3(abc )23＝9(abc )－23时，③式等号成立．即当且仅当a ＝b ＝c ＝314时，原式等号成立．法二：因为a ，b ，c 均为正数，由根本不等式得a 2＋b 2≥2ab ，b 2＋c 2≥2bc ，c 2＋a 2≥2ac .所以a 2＋b 2＋c 2≥ab ＋bc ＋ac ①同理1a 2＋1b 2＋1c 2≥1ab ＋1bc ＋1ac② 故a 2＋b 2＋c 2＋⎝ ⎛⎭⎪⎫1a ＋1b ＋1c 2 ≥ab ＋bc ＋ac ＋31bc ＋31ab ＋31ac ≥6 3. ③所以原不等式成立．当且仅当a ＝b ＝c 时，①式和②式等号成立，当且仅当a ＝b ＝c ，(ab )2＝(bc )2＝(ac )2＝3时，③式等号成立．即当且仅当a ＝b ＝c ＝314时，原式等号成立．制卷人：歐陽文化、歐陽理複；制卷時間：二O 二二年二月七日。

专题4.4 导数的综合应用（真题测试）一、单选题1．（2017·全国·高考真题（理））已知函数211()2()x x f x x x a e e --+=-++有唯一零点，则=a （ ） A ．12-B ．13C ．12D ．12．（2015·陕西·高考真题（理））对二次函数（为非零整数），四位同学分别给出下列结论，其中有且仅有一个结 论是错误的，则错误的结论是 A ．是的零点 B ．1是的极值点 C ．3是的极值D ．点在曲线上3．（2022·青海·海东市第一中学模拟预测（理））已知函数()2e 2xx f x a x =-+，若有且仅有两个正整数，使得()0f x <成立，则实数a 的取值范围是（ ） A ．211,3e e ⎡⎫⎪⎢⎣⎭B ．3291,5e e ⎡⎫⎪⎢⎣⎭C ．391,5e 3e ⎡⎫⎪⎢⎣⎭D ．212,2e e ⎡⎫⎪⎢⎣⎭4．（2014·全国·高考真题（文））已知函数，若存在唯一的零点，且，则的取值范围是（ ） A ．B ．C ．D ．5．（2022·青海·海东市第一中学模拟预测（理））若函数()()22e e x x f x x ax a a R =+-∈有三个不同的零点，则实数a 的取值范围是（ ） A ．1,e ⎛⎫+∞ ⎪⎝⎭B ．1,1e ⎛⎫ ⎪⎝⎭C ．2110,,1e e e ⎛⎫⎛⎫⋃ ⎪ ⎪-⎝⎭⎝⎭D ．210,e e ⎛⎫ ⎪-⎝⎭6．（2022·河南·开封市东信学校模拟预测（理））对任意0x >，不等式e ln()(1)0x ax a x -+-≥恒成立，则正数a 的最大值为（ ） ABC ．1eD ．e7．（2015·全国·高考真题（理））设函数()(21)xf x e x ax a =--+，其中1a < ，若存在唯一的整数0x ，使得2()f x ax bx c =++a 1-()f x ()f x ()f x (2,8)()y f x =32()31f x ax x =-+()f x 0x 00x >a ()2,+∞()1,+∞(),2-∞-(),1-∞-0()0f x <，则a 的取值范围是（ ）A ．3,12e ⎡⎫-⎪⎢⎣⎭B ．33,2e 4⎡⎫-⎪⎢⎣⎭ C ．33,2e 4⎡⎫⎪⎢⎣⎭ D ．3,12e ⎡⎫⎪⎢⎣⎭8．（2022·内蒙古·海拉尔第二中学模拟预测（理））已知函数()()e ln e (0)xf x a a a =+>，若对任意实数1x >，不等式()()ln 1f x x ≥-总成立，则实数a 的取值范围为（ ） A ．210,e ⎛⎫ ⎪⎝⎭B ．221,e e ⎛⎤⎥⎝⎦C ．21,e ⎛⎫+∞ ⎪⎝⎭D ．21,e ⎡⎫+∞⎪⎢⎣⎭二、多选题9．（2022·辽宁实验中学模拟预测）我们把形如(),,0f x y y '=的方程称为微分方程，符合方程的函数()y f x =称为微分方程的解，下列函数为微分方程0xy y xy +-'=的解的是（ ） A ．e x y = B ．e x y x =C ．e 1x y x =+D ．e (R)x y c x c =⋅∈⋅10．（2022·河北沧州·二模）已知实数,a b 满足e e e a b a b ++=，则（ ） A ．0ab < B ．1a b +> C ．e e 4a b +D ．e 1a b >11．（2022·湖南·模拟预测）已知1x >，1y >，且()()1e 11e y xx y ++=+，则下列结论一定正确的是（ ）A ．()ln 0x y ->B ．122x y +<C ．226x y +>D ．()ln ln3x y +<12．（2022·全国·高考真题）已知函数，则（ ）A ．有两个极值点B ．有三个零点C ．点是曲线的对称中心D ．直线是曲线的切线三、填空题13．（2020·河南高三其他（理））函数()2222ln x f x x e x ax =--，若0a =，则()f x 在[]1,2的最小值为_______；当0x >时，()1f x ≥恒成立，则a 的取值范围是_____. 14．（2022·全国·模拟预测（理））若曲线ln x y x =与212y kx =-仅有1个公共点，则k 的取值范围是3()1f x x x =-+()f x ()f x (0,1)()y f x =2y x =()y f x =___________.15．（2012·福建·高考真题（理））对于实数a 和b ，定义运算“*”： 设f （x ）=（2x -1）*（x -1），且关于x 的方程为f （x ）=m （m ∈R ）恰有三个互不相等的实数根x 1，x 2，x 3，则x 1x 2x 3的取值范围是_________________16．（2022·江苏·常州高级中学模拟预测）已知函数22()ln 2e f x x x mx =-+，若()0f x ≥的解集中恰有一个整数，则m 的取值范围为________． 四、解答题17．（2018·全国·高考真题（文））已知函数．（1）求曲线在点处的切线方程； （2）证明：当时，．18．（2017·全国·高考真题（理））已知函数（1）讨论的单调性；（2）若有两个零点，求的取值范围.19．（2017·全国·高考真题（文））已知函数.（1）讨论的单调性； （2）当时，证明. 20．（2016·全国·高考真题（文））设函数． （Ⅰ）讨论的单调性； （Ⅱ）证明当时，； （Ⅲ）设，证明当时，.21．（2015·全国·高考真题（理））设函数．（1）证明：在单调递减，在单调递增；（2）若对于任意，都有，求m 的取值范围．22．（2014·四川·高考真题（理））已知函数，其中，为自然对数的底数.（Ⅰ）设是函数的导函数，求函数在区间上的最小值；22,,a ab a ba b b ab a b ⎧-≠=⎨->⎩()21x ax x f x e +-=()y f x =()0,1-1a ≥()0f x e +≥()()2e 2e x xf x a a x =+--()f x ()f x a 2()ln (21)f x x ax a x =+++()f x 0a <3()24f x a≤--()ln 1f x x x =-+()f x (1,)x ∈+∞11ln x x x-<<1c >(0,1)x ∈1(1)xc x c +->2()e mx f x x mx =+-()f x (,0)-∞(0,)+∞12,[1,1]x x ∈-12|()()|1f x f x e -≤-2()1x f x e ax bx =---,a b R ∈ 2.71828e =()g x ()f x ()g x [0,1]（Ⅱ）若，函数在区间内有零点，求的取值范围(1)0f ()f x (0,1)a专题4.4 导数的综合应用（真题测试）一、单选题1．（2017·全国·高考真题（理））已知函数211()2()x x f x x x a e e --+=-++有唯一零点，则=a （ ） A ．12-B ．13C ．12D ．1【答案】C 【解析】 【分析】 【详解】因为()221111()2()1()1x x x x f x x x a e e x a e e --+--+=-++=-++-，设1t x =-，则()()()21t t f x g t t a e e -==++-，因为()()g t g t =-，所以函数()g t 为偶函数，若函数()f x 有唯一零点，则函数()g t 有唯一零点，根据偶函数的性质可知，只有当0=t 时，()0g t =才满足题意，即1x =是函数()f x 的唯一零点，所以210a -=，解得12a =.故选：C. 2．（2015·陕西·高考真题（理））对二次函数（为非零整数），四位同学分别给出下列结论，其中有且仅有一个结 论是错误的，则错误的结论是 A ．是的零点 B ．1是的极值点 C ．3是的极值 D ．点在曲线上【答案】A 【解析】 【详解】若选项A 错误时，选项B 、C 、D 正确，，因为是的极值点，是的极值，所以，即，解得：，因为点在曲线上，所以，即，解得：，所以，，所以，因为，所以不是的零点，所以选项A 错误，选项B 、C 、D 正确，故选A ．3．（2022·青海·海东市第一中学模拟预测（理））已知函数()2e 2xx f x a x =-+，若有且仅有两个正整2()f x ax bx c =++a 1-()f x ()f x ()f x (2,8)()y f x =()2f x ax b ='+1()f x 3()f x ()()10{13f f '==203a b a b c +=⎧⎨++=⎩2{3b a c a =-=+()2,8()y f x =()42238a a a +⨯-++=5a =10b =-8c =()25108f x x x =-+()()()21511018230f -=⨯--⨯-+=≠1-()f x数，使得()0f x <成立，则实数a 的取值范围是（ ） A ．211,3e e ⎡⎫⎪⎢⎣⎭B ．3291,5e e ⎡⎫⎪⎢⎣⎭C ．391,5e 3e ⎡⎫⎪⎢⎣⎭D ．212,2e e ⎡⎫⎪⎢⎣⎭【答案】C 【解析】 【分析】将()0f x <转化为2(2)exx a x +<，再分别求导分析2()e x x g x =和()(2)h x a x =+的图象，再分别求得1,1g ，()()2,2g ，()()3,3g 到()20-，的斜率，分析临界情况即可 【详解】由()0f x <且0x >，得2(2)exx a x +<，设2()e x x g x =，()(2)h x a x =+， 22()exx x g x '-=，已知函数()g x 在（0，2）上单调递增，在(2,)+∞上单调递减， 函数()(2)h x a x =+的图象过点(2,0)-，(1)11(2)3e g =--，2(2)12(2)e g =--，3(3)93(2)5e g =--，结合图象，因为329115e 3e e <<，所以3915e 3ea ≤<． 故选：C4．（2014·全国·高考真题（文））已知函数，若存在唯一的零点，且，则的取值范围是（ ） A ． B ． C ． D ．【答案】C 【解析】 【详解】试题分析：当时，，函数和，不满足题意，舍去；当时，，令，得或．时，；时，；时，，且，此时在必有零点，故不满足题意，舍去；当时，时，32()31f x ax x =-+()f x 0x 00x >a ()2,+∞()1,+∞(),2-∞-(),1-∞-0a =2()31f x x =-+()f x 0a >2()36f x ax x '=-()0f x '=0x =2x a =(,0)x ∈-∞()0f x '>2(0,)x a ∈()0f x '<2(,)x a∈+∞()0f x '>(0)0f >(,0)x ∈-∞0a <2(,)x a∈-∞；时，；时，，且，要使得存在唯一的零点，且，只需，即，则，选C ．5．（2022·青海·海东市第一中学模拟预测（理））若函数()()22e e x xf x x ax a a R =+-∈有三个不同的零点，则实数a 的取值范围是（ ） A ．1,e ⎛⎫+∞ ⎪⎝⎭B ．1,1e ⎛⎫ ⎪⎝⎭C ．2110,,1e e e ⎛⎫⎛⎫⋃ ⎪ ⎪-⎝⎭⎝⎭D ．210,e e ⎛⎫ ⎪-⎝⎭【答案】D 【解析】 【分析】令()0f x =得20e e x xx xa a ⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭，利用导数研究()e x x g x =的图像，由函数()f x 有三个零点可知，若令1e e xxt t ⎛⎫=≤ ⎪⎝⎭，则可知方程20t at a +-=的一根1t 必在10,e ⎛⎫ ⎪⎝⎭内，另一根21e t =或20t =或()2,0t ∈-∞上，分类讨论即可求解. 【详解】由22e e 0xxx ax a +-=得20e ex xx xa a ⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭，令()e x x g x =， 由()10e xxg x -'==，得1x ＝，因此函数()g x 在(),1-∞上单调递增，在()1,+∞上单调递减，且()00g =，当0x >时，()0e x x g x =>，则()ex xg x =的图像如图所示： 即函数()g x 的最大值为()11eg =，令1e e xx t t ⎛⎫=≤ ⎪⎝⎭，则()20h t t at a =+-=，由二次函数的图像可知，二次方程的一根1t 必在10,e ⎛⎫ ⎪⎝⎭内，另一根21e t =或20t =或()2,0t ∈-∞上，当21e t =时，21e ea =-，则另一根111e t =-，不满足题意，当20t =时，a ＝0，则另一根10t =，不满足题意，()0f x '<2(,0)x a ∈()0f x '>(0,)x ∈+∞()0f x '<(0)0f >()f x 0x 00x >2()0f a>24a >2a <-当()2,0t ∈-∞时，由二次函数()20h t t at a =+-=的图像可知22000110e e a a a a ⎧+⋅-<⎪⎨⎛⎫+⋅->⎪ ⎪⎝⎭⎩， 解得210e ea <<-， 则实数a 的取值范围是210,e e ⎛⎫ ⎪-⎝⎭，故选：D.6．（2022·河南·开封市东信学校模拟预测（理））对任意0x >，不等式e ln()(1)0x ax a x -+-≥恒成立，则正数a 的最大值为（ ） ABC ．1eD ．e【答案】D 【解析】 【分析】将不等式化为ln()e ln()e x ax x ax +≥+，构造()e x f x x =+有()(ln())f x f ax ≥，利用函数的单调性及参变分离法有e xa x ≤在0x >上恒成立，应用导数求右侧最小值，即可得结果.【详解】∵e ln()(1)0x ax a x -+-≥，∴ln()e ln()ln()e x ax x ax ax ax +≥+=+．令()e x f x x =+，则不等式化为()(ln())f x f ax ≥． ∵()e (0)x f x x x =+>为增函数，∴ln()x ax ≥，即e xa x≤．令e ()=x g x x ，则2(1)e ()x x g x x '-=，当01x <<时，()0g x '<，即()g x 递减；当1x >时，()0g x '>，即()g x 递增； 所以()()min 1e e g x g a ⇒≤==． ∴实数a 的最大值为e ． 故选：D7．（2015·全国·高考真题（理））设函数()(21)xf x e x ax a =--+，其中1a < ，若存在唯一的整数0x ，使得0()0f x <，则a 的取值范围是（ ）A ．3,12e ⎡⎫-⎪⎢⎣⎭B ．33,2e 4⎡⎫-⎪⎢⎣⎭C ．33,2e 4⎡⎫⎪⎢⎣⎭D ．3,12e ⎡⎫⎪⎢⎣⎭【答案】D 【解析】 【分析】设()()21xg x e x =-，()1y a x =-，问题转化为存在唯一的整数0x 使得满足()()01g x a x <-，求导可得出函数()y g x =的极值，数形结合可得()01a g ->=-且()312g a e-=-≥-，由此可得出实数a 的取值范围.【详解】设()()21xg x e x =-，()1y a x =-，由题意知，函数()y g x =在直线y ax a =-下方的图象中只有一个点的横坐标为整数，()()21x g x e x '=+，当12x <-时，()0g x '<；当12x >-时，()0g x '>.所以，函数()y g x =的最小值为12122g e -⎛⎫-=- ⎪⎝⎭.又()01g =-，()10g e =>.直线y ax a =-恒过定点()1,0且斜率为a ， 故()01a g ->=-且()31g a a e -=-≥--，解得312a e≤<，故选D.8．（2022·内蒙古·海拉尔第二中学模拟预测（理））已知函数()()e ln e (0)xf x a a a =+>，若对任意实数1x >，不等式()()ln 1f x x ≥-总成立，则实数a 的取值范围为（ ）A ．210,e ⎛⎫ ⎪⎝⎭B ．221,e e ⎛⎤⎥⎝⎦C ．21,e ⎛⎫+∞ ⎪⎝⎭D ．21,e ⎡⎫+∞⎪⎢⎣⎭【答案】D 【解析】 【分析】将所求不等式变形为()()ln 1ln eln eln 1x x ax a x -+++≥+-，构造函数()e xg x x =+，可知该函数在R 上为增函数，由此可得出()ln ln 1a x x ≥--，其中1x >，利用导数求出()()ln 1h x x x =--的最大值，即可求得实数a 的取值范围. 【详解】当1x >时，由()()ln 1f x x ≥-可得()ln eln 1ln 1x aa x +++≥-， 即()()()ln 1ln eln 1ln 1eln 1x x ax a x x x -+++≥-+-=+-，构造函数()e xg x x =+，其中x ∈R ，则()e 10x g x '=+>，所以，函数()g x 在R 上为增函数， 由()()ln 1ln eln eln 1x x ax a x -+++≥+-可得()()ln ln 1g x a g x +≥-⎡⎤⎣⎦，所以，()ln ln 1x a x +≥-，即()ln ln 1a x x ≥--，其中1x >， 令()()ln 1h x x x =--，其中1x >，则()12111xh x x x -'=-=--. 当12x <<时，()0h x '>，函数()h x 单调递增， 当2x >时，()0h x '<，函数()h x 单调递减， 所以，()()max ln 22a h x h ≥==-，21e a ∴≥. 故选：D.二、多选题9．（2022·辽宁实验中学模拟预测）我们把形如(),,0f x y y '=的方程称为微分方程，符合方程的函数()y f x =称为微分方程的解，下列函数为微分方程0xy y xy +-'=的解的是（ ） A ．e x y = B ．e x y x =C ．e 1x y x =+D ．e (R)x y c x c =⋅∈⋅【答案】CD 【解析】 【分析】根据导数的运算求得导函数y '，代入微分方程检验即可． 【详解】选项A ，e x y =，则e x y '=，e e e e 0x x x x xy y xy x x '+-=+-=≠，不是解；选项B ，e x y x =，e e x x y x '=+，22e e e e 0x x x x xy y xy x x x x '+-=+--=，是方程的解；选项C ，e 1x y x =+，e e x x y x '=+，22e e 1e e 10x x x x xy y xy x x x x x x '+-=+++--=+≠，不是方程的解； 选项D ，e (R)x y c x c =⋅∈⋅，e e x x y c cx '=+，22e e e e 0x x x x xy y xy cx cx cx cx '+-=+--=，是方程的解． 故选：CD ．10．（2022·河北沧州·二模）已知实数,a b 满足e e e a b a b ++=，则（ ） A ．0ab < B ．1a b +> C ．e e 4a b + D ．e 1a b >【答案】BCD 【解析】 【分析】A.由e e e a b a b ++=得到111e ea b +=判断；BC.由e e e 2e e a b a b a b ++==2b 判断；D. 由111e e a b +=，得到e e e 1e 11e 1e 1b b b ab b b b b -+-=-=--，令()e e 1,0b b f b b b =-+>，用导数法判断. 【详解】 由e e e a b a b ++=得111e ea b +=，又e 0,e 0a b >>，所以e 1,e 1a b >>，所以0,0a b >>，所以0ab >，选项A 错误；因为e e e 2e e a b a b a b ++==2b ，即e e e 4a b a b ++=，所以ln41a b +>，选项B C ,正确，因为111e e a b +=，所以e e e 1b ab =-，所以e e e 1e 11e 1e 1b b b a bbb b b -+-=-=--.令()e e 1,0b b f b b b =-+>，则()e 0b f b b '=>，所以f b 在区间()0,∞+上单调递增，所以()()00f b f >=，即e e 10b b b -+>，又e 10b ->，所以e 10a b ->，即e 1a b >，选项D 正确. 故选：BCD11．（2022·湖南·模拟预测）已知1x >，1y >，且()()1e 11e y xx y ++=+，则下列结论一定正确的是（ ）A ．()ln 0x y ->B ．122x y +<C ．226x y +>D ．()ln ln3x y +<【答案】AC 【解析】 【分析】构造函数()e xf x x=，利用导数判断函数的单调性，得出1x y >+，结合不等式以及指、对数函数的性质逐一判断即可. 【详解】令()e x f x x=，则()()2e 1e e xx x x x f x x x --'==， 所以当1x >时，()0f x '>，所以()f x 在()1,+∞上单调递增； 由()()1e 11e yxx y ++=+得1e e 111x y x y y +=+++，即1e e 111x y x y y +-=++，∵1y >，∴11012y <<+， ∴1e e 1012x y x y +<-<+，即()()1012f x f y <-+<， ∴1x y >+，即1->x y ，∴()ln 0x y ->，A 正确；由1x y >+知12x y +>+，所以12222x y y ++>>，所以选项B 错误； 由1x y >+知12222326x y y y y ++>+=⋅>，所以选项C 正确．由1x y >+，1y >知213x y y +>+>，所以()()ln ln 21ln3x y y +>+>， 所以D 错误，故选：AC ．12．（2022·全国·高考真题）已知函数，则（ ）A ．有两个极值点B ．有三个零点C ．点是曲线的对称中心D ．直线是曲线的切线【答案】AC 【解析】 【分析】利用极值点的定义可判断A ，结合的单调性、极值可判断B ，利用平移可判断C ；利用导数的几何意义3()1f x x x =-+()f x ()f x (0,1)()y f x =2y x =()y f x =()f x判断D. 【详解】由题，，令得或令得， 所以在上单调递减，在，上单调递增， 所以是极值点，故A 正确；因，，， 所以，函数在上有一个零点， 当时，，即函数在上无零点， 综上所述，函数有一个零点，故B 错误；令，该函数的定义域为，，则是奇函数，是的对称中心， 将的图象向上移动一个单位得到的图象， 所以点是曲线的对称中心，故C 正确；令，可得，又，当切点为时，切线方程为，当切点为时，切线方程为， 故D 错误.故选：AC.三、填空题13．（2020·河南高三其他（理））函数()2222ln x f x x e x ax =--，若0a =，则()f x 在[]1,2的最小值为_______；当0x >时，()1fx ≥恒成立，则a 的取值范围是_____.【答案】e (],1-∞ 【解析】当0a =时，∵()222ln x f x x ex =-，∴()222222x x f x xe x xe x'=+⋅-. 当1x >时，()0f x '>恒成立，()231f x x '=-()0fx '>x >x <()0f x '<x <()f x ((,-∞)+∞x =(10f =+>10f =>()250f -=-<()f x ,⎛-∞ ⎝⎭x ≥()0f x f ≥>⎝⎭()f x ⎫∞⎪⎪⎝⎭()f x 3()h x x x =-R ()()()()33h x x x x x h x -=---=-+=-()h x (0,0)()h x ()h x ()f x (0,1)()y f x =()2312f x x '=-=1x =±()(1)11f f =-=(1,1)21y x =-(1,1)-23y x =+∴()f x 在[]1,2上单调递增.∴()f x 在[]1,2上最小值为()1f e =.又0x >时，()1f x ≥恒成立，令 ()1xg x e x =--,()()100xg x e g ''=->=,所以()g x 在()0,∞+ 递增，()()00g x g >= 所以1x e x >+ ∴()22222ln 22ln 2ln x x x f x x e x ax e x ax +=--=--()2222ln 12ln 111x x x ax a x ≥++--=-+≥恒成立，∴1a ≤.故答案为e ；(],1-∞.14．（2022·全国·模拟预测（理））若曲线ln x y x =与212y kx =-仅有1个公共点，则k 的取值范围是___________. 【答案】(]1,02⎧⎫-∞⋃⎨⎬⎩⎭##1|02k k k ⎧⎫≤=⎨⎬⎩⎭或【解析】 【分析】将原问题转化为32ln 12x k x x =+只有一个解,令()()32ln 102x g x x x x =+>,利用导数求出()g x 的单调性及最值即可得答案. 【详解】 由题意可得:2ln 12x kx x =-只有一个解()0x >, 即32ln 12x k x x=+只有一个解. 令()32ln 12x g x x x=+, ()0x >原问题等价于y k =与()y g x =只有一个交点. 因为()43413ln 113ln x x xg x x x x '---=-= 因为13ln y x x =--在()0,∞+上单调递减, 且在1x =处的值为0 ,所以当()0,1x ∈时, ()()0,g x g x '>单调递增,当()1,x ∈+∞时, ()()0,g x g x '<单调递减且恒为正, 所以()()max 112g x g ==, 又因为y k =与()y g x =只有一个交点, 所以(]1,02k ⎧⎫∈-∞⎨⎬⎩⎭.故答案为: (]1,02⎧⎫-∞⋃⎨⎬⎩⎭.15．（2012·福建·高考真题（理））对于实数a 和b ，定义运算“*”： 设f （x ）=（2x -1）*（x -1），且关于x 的方程为f （x ）=m （m ∈R ）恰有三个互不相等的实数根x 1，x 2，x 3，则x 1x 2x 3的取值范围是_________________ 【答案】【解析】 【详解】由定义运算“*”可知 即，该函数图像如下：由，假设当关于x 的方程为f （x ）=m （m ∈R ）恰有三个互不相等的实数根时， m 的取值范围是，且满足方程，所以令则， 所以令22,,a ab a ba b b ab a b ⎧-≠=⎨->⎩⎫⎪⎪⎝⎭22(21)(21)(1)0()?(1)(21)(1)0x x x x f x x x x x ⎧----=⎨---->⎩2220()0x x x f x x x x ⎧-=⎨-+>⎩1124f ⎛⎫= ⎪⎝⎭1230x x x <<<10,4⎛⎫⎪⎝⎭23,x x 2-+=x x m 23=x x m 22-=x x m 1=x 123==x x x m 10,4⎛⎫=∈ ⎪⎝⎭y m所以， 又在递增的函数， 所以，所以，所以在递减， 则当时，；当时，所以.16．（2022·江苏·常州高级中学模拟预测）已知函数22()ln 2e f x x x mx =-+，若()0f x ≥的解集中恰有一个整数，则m 的取值范围为________．【答案】22ln 22e ,4e 2⎡⎫-⎪⎢⎣⎭【解析】【分析】由()0f x ≥且0x >，得出2ln 2e x x m x -+≥-，构造函数()ln =-xg x x，利用导数研究()g x 的单调性，画出()ln =-x g x x 和22e y x =-的大致图象，由图可知0m >，设0x 为()ln =-xg x x和22e y x m =-+的交点的横坐标，结合题意可知该整数为1，即012x ≤<，当直线22e y x m =-+过1,0A 和ln 22,2B ⎛⎫- ⎪⎝⎭时，即可求出求出m 的值，从而得出m 的取值范围.【详解】由题可知，22()ln 2e f x x x mx =-+，0x >， 由于()0f x ≥的解集中恰有一个整数，即22ln 2e 0x x mx -+≥，即222e ln x mx x -+≥-，因为0x >，所以2ln 2e xx m x-+≥-的解集中恰有一个整数， 令()ln =-x g x x ，则()2ln 1-'=x g x x ， 当1e x <<时，()0g x '<；当e x >时，()0g x '>， 所以()g x 在()1,e 上单调递减，在()e,+∞上单调递增， 画出()ln xy xg x ==-和22e y x =-的大致图象，如图所示： 要使得2ln 2e xx m x-+≥-，可知0m >， 114'⎛= ⎝y ()=h m 10,4⎛⎫⎪⎝⎭()()01>=h m h 0y '<=y 10,4⎛⎫ ⎪⎝⎭0m =0y =14m ==y 123⎫∈⎪⎪⎝⎭x x x设0x 为()ln =-xg x x和22e y x m =-+的交点的横坐标， 而2ln 2e xx m x-+≥-的解集中恰有一个整数，可知该整数为1，即012x ≤<， 当01x =时，得()10g =；当02x =时，得()ln 222g =-， 即1,0A ，ln 22,2B ⎛⎫- ⎪⎝⎭，当直线22e y x m =-+过点1,0A 时，得22e m =，当直线22e y x m =-+过点ln 22,2B ⎛⎫- ⎪⎝⎭时，得2ln 24e 2m =-， 所以m 的取值范围为22ln 22e ,4e 2⎡⎫-⎪⎢⎣⎭.故答案为：22ln 22e ,4e 2⎡⎫-⎪⎢⎣⎭四、解答题17．（2018·全国·高考真题（文））已知函数．（1）求曲线在点处的切线方程； （2）证明：当时，．【答案】（1）切线方程是（2）证明见解析 【解析】 【分析】（1）求导，由导数的几何意义求出切线方程．（2）当时，,令，只需证明即可．【详解】()21x ax x f x e +-=()y f x =()0,1-1a ≥()0f x e +≥210x y --=a 1≥()12f x e 1x x e x x e +-+≥++-（）12gx 1x e x x +=++-gx 0≥（1），．因此曲线在点处的切线方程是．（2）当时，．令，则，当时，，单调递减；当时，，单调递增； 所以 ．因此．18．（2017·全国·高考真题（理））已知函数（1）讨论的单调性；（2）若有两个零点，求的取值范围. 【答案】（1）见解析；（2）. 【解析】 【详解】试题分析：（1）讨论单调性，首先进行求导，发现式子特点后要及时进行因式分解，再对按，进行讨论，写出单调区间；（2）根据第（1）问，若，至多有一个零点.若，当时，取得最小值，求出最小值，根据，，进行讨论，可知当时有2个零点.易知在有一个零点；设正整数满足，则.由于，因此在有一个零点.从而可得的取值范围为.试题解析：（1）的定义域为，，（ⅰ）若，则，所以在单调递减. （ⅱ）若，则由得.当时，；当时，，所以在单调递减，在单调递增.（2）（ⅰ）若，由（1）知，至多有一个零点.（ⅱ）若，由（1）知，当时，取得最小值，最小值为. ()()2212xax a x f x e-++'-=()02f '=()y f x =()0,1-210x y --=1a ≥()()211x xf x e x x e e +-+≥+-+()211xg x x x e +=+-+()121x g x x e +=++'()120x g x e +''=+>1x <-()()10g x g '-'<=()g x 1x >-()()10g x g '-'>=()g x ()g x ()1=0g ≥-()0f x e +≥()()2e 2e x xf x a a x =+--()f x ()f x a (0,1)()f x a 0a ≤0a >0a ≤()f x 0a >ln x a =-()f x 1(ln )1ln f a a a-=-+1a =(1,)∈+∞a (0,1)a ∈(0,1)a ∈()f x (,ln )a -∞-0n 03ln(1)n a>-00000000()e (e 2)e 20n n n n f n a a n n n =+-->->->3ln(1)ln a a->-()f x (ln ,)a -+∞a (0,1)()f x (),-∞+∞()()()()2221121x x x xf x ae a e ae e =+---'=+0a ≤()0f x '<()f x (),-∞+∞0a >()0f x '=ln x a =-(),ln x a ∈-∞-()0f x '<()ln ,x a ∈-+∞()0f x '>()f x (),ln a -∞-()ln ,a -+∞0a ≤()f x 0a >ln x a =-()f x ()1ln 1ln f a a a-=-+①当时，由于，故只有一个零点； ②当时，由于，即，故没有零点； ③当时，，即. 又，故在有一个零点.设正整数满足，则.由于，因此在有一个零点. 综上，的取值范围为.19．（2017·全国·高考真题（文））已知函数.（1）讨论的单调性； （2）当时，证明. 【答案】（1）见解析；（2）见解析. 【解析】 【分析】（1）先求函数导数，再根据导函数符号的变化情况讨论单调性：当时，，则在单调递增；当时，在单调递增，在单调递减. （2）证明，即证，而，所以需证，设g （x ）=ln x -x +1 ，利用导数易得，即得证. 【详解】（1） 的定义域为（0，+），. 若a ≥0，则当x ∈（0，+）时，，故f （x ）在（0，+）单调递增.若a ＜0，则当时，时；当x ∈时，. 故f （x ）在单调递增，在单调递减. （2）由（1）知，当a ＜0时，f （x ）在取得最大值，最大值为. 1a =()ln 0f a -=()f x ()1,a ∈+∞11ln 0a a-+>()ln 0f a ->()f x ()0,1a ∈11ln 0a a-+<()ln 0f a -<()()4222e 2e 22e 20f a a ----=+-+>-+>()f x (),ln a -∞-0n 03ln 1n a ⎛⎫>- ⎪⎝⎭()()00000000e e 2e 20n n n nf n a a n n n =+-->->->3ln 1ln a a ⎛⎫->- ⎪⎝⎭()f x ()ln ,a -+∞a ()0,12()ln (21)f x x ax a x =+++()f x 0a <3()24f x a≤--(21)(1)'()(0)ax x f x x x++=>0a ≥'()0f x >()f x (0,)+∞0a <()f x 1(0,)2a -1(,)2a-+∞3()24f x a ≤--max 3()24f x a ≤--max 1()()2f x f a=-11ln()1022a a -++≤max ()(1)0g x g ==()f x ∞()()‘1211)22(1x ax f x ax a x x++=+++=∞’)(0f x ＞∞10,2x a ⎛⎫∈- ⎪⎝⎭()0f x '＞1()2a ∞-+，’)(0f x <’)(0f x ＞1()2a∞-+，12x a=-111()ln()1224f a a a -=---所以等价于，即. 设g （x ）=ln x -x +1，则. 当x ∈（0,1）时，；当x ∈（1，+）时，.所以g （x ）在（0,1）单调递增，在（1，+）单调递减.故当x =1时，g （x ）取得最大值，最大值为g （1）=0.所以当x ＞0时，g （x ）≤0.从而当a ＜0时，，即. 20．（2016·全国·高考真题（文））设函数．（Ⅰ）讨论的单调性； （Ⅱ）证明当时，； （Ⅲ）设，证明当时，.【答案】（Ⅰ）当时，单调递增；当时，单调递减；（Ⅱ）见解析；（Ⅲ）见解析． 【解析】 【详解】试题分析：（Ⅰ）首先求出导函数，然后通过解不等式或可确定函数的单调性；（Ⅱ）左端不等式可利用（Ⅰ）的结论证明，右端将左端的换为即可证明；（Ⅲ）变形所证不等式，构造新函数，然后通过利用导数研究函数的单调性来处理． 试题解析：（Ⅰ）由题设，的定义域为，，令，解得. 当时，，单调递增；当时，，单调递减. （Ⅱ）由（Ⅰ）知，在处取得最大值，最大值为. 所以当时，. 故当时，，，即. （Ⅲ）由题设，设，则，令，解得.当时，，单调递增；当时，，单调递减. 由（Ⅱ）知，，故，又，故当时，. 所以当时，.3()24f x a≤--113ln()12244a a a ---≤--11ln()1022a a -++≤’1(1)g x x=-()0g x '>∞()0g x '<∞11ln()1022a a -++≤3()24f x a≤--()ln 1f x x x =-+()f x (1,)x ∈+∞11ln x x x-<<1c >(0,1)x ∈1(1)xc x c +->01x <<()f x 1x >()f x ()f x '()0f x '>()0f x '<()f x x 1x()f x (0,)+∞1()1f x x=-'()0f x '=1x =01x <<()0f x '>()f x 1x >()0f x '<()f x ()f x 1x =(1)0f =1x ≠ln 1x x <-(1,)x ∈+∞ln 1x x <-11ln1x x <-11ln x x x-<<1c >()1(1)x g x c x c =+--'()1ln xg x c c c =--'()0g x =01lnln ln c c x c-=0x x <'()0g x >()g x 0x x >'()0g x <()g x 11ln c c c-<<001x <<(0)(1)0g g ==01x <<()0g x >(0,1)x ∈1(1)xc x c +->21．（2015·全国·高考真题（理））设函数．（1）证明：在单调递减，在单调递增；（2）若对于任意，都有，求m 的取值范围．【答案】（1）在单调递减，在单调递增；（2）.【解析】【详解】（Ⅰ）．若，则当时，，；当时，，．若，则当时，，；当时，，．所以，在单调递减，在单调递增．（Ⅱ）由（Ⅰ）知，对任意的，在单调递减，在单调递增，故在处取得最小值．所以对于任意，的充要条件是：即①，设函数，则．当时，；当时，．故在单调递减，在单调递增．又，，故当时，．当时，，，即①式成立．当时，由的单调性，，即；当时，，即．综上，的取值范围是．22．（2014·四川·高考真题（理））已知函数，其中，为自然对数的底数.（Ⅰ）设是函数的导函数，求函数在区间上的最小值；（Ⅱ）若，函数在区间内有零点，求的取值范围【答案】（Ⅰ）当时， ；当 时， ； 当时， .（Ⅱ） 的范围为. 【解析】【详解】试题分析：（Ⅰ）易得，再对分情况确定的单调区间，根据在上的单调性即可得在上的最小值.（Ⅱ）设为在区间内的一个零点，注意到2()e mx f x x mx =+-()f x (,0)-∞(0,)+∞12,[1,1]x x ∈-12|()()|1f x f x e -≤-()f x (,0)-∞(0,)+∞[1,1]-()(1)2mx f x m e x -'=+0m ≥(,0)x ∈-∞10mx e -≤()0f x '<(0,)x ∈+∞10mx e -≥()0f x '>0m <(,0)x ∈-∞10mx e ->()0f x '<(0,)x ∈+∞10mx e -<()0f x '>()f x (,0)-∞(0,)+∞m ()f x [1,0]-[0,1]()f x 0x =12,[1,1]x x ∈-12()()1f x f x e -≤-(1)(0)1,{(1)(0)1,f f e f f e -≤---≤-1,{1,m m e m e e m e --≤-+≤-()1t g t e t e =--+()1t g t e =-'0t <()0g t '<0t >()0g t '>()g t (,0)-∞(0,)+∞(1)0g =1(1)20g e e --=+-<[1,1]t ∈-()0g t ≤[1,1]m ∈-()0g m ≤()0g m -≤1m >()g t ()0g m >1m e m e ->-1m <-()0g m ->1m e m e -+>-m [1,1]-2()1x f x e ax bx =---,a b R ∈ 2.71828e =()g x ()f x ()g x [0,1](1)0f =()f x (0,1)a 12a ≤()(0)1g x g b ≥=-122e a <≤()22ln(2)g x a a a b ≥--2e a >()2g x e a b ≥--a ()2,1e -()2,()2x x g x e ax b g x e a -='=--a ()g x ()g x [0,1]()g x [0,1]0x ()f x (0,1).联系到函数的图象可知，导函数在区间内存在零点，在区间内存在零点，即在区间内至少有两个零点. 由（Ⅰ）可知，当及时，在内都不可能有两个零点.所以.此时，在上单调递减，在上单调递增，因此，且必有.由得：，代入这两个不等式即可得的取值范围.试题解答：（Ⅰ）①当时，，所以.②当时，由得.若，则；若，则. 所以当时，在上单调递增，所以. 当时，在上单调递减，在上单调递增，所以. 当时，在上单调递减，所以. （Ⅱ）设为在区间内的一个零点，则由可知，在区间上不可能单调递增，也不可能单调递减.则不可能恒为正，也不可能恒为负.故在区间内存在零点.同理在区间内存在零点.所以在区间内至少有两个零点.由（Ⅰ）知，当时，在上单调递增，故在内至多有一个零点. 当时，在上单调递减，故在内至多有一个零点. 所以. 此时，在上单调递减，在上单调递增，因此，必有.由得：，有(0)0,(1)0f f ==()g x 0(0,)x 1x ()g x 0(),1x 2x ()g x (0,1)12a ≤2e a ≥()g x (0,1)122e a <<()g x [0,ln 2]a [ln 2,1]a 12(0,ln(2)],(ln(2),1)x a x a ∈∈(0)10,(1)20g b g e a b =->=-->(1)10f e a b =---=1b e a =--a ()2,()2x xg x e ax b g x e a -='=--0a ≤()20x g x e a -'=>()(0)1g x g b ≥=-0a >()20x g x e a -'=>2,ln(2)x e a x a >>12a >ln(2)0a >2e a >ln(2)1a >102a <≤()g x [0,1]()(0)1g x g b ≥=-122e a <≤()g x [0,ln 2]a [ln 2,1]a ()(ln 2)22ln 2g x g a a a a b ≥=--2e a >()g x [0,1]()(1)2g x g e a b ≥=--0x ()f x (0,1)0(0)()0f f x ==()f x 0(0,)x ()g x ()g x 0(0,)x 1x ()g x 0(),1x 2x ()g x (0,1)12a ≤()g x [0,1]()g x (0,1)2e a ≥()g x [0,1]()g x (0,1)122e a <<()g x [0,ln 2]a [ln 2,1]a 12(0,ln(2)],(ln(2),1)x a x a ∈∈(0)10,(1)20g b g e a b =->=-->(1)10f e a b =---=12a b e +=-<.解得.当时，在区间内有最小值.若，则，从而在区间上单调递增，这与矛盾，所以.又，故此时在和内各只有一个零点和.由此可知在上单调递增，在上单调递减，在上单调递增.所以，，故在内有零点.综上可知，的取值范围是. (0)120,(1)210g b a e g e a b a =-=-+>=--=->21e a -<<21e a -<<()g x [0,1](ln(2))g a (ln(2))0g a ≥()0([0,1])g x x ≥∈()f x [0,1](0)(1)0f f ==(ln(2))0g a <(0)20,(1)10g a e g a =-+>=->()g x (0,ln(2))a (ln(2),1)a 1x 2x ()f x 1[0,]x 1(,x 2)x 2[,1]x 1()(0)0f x f >=2()(1)0f x f <=()f x 1(,x 2)x a (2,1)e -。

1 高考数学一轮复习课时检测 第四章 第四节 数系的扩充与复数的引入 理 一、选择题 1．(2011·广东高考)设复数z满足iz＝1，其中i为虚数单位，则z＝( ) A．－i B．i C．－1 D．1

解析：由iz＝1得z＝1i＝－i. 答案：A 2．(2012·宝鸡模拟)若复数z＝1＋i，i为虚数单位，则(1＋z)·z＝( ) A．1＋3i B．3＋3i C．3－i D．3 解析：∵(1＋z)·z＝z＋z2＝1＋i＋(1＋i)2＝1＋i＋2i＝1＋3i. 答案：A 3．(2011·江西高考)若(x－i)i＝y＋2i，x、y∈R，则复数 x＋yi＝( )

A．－2＋i B．2＋i C．1－2i D．1＋2i 解析：由题意得，xi＋1＝y＋2i，故x＝2，y＝1， 即x＋yi＝2＋i. 答案：B

4．已知f(x)＝x2，i是虚数单位，则在复平面中复数f1＋i3＋i对应的点在( ) A．第一象限 B．第二象限 C．第三象限 D．第四象限

解析：f(1＋i)＝(1＋i)2＝2i，∴f1＋i3＋i＝2i3＋i＝2＋6i10＝15＋35i，故对应点在第一象限． 答案：A 5．(2011·湖南高考)若a、b∈R，i为纯虚数单位，且(a＋i)i＝b＋i，则( ) A．a＝1，b＝1 B．a＝－1，b＝1 C．a＝1，b＝－1 D．a＝－1，b＝－1 解析：由(a＋i)i＝b＋i，得－1＋ai＝b＋i，根据两复数相等的充要条件得a＝1，b＝－1. 2

答案：C 6．(2012·荆州模拟)设i是虚数单位，复数1＋ai2－i为纯虚数，则实数a为( ) A．2 B．－2 C．－12 D.12

解析：法一：1＋ai2－i＝1＋ai2＋i2－i2＋i＝2－a＋2a＋1i5为纯虚数，所以2－a＝0，a＝2；

法二：1＋ai2－i＝ia－i2－i为纯虚数，所以a＝2. 答案：A 二、填空题

7．(2011·辽宁高考改编)i为虚数单位，1i＋1i3＋1i5＋1i7＝________.

第四章 三角函数、解三角形第一节任意角和弧度制及任意角的三角函数1．角的概念的推广(1)定义：角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形． (2)分类：①按旋转方向不同分为正角、负角、零角；②按终边位置不同分为象限角和轴线角．(3)终边相同的角❶：所有与角α终边相同的角，连同角α在内，可构成一个集合S ＝{β|β＝α＋2k π，k ∈Z}．2．弧度制的定义和公式(1)定义：把长度等于半径长的弧所对的圆心角叫做1弧度的角，弧度记作rad. (2)公式：(1)定义：设α是一个任意角，它的终边与单位圆交于点P (x ，y )，那么sin α＝y ，cos α＝x ，tan α＝yx (x ≠0)．(2)几何表示：三角函数线可以看作是三角函数的几何表示．正弦线的起点都在x 轴上，余弦线的起点都是原点，正切线的起点都是(1,0)．如图中有向线段MP ，OM ，AT 分别叫做角α的正弦线、余弦线和正切线❷.(3)三角函数值在各象限内的符号,(1)终边相同的角不一定相等．(2)“锐角”不等同于“第一象限的角”，锐角的集合为{α|0°＜α＜90°}，第一象限的角的集合为{α|k ·360°＜α＜k ·360°＋90°，k ∈Z}，小于90°的角包括锐角、负角、零角．(3)角的集合的表示形式不是唯一的，如⎩⎨⎧⎭⎬⎫α|α＝2k π＋π3，k ∈Z ＝⎩⎨⎧⎭⎬⎫β|β＝2k π＋7π3，k ∈Z . 当角α的终边与x 轴重合时，正弦线、正切线都变成一个点，此时角α的正弦值和正切值都为0；当角α的终边与y 轴重合时，余弦线变成一个点，正切线不存在，此时角α的余弦值为0，正切值不存在．[熟记常用结论]1．象限角2．轴线角3．若α∈⎝⎛⎭⎫0，π2，则tan α＞α＞sin α. [小题查验基础]一、判断题(对的打“√”，错的打“×”) (1)小于90°的角是锐角．( )(2)锐角是第一象限角，反之亦然．( )(3)相等的角终边一定相同，终边相同的角也一定相等．( ) (4)三角形的内角必是第一、二象限角．( ) 答案：(1)× (2)× (3)× (4)× 二、选填题1．下列与9π4的终边相同的角的表达式中正确的是( )A ．2k π＋45°(k ∈Z)B ．k ·360°＋94π(k ∈Z)C ．k ·360°－315°(k ∈Z)D ．k π＋5π4(k ∈Z) 解析：选C 由定义知终边相同的角中不能同时出现角度和弧度，应为π4＋2k π(k ∈Z)或k ·360°＋45°(k ∈Z)，结合选项知C 正确．2.若角α＝2 rad(rad 为弧度制单位)，则下列说法错误的是( ) A ．角α为第二象限角 B ．α＝⎝⎛⎭⎫360π°C ．sin α＞0D ．sin α＜cos α解析：选D 对于A ，∵π2＜α＜π，∴角α为第二象限角，故A 正确；对于B ，α＝2×⎝⎛⎭⎫180π°＝2 rad ，故B 正确；对于C ，sin α＞0，故C 正确；对于D ，sin α＞0，cos α＜0，故D 错误．选D.3．已知角α的终边与单位圆的交点P ⎝⎛⎭⎫x ，32，则tan α＝( ) A. 3 B ．±3 C.33D ．±33解析：选B 由|OP |2＝x 2＋34＝1，得x ＝±12.所以tan α＝yx＝±3.故选B.4．已知扇形的圆心角为60°，其弧长为2π，则此扇形的面积为________． 解析：设此扇形的半径为r ，由题意得π3r ＝2π，所以r ＝6，所以此扇形的面积为12×2π×6＝6π.答案：6π5．在0到2π范围内，与角－4π3终边相同的角是________． 解析：与角－4π3终边相同的角是2k π＋⎝⎛⎭⎫－4π3，k ∈Z ，令k ＝1，可得在0到2π范围内与角－4π3终边相同的角是2π3.答案：2π3考点一象限角及终边相同的角[基础自学过关][题组练透]1．设集合M ＝⎩⎨⎧⎭⎬⎫x |x ＝k 2·180°＋45°，k ∈Z ，N ＝⎩⎨⎧⎭⎬⎫x |x ＝k 4·180°＋45°，k ∈Z ，那么( )A ．M ＝NB ．M ⊆NC ．N ⊆MD ．M ∩N ＝∅解析：选B 由于M 中，x ＝k2·180°＋45°＝k ·90°＋45°＝(2k ＋1)·45°，2k ＋1是奇数；而N 中，x ＝k4·180°＋45°＝k ·45°＋45°＝(k ＋1)·45°，k ＋1是整数，因此必有M ⊆N .2．若角α是第二象限角，则α2是( )A ．第一象限角B ．第二象限角C ．第一或第三象限角D ．第二或第四象限角解析：选C ∵α是第二象限角， ∴π2＋2k π＜α＜π＋2k π，k ∈Z ， ∴π4＋k π＜α2＜π2＋k π，k ∈Z. 当k 为偶数时，α2是第一象限角；当k 为奇数时，α2是第三象限角．∴α2是第一或第三象限角． 3．集合⎩⎨⎧⎭⎬⎫α⎪⎪k π＋π4≤α≤k π＋π2，k ∈Z 中的角所表示的范围(阴影部分)是( )解析：选C 当k ＝2n (n ∈Z)时，2n π＋π4≤α≤2n π＋π2(n ∈Z)，此时α的终边和π4≤α≤π2的终边一样；当k ＝2n ＋1(n ∈Z)时，2n π＋π＋π4≤α≤2n π＋π＋π2(n ∈Z)，此时α的终边和π＋π4≤α≤π＋π2的终边一样，结合选项知选C.4．与－2 010°终边相同的最小正角是________．解析：因为－2 010°＝(－6)×360°＋150°，所以150°与－2 010°终边相同，又终边相同的两个角相差360°的整数倍，所以在0°～360°中只有150°与－2 010°终边相同，故与－2 010°终边相同的最小正角是150°.答案：150°5．终边在直线y ＝3x 上，且在[－2π，2π)内的角α的集合为______________________． 解析：如图，在平面直角坐标系中画出直线y ＝3x ，可以发现它与x轴的夹角是π3，在[0,2π)内，终边在直线y ＝3x 上的角有两个：π3，4π3；在[－2π，0)内满足条件的角有两个：－2π3，－5π3，故满足条件的角α构成的集合为⎩⎨⎧⎭⎬⎫－5π3，－2π3，π3，4π3.答案：⎩⎨⎧⎭⎬⎫－5π3，－2π3，π3，4π3[名师微点]1．判断象限角的2种方法 2.确定kα，αk (k ∈N *)的终边位置3步骤 (1)用终边相同角的形式表示出角α的范围； (2)再写出kα或αk 的范围；(3)然后根据k 的可能取值讨论确定kα或αk 的终边所在的位置．3．求终边在某直线上角的4个步骤(1)数形结合，在平面直角坐标系中画出该直线； (2)按逆时针方向写出[0,2π]内的角；(3)再由终边相同角的表示方法写出满足条件角的集合； (4)求并集化简集合．考点二扇形的弧长及面积公式的应用[师生共研过关][典例精析]已知扇形的圆心角是α，半径是r ，弧长为l . (1)若α＝100°，r ＝2，求扇形的面积；(2)若扇形的周长为20，求扇形面积的最大值，并求此时扇形圆心角的弧度数． [解] (1)因为α＝100°＝100×π180＝5π9， 所以S 扇形＝12lr ＝12αr 2＝12×5π9×4＝10π9.(2)由题意知，l ＋2r ＝20，即l ＝20－2r ， 故S 扇形＝12l ·r ＝12(20－2r )·r ＝－(r －5)2＋25，当r ＝5时，S 的最大值为25，此时l ＝10，则α＝lr＝2.[解题技法]有关弧长及扇形面积问题的注意点(1)利用扇形的弧长和面积公式解题时，要注意角的单位必须是弧度．(2)求扇形面积最大值的问题时，常转化为二次函数的最值问题，利用配方法使问题得到解决．(3)在解决弧长问题和扇形面积问题时，要合理地利用圆心角所在的三角形．[过关训练]1．已知2弧度的圆心角所对的弦长为2，那么这个圆心角所对的弧长是( ) A ．2 B ．sin 2 C.2sin 1D ．2sin 1解析：选C 如图，∠AOB ＝2弧度，过O 点作OC ⊥AB 于C ，并延长OC 交AB 于D .则∠AOD ＝∠BOD ＝1弧度， 且AC ＝12AB ＝1，在Rt △AOC 中，AO ＝AC sin ∠AOC ＝1sin 1，即r ＝1sin 1，从而AB 的长l ＝α·r ＝2sin 1. 2．若圆弧长度等于圆内接正三角形的边长，则其圆心角的弧度数为( ) A.π6 B.π3 C ．3D. 3解析：选D 如图，等边三角形ABC 是半径为r 的圆O 的内接三角形，则线段AB 所对的圆心角∠AOB ＝2π3，作OM ⊥AB ，垂足为M ，在Rt △AOM 中，AO ＝r ，∠AOM ＝π3，∴AM ＝32r ，AB ＝3r ， ∴l ＝3r ，由弧长公式得α＝l r ＝3rr ＝ 3.3．已知扇形的面积为2，扇形圆心角的弧度数是4，则扇形的周长为( ) A ．2 B ．4 C ．6D ．8解析：选C 设扇形的半径为r (r ＞0)，弧长为l ，则由扇形面积公式可得2＝12lr ＝12|α|r 2＝12×4×r 2，解得r ＝1，l ＝|α|r ＝4，所以所求扇形的周长为2r ＋l ＝6. 考点三三角函数的定义及应用[师生共研过关][典例精析](1)若sin αtan α＜0，且cos αtan α＜0，则角α是( )A ．第一象限角B ．第二象限角C ．第三象限角D ．第四象限角(2)(2019·广州模拟)在平面直角坐标系中，以x 轴的非负半轴为角的始边，角α，β的终边分别与单位圆交于点⎝⎛⎭⎫1213，513和⎝⎛⎭⎫－35，45，则sin(α＋β)＝( )A ．－3665 B.4865 C ．－313D.3365(3)已知角α的终边经过点P (－x ，－6)，且cos α＝－513，则1sin α＋1tan α＝________. [解析] (1)由sin αtan α＜0可知sin α，tan α异号， 则α为第二象限角或第三象限角． 由cos αtan α＜0可知cos α，tan α异号， 则α为第三象限角或第四象限角． 综上可知，α为第三象限角．(2)因为角α，β的终边分别与单位圆交于点⎝⎛⎭⎫1213，513和⎝⎛⎭⎫－35，45，所以sin α＝513，cos α＝1213，sin β＝45，cos β＝－35，所以sin(α＋β)＝sin αcos β＋cos αsin β＝513×⎝⎛⎭⎫－35＋1213×45＝3365. (3)因为角α的终边经过点P (－x ，－6)，且cos α＝－513， 所以cos α＝－xx 2＋36＝－513，解得x ＝52或x ＝－52(舍去)，所以P ⎝⎛⎭⎫－52，－6，所以sin α＝－1213， 所以tan α＝sin αcos α＝125，则1sin α＋1tan α＝－1312＋512＝－23. [答案] (1)C (2)D (3)－23[解题技法]利用三角函数定义解题的常见类型及方法(1)已知角α终边上一点P 的坐标求三角函数值．先求出点P 到原点的距离r ，然后利用三角函数定义求解．(2)已知角α的终边与单位圆的交点坐标求三角函数值．可直接根据三角函数线求解． (3)已知角α的终边所在的直线方程求三角函数值．先设出终边上一点的坐标，求出此点到原点的距离，然后利用三角函数定义求解相关问题，同时注意分类讨论．(4)判断三角函数值的符号问题．先判断角所在的象限，再根据各象限的符号规律判断．[过关训练]1．下列各选项中正确的是( ) A ．sin 300°＞0 B ．cos(－305°)＜0 C ．tan ⎝⎛⎭⎫－223π＞0 D ．sin 10＜0解析：选D 300°＝360°－60°，则300°是第四象限角，故sin 300°＜0；－305°＝－360°＋55°，则－305°是第一象限角，故cos(－305°)＞0；而－223π＝－8π＋2π3，所以－223π是第二象限角，故tan ⎝⎛⎭⎫－22π3＜0；因为3π＜10＜7π2，所以10是第三象限角，故sin 10＜0. 2．已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线y ＝2x 上，则cos 2θ＝( )A ．－45B ．－35C.35D.45解析：选B 设P (t,2t )(t ≠0)为角θ终边上任意一点，则cos θ＝t 5|t |.当t ＞0时，cos θ＝55；当t ＜0时，cos θ＝－55.因此cos 2θ＝2cos 2θ－1＝25－1＝－35. 3．已知角α的终边上一点P (－3，m )(m ≠0)，且sin α＝2m4，求cos α，tan α的值． 解：设P (x ，y )．由题设知x ＝－3，y ＝m ，所以r 2＝|OP |2＝(－3)2＋m 2(O 为原点)，r ＝3＋m 2， 所以sin α＝m r ＝2m 4＝m22，所以r ＝3＋m 2＝22，即3＋m 2＝8， 解得m ＝±5.当m ＝5时，r ＝22，x ＝－3，y ＝5， 所以cos α＝－322＝－64，tan α＝－153；当m ＝－5时，r ＝22，x ＝－3，y ＝－5， 所以cos α＝－322＝－64，tan α＝153.综上，cos α＝－64，tan α＝－153或cos α＝－64，tan α＝153.。

大题冲关集训(四)1. (2013广东十校联考)在如图所示的几何体中,△ABC是边长为2的正三角形.若AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.(1)求证:AE∥平面BCD;(2)求三棱锥D BCE的体积.(1)证明:取BC的中点M,连接DM、AM,因为BD=CD,所以DM⊥BC,又因为平面BCD⊥平面ABC,BC为交线,所以DM⊥平面ABC,因为AE⊥平面ABC,所以AE∥DM,又因为AE⊄平面BCD,DM⊂平面BCD,所以AE∥平面BCD.(2)解:由(1)知AE∥DM,在△BCD中,CD⊥BD,CD=BD,所以MD=BC=1=AE,所以四边形AMDE是平行四边形,所以DE∥AM,且DE=AM=,因为DM⊥平面ABC,所以DM⊥AM,又AM⊥BC,BC∩DM=M,所以AM⊥平面BCD,所以DE⊥平面BCD,DE=×·BC·DM·DE=××2×1×=.则==S2. 如图所示,在体积为1的三棱柱ABC A1B1C1中,侧棱AA1⊥底面ABC,AC⊥AB,AC=AA1=1,P为线段AB上的动点.(1)求证:CA1⊥C1P;(2)线段AB上是否存在一点P,使四面体PAB1C1的体积为?若存在,请确定点P的位置;若不存在,请说明理由.(1)证明:易知四边形ACC1A1为正方形,所以CA1⊥AC1.由AC⊥AB,AA1⊥底面ABC知AB⊥平面AA1C1C,所以CA1⊥AB.所以CA1⊥平面C1AP,故CA1⊥C1P.(2)解:存在.由于=--=1--=,所以当PAB1C1的体积为时,P为AB的中点.3.(2013深圳一调)如图甲,☉O的直径AB=2,圆上两点C,D在直径AB的两侧,使∠CAB=,∠DAB=.沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC 的中点,E为AO的中点.根据图乙解答下列各题:(1)求三棱锥C BOD的体积;(2)求证:CB⊥DE;(3)在上是否存在一点,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.(1)解:∵C为圆周上一点,且AB为直径,∴∠C=90°.∵∠CAB=,∴AC=BC,∵O为AB的中点,∴CO⊥AB,∵两个半圆所在平面ACB与平面ADB互相垂直且其交线为AB, ∴CO⊥平面ABD,∴CO⊥平面BOD.∴CO就是点C到平面BOD的距离,在Rt△ABD中,S △BOD=S△ABD=××1×=,∴=S △BOD·CO=××1=.(2)证明:在△AOD中,∵∠OAD=60°,OA=OD,∴△AOD为正三角形,又∵E为OA的中点,∴DE⊥AO,∵两个半圆所在平面ACB与平面ADB互相垂直且其交线为AB, ∴DE⊥平面ABC,∴CB⊥DE.(3)解:存在,G为的中点,证明如下:连接OG,OF,FG,∴OG⊥BD,∵AB为☉O的直径,∴AD⊥BD,∴OG∥AD,∵OG⊄平面ACD,AD⊂平面ACD,∴OG∥平面ACD.在△ABC中,O,F分别为AB,BC的中点,∴OF∥AC,OF⊄平面ACD,∴OF∥平面ACD,∵OG∩OF=O,∴平面OFG∥平面ACD,又FG⊂平面OFG,∴FG∥平面ACD.4.(2013潮州市高三期末质检)已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=,AB=BC=2AD=4,E,F分别是AB,CD上的点,EF∥BC,AE=x.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图),G是BC的中点.(1)当x=2时,求证:BD⊥EG;(2)当x变化时,求三棱锥D BCF的体积f(x)的函数式.(1)证明:作DH⊥EF,垂足为H,连接BH,GH,EG,∵平面AEFD⊥平面EBCF,交线为EF,DH⊂平面AEFD.∴DH⊥平面EBCF,又EG⊂平面EBCF,故EG⊥DH,∵EH=AD=BC=BG,EF∥BC,∠ABC=90°.∴四边形BGHE为正方形,故EG⊥BH.又BH,DH⊂平面DBH,且BH∩DH=H,故EG⊥平面DBH.又BD⊂平面DBH,故EG⊥BD.(2)解:∵AE⊥EF,平面AEFD⊥平面EBCF,交线为EF,AE⊂平面AEFD.∴AE⊥平面EBCF.又由(1)知DH⊥平面EBCF,故AE∥DH,∴四边形AEHD是矩形,DH=AE,故以F,B,C,D为顶点的三棱锥D BCF的高DH=AE=x.又S△BCF=BC·BE=×4×(4-x)=8-2x.∴三棱锥D BCF的体积f(x)=S△BFC·DH=S△BFC·AE=(8-2x)x=-x2+x.5.(2013山东潍坊一模)如图所示,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABEF⊥平面EFDC,设AD中点为P.(1)当E为BC中点时,求证:CP∥平面ABEF.(2)设BE=x,问当x为何值时,三棱锥A CDF的体积有最大值?并求出这个最大值. 解:(1)取AF的中点Q,连QE、QP,则QP DF,又DF=4,EC=2,且DF∥EC,所以QP EC,即四边形PQEC为平行四边形,所以CP∥EQ,又EQ⊂平面ABEF,CP⊄平面ABEF,故CP∥平面ABEF.(2)因为平面ABEF⊥平面EFDC,平面ABEF∩平面EFDC=EF,AF⊥EF,所以AF⊥平面EFDC.由已知BE=x,所以AF=x(0<x≤4),FD=6-x,故=S △CDF·AF=××2×(6-x)·x=(6x-x2)=[-(x-3)2+9]=-(x-3)2+3.所以,当x=3时,有最大值,最大值为3.6.(2013清远市高三调研)图1是两个全等的纸板梯形P1BCP2和P3CDP4叠合一起形成的,重叠部分是边长为2的正方形ABCD,P 1A=P4A=2,P2D=P3B=2,将图1中的四个纸板三角形沿虚线折起,使四点P1,P2,P3,P4聚为一点P,就形成了四棱锥P ABCD,如图2所示,其中E,F分别是AD,PB的中点.(1)证明:AD⊥AF;(2)证明:AF∥平面PEC;(3)求三棱锥F AEC的体积.(1)证明:∵PA⊥AD,AD⊥AB,PA∩AB=A,∴AD⊥平面PAB.∵AF⊂平面PAB,∴AF⊥AD.(2)证明:取PC的中点G,连接FG,GE.∵FG BC,AE BC,∴AE FG,∴四边形AEGF是平行四边形,∴AF∥EG.∵AF⊄平面PEC,EG⊂平面PEC,∴AF∥平面PEC.(3)作FH⊥AB于点H,则FH PA,∴FH⊥平面ABCD,即FH⊥平面AEC,FH=1.∵S△AEC=S正方形ABCD=1,∴=FH·S △AEC=.。

课时作业46 空间向量的运算及应用1．已知a ＝(－2,1,3)，b ＝(－1,2,1)，若a ⊥(a －λb )，则实数λ的值为( D )A ．－2B ．－143 C.145 D ．2解析：由题意知a ·(a －λb )＝0，即a 2－λa ·b ＝0，所以14－7λ＝0，解得λ＝2.2．若A ，B ，C 不共线，对于空间任意一点O 都有OP →＝34OA →＋18OB →＋18OC →，则P ，A ，B ，C 四点( B )A ．不共面B ．共面C ．共线D ．不共线解析：由已知可得OP →－OA →＝－14OA →＋18OB →＋18OC →， 即OP →－OA →＝－18OA →＋18OB →＋18OC →－18OA →，可得AP →＝－18(OA →－OB →)＋18(OC →－OA →)＝－18BA →＋18AC →＝18(AC →＋AB →)，所以AP →，AC →，AB →共面但不共线，故P ，A ，B ，C 四点共面． 3．A ，B ，C ，D 是空间不共面的四点，且满足AB →·AC →＝0，AC →·AD→＝0，AB →·AD →＝0，M 为BC 的中点，则△AMD 是( C )A ．钝角三角形B ．锐角三角形C ．直角三角形D ．不确定解析：∵M 为BC 的中点，∴AM →＝12(AB →＋AC →)． ∴AM →·AD →＝12(AB →＋AC →)·AD → ＝12AB →·AD →＋12AC →·AD →＝0.∴AM ⊥AD ，即△AMD 为直角三角形．4．如图，已知空间四边形OABC ，其对角线为OB ，AC ，M ，N 分别是对边OA ，BC 的中点，点G 在线段MN 上，且分MN 所成的比为2，现用基向量OA →，OB →，OC →表示向量OG →，设OG →＝xOA →＋yOB →＋zOC →，则x ，y ，z 的值分别是( D )A ．x ＝13，y ＝13，z ＝13 B ．x ＝13，y ＝13，z ＝16 C ．x ＝13，y ＝16，z ＝13D ．x ＝16，y ＝13，z ＝13解析：设OA →＝a ，OB →＝b ，OC →＝c ， ∵G 分MN 的所成比为2，∴MG →＝23MN →，∴OG →＝OM →＋MG →＝OM →＋23(ON →－OM →)＝12a ＋23⎝⎛⎭⎪⎫12b ＋12c －12a ＝12a＋13b ＋13c －13a ＝16a ＋13b ＋13c ，即x ＝16，y ＝13，z ＝13.5．已知空间向量a ，b 满足|a |＝|b |＝1，且a ，b 的夹角为π3，O 为空间直角坐标系的原点，点A ，B 满足OA →＝2a ＋b ，OB →＝3a －b ，则△OAB 的面积为( B )A.52 3 B.54 3 C.74 3D.114解析：|OA →|＝(2a ＋b )2＝4|a |2＋|b |2＋4a ·b ＝7，同理|OB →|＝7，则cos ∠AOB ＝OA →·OB →|OA →||OB →|＝6|a |2－|b |2＋a ·b 7＝1114，从而有sin ∠AOB ＝5314，∴△OAB 的面积S ＝12×7×7×5314＝534，故选B.6．如图，在空间四边形OABC 中，OA ＝8，AB ＝6，AC ＝4，BC ＝5，∠OAC ＝45°，∠OAB ＝60°，则OA 与BC 所成角的余弦值为( A )A.3－225 B.2－26 C.12D.32解析：因为BC →＝AC →－AB →， 所以OA →·BC →＝OA →·AC →－OA →·AB →＝|OA →||AC →|cos 〈OA →，AC →〉－|OA →||AB →|cos 〈OA →，AB →〉＝8×4×cos135°－8×6×cos120°＝－162＋24.所以cos 〈OA →，BC →〉＝OA →·BC →|OA →||BC →|＝24－1628×5＝3－225.即OA 与BC 所成角的余弦值为3－225.7．已知2a ＋b ＝(0，－5,10)，c ＝(1，－2，－2)，a ·c ＝4，|b |＝12，则以b ，c 为方向向量的两直线的夹角为 60° .解析：由题意，得(2a ＋b )·c ＝0＋10－20＝－10， 即2a ·c ＋b ·c ＝－10. 又∵a ·c ＝4，∴b ·c ＝－18，∴cos 〈b ，c 〉＝b ·c |b ||c |＝－1812×1＋4＋4＝－12，又∵〈b ，c 〉∈[0°，180°]，∴〈b ，c 〉＝120°，∴两直线的夹角为60°.8．已知O 点为空间直角坐标系的原点，向量OA →＝(1,2,3)，OB →＝(2,1,2)，OP →＝(1,1,2)，且点Q 在直线OP 上运动，当QA →·QB →取得最小值时，OQ →的坐标是 ⎝ ⎛⎭⎪⎫43，43，83 .解析：∵点Q 在直线OP 上，∴设点Q (λ，λ，2λ)， 则QA →＝(1－λ，2－λ，3－2λ)，QB →＝(2－λ，1－λ，2－2λ)， QA →·QB →＝(1－λ)(2－λ)＋(2－λ)(1－λ)＋(3－2λ)(2－2λ)＝6λ2－16λ＋10＝6⎝ ⎛⎭⎪⎫λ－432－23.即当λ＝43时，QA →·QB →取得最小值－23. 此时OQ →＝⎝⎛⎭⎪⎫43，43，83.9．已知V 为矩形ABCD 所在平面外一点，且VA ＝VB ＝VC ＝VD ，VP →＝13VC →，VM →＝23VB →，VN →＝23VD →.则VA 与平面PMN 的位置关系是 VA ∥平面PMN .解析：如图，设VA →＝a ，VB →＝b ，VC →＝c ，则VD →＝a ＋c －b ， 由题意知PM →＝23b －13c ， PN →＝23VD →－13VC →＝23a －23b ＋13c . 因此VA →＝32PM →＋32PN →， ∴VA →，PM →，PN →共面．又∵VA ⊄平面PMN ，∴VA ∥平面PMN .10．如图，在四棱柱ABCD -A 1B 1C 1D 1中，底面ABCD 是平行四边形，E ，F ，G 分别是A 1D 1，D 1D ，D 1C 1的中点．(1)试用向量AB →，AD →，AA 1→表示AG →； (2)用向量方法证明平面EFG ∥平面AB 1C . 解：(1)设AB →＝a ，AD →＝b ， AA 1→＝c .由图得AG →＝AA 1→＋A 1D 1→＋D 1G →＝c ＋b ＋12DC →＝12a ＋b ＋c ＝12AB →＋AD →＋AA 1→.(2)证明：由题图，得AC →＝AB →＋BC →＝a ＋b ， EG →＝ED 1→＋D 1G →＝12b ＋12a ＝12AC →， ∵EG 与AC 无公共点，∴EG ∥AC ， ∵EG ⊄平面AB 1C ，AC ⊂平面AB 1C ， ∴EG ∥平面AB 1C .又∵AB 1→＝AB →＋BB 1→＝a ＋c ，FG →＝FD 1→＋D 1G →＝12c ＋12a ＝12AB 1→， ∵FG 与AB 1无公共点，∴FG ∥AB 1， ∵FG ⊄平面AB 1C ，AB 1⊂平面AB 1C ， ∴FG ∥平面AB 1C ，又∵FG ∩EG ＝G ，FG ，EG ⊂平面EFG ， ∴平面EFG ∥平面AB 1C.11．已知正方体ABCD -A 1B 1C 1D 1的棱长为a ，点M 在AC 1上，且AM →＝12MC 1→，N 为B 1B 的中点，则|MN →|为( A )A.216aB.66aC.156aD.153a解析：以D 为原点建立如图所示的空间直角坐标系D -xyz ，则A (a,0,0)，C 1(0，a ，a )， N ⎝⎛⎭⎪⎫a ，a ，a 2.设M (x ，y ，z )，因为点M 在AC 1上，且AM →＝12MC 1→， 则(x －a ，y ，z )＝12(－x ，a －y ，a －z )，得x ＝23a ，y ＝a 3，z ＝a3，即M ⎝ ⎛⎭⎪⎫2a 3，a 3，a 3，所以|MN →|＝⎝⎛⎭⎪⎫a －23a 2＋⎝ ⎛⎭⎪⎫a －a 32＋⎝ ⎛⎭⎪⎫a 2－a 32＝216a . 12．如图，已知直三棱柱ABC -A 1B 1C 1，在底面△ABC 中，CA ＝CB ＝1，∠BCA ＝90°，棱AA 1＝2，M ，N 分别是A 1B 1，A 1A 的中点.(1)求BN →的模；(2)求cos 〈BA 1→，CB 1→〉的值；(3)求证：A 1B ⊥C 1M .解：(1)如图，以点C 作为坐标原点O ，CA ，CB ，CC 1所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系．由题意得B (0,1,0)，N (1,0,1)，所以|BN →|＝(1－0)2＋(0－1)2＋(1－0)2＝ 3.(2)由题意得A 1(1,0,2)，B (0,1,0)，C (0,0,0)，B 1(0,1,2)，所以BA 1→＝(1，－1,2)，CB 1→＝(0,1,2)，BA 1→·CB 1→＝3，|BA 1→|＝6，|CB 1→|＝5，所以cos 〈BA 1→，CB 1→〉＝BA 1→·CB 1→|BA 1→||CB 1→|＝3010.(3)证明：由题意得C 1(0,0,2)，M ⎝ ⎛⎭⎪⎫12，12，2，A 1B →＝(－1,1，－2)，C 1M →＝⎝⎛⎭⎪⎫12，12，0，所以A 1B →·C 1M →＝－12＋12＋0＝0， 所以A 1B →⊥C 1M →， 即A 1B ⊥C 1M .。

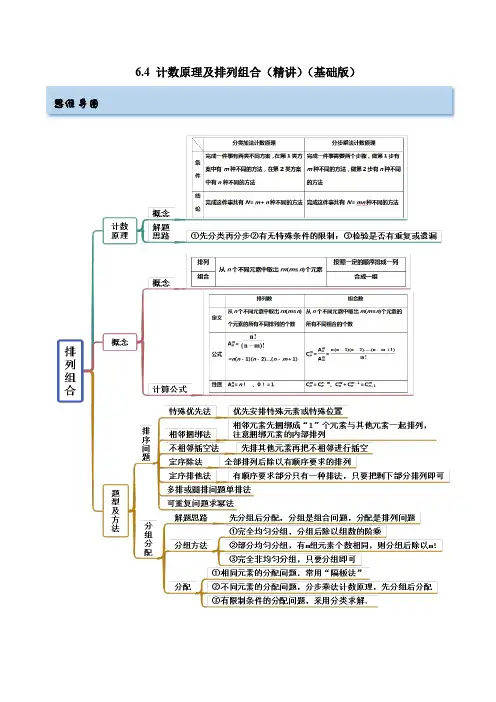
6.4 计数原理及排列组合（精讲）（基础版）思维导图考点一 排队问题【例1】（2022·广东）有7名同学，其中3名男生、4名女生，求在下列不同条件下的排法种数． (1)选5人排成一排；(2)全体站成一排，女生互不相邻；(3)全体站成一排，其中甲不站在最左边，也不站在最右边； (4)全体站成一排，其中甲不站在最左边，乙不站在最右边； (5)男生顺序已定，女生顺序不定；(6)站成三排，前排2名同学，中间排3名同学，后排2名同学，其中甲站在中间排的中间位置； (7)7名同学站成一排，其中甲、乙相邻，但都不与丙相邻； (8)7名同学坐圆桌吃饭，其中甲、乙相邻．【答案】(1)2520(2)144(3)3600(4)3720(5)840(6)720(7)960(8)240【解析】（1）从7人中选5人排列，排法有57A 2520=（种）．（2）先排男生，有33A 种排法，再在男生之间及两端的4个空位中排女生，有44A 种排法．故排法共有3434A A 144=（种）． （3）方法一（特殊元素优先法） 先排甲，有5种排法，其余6人有66A 种排法，故排法共有665A 3600⨯=（种）．方法二（特殊位置优先法） 左右两边位置可安排除甲外其余6人中的2人，有26A 种排法，其他位置有55A 种排法，故排法共有2565A A 3600=（种）．（4）方法一 分两类：第一类，甲在最右边，有66A 种排法；第二类，甲不在最右边，甲可从除去两端后剩考点呈现例题剖析下的5个位置中任选一个，有5种排法，而乙可从除去最右边的位置及甲的位置后剩下的5个位置中任选一个，有5种排法，其余人全排列，有55A 种排法．故排法共有6565A 55A 3720+⨯⨯=（种）．方法二 7名学生全排列，有77A 种排法，其中甲在最左边时，有66A 种排法，乙在最右边时，有66A 种排法，甲在最左边、乙在最右边都包含了甲在最左边且乙在最右边的情形，有55A 种排法，故排法共有765765A 2A A 3720-+=（种）．（5）7名学生站成一排，有77A 种排法，其中3名男生的排法有33A 种，由于男生顺序已定，女生顺序不定，故排法共有7733A 840A =（种）．（6）把甲放在中间排的中间位置，则问题可以看成剩余6人的全排列，故排法共有66A 720=（种）．（7）先把除甲、乙、丙3人外的4人排好，有44A 种排法，由于甲、乙相邻，故再把甲、乙排好，有22A 种排法，最后把排好的甲、乙这个整体与丙分别插入原先排好的4人之间及两端的5个空隙中，有25A 种排法．故排法共有422425A A A 960=（种）．（8）将甲、乙看成一个整体，相当于6名同学坐圆桌吃饭，有661A 6种排法，甲、乙两人可交换位置，故排法共有62621A A 2406=（种）．【一隅三反】1．（2022·河北·藁城新冀明中学）有5名男生和甲、乙2名女生排成一排，求下列情况各有多少种不同的排法？(1)女生甲排在正中间； (2)2名女生不相邻；(3)女生甲必须排在女生乙的左边（不一定相邻）； (4)2名女生中间恰有1名男生．【答案】(1)720种；(2)3600种；(3)2520种；(4)1200种.【解析】(1)女生甲排在正中间，其余6人有66A 种排法，因此不同排法种数为66A 720=种；(2)将5名男生排成一排，有55A 种排法，2名女生可以在每2名男生之间及两端共6个位置中选出2个排，有26A 种排法，因此不同排法种数为5256A A 3600=种；(3)对7名学生全排列有77A 种排法，因此不同排法种数为771A 25202=种；(4)选1名男生排在2名女生中间，有15C 种排法，将3人看成1个元素，与4名男生共5个元素排成一排，不同的排法有55A 种，又因为2名女生有22A 种排法，因此不同排法种数为125525C A A 1200=种.2．（2022·全国·高三专题练习）某种产品的加工需要经过,,,,,5A B C D E 道工序． (1)如果工序A 不能放在最后，那么有多少种加工顺序？（数字作答） (2)如果工序,A B 必须相邻，那么有多少种加工顺序？（数字作答） (3)如果工序C ，D 必须不能相邻，那么有多少种加工顺序？（数字作答） 【答案】(1)96(2)48(3)72【解析】(1)先从另外4道工序中任选1道工序放在最后，有14C 4=种不同的排法，再将剩余的4道工序全排列，有4424A =种不同的排法，故由分步乘法原理可得，共有42496⨯=种加工顺序；(2)先排A ，B 这2道工序，有222A =种不同的排法，再将它们看做一个整体，与剩余的工序全排列，有4424A =种不同的排法，故由分步乘法原理可得，共有22448⨯=种加工顺序；(3)先排其余的3道工序，有336A =种不同的排法，出现4个空位，再将C ，D 这2道工序插空，有2412A =种不同的排法，所以由分步乘法原理可得，共有61272⨯=种加工顺序. 3．（2022·全国·高三专题练习）现有8个人(5男3女）站成一排. (1)女生必须排在一起，共有多少种不同的排法？ (2)其中甲必须站在排头有多少种不同排法？(3)其中甲、乙两人不能排在两端有多少种不同的排法？ (4)其中甲、乙两人不相邻有多少种不同的排法？ (5)其中甲在乙的左边有多少种不同的排法？ (6)其中甲乙丙不能彼此相邻，有多少种不同排法？ (7)男生在一起，女生也在一起，有多少种不同排法？ (8)第3和第6个排男生，有多少种不同排法？ (9)甲乙不能排在前3位，有多少种不同排法？ (10)女生两旁必须有男生，有多少种不同排法？【答案】(1)3636A A (2)77A (3)2666A A (4)2676A A (5)8812A (6)5356A A (7)235235A A A (8)2656A A (9)2656A A (10)5354A A【解析】(1)根据题意，先将3名女生看成一个整体，考虑三人之间的顺序，有33A 种情况，将这个整体与5名男生全排列，有66A 种情况，则女生必须排在一起的排法有3636A A 种；(2)根据题意，甲必须站在排头，有1种情况，将剩下的7人全排列，有77A 种情况，则甲必须站在排头有77A 种排法；(3)根据题意，将甲乙两人安排在中间6个位置，有26A 种情况，将剩下的6人全排列，有66A 种情况， 则甲、乙两人不能排在两端有2666A A 种排法；(4)根据题意，先将出甲乙之外的6人全排列，有66A 种情况，排好后有7个空位，则7个空位中，任选2个，安排甲乙二人，有27A 种情况，则甲、乙两人不相邻有2676A A 种排法； (5)根据题意，将8人全排列，有88A 种情况，其中甲在乙的左边与甲在乙的右边的情况数目相同， 则甲在乙的左边有8812A 种不同的排法；(6)根据题意，先将出甲乙丙之外的5人全排列，有55A 种情况，排好后有6个空位，则6个空位中，任选3个，安排甲乙丙三人，有36A 种情况，其中甲乙丙不能彼此相邻有5356A A 种不同排法； (7)根据题意，先将3名女生看成一个整体，考虑三人之间的顺序，有33A 种情况， 再将5名男生看成一个整体，考虑5人之间的顺序，有55A 种情况，将男生、女生整体全排列，有22A 种情况，则男生在一起，女生也在一起，有235235A A A 种不同排法； (8)根据题意，在5个男生中任选2个，安排在第3和第6个位置，有222525C A A 种情况， 将剩下的6人全排列，有66A 种情况，则第3和第6个排男生，有2656A A 种不同排法； (9)根据题意，将甲乙两人安排在后面的5个位置，有25A 种情况，将剩下的6人全排列，有66A 种情况，甲乙不能排在前3位，有2656A A 种不同排法； (10)根据题意，将5名男生全排列，有55A 种情况，排好后除去2端有4个空位可选，在4个空位中任选3个，安排3名女生，有34A 种情况，则女生两旁必须有男生，有5354A A 种不同排法.考点二 排数问题【例2】（2022·江苏）用0，1，2，3，4这五个数字组成无重复数字的自然数．（1）在组成的五位数中，所有奇数的个数有多少?（2）在组成的五位数中，数字1和3相邻的个数有多少? （3）在组成的五位数中，若从小到大排列，30124排第几个? 【答案】（1）36个（2）36个（2）49个【解析】（1）在组成的五位数中，所有奇数的个数有113233=236=36C C A⨯⨯个；（2）在组成的五位数中，数字1和3相邻的个数有21323323636A C A=⨯⨯=个；（3）要求在组成的五位数中，要求得从小到大排列，30124排第几个，则计算出比30124小的五位数的情况，比30124小的五位数，则万位为1或2，其余位置任意排，即142422448C A=⨯=，故在组成的五位数中比30124小的数有48个，所以在组成的五位数中，若从小到大排列，30124排第49个.【一隅三反】1．（2022·吉林）从1到7的7个数字中取两个偶数和三个奇数组成没有重复数字的五位数．试问：（1）能组成多少个不同的五位偶数？（2）五位数中，两个偶数排在一起的有几个？（3）两个偶数不相邻且三个奇数也不相邻的五位数有几个？（所有结果均用数值表示）【答案】（1）576；（2）576；（3）144【解析】（1）偶数在末尾，五位偶数共有23413442C C A A＝576个．（2）五位数中，偶数排在一起的有23423442C C A A＝576个．（3）两个偶数不相邻且三个奇数也不相邻的五位数有23233423C C A A＝144．2．（2022·全国·高三专题练习）用数字1，2，3，4，5组成没有重复数字的数，问（1）能够组成多少个五位奇数？（2）能够组成多少个正整数？（3）能够组成多少个大于40000的正整数？【答案】（1）72；（2）325；（3）48；【解析】（1）首先排最个位数字，从1、3、5中选1个数排在个位有133A=种，其余4个数全排列有4424A=种，按照分步乘法计数原理可得有143472A A=个五位奇数；（2）根据题意，若组成一位数，有5种情况，即可以有5个一位数；若组成两位数，有2520A=种情况，即可以有20个两位数；若组成三位数，有3560A=种情况，即可以有60个三位数；若组成四位数，有45120A=种情况，即可以有120个四位数；若组成五位数，有55120A=种情况，即可以有120个五位数；则可以有52060120120325++++=个正整数；（3）根据题意，若组成的数字比40000大的正整数，其首位数字为5或4，有2种情况；在剩下的4个数，安排在后面四位，共有142448C A =种情况，则有48个比40000大的正整数；3．（2021·民大附中海南陵水分校）用0、1、2、3、4五个数字: (1)可组成多少个五位数；(2)可组成多少个无重复数字的五位数；(3)可组成多少个无重复数字的且是3的倍数的三位数； (4)可组成多少个无重复数字的五位奇数． 【答案】(1)2500(2)96(3)20(4)36 【解析】(1)用0、1、2、3、4五个数字组成五位数,相当于从1、2、3、4四个数字中抽取一个放在万位，有14C 种情况，从0、1、2、3、4五个数字中抽取一个放在千位，有15C 种情况，从0、1、2、3、4五个数字中抽取一个放在百位，有15C 种情况，从0、1、2、3、4五个数字中抽取一个放在十位，有15C 种情况，从0、1、2、3、4五个数字中抽取一个放在个位，有15C 种情况，所以可组成11111445555C C C C C 452500⨯⨯⨯⨯=⨯=个五位数.(2)用0、1、2、3、4五个数字组成无重复数字的五位数,相当于先从1、2、3、4四个数字中抽取一个放在万位，有14C 种情况，再把剩下的三个数字和0全排列，有44A 种情况，所以可组成1444C A 42496=⨯=个无重复数字的五位数.(3)无重复数字的3的倍数的三位数组成它的三个数字之和必须是3的倍数， 所以三个数字必须是0、1、2或0、2、4或1、2、3或2、3、4，若三个数字是0、1、2，则0不能放在百位，从1和2两个数字中抽取一个放在百位，有12C 种情况，再把剩下的一个数字和0全排列，有22A 种情况；若三个数字是0、2、4，则0不能放在百位，从2和4两个数字中抽取一个放在百位，有12C 种情况，再把剩下的一个数字和0全排列，有22A 种情况；若三个数字是1、2、3，则相当于对这三个数字全排列，有33A 种情况; 若三个数字是2、3、4，则相当于对这三个数字全排列，有33A 种情况.所以根据分类计数原理，共可组成121233222233C A C A A A 22226620⨯+⨯++=⨯+⨯++=个无重复数字的且是3的倍数的三位数.(4)由数字0、1、2、3、4五个数字组成无重复数字的五位奇数，则放在个位的数字只能是奇数，所以放在个位数字只能是1或3，所以相当于先从1、3两个数字中抽取一个放在个位，有12C 种情况，再从剩下的四个数字中除去0抽取一个放在万位，有13C 种情况，再对剩下的三个数字全排列，有33A 种情况，所以可组成113233C C A 23636⨯⨯=⨯⨯=个无重复数字的五位奇数.考点三 分组分配【例3】（2022·全国·高三专题练习）按下列要求分配6本不同的书,各有多少种不同的分配方式? （1）分成三份,1份1本,1份2本,1份3本;（2）甲、乙、丙三人中,一人得1本,一人得2本,一人得3本; （3）平均分成三份,每份2本;（4）平均分配给甲、乙、丙三人,每人2本; （5）分成三份,1份4本,另外两份每份1本;（6）甲、乙、丙三人中,一人得4本,另外两人每人得1本; （7）甲得1本,乙得1本,丙得4本.【答案】（1）60；（2）360；（3）15；（4）90；（5）15；（6）90；（7）30【解析】（1）无序不均匀分组问题.先选1本有16C 种选法;再从余下的5本中选2本有25C 种选法;最后余下的3本全选有33C 种选法.故共有12365360C C C = (种)选法.（2）有序不均匀分组问题.由于甲、乙、丙是不同三人,在1题的基础上,还应考虑再分配,共有12336533360C C C A =.（3）无序均匀分组问题.先分三步,则应是222642C C C 种选法,但是这里出现了重复.不妨记六本书为A ,B ,C ,D ,E ,F ,若第一步取了AB ,第二步取了CD ,第三步取了EF ,记该种分法为(AB ,CD ,EF ),则222642C C C 种分法中还有(AB ,EF ,CD ),(CD ,AB ,EF ),(CD ,EF ,AB ),(EF ,CD ,AB ),(EF ,AB ,CD ),共有33A 种情况,而这33A 种情况仅是AB ,CD ,EF 的顺序不同,因此只能作为一种分法,故分配方式有2226423315C C C A =. （4）有序均匀分组问题.在3题的基础上再分配给3个人,共有分配方式222364233390C C C A A ⋅= (种).（5）无序部分均匀分组问题.共有4116212215C C C A = (种)分法. （6）有序部分均匀分组问题.在5题的基础上再分配给3个人,共有分配方式411362132290C C C A A ⋅= (种). （7）直接分配问题.甲选1本有16C 种选法,乙从余下5本中选1本有15C 种选法,余下4本留给丙有44C 种选法,共有11465430C C C = (种)选法.【一隅三反】1．（2023·全国·高三专题练习）为宣传城市文化，提高城市知名度，我市某所学校5位同学各自随机从“趵突腾空”、“ 历山览胜”、“明湖汇泊”三个城市推荐词中选择一个，来确定该学校所推荐的景点，则三个推荐词都有人选的概率是（ ） A ．5081B ．2081C ．81125D ．27125【答案】A【解析】5位同学任意选取1个景点的方法数为53243=，三个推荐词都有人选，可以先把5人分成三组，然后每组选一个，方法数为2233535322C C (C )A 150A +=，所以所求概率为1505024381P ==．故选：A ． 2．（2022·河北·邢台市南和区第一中学）某研究机构采访了“—带一路”沿线20国的青年，让他们用一个关键词表达对中国的印象，使用频率前12的关键词为高铁，移动支付，网购，共享单车、一带一路、无人机、大熊猫、广场舞、中华美食、长城、京剧、美丽乡村．其中使用频率排前4的关键词“高铁、移动支付、网购、共享单车”也成为了他们眼中的“新四大发明”．若将这12个关键词平均分成3组，且各组都包含“新四大发明”关键词．则不同的分法种数为（ ）A ．1680 B ．3360 C ．6720 D ．10080【答案】B【解析】先将4个“新四大发明”分成1，1，2三组，有11243222C C C 6A =种不同的分法， 再将余下的8个分成3，3，2三组，有33285222C C C 280A =种不同的分法，最后配成三组，所以共有628023360⨯⨯=种不同的分法．故选：B.3．（2022·河北省曲阳县第一高级中学）某地区安排A ，B ，C ，D ，E ，F 六名党员志愿者同志到三个基层社区开展防诈骗宣传活动，每个地区至少安排一人，至多安排三人，且A ，B 两人安排在同一个社区，C ，D 两人不安排在同一个社区，则不同的分配方法总数为（ ） A ．72 B ．84 C ．90 D ．96【答案】B【解析】第一种分配方式为每个社区各两人，则CE 一组，DF 一组，或CF 一组，DE 一组，由2种分组方式，再三组人，三个社区进行排列，则分配方式共有332A 12=种；第二种分配方式为一个社区1人，一个社区2人，一个社区3人，当AB 两人一组去一个社区，则剩下的4人，1人为一组，3人为一组，则必有C 或D 为一组，有1323C C 种分配方法，再三个社区，三组人，进行排列，有133233C C A 12=种分配方法；当AB 加上另一人三人去一个社区，若选择的是C 或D ，则有12C 种选择，再将剩余3人分为两组，有1232C C 种分配方法，将将三个社区，三组人，进行排列，有11232323C C C A 36=种分配方法；若选择的不是C 或D ，即从E 或F 中选择1人和AB 一起，有12C 种分配方法，再将CD 和剩余的1人共3人分为两组，有2种分配方法，将三个社区，三组人，进行排列，有13232C A 24=种分配方法，综上共有12+12+36+24=84种不同的分配方式故选：B考点四 涂色【例4】（2022·浙江·）如图，用五种不同的颜色给图中的O ，A ，B ，C ，D ，E 六个点涂色（五种颜色不一定用完），要求每个点涂一种颜色，且图中每条线段的两个端点涂不同的颜色，则不同的涂法种数是（ ）A ．480B ．720C ．1080D ．1200【答案】D 先给O 涂色，有15C 种方法，接着给A 涂色，有14C 种方法，接着给B 涂色，有13C 种方法，①若C 与A 同色，则有1种涂色方法，接着给D 涂色，有3种涂色方法， 最后E 有2种涂色方法；①若C 与A 不同色，则有2种涂色方法，接着给D 涂色，若D 与A 同色，则有1种涂色方法，最后E 有3种涂色方法；若D 与A 不同色，则有2种涂色方法，最后E 有2种涂色方法.综上，涂色方法总数为15C 14C []13C 1322(1322)1200⨯⨯+⨯⨯+⨯=故选：D【举一反三】1．（2022·山东烟台）我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”.后人称其为“赵爽弦图”.如图，现提供5种颜色给图中的5个小区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不相同.记事件A ：“区域1和区域3颜色不同”，事件B ：“所有区域颜色均不相同”，则()P B A =（ ）A ．27B ．12C ．23 D ．34【答案】B【解析】A 事件有21115322A C C C 个基本事件，B 事件有55A 个基本事件，()5521115322A 1|A C C C 2p B A ∴== ； 故选：B.2．（2022·河北·藁城新冀明中学）有4种不同颜色的涂料，给图中的6个区域涂色，要求相邻区域的颜色不相同，则不同的涂色方法共有（ ）A ．1512种B ．1346种C ．912种D ．756种【答案】D【解析】1、先涂A 区域，则有4种方法，若B ，D 区域涂相同颜色，则有3种方法，C ，E ，F 区域分别有3种方法，共有4×3×3×3×3=324种方法．2、先涂A区域，则有4种方法，若B，D区域涂不同颜色，则有3×2种方法，则E区域有2种方法，C，F 分别有3种方法，共有4×3×2×2×3×3=432种方法．故不同的涂色方法共有756种．故选：D3（2022·广东广州）如图，用4种不同的颜色对A，B，C，D四个区域涂色，要求相邻的两个区域不能用同一种颜色，则不同的涂色方法有（）A．24种B．48种C．72种D．96种【答案】B【解析】按涂色顺序进行分四步：涂A部分时，有4种涂法；涂B部分时，有3种涂法；涂C部分时，有2种涂法；涂D部分时，有2种涂法.⨯⨯⨯=种.故选：B.由分步乘法计数原理，得不同的涂色方法共有432248。

热点探究课(二) 函数、导数与不等式[命题解读] 函数是中学数学的核心内容，导数是研究函数的重要工具，因此，导数的应用是历年高考的重点与热点，常涉及的问题有：讨论函数的单调性(求函数的单调区间)、求极值、求最值、求切线方程、求函数的零点或方程的根、求参数的X 围、证明不等式等，涉及的数学思想有：函数与方程、分类讨论、数形结合、转化与化归思想等，中、高档难度均有.热点1 利用导数研究函数的单调性、极值与最值(答题模板)函数的单调性、极值是局部概念，函数的最值是整体概念，研究函数的性质必须在定义域内进行，因此，务必遵循定义域优先的原则，本热点主要有三种考查方式：(1)讨论函数的单调性或求单调区间；(2)求函数的极值或最值；(3)利用函数的单调性、极值、最值，求参数的X 围.(本小题满分14分)已知函数f (x )＝ln x ＋a (1－x )． (1)讨论f (x )的单调性；(2)当f (x )有最大值，且最大值大于2a －2时，求a 的取值X 围.【导学号：62172114】[思路点拨] (1)求出导数后对a 分类讨论，然后判断单调性；(2)运用(1)的结论分析函数的最大值，对得到的不等式进行等价转化，通过构造函数并分析该函数的单调性求a 的X 围．[规X 解答] (1)f (x )的定义域为(0，＋∞)，f ′(x )＝1x－a .2分若a ≤0，则f ′(x )>0，所以f (x )在(0，＋∞)上单调递增.3分若a >0，则当x ∈⎝⎛⎭⎪⎫0，1a 时，f ′(x )>0；当x ∈⎝ ⎛⎭⎪⎫1a，＋∞时，f ′(x )<0.5分所以f (x )在⎝ ⎛⎭⎪⎫0，1a 上单调递增，在⎝ ⎛⎭⎪⎫1a ，＋∞上单调递减.6分 (2)由(1)知，当a ≤0时，f (x )在(0，＋∞)上无最大值； 当a >0时，f (x )在x ＝1a处取得最大值，最大值为f ⎝ ⎛⎭⎪⎫1a ＝ln ⎝ ⎛⎭⎪⎫1a ＋a ⎝ ⎛⎭⎪⎫1－1a ＝－ln a ＋a －1.11分 因此f ⎝ ⎛⎭⎪⎫1a>2a －2等价于ln a ＋a －1<0.12分令g (a )＝ln a ＋a －1，则g (a )在(0，＋∞)上单调递增，g (1)＝0.于是，当0<a <1时，g (a )<0；当a >1时，g (a )>0. 因此，a 的取值X 围是(0,1).14分[答题模板] 讨论含参函数f (x )的单调性的一般步骤 第一步：求函数f (x )的定义域(根据已知函数解析式确定)． 第二步：求函数f (x )的导数f ′(x )．第三步：根据f ′(x )＝0的零点是否存在或零点的大小对参数分类讨论． 第四步：求解(令f ′(x )>0或令f ′(x )<0)． 第五步：下结论．第六步：反思回顾，查看关键点、易错点、注意解题规X ．温馨提示：1.讨论函数的单调性，求函数的单调区间、极值问题，最终归结到判断f ′(x )的符号问题上，而f ′(x )＞0或f ′(x )＜0，最终可转化为一个一元一次不等式或一元二次不等式问题．2.若已知f (x )的单调性，则转化为不等式f ′(x )≥0或f ′(x )≤0在单调区间上恒成立问题求解.[对点训练1] 已知函数f (x )＝x 3＋ax 2－x ＋c ，且a ＝f ′⎝ ⎛⎭⎪⎫23.(1)求a 的值；(2)求函数f (x )的单调区间；(3)设函数g (x )＝(f (x )－x 3)·e x，若函数g (x )在x ∈[－3,2]上单调递增，某某数c 的取值X 围．[解] (1)由f (x )＝x 3＋ax 2－x ＋c ， 得f ′(x )＝3x 2＋2ax －1.2分当x ＝23时，得a ＝f ′⎝ ⎛⎭⎪⎫23＝3×⎝ ⎛⎭⎪⎫232＋2a ×23－1，解得a ＝－1.4分(2)由(1)可知f (x )＝x 3－x 2－x ＋c ，则f ′(x )＝3x 2－2x －1＝3⎝ ⎛⎭⎪⎫x ＋13(x －1)，列表如下：所以f (x )的单调递增区间是⎝⎛⎭⎪⎫－∞，－3和(1，＋∞)； f (x )的单调递减区间是⎝ ⎛⎭⎪⎫－13，1.8分(3)函数g (x )＝(f (x )－x 3)·e x ＝(－x 2－x ＋c )·e x， 有g ′(x )＝(－2x －1)e x ＋(－x 2－x ＋c )e x＝(－x 2－3x ＋c －1)e x，因为函数g (x )在x ∈[－3,2]上单调递增，所以h (x )＝－x 2－3x ＋c －1≥0在x ∈[－3,2]上恒成立， 只要h (2)≥0，解得c ≥11，所以c 的取值X 围是[11，＋∞).14分热点2 利用导数研究函数的零点或曲线交点问题研究函数零点的本质就是研究函数的极值的正负，为此，我们可以通过讨论函数的单调性来解决，求解时应注重等价转化与数形结合思想的应用，其主要考查方式有：(1)确定函数的零点、图象交点的个数；(2)由函数的零点、图象交点的情况求参数的取值X 围.(2016·高考节选)设函数f (x )＝x 3＋ax 2＋bx ＋c . (1)求曲线y ＝f (x )在点(0，f (0))处的切线方程；(2)设a ＝b ＝4，若函数f (x )有三个不同零点，求c 的取值X 围． [解] (1)由f (x )＝x 3＋ax 2＋bx ＋c ，得f ′(x )＝3x 2＋2ax ＋b .2分 因为f (0)＝c ，f ′(0)＝b ，所以曲线y ＝f (x )在点(0，f (0))处的切线方程为y ＝bx ＋c .4分 (2)当a ＝b ＝4时，f (x )＝x 3＋4x 2＋4x ＋c ， 所以f ′(x )＝3x 2＋8x ＋4.6分令f ′(x )＝0，得3x 2＋8x ＋4＝0，解得x ＝－2或x ＝－23.8分f (x )与f ′(x )在区间(－∞，＋∞)上的情况如下：x (－∞，－2)－2 ⎝⎛⎭⎪⎫－2，－23 －23 ⎝ ⎛⎭⎪⎫－23，＋∞ f ′(x ) ＋－＋f (x )c c －3227所以，当c ＞0且c －27＜0时，存在x 1∈(－4，－2)，x 2∈⎝ ⎛⎭⎪⎫－2，－3，x 3∈⎝ ⎛⎭⎪⎫－3，0，使得f (x 1)＝f (x 2)＝f (x 3)＝0.由f (x )的单调性知，当且仅当c ∈⎝ ⎛⎭⎪⎫0，3227时，函数f (x )＝x 3＋4x 2＋4x ＋c 有三个不同零点.14分[规律方法] 用导数研究函数的零点，常用两种方法：一是用导数判断函数的单调性，借助零点存在性定理判断；二是将零点问题转化为函数图象的交点问题，利用数形结合来解决．[对点训练2] 设函数f (x )＝ln x ＋m x，m ∈R .(1)当m ＝e(e 为自然对数的底数)时，求f (x )的极小值；(2)讨论函数g (x )＝f ′(x )－x3零点的个数. 【导学号：62172115】[解] (1)由题设，当m ＝e 时，f (x )＝ln x ＋ex，则f ′(x )＝x －ex 2，由f ′(x )＝0，得x ＝e.2分 ∴当x ∈(0，e)时，f ′(x )＜0，f (x )在(0，e)上单调递减； 当x ∈(e ，＋∞)时，f ′(x )＞0，f (x )在(e ，＋∞)上单调递增， ∴当x ＝e 时，f (x )取得极小值f (e)＝ln e ＋ee ＝2，∴f (x )的极小值为2.4分(2)由题设g (x )＝f ′(x )－x 3＝1x －m x 2－x3(x ＞0)，令g (x )＝0，得m ＝－13x 3＋x (x ＞0).6分设φ(x )＝－13x 3＋x (x >0)，则φ′(x )＝－x 2＋1＝－(x －1)(x ＋1)，当x ∈(0,1)时，φ′(x )＞0，φ(x )在(0,1)上单调递增； 当x ∈(1，＋∞)时，φ′(x )＜0，φ(x )在(1，＋∞)上单调递减，∴x ＝1是φ(x )唯一的极值点，且是极大值点，因此x ＝1也是φ(x )的最大值点， ∴φ(x )的最大值为φ(1)＝23.10分又φ(0)＝0，结合y ＝φ(x )的图象(如图)，可知①当m ＞23时，函数g (x )无零点；②当m ＝23时，函数g (x )有且只有一个零点；③当0＜m ＜23时，函数g (x )有两个零点；④当m ≤0时，函数g (x )有且只有一个零点． 综上所述，当m ＞23时，函数g (x )无零点；当m ＝23或m ≤0时，函数g (x )有且只有一个零点；当0＜m ＜23时，函数g (x )有两个零点.14分热点3 利用导数研究不等式问题导数在不等式中的应用问题是每年高考的必考内容，且以解答题的形式考查，难度较大，属中高档题．归纳起来常见的命题角度有：(1)证明不等式；(2)不等式恒成立问题；(3)存在型不等式成立问题. ☞角度1 证明不等式设a 为实数，函数f (x )＝e x －2x ＋2a ，x ∈R .(1)求f (x )的单调区间与极值；(2)求证：当a ＞ln 2－1且x ＞0时，e x＞x 2－2ax ＋1.[解] (1)由f (x )＝e x－2x ＋2a ，x ∈R ，f ′(x )＝e x－2，x ∈R .令f ′(x )＝0，得x ＝ln 2.于是当x 变化时，f ′(x )，f (x )的变化情况如下表：x (－∞，ln 2)ln 2 (ln 2，＋∞)f ′(x ) － 0 ＋ f (x )单调递减2(1－ln 2＋a )单调递增故f (x )的单调递减区间是(－∞，ln 2)，单调递增区间是(ln 2，＋∞)，f (x )在x ＝ln 2处取得极小值，极小值为f (ln 2)＝e ln 2－2ln 2＋2a ＝2(1－ln 2＋a ).6分(2)设g (x )＝e x －x 2＋2ax －1，x ∈R .于是g ′(x )＝e x－2x ＋2a ，x ∈R .由(1)知当a ＞ln 2－1时，g ′(x )最小值为g ′(ln 2)＝2(1－ln 2＋a )＞0.于是对任意x ∈R ，都有g ′(x )＞0，所以g (x )在R 内单调递增．于是当a ＞ln 2－1时，对任意x ∈(0，＋∞)，都有g (x )＞g (0)． 又g (0)＝0，从而对任意x ∈(0，＋∞)，g (x )＞0. 即e x－x 2＋2ax －1＞0，故e x ＞x 2－2ax ＋1.14分 ☞角度2 不等式恒成立问题(2016·全国卷Ⅱ)已知函数f (x )＝(x ＋1)ln x －a (x －1)．(1)当a ＝4时，求曲线y ＝f (x )在(1，f (1))处的切线方程；(2)若当x ∈(1，＋∞)时，f (x )>0，求a 的取值X 围． [解] (1)f (x )的定义域为(0，＋∞).1分 当a ＝4时，f (x )＝(x ＋1)ln x －4(x －1)，f (1)＝0，f ′(x )＝ln x ＋1x－3，f ′(1)＝－2.3分故曲线y ＝f (x )在(1，f (1))处的切线方程为2x ＋y －2＝0.6分 (2)当x ∈(1，＋∞)时，f (x )＞0等价于ln x －a x －1x ＋1＞0.设g (x )＝ln x －a x －1x ＋1，则g ′(x )＝1x－2a x ＋12＝x 2＋21－a x ＋1x x ＋12，g (1)＝0.9分 ①当a ≤2，x ∈(1，＋∞)时，x 2＋2(1－a )x ＋1≥x 2－2x ＋1＞0，故g ′(x )＞0，g (x )在(1，＋∞)单调递增，因此g (x )＞0；②当a ＞2时，令g ′(x )＝0得x 1＝a －1－a －12－1，x 2＝a －1＋a －12－1.由x 2＞1和x 1x 2＝1得x 1＜1，故当x ∈(1，x 2)时，g ′(x )＜0，g (x )在(1，x 2)单调递减，因此g (x )＜0.综上，a 的取值X 围是(－∞，2].14分 ☞角度3 存在型不等式成立问题设函数f (x )＝a ln x ＋1－a 2x 2－bx (a ≠1)，曲线y ＝f (x )在点(1，f (1))处的切线斜率为0.(1)求b ；(2)若存在x 0≥1，使得f (x 0)<aa －1，求a 的取值X 围．[解] (1)f ′(x )＝a x＋(1－a )x －b . 由题设知f ′(1)＝0，解得b ＝1.3分 (2)f (x )的定义域为(0，＋∞)， 由(1)知，f (x )＝a ln x ＋1－a 2x 2－x ，f ′(x )＝a x ＋(1－a )x －1＝1－a x ⎝ ⎛⎭⎪⎫x －a 1－a (x －1).5分①若a ≤12，则a1－a ≤1，故当x ∈(1，＋∞)时，f ′(x )>0，f (x )在(1，＋∞)单调递增．所以，存在x 0≥1，使得f (x 0)<aa －1的充要条件为f (1)<a a －1，即1－a 2－1<aa －1，解得－2－1<a <2－1.7分②若12<a <1，则a 1－a >1，故当x ∈⎝ ⎛⎭⎪⎫1，a 1－a 时，f ′(x )<0，当x ∈⎝ ⎛⎭⎪⎫a 1－a ，＋∞时，f ′(x )>0，f (x )在⎝⎛⎭⎪⎫1，a 1－a 上单调递减，在⎝ ⎛⎭⎪⎫a 1－a ，＋∞上单调递增.10分所以存在x 0≥1，使得f (x 0)<aa －1的充要条件为f ⎝ ⎛⎭⎪⎫a 1－a <aa －1. 而f ⎝ ⎛⎭⎪⎫a 1－a ＝a ln a 1－a ＋a 221－a ＋a a －1>a a －1，所以不合题意． ③若a >1，则f (1)＝1－a 2－1＝－a －12<a a －1恒成立，所以a ＞1.综上，a 的取值X 围是(－2－1，2－1)∪(1，＋∞).14分 [规律方法] 1.运用导数证明不等式，常转化为求函数的最值问题．2.不等式恒成立通常可以利用函数的单调性求出最值解决．解答相应的参数不等式，如果易分离参数，可先分离变量，构造函数，直接转化为函数的最值问题，避免参数的讨论．3.“恒成立”与“存在性”问题的求解是“互补”关系，即f (x )≥g (a )对于x ∈D 恒成立，应求f (x )的最小值；若存在x ∈D ，使得f (x )≥g (a )成立，应求f (x )的最大值．应特别关注等号是否成立问题．热点探究训练(二)1.设函数f (x )＝3x 2＋axex(a ∈R )． (1)若f (x )在x ＝0处取得极值，确定a 的值，并求此时曲线y ＝f (x )在点(1，f (1))处的切线方程；(2)若f (x )在[3，＋∞)上为减函数，求a 的取值X 围. 【导学号：62172116】 [解] (1)对f (x )求导得f ′(x )＝ 6x ＋a e x －3x 2＋ax exe x 2＝－3x 2＋6－a x ＋aex.3分 因为f (x )在x ＝0处取得极值，所以f ′(0)＝0，即a ＝0.当a ＝0时，f (x )＝3x 2e x ，f ′(x )＝－3x 2＋6x e x，故f (1)＝3e ，f ′(1)＝3e ，从而f (x )在点(1，f (1))处的切线方程为y －3e ＝3e(x －1)，化简得3x －e y ＝0.7分(2)由(1)知f ′(x )＝－3x 2＋6－a x ＋aex， 令g (x )＝－3x 2＋(6－a )x ＋a ，由g (x )＝0解得x 1＝6－a －a 2＋366，x 2＝6－a ＋a 2＋366.9分当x <x 1时，g (x )<0，即f ′(x )<0，故f (x )为减函数； 当x 1<x <x 2时，g (x )>0，即f ′(x )>0，故f (x )为增函数； 当x >x 2时，g (x )<0，即f ′(x )<0，故f (x )为减函数.11分由f (x )在[3，＋∞)上为减函数，知x 2＝6－a ＋a 2＋366≤3，解得a ≥－92.故a 的取值X 围为⎣⎢⎡⎭⎪⎫－92，＋∞.14分2.(2017·某某模拟)设函数f (x )＝e xx2－k ⎝ ⎛⎭⎪⎫2x ＋ln x (k 为常数，e ＝2.718 28…是自然对数的底数)．(1)当k ≤0时，求函数f (x )的单调区间；(2)若函数f (x )在(0,2)内存在两个极值点，求k 的取值X 围． [解] (1)函数y ＝f (x )的定义域为(0，＋∞)．f ′(x )＝x 2e x －2x e x x 4－k ⎝ ⎛⎭⎪⎫－2x 2＋1x＝x e x －2e x x 3－k x －2x 2＝x －2e x－kx x 3.由k ≤0可得e x－kx >0，所以当x ∈(0,2)时，f ′(x )<0，函数y ＝f (x )单调递减，当x ∈(2，＋∞)时，f ′(x )>0，函数y ＝f (x )单调递增．所以f (x )的单调递减区间为(0,2)，单调递增区间为(2，＋∞).6分 (2)由(1)知，k ≤0时，函数f (x )在(0,2)内单调递减， 故f (x )在(0,2)内不存在极值点；当k >0时，设函数g (x )＝e x－kx ，x ∈[0，＋∞)． 因为g ′(x )＝e x－k ＝e x－e ln k，当0<k ≤1时，当x ∈(0,2)时，g ′(x )＝e x－k >0，y ＝g (x )单调递增， 故f (x )在(0,2)内不存在两个极值点； 当k >1时，得x ∈(0，ln k )时，g ′(x )<0，函数y ＝g (x )单调递减，x ∈(ln k ，＋∞)时，g ′(x )>0，函数y ＝g (x )单调递增．所以函数y ＝g (x )的最小值为g (ln k )＝k (1－ln k )． 函数f (x )在(0,2)内存在两个极值点，当且仅当⎩⎪⎨⎪⎧g 0>0，g ln k <0，g 2>0，0<ln k <2，解得e<k <e22.13分综上所述，函数f (x )在(0,2)内存在两个极值点时，k 的取值X 围为⎝ ⎛⎭⎪⎫e ，e 22. 14分3.(2016·全国卷Ⅰ)已知函数f (x )＝(x －2)e x＋a (x －1)2. (1)讨论f (x )的单调性；(2)若f (x )有两个零点，求a 的取值X 围．[解] (1)f ′(x )＝(x －1)e x＋2a (x －1)＝(x －1)(e x＋2a ).1分 (ⅰ)设a ≥0，则当x ∈(－∞，1)时，f ′(x )＜0； 当x ∈(1，＋∞)时，f ′(x )＞0.所以f (x )在(－∞，1)上单调递减，在(1，＋∞)上单调递增.3分 (ⅱ)设a ＜0，由f ′(x )＝0得x ＝1或x ＝ln(－2a )． ①若a ＝－e 2，则f ′(x )＝(x －1)(e x－e)，所以f (x )在(－∞，＋∞)上单调递增． ②若a ＞－e2，则ln(－2a )＜1，故当x ∈(－∞，ln(－2a ))∪(1，＋∞)时，f ′(x )＞0； 当x ∈(ln(－2a )，1)时，f ′(x )＜0.所以f (x )在(－∞，ln(－2a ))，(1，＋∞)上单调递增，在(ln(－2a )，1)上单调递减.5分③若a ＜－e2，则ln(－2a )＞1，故当x ∈(－∞，1)∪(ln(－2a )，＋∞)时，f ′(x )＞0； 当x ∈(1，ln(－2a ))时，f ′(x )＜0.所以f (x )在(－∞，1)，(ln(－2a )，＋∞)上单调递增，在(1，ln(－2a ))上单调递减.7分(2)(ⅰ)设a ＞0，则由(1)知，f (x )在(－∞，1)上单调递减，在(1，＋∞)上单调递增．又f (1)＝－e ，f (2)＝a ，取b 满足b ＜0且b ＜ln a 2，则f (b )＞a 2(b －2)＋a (b －1)2＝a ⎝ ⎛⎭⎪⎫b 2－32b ＞0，所以f (x )有两个零点.9分(ⅱ)设a ＝0，则f (x )＝(x －2)e x，所以f (x )只有一个零点．(ⅲ)设a ＜0，若a ≥－e2，则由(1)知，f (x )在(1，＋∞)上单调递增．又当x ≤1时f (x )＜0，故f (x )不存在两个零点；若a ＜－e2，则由(1)知，f (x )在(1，ln(－2a ))上单调递减，在(ln(－2a )，＋∞)上单调递增．又当x ≤1时，f (x )＜0，故f (x )不存在两个零点．综上，a 的取值X 围为(0，＋∞).14分4.(2017·某某模拟)已知函数f (x )＝a ln x －ax －3(a ∈R )． (1)求函数f (x )的单调区间；(2)若函数y ＝f (x )的图象在点(2，f (2))处的切线的倾斜角为45°，对于任意的t ∈[1,2]函数g (x )＝x 3＋x 2⎣⎢⎡⎦⎥⎤f ′x ＋m 2在区间(t,3)上总不是单调函数，求m 的取值X 围；(3)求证：ln 22×ln 33×ln 44×…×ln n n <1n (n ≥2，n ∈N ＋). 【导学号：62172117】[解] (1)f ′(x )＝a 1－xx(x >0)． 当a >0时，f (x )的单调增区间为(0,1]，减区间为[1，＋∞)； 当a <0时，f (x )的单调增区间为[1，＋∞)，减区间为(0,1]； 当a ＝0时，f (x )不是单调函数.4分(2)由f ′(2)＝－a 2＝1得a ＝－2，∴f ′(x )＝2x －2x.∴g (x )＝x 3＋⎝ ⎛⎭⎪⎫m2＋2x 2－2x ，∴g ′(x )＝3x 2＋(m ＋4)x －2.∵g (x )在区间(t,3)上总不是单调函数，且g ′(0)＝－2， ∴⎩⎪⎨⎪⎧g ′t <0，g ′3>0.由题意知：对于任意的t ∈[1,2]，g ′(t )<0恒成立，所以有：⎩⎪⎨⎪⎧g ′1<0，g ′2<0，g ′3>0，∴－373<m <－9.8分(3)证明：令a ＝－1，此时f (x )＝－ln x ＋x －3，所以f (1)＝－2，由(1)知f (x )＝－ln x ＋x －3在(1，＋∞)上单调递增，∴当x ∈(1，＋∞)时f (x )>f (1)，即－ln x ＋x －1>0，∴ln x <x －1对一切x ∈(1，＋∞)成立，∵n ≥2，n ∈N ＋，则有0<ln n <n －1，∴0<ln n n <n －1n.word11 / 11 ∴ln 22×ln 33×ln 44×ln n n <12×23×34×…×n －1n ＝1n(n ≥2，n ∈N ＋).16分。

课时作业(十八)一、选择题1．设f (n )＝1＋12＋13＋…＋13n －1(n ∈N *)，那么f (n ＋1)－f (n )等于( )A.13n ＋2B.13n ＋13n ＋1C.13n ＋1＋13n ＋2D.13n ＋13n ＋1＋13n ＋2答案 D2．已知1＋2×3＋3×32＋4×33＋…＋n ×3n －1＝3n (na －b )＋c 对一切n ∈N *都成立，则a 、b 、c 的值为( )A ．a ＝12，b ＝c ＝14B ．a ＝b ＝c ＝14C ．a ＝0，b ＝c ＝14D ．不存在这样的a 、b 、c答案 A解析 ∵等式对一切n ∈N *均成立， ∴n ＝1,2,3时等式成立，即⎩⎪⎨⎪⎧1＝3a －b ＋c ，1＋2×3＝322a －b ＋c ，1＋2×3＋3×32＝333a －b ＋c ，整理得⎩⎪⎨⎪⎧3a －3b ＋c ＝1，18a －9b ＋c ＝7，81a －27b ＋c ＝34，解得a ＝12，b ＝c ＝14.3．在数列{a n }中，a 1＝13，且S n ＝n (2n －1)a n ，通过求a 2，a 3，a 4，猜想a n 的表达式为( )A.1n －1n ＋1B.12n2n ＋1C.12n －12n ＋1D.12n ＋12n ＋2答案 C解析 由a 1＝13，S n ＝n (2n －1)a n ，得S 2＝2(2×2－1)a n ，即a 1＋a 2＝6a 2， ∴a 2＝115＝13×5，S 3＝3(2×3－1)a 3，即13＋115＋a 3＝15a 3. ∴a 3＝135＝15×7，a 4＝17×9.故选C.二、填空题4．n 为正奇数时，求证：x n ＋y n被x ＋y 整除，当第二步假设n ＝2k －1命题为真时，进而需证n ＝________，命题为真．答案 2k ＋1 三、解答题5．用数学归纳法证明：当n 是不小于5的自然数时，总有2n >n 2成立． 解析 ①当n ＝5时，25>52，结论成立；②假设当n ＝k (k ∈N *，k ≥5)时，结论成立，即2k >k 2. 那么当n ＝k ＋1时，左边＝2k ＋1＝2·2k >2·k 2＝(k ＋1)2＋(k 2－2k －1)＝(k ＋1)2＋(k －1－2)(k －1＋2)>(k ＋1)2＝右边．也就是说，当n ＝k ＋1时，结论也成立．∴由①②可知，不等式2n >n 2对满足n ∈N *，n ≥5时的n 恒成立．6．设数列{a n }的前n 项和为S n ，且对任意的自然数n 都有：(S n －1)2＝a n S n . (1)求S 1，S 2，S 3；(2)猜想S n 的表达式并证明． 解析 (1)由(S 1－1)2＝S 21得：S 1＝12；由(S 2－1)2＝(S 2－S 1)S 2得：S 2＝23；由(S 3－1)2＝(S 3－S 2)S 3得：S 3＝34.(2)猜想：S n ＝nn ＋1.证明：①当n ＝1时，显然成立； ②假设当n ＝k (k ≥1且k ∈N *)时，S k ＝kk ＋1成立．则当n ＝k ＋1时，由(S k ＋1－1)2＝a k ＋1S k ＋1得：S k ＋1＝12－S k ＝12－kk ＋1＝k ＋1k ＋2， 从而n ＝k ＋1时，猜想也成立． 综合①②得结论成立．7．在数列{a n }，{b n }中，a 1＝2，b 1＝4，且a n ，b n ，a n ＋1成等差数列，b n ，a n ＋1，b n ＋1成等比数列(n ∈N *)．(1)求a 2，a 3，a 4及b 2，b 3，b 4，由此猜测{a n }，{b n }的通项公式，并证明你的结论； (2)证明：1a 1＋b 1＋1a 2＋b 2＋…＋1a n ＋b n <512. 解析 (1)由条件得 2b n ＝a n ＋a n ＋1，a 2n ＋1＝b n b n ＋1.由此可得a 2＝6，b 2＝9，a 3＝12，b 3＝16，a 4＝20，b 4＝25. 猜测a n ＝n (n ＋1)，b n ＝(n ＋1)2. 用数学归纳法证明：①当n ＝1时，由上可得结论成立． ②假设当n ＝k 时，结论成立，即a k ＝k (k ＋1)，b k ＝(k ＋1)2.那么当n ＝k ＋1时， a k ＋1＝2b k －a k ＝2(k ＋1)2－k (k ＋1)＝(k ＋1)(k ＋2)， b k ＋1＝a 2k ＋1b k＝(k ＋2)2.所以当n ＝k ＋1时，结论也成立．由①②，可知a n ＝n (n ＋1)，b n ＝(n ＋1)2对一切正整数都成立． (2)1a 1＋b 1＝16<512. n ≥2时，由(1)知a n ＋b n ＝(n ＋1)(2n ＋1)>2(n ＋1)·n .故1a 1＋b 1＋1a 2＋b 2＋…＋1a n ＋b n<16＋12(12×3＋13×4＋…＋1nn ＋1) ＝16＋12(12－13＋13－14＋…＋1n －1n ＋1) ＝16＋12(12－1n ＋1)<16＋14＝512. 8．已知数列{a n }的各项都是正数，且满足：a 0＝1，a n ＋1＝12a n ·(4－a n )，(n ∈N)．证明：a n <a n ＋1<2，(n ∈N)．证明 解法一 用数学归纳法证明： (1)当n ＝0时，a 0＝1，a 1＝12a 0(4－a 0)＝32，所以a 0<a 1<2，命题正确．(2)假设n ＝k 时命题成立，即a k －1<a k <2. 则当n ＝k ＋1时，a k －a k ＋1＝12a k －1(4－a k －1)－12a k (4－a k ) ＝2(a k －1－a k )－12(a k －1－a k )(a k －1＋a k )＝12(a k －1－a k )(4－a k －1－a k )． 而a k －1－a k <0,4－a k －1－a k >0，所以a k －a k ＋1<0. 又a k ＋1＝12a k (4－a k )＝12[4－(a k －2)2]<2.所以n ＝k ＋1时命题成立．由(1)(2)可知，对一切n ∈N 时有a n <a n ＋1<2. 解法二 用数学归纳法证明：(1)当n ＝0时，a 0＝1，a 1＝12a 0(4－a 0)＝32，所以0<a 0<a 1<2；(2)假设n ＝k 时有a k －1<a k <2成立，令f (x )＝12x (4－x )，f (x )在[0,2]上单调递增，所以由假设有：f (a k －1)<f (a k )<f (2)， 即12a k －1(4－a k －1)<12a k (4－a k )<12×2×(4－2)， 也即当n ＝k ＋1时，a k <a k ＋1<2成立． 所以对一切n ∈N ，有a k <a k ＋1<2.9．(09·安徽)首项为正数的数列{a n }满足a n ＋1＝14(a 2n ＋3)，n ∈N *.(Ⅰ)证明：若a 1为奇数，则对一切n ≥2，a n 都是奇数； (Ⅱ)若对一切n ∈N *都有a n ＋1>a n ，求a 1的取值范围．解析 (Ⅰ)已知a 1是奇数，假设a k ＝2m －1是奇数，其中m 为正整数， 则由递推关系得a k ＋1＝a 2k ＋34＝m (m －1)＋1是奇数．根据数学归纳法可知，对任何n ∈N *，a n 是奇数．(Ⅱ)解法一 由a n ＋1－a n ＝14(a n －1)(a n －3)知，当且仅当a n <1或a n >3时，a n ＋1>a n .另一方面，若0<a k <1，则0<a k ＋1<1＋34＝1；若a k >3，则a k ＋1>32＋34＝3.根据数学归纳法可知∀n ∈N *,0<a 1<1⇔0<a n <1；∀n ∈N *，a 1>3⇔a n >3. 综上所述，对一切n ∈N *都有a n ＋1>a n 的充要条件是0<a 1<1或a 1>3.解法二 由a 2＝a 21＋34>a 1，得a 21－4a 1＋3>0，于是0<a 1<1或a 1>3. a n ＋1－a n ＝a 2n ＋34－a 2n －1＋34＝a n ＋a n －1a n －a n －14，因为a 1>0，a n ＋1＝a 2n ＋34，所以所有的a n 均大于0，因此a n ＋1－a n 与a n －a n －1同号．根据数学归纳法可知，∀n ∈N *，a n ＋1－a n 与a 2－a 1同号． 因此，对于一切n ∈N *都有a n ＋1>a n 的充要条件是0<a 1<1或a 1>3.10．(2020·济南统考)已知等差数列{a n }的公差d 大于0，且a 2，a 5是方程x 2－12x ＋27＝0，的两根，数列{b n }的前n 项和为T n ，且T n ＝1－12b n .(1)求数列{a n }、{b n }的通项公式；(2)设数列{a n }的前n 项的和为S n ，试比较1b n与S n ＋1的大小，并说明理由．思路分析 (1)求得a 2、a 5的值即可得a n 的表达式，再利用T n －T n －1＝b n 求出{b n }的通项公式；(2)首先求出S n ＋1与1b n的表达式，先进行猜想，再进行证明．解析 (1)由已知得⎩⎪⎨⎪⎧a 2＋a 5＝12，a 2a 5＝27.又∵{a n }的公差大于0，∴a 5>a 2. ∴a 2＝3，a 5＝9. ∴d ＝a 5－a 23＝9－33＝2，a 1＝1.∵T n ＝1－12b n ，b 1＝23，当n ≥2时，T n －1＝1－12b n －1，∴b n ＝T n －T n －1＝1－12b n －(1－12b n －1)，化简，得b n ＝13b n －1，∴{b n }是首项为23，公比为13的等比数列，即b n ＝23·(13)n －1＝23n .∴a n ＝2n －1，b n ＝23n .(2)∵S n ＝1＋2n －12n ＝n 2，∴S n ＋1＝(n ＋1)2，1b n ＝3n2，以下比较1b n与S n ＋1的大小：当n ＝1时，1b 1＝32，S 2＝4，∴1b 1<S 2.当n ＝2时，1b 2＝92，S 3＝9，∴1b 2<S 3.当n ＝3时，1b 3＝272，S 4＝16，则1b 3<S 4.当n ＝4时，1b 4＝812，S 5＝25，得1b 4>S 5.猜想：n ≥4时，1b n>S n ＋1.下面用数学归纳法证明： ①当n ＝4时，已证．②假设当n ＝k (k ∈N *，k ≥4)时，1b k>S k ＋1，即3k2>(k ＋1)2， 那么，n ＝k ＋1时， 1b k ＋1＝3k ＋12＝3·3k2>3(k ＋1)2＝3k 2＋6k ＋3＝(k 2＋4k ＋4)＋2k 2＋2k －1>[(k ＋1)＋1]2＝S (k ＋1)＋1， ∴n ＝k ＋1时，1b n>S n ＋1也成立．由①②可知n ∈N *，n ≥4时，1b n>S n ＋1成立．综上所述，当n ＝1,2,3时，1b n<S n ＋1，当n ≥4时，1b n>S n ＋1.。

专题4.2 应用导数研究函数的单调性（真题测试）一、单选题1.（2022·上海松江·二模）下列函数中，与函数3y x =的奇偶性和单调性都一致的函数是（ ） A ．2yxB ．sin y x x =+C ．||2x y =D ．tan y x =【答案】B 【解析】 【分析】根据初等函数的奇偶性与单调性，再结合导数即可判断答案. 【详解】容易判断()3R y x x =∈是奇函数，且在R 上是增函数，而2||,2x y x y ==是偶函数，tan y x =在R 上不是增函数，所以排除A,C,D.对B ，函数()sin R y x x x =+∈是奇函数，且1cos 0y x '=+≥，则函数在R 上是增函数. 故选：B.2．（2015·陕西·高考真题（文））设()sin f x x x =-，则()f x =（ ） A ．既是奇函数又是减函数 B ．既是奇函数又是增函数 C ．是有零点的减函数 D ．是没有零点的奇函数【答案】B 【解析】 【详解】 试题分析：函数的定义域为，关于原点对称，，因此函数是奇函数，不恒等于0，函数是增函数，故答案为B ．3．（2016·全国·高考真题（文））函数2||2x y x e =-在[]–2,2的图象大致为（ ）A ．B ．C ．D ．【答案】D 【解析】 【详解】试题分析：函数2||()2x f x x e =-|在[–2,2]上是偶函数，其图象关于y 轴对称， 因为22(2)8e ,08e 1f =-<-<， 所以排除,A B 选项；当[]0,2x ∈时，4x y x e '=-有一零点，设为0x ，当0(0,)x x ∈时，()f x 为减函数， 当0(,2)x x ∈时，()f x 为增函数． 故选：D.4.（2009·湖南·高考真题（文））若函数()y f x =的导函数在区间[,]a b 上是增函数，则函数()y f x =在区间[,]a b 上的图象可能是（ ）A ．B ．C ．D ．【答案】A 【解析】 【详解】试题分析：∵函数y=f （x ）的导函数在区间[a ，b]上是增函数，∴对任意的a ＜x 1＜x 2＜b ，有也即在a,x 1,x 2,b 处它们的斜率是依次增大的．∴A 满足上述条件，对于B 存在使，对于C 对任意的a ＜x 1＜x 2＜b ，都有，对于D 对任意的x ∈[a ，b]，不满足逐渐递增的条件，故选A ．5．（2013·全国·高考真题（理））若函数21()f x x ax x =++在1(,)2+∞是增函数，则a 的取值范围是（ ） A ．[1,0]- B ．[1,)-+∞ C ．[0,3] D ．[3,)+∞【答案】D 【解析】 【详解】试题分析：由条件知()2120f x x a x -'=+≥在1,+2⎛⎫∞ ⎪⎝⎭上恒成立，即212a x x ≥-在1,+2⎛⎫∞ ⎪⎝⎭上恒成立． ∵函数212y x x =-在1,+2⎛⎫∞ ⎪⎝⎭上为减函数，∴max21123212y <-⨯=⎛⎫⎪⎝⎭, ∴．故选D ．6．（2015·福建·高考真题（理））若定义在R 上的函数()f x 满足()01f =-，其导函数()f x '满足()1f x k '>>，则下列结论中一定错误的是（ ） A ．11f k k⎛⎫< ⎪⎝⎭B ．111f k k ⎛⎫> ⎪-⎝⎭C ．1111f k k ⎛⎫< ⎪--⎝⎭ D ．111k f k k ⎛⎫> ⎪--⎝⎭ 【答案】C【解析】 【详解】试题分析：令()g()x f x kx =-，则()'()0g x f x k '=->，因此1111g()(0)(0)1111111k k g f f f k k k k k k ⎛⎫⎛⎫>⇒->⇒>-= ⎪ ⎪------⎝⎭⎝⎭，所以选C. 7．（2011·辽宁·高考真题（文））函数()f x 的定义域为R ，()12f -=，对任意x ∈R ，()2f x '>，则()24f x x >+的解集为（ ） A ．()1,1- B ．()1,-+∞C ．(),1-∞-D ．(),-∞+∞【答案】B 【解析】 【分析】构造函数()()24g x f x x =--，利用导数判断出函数()y g x =在R 上的单调性，将不等式()24f x x >+转化为()()1g x g >-，利用函数()y g x =的单调性即可求解. 【详解】依题意可设()()24g x f x x =--，所以()()20g x f x ''=->. 所以函数()y g x =在R 上单调递增，又因为()()11240g f -=-+-=. 所以要使()()240g x f x x =-->，即()()1g x g >-，只需要1x >-，故选B. 8．（2022·青海·模拟预测（理））若01a b <<<，则（ ） A ．e e ln ln b a b a -<- B ．e e ln ln b a b a -≥- C ．e e a b b a ≤ D ．e e a b b a >【答案】D 【解析】 【分析】对于A,B ，构造函数()e ln x f x x =-，利用导数判断其单调性，根据01a b <<<，比较()e ln ,()e ln abf a a f b b =-=-，可判断A,B ；对于C,D, 设e g()=x x x,利用导数判断其单调性，根据01a b <<<，比较(),()g a g b ，可判断C,D. 【详解】对于A,B,令()e ln x f x x =- ，则1()e xf x x '=-，当01x <<时，1()e xf x x'=-单调递增，且2132123()e 20,()e 0232f f ''=-<=-=>>故存在012(,)23x ∈ ，使得0()0f x '=，则当0(0,)x x ∈时，()e ln x f x x =-递减，当0(,1)x x ∈时，()e ln x f x x =-递增， 由于01a b <<<，此时()e ln ,()e ln a b f a a f b b =-=-大小关系不确定， 故A,B 均不正确；对于C,D,设e g()=x x x ，则e (1)g ()=x x x x -'，当01x <<时，()0g x '<，故eg()=xx x单调递减，所以当01a b <<<时，()()g a g b > ，即e ea b a b> ，即e e a b b a >，故C 错误，D 正确， 故选：D 二、多选题9．（2022·全国·模拟预测）已知定义在R 上的函数()f x 满足()()0f x f x +'>，则下列式子成立的是（ ） A ．()()20212022f ef < B ．()()20212022f ef >C ．()f x 是R 上的增函数D ．0t ∀>，则()()tf x e f x t <+【答案】AD 【解析】 【分析】构造函数()xy e f x =，由已知可得函数单调递增，即可判断选项ABD ，举特例可判断选项C.【详解】由()()0f x f x +'>，得()()0x x e f x e f x '+>，即()0x e f x '⎡⎤>⎣⎦，所以函数()x y e f x =为R 上的增函数，故()()2021202220212022e f e f <，所以()()20212022f ef <，故A 正确，B 不正确；函数()xe f x 为增函数时，()f x 不一定为增函数，如()12x f x =，显然()x e f x 是增函数，但()f x 是减函数，所以C 不正确；因为函数()x e f x 为增函数，所以0t >时，有()()x x t e f x e f x t +<+，故有()()tf x e f x t <+成立，所以D 正确.故选：AD.10．（2022·湖北·模拟预测）已知正实数a ，b ，c 满足1log b ac c b a <<<，则一定有（ ）A ．1a <B ．a b <C ．b c <D ．c a <【答案】AB 【解析】 【分析】根据1b c <，1a b <可得(),0,1c b ∈，进而判断出1a c <<，A 正确； 构造()ln xf x x=，0x >得到单调性，从而求出a b <，B 正确；CD 选项可以举出反例. 【详解】由正实数a ，b ，c ，以及1b c <，1a b <可得(),0,1c b ∈， 又log 1log c c a c >=，所以1a c <<． 所以b b a c <，又b a c b <，所以b a a b <， 即ln ln b a a b <，等价于ln ln a ba b<， 构造函数()ln xf x x=，0x > ()21ln xf x x -'=， 当()0,1x ∈时，()21ln 0xf x x -'=> 故()ln xf x x=在()0,1上递增，从而a b <． 又取b c =时，原式为1log b ab b b a <<<同样成立，故CD 不正确，故选：AB 11．（2022·辽宁沈阳·二模）已知奇函数()f x 在R 上可导，其导函数为()f x '，且()()1120f x f x x --++=恒成立，若()f x 在[]0,1单调递增，则（ ）A ．()f x 在[]1,2上单调递减B ．()00f =C ．()20222022f =D ．()20231f '=【答案】BCD 【解析】 【分析】根据函数的的对称性和周期性，以及函数的导数的相关性质，逐个选项进行验证即可. 【详解】 方法一：对于A ，若()f x x =，符合题意，故错误，对于B ，因已知奇函数()f x 在R 上可导，所以()00f =，故正确， 对于C 和D ，设()()g x f x x =-，则()g x 为R 上可导的奇函数，()00g =，由题意()()1111f x x f x x -+-=+--，得()()11g x g x -=+，()g x 关于直线1x =对称， 易得奇函数()g x 的一个周期为4，()()()2022200g g g ===，故C 正确，由对称性可知，()g x 关于直线1x =-对称，进而可得()10g '-=，（其证明过程见备注） 且()g x '的一个周期为4，所以()()202310g g '='-=，故D 正确．备注：()()11g x g x -=+，即()()11g x g x --=-+，所以()()11g x g x -+=--， 等式两边对x 求导得，()()11g x g x '-+=-'--， 令0x =，得()()11g g '-=-'-，所以()10g '-=． 方法二：对于A ，若()f x x =，符合题意，故错误，对于B ，因已知奇函数()f x 在R 上可导，所以()00f =，故正确，对于C ，将()()1120f x f x x --++=中的x 代换为1x +，得()()2220f x f x x --+++=，所以()()222f x f x x ++=+，可得()()4226f x f x x +++=+，两式相减得，()()44f x f x +-=，则()()624f f -=，()()1064f f -=，…，()()202220184f f -=， 叠加得()()202222020f f -=，又由()()222f x f x x ++=+，得()()2022f f =-+=， 所以()()2022220202022f f =+=，故正确，对于D ，将()()1120f x f x x --++=的两边对x 求导，得()()1120f x f x ''---++=， 令0x =得，()11f '=，将()()f x f x --=的两边对x 求导，得()()f x f x '-='，所以()11f '-=， 将()()44f x f x +-=的两边对x 求导，得()()4f x f x ''+=， 所以()()()2023201911f f f '''==⋅⋅⋅=-=，故正确． 故选：BCD12．（2021·福建·福州三中高三阶段练习）已知函数()xf x xe ax =+.则下列说法正确的是（ ）A ．当0a =时，min ()0f x =B ．当1a =时，直线2y x =与函数()f x 的图像相切C ．若函数()f x 在区间[)0,∞+上单调递增，则0a ≥D ．若在区间[]0,1上，()2f x x ≤恒成立，则1a e -≤【答案】BD 【解析】 【分析】对于A ：当0a =时，()e xf x x =，求导函数，分析导函数的符号，得出函数()f x 的单调性，从而求得函数()f x 的最小值；对于B ：当1a =时，()e +xf x x x '=，求导函数，设切点为()00,x y ，则过切点的切线方程为：()()()0000000e +e +e +1x x x y x x x x x -=-，由切线过原点，求得00x =，继而求得过原点的切线方程；对于C ：问题等价于()+e 0xf x x x a '=+≥在区间[)0,∞+上恒成立，分离参数得e x a x x ≥--在区间[)0,∞+上恒成立，令()e xg x x x =--，求导函数，分析导函数的符号，得函数()g x 的单调性和最值，由此可判断；对于D ：问题等价于2e x x x ax +≤在区间[]0,1上恒成立，0x =时，不等式恒成立；当01x <≤时，分离参数e x a x ≤-，令()e xh x x =-，求导函数，分析()h x '的符号，得函数()h x 的单调性和最值，由此可判断.【详解】对于A ，当0a =时，()()()e ,1e x xf x x f x x ==+'，易知函数()f x 在(),1-∞-上单调递减，在()1,-+∞上单调递增，()min 1()1ef x f ∴=-=-，故选项A 不正确；对于B ，当1a =时，()()()()e ,1e 1,02x xf x x x f x x f +''=+=+=，∴函数()f x 在()0,0处的切线方程为2y x =，故选项B 正确；对于C ，()()1e xf x x a =++'，若函数()f x 在区间[)0,∞+上单调递增，则()0f x '在[)0,∞+上恒成立，()1e x a x ∴-+，令()()1e ,0x g x x x =-+，则()()2e 0x g x x =-+<'， ∴函数()g x 在[)0,∞+上单调递减，()max ()01a g x g ∴==-，故选项C 错误；对于D ，当0x =时，a ∈R 恒成立；当(]0,1x ∈时，()2f x x 恒成立等价于2e x x ax x +恒成立，即e x a x +，即e x a x -恒成立，设()e ,01x h x x x =-<，则()10e xh x '=-<在(]0,1上恒成立，()h x ∴在(]0,1上单调递减，()min ()11e a h x h ∴==-，故选项D 正确.故选：BD. 三、填空题13．（2009·江苏·高考真题）函数32()15336f x x x x =--+的单调减区间为_____. 【答案】(1,11)- 【解析】 【详解】f ′(x )＝3x 2－30x －33＝3(x －11)(x ＋1)，令f ′(x )＜0，得－1＜x ＜11，所以单调减区间为(－1,11)．14．（2022·河北衡水·高三阶段练习）已知函数()f x 的导函数为'()f x ，定义域为(0,)+∞，且满足'()()0xf x f x -<，则不等式2(2022)(2022)(2)f m m f ->-恒成立时m 的取值范围为__________. 【答案】()2022,2024【解析】 【分析】 设()()f x F x x=，根据题意得到()0F x '<，得出函数()F x 在(0,)+∞上单调递减，结合不等式2(2022)(2022)(2)f m m f ->-，得到020222m <-<，即可求解.【详解】由题意，函数()f x 的定义域为(0,)+∞，因为()()0xf x f x '-<，可得2()'()()'0f x xf x f x x x -⎡⎤=<⎢⎥⎣⎦， 设()()f x F x x=，可得()0F x '<，所以函数()F x 在(0,)+∞上单调递减，又由2(2022)(2022)(2)f m m f ->-，所以20220m ->，且(2022)(2)20222f m f m ->-，则020222m <-<，解得20222024m <<，即m 的取值范围为()2022,2024. 故答案为：()2022,2024.15．（2022·江苏盐城·三模）已知()f x '为()f x 的导函数，且满足()01f =，对任意的x 总有()()22f x f x '->，则不等式()223xf x e +≥的解集为__________． 【答案】[)0,+∞##{|0}x x ≥ 【解析】 【分析】 构造新函数()()22exf xg x +=，利用已知条件()()22f x f x '->，可以判断()g x 单调递增，利用()g x 的单调性即可求出不等式的解集 【详解】设函数()()22e x f x g x +=，则()()()()222221()22222e x x x x f x e e f x f x f x g x e '⋅-⋅⋅+⎡⎤⎣⎦'--'==⎛⎫ ⎪⎝⎭又()()22f x f x '-> ()0g x '∴>所以()g x 在R 上单调递增，又()()0023g f =+=故不等式2()23xf x e +≥ 可化为()(0)g x g ≥ 由()g x 的单调性可得该不等式的解集为[)0,+∞． 故答案为：[)0,+∞16．（2022·浙江·海亮高级中学模拟预测）已知函数()33x f x ax b =-+，则对任意的x ∈R ，存在a 、b （其中a 、b ∈R 且1a ≥），能使以下式子恒成立的是___________.①()()221f x f x ≤+；②()()2021f x f x +-=；③()()21f x f a -≤+；④()()221a f x f ->-.【答案】①②③ 【解析】 【分析】取1a =-，0b =，利用导数研究函数()f x 的单调性，可判断①；取20212=b 可判断②；取1a =-，利用导数研究函数()f x 的单调性，可判断③；分1a ≤-、1a ≥两种情况讨论，利用导数分析函数()f x 的单调性，可判断④. 【详解】对于①，取1a =-，0b =，则()33x f x x =+，()210f x x '=+>，所以，函数()f x 在R 上为增函数，因为()221210x x x +-=-≥，即221x x ≤+，故()()221f x f x ≤+恒成立，①对；对于②，取1a =-，20212=b ，则()3202132x f x x =++，所以，()()33202120213232x x f x x x --=-+=--+，则()()2021f x f x +-=，②对； 对于③，当1a =-时，()33x f x x b =++，则()210f x x '=+>，所以，函数()f x 在R 上为增函数，20x -≤，故()()21f x f a -≤+，③对；对于④，当1a ≥时，()2f x x a '=-.由()0f x '>可得x <x ()0f x '<可得x <此时，函数()f x 的增区间为(,-∞、)+∞，减区间为(，所以，函数()f x 的极大值为(f b b =+>，极小值为fb b =<，20x ≥，所以，()2f x fb ≥=，1210a a --≤-<-<，所以，(()()210af f f b f->->=>，则()()221af x f ->-不恒成立；当1a ≤-时，()20f x x a '=->，则()f x 在R 上为增函数，因为20x ≥，211--≥a ，所以，()2f x 、()21af --的大小关系无法确定，④错.故答案为：①②③. 四、解答题17．（2014·全国·高考真题（文））函数f(x)=ax 3+3x 2+3x(a≠0). （1）讨论函数f(x)的单调性；（2）若函数f(x)在区间（1，2）是增函数，求a 的取值范围. 【答案】（1）见解析；（2）5[,0)(0,)4-⋃+∞【解析】 【分析】 【详解】试题分析：（1）首先求出函数的导数，然后求出使()0f x '>或()0f x '<的解集即可. （2）分类讨论在区间（1，2）上使()0f x '>成立的条件，并求出参数a 的取值范围即可 试题解析：（1）2()363f x ax x '=++，2()3630f x ax x ++'==的判别式△=36（1-a ）. （i ）若a≥1，则()0f x '≥，且()0f x '=当且仅当a=1，x=-1，故此时f （x ）在R 上是增函数.（ii ）由于a≠0，故当a<1时，()0f x '=有两个根：12x x ==， 若0<a<1,则当x ∈（－∞，x 2）或x ∈（x 1，+∞）时，()0f x '>，故f （x ）在（－∞，x 2），（x 1，+∞）上是增函数；当x ∈（x 2，x 1）时，()0f x '<，故f （x ）在（x 2，x 1）上是减函数；若a<0，则当x ∈（－∞，x 2）或x ∈（x 1，+∞）时，()0f x '<，故f （x ）在（－∞，x 2），（x 1，+∞）上是减函数；当x ∈（x 2，x 1）时，()0f x '>，故f （x ）在（x 2，x 1）上是增函数；（2）当a>0，x>0时,()0f x '>，所以当a>0时，f （x ）在区间（1，2）是增函数. 若a<0时，f （x ）在区间（1,2）是增函数当且仅当(1)0f '≥且(2)0f '≥，解得504a -≤<.综上，a 的取值范围是5[,0)(0,)4-⋃+∞.18．（2008·四川·高考真题（文））设1x =和2x =是函数()531f x x ax bx =+++的两个极值点．（1）求a 和b 的值；（2）求()f x 的单调区间 【答案】（1）25,203a b =-= （2）单调增区间是()()(),2,1,1,2,-∞--+∞，单调减区间是()()2,1,1,2-- 【解析】 【分析】（1）根据极值点为导函数的零点，且在零点两边导函数符号相反，列出方程组，求出a 和b 的值，代入检验是否符合要求；（2）在第一问的基础上求出导函数，解不等式，求出单调区间. 【详解】（1）因为()4253f x x ax b =++'，由题设知：()1530f a b '=++=()42225230f a b =⨯⨯+'+=，解得：25,203a b =-=，此时()53252013f x x x x +-=+，()()()422252520514f x x x x x =+=-'--，令()0f x '>得：2x <-或11x -<<或2x >，令()0f x '<得：21x -<<-或12x <<，故1x =是函数的极大值点，2x =是函数的极小值点，满足要求，综上：25,203a b =-=； （2）由（1）知()()()()()()()42245351451212f x x ax b x x x x x x =++=--=++--'当()()(),21,12,x ∈-∞-⋃-⋃+∞时，()0f x '>；当()()2,11,2x ∈--⋃时，()0f x '<. 因此()f x 的单调增区间是()()(),2,1,1,2,-∞--+∞，()f x 的单调减区间是()()2,1,1,2-- 19．（2017·全国·高考真题（文））已知函数f (x )＝e x (e x －a )－a 2x ，其中参数a ≤0. (1)讨论f (x )的单调性； (2)若f (x )≥0，求a 的取值范围.【答案】(1) f (x )在,ln 2⎛⎫⎛⎫-∞- ⎪ ⎪⎝⎭⎝⎭a 上单调递减，在区间ln ,2⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭a 上单调递增.（2）3420e ⎡⎤-⎢⎥⎣⎦，【解析】 【分析】(1)求f (x )的导函数为f ′(x )＝(2e x ＋a )(e x －a )，通过讨论a ，求函数的单调区间即可. (2)因为f (x )≥0，所以即求f (x )的最小值大于等于0，由第(1)的结果求的f (x )的最小值，解关于a 的不等式即可求出a 的范围. 【详解】(1)函数f (x )的定义域为(－∞，＋∞)，且a ≤0. f ′(x )＝2e 2x －a e x －a 2＝(2e x ＋a )(e x －a ).①若a ＝0，则f (x )＝e 2x ，在(－∞，＋∞)上单调递增.②若a <0，则由f ′(x )＝0，得x ＝ln 2a ⎛⎫- ⎪⎝⎭.当x ∈,ln 2⎛⎫⎛⎫-∞- ⎪ ⎪⎝⎭⎝⎭a 时，f ′(x )<0；当x ∈ln ,2⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭a 时，f ′(x )>0.故f (x )在,ln 2⎛⎫⎛⎫-∞- ⎪ ⎪⎝⎭⎝⎭a 上单调递减，在区间ln ,2⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭a 上单调递增.(2)①当a ＝0时，f (x )＝e 2x ≥0恒成立.②若a <0，则由(1)得，当x ＝ln 2a ⎛⎫- ⎪⎝⎭时，f (x )取得最小值，最小值为f ln 2a ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭＝a 23ln 42a ⎡⎤⎛⎫-- ⎪⎢⎥⎝⎭⎣⎦，故当且仅当a 23ln 42a ⎡⎤⎛⎫-- ⎪⎢⎥⎝⎭⎣⎦≥0，即0>a ≥342e -时，f (x )≥0. 综上a 的取值范围是[342e -，0]. 20．（2014·山东·高考真题（文））设函数若，求曲线处的切线方程；讨论函数的单调性.【答案】（1）210x y --=.（2）当0a ≥时，函数()f x 在(0,)+∞上单调递增；当12a ≤-时，函数()f x 在(0,)+∞上单调递减；当102a -<<时，()f x 在，)+∞上单调递减，在上单调递增.【解析】 【详解】试题分析：（1）由题意知0a =时，1(),(0,)1x f x x x -=∈+∞+，求切线的斜率，即1(1)2f '=，又(1)0f =，由直线方程的点斜式进一步整理，得到切线方程为210x y --=.（2）函数()f x 的定义域为(0,)+∞，2222(22)()(1)(1)a ax a x af x x x x x +++'=+=++，根据a 的不同情况，讨论导函数值的正负，以确定函数的单调性.其中0a ≥时，情况较为单一，()0f x '>，函数()f x 在(0,)+∞上单调递增， 当0a <时，令2()(22)g x ax a x a =+++，由于22(22)44(21)a a a ∆=+-=+，再分12a =-，12a <-，102a -<<等情况加以讨论.试题解析：（1）由题意知0a =时，1(),(0,)1x f x x x -=∈+∞+， 此时22()(1)f x x ='+，可得1(1)2f '=，又(1)0f =， 所以曲线()y f x =在(1,(1))f 处的切线方程为210x y --=. （2）函数()f x 的定义域为(0,)+∞， 2222(22)()(1)(1)a ax a x af x x x x x +++'=+=++，当0a ≥时，()0f x '>，函数()f x 在(0,)+∞上单调递增， 当0a <时，令2()(22)g x ax a x a =+++， 由于22(22)44(21)a a a ∆=+-=+， 当12a =-时，0∆=，221(1)2()0(1)x f x x x --=≤+'，函数()f x 在(0,)+∞上单调递减，当12a <-时，0,()0g x ∆<<，()0f x '<，函数()f x 在(0,)+∞上单调递减，当102a -<<时，0∆>，设1212,()x x x x <是函数()g x 的两个零点，则1x =2x =由1x =0=>，所以1(0,)x x ∈时，()0,()0g x f x '<<，函数()f x 单调递减， 12(,)x x x ∈时，()0,()0g x f x '>>，函数()f x 单调递增，2(,)x x ∈+∞时，()0,()0g x f x '<<，函数()f x 单调递减，综上可知，当0a ≥时，函数()f x 在(0,)+∞上单调递增； 当12a ≤-时，函数()f x 在(0,)+∞上单调递减；当102a -<<时，()f x 在，)+∞上单调递减，在上单调递增.21．（2021·全国·高考真题（理））已知0a >且1a ≠，函数()(0)ax x f x x a =>．（1）当2a =时，求()f x 的单调区间；（2）若曲线()y f x =与直线1y =有且仅有两个交点，求a 的取值范围． 【答案】（1）20,ln2⎛⎤⎥⎝⎦上单调递增；2,ln2⎡⎫+∞⎪⎢⎣⎭上单调递减；（2）()()1,,+∞e e .【解析】 【分析】（1）求得函数的导函数，利用导函数的正负与函数的单调性的关系即可得到函数的单调性；（2）方法一：利用指数对数的运算法则，可以将曲线()y f x =与直线1y =有且仅有两个交点等价转化为方程ln ln x ax a =有两个不同的实数根，即曲线()y g x =与直线ln a y a=有两个交点，利用导函数研究()g x 的单调性，并结合()g x 的正负，零点和极限值分析()g x 的图象，进而得到ln 10a a e<<，发现这正好是()()0g a g e <<，然后根据()g x 的图象和单调性得到a 的取值范围.【详解】（1）当2a =时，()()()()22222ln 2222ln 2,242xx x x x x x x x x x f x f x ⋅-⋅-⋅===', 令()'0f x =得2ln 2x =,当20ln 2x <<时，()0f x '>,当2ln 2x >时，()0f x '<, ∴函数()f x 在20,ln2⎛⎤⎥⎝⎦上单调递增；2,ln2⎡⎫+∞⎪⎢⎣⎭上单调递减； （2）[方法一]【最优解】：分离参数()ln ln 1ln ln a x a x x x af x a x x a a x a x a==⇔=⇔=⇔=,设函数()ln x g x x =, 则()21ln xg x x -'=,令()0g x '=，得x e =, 在()0,e 内()0g x '>,()g x 单调递增；在(),e +∞上()0g x '<,()g x 单调递减；()()1max g x g e e∴==,又()10g =，当x 趋近于+∞时，()g x 趋近于0，所以曲线()y f x =与直线1y =有且仅有两个交点，即曲线()y g x =与直线ln ay a=有两个交点的充分必要条件是ln 10a a e<<,这即是()()0g a g e <<, 所以a 的取值范围是()()1,,+∞e e .[方法二]：构造差函数由()y f x =与直线1y =有且仅有两个交点知()1f x =，即a x x a =在区间(0,)+∞内有两个解，取对数得方程ln ln a x x a =在区间(0,)+∞内有两个解．构造函数()ln ln ,(0,)g x a x x a x =-∈+∞，求导数得ln ()ln a a x a g x a x x'-=-=． 当01a <<时，ln 0,(0,),ln 0,()0,()a x a x a g x g x '<∈+∞->>在区间(0,)+∞内单调递增，所以，()g x 在(0,)+∞内最多只有一个零点，不符合题意； 当1a >时，ln 0a >，令()0g x '=得ln a x a =，当0,ln a x a ⎛⎫∈ ⎪⎝⎭时，()0g x '>；当,ln a x a ⎛⎫∈+∞ ⎪⎝⎭时，()0g x '<；所以，函数()g x 的递增区间为0,ln a a ⎛⎫ ⎪⎝⎭，递减区间为,ln a a ⎛⎫+∞⎪⎝⎭． 由于1110e1,e 1e ln 0ln aaa a g a a ---⎛⎫<<<=--< ⎪⎝⎭，当x →+∞时，有ln ln a x x a <，即()0g x <，由函数()ln ln g x a x x a =-在(0,)+∞内有两个零点知ln 10ln ln a a g a a a ⎛⎫⎛⎫=->⎪ ⎪⎝⎭⎝⎭，所以e ln aa >，即eln 0a a ->．构造函数()eln h a a a =-，则e e()1a h a a a'-=-=，所以()h a 的递减区间为(1,e)，递增区间为(e,)+∞，所以()(e)0h a h ≥=，当且仅当e a =时取等号，故()0>h a 的解为1a >且e a ≠．所以，实数a 的取值范围为(1,e)(e,)⋃+∞． [方法三]分离法：一曲一直曲线()y f x =与1y =有且仅有两个交点等价为1ax xa=在区间(0,)+∞内有两个不相同的解．因为a x x a =，所以两边取对数得ln ln a x x a =，即ln ln x a x a=，问题等价为()ln g x x =与ln ()x ap x a =有且仅有两个交点．①当01a <<时，ln 0,()ap x a<与()g x 只有一个交点，不符合题意． ②当1a >时，取()ln g x x =上一点()()000011,ln ,(),,()x x g x g x g x xx ''==在点()00,ln x x 的切线方程为()0001ln y x x x x -=-，即0011ln y x x x =-+． 当0011ln y x x x =-+与ln ()x a p x a =为同一直线时有00ln 1,ln 10,a ax x ⎧=⎪⎨⎪-=⎩得0ln 1,e e.a a x ⎧=⎪⎨⎪=⎩ 直线ln ()x a p x a =的斜率满足：ln 1e0a a <<时，()ln g x x =与ln ()x ap x a =有且仅有两个交点．记2ln 1ln (),()a a h a h a a a'-==，令()0h a '=，有e a =．(1,e),()0,()a h a h a '∈>在区间(1,e)内单调递增；(e,),()0,()a h a h a '∈+∞<在区间(,)e +∞内单调递减；e a =时，()h a 最大值为1(e)eg =，所当1a >且e a ≠时有ln 1e0a a <<． 综上所述，实数a 的取值范围为(1,e)(e,)⋃+∞． [方法四]：直接法()112ln (ln )()(0),()a a x x a a x xx x ax a a a x x a x a f x x f x a a a --'⋅-⋅-=>==． 因为0x >，由()0f x '=得ln a x a=． 当01a <<时，()f x 在区间(0,)+∞内单调递减，不满足题意；当1a >时，0ln aa >，由()0f x '>得0,()ln a x f x a<<在区间0,ln a a ⎛⎫ ⎪⎝⎭内单调递增，由()0f x '<得,()ln ax f x a >在区间,ln a a ⎛⎫+∞ ⎪⎝⎭内单调递减． 因为lim ()0x f x →+∞=，且0lim ()0x f x +→=，所以1ln a f a ⎛⎫> ⎪⎝⎭，即ln ln ln 1(ln )aaa a a a aa a a a a -⎛⎫ ⎪⎝⎭=>，即11ln ln (ln ),ln a a a a a a a a a -->>，两边取对数，得11ln ln(ln )ln a a a ⎛⎫-> ⎪⎝⎭，即ln 1ln(ln )a a ->．令ln a t =，则1ln t t ->，令()ln 1h x x x =-+，则1()1h x x'=-，所以()h x 在区间(0,1)内单调递增，在区间(1,)+∞内单调递减，所以()(1)0h x h ≤=，所以1ln t t -≥，则1ln t t ->的解为1t ≠，所以ln 1a ≠，即e a ≠． 故实数a 的范围为(1,e)(e,)⋃+∞．] 【整体点评】本题考查利用导数研究函数的单调性，根据曲线和直线的交点个数求参数的取值范围问题，属较难试题， 方法一：将问题进行等价转化，分离参数，构造函数，利用导数研究函数的单调性和最值，图象，利用数形结合思想求解.方法二：将问题取对，构造差函数，利用导数研究函数的单调性和最值. 方法三：将问题取对，分成()ln g x x =与ln ()x ap x a=两个函数，研究对数函数过原点的切线问题，将切线斜率与一次函数的斜率比较得到结论．方法四：直接求导研究极值，单调性，最值，得到结论.22．（2022·江苏江苏·三模）设函数()()2e sin 1xf x a x ax a x =+--+.(1)当0a ≤时，讨论()f x 的单调性； (2)若()f x 在R 上单调递增，求a .【答案】(1)在(),0∞-上单调递减，在()0,∞+上单调递增 (2)12 【解析】 【分析】（1）求得()()e cos 21xf x a x ax a =+--+'，设()()g x f x '=，得到()()e 2sin x g x a x +'=-，得到()y g x =在R 上单调递增，得到()y f x '=在R 上单调递增，结合()00f '=，即可求解；（2）令()e 1xh x x =--，利用导数求得()()00h x h ≥=，得到e 10x x --≥和e 1x x -≥-，令()sin x x x ϕ=-，得出0x ≥时，sin x x ≥；0x ≤，得到sin x x ≤，分0a ≤，102a <<，12a >和12a =，四种情况讨论，结合导数求得函数的单调性与最值，即可求解. (1)解：因为()()2e sin 1xf x a x ax a x =+--+，可得()()e cos 21x f x a x ax a =+--+'，设()()g x f x '=，则()()e 2sin xg x a x +'=-所以当0a ≤时，()0g x '>，函数()y g x =在R 上单调递增， 即函数()y f x '=在R 上单调递增，又由()00f '=，所以当0x <时，()0f x '<；当0x >时，()0f x '>，所以当0a ≤时，()f x 在(),0∞-上单调递减，在()0,∞+上单调递增. (2)解：令()e 1x h x x =--，可得()e 1xh x '=-，当0x >时，()0h x '>，()h x 单调递增； 当0x <时，()0h x '<，()h x 单调递减，又由()00h =，所以()()00h x h ≥=，即e 10x x --≥， 所以e 1x x ≥+，所以e 1x x -≥-；令()sin x x x ϕ=-，可得()1cos 0x x ϕ'=-≥，所以函数()x ϕ单调递增， 因为()00ϕ=，当0x ≥，可得()()00x ϕϕ≥=，即sin 0x x -≥，即sin x x ≥； 当0x ≤，可得()()00x ϕϕ≤=，即sin 0x x -≤，即sin x x ≤， （2.1）当0a ≤时，由（1）知不合题意；（2.2）当102a <<时，若(),0x ∈-∞，()()e cos 21xf x a x ax a =+--+'()1cos 211a x ax a x≤+--+- 121212111ax x a a ax a x x⎡⎤⎛⎫-- ⎪⎢⎥⎝⎭⎣⎦≤+---=--； 当1102x a-<<时，()0f x '<，()f x 单调递减，不合题意； （2.3）当12a >时，若()0,1x ∈，同理可得()12121ax x a f x x⎡⎤⎛⎫-- ⎪⎢⎝⎣'⎥⎭⎦≤-， 当1012x a<<-时，()0f x '<，()f x 单调递减，不合题意； （2.4）当12a =时，()2113e sin 222x f x x x x =+--，可得()13e cos 22xf x x x =+--'， 设()()g x f x '=，则()1e sin 12xg x x '=--，①当0x >时，()111e sin 11sin 10222xg x x x x x x =-'-≥+--≥->，所以()g x 在()0,∞+上单调递增，()f x '在()0,∞+上单调递增， ②当0x >时，若[)1,0x ∈-，()()()1111e sin 11021221x x x g x x x x x +=--≤--=≤--'， 若(],1x ∈-∞-，()111e sin 1102e 2x g x x -≤+'=--<， 所以()g x 在(),0∞-上单调递增，()f x '在(),0∞-上单调递增， 由①②可知，()()00f x f ''≥=，所以()f x 在R 上单调递增， 综上所述，12a =.。

6.4 求和方法（精练）（提升版）1．（2022·黑龙江）已知等差数列{}n a 满足a 1+a 2＝4，a 4+a 5+a 6＝27． （1）求数列{}n a 的通项公式；（2）若2nn b =，求数列{}n a b 的前n 项和S n ．【答案】（1）21n a n =-；（2）21223n +-．【解析】（1）由题意，设等差数列{}n a 的公差为d ，则112431227a d a d +=⎧⎨+=⎩∴112a d =⎧⎨=⎩，∴12(1)21n a n n =+-=-．（2）2nn b =，∴2n n aa b =，∵1124n n n n a a a a b b ---==，又112a b b ==，∴数列{}n a b 为等比数列，且首项为2，公比为4，∴()2121422143n n nS +--==-．2．（2021·四川攀枝花市）在公差不为零的等差数列{}n a 中，11a =，且125,,a a a 成等比数列. （1）求{}n a 的通项公式；（2）设12na nb ⎛⎫= ⎪⎝⎭，求数列{}n b 的前n 项和n S .【答案】（1）21n a n =-；（2）21[1()]34n n S =-. 【解析】（1）设等差数列{}n a 的公差为d ，由已知得2125a a a =⋅，则2111()(4)a d a a d +=⋅+，将11a =代入并化简得220d d -=，解得2d =或0d =(舍去).所以1(1)221n a n n =+-⨯=-.（2）由（1）知2111()()22n a n n b -==，所以2111()2n n b ++=，题组一 公式法求和所以21(21)111()24n n n n b b +--+==，即数列{}n b 是首项为12，公比为14的等比数列. 所以11[1()]2124[1()]13414n n n S -==--. 3．（2022·全国·高三专题练习）已知各项为正数的等差数列{}n a 的前n 项和为n S ，426S =，且1a ，3a ，36S a +成等比数列. (1)求n a ； (2)若1n n b S n=+，求{}n b 的前n 项和n T . 【答案】(1)31n a n =-(2)233n nT n =+ 【解析】(1)设等差数列{}n a 的公差为()0d d >，由426S =，且1a ，3a ，36S a +成等比数列可得()()12111146262335a d a d a a d a d +=⎧⎪⎨+=+++⎪⎩， 解得12a =，3d =，所以()()1123131n a a n d n n =+-=+-=-. (2)由31n a n =-可得()()()13131222n n n a a n n n n S n n n ++++=+=+=， 所以()22113131n b n n n n ⎛⎫==- ⎪++⎝⎭，所以211111111322311n T n n n n ⎛⎫=-+-++-+- ⎪-+⎝⎭21213133n n n ⎛⎫=-=⎪++⎝⎭. 1．（2022·江苏江苏·一模）已知数列{}n a ，11a =，且()111n n a a n n +=-+，*n ∈N .(1)求数列{}n a 的通项公式；(2)记数列{}2n a 的前n 项和为n S ，求证：421n nS n <+. 【答案】(1)1n a n=(2)证明见解析 题组二 裂项相消求和【解析】(1)解：因为()111n n a a n n +=-+，所有1111(1)1n n a a n n n n+-=-=-++，当2n ≥时，211121a a -=-，321132a a -=-，……，1111n n a a n n --=--， 相加得1111n a a n -=-，所以1n a n =，当1n =时，11a =也符合上式， 所以数列{}n a 的通项公式1n a n=； (2)证明：由（1）得221na n =， 所以222111111111142222n a n n n n n n =<==-⎛⎫⎛⎫--+-+ ⎪⎪⎝⎭⎝⎭， 所以222111111111111111121122222222n S n n n =++⋅⋅⋅+<-+-+⋅⋅⋅+--+-+-+， 1141121122nn n =-=+-+．所以421n nS n <+． 2．（2022·浙江台州·二模）在数列{}n a 中，12a =，且对任意的正整数n ，都有()1210n n na n a +++=. (1)证明数列n a n ⎧⎫⎨⎬⎩⎭是等比数列，并求数列{}n a 的通项公式；(2)设()132(2)n nn n n b a a ++-=，求数列{}n b 的前n 项和n S .【答案】(1)证明见解析，()112 n n n a n -=-⋅(2)()()1111212n n n S n ++-=++⋅ 【解析】(1)解：（1）由()1210n n na n a +++=，得121n n a a n n +=-⨯+.又因为12a =，所以数列n a n ⎧⎫⎨⎬⎩⎭是以2为首项，2-为公比的等比数列. 故()122n n a n-=⨯-，即()112 n n n a n -=-⋅. (2)由()112n n n a n -=-⋅，故()()()()()()()()1111322322*********nn n n n n n n n n n n b n n n n +-+++-+==-⋅⨯+⋅-⋅⨯-+⋅ ()()11111212n n n n n ++⎡⎤=-+⎢⎥⋅+⋅⎣⎦， 故123n n S b b b b =+++⋅⋅⋅+()()1223341111111111122222322232212n n n n n +-⎡⎤⎡⎤⎡⎤⎡⎤=+-+++-⋅⋅⋅+-+⎢⎥⎢⎥⎢⎥⎢⎥⨯⨯⨯⨯⨯⨯⋅+⎣⎦⎣⎦⎣⎦⎣⎦()()1111212n n n ++-=++⋅． 3．（2022·广东·广州市第四中学高三阶段练习）已知数列{}n a 满足112(1)0,4n n n a na a ++-==． (1)求数列{}n a 的通项公式；(2)设数列24n n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为n T ，求证：364n T <． 【答案】(1)12n n a n +=⋅(2)证明见解析【解析】(1)因为数列{}n a 满足112(1)0,4n n n a na a ++-==， 所以121n n a a n n +=+，所以141a=， 所以数列n a n ⎧⎫⎨⎬⎩⎭是首项为4，公比为2的等比数列，则有11422n n n a n -+=⨯=，12n n a n +=⋅.(2)()()132441111222162322+++⎛⎫===- ⎪+⋅⋅++⎝⎭n n n n n n a a n n n n n n ， 所以1111111311132324232212⎛⎫⎛⎫=-+-++-=-- ⎪ ⎪+++⎝⎭⎝⎭n T n n n n ， 因为n *∈N ，所以364n T <. 4．（2022·辽宁·沈阳市第一二〇中学高三阶段练习）已知数列{}n a 的前n 项和()12n n n a a S +=，且0n a >． (1)证明：数列{}n a 为等差数列；(2)若122nn n n n a b a a ++⋅⋅=，求数列{}n b 的前n 项和n T ．【答案】(1)证明见解析；(2)1212n n +-+. 【解析】(1)当1n =时，由()11112a a a +=，得11a =或10a =，∵0n a >，∵11a =， 由()12n n n a a S +=，得22n n n S a a =+①当2n ≥时，21112n n n S a a ---=+②由-①②，得()()22112n n n n n a a a a a --=+-+，整理得()()1110n n n n a a a a --+--=， ∵0n a >，∵1n n a a -+≠0，∵11n n a a --=， ∵数列{}n a 是首项为1，公差为1的等差数列； (2)由（1）得()111n a n n =+-⨯=， ()()11222221221n n n nn n n n a n b a a n n n n +++⋅⋅==-++⋅=++，∵213211112222222221324321222n n n n n T n n n n +++⎛⎫⎛⎫⎛⎫=-+-++-=-+=- ⎪ ⎪ ⎪++++⎝⎭⎝⎭⎝⎭． 5．（2022·陕西·模拟预测（理））已知正项等比数列{}n a 的前n 项和为n S ，且11231,2a a a a =+=，数列{}n b 满足()241n bn n a S =+．(1)证明：数列{}n b 为等差数列； (2)记n T 为数列11n n b b +⎧⎫⎨⎬⎩⎭的前n 项和，证明：11156n T ≤<．【答案】(1)证明见解析；(2)证明见解析.【解析】(1)设等比数列{}n a 的公比为q ，因为11231,2a a a a =+=，故22q q +=，解得2q =或1q =-（舍），故12n n a -=，21nn S =-，因为()241n b n n a S =+121222n n n ++=⨯=，故21n b n =+，又()123212n n b b n n +-=+-+=， 故数列{}n b 是公差为2的等差数列. (2)因为()()111111212322123n n b b n n n n +⎛⎫==- ⎪++++⎝⎭， 故n T ()1111111111235572123232332369n n n n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-=-== ⎪ ⎪ ⎪ ⎪⎢⎥+++++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦，又()119696x y x x x==≥++是单调增函数，且16y <， 又当1n =时，115n T =，故11156n T ≤<，即证. 6．（2022·安徽安庆·二模）已知数列{}n a 的前n 项和为n S ，且满足()213n n S n a =+-，n ∈+N . (1)求{}n a 的通项公式；(2)若()()231nn n b n a =+-，求{}n b 的前n 项和n T .【答案】(1)()()612n a n n =++，n ∈+N (2)()6312nn -+-+ 【解析】(1)解：1n =时，1143a a =-，解得11a =.当2N n n +≥∈，时，2113n n S n a --=-，故()22111n n n n n a S S n a n a --=-=+-，所以12n n a na n -=+， 故()()1321122113261215412n n n n n a a a a n n a a a a a a n n n n ----=⋅⋅⋅=⋅⋅⋅=++++.1a 符合上式故{}n a 的通项公式为()()612n a n n =++，N n +∈.(2)解：结合（1）得()()()112316112n n n n b n a n n ⎛⎫=+-=-+ ⎪++⎝⎭，所以()1211111166********n n n T b b b n n ⎛⎫⎛⎫⎛⎫=+++=-+++++-+ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭()6312nn =-+-+.1．（2022·广东·模拟预测）在∵121(1)2n a a a n n +++=+，∵21n n a S =-，∵()221210n n n a a n a --=->这三个条件中任选一个，补充在下面的问题中，并作答．问题：已知数列{}n a 的前n 和为n S ，若11a =，且 ，求数列{}2nn a 的前n 项和n T ．【答案】选∵，1(1)22n n T n +=-⋅+；选∵，21(2)3n n T ⎡⎤=--⎣⎦；选∵，1(1)22n n T n +=-⋅+. 【解析】选∵：当n ≥2时，因为121(1)2n a a a n n +++=+，题组三 错位相减求和所以()121112n a a a n n -+++=-， 上面两式相减得(2)n a n n =．当n ＝1时，11212a =⨯=，满足上式，所以n a n =．因为212222n n T n =⨯+⨯++⨯， 所以231212222n n T n +=⨯+⨯++⨯，上面两式相减，得：212222n n n T n +-=+++-⨯，所以1(1)22n n T n +=-⋅+．选∵：当2n 时，因为21n n a S =-，所以1121n n a S --=-，上面两式相减得12n n n a a a --=，即1n n a a -=-，经检验，21a a =-，所以{}n a 是公比为－1的等比数列，111(1)(1)n n n a --=⨯-=-．因为12(1)(2)n n n --=--，所以221(2)2(2)(2)(2)1(2)1(2)3n n n n T ⎡⎤---⎣⎦⎡⎤⎡⎤=--+-++-=-=--⎣⎦⎣⎦--． 选∵：由22121n n a a n --=-，得：22222212232123,25,,3n n n n a a n a a n a a -----=--=--=，由累加法得：()()2222121311,2n nn n a n a n --+-==-=．又0n a >，所以n a n =．因为212222n n T n =⨯+⨯++⨯，所以231212222n n T n +=⨯+⨯++⨯，上面两式相减得212222n n n T n +-=+++-⨯，所以1(1)22n n T n +=-⋅+．2．（2022·广东肇庆·二模）已知数列{}n a 满足112a =，121n n a a +=+. (1)证明：数列{}1n a -是等比数列； (2)求数列{}n na 的前n 项和n T .【答案】(1)证明见解析(2)24222n n n n +-++【解析】(1)证明：由121n n a a +=+，得1221n n a a +-=-， 又1112a -=-，所以10n a -≠，故11112n na a +-=-， 故{}1n a -是以12-为首项，以12为公比的等比数列；(2)解：由（1）得112n n a ⎛⎫=- ⎪⎝⎭-，得112nn a ⎛⎫=- ⎪⎝⎭，所以12n n na n n ⎛⎫=- ⎪⎝⎭，设12n n ⎧⎫⎪⎪⎛⎫⎨⎬ ⎪⎝⎭⎪⎪⎩⎭的前n 项和为n P ， 则211112222nn P n ⎛⎫⎛⎫=⨯+⨯++ ⎪ ⎪⎝⎭⎝⎭，∵ 2311111122222n n P n +⎛⎫⎛⎫⎛⎫=⨯+⨯++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，∵由∵-∵，得231111111222222n n n P n +⎛⎫⎛⎫⎛⎫⎛⎫=++++- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭11111221*********nn n n n n ++⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎛⎫⎛⎫⎛⎫⎣⎦=-=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭-，则()1222n n P n ⎛⎫=-+ ⎪⎝⎭， 故2242123222n n n n n n n n n T n P P ++-+=++++-=-=+. 3．（2022·广东韶关·一模）在∵112,2n n n a a a +=+=；∵22n n S a =-；∵122n n S +=-这三个条件中任选一个，补充在下列问题中，并做出解答.设数列{}n a 的前n 项和为n S ，__________，数列{}n b 是等差数列，12461,21o b b b =++=.(1)求数列{}n a 和{}n b 的通项公式； (2)设n n n c a b =⋅，求数列{}n c 的前n 项和n T .【答案】(1)选∵：()*2n n a n =∈N ，21n b n =-；选∵：()*2n n a n =∈N ，21n b n =-；选∵：()*2n n a n =∈N ，21n b n =- (2)()12326n n +-⨯+【解析】(1)解：若选∵：由12n n n a a +=+，则12nn n a a +-=，可得1222111232212,22,,,2n n n n n a a a a a a a a ------=-=-=-=将上述1n -个式子相加，整理的22112222n n n a a ---=++++()12212221n n --==--又因为12a =，所以()*2n n a n =∈N .若选∵：22n n S a =-，当1n =时，12a =， 当2n ≥时，()()112222n n n n n a S S a a --=-=--- 所以12nn a a -=，所以2n n a =. 综上，()*2n n a n =∈N若选∵：122n n S +=-，当1n =时，12a =，当2n ≥时，由122n n S +=-可得122n n S -=-，所以12nn n n a S S -=-=，所以2n n a =.经检验当1n =时2n n a =也成立，所以2n n a =()*n N ∈；设等差数列{}n b 的公差为d ，由题有12461,21b b b b =++=，即1113521d d b d b b +++=++，解得2d = 从而21n b n =-(2)解：由（1）可得()212nn c n =-⨯，令n c 的前n 项和是n T ，则()123123252212n n T n =⨯+⨯+⨯++-⨯，()23412123252212n n T n +=⨯+⨯+⨯++-⨯，两式相减得()()123112222222212n n n T n +-=⨯+⨯+⨯++⨯--⨯，()211821221212n n n T n ++--=⨯+--⨯-，整理得()21123262326n n n n T n n +++=⨯-⨯+=-⨯+；4．（2022·广东·模拟预测）已知数列{}n a 满足112a =，121n n a a +=+． (1)证明：数列{}1n a -是等比数列；(2)求数列{}n na 的前n 项和n T ．【答案】(1)证明见解析(2)24222n n n n n T +-+=+【解析】(1)证明：由121n n a a +=+，得1221n n a a +-=-， 又1112a -=-，所以10n a -≠，故11112n n a a +-=-， 故{}1n a -是以12-为首项，以12为公比的等比数列．(2)由（1）得112n n a ⎛⎫=- ⎪⎝⎭-，得112nn a ⎛⎫=- ⎪⎝⎭，所以12n n na n n ⎛⎫=- ⎪⎝⎭，设12n n ⎧⎫⎪⎪⎛⎫⎨⎬ ⎪⎝⎭⎪⎪⎩⎭的前n 项和为n P ，则211112222nn P n ⎛⎫⎛⎫=⨯+⨯+⋅⋅⋅+ ⎪ ⎪⎝⎭⎝⎭，∵2311111122222n n P n +⎛⎫⎛⎫⎛⎫=⨯+⨯+⋅⋅⋅+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，∵由∵-∵，得23111112211111111222222212nn n n n P n n ++⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎣⎦=+++⋅⋅⋅+-=- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭-111122n n n +⎛⎫⎛⎫=-- ⎪ ⎪⎝⎭⎝⎭，则()1222nn P n ⎛⎫=-+ ⎪⎝⎭，故2242123222n n n n n n n n n T n P P ++-+=+++⋅⋅⋅+-=-=+．5．（2022·广东佛山·模拟预测）已知数列{}n a 满足11a =，22a =，且对任意*N n ∈，都有2132n n n a a a ++=-． (1)求证：{}1n n a a +-是等比数列，并求{}n a 的通项公式； (2)求使得不等式1212154m m a a a ++⋅⋅⋅+≤成立的最大正整数m ． 【答案】(1)证明见解析；12n na (2)6m =【解析】(1)由2132n n n a a a ++=-，得()2112n n n n a a a a +++-=-， 所以{}1n n a a +-是等比数列.所以()1112122n n n n a a a a --+-=-⨯=从而()()()()11232211n n n n n a a a a a a a a a a ---=-+-+⋅⋅⋅+-+-+ 230231122222112n n n n n a -----=++⋅⋅⋅++=++⋅⋅⋅++=所以，12n na ．(2)设1212m mm S a a a =++⋅⋅⋅+ 即221123112222m m m m m S ---=+++⋅⋅⋅++，所以，32231221222m m m m mS ---=+++⋅⋅⋅++，于是，32111111224122222m m m m m m mS ----+=+++⋅⋅⋅++-=-．因为112m m m m m S S S ++=+>，且6154S =， 所以，使1212154m m a a a ++⋅⋅⋅+≤成立的最大正整数6m =． 1．（2022·甘肃·一模）已知数列{}n a 满足11a =，12n n a a +=．数列{}n b 满足11b =，22b =，212n n n b b b +++=，*n ∈N ．(1)求数列{}n a 及{}n b 的通项公式；(2)求数列{}n n a b +的前n 项和n T ．【答案】(1)1*1(),2n n a n N -=∈，*,n b n n N =∈；(2)1*1(1)2(),.22n n n T n N -+=-+∈π 【解析】(1)由12n n a a +=得112n n a a +=， 所以数列{}n a 是以11a =为首项，12为公比的等比数列，故1*1(),2n n a n N -=∈，由212n n n b b b +++=可知数列{}n b 是等差数列，首项11b =，公差211d b b =-=，所以*,n b n n N =∈.(2)11221212()()n n n n n T a b a b a b a a a b b b =++++++=+++++++02211111()()()()1232222n n -=+++++++++111()(1)1(1)22().122212nn n n n n --++=+=-+-即1*1(1)2(),.22n n n T n N -+=-+∈π2．（2022·江苏南京·高三开学考试）设数列{}n a 是公差不为零的等差数列，11a =，若125,,a a a 成等比数列 (1)求数列{}n a 的通项公式；题组四 分组求和(2)设21131n a n n b a+=+-()*N n ∈，求数列{}n b 的前n 项和为n S .【答案】(1)21n a n =-；(2)3(91)448n n n S n =+-+. 【解析】(1)解：设数列{an }是公差为d （d ≠0）的等差数列，a 1=1 若a 1，a 2，a 5成等比数列，可得a 1a 5=a 22，即有21(14)(1)d d ⨯+=+，解得2d =或d =0（舍去） 则12(1)21n a n n =+-=-. (2)解：21131n a n n b a +=+-()2121211113341211n n n n n --⎛⎫=+=-+ ⎪+⎝⎭+- 可得前n 项和()211111111327342231n n S n n -⎛⎫=-+-++-++++ ⎪+⎝⎭()()3191131914119448nn n n n -⎛⎫=-+=+- ⎪+-+⎝⎭.3．（2022·全国·高三专题练习）已知正项等比数列{}n a ，满足241a a =，5a 是112a 与35a 的等差中项.(1)求数列{}n a 的通项公式； (2)设()()444(2)11n n n n n a a a b n +++=+--⋅-，求数列{}n b 的前n 项和n S .【答案】(1)32n n a -=(2)当n 为偶数时，111212n n nS +=-+-；当n 为奇数时，111221nn n S +-=--. 【解析】(1{}n a 是正项等比数列，故22431a a a ==，所以31a =，又5132125a a a =+，设公比为q （q >0），即233322125a a q a q =+，即221225q q=+，解得：2q ，则数列{}n a 的通项公式为3332n n n a a q --==(2)()()()()()()411141422(1)(1)(1)2221212211n n n nn n n n n n n n n a b n n a a n +++++++=+-⋅=+-⋅=+-⋅------111(1)2121n nn n +=-+-⋅-- 则()22311111111231212121212121nn n n S n +⎡⎤=-+-++-+-+-++-⎣⎦------当n 为偶数时，111212n n nS +=-+-；当n 为奇数时，1111111212221nn n n n S +++-=--=---. 4．（2022·全国·高三专题练习）已知等差数列{}n a 的前n 项和为n S ，且5251025,31S a a a =++=. (1)求数列{}n a 的通项公式以及前n 项和n S ；(2)若22,1,n a n n n n b n a a+⎧⎪=⎨⎪⎩为奇数为偶数，求数列{}n b 的前2n －1项和21n T -.【答案】(1)2n S n =；(2)41221153(41)n n n S n +=--+-. 【解析】(1)依题意，53525S a ==，则35a =，故25103332731a a a a d a d a d ++=-++++=，解得d ＝2，∵1321a a d =-=， 故21n a n =-，21212n n S n n +-=⋅=. (2)依题意，得211111(21)(23)42123n n a a n n n n +⎛⎫==- ⎪-+-+⎝⎭， 故212,111,42123n n n b n n n -⎧⎪=⎨⎛⎫- ⎪⎪-+⎝⎭⎩为奇数为偶数，故154321111111111222437471144541n n T n n --⎛⎫⎛⎫⎛⎫=+-++-++-+ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭154311111112224377114541n n n -⎛⎫=++++-+-++- ⎪--⎝⎭()4412121112211164341153(41)n n n n n +---⎛⎫=+-=+ ⎪---⎝⎭5．（2022·河南·模拟预测（理））在等比数列{}n a 中，748a a =，且214a ，35a -，412a -成等差数列.(1)求{}n a 的通项公式； (2)若22111log n n n b n a a -=+，证明：数列{}n b 的前n 项和43n T <. 【答案】(1)12n n a +=(2)证明见解析【解析】(1)设数列{}n a 的公比为q ，由748a a =，得3448a q a =，所以2q.因为214a ，35a -，412a -成等差数列，所以()324125124a a a -=+-，即11118108122a a a -=+-，解得14a =.因此11422n n n a -+=⨯=.(2)因为()22211111111log 1214n n n n n b n a a n n n n -⎛⎫=+=+=-+ ⎪++⎝⎭，所以21111111112231444n n T n n ⎛⎫⎛⎫=-+-++-++++ ⎪ ⎪+⎝⎭⎝⎭1111111441111113414n n n n ⎛⎫⨯- ⎪⎛⎫⎛⎫⎛⎫⎝⎭=-+=-+⨯- ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭-. 因为1111n -<+，1111343n ⎛⎫⨯-< ⎪⎝⎭，所以43n T <.6．（2022·云南·一模（理））已知数列{}n a 的前n 项和为n S ，42310nn n a S --+=.(1)求数列{}3nn a -的通项公式；(2)记23log 3n nn n n b a a =-+-，求数列{}21n b -的前n 项和n T .【答案】(1)32n n n a -=-(2)n T 2122233n n +=+-【解析】(1)∵42310n n n a S --+=，∵2431nn n S a =-+.∵1112431n n n S a +++=-+.∵数列{}n a 的前n 项和为n S ，∵()111112222431431n nn n n n n n n S S S S a a a +++++-=-==-+-+-.∵()11323n n n n a a ++-=-.所以数列{}3n n a -是首项为13a -，公比为2的等比数列.∵()11332n n n a a --=-⨯.当1n =时，由42310nn n a S --+=和11S a =得111142314220a S a a --+=--=，解方程得11a =.∵()111332222n n n n n a a ---=-⨯=-⨯=-.∵数列{}3nn a -的通项公式为32n n n a -=-.(2)由（1）知：32n n n a -=-.∵223log 32log 22n n n n nn n n b a a n =-+-=-+=-.∵2121212n n b n --=--. ∵[]()352113(21)2222n n T n -=+++--++++()22212(121)212n n n -+-=--2122233n n +=+-. 7．（2022·天津三中三模）已知在各项均不相等的等差数列{}n a 中，11a =，且1a 、2a 、5a 成等比数列，数列{}n b 中，()122log 1b a =+，1142n n n b b ++=+，N n *∈.(1)求{}n a 的通项公式及其前n 项和n S ；(2)求证：{}2nn b +是等比数列，并求{}n b 的通项公式；(3)设1,2,N 232,21,N 422k k kn kk k a n k k b c n k k b **+⎧=∈⎪+⎪=⎨⨯⎪=-∈⎪-+⎩求数列{}n c 的前2n 项的和2n T . 【答案】(1)21n a n =-，2n S n =(2)证明见解析，42nnn b =-(3)()2132156599421n n nn n T +-+=-+⋅- 【解析】(1)解：设等差数列{}n a 的公差为d ，则0d ≠，由已知可得2215a a a =，即()2114d d +=+，解得2d =，故()1121n a a n d n =+-=-，()122n n n a a S n +==. (2)证明：因为()122log 12b a =+=，1142n n n b b ++=+，则()12124242n n n n n n b b b ++++=+=+，因为124b +=，故数列{}2nn b +是以4为首项和公比的等比数列，因此，12444n n n n b -+=⨯=，因此，42n nn b =-.(3)解：设数列{}n c 的前2n 项和中，奇数项的和记为A ，偶数项的和记为B .当()2N n k k *=∈，214n kk c -=， 则23135214444nn A -=++++， 231113232144444nn n n A +--=++++， 上式-下式得1231111131222211218414444444414n n n n n n A -++⎛⎫- ⎪--⎛⎫⎝⎭=++++-=+- ⎪⎝⎭-15651234n n ++=-⋅， 故565994nn A +=-⋅. 当()21N n k k *=-∈时，()1113232432244222k kn k k k k k c +++⨯⨯==-⋅+--+ ()()()()1111132323112212121222121k k k k k k k k-++++⨯⨯⎛⎫===- ⎪------⎝⎭，所以，223131111112212121212121n n B +⎡⎤⎛⎫⎛⎫⎛⎫=-+-++- ⎪ ⎪ ⎪⎢⎥------⎝⎭⎝⎭⎝⎭⎣⎦()1132131122121nn n ++-⎛⎫=-= ⎪--⎝⎭， 因此，()2132156599421n n nn n T +-+=-+⋅-. 1．（2021·全国·高三专题练习（理））已知数列{}n a 的通项公式为(1)sin 2n n a n n π=+⋅(n ∈+N )，其前n 项和为n S ，则8S =_______.【答案】36-【解析】4342414(43)(43)(42)sin 2k k k k k k c a a a a k k π----=+++=--⋅ (42)(41)4(42)(41)sin(41)4sin 4(41)sin 222k k k k k k k k k πππ--+--⋅+-⋅++⋅(43)(42)1(42)(41)0(41)4(1)4(41)0k k k k k k k k =--⨯+--⨯+-⨯-++⨯166k =-+，∵81216(12)6236S c c =+=-⨯++⨯=-.故答案为：36-2．（2020·河南郑州·三模）设数列{an }的前n 项和为Sn ，已知13a =对任意的正整数n 满足()()11cos 2213,n n n n n n S S n a a a π++-=+-+则19a =______．【答案】3.17-【解析】由()()11cos 2213,n n n n n n S S n a a a π++-=+-+得()()11cos 2213n n n n n a a n a a π++--=-.又因为13a =,故0n a ≠.故()()1cos 211213n n n n a a π+--=--. 故()21cos 113a a π--=-,3211cos 033a a -=-⨯…，191811cos16353a a π-=-⨯. 累加可得1911113573529 (6333333)a a -⨯-=-+-+-==-. 故191117633a =-+=-,故193.17a -= 故答案为：3.17-题组五 周期数列题组六 倒序相加法1．（2022·全国·高三专题练习）已知函数()y f x =满足()(1)1f x f x +-=，若数列{}n a 满足121(0)(1)n n a f f f f f n n n -⎛⎫⎛⎫⎛⎫=+++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则数列{}n a 的前20项和为（ ）A ．100B ．105C ．110D ．115【答案】D【解析】因为函数()y f x =满足()(1)1f x f x +-=，121(0)(1)n n a f f f f f n n n -⎛⎫⎛⎫⎛⎫=+++⋯⋯++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∵，121(1)(0)n n n a f f f f f n n n --⎛⎫⎛⎫⎛⎫∴=+++⋯⋯++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∵， 由∵+∵可得21n a n =+，12n n a +∴=，所以数列{}n a 是首项为1，公差为12的等差数列，其前20项和为20120121152+⎛⎫+ ⎪⎝⎭=.故选：D. 2．（2022·全国·高三专题练习）已知22()(),1f x x x =∈+R 若等比数列{}n a 满足120201,a a =则122020()()()f a f a f a +++=（ ）A ．20192B ．1010C ．2019D ．2020【答案】D 【解析】22()(),1f x x x =∈+R 22222122()11122211f x f x x x x x x ⎛⎫∴+=+ ⎪+⎝⎭⎛⎫+ ⎪⎝⎭=+=++等比数列{}n a 满足120201,a a =120202019220201...1,a a a a a a ∴====()()()()()()120202019202012...2f a f a f a f a f a f a ∴+=+==+=即122020()()()f a f a f a +++=2020故选：D3．（2022·全国·高三专题练习）设函数()221xf x =+，利用课本（苏教版必修5）中推导等差数列前n 项和的方法，求得()()()()()54045f f f f f -+-+⋅⋅⋅++⋅⋅⋅++的值为（ ） A ．9 B ．11C ．92D ．112【答案】B【解析】()221x f x =+，()()()22222212121221x x x x x x f x f x --⋅∴+-=+=+++++()2122222211221x x x x x +⋅=+==+++，设()()()()()54045S f f f f f =-+-+⋅⋅⋅++⋅⋅⋅++， 则()()()()()54045S f f f f f =+++++-+-，两式相加得()()2115511222S f f ⎡⎤=⨯+-=⨯=⎣⎦，因此，11S =.故选：B.4．（2022·全国·高三专题练习）对于三次函数()()320f x ax bx cx d a =+++≠，给出定义：设()'f x 是函数()y f x =的导数，()f x "是()'f x 的导数，若方程()0f x "=有实数解0x ，则称点()()00,x f x 为函数()y f x =的“拐点”.经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心.设函数()3211533212g x x x x =-+-，则122018(201920192019g g g ⎛⎫⎛⎫⎛⎫++⋯+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭)A ．2016B ．2017C ．2018D ．2019【答案】C【解析】函数()3211533212g x x x x =-+-，函数的导数()2'3g x x x =-+，()'21g x x =-，由()0'0g x =得0210x -=，解得012x =，而112g ⎛⎫= ⎪⎝⎭，故函数()g x 关于点1,12⎛⎫⎪⎝⎭对称，()()12g x g x ∴+-=，故设122018...201920192019g g g m ⎛⎫⎛⎫⎛⎫+++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则201820171...201920192019g g g m ⎛⎫⎛⎫⎛⎫+++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，两式相加得220182m ⨯=，则2018m =，故选C.5．（2022·全国·高三专题练习）已知数列{}n a 的前n 项和为n S ，满足2n S an bn =+，（,a b 均为常数），且72a π=.设函数2()sin 22cos2xf x x =+，记()n n y f a =，则数列{}n y 的前13项和为（ ） A ．132πB ．7πC ．7D ．13【答案】D【解析】因为2()sin 22cossin 2cos 12xf x x x x =+=++， 由2n S an bn =+，得()()()2211122n n n S S an bn a n b n an a b n a -=-=+----=-+≥，又11a S a b ==+也满足上式，所以2n a an a b =-+， 则12n n a a a --=为常数，所以数列{}n a 为等差数列；所以11372a a a π+==，()()111131131313sin 2cos 1sin 2cos 1y f a f a a a a y a =+=++++++()()1111sin 2cos 1sin 22cos 12a a a a ππ=+++-+-+=.则数列{}n y 的前13项和为()()()1213...f a f a f a +++，记()()()1213...M f a f a f a =+++，则()()()13121...M f a f a f a =+++， 所以()()11321326M f a f a ⎡⎤=+=⎣⎦，因此13M =. 故选：D ．6．（2022·湖南岳阳·二模）德国数学家高斯是近代数学奠基者之一，有“数学王子”之称，在历史上有很大的影响.他幼年时就表现出超人的数学天赋，10岁时，他在进行123100++++的求和运算时，就提出了倒序相加法的原理，该原理基于所给数据前后对应项的和呈现一定的规律生成，因此，此方法也称之为高斯算法.已知某数列通项21002101n n a n -=-，则12100...a a a +++=（ ）A ．98B ．99C ．100D ．101【答案】C【解析】由已知，数列通项21002101n n a n -=-，所以10121002(101)100210010224202221012(101)101210110122101n nn n n n n a a n n n n n -------+=+=+==------， 所以91110029398012n n a a a a a a a a -+=+=+==+，所以12100...502100a a a +++=⨯=.故选：C.。

【创新方案】2017届高考数学一轮复习 第二章 函数概念与基本初等函数I 第四节 二次函数与幂函数课后作业 理[全盘巩固]一、选择题1．(2016·枣庄模拟)已知函数f (x )＝x 2＋2|x |，若f (－a )＋f (a )≤2f (2)，则实数a 的取值X 围是( )A ．[－2,2]B ．(－2,2]C ．[－4,2]D ．[－4,4]2．(2016·某某模拟)已知f (x )＝ax 2－x －c ，若f (x )>0的解集为(－2,1)，则函数y ＝f (－x )的大致图象是( )A B C D3．已知二次函数f (x )满足f (2＋x )＝f (2－x )，且f (x )在[0,2]上是增函数，若f (a )≥f (0)，则实数a 的取值X 围是( )A ．[0，＋∞) B．(－∞，0] C ．[0,4] D ．(－∞，0]∪[4，＋∞)4．方程x 2＋ax －2＝0在区间[1,5]上有根，则实数a 的取值X 围为( )A.⎝ ⎛⎭⎪⎫－235，＋∞B ．(1，＋∞) C.⎣⎢⎡⎦⎥⎤－235，1 D.⎝⎛⎦⎥⎤－∞，－2355．(2016·某某模拟)若函数f (x )＝ax 2＋b |x |＋c (a ≠0)有四个单调区间，则实数a ，b ，c 满足( )A ．b 2－4ac >0，a >0 B ．b 2－4ac >0 C ．－b 2a >0 D ．－b2a <0二、填空题6．若幂函数y ＝(m 2－3m ＋3)·xm 2－m －2的图象不过原点，则m 的取值是________．7．已知二次函数f (x )是偶函数，且f (4)＝4f (2)＝16，则函数f (x )的解析式为________． 8．设f (x )是定义在R 上的奇函数，且当x ≥0时，f (x )＝x 2若对任意的x ∈[t ，t ＋2]，不等式f (x ＋t )≥2f (x )恒成立，则实数t 的取值X 围是________．三、解答题9．已知函数f (x )＝ax 2＋bx ＋1(a ，b ∈R )，x ∈R .(1)若函数f (x )的最小值为f (－1)＝0，求f (x )的解析式，并写出单调区间； (2)在(1)的条件下，f (x )>x ＋k 在区间[－3，－1]上恒成立，试求k 的取值X 围． 10．已知a 是实数，函数f (x )＝2ax 2＋2x －3在x ∈[－1,1]上恒小于零，某某数a 的取值X 围．[冲击名校]1．已知y ＝f (x )为偶函数，当x ≥0时，f (x )＝－x 2＋2x ，则满足f (f (a ))＝12的实数a的个数为( )A ．8B ．6C ．4D ．22．已知函数f (x )满足f (x )＝x 2－2(a ＋2)x ＋a 2，g (x )＝－x 2＋2(a －2)x －a 2＋8.设H 1(x )＝max{f (x )，g (x )}，H 2(x )＝min{f (x )，g (x )}(max(p ，q )表示p ，q 中的较大值，min(p ，q )表示p ，q 中的较小值)，记H 1(x )的最小值为A ，H 2(x )的最大值为B ，则A －B ＝()A ．a 2－2a －16 B ．a 2＋2a －16 C ．－16 D ．163．已知函数f (x )＝x 2－2x ，g (x )＝ax ＋2(a >0)，若∀x 1∈[－1,2]，∃x 2∈[－1,2]，f (x 1)＝g (x 2)，则实数a 的取值X 围是________．4．已知函数f (x )＝ax 2－2ax ＋2＋b (a ≠0)，若f (x )在区间[2,3]上有最大值5，最小值2.(1)求a ，b 的值；(2)若b <1，g (x )＝f (x )－mx 在[2,4]上单调，求m 的取值X 围．5．已知函数f (x )＝x 2－2ax ＋5(a ＞1)．若f (x )在区间(－∞，2]上是减函数，且对任意的x 1，x 2∈[1，a ＋1]，总有|f (x 1)－f (x 2)|≤4，某某数a 的取值X 围．答 案 [全盘巩固]一、选择题1．解析：选A 由f (x )＝x 2＋2|x |，f (2)＝8知，f (－a )＋f (a )＝2a 2＋4|a |≤16，解得a ∈[－2,2]．2．解析：选C 法一：由f (x )>0的解集为(－2,1)，可得a ＝－1，c ＝－2，所以f (x )＝－x 2－x ＋2，f (－x )＝－x 2＋x ＋2＝－(x ＋1)(x －2)，故选C.法二：由f (x )>0的解集为(－2,1)，可知函数f (x )的大致图象为选项D ，又函数f (x )与f (－x )的图象关于y 轴对称，所以f (－x )的大致图象为选项C.3．解析：选C 由f (2＋x )＝f (2－x )可知，函数f (x )图象的对称轴为x ＝2＋x ＋2－x2＝2，又函数f (x )在[0,2]上单调递增，所以由f (a )≥f (0)可得0≤a ≤4.4．解析：选C 法一：令f (x )＝x 2＋ax －2，由题意知f (x )的图象与x 轴在[1,5]上有交点，又f (0)＝－2<0，∴⎩⎪⎨⎪⎧f 1≤0，f 5≥0，即⎩⎪⎨⎪⎧a －1≤0，5a ＋23≥0，∴－235≤a ≤1.法二：方程x 2＋ax －2＝0在区间[1,5]上有根，即方程x ＋a －2x ＝0，也即方程a ＝2x－x在区间[1,5]上有根，而函数y ＝2x －x 在区间[1,5]上是减函数，所以－235≤y ≤1，则－235≤a ≤1.5．解析：选C x >0时，f (x )＝ax 2＋bx ＋c ，此时f (x )应该有两个单调区间，∴对称轴x ＝－b 2a >0；x <0时，f (x )＝ax 2－bx ＋c ，对称轴x ＝b2a<0，∴此时f (x )有两个单调区间，∴当－b2a>0时，f (x )有四个单调区间． 二、填空题6．解析：由幂函数性质可知m 2－3m ＋3＝1，∴m ＝2或m ＝1.又幂函数图象不过原点，∴m 2－m －2≤0，即－1≤m ≤2，∴m ＝2或m ＝1.答案：1或27．解析：由题意可设函数f (x )＝ax 2＋c (a ≠0)，则f (4)＝16a ＋c ＝16,4f (2)＝4(4a ＋c )＝16a ＋4c ＝16，解得a ＝1，c ＝0，故f (x )＝x 2.答案：f (x )＝x 28．解析：∵当x ≥0时，f (x )＝x 2，且f (x )是定义在R 上的奇函数，∴f (x )在R 上是增函数，又f (x ＋t )≥2f (x )＝f (2x )，∴x ＋t ≥2x ，∴t ≥(2－1)x .∵x ∈[t ，t ＋2]，∴t ≥(2－1)(t ＋2)，∴t ≥ 2.答案：[2，＋∞) 三、解答题9．解：(1)由题意得f (－1)＝a －b ＋1＝0，a ≠0，且－b2a ＝－1，∴a ＝1，b ＝2.∴f (x )＝x 2＋2x ＋1，单调减区间为(－∞，－1]，单调增区间为[－1，＋∞)． (2)f (x )>x ＋k 在区间[－3，－1]上恒成立， 转化为x 2＋x ＋1>k 在区间[－3，－1]上恒成立．设g (x )＝x 2＋x ＋1，x ∈[－3，－1]， 则g (x )在[－3，－1]上递减． ∴g (x )min ＝g (－1)＝1.∴k <1，即k 的取值X 围为(－∞，1)． 10．解：2ax 2＋2x －3<0在[－1,1]上恒成立． 当a ＝0时，适合；当a ≠0时，x ＝0时，有－3<0恒成立；x ≠0时，a <32⎝ ⎛⎭⎪⎫1x －132－16，因为1x ∈(－∞，－1]∪[1，＋∞)，当x ＝1时，右边取最小值12，所以a <12，且a ≠0.综上，实数a 的取值X 围是⎝⎛⎭⎪⎫－∞，12. [冲击名校]1．解析：选A 由题意知， f (x )＝⎩⎪⎨⎪⎧－x 2＋2x ，x ≥0，－x 2－2x ，x <0，其图象如图所示．令t ＝f (a )，则t ≤1，令f (t )＝12，解得t ＝1－22或t ＝－1±22，即f (a )＝1－22或f (a )＝－1±22，由数形结合得，共有8个交点． ．2．解析：选C 取a ＝－2，则f (x )＝x 2＋4，g (x )＝－x 2－8x ＋4，画出它们的图象，如图所示．则H 1(x )的最小值为两图象右边交点的纵坐标，H 2(x )的最大值为两图象左边交点的纵坐标，由⎩⎪⎨⎪⎧x 2＋4＝y ，－x 2－8x ＋4＝y ，解得⎩⎪⎨⎪⎧x ＝0，y ＝4或⎩⎪⎨⎪⎧x ＝－4，y ＝20，∴A ＝4，B ＝20，A －B ＝－16.3．解析：由题意得g (x )min ≤f (x )min 且g (x )max ≥f (x ) max ，f (x )在区间[－1,2]上的最大值f (x ) max ＝f (－1)＝3，f (x )在区间[－1,2]上的最小值f (x ) min ＝f (1)＝－1.由于g (x )＝ax ＋2(a >0)在区间[－1,2]上单调递增，则g (x ) min ＝g (－1)＝－a ＋2，g (x ) max ＝g (2)＝2a ＋2，故⎩⎪⎨⎪⎧－a ＋2≤－1，2a ＋2≥3，解得a ≥3.答案：[3，＋∞)4．解：(1)f (x )＝a (x －1) 2＋2＋b －a . 当a >0时，f (x )在[2,3]上为增函数，故⎩⎪⎨⎪⎧ f 3＝5，f 2＝2，⇒⎩⎪⎨⎪⎧ 9a －6a ＋2＋b ＝5，4a －4a ＋2＋b ＝2，⇒⎩⎪⎨⎪⎧a ＝1，b ＝0.当a <0时，f (x )在[2,3]上为减函数，故⎩⎪⎨⎪⎧f3＝2，f 2＝5，⇒⎩⎪⎨⎪⎧9a －6a ＋2＋b ＝2，4a －4a ＋2＋b ＝5，⇒⎩⎪⎨⎪⎧a ＝－1，b ＝3.(2)∵b <1，∴a ＝1，b ＝0，即f (x )＝x 2－2x ＋2.g (x )＝x 2－2x ＋2－mx ＝x 2－(2＋m )x ＋2，∵g (x )在[2,4]上单调，∴2＋m 2≤2或m ＋22≥4.∴m ≤2或m ≥6.故m 的取值X 围为(－∞，2]∪[6，＋∞)．5．解：∵f (x )在区间(－∞，2]上是减函数，∴a ≥2. 又x ＝a ∈[1，a ＋1]，且(a ＋1)－a ≤a －1， ∴f (x )max ＝f (1)＝6－2a ，f (x )min ＝f (a )＝5－a 2. ∵对任意的x 1，x 2∈[1，a ＋1]， 总有|f (x 1)－f (x 2)|≤4，∴f (x ) max －f (x ) min ≤4，得－1≤a ≤3. 又a ≥2，∴2≤a ≤3.故实数a 的取值X 围是[2,3]．。

7.4 数列求和、数列的综合基础篇 固本夯基考点一 数列求和1.(2021浙江,10,4分)已知数列{a n }满足a 1=1,a n+1=n 1+√a (n ∈N *).记数列{a n }的前n 项和为S n ,则( ) A.32<S 100<3 B.3<S 100<4 C.4<S 100<92 D.92<S 100<5 答案 A2.(2020山东仿真联考3)已知正项数列{a n }满足a n+1>2a n ,S n 是{a n }的前n 项和,则下列四个命题中错误的是( )A.a n+1>2na 1 B.S 2k >(1+2k)S k C.S n <2a n -a 1(n ≥2) D.{a n+1a n}是递增数列 答案 D3.(2020浙江,11,4分)我国古代数学家杨辉,朱世杰等研究过高阶等差数列的求和问题,如数列{n(n+1)2}就是二阶等差数列.数列{n(n+1)2}(n ∈N *)的前3项和是 . 答案 104.(2022届T8联考,18)设等差数列{a n }的前n 项和为S n ,已知a 1=3,S 3=5a 1. (1)求数列{a n }的通项公式;(2)设b n =1+2S n,数列{b n }的前n 项和为T n .定义[x]为不超过x 的最大整数,例如[0.3]=0,[1.5]=1.当[T 1]+[T 2]+…+[T n ]=63时,求n 的值.解析 (1)设等差数列{a n }的公差为d,因为a 1=3,所以S 3=3a 1+3d=9+3d. 又因为S 3=5a 1=15,所以9+3d=15,得d=2. 所以数列{a n }的通项公式是a n =3+2(n-1)=2n+1. (2)因为S n =3n+n(n−1)2×2=n 2+2n,所以b n =1+2S n =1+2n(n+2)=1+1n -1n+2. 所以T n =n+(1−13)+(12−14)+(13−15)+…+(1n−1−1n+1)+(1n −1n+2)=n+1+12-1n+1-1n+2. 当n ≤2时,因为-13≤12-1n+1-1n+2<0,所以[T n ]=n.当n ≥3时,因为0<12-1n+1-1n+2<12,所以[T n ]=n+1.因为[T 1]+[T 2]+…+[T n ]=63, 所以1+2+4+5+…+(n+1)=63, 即3+(n−2)(4+n+1)2=63,即n 2+3n-130=0,即(n-10)·(n+13)=0.因为n ∈N *,所以n=10.5.(2022届华中师范大学琼中附中月考,17)已知等差数列{a n }中,a 2=3,a 4+a 6=18. (1)求数列{a n }的通项公式;(2)若数列{b n }满足b n+1=2b n ,并且b 1=a 5,试求数列{b n }的前n 项和S n .解析 (1)设数列{a n }的公差为d,根据题意得{a 1+d =3,2a 1+8d =18,解得{a 1=1,d =2,∴a n =a 1+(n-1)d=2n-1.(2)∵b n+1=2b n ,∴数列{b n }是公比为2的等比数列, 又b 1=a 5=2×5-1=9,∴S n =b 1(1−q n )1−q =9(1−2n )1−2=-9+9×2n.6.(2022届长沙雅礼中学月考,17)已知数列{a n }中,a 1=1,a 2=3,其前n 项和S n 满足S n+1+S n-1=2S n +2(n ≥2,n ∈N *).(1)求数列{a n }的通项公式;(2)若b n =a n +2a n ,求数列{b n }的前n 项和T n .解析 (1)由题意得S n+1-S n =S n -S n-1+2(n ≥2),即a n+1-a n =2(n ≥2),又a 2-a 1=3-1=2,所以a n+1-a n =2(n ∈N *).所以数列{a n }是以1为首项,2为公差的等差数列,所以a n =2n-1(n ∈N *).(2)b n =a n +2a n=2n-1+22n-1=2n-1+12·4n ,所以T n =[1+3+5+…+(2n-1)]+12×(4+42+43+…+4n )=n 2+2(4n−1)3.7.(2022届广东深圳七中月考)已知等比数列{a n }中,a 1=1,且2a 2是a 3和4a 1的等差中项.等差数列{b n }满足b 1=1,b 7=13.(1)求数列{a n }的通项公式; (2)求数列{a n -b n }的前n 项和T n .解析 (1)设数列{a n }的公比为q,由题意可得2×2a 2=a 3+4a 1,即4a 1q=a 1q 2+4a 1,又a 1=1,所以q=2,则数列{a n }的通项公式为a n =2n-1.(2)设数列{b n }的公差为d,由题意可得b 7-b 1=12=6d,即d=2,则数列{b n }的通项公式为b n =1+(n-1)×2=2n-1.a n -b n =2n-1-(2n-1),则T n =(20-1)+(21-3)+…+[2n-1-(2n-1)]=(20+21+…+2n-1)-(1+3+…+2n-1)=1−2n 1−2-(1+2n−1)·n 2=2n -1-n 2.8.(2022届河北秦皇岛青龙8月测试,18)已知数列{a n }的前n 项和为S n ,且满足S n =2a n -1(n ∈N *). (1)求数列{a n }的通项公式a n 及S n ;(2)若数列{b n }满足b n =|S n -15|,求数列{b n }的前n 项和T n . 解析 (1)当n=1时,S 1=2a 1-1,即a 1=1,由S n =2a n -1得S n+1=2a n+1-1,两式相减得a n+1=2a n+1-2a n ,即a n+1=2a n ,即数列{a n }是以1为首项,2为公比的等比数列,则a n =2n-1,则S n =1−2n 1−2=2n-1.(2)由(1)知b n =|2n-16|,则b n ={16−2n (1≤n ≤4),2n −16(n >4).记{2n -16}的前n 项和为A n ,则A n =(21+22+…+2n)-16n=2·(1−2n )1−2-16n=2n+1-16n-2.则当1≤n ≤4时,T n =-A n =16n-2n+1+2.当n>4时,T n =(16-21)+(16-22)+…+(16-24)+(25-16)+(26-16)+…+(2n-16)=-A 4+A n -A 4=A n -2A 4=2n+1-16n+66,则T n ={16n −2n+1+2(1≤n ≤4),2n+1−16n +66(n >4).9.(2021浙江“山水联盟”开学考)已知数列{a n }满足:a 1=1,a n+1a n =nn+1;数列{b n }是等比数列,并满足b 1=2,且b 1-1,b 4,b 5-1成等差数列. (1)求数列{a n },{b n }的通项公式;(2)若数列{b n }的前n 项和是S n ,数列{c n }满足c n =a n a n+1a n+2(S n +2),求证:c 1+c 2+…+c n <12.解析 (1)由于a 1=1,na n =(n+1)a n+1,所以{na n }是常数列,所以na n =1·a 1=1,故a n =1n. 设{b n }的公比是q,由已知得2b 4=(b 1-1)+(b 5-1),所以4q 3=2q 4,所以q=2,故b n =2n.(2)证明:由(1)得S n =2(1−2n )1−2=2n+1-2,则c n =a n a n+1a n+2(S n +2)=n+2n(n+1)·2n+1=1n·2n -1(n+1)·2n+1, 则c 1+c 2+…+c n =11×2-12×22+12×22-13×23+…+1n·2n-1(n+1)·2n+1,所以c 1+c 2+…+c n =12-1(n+1)·2n+1<12. 10.(2020天津,19,15分)已知{a n }为等差数列,{b n }为等比数列,a 1=b 1=1,a 5=5(a 4-a 3),b 5=4(b 4-b 3). (1)求{a n }和{b n }的通项公式;(2)记{a n }的前n 项和为S n ,求证:S n S n+2<S n+12(n ∈N *);(3)对任意的正整数n,设c n ={(3a n −2)b na n a n+2,n 为奇数,a n−1b n+1,n 为偶数.求数列{c n }的前2n 项和.解析 (1)设等差数列{a n }的公差为d,等比数列{b n }的公比为q.由a 1=1,a 5=5(a 4-a 3),可得d=1,从而{a n }的通项公式为a n =n.由b 1=1,b 5=4(b 4-b 3),又q ≠0,可得q 2-4q+4=0,解得q=2,从而{b n }的通项公式为b n =2n-1.(2)证明:由(1)可得S n =n(n+1)2,故S n S n+2=14n(n+1)·(n+2)(n+3),S n+12=14(n+1)2(n+2)2,从而S n S n+2-S n+12=-12(n+1)(n+2)<0,所以S n S n+2<S n+12.(3)当n 为奇数时,c n =(3a n −2)b n a n a n+2=(3n−2)2n−1n(n+2)=2n+1n+2-2n−1n ;当n 为偶数时,c n =a n−1b n+1=n−12n.对任意的正整数n,有∑k=1nc 2k-1=∑k=1n(22k 2k+1−22k−22k−1)=22n 2n+1-1和∑k=1n c 2k =∑k=1n 2k−14k =14+342+543+…+2n−14n ①. 由①得14∑k=1n c 2k =142+343+…+2n−34n +2n−14n+1②. 由①-②得34∑k=1n c 2k =14+242+…+24n -2n−14n+1=24(1−14n )1−14-14-2n−14n+1,从而得∑k=1n c 2k =59-6n+59×4n .因此,∑k=12nc k =∑k=1nc 2k-1+∑k=1nc 2k =4n 2n+1-6n+59×4n -49.所以,数列{c n }的前2n 项和为4n 2n+1-6n+59×4n -49.考点二 数列的综合1.(2020福建泉州线上测试)已知{a n }是公差为3的等差数列.若a 1,a 2,a 4成等比数列,则{a n }的前10项和S 10=( )A.165B.138C.60D.30 答案 A2.数学家也有许多美丽的错误,如法国数学家费马于1640年提出了以下猜想:F n =22n+1(n=0,1,2,…)是质数.直到1732年才被善于计算的大数学家欧拉算出F 5=641×6700417,不是质数.现设a n =log 2(F n -1),n=1,2,…,S n表示数列{a n }的前n 项和.则使不等式2S 1S 2+22S 2S 3+…+2n S n S n+1<2n2 020成立的最小正整数n 的值是( )A.11B.10C.9D.8 答案 C3.(2022届浙江“山水联盟”开学考,20)已知数列{a n }的前n 项和为S n ,2S n =(2n+1)a n -2n 2(n ∈N *),数列{b n }满足b 1=a 1,nb n+1=a n b n .(1)求数列{a n }和{b n }的通项公式; (2)设数列{c n }满足:c 1=4,c n+1=c n -a n b n (n ∈N *),若不等式λ+3n+92n ≥c n (n ∈N *)恒成立,求实数λ的取值范围. 解析 (1)当n=1时,2a 1=3a 1-2,∴a 1=2.当n ≥2时,由{2S n =(2n +1)a n −2n 2,2S n−1=(2n −1)a n−1−2(n −1)2得2a n =(2n+1)a n -(2n-1)a n-1-2n 2+2(n-1)2,即a n -a n-1=2,∴数列{a n }是公差为2的等差数列, ∵a 1=2,∴a n =2n.由条件得b 1=2,nb n+1=2nb n ,∴b n+1=2b n ,即数列{b n }是公比为2的等比数列,∴b n =2n.(2)由(1)得a n b n =2n 2n =n 2n−1,设数列{a n b n }的前n 项和为T n ,则T n =1+22+322+423+…+n2n−1, ∴12T n =12+222+323+…+n−12n−1+n2n , ∴12T n =1+12+122+123+…+12n−1-n 2n =1−12n 1−12-n 2n =2-n+22n , ∴T n =4-n+22n−1,由c n+1=c n -a nb n 得c n+1-c n =-a n b n ,所以c n -c n-1=-a n−1b n−1,……,c 2-c 1=-a 1b 1,累加得c n -c 1=-T n-1,即c n -4=-4+n+12n−2,∴c n =n+12n−2,∴λ≥n+12n−2-3n+92n =n−52n 对任意n ∈N *恒成立, 令f(n)=n−52n ,则f(n+1)-f(n)=n−42n+1-n−52n =−n+62n+1, ∴f(1)<f(2)<…<f(6)=f(7),f(7)>f(8)>…, ∴f(n)max =f(6)=f(7)=164,∴λ≥164. 故λ的取值范围是[164,+∞). 4(2022届校际联合考试)我国南宋时期的数学家杨辉,在他1261年所著的《详解九章算法》一书中,用如图的三角形解释二项和的乘方规律,此图称为“杨辉三角”.在此图中,从第三行开始,首尾两数为1,其他各数均为它肩上两数之和.(1)把“杨辉三角”中第三斜列的各数取出,按原来的顺序排列得一数列:1,3,6,10,15,…,写出a n 与a n-1(n ∈N *,n ≥2)的递推关系,并求出数列{a n }的通项公式;(2)已知数列{b n }满足b 1+12b 2+13b 3+ (1)b n =2a n (n ∈N *),设数列{c n }满足c n =2n+1b n b n+1,数列{c n }的前n 项和为T n ,若T n <n n+1λ(n ∈N *)恒成立,试求实数λ的取值范围. 解析 (1)由题意可知a 1=1,n ≥2时,a n -a n-1=n,所以a n =(a n -a n-1)+(a n-1-a n-2)+…+(a 2-a 1)+a 1=n+(n-1)+…+2+1=n(n+1)2,故a n =n(n+1)2. (2)数列{b n }满足b 1+12b 2+13b 3+ (1)b n =n 2+n,① 当n ≥2时,b 1+12b 2+13b 3+…+1n−1b n-1=(n-1)2+(n-1),② ①-②得1nb n =2n,故b n =2n 2(n ≥2),又n=1时亦成立,所以b n =2n 2(n ∈N *). 数列{c n }满足c n =2n+1b n b n+1=2n+14n 2(n+1)2=14[1n 2−1(n+1)2], 则T n =14[1−122+122−132+⋯+1n 2−1(n+1)2]=14[1−1(n+1)2],由T n <n n+1λ(n ∈N *)恒成立, 得14[1−1(n+1)2]<n n+1λ,整理得λ>n+24n+4,因为y=n+24n+4=14(1+1n+1)在n ∈N *上单调递减,故当n=1时,(n+24n+4)max =38,即λ>38,所以实数λ的取值范围为(38,+∞). 5.(2022届长沙长郡中学月考,18)已知数列{a n }满足a n+1-2a n =0,a 3=8. (1)求数列{a n }的通项公式; (2)设b n =n a n,数列{b n }的前n 项和为T n .若2T n >m-2021对n ∈N *恒成立,求正整数m 的最大值. 解析 (1)由a n+1-2a n =0得a n+1=2a n ,则{a n }是以2为公比的等比数列, 又a 3=8,即4a 1=8,解得a 1=2,所以a n =2n.(2)由(1)可得b n =n a n =n 2n ,则T n =12+222+323+…+n 2n ,12T n =122+223+324+…+n 2n+1,两式相减可得12T n =12+122+123+…+12n -n 2n+1=12(1−12n)1−12-n 2n+1, 化简可得T n =2-n+22n (n ∈N *),因为T n+1-T n =2-n+32n+1-2+n+22n =n+12n+1>0,所以{T n }逐项递增,T 1最小,为12,所以2×12>m-2021,解得m<2022,又m ∈N *,所以m 的最大值为2021. 6.(2021南京三模,18)已知等差数列{a n }满足:a 1+3,a 3,a 4成等差数列,且a 1,a 3,a 8成等比数列. (1)求数列{a n }的通项公式;(2)在任意相邻两项a k 与a k+1(k=1,2,…)之间插入2k个2,使它们和原数列的项构成一个新的数列{b n },记S n为数列{b n }的前n 项和,求满足S n <500的n 的最大值. 解析 (1)设等差数列{a n }的公差为d, 由题意知a 1+3+a 4=2a 3, 即2a 1+3+3d=2a 1+4d,解得d=3, 又a 1a 8=a 32,即a 1·(a 1+7×3)=(a 1+2×3)2,解得a 1=4,故a n =3n+1.(2)因为b n >0,所以{S n }是单调递增数列,又因为a k+1前的所有项的项数为k+21+22+ (2)=k+2k+1-2,所以S k+2k+1−2=(a 1+a 2+…+a k )+2(21+22+23+ (2))=k(4+3k+1)2+2×2(1−2k )1−2=3k 2+5k 2+2k+2-4.当k=6时,S 132=321<500;当k=7时,S 261=599>500, 令S 132+a 7+2(n-133)<500,即321+22+2(n-133)<500, 解得n<211.5,所以满足S n <500的n 的最大值为211.7.(2020辽宁葫芦岛兴城高中模拟)设函数f(x)=x 2,过点C 1(1,0)作x 轴的垂线l 1,交函数f(x)的图象于点A 1,以A 1为切点作函数f(x)图象的切线交x 轴于点C 2,再过C 2作x 轴的垂线l 2,交函数f(x)的图象于点A 2,……,以此类推得点A n ,记A n 的横坐标为a n ,n ∈N *.(1)证明数列{a n }为等比数列,并求出通项公式;(2)设直线l n 与函数g(x)=lo g 12x 的图象相交于点B n ,记b n =OA⃗⃗⃗⃗ n ·OB ⃗⃗⃗⃗ n (其中O 为坐标原点),求数列{b n }的前n 项和S n .解析 (1)以点A n-1(a n-1,a n−12)(n ≥2)为切点的切线方程为y-a n−12=2a n-1(x-a n-1).当y=0时,x=12a n-1,即a n =12a n-1,又∵a 1=1,∴数列{a n }是以1为首项,12为公比的等比数列,∴a n =(12)n−1. (2)由题意,得B n ((12)n−1,n −1), ∴b n =OA⃗⃗⃗⃗ n ·OB ⃗⃗⃗⃗ n =(14)n−1+(14)n−1·(n-1)=n ·(14)n−1, ∴S n =1×(14)0+2×(14)1+…+n ×(14)n−1,14S n =1×(14)1+2×(14)2+…+n ×(14)n. 两式相减,得34S n =1×(14)0+14+…+(14)n−1-n ×(14)n=1−(14)n1−14-n ×(14)n,化简,得S n =169-(4n 3+169)×(14)n =169-3n+49×4n−1.综合篇 知能转换A 组考法一 错位相减法求和1.(2022届全国学业质量联合检测)已知正项数列{a n }的前n 项和为S n ,且满足a n 2,S n ,a n 成等差数列. (1)求数列{a n }的通项公式;(2)请从以下三个条件中任意选择一个,求数列{b n }的前n 项和T n . 条件①:设数列{b n }满足b n =(-1)na n ;条件②:设数列{b n }满足b n =2a n ·a n ; 条件③:设数列{b n }满足b n =√a +√a .解析 (1)因为a n 2,S n ,a n 成等差数列,所以2S n =a n 2+a n ,当n ≥2时,2S n-1=a n−12+a n-1,两式作差化简,得(a n +a n-1)·(a n -a n-1-1)=0.因为该数列是正项数列,所以a n +a n-1≠0, 所以a n -a n-1-1=0,即a n -a n-1=1, 所以数列{a n }是公差为1的等差数列, 又当n=1时,2a 1=a 12+a 1,解得a 1=1, 所以a n =n(n ∈N *).(2)选择条件①:数列{b n }满足b n =(-1)n a n =(-1)nn. 所以T n =-1+2-3+4-5+6-…+(-1)nn,当n 为偶数时,T n =(-1+2)+(-3+4)+(-5+6)+…+[-(n-1)+n]=n2×1=n 2; 当n 为奇数时,T n =(-1+2)+(-3+4)+(-5+6)+…+[-(n-2)+(n-1)]-n=n−12×1-n=-1+n2.所以T n ={n2,n 为偶数,−1+n 2,n 为奇数.选择条件②:数列{b n }满足b n =2a n ·a n =n ·2n,可得T n =1×21+2×22+…+n ·2n,①2T n =1×22+2×23+…+n ·2n+1,②①-②得-T n =2+22+23+ (2)-n ·2n+1=2(1−2n )1−2-n ·2n+1=(1-n)·2n+1-2,则T n =(n-1)·2n+1+2.选择条件③:数列{b n }满足b n =√a +√a =√n+1+√n=√n +1-√n ,则T n =(√2-1)+(√3-√2)+…+(√n +1-√n )=√n +1-1.2.(2022届山东德州夏津一中入学考试)设数列{a n }是等差数列,数列{b n }是公比大于0的等比数列,已知a 1=1,b 1=3,b 2=3a 3,b 3=12a 2+3.(1)求数列{a n }和数列{b n }的通项公式;(2)设数列{c n }满足c n ={1,n ≤5,b n−5,n ≥6,求数列{a n c n }的前n 项和T n .解析 (1)设等差数列{a n }的公差为d,等比数列{b n }的公比为q(q>0),根据题意得{3q =3(1+2d),3q 2=12(1+d)+3,解得{d =1,q =3或{d =−1,q =−1(舍),所以a n =1+(n-1)×1=n,b n =3·3n-1=3n .(2)当n ≤5时,c n =1,所以T n =a 1+a 2+…+a n =1+2+…+n=n(n+1)2.当n ≥6时,c n =b n-5=3n-5,所以T n =T 5+a 6b 1+a 7b 2+…+a n b n-5=15+6×31+7×32+…+n ·3n-5.令M=6×31+7×32+…+n ·3n-5,则3M=6×32+7×33+…+(n-1)·3n-5+n ·3n-4,两式相减得-2M=6×31+(32+33+…+3n-5)-n ·3n-4=18+32(1−3n−6)1−3-n ·3n-4,整理得M=-274+2n−14·3n-4,所以T n =334+2n−14·3n-4.综上,T n ={n(n+1)2,n ≤5,334+2n−14·3n−4,n ≥6.3.(2022届山东泰安肥城摸底考试)已知数列{a n }各项均为正数,a 1=1,{a n 2}为等差数列,公差为2. (1)求数列{a n }的通项公式.(2)求S n =2a 12+22a 22+23a 32+ (2)a n 2.解析 (1)∵a 1=1,∴a 12=1,又∵{a n 2}为等差数列,公差为2,∴a n 2=a 12+(n-1)×2=2n-1,又∵a n >0,∴a n =√2n −1.(2)由(1)可得S n =1×2+3×22+5×23+…+(2n-1)·2n ,2S n =1×22+3×23+5×24+…+(2n-1)·2n+1, 两式相减得-S n =1×2+2×22+2×23+…+2·2n-(2n-1)·2n+1=2+2n+2-23-(2n-1)·2n+1=-6-(2n-3)·2n+1,∴S n =6+(2n-3)·2n+1.4.(2021浙江,20,15分)已知数列{a n }的前n 项和为S n ,a 1=-94,且4S n+1=3S n -9(n ∈N *). (1)求数列{a n }的通项公式;(2)设数列{b n }满足3b n +(n-4)a n =0(n ∈N *),记{b n }的前n 项和为T n ,若T n ≤λb n 对任意n ∈N *恒成立,求实数λ的取值范围.解析 (1)解法一:由4S n+1=3S n -9,得4S n =3S n-1-9(n ≥2),两式相减,得4a n+1=3a n ,则a n+1=34a n (n ≥2).又由4S n+1=3S n -9,得4S 2=3S 1-9,即4(a 1+a 2)=3a 1-9, 又a 1=-94,所以a 2=-2716,则a 2=34a 1, 所以数列{a n }是以-94为首项,34为公比的等比数列, 所以数列{a n }的通项公式为a n =-94·(34)n−1=-3·(34)n . 解法二:由4S n+1=3S n -9,得S n+1=34S n -94,则S n+1+9=34S n -94+9=34S n +274=34(S n +9),又S 1+9=-94+9=274≠0,所以数列{S n +9}是以274为首项,34为公比的等比数列,则S n +9=274·(34)n−1=9·(34)n ,所以S n =9·(34)n-9.当n ≥2时,a n =S n -S n-1=[9·(34)n −9]-[9·(34)n−1−9]=-3·(34)n .当n=1时,a 1=-94也满足上式,所以数列{a n }的通项公式为a n =-3·(34)n.(2)由(1)知a n =-3·(34)n.由3b n +(n-4)a n =0,得b n =-n−43a n =(n-4)(34)n. 则T n =(-3)×34+(-2)×(34)2+(-1)×(34)3+0×(34)4+…+(n-5)(34)n−1+(n-4)(34)n,① 因此34T n =(-3)×(34)2+(-2)×(34)3+(-1)×(34)4+0×(34)5+…+(n-5)(34)n +(n-4)(34)n+1,②由①-②,得14T n =-3×34+(34)2+(34)3+(34)4+…+(34)n -(n-4)(34)n+1 =-94+(34)2−(34)n ·341−34-(n-4)(34)n+1=-n (34)n+1, 所以T n =-4n (34)n+1.由T n ≤λb n ,得-4n (34)n+1≤λ(n-4)(34)n 恒成立,即λ(n-4)≥-3n 恒成立. 当n<4时,λ≤-3n n−4,设f(n)=-3n n−4=-3+−12n−4,当n<4且n ∈N *时,f(n)min =f(1)=1,所以λ≤1;当n=4时,不等式恒成立; 当n>4时,λ≥-3n n−4,设f(n)=-3n n−4=-3+−12n−4,当n>4且n ∈N *,n →+∞时,f(n)→-3,所以λ≥-3.综上所述,实数λ的取值范围是[-3,1].5.(2021全国乙文,19,12分)设{a n }是首项为1的等比数列,数列{b n }满足b n =na n3.已知a 1,3a 2,9a 3成等差数列.(1)求{a n }和{b n }的通项公式;(2)记S n 和T n 分别为{a n }和{b n }的前n 项和.证明:T n <S n 2. 解析 (1)设等比数列{a n }的公比为q. ∵a 1,3a 2,9a 3成等差数列,∴6a 2=a 1+9a 3,又∵{a n }是首项为1的等比数列,∴6a 1q=a 1+9a 1q 2,∴9q 2-6q+1=0,解得q 1=q 2=13,∴a n =a 1·q n-1=(13)n−1,∵b n =na n 3,∴b n =n ·(13)n. (2)证明:∵S n 为{a n }的前n 项和, ∴S n =a 1(1−q n )1−q =32[1−(13)n]. ∵T n 为{b n }的前n 项和, ∴T n =b 1+b 2+…+b n =1×(13)1+2×(13)2+…+n (13)n,① 13T n =1×(13)2+2×(13)3+…+n (13)n+1.② ①-②可得23T n =13+(13)2+…+(13)n-n ·(13)n+1=13[1−(13)n ]1−13-n ·(13)n+1=-(13n +12)(13)n +12,∴T n =-(12n +34)(13)n +34, ∴T n -S n 2=-12n ·(13)n <0,∴T n <S n2.6.(2020课标Ⅲ理,17,12分)设数列{a n }满足a 1=3,a n+1=3a n -4n. (1)计算a 2,a 3,猜想{a n }的通项公式并加以证明; (2)求数列{2na n }的前n 项和S n . 解析 (1)a 2=5,a 3=7. 猜想a n =2n+1.由已知可得 a n+1-(2n+3)=3[a n -(2n+1)], a n -(2n+1)=3[a n-1-(2n-1)], ……a 2-5=3(a 1-3).因为a 1=3,所以a n =2n+1. (2)由(1)得2na n =(2n+1)2n,所以S n =3×2+5×22+7×23+…+(2n+1)×2n.①从而2S n =3×22+5×23+7×24+…+(2n+1)×2n+1.②①-②得-S n =3×2+2×22+2×23+…+2×2n-(2n+1)×2n+1.所以S n =(2n-1)2n+1+2.7.(2017山东文,19,12分)已知{a n }是各项均为正数的等比数列,且a 1+a 2=6,a 1a 2=a 3. (1)求数列{a n }的通项公式;(2){b n }为各项非零的等差数列,其前n 项和为S n .已知S 2n+1=b n b n+1,求数列{b na n}的前n 项和T n . 解析 (1)设{a n }的公比为q,由题意知a 1(1+q)=6,a 12q=a 1q 2,又a n >0,所以解得a 1=2,q=2,所以a n =2n. (2)由题意知S 2n+1=(2n+1)(b 1+b 2n+1)2=(2n+1)b n+1,又S 2n+1=b n b n+1,b n+1≠0,所以b n =2n+1.令c n =b n a n ,则c n =2n+12n .因此T n =c 1+c 2+…+c n =32+522+723+…+2n−12n−1+2n+12n ,又12T n =322+523+724+…+2n−12n +2n+12n+1,两式相减得12T n =32+(12+122+⋯+12n−1)-2n+12n+1,所以T n =5-2n+52n. 8.(2017天津理,18,13分)已知{a n }为等差数列,前n 项和为S n (n ∈N *),{b n }是首项为2的等比数列,且公比大于0,b 2+b 3=12,b 3=a 4-2a 1,S 11=11b 4. (1)求{a n }和{b n }的通项公式;(2)求数列{a 2n b 2n-1}的前n 项和(n ∈N *).解析 (1)设等差数列{a n }的公差为d,等比数列{b n }的公比为q.由已知b 2+b 3=12,得b 1(q+q 2)=12,因为b 1=2,所以q 2+q-6=0,解得q=2或q=-3,又因为q>0,所以q=2.所以,b n =2n.由b 3=a 4-2a 1,可得3d-a 1=8①.由S 11=11b 4,可得a 1+5d=16②,联立①②,解得a 1=1,d=3,由此可得a n =3n-2. 所以,数列{a n }的通项公式为a n =3n-2,数列{b n }的通项公式为b n =2n.(2)设数列{a 2n b 2n-1}的前n 项和为T n ,由a 2n =6n-2,b 2n-1=2×4n-1,得a 2n b 2n-1=(3n-1)×4n, 故T n =2×4+5×42+8×43+…+(3n-1)×4n,4T n =2×42+5×43+8×44+…+(3n-4)×4n +(3n-1)×4n+1, 上述两式相减,得-3T n =2×4+3×42+3×43+…+3×4n-(3n-1)×4n+1=12×(1−4n )1−4-4-(3n-1)×4n+1=-(3n-2)×4n+1-8.得T n =3n−23×4n+1+83.所以,数列{a 2n b 2n-1}的前n 项和为3n−23×4n+1+83. 9.(2018浙江,20,15分)已知等比数列{a n }的公比q>1,且a 3+a 4+a 5=28,a 4+2是a 3,a 5的等差中项.数列{b n }满足b 1=1,数列{(b n+1-b n )·a n }的前n 项和为2n 2+n. (1)求q 的值;(2)求数列{b n }的通项公式.解析 (1)由a 4+2是a 3,a 5的等差中项得a 3+a 5=2a 4+4,所以a 3+a 4+a 5=3a 4+4=28,解得a 4=8. 由a 3+a 5=20得8(q +1q )=20,解得q=2或q=12, 因为q>1,所以q=2.(2)设c n =(b n+1-b n )a n ,数列{c n }的前n 项和为S n . 由c n ={S 1,n =1,S n −S n−1,n ≥2,解得c n =4n-1. 由(1)可知a n =2n-1,所以b n+1-b n =(4n-1)·(12)n−1,故b n -b n-1=(4n-5)·(12)n−2,n ≥2, 所以b n -b 1=(b n -b n-1)+(b n-1-b n-2)+…+(b 3-b 2)+(b 2-b 1)=(4n-5)·(12)n−2+(4n-9)·(12)n−3+…+7×12+3.设T n =3+7×12+11×(12)2+…+(4n-5)·(12)n−2,n ≥2,则12T n =3×12+7×(12)2+…+(4n-9)·(12)n−2+(4n-5)·(12)n−1, 所以12T n =3+4×12+4×(12)2+…+4·(12)n−2-(4n-5)·(12)n−1,因此T n =14-(4n+3)·(12)n−2,n ≥2,又b 1=1,所以b n =15-(4n+3)·(12)n−2. 10.(2021浙江嘉兴教学测试,20)已知数列{a n }的前n 项和为S n ,S n =2a n -n,n ∈N *. (1)求数列{a n }的通项公式;(2)令b n =2na n ,求数列{b n }的前n 项和T n . 解析 (1)当n=1时,S 1=a 1=2a 1-1,得a 1=1;当n ≥2时,由S n =2a n -n,得S n-1=2a n-1-(n-1),两式相减得a n =2a n-1+1,变形得a n +1=2(a n-1+1), ∴数列{a n +1}是等比数列,且公比为2.又∵a 1+1=2,∴a n +1=2n,∴a n =2n-1.(2)b n =2na n =2n(2n -1)=n ·2n+1-2n,于是T n =b 1+b 2+…+b n =(1×22-2)+(2×23-4)+…+(n ×2n+1-2n)=(1×22+2×23+…+n ×2n+1)-2(1+2+…+n),令A n =1×22+2×23+…+n ·2n+1,即T n =A n -n(n+1).A n =1×22+2×23+…+(n-1)·2n +n ·2n+1,① 2A n =1×23+2×24+…+(n-1)·2n+1+n ·2n+2,②①-②得-A n =22+23+…+2n+1-n ·2n+2=4(1−2n )1−2-n ·2n+2=-4+2n+2-n ·2n+2=-(n-1)·2n+2-4,∴A n =(n-1)·2n+2+4,∴T n =(n-1)·2n+2+4-n 2-n.考法二 裂项相消法求和1.(2020长沙明德中学3月月考)在各项都为正数的等比数列{a n }中,若a 1=2,且a 1a 5=64,则数列{a n(an −1)(a n+1−1)}的前n 项和是( )A.1-12n+1−1B.1-12n+1C.1-12n+1 D.1-12n −1答案 A2.(多选)(2021辽宁百校联盟质检,10)已知数列{a n }满足a 2=4,n(n-1)a n+1=(n-1)a n -na n-1(n>1且n ∈N *),数列{a n }的前n 项和为S n ,则( ) A.a 1+a 3=2 B.a 1+a 3=4C.2020S 2021-a 2020=8080D.2021S 2021-a 2020=4040 答案 AC3.(2017课标Ⅱ,15,5分)等差数列{a n }的前n 项和为S n ,a 3=3,S 4=10,则∑k=1n1S k = . 答案2nn+14.(2020浙江丽水四校联考,14)已知数列{a n }满足:a 1=12,a n+1=a n 2+a n ,用[x]表示不超过x 的最大整数,则[1a1+1+1a 2+1+⋯+1a 2 012+1]的值等于 . 答案 15.(2022届河北邢台入学考试)在①a3+a6=18,②{a n}的前n项和S n=n2+pn,③a3+a4=a7这三个条件中任选一个,补充在下面的问题中并解答.问题:在等差数列{a n}中,a1=2,且.(1)求数列{a n}的通项公式;(2)若b n=1a n a n+1,求数列{b n}的前n项和T n.注:若选择多个条件分别解答,则按第一个解答计分.解析(1)选①.设{a n}的公差为d.由题意可得a1+2d+a1+5d=2a1+7d=18.因为a1=2,所以d=2,则a n=a1+(n-1)d=2n.选②.设{a n}的公差为d.因为S n=n2+pn,所以S n-1=(n-1)2+p(n-1)=n2+pn-2n-p+1(n≥2),两式相减得a n=2n+p-1(n≥2),又因为a1=S1=p+1满足上式,所以a n=2n+p-1(n∈N*).由a1=2得p+1=2,所以p=1,所以a n=2n. 选③.设{a n}的公差为d.因为a3+a4=a7,所以a1+2d+a1+3d=a1+6d,即a1=d.因为a1=2,所以d=2,所以a n=a1+(n-1)d=2n.(2)由(1)可得a n+1=2(n+1),则b n=12n·2(n+1)=14(1n−1n+1).故T n=14[(1−12)+(12−13)+⋯+(1n−1n+1)]=14(1−1n+1)=n4n+4.6.(2022届河北唐山玉田一中开学考试)在①S7=49,②S5=a8+10,③S8=S6+28这三个条件中任选一个,补充在下面问题中,并完成解答.问题:已知等差数列{a n}的前n项和为S n,a5=9,,若数列{b n}满足b n=1a n a n+1,证明:数列{b n}的前n项和T n<12.注:若选择多个条件分别解答,则按第一个解答计分.证明 选择①.设数列{a n }的公差为d,由{S 7=49,a 5=9,得{7a 1+7×(7−1)2d =49,a 1+4d =9,解得{a 1=1,d =2,所以a n =2n-1.又因为b n =1a n a n+1=1(2n−1)(2n+1)=12(12n−1−12n+1),所以T n =b 1+b 2+b 3+…+b n =12(1−13+13−15+15−17+⋯+12n−1−12n+1), 所以T n =12(1−12n+1)<12. 选择②.设数列{a n }的公差为d,由S 5=a 8+10,可得4a 1+3d=10,又a 5=a 1+4d=9,联立解得d=2,a 1=1,所以a n =2n-1.下面同选择①.选择③.设数列{a n }的公差为d,由S 8-S 6=28,可得a 7+a 8=2a 5+5d=28,又因为a 5=9,所以d=2,所以a 1=a 5-4d=9-4×2=1,所以a n =2n-1.下面同选择①.7.(2022届湖北黄冈调研,19)已知数列{a n }的前n 项和为S n ,2S n =(n+1)a n ,且a 1>1,a 2-1,a 4-2,a 6成等比数列. (1)求数列{a n }的通项公式; (2)设b n =4a n a n+1+2−a n ,数列{b n }的前n 项和为T n ,求证:T n <43.解析 (1)∵2S n =(n+1)a n ,∴S n =(n+1)a n 2,当n ≥2时,a n =S n -S n-1=n+12·a n -n 2·a n-1,化简得a n n =a n−1n−1,即a n n =a n−1n−1=…=a 11,∴a n =na 1,又a 2-1,a 4-2,a 6成等比数列,∴(a 2-1)·a 6=(a 4-2)2,即(2a 1-1)·6a 1=(4a 1-2)2,解得a 1=2或a 1=12.又a 1>1,∴a 1=2,∴a n =2n(n ∈N *). (2)证明:由(1)可得b n =4a n a n+1+2−a n =42n·2(n+1)+2-2n =1n -1n+1+(14)n ,∴T n =b 1+b 2+…+b n =[(1−12)+14]+[(12−13)+(14)2]+…+[(1n −1n+1)+(14)n ]=(1−12+12−13+⋯+1n −1n+1)+14+(14)2+…+(14)n=1-1n+1+14[1−(14)n]1−14=43-1n+1-13(14)n ,∵n ∈N *,∴T n <43. 8.(2021广东深圳外国语学校第一次月考)设数列{a n }的前n 项和为S n ,∀m ∈N *,都有a m+1-a m =-1,且a 2+S 2=-5. (1)求数列{a n }的通项公式; (2)求证:1a 1a 2+1a 2a 3+…+1a n a n+1<1. 解析 (1)∵∀m ∈N *,都有a m+1-a m =-1, ∴{a n }是等差数列,设公差为d,则d=-1.由a 2+S 2=3a 1+2d=-5,解得a 1=-1, 所以a n =-1-(n-1)=-n. (2)证明:由a n =-n,得1a n a n+1=1n(n+1)=1n -1n+1,所以1a 1a 2+1a 2a 3+…+1a n a n+1=(1−12)+(12−13)+…+(1n −1n+1)=1-1n+1<1. 9.(2021湖北八市3月联考,18)已知数列{a n },其前n 项和为S n ,请在下列三个条件中补充一个在下面问题中,使得最终结论成立并证明你的结论. 条件①:S n =-a n +t(t 为常数);条件②:a n =b n b n+1,其中数列{b n }满足b 1=1,(n+1)b n+1=nb n ;条件③:3a n 2=3a n+12+a n+1+a n .数列{a n }中,a 1是(2√301x)6展开式中的常数项,且 .求证:S n <1对任意n ∈N *恒成立.注:如果选择多个条件作答,则按第一个条件的解答计分.解析 (2√30+1x )6的展开式的通项为T r+1=C 6r·(2√30)6−r(1x )r =C 6r (√30)6−r x 12-3r,令12-3r=0,得r=4,得展开式的常数项为12,即a 1=12.若选择①:在S n =-a n +t 中,令n=1,得2a 1=t,即t=1, 当n ≥2时,S n-1=-a n-1+1.两式相减得a n =12a n-1, 故{a n }是以12为首项,12为公比的等比数列, 所以S n =a 1(1−q n )1−q =1-(12)n <1对任意n ∈N *恒成立. 若选择②:由(n+1)b n+1=nb n 得b n+1b n =nn+1, 所以b n =b n b n−1·b n−1b n−2·…·b 2b 1·b 1=1n (n ≥2),n=1时也满足,故b n =1n (n ∈N *),则a n =1n(n+1)=1n -1n+1, S n =(1−12)+(12−13)+…+(1n −1n+1)=1-1n+1<1对任意n ∈N *恒成立. 若选择③:由题意得3a n+12-3a n 2=-(a n+1+a n ),得a n+1-a n =-13或a n+1+a n =0,又a 1=12,当a n+1+a n =0时,有S n ={0,n 为偶数,12,n 为奇数,所以S n <1;当a n+1-a n =-13时,有S n =n 2-n(n−1)6=-16(n 2-4n),当n=2时,S n 取最大值,为-16×(22-4×2)=23,因为23<1,所以S n <1对任意的n ∈N *恒成立.10.(2022届广东阶段测,17)设{a n }是各项均为正数的数列,a 1=3,a n+1=√a n 2+4a n+1+4a n . (1)求数列{a n }的通项公式;(2)若S n 为数列{a n }的前n 项和,且b n =n(n+1)S n+1S n,求数列{b n }的前n 项和.解析 (1)由a n+1=√a n 2+4a n+1+4a n 得a n+12=a n 2+4a n+1+4a n ,整理得(a n+1-a n -4)(a n+1+a n )=0,又a n+1+a n >0,所以a n+1-a n =4,所以{a n }是首项为3,公差为4的等差数列,故a n =4n-1. (2)由(1)可知,S n =n(3+4n−1)2=n(2n+1),S n+1=(n+1)(2n+3),所以b n =n(n+1)S n+1S n =1(2n+1)(2n+3)=12(12n+1−12n+3),设数列{b n }的前n 项和为T n , 则T n =12[(13−15)+(15−17)+⋯+(12n+1−12n+3)] =12(13−12n+3)=n6n+9.B 组1.(2022届重庆西南大学附中月考,8)设数列{a n }的前n 项和是S n ,令T n =S 1+S 2+⋯+S nn,称T n 为数列a 1,a 2,…,a n 的“超越数”.已知数列a 1,a 2,…,a 504的“超越数”为2020,则数列5,a 1,a 2,…,a 504的“超越数”为( )A.2018B.2019C.2020D.2021 答案 D2.(2022届河北张家口宣化一中考试,6)将正整数12分解成两个正整数的乘积,有1×12,2×6,3×4三种分解方式,其中3×4是这三种分解方式中两数差的绝对值最小的一种,我们称3×4为12的最佳分解.当p ·q(p,q ∈N *)是正整数n 的最佳分解时,我们定义函数f(n)=|p-q|,例如f(12)=|4-3|=1,则∑i=12 021f(2i)=( )A.21011-1B.21011C.21010-1 D.21010答案 A3.(2021山东菏泽期末,7)已知数列{a n }的前n 项和是S n ,且S n =2a n -1,若a n ∈(0,2021),则称项a n 为“和谐项”,则数列{a n }的所有“和谐项”的和为( ) A.1022 B.1023 C.2046 D.2047 答案 D4.(2021河北衡水中学联考二,11)若P(n)表示正整数n 的个位数字,a n =P(n 2)-P(2n),数列{a n }的前n 项和为S n ,则S 2021=( )A.-1B.0C.1009D.1011 答案 C5.(多选)(2021新高考Ⅱ,12,5分)若正整数n=a 0·20+a 1·2+…+a k-1·2k-1+a k ·2k ,其中a i ∈{0,1}(i=0,1,…,k),记ω(n)=a 0+a 1+…+a k ,则( )A.ω(2n)=ω(n)B.ω(2n+3)=ω(n)+1C.ω(8n+5)=ω(4n+3)D.ω(2n-1)=n 答案 ACD6.(多选)(2021广州一模,12)在数学课堂上,教师引导学生构造新数列:在数列的每相邻两项之间插入此两项的和,形成新的数列,再把所得数列按照同样的方法不断构造出新的数列.将数列1,2进行构造,第1次得到数列1,3,2;第2次得到数列1,4,3,5,2;……;第n(n ∈N *)次得到数列1,x 1,x 2,x 3,…,x k ,2.记a n =1+x 1+x 2+…+x k +2,数列{a n }的前n 项和为S n ,则( ) A.k+1=2nB.a n+1=3a n -3C.a n =32(n 2+3n) D.S n =34(3n+1+2n-3) 答案 ABD7.(2020山东师范大学附中最后一卷)对n 个不同的实数a 1,a 2,…,a n 可得n!个不同的排列,每个排列为一行写成一个n!行的数阵.对第i 行a i1,a i2,…,a in ,记b i =-a i1+2a i2-3a i3+…+(-1)nna in ,i=1,2,3,…,n!.例如用1,2,3可得数阵如图,此数阵中每一列各数之和都是12,所以b 1+b 2+…+b 6=-12+2×12-3×12=-24.那么,在用1,2,3,4,5形成的数阵中,b 1+b 2+…+b 120等于( )1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1A.-3600B.-1800C.-1080D.-720 答案 C8.(2021湖南岳阳一模,4)“中国剩余定理”又称“孙子定理”,讲的是一个关于整除的问题.现有这样一个整除问题:将1到2021这2021个数中能被3整除余2且被5整除余2的数按从小到大的顺序排成一列,构成数列{a n },则此数列的所有项中,中间项的值为( ) A.992 B.1022 C.1007 D.1037 答案 C9.(多选)(2021济南十一学校联考,11)已知数列{F n }:1,1,2,3,5,8,13,…,从第三项开始,每项等于其前相邻两项之和.记数列{F n }的前n 项和为S n ,则下列结论中正确的是( ) A.S 6=F 8 B.S 2019=F 2021-1C.F 1+F 3+F 5+…+F 2021=F 2022D.F 12+F 22+F 32+…+F 2 0202=F 2020F 2021答案 BCD10.(2022届南京调研,7)取一条长度为1的直线段,将它三等分,去掉中间一段,留剩下的两段;再将剩下的两段分别三等分,各去掉中间一段,留剩下的更短的四段;……;将这样的操作一直继续下去,直至无穷,由于在不断分割舍弃的过程中,所形成的线段数目越来越多,长度越来越小,在极限的情况下,得到一个离散的点集,称为康托尔三分集.若在第n 次操作中去掉的线段长度之和不小于160,则n 的最大值为(参考数据:lg2≈0.3010,lg3≈0.4771)( ) A.6 B.7 C.8 D.9 答案 C应用篇知行合一应用构建数列模型解决实际生活中的问题1.(2020山东潍坊6月模拟数学文化与等差数列)在我国古代著名的数学专著《九章算术》里有一段叙述:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增十三里;驽马初日行九十七里,日减半里;良马先至齐,复还迎驽马,二马相逢.相逢时良马比驽马多行()A.540里B.426里C.963里D.114里答案A2.(2020山东省实验中学期中数学文化与等比数列)古代数学著作《九章算术》有如下问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”意思是“一女子善于织布,每天织的布都是前一天的2倍,已知她5天共织布5尺,问这女子每天分别织布多少?”根据上述已知条件,若要使织布的总尺数不少于30尺,则至少需要()A.6天B.7天C.8天D.9天答案C3.(2022届全国联考,6实际生活)某微生物科研机构为了记录微生物在不同时期的存活状态,计划将微生物分批次培养,第一批次,培养1个;从第二批次开始,每一批次培养的个数是前一批次的2倍,按照这种培养方式(假定每一批次的微生物都能成活),要使微生物的总个数不少于950,大概经过的批次为()A.10B.9C.8D.7答案A4.(2022届湖南湘潭月考,4数学文化与等比数列)我国古代数学名著《算法统宗》是明代数学家程大位(1533年—1606年)所著.程大位少年时,读书极为广博,对书法和数学颇感兴趣.20岁起便在长江中下游一带经商,因商业计算的需要,他随时留心数学,遍访名师,搜集了很多数学书籍,刻苦钻研,时有心得,终于在他60岁时,完成了《算法统宗》这本著作.该书中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”根据诗词的意思,可得塔的最底层共有灯()A.192盏B.128盏C.3盏D.1盏答案 A5.(多选)(2022届江苏南通海门一中月考数学文化)《张丘建算经》是中国古代众多数学名著之一.书中有如下问题:“今有女善织,日益功疾,初日织五尺,今一月日织九匹三丈,问日益几何?”其大意为:“有一女子擅长织布,织布的速度一天比一天快,从第二天起,每天比前一天多织相同数量的布,第一天织5尺,一个月共织了9匹3丈,问从第二天起,每天比前一天多织多少尺布?”已知1匹=4丈,1丈=10尺,若这个月有30天,记该女子这个月中第n 天所织布的尺数为a n ,b n =2a n ,则( )A.b 10=8b 5B.数列{b n }是等比数列C.a 1b 30=105D.a 3+a 5+a 7a 2+a 4+a 6=209193答案 BD6.(多选)(2021江苏栟茶中学学情调研数学文化与等比数列)在《增减算法统宗》中有这样一则故事:“三百七十八里关,初行健步不为难,次日脚痛减一半,如此六日过其关.”则下列说法正确的是( )A.此人第二天走了九十六里路B.此人第一天走的路程比后五天走的路程多六里C.此人第三天走的路程占全程的18D.此人后三天共走了42里路答案 ABD7.(多选)(2021湖南、河北联考,11数学文化与等差数列)朱世杰是元代著名数学家,他所著的《算学启蒙》是一部在中国乃至世界最早的科学普及著作.《算学启蒙》中涉及一些“堆垛”问题,主要利用“堆垛”研究数列以及数列的求和问题.现有100根相同的圆形铅笔,小明模仿“堆垛”问题,将它们全部堆放成纵断面为等腰梯形的“垛”,要求层数不小于2,且从最下面一层开始,每一层比上一层多1根,则该“等腰梯形垛”应堆放的层数可以是( )。

专题十计数原理10.1计数原理、排列与组合基础篇固本夯基考点计数原理、排列、组合1.(2022届山东平邑一中收心考)某旅馆有三人间、两人间、单人间各一间可入住,现有三个成人带两个小孩前来住宿,若小孩不单独入住一个房间(必须有成人陪同),且三间房都要安排给他们入住,则不同的安排方法有()A.18种B.12种C.27种D.15种答案A2.(2022届广东开学联考)四色定理又称四色猜想,是世界近代三大数学难题之一.其内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色.”四色问题的证明进程缓慢,直到1976年,美国数学家运用电子计算机证明了四色定理.现某校数学兴趣小组给一个底面边长互不相等的直四棱柱容器的侧面和下底面染色,提出如下的“四色问题”:要求相邻两个面不得使用同一种颜色,现有4种颜色可供选择,则不同的染色方案有()A.18种B.36种C.48种D.72种答案D3.(2020新高考Ⅰ,3,5分)6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排3名,则不同的安排方法共有()A.120种B.90种C.60种D.30种答案C4.(2021上海杨浦一模,15)从正方体的8个顶点中选取4个作为顶点,可得到四面体的个数为()A.C84-12B.C84-8C.C84-6D.C84-4答案A5.(2020山东潍坊临朐模拟,8)现有4种不同颜色,要对如图所示的四个部分进行着色,要求有公共边界的两块不能用同一种颜色,则不同的着色方法共有()A.24种B.30种C.36种D.48种答案D6.(2021沈阳市郊联体一模,8)中国古典乐器一般按“八音”分类,这是我国最早按乐器的制造材料来对乐器进行分类的方法,最早见于《周礼·春官·大师》.八音分为“金、石、土、革、丝、木、匏、竹”,其中“金、石、木、革”为打击乐器,“土、匏、竹”为吹奏乐器,“丝”为弹拨乐器.某同学安排了包括“土、匏、竹”在内的六种乐器的学习,每种乐器安排一节,连排六节,并要求“土”与“匏”相邻排课,但均不与“竹”相邻排课,且“丝”不能排在第一节,则不同的排课方式的种数为()A.960B.1024C.1296D.2021答案C7.(多选)(2021山东师大附中模拟)“二进制”与我国古代的《易经》有着一定的联系,该书中有两类最基本的符号:“——”和“——”,其中“——”在二进制中记作“1”,“——”在二进制中记作“0”,其变化原理与“逢二进一”的法则相通.若从两类符号中任取2个符号排列,则可以组成的不同的十进制数为()A.0B.1C.2D.3答案ABCD8.(2018浙江,16,4分)从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成个没有重复数字的四位数.(用数字作答)答案12609.(2021江苏盐城二模,13)某班4名同学去参加3个社团,每人只参加1个社团,每个社团都有人参加,则满足上述要求的不同方案共有种.(用数字填写答案)答案36综合篇知能转换考法一排列问题的解决方法1.(2022届河北邯郸开学摸底,5)由1,2,3,4,5,6六个数字按如下要求组成无重复数字的六位数,1必须排在前两位,且2,3,4必须排在一起,则这样的六位数共有()A.48个B.60个C.72个D.84个答案B2.(2022届广东深圳七中月考,5)某次演出有5个节目,若甲、乙、丙3个节目间的先后顺序已确定,则不同的排法有()A.120种B.80种C.20种D.48种答案C3.(2022届河北玉田一中开学考)高三(2)班某天安排6节课,其中语文、数学、英语、物理、生物、地理各一节.若要求物理课比生物课先上,语文课与数学课相邻,则编排方案共有()A.42种B.96种C.120种D.144种答案C4.(2022届广东珠海二中10月月考,3)五名同学国庆假期相约去珠海日月贝采风观景,结束后五名同学排成一排照相留念,若甲乙二人不相邻,则不同的排法共有()A.36种B.48种C.72种D.120种答案C5.(2022届河北廊坊十二中一模,7)由0,1,2,3,4这5个数组成无重复数字的五位数且为偶数,共有种不同的排法()A.24B.48C.60D.62答案C6.(2021湖北九师联盟2月质量检测,3)若5个人排成一列纵队,则其中甲、乙、丙三人两两不相邻的排法有()A.4种B.14种C.5种D.12种答案D7.(2020广东深圳七中第二次月考,4)7个人排成一排准备照一张合影,其中甲、乙要求相邻,丙、丁要求分开,则不同的排法有()A.480种B.720种C.960种D.1200种答案C8.(2022届广东深圳六校联考,13)一部纪录片在4个不同的场地轮映,每个场地放映一次,则有种轮映次序.答案249.(2021福建三明一中月考一)来自甲、乙、丙3个班级的5名同学站在一排照相,其中甲班有2名同学,乙班有2名同学,丙班有1名同学,则仅有甲班的同学相邻的站法种数为.答案 2410.(2017天津理,14,5分)用数字1,2,3,4,5,6,7,8,9组成没有重复数字,且至多有一个数字是偶数的四位数,这样的四位数一共有 个.(用数字作答)答案 108011.(2020山东济宁一中质量检测,15)“中国梦”的英文翻译为“ChinaDream ”,其中China 又可以简写为CN,从“CNDream ”中取6个不同的字母排成一排,含有“ea ”字母组合(顺序不变)的不同排列共有 种.答案 600考法二 组合问题的常见解法1.(2022届湖北部分重点中学9+N 新高考联盟新起点联考)定义空间直角坐标系中的任意点P(x,y,z)的“N 数”为在P 点的坐标中不同数字的个数,如:N(1,1,1)=1,N(1,3,1)=2,N(1,2,3)=3,若x,y,z ∈{0,1,2,3},则所有这些点P 的“N 数”的平均值为( )A.3716B.64C.2516D.40 答案 A2.(2022届湖南天壹名校联盟摸底)已知文印室内有5份待打印的文件自上而下摞在一起,秘书小王要在这5份文件中再插入甲、乙两份文件,甲文件要在乙文件前打印,且不改变原来次序,则不同的打印方式有( )A.15种B.21种C.28种D.36种答案 B3.(2020长沙一中月考(一),8)中国有十二生肖,又叫十二属相,每一个人的出生年份对应了十二种动物(鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪)中的一种,现有十二生肖的吉祥物各一个,甲、乙、丙三位同学依次选一个作为礼物,甲同学喜欢牛和马,乙同学喜欢牛、兔、狗和羊,丙同学哪个吉祥物都喜欢,如果让三位同学对选取的礼物都满意,那么不同的选法有 ( )A.50种B.60种C.70种D.90种答案 C4. (2021广州一模,6)如图,洛书(古称龟书)是阴阳五行术数之源.在古代传说中有神龟出于洛水,其甲壳上有此图象,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四角黑点为阴数.若从四个阴数和五个阳数中随机选取3个数,则选取的3个数之和为奇数的方法数为 ( )A.30B.40C.44D.70答案 B5.(多选)(2021江苏启东中学检测,9)在100件产品中,有98件合格品,2件不合格品.从这100件产品中任意抽出3件,则下列结论正确的有( )A.抽出的3件产品中恰好有1件是不合格品的抽法有C 21C 982种B.抽出的3件产品中恰好有1件是不合格品的抽法有C 21C 992种C.抽出的3件中至少有1件是不合格品的抽法有(C 21C 982+C 22C 981)种D.抽出的3件中至少有1件是不合格品的抽法有(C 1003-C 983)种答案 ACD6.(2018课标Ⅰ理,15,5分)从2位女生,4位男生中选3人参加科技比赛,且至少有1位女生入选,则不同的选法共有 种.(用数字填写答案)答案 16考法三 分组与分配问题的解题方法1.(2022届南京学情调研,5)将4名志愿者全部安排到某社区参加3项工作,每人参加1项,每项工作至少有1人参加,则不同的安排方式共有( )A.24种B.36种C.60种D.72种答案 B2.(2021全国乙理,6,5分)将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有( )A.60种B.120种C.240种D.480种答案 C3.(2022届重庆西南大学附中开学考,6)A,B,C,D,E,F六名同学进行劳动技术比赛,决出第1名到第6名的名次.A,B,C去询问成绩,回答者对A说:“很遗憾,你们三个都没有得到冠军.”对B说:“你的名次在C之前.”对C说:“你不是最后一名.”从以上的回答分析,6人的名次排列情况种数为()A.108B.120C.144D.156答案A4.(2022届河北沧州十五校摸底)将甲乙等5名志愿者分配到冬奥会三个不同的运动场馆做服务工作,每个岗位至少1人,且甲乙二人必须在一起,则共有种不同的分配方法.答案365.(2020课标Ⅱ理,14,5分)4名同学到3个小区参加垃圾分类宣传活动,每名同学只去1个小区,每个小区至少安排1名同学,则不同的安排方法共有种.答案36。

2025年新人教版高考数学一轮复习讲义含答案解析§1.1集合课标要求1.了解集合的含义，了解全集、空集的含义.2.理解元素与集合的属于关系，理解集合间的包含和相等关系.3.会求两个集合的并集、交集与补集.4.能用自然语言、图形语言、集合语言描述不同的具体问题，能使用Venn图表示集合间的基本关系和基本运算．知识梳理1．集合与元素(1)集合中元素的三个特性：确定性、互异性、无序性．(2)元素与集合的关系是属于或不属于，用符号∈或∉表示．(3)集合的表示法：列举法、描述法、图示法．(4)常见数集的记法集合非负整数集(或自然数集)正整数集整数集有理数集实数集符号NN *(或N ＋)Z QR2.集合的基本关系(1)子集：一般地，对于两个集合A ，B ，如果集合A 中任意一个元素都是集合B 中的元素，就称集合A 为集合B 的子集，记作A ⊆B (或B ⊇A )．(2)真子集：如果集合A ⊆B ，但存在元素x ∈B ，且x ∉A ，就称集合A 是集合B 的真子集，记作A B (或BA )．(3)相等：若A ⊆B ，且B ⊆A ，则A ＝B .(4)空集：不含任何元素的集合叫做空集，记为∅.空集是任何集合的子集，是任何非空集合的真子集．3．集合的基本运算表示集合语言图形语言记法运算并集{x|x∈A，或x∈B}A∪B交集{x|x∈A，且x∈B}A∩B补集{x|x∈U，且x∉A}∁U A常用结论1．若集合A有n(n≥1)个元素，则集合A有2n个子集，2n－1个真子集．2．空集是任何集合的子集，是任何非空集合的真子集．3．A∩B＝A⇔A⊆B，A∪B＝A⇔B⊆A.4．∁U(A∩B)＝(∁U A)∪(∁U B)，∁U(A∪B)＝(∁U A)∩(∁U B)．自主诊断1．判断下列结论是否正确．(请在括号中打“√”或“×”)(1)集合{x∈N|x3＝x}，用列举法表示为{－1,0,1}．(×)(2){x|y＝x2＋1}＝{y|y＝x2＋1}＝{(x，y)|y＝x2＋1}．(×)(3)若1∈{x2，x}，则x＝－1或x＝1.(×)(4)对任意集合A，B，都有(A∩B)⊆(A∪B)．(√)2．(必修第一册P14T4改编)设集合A＝{x|3≤x<7}，B＝{x|2<x<10}，则(∁R A)∩B等于() A．{x|2<x≤3}B．{x|7<x<10}C．{x|2<x<3或7≤x<10}D．{x|2<x≤3或7<x<10}答案C解析因为∁R A＝{x|x<3或x≥7}，B＝{x|2<x<10}，所以(∁R A)∩B＝{x|2<x<3或7≤x<10}．3．(必修第一册P35T9改编)已知集合A＝{1,3，a2}，B＝{1，a＋2}，若A∪B＝A，则实数a ＝________.答案2解析因为A∪B＝A，所以B⊆A，所以a＋2∈A.当a＋2＝3，即a＝1时，A＝{1,3,1}，不满足集合中元素的互异性，不符合题意；当a＋2＝a2时，a＝－1(舍去)或a＝2，此时A＝{1,3,4}，B＝{1,4}，符合题意．综上，实数a＝2.4．(必修第一册P9T5改编)已知集合A＝{x|0<x<a}，B＝{x|0<x<2}，若B⊆A，则实数a的取值范围为________．答案[2，＋∞)解析因为B⊆A，所以利用数轴分析法(如图)，可知a≥2.题型一集合的含义与表示例1(1)(2023·长春模拟)已知集合A＝{(x，y)|x2＋y2＝4}，B＝{(x，y)|x＋y＝0}，则A∩B的子集个数为()A．1B．2C．3D．4答案D解析集合A＝{(x，y)|x2＋y2＝4}表示以(0,0)为圆心，2为半径的圆上的所有点，集合B＝{(x，y)|x＋y＝0}表示直线x＋y＝0上的所有点，因为直线x＋y＝0经过圆心(0,0)，所以直线与圆相交，所以A∩B的元素个数为2，则A∩B的子集个数为4.(2)已知集合A＝{0，m，m2－3m＋2}，且2∈A，则实数m的值为()A．2B．3C．0D．－2答案B解析因为集合A＝{0，m，m2－3m＋2}，且2∈A，则m＝2或m2－3m＋2＝2，解得m∈{0,2,3}．当m＝0时，集合A中的元素不满足互异性；当m＝2时，m2－3m＋2＝0，集合A中的元素不满足互异性；当m＝3时，A＝{0,3,2}，符合题意．综上所述，m＝3.思维升华解决集合含义问题的关键点(1)一是确定构成集合的元素．(2)确定元素的限制条件．(3)根据元素的特征(满足的条件)构造关系式解决相应问题．跟踪训练1(1)(2023·苏州模拟)设集合A＝{1,2,3}，B＝{4,5}，C＝{x＋y|x∈A，y∈B}，则C中元素的个数为()A ．3B ．4C ．5D ．6答案B解析因为集合A ＝{1,2,3}，B ＝{4,5}，C ＝{x ＋y |x ∈A ，y ∈B }，所以C ＝{5,6,7,8}．即C 中元素的个数为4.(2)若含有3，b a ，{a 2，a ＋b,0}，则a 2024＋b 2024＝________.答案1解析，ba，{a 2，a ＋b,0}，显然a ≠0，所以ba ＝0，即b ＝0；此时两集合分别是{a,1,0}，{a ，a 2,0}，则a 2＝1，解得a ＝1或a ＝－1.当a ＝1时，不满足互异性，故舍去；当a ＝－1时，满足题意．所以a 2024＋b 2024＝(－1)2024＋02024＝1.题型二集合间的基本关系例2(1)(2023·海口质检)已知集合A ＝{x |x >5}，B ＝{x |1－log 2x <0}，则()A ．A ⊆B B ．B ⊆AC ．A ∩B ＝∅D ．A ∪B ＝R答案A解析因为集合A ＝{x |x >5}，集合B ＝{x |1－log 2x <0}＝{x |x >2}，所以A ⊆B .(2)已知集合A ＝{x |x <－1或x ≥3}，B ＝{x |ax ＋1≤0}，若B ⊆A ，则实数a 的取值范围是()A.－13，B.－13，1C ．(－∞，－1)∪[0，＋∞)D.－13，(0,1)答案A 解析∵B ⊆A ，∴①若B ＝∅，即ax ＋1≤0无解，此时a ＝0，满足题意．②若B ≠∅，即ax ＋1≤0有解，当a >0时，可得x ≤－1a，要使B ⊆A ，>0，－1a<－1，解得0<a <1；当a <0时，可得x ≥－1a，要使B ⊆A ，<0，－1a≥3，解得－13≤a <0，综上，实数a 的取值范围是－13，思维升华(1)空集是任何集合的子集，在涉及集合关系问题时，必须考虑空集的情况，否则易造成漏解．(2)已知两个集合间的关系求参数时，关键是将条件转化为元素或区间端点间的关系，进而转化为参数所满足的关系，常用数轴、Venn 图等来直观解决这类问题．跟踪训练2(1)已知集合M ＝{x |y ＝1－x 2，x ∈R }，N ＝{x |x ＝m 2，m ∈M }，则集合M ，N 的关系是()A ．MNB ．NMC ．M ⊆∁R ND ．N ⊆∁R M答案B解析因为M ＝{x |y ＝1－x 2，x ∈R }＝{x |－1≤x ≤1}，N ＝{x |x ＝m 2，m ∈M }＝{x |0≤x ≤1}，所以NM .(2)设集合A ＝{x |－1≤x ＋1≤6}，B ＝{x |m －1<x <2m ＋1}，当x ∈Z 时，集合A 的非空真子集的个数为________；当B ⊆A 时，实数m 的取值范围是________．答案254{m |m ≤－2或－1≤m ≤2}解析易得A ＝{x |－2≤x ≤5}．若x ∈Z ，则A ＝{－2，－1,0,1,2,3,4,5}，即A 中含有8个元素，∴A 的非空真子集的个数为28－2＝254.①当m －1≥2m ＋1，即m ≤－2时，B ＝∅，B ⊆A ；②当m >－2时，B ＝{x |m －1<x <2m ＋1}≠∅，因此，要使B ⊆A －1≥－2，m ＋1≤5，解得－1≤m ≤2.综上所述，m 的取值范围是{m |m ≤－2或－1≤m ≤2}．题型三集合的基本运算命题点1集合的运算例3(1)(2022·新高考全国Ⅰ)若集合M ＝{x |x <4}，N ＝{x |3x ≥1}，则M ∩N 等于()A ．{x |0≤x <2}|13≤x <2C ．{x |3≤x <16}|13≤x <16答案D解析因为M ＝{x |x <4}，所以M ＝{x |0≤x <16}；因为N ＝{x |3x ≥1}，所以N |x ≥13所以M ∩N |13≤x <16(2)(多选)已知M ，N 均为实数集R 的子集，且N ∩(∁R M )＝∅，则下列结论中正确的是()A ．M ∩(∁R N )＝∅B ．M ∪(∁R N )＝RC ．(∁R M )∪(∁R N )＝∁R MD ．(∁R M )∩(∁R N )＝∁R M 答案BD解析∵N ∩(∁R M )＝∅，∴N ⊆M ，如图，若N 是M 的真子集，则M ∩(∁R N )≠∅，故A 错误；由N ⊆M 可得M ∪(∁R N )＝R ，故B 正确；由N ⊆M 可得∁R N ⊇∁R M ，故C 错误，D 正确．命题点2利用集合的运算求参数的值(范围)例4(1)(多选)已知A ＝{x |x 2＋x －6＝0}，B ＝{x |mx ＋1＝0}，且A ∪B ＝A ，则m 的值可能为()A ．－13B.13C ．0D ．－12答案BCD解析由题意知A ＝{x |x 2＋x －6＝0}，由x 2＋x －6＝0，解得x ＝2或x ＝－3，所以A ＝{2，－3}，因为A∪B＝A，所以B⊆A，当B＝∅时，m＝0，满足题意；当B≠∅时，B－1m＝2或－1m＝－3，解得m＝－12或m＝13，综上，m＝0或－12或13.(2)(2024·本溪模拟)设集合A＝{x|x<a2}，B＝{x|x>a}，若A∩(∁R B)＝A，则实数a的取值范围为()A．[0,1]B．[0,1)C．(0,1)D．(－∞，0]∪[1，＋∞)答案A解析因为B＝{x|x>a}，所以∁R B＝{x|x≤a}，又A∩(∁R B)＝A，所以A⊆∁R B，又A＝{x|x<a2}，所以a2≤a，解得0≤a≤1，即实数a的取值范围为[0,1]．思维升华对于集合的交、并、补运算，如果集合中的元素是离散的，可用Venn图表示；如果集合中的元素是连续的，可用数轴表示，此时要注意端点的情况．跟踪训练3(1)(多选)已知集合A＝{x|x2－2x>0}，B＝{x|1<x<3}，则()A．(∁R A)∪B＝{x|0≤x<3}B．(∁R A)∩B＝{x|1<x<2}C．A∩B＝{x|2<x<3}D．A∩B是{x|2<x<5}的真子集答案ACD解析由x2－2x>0，得x<0或x>2，所以A＝{x|x<0或x>2}，所以∁R A＝{x|0≤x≤2}，对于A，因为B＝{x|1<x<3}，所以(∁R A)∪B＝{x|0≤x<3}，所以A正确；对于B，因为B＝{x|1<x<3}，所以(∁R A)∩B＝{x|1<x≤2}，所以B错误；对于C ，因为A ＝{x |x <0或x >2}，B ＝{x |1<x <3}，所以A ∩B ＝{x |2<x <3}，所以C 正确；对于D ，因为A ∩B ＝{x |2<x <3}，所以A ∩B 是{x |2<x <5}的真子集，所以D 正确．(2)已知集合A ，B 满足A ＝{x |x >1}，B ＝{x |x <a －1}，若A ∩B ＝∅，则实数a 的取值范围为()A ．(－∞，1]B ．(－∞，2]C ．[1，＋∞)D ．[2，＋∞)答案B解析因为集合A ，B 满足A ＝{x |x >1}，B ＝{x |x <a －1}，且A ∩B ＝∅，则a －1≤1，解得a ≤2.题型四集合的新定义问题例5(多选)群论是代数学的分支学科，在抽象代数中具有重要地位，且群论的研究方法也对抽象代数的其他分支有重要影响，例如一元五次及以上的方程没有根式解就可以用群论知识证明．群的概念则是群论中最基本的概念之一，其定义如下：设G 是一个非空集合，“·”是G 上的一个代数运算，即对所有的a ，b ∈G ，有a ·b ∈G ，如果G 的运算还满足：①∀a ，b ，c ∈G ，有(a ·b )·c ＝a ·(b ·c )；②∃e ∈G ，使得∀a ∈G ，有e ·a ＝a ·e ＝a ；③∀a ∈G ，∃b ∈G ，使a ·b ＝b ·a ＝e ，则称G 关于“·”构成一个群．则下列说法正确的有()A ．G ＝{－1,0,1}关于数的乘法构成群B ．G |x ＝1k ，k ∈Z ，k ≠0{x |x ＝m ，m ∈Z ，m ≠0}关于数的乘法构成群C ．实数集关于数的加法构成群D ．G ＝{m ＋2n |m ，n ∈Z }关于数的加法构成群答案CD解析对于A ，若G ＝{－1,0,1}，则对所有的a ，b ∈G ，有a ·b ∈{1,0，－1}＝G ，满足乘法结合律，即①成立，满足②的e 为1，但当a ＝0时，不存在b ∈G ，使得a ·b ＝b ·a ＝e ＝1，即③不成立，故A 错误；对于B ，因为a ＝12∈G ，且b ＝3∈G ，但a ·b ＝12×3＝32∉G ，故B 错误；对于C ，若G ＝R ，则对所有的a ，b ∈R ，有a ＋b ∈R ，满足加法结合律，即①成立，满足②的e 为0，∀a ∈R ，∃b ＝－a ∈R ，使a ＋b ＝b ＋a ＝0，即③成立，故C 正确；对于D ，若G ＝{m ＋2n |m ，n ∈Z }，则对所有的a ＝m 1＋2n 1，b ＝m 2＋2n 2∈G ，有a＋b＝(m1＋m2)＋2(n1＋n2)∈G，∀a，b，c∈G，(a＋b)＋c＝a＋(b＋c)成立，即①成立，当a＝b＝0时，a＋2b＝0，满足②的e＝0，即②成立，∀a＝m＋2n∈G，∃b＝－m－2n∈G，使a＋b＝b＋a＝0，即③成立，故D正确．思维升华集合新定义问题的“三定”(1)定元素：确定已知集合中所含的元素，利用列举法写出所有元素．(2)定运算：根据要求及新定义运算，将所求解集合的运算问题转化为集合的交集、并集或补集的基本运算问题，或转化为数的有关运算问题．(3)定结果：根据定义的运算进行求解，利用列举法或描述法写出所求集合中的所有元素．跟踪训练4(多选)设A为非空实数集，若对任意x，y∈A，都有x＋y∈A，x－y∈A，且xy∈A，则称A为封闭集．下列叙述中，正确的为()A．集合A＝{－2，－1,0,1,2}为封闭集B．集合A＝{n|n＝2k，k∈Z}为封闭集C．封闭集一定是无限集D．若A为封闭集，则一定有0∈A答案BD解析对于A，在集合A＝{－2，－1,0,1,2}中，－2－2＝－4不在集合A中，∴集合A不是封闭集，故A错误；对于B，集合A＝{n|n＝2k，k∈Z}，设x，y∈A，则x＝2k1，y＝2k2，k1，k2∈Z，∴x＋y＝2(k1＋k2)∈A，x－y＝2(k1－k2)∈A，xy＝4k1k2∈A，∴集合A＝{n|n＝2k，k∈Z}为封闭集，故B正确；对于C，封闭集不一定是无限集，如：{0}为封闭集，故C错误；对于D，若A为封闭集，则取x＝y，得x－y＝0∈A，故D正确．课时精练一、单项选择题1．(2022·全国乙卷)设全集U＝{1,2,3,4,5}，集合M满足∁U M＝{1,3}，则()A．2∈M B．3∈M C．4∉M D．5∉M答案A解析由题意知M＝{2,4,5}．2．(2023·新高考全国Ⅰ)已知集合M＝{－2，－1,0,1,2}，N＝{x|x2－x－6≥0}，则M∩N等于()A．{－2，－1,0,1}B．{0,1,2}C．{－2}D．{2}答案C解析方法一因为N＝{x|x2－x－6≥0}＝(－∞，－2]∪[3，＋∞)，而M＝{－2，－1,0,1,2}，所以M∩N＝{－2}．方法二因为M＝{－2，－1,0,1,2}，将－2，－1，0,1,2代入不等式x2－x－6≥0，只有－2使不等式成立，所以M∩N＝{－2}．3．(2024·南京模拟)集合A＝{x∈N|1<x<4}的子集个数为()A．2B．4C．8D．16答案B解析A＝{x∈N|1<x<4}＝{2,3}，故子集个数为22＝4.4．已知全集U，若集合A和集合B都是U的非空子集，且满足A∪B＝B，则下列集合中表示空集的是()A．(∁U A)∩B B．A∩BC．(∁U A)∩(∁U B)D．A∩(∁U B)答案D解析由Venn图表示集合U，A，B如图，由图可得(∁U A)∩B＝∁B A，A∩B＝A，(∁U A)∩(∁U B)＝∁U B，A∩(∁U B)＝∅. 5．(2024·绵阳模拟)已知A＝{1,4，m2}，B＝{1，m}，若B⊆A，则m等于()A．0或4B．1或4C．0D．4答案A解析∵B⊆A且A＝{1,4，m2}，B＝{1，m}，∴m＝4或m＝m2，当m＝4时，A＝{1,4,16}，B＝{1,4}，满足题意；当m＝m2时，得m＝0或m＝1，当m＝0时，A＝{1,4,0}，B＝{1,0}，满足题意；当m＝1时，代入集合中，不满足集合的互异性．综上，m可取0,4.6．已知M，N均为R的子集，若存在x使得x∈M，且x∉∁R N，则()A．M∩N≠∅B．M⊆NC．N⊆M D．M＝N答案A解析因为x∉∁R N，所以x∈N，又因为x∈M，所以x∈M∩N，故M∩N≠∅，故A正确；由于题目条件是存在x，所以不能确定集合M，N之间的包含关系，故B，C，D错误．7.已知全集U＝R，集合A＝{x|0≤x≤2}，B＝{x|x2－x>0}，则图中的阴影部分表示的集合为()A．(－∞，1]∪(2，＋∞)B．(－∞，0)∪(1,2)C．[1,2)D．(1,2]答案A解析B＝{x|x2－x>0}＝{x|x<0或x>1}，由题意可知阴影部分对应的集合为∁U(A∩B)∩(A∪B)，所以A∩B＝{x|1<x≤2}，A∪B＝R，即∁U(A∩B)＝{x|x≤1或x>2}，所以∁U(A∩B)∩(A∪B)＝(－∞，1]∪(2，＋∞)．8．设集合I＝{1,3,5,7}，若非空集合A同时满足：①A⊆I；②|A|≤min(A)(其中|A|表示A中元素的个数，min(A)表示集合A中最小的元素)，称集合A为I的一个“好子集”，则I的所有“好子集”的个数为()A．7B．8C．9D．10答案B解析当|A|＝1时，即集合A中元素的个数为1时，A的可能情况为{1}，{3}，{5}，{7}；当|A|＝2时，即集合A中元素的个数为2时，A的可能情况为{3,5}，{3,7}，{5,7}；当|A|＝3时，即集合A中元素的个数为3时，A的可能情况为{3,5,7}，综上所述，I的所有“好子集”的个数为8.二、多项选择题9．已知I为全集，集合M，N⊆I，若M⊆N，则()A．M∪N＝N B．M∩N＝NC．∁I M⊆∁I N D．(∁I N)∩M＝∅答案AD解析因为M⊆N，则M∪N＝N，M∩N＝M，则A正确，B错误；又I为全集，集合M，N⊆I，则∁I M⊇∁I N，(∁I N)∩M＝∅，C错误，D正确．10．已知集合A＝{x|x2＝1}，B＝{x|ax＝1}，且A∪B＝A，则实数a的取值可以是() A．－1B．0C．1D．2答案ABC解析A＝{x|x2＝1}＝{－1,1}，集合B表示关于x的方程ax＝1的解集，因为A∪B＝A，所以B⊆A，当a＝0时方程ax＝1无解，此时B＝∅，符合题意；当B＝{1}时，a＝1；当B＝{－1}时，－a＝1，解得a＝－1，综上可得a＝0或±1.三、填空题11．已知集合A＝{(x，y)|x，y∈N*，y≥x}，B＝{(x，y)|x＋y＝8}，则A∩B中元素的个数为________．答案4解析根据题意，A∩B的元素是x＋y＝8上满足x，y∈N*且y≥x的点，即点(1,7)，(2,6)，(3,5)，(4,4)．12．已知集合A＝{1,2,3}，B＝{m,4,5}，且A∪B中的所有元素的和为12，则m＝________.答案－3解析当m＝1或m＝2或m＝3时，A∪B＝{1,2,3,4,5}，所有元素的和为15，不符合题意；当m≠1且m≠2且m≠3时，A∪B＝{1,2,3，m,4,5}，由题意得1＋2＋3＋m＋4＋5＝12，所以m＝－3.13．高三某班共有55人，其中有14人参加了球类比赛，16人参加了田径比赛，4人既参加了球类比赛，又参加了田径比赛，则该班这两项比赛都没有参加的人数是________．答案29解析由题意画出Venn图，如图所示，由Venn图知，参加比赛的人数为26，所以该班这两项比赛都没有参加的人数是29.14．对于任意两集合A，B，定义A－B＝{x|x∈A且x∉B}，A*B＝(A－B)∪(B－A)，记A＝{x|x≥0}，B＝{x|y＝lg(9－x2)}，则B－A＝________，A*B＝________.答案{x|－3<x<0}{x|－3<x<0或x≥3}解析由题意得A＝{x|x≥0}，B＝{x|－3<x<3}，所以A－B＝{x|x≥3}，B－A＝{x|－3<x<0}．因此A*B＝{x|x≥3}∪{x|－3<x<0}＝{x|－3<x<0或x≥3}．15．(多选)由无理数引发的数学危机一直延续到19世纪，直到1872年，德国数学家戴德金从连续性的要求出发，用有理数的“分割”来定义无理数(史称戴德金分割)，并把实数理论建立在严格的科学基础上，才结束了无理数被认为“无理”的时代，也结束了持续2000多年的数学史上的第一次大危机．所谓戴德金分割，是指将有理数Q划分为两个非空的子集M 与N，且满足M∪N＝Q，M∩N＝∅，M中的每一个元素小于N中的每一个元素，则称(M，N)为戴德金分割．下列选项中可能成立的是()A．M＝{x|x<0}，N＝{x|x>0}，(M，N)是一个戴德金分割B．M没有最大元素，N有一个最小元素C．M有一个最大元素，N有一个最小元素D．M没有最大元素，N也没有最小元素答案BD解析对于A，因为M＝{x|x<0}，N＝{x|x>0}，M∪N＝{x|x≠0}≠Q，故A错误；对于B，设M＝{x∈Q|x<0}，N＝{x∈Q|x≥0}，满足戴德金分割，则M中没有最大元素，N有一个最小元素0，故B正确；对于C，若M有一个最大元素，N有一个最小元素，则不能同时满足M∪N＝Q，M∩N＝∅，故C错误；对于D，设M＝{x∈Q|x<2}，N＝{x∈Q|x≥2}，满足戴德金分割，此时M没有最大元素，N也没有最小元素，故D正确．16．设集合M＝{1,2,3，…，12}，现对M的任一非空子集A，令x A为A中最大数与最小数之和，则所有这样的x A的算术平均值为________．答案13解析集合M的非空子集共有(212－1)个，其中，最小值为1的子集可视为{2,3，…，12}的子集与集合{1}的并集，共有211个，同上可知，最小值为2的子集共有210个，最小值为3的子集共有29个，…，最小值为12的子集共有20个．最大值为12的子集可视为{1,2,3，…，11}的子集与集合{12}的并集，共有211个，同上可知，最大值为11的子集共有210个，最大值为10的子集共有29个，…，最大值为1的子集共有20个．所以M的所有非空子集中的最小值之和为211＋2×210＋3×29＋…＋12×20，最大值之和为12×211＋11×210＋10×29＋ (20)所以x A的算术平均值为211＋2×210＋3×29＋…＋12×20＋12×211＋11×210＋10×29＋…＋20212－1＝13(211＋210＋29＋ (20)212－1＝13×1－2121－2212－1＝13.。