当前位置：文档之家 › 6第6章电介质和电介质中的高斯定理

6第6章电介质和电介质中的高斯定理

  • 格式：ppt
  • 大小：1.16 MB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

介质的极化和介质中的高斯定理

介质的极化和介质中的高斯定理

部电都介产质生内附部加的电总场场E强'。E
E0
E'
E0
'
'
极化电荷所产生的附加电场不足以将介质中的外电
场完全抵消，它只能削弱外电场。称为退极化场。
介质内部的总场强不为零！ 在各向同性均匀电介质中： E
E0
r
r称为相对介电常数或电容率。
3
二、介质中的高斯定理 电位移矢量
1.介质中的高斯定理
d
D2S 0S D1 D2 0 , D2 0
E2
D2
0r
0 0r
11
I区：D1
0,
E1
0 0
0
II区：D2 0 ,
②.求电容C
E2
0 0r
由C q U ab
与 U ab
Ed
高 斯
C q
0S
面
U ab E1(d d ' ) E 2d '
d' 0
D P1 P2
r
d
质中的高斯定理求场强：先根据自由电荷的分布利用 介质中的高斯定理求出电位移矢量的分布，再根据电 位移矢量与场强的关系求出场强的分布。
7
例1：将电荷 q 放置于半径为 R 相对电容率为 r 的介
质球中心，求：I 区、II区的 D、E、 及 U。
解：在介质球内、外各作半径为 r 的
高斯球面。
SD dS q0
荷密度为 0 , 其间插有厚度为 d’ 、电容率为 r 的电介质。
求 ： ①. P1 、P2点的场强E；②.电容器的电容。
解： ①. 过 P1 点作高斯柱面, 左右底面分别经过导体
和 P1 点。
D SD dS q0

第6章 静电场中导体和电介质 重点与知识点

第6章 静电场中导体和电介质 重点与知识点

理学院物理系 王 强
第六章 静电场中的导体和电介质
大学物理
第六章 重点与知识点
一、静电场中的导体
2、空腔导体(带电荷 、空腔导体 带电荷 带电荷Q)
1）、腔内无电荷，导体的净电荷只能分布在外表面。 腔内无电荷，导体的净电荷只能分布在外表面。 净电荷只能分布在外表面 Q
在静电平衡状态下,导体 在静电平衡状态下, 空腔内各点的场强等于零, 空腔内各点的场强等于零, 空腔的内表面上处处没有 空腔的内表面上处处没有 净电荷分布。 净电荷分布。
C2 U
Cn
2、电容器的并联
C = C1 + C2 + ⋅ ⋅ ⋅ + Cn
= ∑ Ci
i =1
nq1C1来自q2C2qn U
Cn
2012年3月23日星期五
理学院物理系 王 强
第六章 静电场中的导体和电介质
大学物理
第六章 重点与知识点
四、 电场的能量
（一）、静电场的能量
电场能量密度: 电场能量密度
We 1 2 1 we = = εE = ED V 2 2
ε
电容率, : 电容率,决定于电介质种类的常数
2）、电介质中的高斯定理 ）
v r D ⋅ dS = ∑ Q0i ∫
S i (自由电荷)
2012年3月23日星期五
电介质中通过任 一闭合曲面的电位 一闭合曲面的电位 移通量等于该曲面 移通量等于该曲面 所包围的自由电荷 所包围的自由电荷 的代数和
第六章 静电场中的导体和电介质
一般电场所存储的能量: 一般电场所存储的能量
dWe = wedV
1 2 We = ∫ dWe = ∫ ε E dV V V 2
适用于所有电场） （适用于所有电场）

四川大学大学物理练习册答案第六章 静电场中的导体与电介质

四川大学大学物理练习册答案第六章 静电场中的导体与电介质

(2) 如用导线将球和球壳连接起来，则 壳的内表面和球表面的电荷会完全中和 而使这两个表面不带电，二者之间的电 场也变为0,二者成为等势体，球壳外表 面上的电荷仍保持为 q 3 , 并均匀分布， 它外面的电场分布也不变，仍为
B
A
o
q3
q3 B R3 E 2 2 4πε0 r r
R3 R2
R

同理，在导体表面上距O点 为 r 的P点附近的P处场强也应为 零。沿 x 轴分量为
a
P r O
X
由此得
由对称性分析，感应电荷应呈以O点为中心的圆对称分布。 在导体表面取 r—r+dr 的细圆环，则环面上的感应电荷为
整个导体表面的感应电荷总量为
q0
+ + + + + + + ++
尖端放电现象 带电导体尖端附 近的电场特别大，可 使尖端附近的空气发 生电离而成为导体产 生放电现象． 电 风 实 验
+++ ++
σE
+ +
+ + +
尖端放电有弊有利。
避雷针的工作原理
+ +
－
+ + +
+ +
－－ － － －
（二） 空腔导体 空腔内无电荷时
0

B




q

+



三
静电屏蔽
静电屏蔽——在静电场中，因导体的存在使某些特 定的区域不受电场影响的现象。

有电介质时的高斯定理

有电介质时的高斯定理
3.电位移线起于正的自由电荷而止于负的自由电荷.
∬ΣD→ ⋅ dS→ = Q0
Processing math: 100%
问题分析
εr− 1
由于Q = εr Q0, 真空电容率ε = ε0εr 从而：
def
定义:点位移矢量:D = ε
从而上式简化为:
有电介质时的高斯定理
Q0
∬ΣE→ ⋅ dS→ = ε0εr
∬ ∑ ΣD→ ⋅ dS→ = i=1Q0i
说明:
1. 电位移矢量D→ = ε0εrE→ = εE→ = P→ + ε0E→ 2.公式考虑了极化电荷的影响。
以充满各向同性的电介质平行板电容器为例在正极板与电介质交界处去圆柱体高斯面利用高斯定律有
有电介质时的高斯定理
问题引入：
以充满各向同性的电介质平行板电容器为例，在正极板与电介质交界处去圆柱体高斯面, 利用高斯定律有： 1
∬ΣE→ ⋅ dS→ = ε0 (Q0 − Q′)
其中，Q0表示自由电荷，Q′表示极化电荷。 可见在电介质中计算电场与Q′有关，直接计算很困难。

9-6有电介质时的高斯定理 电位移

9-6有电介质时的高斯定理 电位移

∫∫ D S
S1
= D 1 S＝S σ
σ σ E1 = = ε 1 ε r 1ε 0
v v v v 再利用 D 1＝ ε 1 E 1 , D 2＝ ε 2 E 2 可求得
σ σ E2 = = ε 2 ε r 2ε 0
方向都是由左指向右。 方向都是由左指向右。
有电介质时的高斯定理 电位移
负两极板A、 间的电势差为 （2）正、负两极板 、B间的电势差为 ）
例题9-6 一半径为 的金属球，带有电荷 0,浸埋在均匀 一半径为R的金属球 带有电荷q 浸埋在均匀 的金属球， 例题 无限大”电介质（电容率为ε），求球外任一点P的场 ），求球外任一点 “无限大”电介质（电容率为 ），求球外任一点 的场 强及极化电荷分布。 强及极化电荷分布。 P 根据金属球是等势体， 解: 根据金属球是等势体，而 ε r 且介质又以球体球心为中心对 称分布，可知电场分布必仍具 称分布， R Q0 球对称性， 球对称性，用有电介质时的高 斯定理来。 斯定理来。 S 如图所示， 如图所示，过P点作一半 点作一半 径为r并与金属球同心的闭合 径为 并与金属球同心的闭合 球面S， 球面 ，由高斯定理知
4εr（εr 2 1) 3 ′ σ 上负下正 σ2 = ε0 (εr2 1)E2 = εr1εr 2 +εr1εr3 + 2εr 2εr3
′ σ3 = ε0 (εr3 1)E3 =
4εr（εr3 1) 2 σ εr1εr 2 + εr1εr3 + 2εr 2εr3
上负下正
有电介质时的高斯定理 电位移
r r 由 P = ε0 (εr 1)E 得电极化强度矢量的分布
P=
r r 由 σ′ = P n 得束缚电荷的分布

电介质的极化和介质中的高斯定理

电介质的极化和介质中的高斯定理

1.真空中 P = 0 ，真空中无电介质。 真空中 真空中无电介质。 2.导体内 P = 0 ，导体内不存在电偶极子。 导体内 导体内不存在电偶极子。
8
（2）极化（束缚）电荷与极化强度的关系 ）极化（束缚） 在电介质的表面上， 在电介质的表面上，极化强度与极化电荷之间有 r r 如下关系： 如下关系： ' = P = P cosθ = P ⋅ e σ
r E'
r E
r E0
εr 称为相对
介电常数或 电容率。 电容率。
2.电介质极化的微观机制 2.电介质极化的微观机制 从电学性质看电介质的分子可分为两类：无极分子、 从电学性质看电介质的分子可分为两类：无极分子、 有极分子。 有极分子。 每个分子负电荷对外影响均可等效为 的作用。 单独一个静止的负电荷 的作用。其大小为 分子中所有负电之和， 分子中所有负电之和，这个等效负电荷的 作用位置称为分子的 负电作用中心” 称为分子的“ 作用位置称为分子的“负电作用中心”。
静电场中的电介质 介质中的高斯定理
1
从电场这一角度看，电介质就是绝缘体。 从电场这一角度看，电介质就是绝缘体。 特点：电介质体内只有极少自由电子。 特点：电介质体内只有极少自由电子。 我们只讨论静电场与各向同性电介质的相互作用。 我们只讨论静电场与各向同性电介质的相互作用。
一、静电场对电介质的作用—电介质的极化 静电场对电介质的作用—
∫ P ⋅ dS = − ∑ q
S S inside
在任一闭合曲面内极化电荷的负值等于极化强度的通量。 在任一闭合曲面内极化电荷的负值等于极化强度的通量。
9
四、介质中的高斯定理 电位移矢量
1.介质中的高斯定理 1.介质中的高斯定理 真空中的高斯定理 φ =

6-5电介质中的高斯定理

6-5电介质中的高斯定理

ε ε ε ε E 2 = D 2 = σ
0r
0r
结束 返回
C
B
UA
UB =
A
E1. d l
+
C
E
.
2
d
l
ε ε ε = σ
C
dl +
σ
B
dl
0A
0r C
ε ε ε σ σ =
d 1+
0
0 r d2
ε E 1= σ 0
E
2
=ε
σ
ε0
r
C
=
σ
UA
S UB
ε =
0S d1 + d2
εr
§6-5 静电场中的介质 介质中的高斯定理
一、电介质的电结构和电极化 1. 电介质的电结构
电介质：电阻率很大，导电能力很差的物质, 即绝缘体。
电结构特点：分子中的正负电荷束缚的很紧，介质内
部几乎没有自由电荷。
H+
两类电介质分子结构：
+ -
无极 分子
H+
C--
H+
e+
H+
CH4
+
O--
-q
-
有极 H+
= + H+
分子
H2O
+q
电介质极化: 在外电场的作用下,介质表 面产生极化电荷的现象。
描述真空静电场性质有场强环路定律和 高斯定理，它们是：
LE .dl = 0
s
E
.
dS
=
Σq
ε0
下面来讨论有介质时环路定律和高斯定
理的形式。

电容器、电介质、介质中的高斯定理

电容器、电介质、介质中的高斯定理

i
E总 E0 E 0
被约束在分子内
不一定与表面垂直
9
有极分子电介质
H
H
104
o
F
+ - pi
E0 F
+
+
+
E
无外场
pi 0
pi
0
i
外场中(转向极化)
pi 0
pi
0
i
出现束缚电荷和附加电场
位移极化和转向极化微观机 制不同，宏观效果相同。10
统一描述
pi
0
i
出现束缚电荷(面电荷、体电荷)
实验发现:
A
插入前： U 0
C0
q U0
插入后：U AB
C q U AB
U0 U AB
r,
C C0
r
r 1,常量 由电介质的种类和状态决定
0
真空介电常数
r
相对介电常数(电容率)
= 0 r 介电常数
13
E0
0 0
, U0
E0d ,
E
0
内部的场由自由电荷和
+
+
+
+
E0 E
+
+
极化电荷共同产生
静电感应
无极分子电介质: 位移极化 有极分子电介质: 转向极化
宏观 效果
静电平衡 导体内 E 0, 0 导体表面 E表面 感应电荷 0 E
内为部零：分子pi偶极0 矩矢量和不
i
出现束缚电荷（极化电荷）
12
二、电介质对电场的影响
+ + + + +
B

电介质中高斯定理

电介质中高斯定理

1
r r 1 Q Q r 0 0
)
Q Q0 (1
1
)
⑤极化电荷密度 与
E 0 rE
1 0 P ( 1 ) ( r 1 ) 0 0 0E 0 ( r 1 ) 0E 0E
r
r
R2
R1

r
R2
解（1）
R1

d S l D
S
D 2 π rl l
D
E ( R r R ) 1 2 r 2 π rr 0 0
D 2π r
r
R2
R1

( R r R ) （2）由（１）可知 E 1 2 2π 0r r R R d r 2 U E d r ln R 2 π r 2 π 0r R 0 r 1
2.极化电荷与电极化强度之间的关系 （以位移极化为例） 电场中每个分子产生电矩：
++++-
++++-
++++-
++++-
均匀介质
E
++++-
pe ql
单位体积中分子电矩 的矢量和为：
p P V
nql
e
npe
式中 n 为介质中单位体积的分子数。
电极化强度和极化电荷面密度的关系
6 2 P ( ε 1 ) ε E 5 . 89 10 C m r 0 6 2 σ ε E 8 . 85 10 C m 0 00 6 2 σ ' P 5 . 89 10 C m 6 2 D ε ε E ε E σ 8 . 85 10 C m 0 r 0 0 0

有电介质的高斯定理

有电介质的高斯定理

S
有电介质存在时的高斯定理的应用
（1）分析自由电荷分布的对称性，选择适当的高斯面 求出电位移矢量。 （2）根据电位移矢量与电场的关系，求出电场。
（3）根据电极化强度与电场的关系，求出电极化强度。
（4）根据束缚电荷与电极化强度关系，求出束缚电荷。
例1 平行板电容器上自由电荷面密度为 0 充满相对介电常数为 r 的均匀各向同
vv
Ò D dS D1S D2S 0
S1
所以 D1＝D2
即在两电介质内，电位移
uur uur uur
D1和uuDr2
的量值相等。由于
D1 1 E1, D2 2 E2
所以 E1 2 r 2 E2 1 r1
可见在这两层电介质中场强并不相等，而是和 电容率（或相对电容率）成反比。
作正柱形高斯面S
底面积设S0
vv
Ò D

dS


q 0
S
S S0
x
Ox
vv
Ò
D

dS


q 0
d
S
xd 2
2DS 0 0 2 x S0 D 0 x
E D 0 x
x

P d 2

0 r
0r 1E
2DS 0
0 r
r 1
0dS0
U2
r
E
2
dr

q
r 4 0r 2 dr

q
4 0r
例. 平行板电容器的电容
s
已知: 平行板电容器 d, S ,r
求: 其电容.
Q
解: • 设电容器带电量 Q

高斯定理

高斯定理
31
1.2.4
高斯定律的应用
高斯定律适用于任何情况，但仅具有一定对称
性的场才有解析解。 计算技巧：
a） 分析场分布的对称性，判断能否用高斯定律 求解。 b）选择适当的闭合面作为高斯面，使 中的 D 可作为常数提出积分号外。
32
S D dS
例
求电荷线密度为 的无限长均匀带电体的电场。
解：电场分布特点： D 线皆垂直于导线，呈辐射状态； 等 r 处D 值相等； 取长为L，半径为 r 的封闭圆柱面 为高斯面。

2
1-2 静电场中的导体

导体的定义：其内存在着能够自由运动的电荷的物质。 自由运动的电荷可以是自由电子或离子，金属是最常见 的导体。 当我们把导体放入外电场中，则外电场对导体内的自由 电荷将产生作用力，使它们沿着（或逆着）电场的方向 运动，导体表面会出现感应电荷。

Eex
17

根据电荷守恒原理，这两部分极化电荷的总和
P dV ' P e dS ' 0
V ' S ' n

在均匀极化的电介质内，极化电荷体密度
p 0
有电介质存在的场域中，任一点的电位及电场 强度表示为
) ( ) 1 ( f p f p ( r ) dV ' dS ' V ' S ' 4 r ' r r ' 0 r
27
D 线从正的自由电荷发出而终止于负的自由电荷。 在各向同性介质中
D E P E E 0 0 e 0
其中
( 1 ) E E E 0 e r 0

第六章 电介质导体与电场 电学

第六章 电介质导体与电场 电学

1 E dS
S
0
(q
S
0
q )
'
北京建筑大学 理学院
1.电位移矢量 （电位移是一个辅助量 ）
定义：
D r 0 E E
单位：cm-2
其中 r 0
F 电容率或介电常量 的 单 位 ： m
2.电位移线： （线的性质：切线方向，疏密） D线起始于正自由电荷，终止于负自由电荷，与 束缚电荷无关。而电力线起始于正电荷终止于负电荷， 包括自由电荷和束缚电荷。
北京建筑大学 理学院
2.有极分子（Polar molecule） 分子的正电荷中心同负电荷中心不重合，（等效 电偶极子）在无外场作用下存在固有电矩。例如， H2O NH3,CO SO2等.
O H+
-
H+
+
H+
+
H2O
+
+
+ +
+
N
H+
+
+ H NH3（氨）
因无序排列对外不呈现电性。 Pi 0
如图
E ds 0
s
q
i
i
0
2. 导体表面电荷面密度与表面邻近处的场强成正比。
E ds ES1 S1 / 0
s
E 0
北京建筑大学 理学院
3. 孤立导体处于静电平衡时，它的表面各处的面电荷 密度与各处表面的曲率（曲率圆半径的倒数）有关。
E0
电介质的击穿：电介质的绝缘性能遭到破坏，变为导体。
北京建筑大学 理学院
三.电介质对电场的影响
在外电场 E0中，介质极化产生的束缚 电荷，产生附加电场 E '

电介质中的高斯定理公式

电介质中的高斯定理公式

高斯定理是电磁学中的基本定理之一，它描述了电场的分布与电场通量之间的关系。

在电介质中应用高斯定理时，可以使用以下公式：
∮S E · dA = 1/ε₀ ∫V ρ dV
其中，
∮S E · dA 表示闭合曲面S上电场E与面元dA的点积的总和，也称为电场通量。

1/ε₀ 是真空中的电介质常数，ε₀ ≈ 8.85 × 10⁻¹² C²/(N·m²)。

∫V ρ dV 表示电介质内电荷密度ρ与体积元dV的乘积的积分，表示电荷分布的总量。

这个公式可以用于计算闭合曲面内的电场通量，其中电介质内的电荷分布由体积积分来表示。

根据高斯定理，如果闭合曲面内没有电荷分布（即电介质内无净电荷），那么电场通量为零；如果闭合曲面内有电荷分布，电场通量将与闭合曲面内的净电荷量成正比。

07--4、电介质中的电场高斯定理

07--4、电介质中的电场高斯定理

解： （1）自由电荷所产生旳场强（在真空中）为
E0
σ0 ε0
9.0 106 8.85 1012
1.02 106 V/m
(2)
由
E
E0 εr
εσrε00
σ0 ε
可知电介质内的场强为
E
σ0 ε
9.0 106 3.5 1011
2.57 105
V/m
（3）极化电荷面密度为：
0
0
3.5 1011 8.85 1010 3.5 1011
有电介质时旳高斯定理得（注意导体中
D=0）：
D dS S2
D dS
右底面
D1 A
A
与前面的式子相比较， 有D1 D2
+ +
S2
利用 D1 1E1 ，D2 2 E2 ，可求得：
E1
1
r1 0
,
E2
2
r 2 0
（2）正、负两极板间旳电势差为：
U
E1d1
E2d2
(d1 1
E1 E2
S D dS D S 0 S
D＝ 0
E1
D
1
0 0 r
E2
D
0
0 0
U
E1
d 2
E2
d 2
0d 2 0 r
0d 2 0
0d 0
r 1 2 r
3 5 U0
C1
Q1 U1
2 r 0 S
d
C2
Q2 U2
2 0 S
d
C1，C2串联：
C
C1C2 C1 C2
5 3 C0
由前面知：
例6、同轴电缆半径分别为R1和R2，其间充斥电介质 r1,，r2 ，

大学物理第六章课后习题答案

大学物理第六章课后习题答案

第六章 静电场中的导体与电介质 6 －1 将一个带正电的带电体A 从远处移到一个不带电的导体B 附近，则导体B 的电势将（ ）（A ） 升高 （B ） 降低 （C ） 不会发生变化 （D ） 无法确定 分析与解 不带电的导体B 相对无穷远处为零电势。

由于带正电的带电体A 移到不带电的导体B 附近时，在导体B 的近端感应负电荷；在远端感应正电荷，不带电导体的电势将高于无穷远处，因而正确答案为（A ）。

6 －2 将一带负电的物体M 靠近一不带电的导体N ，在N 的左端感应出正电荷，右端感应出负电荷。

若将导体N 的左端接地（如图所示），则（ ）（A ） N 上的负电荷入地 （B ）N 上的正电荷入地（C ） N 上的所有电荷入地 （D ）N 上所有的感应电荷入地分析与解 导体N 接地表明导体N 为零电势，即与无穷远处等电势，这与导体N 在哪一端接地无关。

因而正确答案为（A ）。

6 －3 如图所示将一个电量为q 的点电荷放在一个半径为R 的不带电的导体球附近，点电荷距导体球球心为d ，参见附图。

设无穷远处为零电势，则在导体球球心O 点有（ ）（A ）d εq V E 0π4,0== （B ）dεq V d εq E 020π4,π4== （C ）0,0==V E（D ）R εq V d εq E 020π4,π4==分析与解 达到静电平衡时导体内处处各点电场强度为零。

点电荷q 在导 体球表面感应等量异号的感应电荷±q′，导体球表面的感应电荷±q′在球心O 点激发的电势为零，O 点的电势等于点电荷q 在该处激发的电势。

因而正确答案为（A ）。

6 －4 根据电介质中的高斯定理，在电介质中电位移矢量沿任意一个闭合曲面的积分等于这个曲面所包围自由电荷的代数和。

下列推论正确的是( )（A ） 若电位移矢量沿任意一个闭合曲面的积分等于零，曲面内一定没有自由电荷（B ） 若电位移矢量沿任意一个闭合曲面的积分等于零，曲面内电荷的代数和一定等于零（C ） 若电位移矢量沿任意一个闭合曲面的积分不等于零，曲面内一定有极化电荷（D ） 介质中的高斯定律表明电位移矢量仅仅与自由电荷的分布有关 （E ） 介质中的电位移矢量与自由电荷和极化电荷的分布有关分析与解 电位移矢量沿任意一个闭合曲面的通量积分等于零，表明曲面 内自由电荷的代数和等于零；由于电介质会改变自由电荷的空间分布，介质中的电位移矢量与自由电荷与位移电荷的分布有关。

介质中的高斯定理

介质中的高斯定理

v E
D
介质中的高斯定理
例 自由电荷面密度为0的平行板电容器，其极化电荷面密度
为多少？
解: 由介质中的高斯定理
-+´0
DS 0S D 0
D +´
E
D
0r
0 0 r
- 0
0 0
E0
0 0
E 0
E E0 E
0 r 0 0
1
1
r
0
E
dS S
++++++
-q - - - - - -
移出S面
qi
留在S面内
介质中的高斯定理
v v E dS
S
1
0
qi
1
0
vv P dS
S
S 0E P dS qi
定义电位移矢量: D 0 E P C m2
介质中的高斯定理: 在任何静电场中，通过任意闭合曲面 的电位移通量等于该曲面所包围的自由电荷的代数和.
D S
dS
qi
说明:
D S
dS
qi
介质中的高斯定理
1. 介质中的高斯定理虽说是从平板电容器这一特例推 导出，但它却有普适性.
2. 介质中的高斯定理包含了真空中的高斯定理.
真空中: P 0 所以: D 0E P 0E
v D dS
S
S 0E dS qi
vv E dS
S
1
0
qi
3. 电位移矢量D 是一个辅助量.描写电场的基本物理
介质中的高斯定理
大学物理
静电场中的导体和电介质
第4讲 介质中的高斯定理
介质中的高斯定理

第6章 静电场中的导体与介质

第6章 静电场中的导体与介质

第6章 静电场中的导体与电介质一、基本要求1．掌握导体静电平衡的条件和静电平衡条件下导体的性质，并能利用静电平衡条件解决有关问题。

2．理解电容的定义，掌握典型电容器电容的计算方法。

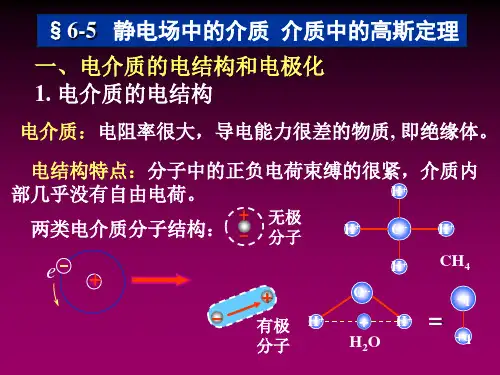
3．了解电介质极化的微观机制，理解电介质对静电场的影响。

掌握介质中静电场的基本规律，掌握应用介质中的高斯定理求解介质中静电场的电位移矢量和电场强度的计算方法。

4．理解静电场能量的概念，能计算一些对称情况下的电场能量。

二、知识框架三、知识要点 1．重点 （2）电介质中的高斯定理及其应用。

1C ++n C ++d 0L =⎰E l 保守场Sd q ⋅=∑⎰⎰D S 静电场能量密度:1四、基本概念及规律1．导体的静电平衡条件及其性质（1）导体的静电平衡条件 导体内部电场强度处处为零，即 0=内E （2）导体处于静电平衡时的性质 ① 导体是等势体，导体表面是等势面。

② 导体表面的场强处处与导体表面垂直，导体表面附近的场强大小与该处导体表面的面密度σ成正比，即0 E e nσε=表面 ③ 电荷只分布在导体外表面。

（3）静电屏蔽 在静电平衡条件下，空腔导体内部电场不受外部电场的影响，接地空腔导体内部与外部电场互不影响，这种现象称为静电屏蔽。

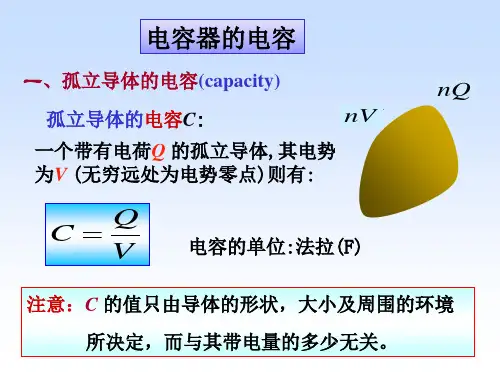
2．电容C（1）孤立导体的电容 Vq C =电容的物理意义：使导体每升高单位电势所需的电量。

（2）电容器的电容 BA V V qC -=（3）电容器两极板间充满电介质后的电容 0C C r ε= 其中C 0是两极板间为真空时的电容，r ε是电介质的相对介电常数。

（4）几种常见电容器的电容① 平行板电容器 dSC r εε0=② 同心球形电容器 AB BA rR R R R C -=επε04 （R B ＞R A ）③ 同轴圆柱形电容器 AB rR R lC ln 20επε= （R B ＞R A ） （5）电容器的串并联① 电容器串联后的总电容3211111C C C C ++=+…+nC 1② 电容器并联后的总电容 C = C 1+ C 2 + C 3+ … + C n 3．电介质中的静电场（1）电极化强度 电介质中任一点的电极化强度等于单位体积中所有分子的电偶极矩的矢量和，即 iV∆∑P P =① 对于各向同性的电介质 00(1)r e εεχε-=P =E E 其中1-=r e εχ称为电介质的极化率。

6 有电介质时的高斯定理

6 有电介质时的高斯定理

于该闭合曲面所包围的自由电荷的代数和.
E dS
S 0r
Q
0i
i
自由电荷 代数和
讨论 电场中充满均匀各向同性电介质的情况下
1、定义：电位移矢量 D 0rE E
: 电容率,决定于电介质种类的常数
说明
(1)是描述电场辅助性矢量
(2) 对应电场线起始于正自由电荷，
(3)
终止于负自由电荷
电位移通量 Ψ D
二、电介质中的静电场环路定理
l E dl 0
D dl 0 l
电位移 有介质时的高斯定理
一、电介质中的高斯定理 电位移矢量 D
加入电介质(εr )
E dS
1
S
0
qi
i
1
0
(
0 )S
'(1 1r Nhomakorabea)
0
EdS Q
S 0r i
E
dS
0S
1
S
0 r 0 r
Q0i
i
0i
自由电荷的代数和
令： D0ErE
电位移矢量
DdS
S
Q0i
i
电介质中通过任一闭合曲面的电位移通量等
D
s
dS
电力线与电位移线的比较
E线
D线
+Q
+Q
r
r
2、电介质中电场 强度
E
、电极化强度
P
和电位移矢量D 之间的 关系
电位移
D 0rE E
电极化强度
P
(r1)0 E
D P 0E
3、电介质中的高斯定理
D dS Q0i
S
i
(自由电荷
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
+++ ++++++++ S
第6章 静电场
E1 + + + + + 1' - - - - - ' 2 d2 E2 + + + + +2' U l E dl E1d1 E2d2 ----- 0 Q0 d1 d 2 ( ) r1 1 0 （ 2） 1 ' 0 S r1 r 2
Q0 0 r1 r 2 S C U r1d 2 r 2 d1
r1 r2 1 2' 0 r2
0 D E1 0 r1 0 r1 0 D E2 0 r2 0 r2
d1
0 S 1+++++ ++++ - - - - - 1 '
第6章 静电场
例2 常用的圆柱形电容器，是由半径为 R1 的长 直圆柱导体和同轴的半径为 R2 的薄导体圆筒组成， 并在直导体与导体圆筒之间充以相对电容率为 r 的 电介质.设直导体和圆筒单位长度上的电荷分别为 和 . 求（1）电介质中的电场强度、电位移； （２）此圆柱形电容器的电容．
金属导体和电介质比较
金属导体
特征 模型 与电场的 相互作用 有大量的 自由电子 “电子气” 静电感应
电介质（绝缘体）
基本无自由电子，正负电荷 只能在分子范围内相对运动
电偶极子
无极分子电介质: 位移极化 有极分子电介质: 转向极化
宏观 效果
静电平衡 内部：分子偶极矩矢量 导体内 E 0, 0 和不为零 p i 0 i 导体表面 E表面 表面：出现束缚电荷 感应电荷 0 E （极化电荷）


H
-
+
-
+
E0

p i 0
i
E 外场中(取向极化) pi 0 pi 0
i
位移极化和取向极化微观机 制不同，宏观效果相同。
出现束缚电荷和附加电场
M p E p // E
第6章 静电场
4. 极化电荷 Polarization charge or bound charge
第6章 静电场
复
习
1. 静电平衡下条件(充要条件)： 推 ①导体是等势体。 ① Einside 0 论 ②导体表面是等势面。 ②
Esurface surface
2. 电容
q Q Q 孤立导体电容 C 电容器电容 C u A u B u AB u
第6章 静电场
九、电介质及其极化(polarization)
S
'
0
+++++++++++
r
S
S ( 0 ) E dS
0
+ + + + + + 0 - - - - - - - - - - '

(1
1
r
) 0

0 0 r
q0 S 0 E dS 0r 0 r S
第6章 静电场
十、电介质对电场的影响
1.电介质对电容的影响
U0
Q
+++++++
U
-------
C0 Q
++++++ r+ ------- C
Q
Q
插入前： U
结论：
U 1
0
r
U0
Q U0 Q Q C0 插入后： U , C r r C0 U0 r U U0 U Ed E E0
1. 电介质 由大量电中性的分子组成的绝缘体。 2 .电介质的分类： 引入重心模型
p ql -q
l
+q
①无极分子（Nonpolar molecule） 在无外场作用下：整个分子无电矩。 例如，CO2 H2 N2 O2 He ②有极分子（Polar molecule） 在无外场作用下：存在固有电矩 例如，H2O HCl CO SO2 因无序排列对外不呈现电性。
在外电场中，均匀介质内部各处仍呈电中性，但 在介质表面要出现电荷，这种电荷不能离开电介质到 其它带电体，也不能在电介质内部自由移动。我们称 它为束缚电荷或极化电荷。它不象导体中的自由电荷 能用传导方法将其引走。 在外电场中，出现束缚电荷的现象～电介质的极化。
E 无极分子 0
有极分子
E0
第6章 静电场
r
R2
R1

第6章 静电场
r
R2
解（1）
R1
D d S l
S


2π r
D 2π rl l
E 0 r 2π 0 r r
D
D
( R1 r R2 )
第6章 静电场
r
R2
R1

( R1 r R2 ) E 2π 0 r r dr R2 ln 2π 0 r R1 2π 0 r r
电介质中的高斯定理

S
s
q
i
i0 (自由电荷 )
D dS : 穿过闭合曲面的电通量仅与
q
s内
0
有关.
第6章 静电场
电力线与电位移线的比较
E 线 D 线
+Q
+Q
r
电力线（E线）不但与 自由电荷有关 ，而且与 束缚电荷有关
r
电位移线（D线）却 只与自由电荷有关
第6章 静电场
例1 一平行平板电容器充满两层厚度各为 d1和 d 2 的电介质，它们的相对电容率分别为 r1 和 r2 , 极板 面积为 S . 求（1）电容器的电容；（2）当极板上的 自由电荷面密度的值为 0时，两介质分界面上的极化 电荷面密度. 0 解（1） D dS 0 S1


0 r1 0 D E2 0 r2 0 r2
D 0 0 D E1

S
0 r1
1 - - d1 E1 + + + + + d2 E2
- 1' + 1 ' - ' 2 + + + + + + ' 2 ---------- 0
C r C0
r
电介质极化减弱了场强
第6章 静电场
0 r
r 相对介电常数 r 1
0 真空介电常数
- - - - - -

介电常数（电容率） 2.电介质对电场的影响 内部的场由自由电荷和 极化电荷共同产生 0 +++++++++++
பைடு நூலகம்
d r E0 E ' E + + + + + +
E E0 E
0 - - - - - - - - - - -
0 E0 , E 0 0 1 E ( 0 ) 0
第6章 静电场
U0 U 0 E0 d d E0
U Ed ,
U0 r U

- - - - - r d E0 E ' E
rE S
0

dS q 0

第6章 静电场

S
0 r E dS
q
i
i0 (自由电荷 )
电场中充满均匀各向同性电介质的情况下
定义： 电位移矢量 D
D dS
D 0 r E E
电介质中任一闭合 曲面的电位移通量 等于该面所包围的 自由电荷的代数和
真空圆柱形 电容器电容
（2）由（１）可知
R2 U E dr
R1
R2 Q r C0 C 2π 0 r l ln U R1 C R2 单位长度电容 2π 0 r ln R1 l
第6章 静电场
本节作业 6—51，53，54，55
+ + +
+++++++++++
E0 U UE0 E d U0 r
0 E0 , 0 1 E ( 0 ) 0
---------- 1 ( 1 ) 0 r
+ + +
自由电荷和束缚电荷的关系
第6章 静电场
十一、有电介质时的高斯定理
高斯定理 qi i E dS 0 S 1 ' E d S ( q q ) S 0 0
i
外场中(位移极化) pi 0 pi 0
i
出现束缚电荷和附加电场
+
H
c
H
+ + + -
+ + + -
E0
----
+ + +
-
++ + ++ + +
第6章 静电场
②有极分子——取向极化 Orientation polarization