下载文档原格式
有介质时的高斯定理，写出其物理意义
高斯定理（也称为高斯通量定理）是电磁学中的一个基本定理，描述了电场或磁场通过一个封闭曲面的总通量与在该曲面内部源的大小之间的关系。
具体表达式为：对一个任意形状的封闭曲面，电场或磁场通过该曲面的总通量等于该曲面内部电荷或磁荷的代数和。
物理意义如下：
1. 电场或磁场通过一个封闭曲面的总通量是该曲面内部电荷或磁荷的性质之一，可以帮助我们了解场的发源和分布。
例如，通过测量通过一个闭合曲面的电场通量，可以推断该闭合曲面内部的电荷分布情况。
2. 高斯定理对于计算电场或磁场的分布以及场源的性质具有重要的应用。
通过选取适当的曲面以及利用高斯定理，可以简化计算复杂电场或磁场的过程，提高计算效率。
3. 高斯定理还有与能量和电荷守恒定律的联系。
当封闭曲面内部不存在电荷时，即电荷守恒定律成立时，通过该曲面的电场通量为零。
这可以用来推导电场能量的守恒。
总的来说，高斯定理在电磁学中具有重要的作用，它可以帮助我们理解场的分布、推断电荷或磁荷的性质，并且简化电场或磁场计算的过程。
第 2 章静电场2.4 介质中的静电场方程2.4.2 介质中的高斯定律1.介质中高斯定律的微分形式ερ=∙∇E 0ερρp+=∙∇E （真空中）（电介质中）定义电位移矢量（Displacement ）∙D 线从正的自由电荷发出而终止于负的自由电荷。
D ——辅助矢量，又称电通密度，C /m 2代入P∙-∇=p ρ)(1P E 0∙∇-=∙∇ρερε=+∙∇)(0P E PE D +=0ε则有ρ=⋅∇D 电介质中高斯定律的微分形式为自由电荷体密度ρ2. 介质中高斯定律的积分形式⎰∑=∙SqS D d 介质中高斯定律的积分形式⎰∑∑+=∙Sq q )(S E p 01dε代入⎰∙-=S p q SP d ⎰⎰∑∙-=∙S S q SP S E d d 0ε⎰∑⎰=∙+∙SSqS P S E d d 0ε⎰∑=∙+SqS P E d )(0εq 为闭合面包围的自由电荷• D 线由正的自由电荷出发，终止于负的自由电荷；• P 线由负的极化电荷出发，终止于正的极化电荷。
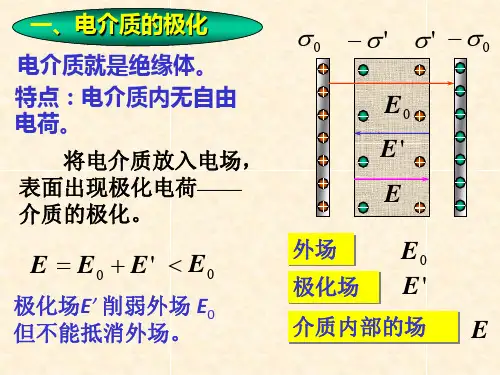
• E 线由正电荷出发，终止于负电荷；D 线E 线P 线D 、E 与P三者之间的关系图示平行板电容器中放入介质板后，其D 线、E 线和P 线的分布。
3.D 和E 的关系D = ε0E + P P = χe ε0E⇒⎭⎬⎫D = ε0E +χe ε0E = ε0(1+χe ) E= ε0εr E = εED = εE介质的本构关系或组成关系er 1χεεε+==ε——介质的电容率（介电常数）F/mεr ——介质的相对电容率（相对介电常数）无量纲χe 、εr 和ε的取值取决于媒质的特性4. 介质特性电场中，介质的特性由其介电常数确定。
E D ε=r ε⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡z y x z y x E E E D D D 333231232221131211εεεεεεεεε均匀、线性、各向同性介质的介电常数是常量--简单介质。
