074电介质中的电场高斯定理

介质中高斯定理的微分形式高斯定理是电磁学中的基本定律之一，也是应用极为广泛的重要定理。

它表明了电场的流量与电场的源的关系，可以用来描述电场在不同介质中的传播和分布情况。

下面，我们来详细介绍介质中高斯定理的微分形式，以期帮助读者更好地理解并应用这一定理。

高斯定理的微分形式可表示为：∇・(ε(r)∇·E(r)) = ρ(r)其中，∇表示梯度运算符，·表示点乘运算符，E(r)表示电场矢量，ε(r)表示介质中的电容率函数，ρ(r)表示自由电荷密度。

这个方程的意义是：介质中的电场流出或流入单位体积的量，等于该体积内所有电荷的代数和。

也可以理解为电场的散度与电荷密度之间的关系。

在研究介质中的电场分布时，高斯定理的微分形式对于求解复杂或不规则情况下的电场非常重要。

通过对方程左边的梯度和散度运算，我们可以得到电场强度的微分形式，利用右边的电荷密度函数，我们可以进一步求解电场的分布情况。

这使得高斯定理在电磁学和电子工程领域中得以广泛应用。

在实际应用中，我们需要考虑不同材料的电容率函数ε(r)。

不同介质中的电容率函数不同，影响电场在介质中的传播和分布。

根据具体情况，我们可以选择不同形式的电容率函数，如常数形式（如真空中的ε0），线性形式或非线性形式，并使用高斯定理的微分形式求解电场分布。

此外，高斯定理的微分形式还可以与其积分形式相结合，形成一套完整的方程体系，用于研究电场与导体、电介质之间的相互作用，从而解决更加复杂的电场问题。

通过对积分形式的运算，我们可以得到电荷分布对电场产生的影响，求解场源分布情况等等。

总之，介质中高斯定理的微分形式是研究电场分布的重要工具之一。

通过对电场强度的微分运算，我们可以得到电场的变化规律，通过电荷密度函数，我们可以进一步求解电场的分布情况。

掌握高斯定理的微分形式，对于电磁学和电子工程领域的学习和应用具有重要意义。

通过深入理解和灵活应用高斯定理的微分形式，我们能够解决更加复杂的电场问题，并为技术创新和工程实践提供有效的指导。

静电场的高斯定理
静电场的高斯定理是电场的一种重要性质描述，它是由德国数学家
卡尔·弗里德里希·高斯在19世纪提出的。

高斯定理表述了电场的通量与电场源之间的关系。

它的数学表达式为：
∮ E · dA = ε₀ * Q
其中，∮ E · dA表示电场E在一个封闭曲面上的通量（通过该曲面
的电场线数目乘以单位面积的大小），ε₀表示真空中的电介质常数，Q表示该曲面内的电荷量。

高斯定理可以理解为：一个空间闭曲面上的电场总通量等于该空间
内的电荷量与真空中的电介质常数的乘积。

高斯定理的实际应用是利用其简化计算电场问题。

通过选择合适的
曲面，可以使电场的计算变得更简单。

这是因为高斯定理允许我们
将电荷分布复杂的问题简化为电荷集中的问题。

总之，静电场的高斯定理提供了描述电场通量与电荷量之间的关系的数学工具，能够方便地帮助解决电场问题。

电学高斯定理-概述说明以及解释1.引言1.1 概述：电学高斯定理，又称高斯电场定理，是电学领域中一个非常重要的定理，它描述了电场在闭合曲面上的总通量与在该曲面内所有点电荷的代数和之间的关系。

通过高斯定理，我们可以更加深入地理解电场的性质和分布。

在本文中，我们将对电学高斯定理进行详细探讨，包括其概念、数学表达以及应用。

通过对电场的分析和计算，我们可以更好地理解高斯定理在电学领域中的重要性和实际应用价值。

同时，我们也将展望未来高斯定理的发展方向，探讨其在电学研究中的潜在应用和意义。

通过本文的学习，读者将能够更加全面地认识和理解电学高斯定理，为其在实际工程和科研中的应用提供帮助和指导。

1.2 文章结构本文将从引言部分开始，首先概述电学高斯定理的重要性和应用价值，然后介绍文章的结构安排。

接着将进入正文部分，详细讨论电学高斯定理的概念、数学表达以及其在现实生活中的应用情况。

最后，结论部分将总结电学高斯定理的重要性和在电学领域的应用，同时展望未来高斯定理的发展趋势。

整篇文章将全面介绍电学高斯定理，帮助读者更好地理解和应用这一重要理论。

1.3 目的电学高斯定理作为电磁学中的重要定律之一，其目的在于帮助我们理解电荷在电场中的行为规律。

通过深入研究高斯定理，我们可以更好地理解电场分布情况，预测电荷的运动轨迹，并解决复杂电学问题。

此外，掌握电学高斯定理还可以为我们提供一种便捷的计算电场强度的方法，简化电场分析的过程。

通过对高斯定理的掌握，我们可以更高效地解决工程中的电学问题，提高电学学科的研究水平和工程应用技术。

因此，本文旨在深入探讨电学高斯定理的概念、数学表达和应用，帮助读者更好地理解电场的特性，拓展电学知识，为电学领域的学习和研究提供有益的参考。

2.正文2.1 电学高斯定理的概念电学高斯定理，也称为高斯通量定理，是电学领域中的一个重要定理。

它描述了电场通过任意闭合曲面的总通量等于该曲面内的电荷总量的1/ε₀倍，其中ε₀为真空介电常数。

静电场的高斯定理
《静电场的高斯定理》
一、概述
静电场是一种重要的物理场，它是电学系统中最基本的物理量。

其中，高斯定理可以很好地描述静电场的行为，它是物理学中最重要的数学定理之一。

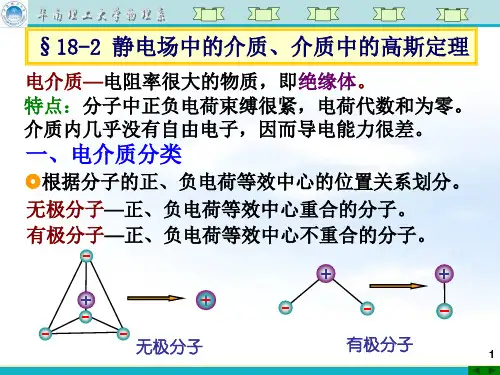
二、高斯定理的定义
高斯定理（Gauss’s law）是一个关于电压、电势和电场强度之间关系的定理，它可以用来求解电场强度和电势。

它可以用如下公式表示：
负电荷面密度和电势的总和*电场强度的积分= n电荷的电量/εo
其中，n是电荷数，εo是真空电介质中的介电常数。

三、高斯定理的应用
高斯定理可用于研究电荷在各种形状的电容器中的分布情况。

在分析电势和电能场时，也会用到高斯定理。

它同时也可以用来在不完全对称情况下分析和计算电场强度。

四、总结
高斯定理是物理学中一个重要的数学定理，它可以用来求解电场强度和电势，并可用于研究电荷在各种形状的电容器中的分布情况。

它可以用来解决电势和电能场的分析问题，也可以用来解决不完全对称情况下的电场强度计算问题。

有电介质的高斯定理好的，那我们就开始聊聊有电介质的高斯定理吧。

电介质的高斯定理啊，听起来就很厉害的样子呢。

其实啊，它就像是一个超级智慧的小管家，管理着电场在电介质中的那些事儿。

你想啊，电场这个东西本来就很神秘，看不见摸不着的，就像一个调皮的小精灵到处乱窜。

但是有了这个高斯定理呢，就好像给这个小精灵套上了一个小缰绳，能让我们更好地去把握它。

在电介质里啊，电荷可不像在真空中那么自由自在了。

电介质会对电场产生影响，就像是给电场设置了一些小障碍一样。

而高斯定理呢，它就像一个聪明的侦探，能透过这些复杂的情况，找到电场和电荷之间的关系。

比如说吧，当有个电介质放在电场里的时候，电介质里的分子会被电场影响，它们会发生极化现象。

这极化就像一群小士兵，被电场这个将军指挥着，重新排列队形。

那高斯定理是怎么做到看透这一切的呢？它通过巧妙地选择一个高斯面，就像在电介质的世界里圈出了一块特殊的领地。

然后呢，根据穿过这个高斯面的电通量，就能知道这个领地里面电荷的情况啦。

这电通量就像是经过这个领地边界的某种流量一样，它能告诉我们很多秘密哦。

你要是把电场想象成水流，那电介质就像是水里的一些小障碍物，会让水流改变方向。

而高斯定理就是那个能算出水流到底是怎么变化的神奇法则。

而且啊，这个定理不仅仅是个干巴巴的公式，它背后有着很多有趣的物理故事呢。

就像每一个科学发现都是人类探索未知的小冒险一样，这个定理的诞生也是科学家们不断思考、不断实验的成果。

理解电介质的高斯定理其实也不是特别难啦，只要你愿意去想象，把那些抽象的东西变成生活中的场景，就像我们刚刚说的小精灵、小士兵、水流这些。

这样的话，这个定理就不再是高高在上、让人望而生畏的东西了，而是像一个可爱的小伙伴，可以跟我们愉快地聊天，告诉我们电介质和电场之间那些有趣的互动呢。

你看，科学有时候就是这么有趣，只要我们换个角度去看，那些看似枯燥的定理也能变得生动起来，就像电介质的高斯定理一样，充满了魅力。