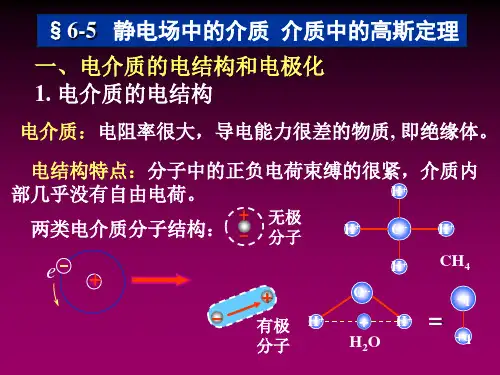
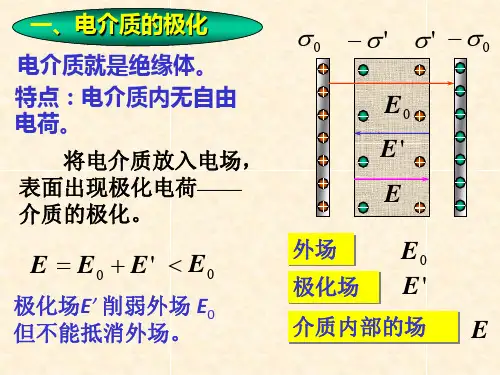
介质中的高斯定理
- 格式:pdf
- 大小:472.30 KB
- 文档页数:7


有介质时的高斯定理,写出其物理意义
高斯定理(也称为高斯通量定理)是电磁学中的一个基本定理,描述了电场或磁场通过一个封闭曲面的总通量与在该曲面内部源的大小之间的关系。
具体表达式为:对一个任意形状的封闭曲面,电场或磁场通过该曲面的总通量等于该曲面内部电荷或磁荷的代数和。
物理意义如下:
1. 电场或磁场通过一个封闭曲面的总通量是该曲面内部电荷或磁荷的性质之一,可以帮助我们了解场的发源和分布。
例如,通过测量通过一个闭合曲面的电场通量,可以推断该闭合曲面内部的电荷分布情况。
2. 高斯定理对于计算电场或磁场的分布以及场源的性质具有重要的应用。
通过选取适当的曲面以及利用高斯定理,可以简化计算复杂电场或磁场的过程,提高计算效率。
3. 高斯定理还有与能量和电荷守恒定律的联系。
当封闭曲面内部不存在电荷时,即电荷守恒定律成立时,通过该曲面的电场通量为零。
这可以用来推导电场能量的守恒。
总的来说,高斯定理在电磁学中具有重要的作用,它可以帮助我们理解场的分布、推断电荷或磁荷的性质,并且简化电场或磁场计算的过程。


真空中和介质中的高斯定理高斯定理,这个听上去有点复杂的名字,其实在物理界可是个大明星,简直就是“物理界的范冰冰”!说到它,大家首先想到的就是电场,没错,电场就像空气一样,围绕着我们,无时无刻不在。
想象一下,咱们周围的电荷,像小小的派对动物,互相排斥又吸引,搞得电场波动不断,真是热闹得很!高斯定理到底是什么呢?其实就是告诉我们,在一个封闭的区域内,电场的总流出量和这个区域里面的电荷量成正比。
简单来说,就是你放多少电荷在里面,电场就会“跑”多少出来。
这样一听,是不是觉得特别有趣?好了,咱们再聊聊真空和介质中的高斯定理。
这两个概念就像是两种不同风格的歌手,各有各的特点。
真空,嘿,它就像个独立的摇滚歌手,潇洒自如,不受任何干扰。
真空中的电场可以轻松发挥作用,根本不用担心周围的环境。
这时候,高斯定理变得格外简单,完全可以依靠电荷的数量来判断电场的强弱。
而介质嘛,就像是个嘈杂的聚会,环境复杂多变,电场的表现就有点“拗口”。
因为介质会影响电场的传播,咱们得考虑到介质的介电常数。
它就像是一个调音师,调整着电场的音量,让它在不同环境下表现得淋漓尽致。
想象一下,如果你把一个电荷放在真空中,它就像一个在阳光下炫耀的明星,电场四处发散,影响周围的一切。
而如果你把它放在一个充满水的泳池里,那就有点像在游泳的明星,周围的水流会干扰它的动作。
真空中电场的流动可以通过简单的公式算出,但在介质中,这个过程就要复杂得多。
介质的介电常数就像是一把调音器,让我们能更好地理解电场在不同环境中的变化。
可别小看这个常数,它可是高斯定理在介质中的关键!你要是搞不清楚,电场就会像失控的音乐节,变得乱七八糟。
再说了,咱们常常在生活中也能找到高斯定理的影子。
比如你在海滩上看着浪花拍打岸边,水流的运动就和电场有点像。
海浪涌向岸边,和电场中的电荷一样,都在不断变化着。
你要是能明白高斯定理,那你就是理解了自然界中一部分奥秘。
电场和电荷的关系,像是阳光和树影,互相依存,缺一不可。





高斯定理是电磁学中的一条基本定理,也被称为高斯电场定理或高斯法则。
它描述了电场在闭合曲面上的通量与该闭合曲面所包围的电荷量之间的关系。
高斯定理可以表述为:闭合曲面上的电场通量等于该闭合曲面所包围的电荷量的代数和的1/ε₀倍,其中ε₀是真空中的介电常数(ε₀ ≈ 8.854 × 10⁻¹² F/m)。
数学上,高斯定理可以用以下方程式表示:
∮ E · dA = Q/ε₀
其中,∮表示曲面积分,E 是电场矢量,dA 是曲面元素的面积矢量,Q 是闭合曲面所包围的电荷量。
高斯定理的应用范围很广,可以用于计算各种电场分布情况下的电场强度。
通过选择合适的闭合曲面和确定其中的电荷分布情况,可以利用高斯定理简化电场问题的计算。
高斯定理也适用于其他物理量的通量计算,例如磁场的磁通量。
第 2 章静电场
2.4 介质中的静电场方程
2.4.2 介质中的高斯定律
1.介质中高斯定律的微分形式
ερ
=
∙∇E 0
ερρp
+=
∙∇E (真空中)(电介质中)定义电位移矢量(Displacement )
∙D 线从正的自由电荷发出而终止于负的自由电荷。
D ——辅助矢量,又称电通密度,C /m 2代入P
∙-∇=p ρ)
(1
P E 0
∙∇-=∙∇ρερ
ε=+∙∇)(0P E P
E D +=0ε则有
ρ
=⋅∇D 电介质中高斯定律的微分形式
为自由电荷体密度
ρ
2. 介质中高斯定律的积分形式
⎰
∑=∙S
q
S D d 介质中高斯定律的积分形式
⎰
∑∑+=
∙S
q q )
(S E p 0
1
d
ε代入⎰∙-=S p q S
P d ⎰⎰∑∙-=∙S S q S
P S E d d 0
ε⎰∑⎰=∙+∙S
S
q
S P S E d d 0
ε⎰∑=∙+S
q
S P E d )(0
εq 为闭合面包围的自由电荷
• D 线由正的自由电荷出发,终止于负的自由电荷;• P 线由负的极化电荷出发,终止于正的极化电荷。
• E 线由正电荷出发,终止于负电荷;
D 线
E 线
P 线
D 、
E 与P
三者之间的关系
图示平行板电容器中放入介质板后,其D 线、E 线和P 线的分布。
3.D 和E 的关系D = ε0E + P P = χe ε0E
⇒⎭
⎬⎫
D = ε0
E +χe ε0E = ε0(1+χe ) E
= ε0εr E = εE
D = εE
介质的本构关系或组成关系
e
r 1χεε
ε+==ε——介质的电容率(介电常数)F/m
εr ——介质的相对电容率(相对介电常数)无量纲
χe 、εr 和ε的取值取决于媒质的特性
4. 介质特性
电场中,介质的特性由其介电常数确定。
E D ε=r ε⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡z y x z y x E E E D D D 3332
31
2322211312
11εεεεεεεεε均匀、线性、各向同性介质的介电常数是常量--简单介质。
各向异性介质的介电常数不是标量,而是矩阵-张量
晶体、地球上空电离层会显示各向异性的特点与空间位置无关,是常数----均匀介质
与空间位置有关,是函数----非均匀介质)
(r
ε与电场大小无关----线性介质与电场大小有关----非线性介质
)(E ε与方向无关----各向同性介质与方向有关----各向异性介质
介质存在时,静电场的基本方程为
总结
⎪⎪
⎩
⎪
⎪⎨⎧==∙=∙⎰⎰E D l E S D ε0d d c S q ⎪⎩
⎪
⎨⎧==⨯∇=∙∇E D E D ερ。