第6讲 找规律

第六讲简单的找规律前续知识点：一年级第一讲；XX模块第X讲后续知识点：X年级第X讲；XX模块第X讲阿瓜萱萱阿呆小高墨莫卡莉娅阿呆阿呆阿呆小高小山羊路人甲路人乙路人丙阿呆把相应的人物换成红字标明的人物．找规律可以分为图形规律和数列规律，我们先来结合图形的变化规律找一找数字的变化规律．【提示】每个方框里小球的数量有什么规律？找规律，补全空白方框．上面的图形除了有图形规律，还有数的规律，我们还可以根据图形数量之间的规律来判断某个位置的图形．同样的，通过数与数之间的规律关系也可以找到某个位置的数．【提示】动手画一画．大淘去采蘑菇，2格2格地跳，每跳一下画一个“○”．大淘都跳在哪些点上？例题2小青蛙从A 向B 跳，3格3格地跳，每跳一下画一个“○”．小青蛙都跳在了哪些点上？这些点上的数有什么规律？123456789 10 11 12BA 例题1 找规律，补全空白方框．练习1 练习2【提示】找到相邻数之间的关系．每个小动物身上都有数，这些数都是按规律排列的，请你在空白处填上正确的数．前面都是找图形与数之间的规律，以及数列的规律，接下来我们在前面学习的基础上继续研究算式之间的规律．15 12 9 618例题3每个小朋友都报了一个数，这些数按一定的规律排列．第六个小朋友报的数是几？8 10 12 2014 16 012 3 4 5 6 7 8 9 10 11 12练习3【提示】观察算式之间的关系．找到算式中的规律，补全算式．例题4根据算式规律，在横线上填数，并计算结果．1 ＋2 ＝3 2 ＋ 3 ＝ 5 3 ＋4 ＝ 7 4 ＋5 ＝ 9 5 ＋__ ＝__ __＋__ ＝__练习4【提示】第一排与第二排数之间的关系是什么？例题6 根据算式规律，在横线上填数，并计算结果．5＋15＝20 10＋12＝22 15＋ 9＝24 20＋ 6＝__ __＋__＝__例题5下面母鸡、鸡蛋和小鸡身上的编号都是按照一定规律排列的，找到规律，并在下面的空圆圈内填上适当的数．123 2135 38836【提示】观察算式之间的关系．课外阅读兔子数列在1、1、2、3、5、8、13、21……中，从第三个数开始，每个数都等于前两个数的和．这一奇特的数列是由意大利数学家斐波那契从兔子繁殖问题中提出的，为了纪念他，人们就把这种数列称为斐波那契数列，也称兔子数列．斐波那契发现兔子繁殖非常快，几个月后，1对兔子就变成了几十对．每对成年兔每个月都能生出1对兔宝宝，而兔宝宝一个月后便有生殖能力，两个月后就能生下第一对小兔．这样一月初有1对兔宝宝，二月初小兔交配，三月初新生1对兔宝宝，有2对兔子，四月初再生1对小兔，有3对兔子，五月初比上月多生1对兔宝宝（三月出生的小兔生的），有2对兔宝宝，共有5对兔子，六月初又比上月多生1对兔宝宝（四月出生的小兔生的），共8对．这样一到六月兔子的对数就是1、1、2、3、5、8，从第三个数开始，每个数都是前两个数的和，继续推理下去仍是如此．作业1. 找规律，补全空白方框．2. 从0开始4格4格地跳，每跳一下画一个“○”，它跳到了哪些点上呢？0 1 2 3 4 5 6 7 8 9 10 11 12 3. 找出藏在大树后面的数，在对应的空格里写出来．20 17 14 84. 茶壶爷爷请小朋友们帮忙填算式．根据算式规律，在空白处填算式，并计算结果．5. 下面各种图形上的编号都是按照一定规律排列的，找出规律，并在下面空着的圆圈里填上适当的数．2 3325562217+ 2 =19 16+ 3 =19 15+ 4 =19 14+__=__第六讲 简单的找规律1. 例题1答案：详解：通过观察可以发现本题中，从第二个方框开始，后一个方框里的小球是在前一个方框里的小球的基础上增加一排小球．所以可以得出第五个方框中有5排小球，第5排有5个小球，所以一共有1234515++++=（个）小球． 2. 例题2答案：详解：因为小青蛙从A 向B 3格3格地跳，从整体看，跳到的点数越来越大，所以小青蛙跳的点数是0、3、6、9、12，把这些点数都画上“○”，并观察这些点之间存在的关系是每两个相邻的数之间相差3． 3.例题3 答案：18 详解：从整体看，后面的数比前面的数大，观察每相邻两个数之间的规律，相邻的两个数相差2．后一个数是前一个数加上2． 4.例题4答案：从上到下，从左到右依次是6、11、6、7、13 详解：从整体看，把算式从“＋”分前后两部分，“＋”前面的数组成一个数列：1、2、3、4、5……题中都是加法算式，每个算式后面的数比前面的数大，相邻两数之间的差1，后一个数是前一个数＋1，由此可以判断“5”后面是“6”．“＋”后面的数组成一个数列：2、3、4、5、6，由此可以判断算式“56+”下面的算式是“6713+=”． 5.例题5答案：从上到下，从左到右依次是5、10、18详解：从整体观察，共有5排数，可以得到这样的规律：下面一排中图形上的编号是上一排中与它相邻的左上角和右上角两个编号相加的和，通过其他的编号也可以验证这个规律．依次推理，可填出全部的数． 6.例题6答案：从上到下，从左到右依次是26、25、3、28详解：从整体看，都是加法算式．20626+=．把算式从“＋”分前后两部分，“＋”前面的数组成一个数列：5、10、15、20、___从整体看，后面的数比前面的数大，相邻两数之间的差为5，后一个数是前一个数＋5．由此可以判断“20”下面是“25”．“＋”后面的数组成一个数列：15、12、9、6、___．从整体看，后面的数比前面的数小，相邻两数之间的差是3，后一个数是前一个数减去3．由此可以判断“6”下面是“3”．25328+=．23456789 10 11 12BA7. 练习1答案：简答：通过观察可以发现本题中，从第二个方框开始，后一个方框里的小球是在前一个方框里的小球的基础上减少一排小球．所以可以得出第五个方框中有1排小球，有1个小球．8. 练习2答案：简答：从整体看，跳到的点数越来越小，所以灰太狼的点数是12、10、8、6、4、2、0把这些点数都画上“○”，并观察这些点之间存在的关系．发现，每两个相邻的数之间相差2．9. 练习3答案：3简答：从整体看，后面的数比前面的数小，观察每相邻两个数之间的规律，相邻的两个数相差3．后一个数是前一个数减去3．10. 练习4答案：从上到下，从左到右依次是7、17、10、19简答：从整体看，都是加法算式．把算式从“＋”分前后两部分，“＋”前面的数组成一个数列：5、6、___、8、9……从整体看，后面的数比前面的数大，相邻两数之间的差为1，后一个数是前一个数加1．由此可以判断“6”后面是“7”．“＋”后面的数组成一个数列：6、7、8、9、___．从整体看，后面的数比前面的数大，相邻两数之间的差是1，后一个数是前一个数加1，由此可以判断“9”后面是“10”．11. 作业1答案：如下图所示简答：通过观察可以发现，从第二个方框开始，后一个方框里比前一个方框里多3个圆．所以可以得出第五个方框中有13个圆．12. 作业2答案：4、8、120 1 2 3 4 5 6 7 8 9 10 1112简答：跟着箭头把小动物跳的路线画出来，并对应的把“○”标出来．13.作业3答案：从左到右依次是11、5简答：通过观察可以发现车厢上的数的规律是：两个相邻的数之间的差是3．20317-=，-=，17314-=．-=，835-=，11381431114.作业4答案：从左到右依次是5、19简答：通过观察可以发现前面三个算式中，“＋”号前面的数依次是17、16、15、14，它们之间的规律是相邻两个数之间的差是1；“＋”号后面的数依次是2、3、4、___，它们之间的规律是相邻两个数之间的差是1，所以第四个数是5；“＝”右边的数都是19；最后的算式与结果：14519+=．15.作业5答案：从左到右依次是11、11简答：通过观察可以发现第二排第一个数“5”是第一排中第一个数与第二个数相加的和，即：=+，所以可以得到这样的规律：下面一排图形上的编号是上一排与它相邻的左上角和右上角523两个编号相加的和，通过其他的编号也可以验证这个规律．。

测试卷6 （找规律篇）时间：15分钟满分5分姓名_________ 测试成绩_________1如果将八个数14，30，33，35，39，75，143，169平均分成两组，使得这两组数的乘积相等，那么分组的情况是什么？2观察1+3=4 ；4+5=9 ；9+7=16 ；16+9=25 ；25+11=36 这五道算式，找出规律，然后填写20012＋（）＝200223一串分数：12123412345612812 ,,,,,,,,,,,,.....,,,......,33,55557777779991111其中的第2000个分数是 .4在2、3两数之间,第一次写上5,第二次在2、5和5、3之间分别写上7、8(如下所示),每次都在已写上的两个相邻数之间写上这两个相邻数之和.这样的过程共重复了六次,问所有数之和是多少? 2......7......5......8 (3)5请你从01、02、03、…、98、99中选取一些数，使得对于任何由0～9当中的某些数字组成的无穷长的一串数当中，都有某两个相邻的数字，是你所选出的那些数中当中的一个。

为了达到这些目的。

(1)请你说明：11这个数必须选出来；(2)请你说明：37和73这两个数当中至少要选出一个；(3)你能选出55个数满足要求吗？【附答案】1 【解】分解质因数，找出质因数再分开，所以分组为33、35、30、169和14、39、75、143。

2 【解】上面的规律是：右边的数和左边第一个数的差正好是奇数数列3、5、7、9、11……，所以下面括号中填的数字为奇数列中的第2001个，即4003。

3 【解】分母为3的有2个，分母为4个，分母为7的为6个，这样个数2+4+6+8…88=1980<2000，这样2000个分数的分母为89，所以分数为20/89。

4 【解】：第一次写后和增加5，第二次写后的和增加15，第三次写后和增加45，第四次写后和增加135，第五次写后和增加405，……它们的差依次为5、15、45、135、405……为等比数列，公比为3。

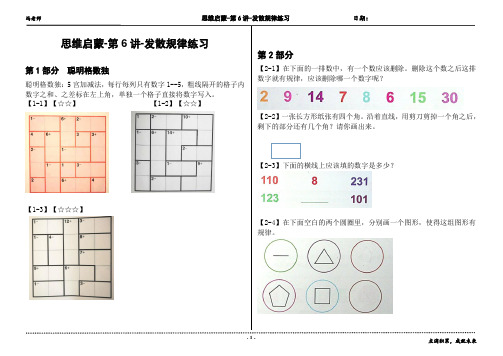
思维启蒙-第6讲-发散规律练习第1部分聪明格数独聪明格数独：5宫加减法，每行每列只有数字1--5，粗线隔开的格子内数字之和、之差标在左上角，单独一个格子直接将数字写入。

【1-1】【☆☆】【1-2】【☆☆】【1-3】【☆☆☆】第2部分【2-1】在下面的一排数中，有一个数应该删除。

删除这个数之后这排数字就有规律，应该删除哪一个数字呢？【2-2】一张长方形纸张有四个角。

沿着直线，用剪刀剪掉一个角之后，剩下的部分还有几个角？请你画出来。

【2-3】下面的横线上应该填的数字是多少？【2-4】在下面空白的两个圆圈里，分别画一个图形，使得这组图形有规律。

【2-5】一条直线可以把一个圆分成两个部分，如图所示。

那么两条直线分几个部分？三条直线最多能分成几个部分呢？四条直线最多能分成几个部分呢？【注意是最多画几条】【假如有10条直线，最多可以分成多少个部分呢？】【2-6】用+、-、×、÷计算出24点，并且要用多种方法： 3、8、8、9，这四个数字的使用顺序可以变化。

（1）--------------------------（2）--------------------------（3）--------------------------【2-7】利用3×8=24、4×6=24求解（1）3、3、6、10（2）2、3、3、7【2-8】利用0、11的运算特性求解。

（1）3、4、4、8（2）4、5、11、13【2-9】（1）利用（a-b）×（c+d）-----2、2、4、10（2）利用（a+b）÷c×d------2、2、4、10（3）利用（a-b÷c）×d------2、2、3、12（4）利用（a+b-c）×d-----2、2、5、9（5）利用a×b+c-d----1、3、10、11（6）利用（a-b）×c+d----1、4、6、6【2-10】填数字【2-11】根据规律填数字：（10 ，20 ，3），（20 ，15 ，9) ，（30 ，10 ，15），（□，□，□）【2-12】三个骰子是一样的，只是转动了方向，现在请你判断出，三组对应的数字分别是谁？（）对（）；（）对（）；（）对（）。

学员编号：年级：课时数：学员姓名：辅导科目：学科教师：授课T (同步知识主题) C （专题方法主题）T （学法与能力主题）类型授课日期时段教学内容第六讲：找规律填数（二）我们常将一个数列与一些规律简单的数列进行比较，例如，偶数数列2，4，6，8…的第100项显然是200，而1 990址第995项，将奇数数列1，3，5，7，…与偶数列比较，就知道第100个奇数是200 -1= 199．而1 989是第995个奇数下面的例1显示一个数列与它的“差数列”间的关系．．找出数列的规律，并在括号内填入适当的数：1，2，4，7，l1，16，( )，( ) ．从第2项起，每一项减去前一项得数列l，2，3，4，5，…，这个由差组成的“差数列”，第6、7项分别是6、7．所以原数列的第7、8项分别是16+6=22．22+7=29．即括号内应填入22，29．找规律，在括号内填入适当的数：2，6，12，20，30，42，( ) ．．找出数列的规律，并在括号内填入适当的数：25，3，22，3，l9，3，( )，( )由观察可以知道，所有偶数项数的项全由3组成．再来看一下奇数项数的项25，22，19，…．从22起，每一个都比前一个少3．所以括号内应该填入16，3．发现规律，并在括号内填入适当的数：15，6，3，7，11，8，( )，( ) ．例2表示，有些数列可以拆成两个数列（或者说，由两个数列组成），分别由奇数项数的项和偶数项数的项构成．而这两个数列的规律都不难发现．）已知算式：1+1，2+3，3+5，4+7，1+9，2+11，3+13，4+15，1+17，…．问：第几个算式的得数是1 992？不难看出，各个算式中，被加数是l，2，3，4，每4个循环一次．加数是1，3，5，7，9，11，13，15，17，…，正好是奇数数列，如果和是1992，那么被加数是l或3（因为2或4加上奇数，不会等于偶数1 992），从而加数是1 991或1 989．因为(1 989 +1)÷2=995所以1989是上面奇数数列的第995项．1 991是第996项又因为995=4×248+3．所以，第995个算式是3+1 989第996个算式是4+1 991没有算式1+1 991．所以第995个算式的得数是1 992．发现规律，在括号内填入适当的数：2，5，8，11，10，13，16，19，18，( )，( )自然数按一定规律排成下表，问第200行的第5个数是多少？12 34 5 67 8 9 10……第1行1个数，第2行2个数，第3行3个数，…，第199行199个数，因此前199行共有1+2+3+…+199=(1+199)×199÷2=19 900个数，即前199行的最末一个数是19 900.第200行第5个数是19 900 +5=19 905上面的表中，100是第几行第几个数？．如右图，将自然数1，2，3，4，…按箭头所指方向顺序排列，依次在2，3，5，7，10，…的位置处拐弯，如果2算第1次拐弯，3算第2次拐弯，那么第13次拐弯处的数是什么？首先，注意到第1次拐弯在东北，笫2次拐弯在东南，第3次拐弯在西南，第4次拐弯扯西北，依此类推，每过4次拐弯就使方向循环出现．因为13=3×4+1所以第13次拐弯在东北其次，东北拐弯处的数组成数列2，10，26，…，它的每一项比数列1，9，25，…的相应项多1．数列1，4，9，16，25，36，49，64，81，100，121，…也就是1×1，2×2，3×3，4×4，5×5，6×6，…叫做平方数数列．数列1，9，25，40，…也就是1×1，3×3，5×5，7×7，…是由奇数平方组成的数列，因此，上述数列（即东北拐弯处的数列）中，26的后一项是7×7 +1=50．即第13个拐弯处的数是50．上图中第21个拐弯处的数是多少？。

[二年级数学]二年级奥数上册1二年级奥数上册:第一讲速算与巧算一、“凑整”先算1.计算:(1)24+44+56(2)53+36+47解:(1)24+44+56=24+(44+56)=24+100=124这样想:因为44+56=100是个整百的数，所以先把它们的和算出来.(2)53+36+47=53+47+36=(53+47)+36=100+36=136这样想:因为53+47=100是个整百的数，所以先把+47带着符号搬家，搬到+36前面;然后再把53+47的和算出来.2.计算:(1)96+15(2)52+69解:(1)96+15=96+(4+11)=(96+4)+11=100+11=1112这样想:把15分拆成15=4+11，这是因为96+4=100，可凑整先算.(2)52+69=(21+31)+69=21+(31+69)=21+100=121这样想:因为69+31=100，所以把52分拆成21与31之和，再把31+69=100凑整先算.3.计算:(1)63+18+19(2)28+28+28解:(1)63+18+19=60+2+1+18+19=60+(2+18)+(1+19)=60+20+20=100这样想:将63分拆成63=60+2+1就是因为2+18和1+19可以凑整先算.(2)28+28+28=(28+2)+(28+2)+(28+2)-63=30+30+30-6=90-6=84这样想:因为28+2=30可凑整，但最后要把多加的三个2减去.二、改变运算顺序:在只有“+”、“-”号的混合算式中，运算顺序可改变计算:(1)45-18+19(2)45+18-19解:(1)45-18+19=45+19-18=45+(19-18)=45+1=46这样想:把+19带着符号搬家，搬到-18的前面.然后先算19-18=1.(2)45+18-19=45+(18-19)=45-1=44这样想:加18减19的结果就等于减 1.三、计算等差连续数的和相邻的两个数的差都相等的一串数就叫等差连续数，又叫等差数列，如: 41，2，3，4，5，6，7，8，91，3，5，7，92，4，6，8，103，6，9，12，154，8，12，16，20等等都是等差连续数.1. 等差连续数的个数是奇数时，它们的和等于中间数乘以个数，简记成:(1)计算:1+2+3+4+5+6+7+8+9=5×9 中间数是 5=45 共9个数(2)计算:1+3+5+7+9=5×5 中间数是 5=25 共有5个数(3)计算:2+4+6+8+10=6×5 中间数是 6=30 共有5个数5(4)计算:3+6+9+12+15=9×5 中间数是9=45 共有5个数(5)计算:4+8+12+16+20=12×5 中间数是12=60 共有5个数2. 等差连续数的个数是偶数时，它们的和等于首数与末数之和乘以个数的一半，简记成:(1)计算:1+2+3+4+5+6+7+8+9+10=(1+10)×5=11×5=55共10个数，个数的一半是5，首数是1，末数是10.(2)计算:3+5+7+9+11+13+15+17=(3+17)×4=20×4=806共8个数，个数的一半是4，首数是3，末数是17.(3)计算:2+4+6+8+10+12+14+16+18+20=(2+20)×5=110共10个数，个数的一半是5，首数是2，末数是20.四、基准数法(1)计算:23+20+19+22+18+21解:仔细观察，各个加数的大小都接近20，所以可以把每个加数先按20相加，然后再把少算的加上，把多算的减去.23+20+19+22+18+21=20×6+3+0-1+2-2+1=120+3=1236个加数都按20相加，其和=20×6=120.23按20计算就少加了“3”，所以再加上“3”;19按20计算多加了“1”，所以再减去“1”，以此类推.(2)计算:102+100+99+101+987解:方法1:仔细观察，可知各个加数都接近100，所以选100为基准数，采用基准数法进行巧算.102+100+99+101+98=100×5+2+0-1+1-2=500方法2:仔细观察，可将5个数重新排列如下:(实际上就是把有的加数带有符号搬家)102+100+99+101+98=98+99+100+101+102=100×5=500可发现这是一个等差连续数的求和问题，中间数是100，个数是 5.习题一1.计算:(1)18+28+72=(2)87+15+13=(3)43+56+17+24=8(4)28+44+39+62+56+21=2.计算:(1)98+67=(2)43+28=(3)75+26=3.计算:(1)82-49+18=(2)82-50+49(3)41-64+294.计算:(1)99+98+97+96+95(2)9+99+9995.计算:(1)5+6+7+8+9(2)5+10+15+20+25+30+359(3)9+18+27+36+45+54(4)12+14+16+18+20+22+24+266.计算:(1)53+49+51+48+52+50(2)87+74+85+83+75+77+80+78+81+847.计算:1+2+3+4+5+6+1+2+3+4+5+6+1+2+3+4+5+6+1+2+3+4+5 10二年级奥数上册:第一讲速算与巧算习题解答111213141516171819第一层 1个第二层 2个第三层 3个第四层 4个第五层 5个20第六层 6个第七层 7个第八层 8个第九层 9个第十层 8个第十一层7个第十二层6个第十三层 5个第十四层 4个第十五层 3个第十六层 2个第十七层 1个总数1+2+3+4+5+6+7+8+9+8+7+6+5+4+3+2+1 =(1+2+3+4+5+6+7+8+9)+(8+7+6+5+4+3+2+1) =45+36=81(利用已学过的知识计算).21第一层 1个第二层 3个第三层 5个第四层 7个第五层 9个第六层 11个第七层 13个第八层 15个第九层 17个总数:1+3+5+7+9+11+13+15+17=81(利用已学过的知识计算).22×101+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=10即等号左边这样的一串数之和等于中间数的自乘积.由此我们猜想: 1=1×11+2+1=2×21+2+3+2+1=3×31+2+3+4+3+2+1=4×41+2+3+4+5+4+3+2+1=5×5231+2+3+4+5+6+5+4+3+2+1=6×61+2+3+4+5+6+7+6+5+4+3+2+1=7×71+2+3+4+5+6+7+8+7+6+5+4+3+2+1=8×8×91+2+3+4+5+6+7+8+9+8+7+6+5+4+3+2+1=9×101+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=10这样的等式还可以一直写下去，能写出很多很多.同学们可以自己检验一下，看是否正确，如果正确我们就发现了一条规律.?由方法2和方法3也可以得出下式:1+3+5+7+9+11+13+15+17+19=10×10.即从1开始的连续奇数的和等于奇数个数的自乘积.由此我们猜想:1+3=2×21+3+5=3×31+3+5+7=4×41+3+5+7+9=5×5241+3+5+7+9+11=6×61+3+5+7+9+11+13=7×71+3+5+7+9+11+13+15=8×81+3+5+7+9+11+13+15+17=9×91+3+5+7+9+11+13+15+17+19=10×10还可往下一直写下去，同学们自己检验一下，看是否正确，如果正确，我们就又发现了一条规律.解:(1)我们已知，两点间的直线部分是一条线段.以A点为共同端点的线段有: AB AC AD AE AF 5条.以B点为共同左端点的线段有:BC BD BE BF 4条.以C点为共同左端点的线段有:CD CE CF 3条.25以D点为共同左端点的线段有:DE DF 2条.以E点为共同左端点的线段有:EF1条.总数5+4+3+2+1=15条.26272829二年级奥数上册:第三讲数数与计数(二)习题3031323334二年级奥数上册:第四讲认识简单数列35363738二年级奥数上册:第四讲认识简单数列习题39二年级奥数上册:第四讲认识简单数列习题解答404142二年级奥数上册:第五讲自然数列趣题第五讲自然数列趣题本讲的习题，大都是关于自然数列方面的计数问题，解题的思维方法一般是运用枚举法及分类统计方法，望同学们能很好地掌握它.例1 小明从1写到100，他共写了多少个数字“1”,解:分类计算:“1”出现在个位上的数有:1，11，21，31，41，51，61，71，81，91共10个;“1”出现在十位上的数有:10，11，12，13，14，15，16，17，18，19共10个;“1”出现在百位上的数有:100共1个;共计10+10+1=21个.43例2 一本小人书共100页，排版时一个铅字只能排一位数字，请你算一下，排这本书的页码共用了多少个铅字,解:分类计算:从第1页到第9页，共9页，每页用1个铅字，共用1×9=9(个);从第10页到第99页，共90页，每页用2个铅字，共用2×90=180(个);第100页，只1页共用3个铅字，所以排100页书的页码共用铅字的总数是: 9+180+3=192(个).44解:(见图5—1)先按题要求，把1到100的一百个自然数全部写出来，再分类进行计算:如图5—1所示，宽竖条带中都是个位数字，共有10条，数字之和是: (1+2+3+4+5+6+7+8+9)×10=45×10=450.窄竖条带中，每条都包含有一种十位数字，共有9条，数字之和是:1×10+2×10+3×10+4×10+5×10+6×10+7×10+8×10+9×10=(1+2+3+4+5+6+7+8+9)×10=45×10,450.另外100这个数的数字和是1+0+0=1.所以，这一百个自然数的数字总和是:45450+450+1=901.顺便提请同学们注意的是:一道数学题的解法往往不只一种，谁能寻找并发现出更简洁的解法来，往往标志着谁有更强的数学能力.比如说这道题就还有更简洁的解法，试试看，你能不能找出来,二年级奥数上册:第五讲自然数列趣题习题1.有一本书共200页，页码依次为1、2、3、,,、199、200，问数字“1”在页码中共出现了多少次,2.在1至100的奇数中，数字“3”共出现了多少次,3.在10至100的自然数中，个位数字是2或是7的数共有多少个,4.一本书共200页，如果页码的每个数字都得用一个单独的铅字排版(比如，“150”这个页码就需要三个铅字“1”、“5”和“0”)，问排这本书的页码一共需要多少个铅字,5.像“21”这个两位数，它的十位数字“2”大于个位数字“1”，问从1至100的所有自然数中有多少个这样的两位数,6.像“101”这个三位数，它的个位数字与百位数字调换以后，数的大小并不改变，问从100至200之间有多少个这样的三位数,467.像11、12、13这三个数，它们的数位上的各个数字相加之和是(1+1)+(1+2)+(1+3)=9.问自然数列的前20个数的数字之和是多少,8.把1到100的一百个自然数全部写出来，用到的所有数字的和是多少,9.从1到1000的一千个自然数的所有数字的和是多少,习题五解答1.解:分类计算，并将有数字“1”的数枚举出来.“1”出现在个位上的数有:1，11，21，31，41，51，61，71，81，91，101，111，121，131，141，151，161，171，181，191 共20个;“1”出现在十位上的数有:10，11，12，13，14，15，16，17，18，19110，111，112，113，114，115，116，117，118，119 共20个;47“1”出现在百位上的数有:100，101，102，103，104，105，106，107，108，109，110，111，112，113，114，115，116，117，118，119，120，121，122，123，124，125，126，127，128，129，130，131，132，133，134，135，136，137，138，139，140，141，142，143，144，145，146，147，148，149，150，151，152，153，154，155，156，157，158，159，160，161，162，163，164，165，166，167，168，169，170，171，172，173，174，175，176，177，178，179，180，181，182，183，184，185，186，187，188，189，190，191，192，193，194，195，196，197，198，199 共100个;数字“1”在1至200中出现的总次数是:20+20+100=140(次).2.解:采用枚举法，并分类计算:48“3”在个位上:3，13，23，33，43，53，63，73，83，93共10个;“3”在十位上:31，33，35，37，39共5个;数字“3”在1至100的奇数中出现的总次数:10+5=15(次).3.解:枚举法:12，17，22，27，32，37，42，47，52，57，62，67，72，77，82，87，92，97共18个.4.解:分段统计，再总计.页数铅字个数1,9共9页1×9=9(个)(每个页码用1个铅字)10,90共90页2×90=180(个)(每个页码用2个铅字)100,199共100页3×100=300(个)(每个页码用3个铅字)第200页共1页3×1=3(个)(这页用3个铅字)总数:9+180+300+3=492(个).5.解:列表枚举，分类统计:10 1个4920 21 2个30 31 32 3个40 41 42 43 4个50 51 52 53 54 5个60 61 62 63 64 65 6个70 71 72 73 74 75 76 7个80 81 82 83 84 85 86 87 8个90 91 92 93 94 95 96 97 98 9个总数1+2+3+4+5+6+7+8+9=45(个).6.解:枚举法，再总计:101，111，121，131，141，151，161，171，181，191共10个.5051二年级奥数上册:第六讲找规律(一)525354二年级奥数上册:第六讲找规律(一)习题5556二年级奥数上册:第六讲找规律(一)习题解答575859二年级奥数上册:第七讲找规律(二) 60。

小学奥数基础教程（三年级）- 1 -小学奥数基础教程（三年级）第1讲加减法的巧算第2讲横式数字谜(一)第3讲竖式数字谜(一)第4讲竖式数字谜(二)第5讲找规律(一)第6讲找规律(二)第7讲加减法应用题第8讲乘除法应用题第9讲平均数第10讲植树问题第11讲巧数图形第12讲巧求周长第13讲火柴棍游戏(一)第14讲火柴棍游戏(二)第15讲趣题巧解第16讲数阵图(一)第17讲数阵图(二)第18讲能被2，5整除的数的特征第19讲能被3整除的数的特征第20讲乘、除法的运算律和性质第21讲乘法中的巧算第22讲横式数字谜(二)第23讲竖式数字谜(三)第24讲和倍应用题第25讲差倍应用题第26讲和差应用题第27讲巧用矩形面积公式第28讲一笔画(一)第29讲一笔画(二)第30讲包含与排除一、两、三位数乘一位数（一）二、两、三位数乘一位数（二）三、乘法分配律数学智慧园（一）四、等量替换五、两、三位数除以一位数（一）六、两、三位数除以一位数（二）七、和差问题数学智慧园（二）八、图形空格填数九、归一问题十、和倍问题十一、差倍问题数学智慧园（三）十二、两积之和第2讲横式数字谜(一)在一个数学式子(横式或竖式)中擦去部分数字，或用字母、文字来代替部分数字的不完整的算式或竖式，叫做数字谜题目。

解数字谜题就是求出这些被擦去的数或用字母、文字代替的数的数值。

例如，求算式324+□=528中□所代表的数。

根据“加数=和-另一个加数”知，□=582-324＝258。

又如，求右竖式中字母A，B所代表的数字。

显然个位数相减时必须借位，所以，由12-B＝5知，B＝12-5＝7；由A-1＝3知，A＝3＋1＝4。

解数字谜问题既能增强数字运用能力，又能加深对运算的理解，还是培养和提高分析问题能力的有效方法。

这一讲介绍简单的算式(横式)数字谜的解法。

解横式数字谜，首先要熟知下面的运算规则：(1)一个加数+另一个加数=和；(2)被减数-减数=差；(3)被乘数×乘数=积；(4)被除数÷除数=商。

06找规律画图拓展题目1、请你根据前两行图片的样子，想一想，小鸡应该是什么样子的，在正确的图片下面画√。

Array2、下面的小物品有什么样的规律呢？你知道后面一个是什么吗？请选择并圈起来！3、请你找出下面图形的规律，并画出横线上的图形。

4、找规律，请根据规律继续往下画。

5、第一排和第二排的规律是一样的，根据这种规律把“？”补充完整。

6、请根据规律在空白圆中涂上相应的颜色。

7、根据下图中前面几幅图的变化规律，画出空格中的图8、小动物们排队玩游戏，每次顺序都不同，请同学们判断一下，第四次排队的顺序应该是什么样的。

9、找规律，请根据规律继续往下画。

10、按规律在空白处补上合适的图形。

11、根据下图中几幅图的变化规律，画出第三幅图。

12、根据下面一串黑白珠子的排列规律，你能继续往下涂吗？13、闹闹在玩耍的时候不小心把妈妈最喜欢的珍珠项链弄断了，有几颗珠子散落下来。

闹闹想要帮妈妈修好项链，但是不知道珠子颜色排列的顺序，同学们能不能帮他找到珠子颜色的顺序呢？（请把红色珠子涂上颜色）14、艾迪和薇儿的自然课作业是培育一棵种子，请同学们根据艾迪和薇儿的培育日记预测一下，到了第五天，他们的植物会变成什么样子？15、同学们玩过超级玛丽的游戏吗？在游戏里，超级玛丽遇到蘑菇就可以吃掉，遇到砖块就可以得到金币，请同学观察一下下面的图片，想想最后一行应该是什么样子？请在正确的下面画√。

16、下面是世界上最早出现的美索不达米亚“数字”，也叫做“楔形文字”他们用这种符号表示“一”，用表示“十”，用表示“百”。

请同学们根据下图，帮助乐乐老师把楔形文字的数字翻译成咱们所认识的阿拉伯数字。

1、【答案与解析】 正确答案：C2、【答案与解析】3、【答案与解析】① ② ③4、【答案与解析】5、【答案与解析】06找规律画图 拓展题目6、【答案与解析】7、【答案与解析】8、【答案与解析】老虎，兔子，羊，猴子。

9、【答案与解析】10、【答案与解析】11、【答案与解析】12、【答案与解析】13、【答案与解析】白色珠子数量不变，红色珠子1、2、3、4……14、【答案与解析】艾迪的植物叶子数量变化：1→3→5→7→9。

第5讲找规律(一)例1找出下列各数列的规律，并按其规律在( )内填上合适的数：(1)4，7，10，13，( )，…(2)84，72，60，( )，( )；(3)2，6，18，( )，( )，…(4)625，125，25，( )，( )；(5)1，4，9，16，( )，…(6)2，6，12，20，( )，( )，…例2找出下列各数列的规律，并按其规律在( )内填上合适的数：(1)1，2，2，3，3，4，( )，( )；(2)( )，( )，10，5，12，6，14，7；(3) 3，7，10，17，27，( )；(4) 1，2，2，4，8，32，( )。

例3找出下列各数列的规律，并按其规律在( )内填上合适的数：(1)18，20，24，30，( )；(2)11，12，14，18，26，( )；(3)2，5，11，23，47，( )，( )。

例4找出下列各数列的规律，并按其规律在( )内填上合适的数：(1)12，15，17，30， 22，45，( )，( )；(2) 2，8，5，6，8，4，( )，( )。

练习5按其规律在下列各数列的( )内填数。

1.56，49，42，35，( )。

2.11， 15， 19， 23，( )，…3.3，6，12，24，( )。

4.2，3，5，9，17，( )，…5.1，3，4，7，11，( )。

6.1，3，7，13，21，( )。

7.3，5，3，10，3，15，( )，( )。

8.8，3，9，4，10，5，( )，( )。

9.2，5，10，17，26，( )。

10.15，21，18，19，21，17，( )，( )。

11.数列1，3，5，7，11，13，15，17。

(1)如果其中缺少一个数，那么这个数是几？应补在何处？(2)如果其中多了一个数，那么这个数是几？为什么？第6讲找规律(二)例1观察下列图形的变化规律，并按照这个规律将第四个图形补充完整。

例2在下列各组图形中寻找规律，并按此规律在“？”处填上合适的数：例3寻找规律填数：例4寻找规律在空格内填数：例5在下列表格中寻找规律，并求出“？”：例6寻找规律填数：练习6寻找规律填数：6.下图中第50个图形是△还是○？○△○○○△○○○△○…第11讲巧数图形例1数出下图中共有多少条线段。