数字积分法
- 格式:ppt
- 大小:720.50 KB
- 文档页数:24

第三四象限直线插补计算1. 引言随着微电子技术,计算机技术的发展,数控机床的性能不断完善,其应用范围也不断增大。
而数控技术作为数控机床的关键技术,越来越得到更多高校的重视。
2.数字积分法直线插补原理设将要加工的直线XOY 平面内第一象限直线OE ,如图.一所示,直线起点在坐标原点,终点为E (Xe ,Ye )。
同样,假设坐标值均为以脉冲当量为单位的整数。
图.一若此时刀具在两坐标轴上的进给速度分量分别是Vx ,Vy ,则刀具在X 轴,Y 轴方向上位移增量分别是△X = Vx △t 式一a△ Y = Vy △t 式一b由图.一 所示的几何关系可得V/OE=Vx/Xe=Vy/Ye=K (常数) 式二将式二中的Vx ,Vy 分别代入式一 可得:△X = KXe △t 式三a△ Y = KYe △t 式三b可见刀具由原点O 走向E 的过程,可以看作式每经过一个单位时间间隔△t ,就分别以增量[KXe],[ KYe]同时在两个坐标轴累加的结果。
也可以这样认为,数字积分法插补实际上就是利用速度分量,进行数字积分来确定刀具在各坐标轴上位置的过程,即XO当取△ti=“1”(一个单位时间间隔)则X = nKXe 式五aY = nKYe 式五b设经过n 次累加后,刀具正好到达终点E(Xe,Ye),则要求式五中常量满足 下式nK=1 式六n 是累加次数必须取整数,所有K 取小数。
为了保证每次分配给坐标轴的进给脉冲不超过一个单位,则△ X=KXe<1 式七a△ Y=KYe<1 式七b上式中Xe ,Ye 的最大允许值受系统中相应寄存器容量的限制。
现假设寄存器 为N 位则容量为2N ,对应存储的最大允许数字量为(2N - 1)将其带入式七得 K<=1/(2N - 1) 式八现不妨取 K =1/2N 式九显然它满足式七,式八的约束条件,再将K 值代入式六可得累加次数为 n =2N 式十如果将n ,K,值代入式五则动点坐标为X = nKXe =Xe 式十一aY = nKYe =Ye 式十一b根据以上分析,在进行直线插补时,先开辟两个被积函数寄存器Jvx ,Jvy 分别存放终点坐标值Xe ,Ye ,还有两个余数寄存器Jrx ,Jry 。



数字积分法(DDA)插补直线参考程序Sub 插补X()标志X = 0If 余数X >= Q Then余数X = 余数X Mod Qx动点= x动点+ 1: 标志X = 1 End IfEnd SubSub 插补Y()标志Y = 0If 余数Y >= Q Then余数Y = 余数Y Mod Qy动点= y动点+ 1: 标志Y = 1End IfEnd SubSub 插补Z()标志Z = 0If 余数Z >= Q Then余数Z = 余数Z Mod Qz动点= z动点+ 1: 标志Z = 1 End IfEnd SubSub 插补公共()余数X = 余数X + x终点余数Y = 余数Y + y终点余数Z = 余数Z + z终点插补X插补Y插补Z插补记录= 插补记录+ 1End SubSub 插补()Dim c As Integer插补记录= 0: 余数X = 0: 余数Y = 0: 余数Z = 0: 划轮廓线PSet (z原点, x原点), vbRedSelect Case 象限标志Case 1: '第一象限插补Do Until 插补记录= Q插补公共Line -Step(z步长×标志Z, x步长×标志X), vbRedLoopCase 2: '第二象限插补c = x终点: x终点= z终点: z终点= -cc = x步长: x步长= z步长: z步长= -cDo Until 插补记录= Q插补公共Line -Step(x步长×标志X, z步长×标志Z), vbRed LoopCase 3: '第三象限插补x终点= -x终点: z终点= -z终点x步长= -x步长: z步长= -z步长Do Until 插补记录= Q插补公共Line -Step(z步长×标志Z, x步长×标志X), vbRed LoopCase 4: '第四象限插补c = x终点: x终点= -z终点: z终点= cc = x步长: x步长= -z步长: z步长= cDo Until 插补记录= Q插补公共Line -Step(x步长×标志X, z步长×标志Z), vbRed LoopEnd SelectEnd Sub。
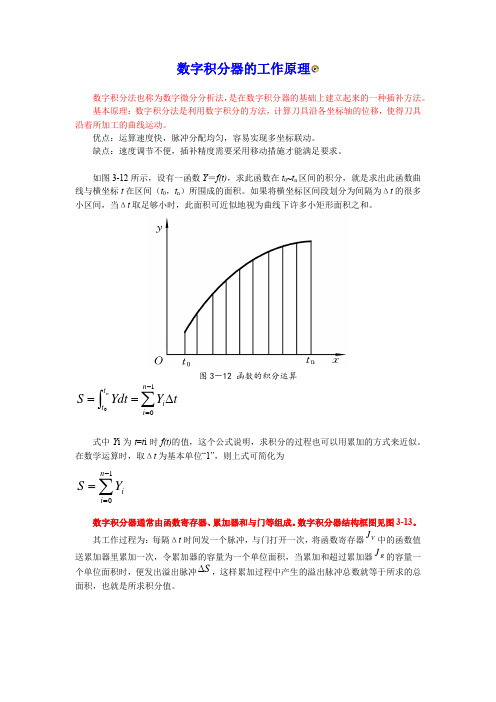
数字积分器的工作原理数字积分法也称为数字微分分析法,是在数字积分器的基础上建立起来的一种插补方法。
基本原理:数字积分法是利用数字积分的方法,计算刀具沿各坐标轴的位移,使得刀具沿着所加工的曲线运动。
优点:运算速度快,脉冲分配均匀,容易实现多坐标联动。
缺点:速度调节不便,插补精度需要采用移动措施才能满足要求。
如图3-12所示,设有一函数Y =f(t),求此函数在t 0~t n 区间的积分,就是求出此函数曲线与横坐标t 在区间(t 0,t n )所围成的面积。
如果将横坐标区间段划分为间隔为Δt 的很多小区间,当Δt 取足够小时,此面积可近似地视为曲线下许多小矩形面积之和。
图3-12 函数的积分运算式中Y i 为t =t i 时f(t)的值,这个公式说明,求积分的过程也可以用累加的方式来近似。
在数学运算时,取Δt 为基本单位“1”,则上式可简化为数字积分器通常由函数寄存器、累加器和与门等组成。
数字积分器结构框图见图3-13。
其工作过程为:每隔Δt 时间发一个脉冲,与门打开一次,将函数寄存器中的函数值送累加器里累加一次,令累加器的容量为一个单位面积,当累加和超过累加器的容量一个单位面积时,便发出溢出脉冲,这样累加过程中产生的溢出脉冲总数就等于所求的总面积,也就是所求积分值。
V J R J S ∆∑⎰-=∆==100n i i t t t Y Ydt S n ∑-==10n i iY S图3-13 积分运算原理图如果S代表位移,y代表速度,则位移可表示为速度值的累加运算。
若要产生直线OE,其起点为坐标原点O,终点坐标为E(7,4)。
设寄存器和累加器容量为1,将X e=7,Y e=4分别分成8段,每一段分别为7/8,4/8,将其存入X和Y函数寄存器中。
第一个时钟脉冲来到时,累加器里的值分别为7/8,4/8,因不大于累加器容量,没有溢出脉冲。
第二个时钟脉冲来到时,X累加器累加结果为7/8+7/8=1+6/8,因累加器容量为1,满1就溢出一个脉冲,则往X方向发出一进给脉冲,余下的6/8仍寄存在累加器里,累加器又称余数寄存器。

数控原理与系统课程设计课题名称:数字积分插补法直线插补专业:班级:姓名:指导老师:数控原理与系统课程设计任务书班级姓名学号课程设计的目的1)了解连续轨迹控制数控系统的组成原理。
2) 掌握数字积分插补的基本原理。
3)掌握数字积分插补的软件实现方法。
二、课程设计的任务数字积分法又称数字微分分析法DDA(Digital Differential Analyzer)。
数字积分法具有运算速度快、脉冲分配均匀、易于实现多坐标联动及描绘平面各种函数曲线的特点,应用比较广泛。
其缺点是速度调节不便,插补精度需要采取一定措施才能满足要求。
由于计算机有较强的计算功能和灵活性,采用软件插补时,上述缺点易于克服。
本次课程设计具体要求如下:1)数字积分插补法基本原理2)数字积分插补法插补软件流程图3)算法描述(逐点比较法算法在VB中的具体实现)4)编写算法程序清单5)软件运行仿真效果二、课程设计报告要求1)按课程设计任务5点要求为标题,编写课程设计报告,最后加一点:此次课程设计小结(包括设计过程中所碰到的问题、解决办法以及有关设计体会等)。
2)字数在3000字左右。
3)仿真软件一份。
三、学生分组数控原理与系统课程设计说明书一、数字积分法直线插补的基本原理数字积分法是利用数字积分的方法,计算刀具沿各坐标轴的位移,使得刀具沿着所加工的轮廓曲线运动利用数字积分原理构成的插补装置称为数字积分器,又称数字微分分析器(Digital Differential Analyzer ),简称DDA 。
数字积分器插补的最大优点在于容易实现多坐标轴的联动插补、能够描述空间直线及平面各种函数曲线等。
因此,数字积分法插补在轮廓数控系统中得到广泛的应用。
从几何角度来看,积分运算就是求出函数Y = f (t )曲线与横轴所围成的面积,从t =t 0到t n 时刻,函数Y= f (t )的积分值可表述为⎰⎰==n n tt t t dt )t (Ydt S 00f 如果进一步将t ∈[t 0,t n ]的时间区划分为若干个等间隔Δt 的小区间,当Δt 足够小时,函数Y 的积分可用下式近似表示t Y Ydt S n i i t t n ∆∑⎰-=≈=100在几何上就是用一系列的小矩形面积之和来近似表示函数f (t )以下的积分面积。
数字积分法第二象限直线插补程序设计数字积分法是利用数字积分的方法,计算刀具沿各坐标轴的位移,使得刀具沿着所加工的轮廓曲线运动利用数字积分原理构成的插补装置称为数字积分器,又称数字微分分析器(Digital Differential Analyzer),简称DDA。
数字积分器插补的最大优点在于容易实现多坐标轴的联动插补、能够描述空间直线及平面各种函数曲线等。
因此,数字积分法插补在轮廓数控系统中得到广泛的应用。
具体设计内容如以下:……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………目录一、课程设计目的 (1)二、课程设计题目描述和要求 (1)三、课程设计报告内容 (1)数字积分法直线插补的基本原理 (2)从几何角度来看积分运算 (2)数字积分法在轮廓插补中的具体应用(数字积分法直线插补)3 插补终点判别的具体实现 (4)插补器的组成 (5)数字积分法稳速控制 (5)提高插补精度的措施 (6)减少误差的方法 (6)数字积分法直线插补框图 (7)数字积分法直线(第二象限)插补程序流程图 (7)四结论 (8)五结束语 (8)参考书目 (10)附录数字积分法直线插补程序清单(第二象限) (11)一、课程设计目的1)了解连续轨迹控制数控系统的组成原理。
dda数字积分法数字积分法(Digital Differential Analyzer,简称DDA)是一种常见的计算机图形学算法,用于绘制直线和曲线。
它通过离散化空间,将连续的线段或曲线分割成若干离散的像素点,从而实现在屏幕上绘制图形的目的。
DDA算法是一种简单而有效的算法,它使用了数学上的差分思想,通过计算直线或曲线的斜率,按照相应的步长在屏幕上绘制出线段或曲线。
在这个过程中,DDA算法仅需进行一次斜率计算和一次像素绘制操作,因此效率较高。
此外,DDA 算法的原理也较为直观,易于理解和实现。
在DDA算法中,首先需要确定直线(或曲线)的起点和终点坐标,然后计算出斜率。
接着,根据斜率选择适当的步长,并在屏幕上按照步长绘制出像素点。
具体的实现步骤如下:1. 输入直线(或曲线)的起点和终点坐标。
2. 计算直线(或曲线)的斜率。
如果是直线,可以使用斜率公式: K = (y2 - y1) / (x2 - x1)。
如果是曲线,可以通过给定函数获取斜率。
3. 确定适当的步长(step),一般可以选择x轴或y轴的最大差值作为步长。
例如,如果x轴的最大差值大于y轴的最大差值,则可以选择x轴差值作为步长。
4. 根据所选择的步长计算出像素点的数量,例如,如果步长是1,则需要+1个像素点。
5. 通过逐步增加步长和计算出相应的像素点坐标,最终绘制出线段或曲线。
为了更好地理解DDA算法的原理和实现,下面将详细介绍一种常见的直线绘制实现方法。
```pythondef dda_line(x1, y1, x2, y2):dx = abs(x2 - x1)dy = abs(y2 - y1)# 确定适当的步长if dx > dy:step = dxelse:step = dy# 计算每一步的增量x_increment = dx / stepy_increment = dy / step# 初始化起点坐标x = x1y = y1# 绘制起点像素点plot_pixel(round(x), round(y))# 迭代绘制每一步for i in range(step):x += x_incrementy += y_increment# 绘制像素点plot_pixel(round(x), round(y))```在以上代码中,plot_pixel函数用于绘制像素点,它可以根据具体的绘图环境进行相应的变换和操作。