初三数学暑假衔接班讲义(好)

第一讲 一元二次方程的解法（一）【基础知识精讲】1．一元二次方程的定义：只含有一个未知数整式方程，并且都可以化为ax 2＋bx+c=0 (a 、b 、c 为常数，a≠0）的形式，这样的方程叫做一元二次方程.注意： 满足是一元二次方程的条件有:(1）必须是一个整式方程;(2）只含有一个未知数；（3）未知数的最高次数是2.(三个条件缺一不可）2．一元二次方程的一般形式:一元二次方程的一般式是ax 2＋bx+c=0 (a 、b 、c 为常数，a≠0）。

其中ax 2是二次项， a 是二次项系数；bx 是一次项，b 是一次项系数；c 是常数项。

3．一元二次方程的解法：⑴ 直接开平方法：如果方程 （x+m ）2= n (n≥0)，那么就可以用两边开平方来求出方程的解. (2） 配方法：配方法是一种以配方为手段,以开平方为基础的一种解一元二次方程的方法．用配方法解一元二次方程：ax 2＋bx+c=0 (a ≠0）的一般步骤是: ① 化二次项系数为1，即方程两边同除以二次项系数;② 移项，即使方程的左边为二次项和一次项，右边为常数项; ③ 配方，即方程两边都加上一次项系数的绝对值一半的平方; ④ 化原方程为（x+m)2=n 的形式;⑤ 如果n≥0就可以用两边开平方来求出方程的解；如果n ＜0，则原方程无解．注意：①方程两边绝不能随便约去含有未知数的代数式．如－2（x ＋4）2=3（x ＋4）中，不能随便约去（x ＋4）.②解一元二次方程时一般不使用配方法（除特别要求外)但又必须熟练掌握,解一元二次方程的一般顺序是：开平方法→因式分解法→公式法．【例题巧解点拨】（一）一元二次方程的定义：例1:1、方程①13122=-x x ②05222=+-y xy x ③0172=+x ④022=y 中一元二次方程是 。

A. ①和②；B.②和③ ；C. ③和④；D. ①和③2、要使方程（a-3）x 2+（b+1)x+c=0是关于x 的一元二次方程，则__________。

目录入门检测:1.一次函数21y x =-的图象与x 轴的交点坐标为 ，与y 轴的交点坐标为 ．<2分钟>【答案】(1,02)，(0,1-)2. 已知一次函数y=kx+b ，y 随着x 的增大而减小，且kb ＞0，则这个函数的大致图象是( )<2分钟>A ．B ．C ．D ．【答案】B3. 将正比例函数y=3x 的图象向下平移4个单位长度后，所得函数图象的解析式为（ ）． <2分钟>A ．34y x =+B ．34y x =-C ．3(4)y x =+D ． 3(4)y x =-【答案】B4. 如图，直线AB 与x 轴交于点A （1，0），与y 轴交于点B （0，－2）. （1）求直线AB 的解析式；（2）若点C 是第一象限内的直线上的一个点，且△BOC 的面积为2，求点C 的坐标. <5分钟>【答案】解：（1）设直线AB 的解析式为)0(≠+=k b kx y , ∵直线AB 经过点A （1，0），点B （0，－2），∴0,2,k b b +=⎧⎨=-⎩解得2,2.k b =⎧⎨=-⎩∴直线AB 的解析式为22-=x y .(2) ∵△BOC 的面积为2，过点C 作CD ⊥y 轴于点D ，∴CD=2.又∵点C 在第一象限内，∴点C 的横坐标是2. 代入22-=x y ，得到点C 的纵坐标是2. ∴点C 的坐标是（2，2）.5. 已知等腰三角形周长为12，其底边长为y ，腰长为x. （1）写出y 关于x 的函数解析式及自变量x 的取值范围；（2）在给出的平面直角坐标系中，画出（1）中函数的图象. <5分钟>【答案】解：(1)依题意212y x +=，212y x ∴=-+.x ，y 是三角形的边，故有002x y x y >⎧⎪>⎨⎪>⎩，将212y x =-+代入，解不等式组得36x <<.(2)-2 -1 -7-6 -5-4-3 -3 -4 -5 -6 -7 12 3 4 5 6 7-1 -2 76 5 4 3 2 1 o yx-2-1-7-6-5-4-3-3-4-5-6-71234567-1-27654321oyx第一讲 二次函数的概念与解析式1.1二次函数的定义及图像 二次函数的定义一般地，形如2(,,0)y axbx c a b c a =++≠是常数，的函数，叫做二次函数，其中，x 是自变量，,,a b c 分别是二次项系数、一次项系数、常数项．【例1】已知函数y=（m+2）x 2m m+是关于x 的二次函数，则满足条件的m 值为______．【答案】m=1【练习1.1】若y=（m －3）232m m x -+是二次函数，求m 的值．【答案】m=0【例2】若y=（k －3）22k x -+x 2－x+1是二次函数，求常数k 的值．【答案】分情况讨论：当k －3=0，即k=3时，y=x 2－x+1是二次函数；当k 2－2=2且k －3+1≠0，即k=－2时，y=－4x 2－x+1是二次函数；当k 2－2=1时，即k=±3时，y=x 2+（3－4）x+1，或y=x 2－（3+4）x+1均是二次函数，还有k 2－2=0时综合上知k=3或－2或±3或±2【练习2.1】若y=（k －2）22k x -+4x 2－x+1是二次函数，求常数k 的值．【答案】21.2 二次函数的性质 与a 有关的性质一函数形式：2(0)y ax a =≠开口：0a >，开口向上；0a <,开口向下.a 相同⇔抛物线的形状大小相同.a越大开口越小，a越小开口越大.对称轴：y 轴（0x =）顶点：原点（0,0）【例3】二次函数y ＝ax 2的图象大致如下，请将图中抛物线字母的序号填入括号内．(1)y ＝2x 2如图( ) ； (2)221x y =如图( )； (3)y ＝－x 2如图( )； (4)231x y -=如图( )；(5)291x y =如图( )；(6)291x y -=如图( )．【答案】(1)D ，(2)C ，(3)A ，(4)B ，(5)F ，(6)E ．【练习3.1】若函数y ＝226a a ax －－是二次函数且图象开口向上，则a ＝( ) A ．－2 B ．4 C ．4或－2 D ．4或3【答案】B⏹ 与a 有关的性质二【例4】已知a<－1，点（a －1，y 1），（a ，y 2），（a+1，y 3）都在函数y=x 2的图象上，则（） A ．y 1<y 2<y 3 B ．y 1<y 3<y 2 C ．y 3<y 2<y 1 D ．y 2<y 1<y 3【答案】C【练习4.1】若二次函数223y x =-的图象上有两个点(3,)A m -、(2,)B n ，则m ___n （填“<”或“=”或“>”）【答案】>⏹ 与a 、b 有关的性质对称轴在y 轴左侧，,a b 同号；对称轴在y 轴右侧，,a b 异号.（左同右异） 对称轴在y 轴上，b=0.【例5】判断下列二次函数的对称轴的位置 (1)y ＝x 2＋6x ＋10 (2)y ＝3x 2－2x (3)y ＝100－5x 2 (4)y ＝(x －2)(2x ＋1)(5)y ＝ax 2－6bx ＋10（a<0,b<0）【答案】左，右，0，右，右【练习5.1】已知二次函数2y ax bx c =++ (a ≠0）的图象如右图所示，则下列结论：①a 、b 同号；②当x =1和x =3时，函数值相等；③4a +b =0；④当y =－2时，x 的值只能取0．其中正确的个数是（）A ．l 个B ．2个C ．3个D ．4个【答案】B与c 有关的性质抛物线与y 轴正半轴相交，0c >；负半轴相交，0c <.抛物线经过原点，c=0【例6】判断下列二次函数与y 轴的交点的位置 (1)y ＝2x 2＋3x ＋10 (2)y ＝－3x 2－2x －3 (3)y ＝100x －5x 2(4)y ＝(x －3)(2x ＋1) (5)y ＝x 2－6x ＋a 2+2a+3【答案】正，负，原点，负，正.【练习6.2】已知二次函数2y ax bx c =++（0a ≠）的图象如图所示，有下列结论：①abc>0；②a+b+c>0；③a-b+c<0；其中正确的结论有（ ）A ．0个B ．1个C ．2个D ．3个【答案】C1.3二次函数的解析式的求法一般式【例7】已知抛物线c bx x y ++=2经过点（1，-4）和（-1，2）.求抛物线解析式.【答案】解：设抛物线解析式为：由题意知：⎩⎨⎧=--=+15b c b c解得：⎩⎨⎧-=-=32b c∴抛物线解析式为232--=x x y【练习7.1】已知：如图，二次函数22y axbx =+-的图象经过A 、B 两点，求出这个二次函数解析式.【答案】解：（1）由图可知A （－1，－1），B （1，1） 依题意，得21,21a b a b --=-⎧⎨+-=⎩解得2,1.a b =⎧⎨=⎩∴ y ＝2x 2＋x －2．顶点式【例8】以直线1x =为对称轴的抛物线过点A （3，0）和点B(0，3)，求此抛物线的解析式.【答案】解：设抛物线的解析式为2(1)y a x b =-+， 抛物线过点A （3，0）和B(0，3). ∴40,3.a b a b +=⎧⎨+=⎩解得1,4.a b =-⎧⎨=⎩∴抛物线的解析式为223y x x =-++.【练习8.1】已知二次函数的图象过坐标原点，它的顶点坐标是（1，－2），求这个二次函数的关系式．【答案】解：设这个二次函数的关系式为2)1(2--=x ay得：2)10(02--=a 解得：2=a∴这个二次函数的关系式是2)1(22--=x y ， 即224.y x x =-双根式【例9】已知抛物线与x 轴相交于两点A(1，0)，B(-3，0)，与y 轴相交于点C(0，3)． (1)求此抛物线的函数表达式； (2)如果点3,2D m ⎛⎫⎪⎝⎭是抛物线上的一点，求△ABD 的面积．【答案】解：(1) ∵抛物线与y 轴相交于点C(0，3),∴设抛物线的解析式为23y ax bx =++. ∵抛物线与x 轴相交于两点(1,0),(3,0)A B -， ∴30,9330.a b a b ++=⎧⎨-+=⎩解得：1,2.a b =-⎧⎨=-⎩ ∴抛物线的函数表达式为：232y x x =-+-. （2）∵点3(,)2D m 是抛物线上一点，∴2(23339)224m =-⨯+=--. ∴119942242ABD D S AB y ∆==⨯⨯=.【练习9.1】已知抛物线过点A (2,0),B (－1,0),与y 轴交于点C ,且OC ＝2.则这条抛物线的解析式是（ ）A.22y x x =--B.22y x x =-++C.22y x x =--或22y x x =-++D.22y x x =---或22y x x =++【答案】C1.4二次函数与图形变换 ⏹ 平移【例10】将函数234y x x =+-向左平移3个单位，向下平移2个单位后的解析式为．【答案】276y x x =++【练习10.1】将抛物线25y x =先向左平移2个单位，再向上平移3个单位后得到新的抛物线，则新抛物线的表达式是（ ） A ．25(2)3y x =++B ．25(2)3y x =-+C ．25(2)3y x =--D ．25(2)3y x =+-【答案】A【练习10.2】把抛物线y ＝－x 2＋4x －3先向左平移3个单位，再向下平移2个单位，则变换后的抛物线解析式是( ) A ．y ＝－(x ＋3)2－2 B ．y ＝－(x ＋1)2－1 C ．y ＝－x 2＋x －5D ．前三个答案都不正确【答案】B⏹ 对称【例11】抛物线234y x x =+-关于x 轴对称的图像解析式为，关于y 轴对称的图像解析式为，关于原点对称的图像解析式为.【答案】234y x x =--+；234y x x =--；234y x x =-++【练习11.1】某抛物线先沿x 轴翻折，再沿y 轴翻折得到新的解析式为223y x x =+，则原抛物线解析式为.【答案】223y x x =-+ 旋转【例12】填空(1)将抛物线21y x =+绕原点O 旋转180°，则旋转后抛物线的解析式为. (2)将抛物线223y x x =++绕点（1,1）旋转180°，则旋转后的抛物线解析式为.【答案】（1）21y x =--（2）269y x x =-+-【练习12.1】将抛物线 224=+y x 绕原点O 旋转180°，则旋转后的抛物线的解析式为（ ）A ． 22=-y xB ． 224=-+y xC ． 224=--y xD ． 224=-y x【答案】C课后作业:1. 把抛物线2=+1y x 向右平移3个单位，再向下平移2个单位，得到抛物线（ ） A ．()231y x =+- B ．()233y x =++ C ．()231y x =-- D ．()233y x =-+【答案】C2.二次函数2y ax bx c =++的图象如图所示，则下列结论中错误．．的是（ ） A ．函数有最小值 B ．当－1 <x < 2时，0y > C ．0a b c ++< D ．当12x <，y 随x 的增大而减小【答案】B3.已知抛物线y =x 2－4x +5，求出它的对称轴和顶点坐标.【答案】解：y =x 2－4x +5 = x 2－4x +4+1 =(x －2)2+1.∴抛物线的对称轴为x =2.顶点坐标为（2，1）.4. 抛物线22y x =平移后经过点(0,3)A ，(2,3)B ，求平移后的抛物线的表达式．【答案】解：设平移后抛物线的表达式为22y x bx c =++．∵平移后的抛物线经过点(0,3)A ，(2,3)B ，∴3,382.c b c =⎧⎨=++⎩解得4,3.b c =-⎧⎨=⎩所以平移后抛物线的表达式为2243y x x =-+．解二：∵平移后的抛物线经过点(0,3)A ，(2,3)B ， ∴平移后的抛物线的对称轴为直线1x =. ∴设平移后抛物线的表达式为()221y x k=-+．∴()23221k=⨯-+．∴1k =．所以平移后抛物线的表达式为()2211y x =-+．5.已知：二次函数2y ax bx c =++(0)a ≠中的x y ，满足下表：（1）的值为 ； （2）若1()A p y ，，2(1)B p y +，两点都在该函数的图象上，且0p <，试比较1y 与2y的大小.【答案】解：（1）m = 0 . （2）0p <，11p p ∴<+<，又因为抛物开口向上，对称轴为1x =， ∴12y y >.6.已知直线y=mx+n 经过抛物线y=ax2+bx+c 的顶点P(1，7)，与抛物线的另一个交点为M （0，6），求直线和抛物线的解析式【答案】解：（1）∵ 直线y mx n =+经过点P （1，7）、M （0，6），∴7,6.m n n +=⎧⎨=⎩解得 1,6.m n =⎧⎨=⎩∴ 直线的解析式为6y x =+． ∵ 抛物线2y ax bx c=++的顶点为P （1，7），∴ 2(1)7y a x =-+．∵ 抛物线经过点M （0，6）， ∴2(01)76a -+=．解得1a =-．∴ 抛物线的解析式为226y x x =-++．7.抛物线2y x bx c =++（b ，c 均为常数）与x 轴交于(1,0),A B 两点，与y 轴交于点(0,3)C ．．（1）求该抛物线对应的函数表达式；（2）若P 是抛物线上一点，且点P 到抛物线的对称轴的距离为3，请直接写出点P 的坐标．【答案】解:(1) ∵抛物线2y x bx c =++与y 轴交于点(0,3)C , ∴c=3 .∴23y x bx =++.又∵抛物线2y x bx c =++与x 轴交于点(1,0)A , ∴b=-4 .∴243y x x =-+. （2）点P 的坐标为(5,8)或(1,8)-．入门检测:1. 下列各式中，y 是x 的二次函数的个数为( )①y ＝2x 2＋2x ＋5；②y ＝－5＋8x －x 2；③y ＝(3x ＋2)(4x －3)－12x 2；④y ＝ax 2＋bx ＋c ；⑤y ＝mx 2＋x ；⑥y ＝bx 2＋1(b 为常数，b ≠0)．<1分钟>A ．3B ．4C ．5D ．6【答案】A2. 已知二次函数,2c bx ax y ++=且0,0>+-<c b a a ，则一定有（）<2分钟> A ．042>-ac b B ．042=-ac b C ．042<-ac b D ．042≤-ac b【答案】A3．在同一直角坐标系中，一次函数y =ax +c 和二次函数y =ax 2+c 的图象为( ) <2分钟>【答案】B4. 抛物线2y x bx c =++图象向右平移2个单位再向下平移3个单位，所得图象的解析式为223y x x =--，则b 、c 的值为（）<2分钟> A .b ＝2，c ＝2 B.b ＝2，c ＝0 C .b ＝－2，c ＝－1 D.b ＝－3，c ＝2 【答案】B5．将抛物线221216y x x =-+绕它的顶点旋转180°，所得抛物线的解析式是（）．<2分钟> A ．221216y x x =--+ B ．221216y x x =-+- C ．221219y x x =-+- D ．221220y x x =-+-【答案】D6．抛物线2y x bx c =-++上部分点的横坐标x ，纵坐标y 的对应值如下表：x… 2-1-0 1 2 … y…4664…从上表可知，下列说法正确的个数是（）<4分钟>①抛物线与x 轴的一个交点为(20)-，②抛物线与y 轴的交点为(06)， ③抛物线的对称轴是：1x = ④在对称轴左侧y 随x 增大而增大 A ．1 B ．2 C ．3 D ．4 【答案】C7．若二次函数52++=bx x y 配方后为k x y +-=2)2(则b 、k 的值分别为（）<1分钟> A ．0，5 B ．0，1 C ．—4，5 D ．—4，1 【答案】D8．由二次函数y ＝－x 2＋2x 可知（）<2分钟>A ．其图象的开口向上B ．其图象的对称轴为x ＝1C ．其最大值为－1D ．其图象的顶点坐标为（－1，1） 【答案】B。

三角形一边的平行线是九年级数学上学期第一章第二节的内容，本讲主要讲解三角形一边平行线性质定理及推论，重点是掌握该定理及其推论，分清该定理及其推论之间的区别和联系，难点是理解该定理和推论的推导过程中所蕴含的分类讨论思想和转化思想，并认识“A”字型和“X ”字形这两个基本图形，为后面学习相似三角形奠定基础．1、三角形一边的平行线性质定理平行于三角形一边的直线截其他两边所在的直线，截得的对应线段成比例．如图，已知ABC∆，直线l // BC，且与AB 、AC 所在直线交于点D和点E，那么AD AEDB EC=．三角形一边的平行线（一）内容分析知识结构模块一：三角形一边的平行线性质定理知识精讲lAB CD EAB CD E AB CDEll2 / 11ABCDEF AB CD EFO ABCE D ABC【例1】 如图，在ABC ∆中，10AB =，8AC =，点D 在直线AB 上，过点D 作DE // BC交直线AC 与点E ．如果4BD =，求AE 的长．【例2】 如图，在ABC ∆中，AB AC >，AD BC ⊥于点D ，点F 是BC 中点，过点F 作BC 的垂线交AB 于点E ，:3:2BD DC =，则:BE EA =．【例3】 如图，已知AB // CD // EF ，14OA =，16AC =，8CE =，12BD =，求OB 、DF 的长．【例4】 如图，已知ABC ∆是边长为2的等边三角形，DE // BC ，:3:4ECD BCD S S ∆∆=，求EC 的长．例题解析ACBDENM ABCD E FGA BCD EF【例5】 如图，P 为平行四边形ABCD 对角线BD 上任意一点．求证：PQ PI PR PS =．【例6】 如图，在平行四边形ABCD 中，CD 的延长线上有一点E ，BE 交AC 于点F ，交AD 于点G ． 求证：2BF FG EF =．【例7】 如图，点C 在线段AB 上，AMC ∆和CBN ∆都是等边三角形．求证：（1）MD AM DC CN=； （2）MD EB ME DC =．【例8】 如图，ABC ∆的面积是10，点D 、E 、F （与A 、B 、C 是不同的点）分别位于AB 、BC 、CA 各边上，而且2AD =，3DB =，如果ABE ∆的面积和四边形DBEF 的面积相等，求ABE ∆的面积．PQR SABCD I4 / 11ABC DP【例9】 如图，在ABC ∆中，6BC =，42AC =，45C ∠=︒，在BC 边上有一动点P ，过P 作PC // AB 与AC 相交于于点D ，联结AP ，设BP x =，APD ∆的面积为y ． （1）求y 与x 之间的函数关系式，并指出自变量x 的取值范围； （2）P 点是否存在这样的位置，使APD ∆的面积是APB ∆的面积的23？若存在，求出BP 的长；若不存在，请说明理由．1、 三角形一边的平行线性质定理推论平行于三角形一边的直线截其他两边所在的直线，截得的三角形的三边与原三角形的三边对应成比例．如图，点D 、E 分别在ABC ∆的边AB 、AC 上，DE // BC ，那么DE AD AEBC AB AC ==． 2、 三角形的重心定义：三角形三条中线交于一点，三条中线交点叫三角形的重心．性质：三角形重心到一个顶点的距离，等于它到这个顶点对边中点的距离的两倍．模块二：三角形一边的平行线性质定理推论知识精讲例题解析ABCD EBAC ABC DE FADCBEFa Nb Qxc PM xNa Qcb P M cNx Qa b P M c NbQa x PM 【例10】 如图，一根直立于水平地面的木杆AB 在灯光下形成影子，当木杆绕点A 按逆时针反向旋转直至到达地面时，影子的长度发生变化.设AB 垂直于地面时的影子为AC （假定AC AB >），影子的最大值为m ，最小值为n ，有下列结论：○1m AC >； ○2m AC =；○3n AB =；○4影子的长度先增大后减小；其中正确的序号是______．【例11】 已知：MN // PQ ，a b ≠，c x ≠，则满足关系式bcx a=的图形是（ ）A ．B ．C ．D ．【例12】 如图，ABC ∆中，DE // BC ，3AE =，4DE =，2DF =，5CF =，求EC 的长．【例13】 如图，在平行四边形ABCD 中，点E 在边DC 上，若:1:2DE EC =，则:BF BE =．6 / 11ABCGH ABCDE FABC DEFGABCDE FG【例14】 如图，在ABC ∆中，6BC =，G 是ABC ∆的重心，过G 作边BC 的平行线交AC于点H ，求GH 的长．【例15】 如图，已知AB // CD // EF ．AB m =，CD n =，求EF 的长（用m 、n 的代数式表示）．【例16】 如图，E 为平行四边形ABCD 的对角线AC 上一点，13AE EC =，BE 的延长线交CD 的延长线于点G ，交AD 于点F ，求:BF FG 的值．【例17】 如图，1l //2l ，:2:5AF FB =，:4:1BC CD =，求:AE EC 的值．A DB CEFAB CD EGOA BCDE【例18】 如图，在梯形ABCD 中，AD // BC ，对角线AC 、BD 交于点O ，点E 在AB 上，且EO // BC ，已知3AD =，6BC =．求EO 的长．【例19】 如图，在梯形ABCD 中，AD // BC ，3AD =，5BC =，E 、F 是两腰上的点，且EF // AD ，:1:2AE EB =，求EF 的长．【例20】 如图，在ABC ∆中，D 是BC 边上的一点，:3:1BD DC =，G 为AD 的中点，联结BG 并延长AC 交于E ，求:EG GB 的值．【例21】 已知点D 是ABC ∆的BC 边上的一点，13CD BC =，E 是AD 的中点，BE 的延长线交AC 于F ，求:AF AC 的值．8 / 11A B CDEF AB CDEFA DB CEF GABCD 【例22】 如图，路灯A 的高度为7米，在距离路灯正下方B 点20米处有一墙壁CD ，CD BD ⊥，如果身高为1.6米的学生EF 站立在线段BD 上（EF BD ⊥，垂足为F ，EF CD <），他的影子的总长度为3米，求该学生到路灯正下方B 点的距离FB 的长．【例23】 如图，平行四边形ABCD 中，点E 、F 分别在AB 、AD 上，EF 交AC 于点G ，若:2:3AE EB =，:1:2AF AD =，求:AG AC 的值．【例24】 如图，在ABC ∆中，设D 、E 是AB 、AC 上的两点，且BD CE =，延长DE交BC 的延长线于点F ，:3:5AB AC =，12cm EF =，求DF 的长．【例25】 如图，已知ABC ∆中，点D 、E 分别在边AB 、AC 上，且:3:2AD DB =，:1:2AE EC =，直线ED 和CB 的延长线交于点F ，求:FB FC ．ABC D EOABCDEF P【例26】 已知：在ABC ∆中，D 、E 是BC 上的两点，且AD // EG ，EG 交AC 于F ，交BA 的延长线于G ，若2EF EG AD +=． 求证：AD 是ABC ∆的中线．【习题1】如图，P 是ABC ∆的中线AD 上一点，PE // AB ，PF // AC ．求证：BE CF =．【习题2】 如图，在ABC ∆中，DE // BC ，且:2:3AD AB =，求:EO EB 的值．【习题3】 在ABC ∆中，AB BC =，如果中线BM 与高AD 相交于点G ，求AGAD．随堂检测10 / 11A BCD EA BC DEFABD C EF G H【习题4】如图ABC ∆，点D 、E 分别在BC 、AC 上，BE 平分ABC ∠，DE // BA ．如果24CE =，26AE =，45AB =，求DE 和CD 的长．【习题5】如图，梯形ABCD 中，DC // EF // GH // AB ，30AB cm =，10CD cm =，::2:3:4DE EG GA =，求EF 与GH 的长度．【作业1】 如图，AB // EF // CD ，2AB =，8CD =，:1:5AE EC =，求EF 的长度．【作业2】平行四边形ABCD ，E 是AB 的中点，在直线AD 上截取2AF FD =，EF交AC 于G ，求AGGC的值．课后作业ABCD EFADBCEGOAB CDBFDEAB C【作业3】 如图，AB // EF // DC ，已知20AB =，80CD =，求EF 的长．【作业4】如图，在ABC ∆中，D 是边BC 上一点，DF // AB ，DE // CA ．（1）求证：AE CFEB FA =； （2）如果2CF =，5AC =，6AB =，求AE 、DE 的长．【作业5】如图，在平行四边形ABCD 中，E 是AD 上一点，CE 与BD 相交于点O ，CE 与BA 的延长线相交于点G ，已知2DE AE =，10CE =，求GE 和CO 的长．【作业6】 如图，DE // BC ，3ADE S ∆=，18CBD S ∆=，求ABC S ∆．。

第1讲 乘法公式【基础知识回顾】 知识点1 平方公式（1）平方差公式 22()()a b a b a b +-=-；（2）完全平方公式 222()2a b a ab b ±=±+．（3）三数和平方公式2222()2()a b c a b c ab bc ac ++=+++++； 知识点2 立方公式（1）立方和公式 2233()()a b a ab b a b +-+=+；（2）立方差公式 2233()()a b a ab b a b -++=-； （3）两数和立方公式 33223()33a b a a b ab b +=+++；（4）两数差立方公式 33223()33a b a a b ab b -=-+-．【合作探究】探究一 平方公式的应用 【例1】计算：（1）)416)(4(2m m m +-+ （2）)41101251)(2151(22n mn m n m ++-（3）)164)(2)(2(24++-+a a a a （4）22222))(2(y xy x y xy x +-++（5）22)312(+-x x归纳总结：【练习1】计算：2(21)x y ++探究二 立方公式的应用【例2】计算：（1）3(1)x + （2）3(23)x -归纳总结：【练习2】用立方和或立方差公式分解下列各多项式：(1) 38x +(2) 30.12527b -探究三 整体代换【例3】已知13x x +=，求：（1）221x x +；（2）331x x +．归纳总结：【练习3-1】已知2310x x +-=，求：（1）221x x +；（2）331x x -．【练习3-2】已知4a b c ++=，4ab bc ac ++=，求222a b c ++的值．【课后作业】1．不论a ，b 为何实数，22248a b a b +--+的值 （ ）A ．总是正数B ．总是负数C ．可以是零D ．可以是正数也可以是负数2．已知22169x y +=， 7x y -=，那么xy 的值为（ ） A ．120 B ．60 C ．30 D ．153．如果多项式29x mx -+是一个完全平方式，则m 的值是4．如果多项式k x x ++82是一个完全平方式，则k 的值是5．()()22_________a b a b +--=()222__________a b a b +=+-6．已知17x y +=，60xy =，则22x y += 7．填空，使之符合立方和或立方差公式或完全立方公式： （1）3(3)()27x x -=- （2）3(23)()827x x +=+ （3）26(2)()8x x +=+ （4）3(32)()278a a -=-（5）3(2)()x +=； （6）3(23)()x y -=（7）221111()()9432a b a b -=+ （8）2222(2)4(a b c a b c +-=+++ )8．若2210x x +-=，则221x x +=____________；331x x -=____________． 9．已知2310x x -+=，求3313x x ++的值．10．观察下列各式：2(1)(1)1x x x -+=-；23(1)(1)1x x x x -++=-；324(1)(1)1x x x x x -+++=-…..根据上述规律可得：1(1)(...1)n n x x x x --++++=_________________第2讲 因式分解【基础知识回顾】 知识点1 因式分解因式分解是代数式的一种重要的恒等变形，它与整式乘法是相反方向的变形．在分式运算、解方程及各种恒等变形中起着重要的作用． 知识点2 因式分解方法因式分解的方法较多，除了初中课本涉及到的提取公因式法和公式法（平方差公式和完全平方公式）外，还有公式法（立方和、立方差公式）、十字相乘法和分组分解法等等．知识点3 常用的乘法公式：（1）平方差公式： ； （2）完全平方和公式： ； （3）完全平方差公式： ．（4）2()a b c ++=（5）33a b +=(立方和公式) （6）33a b -=(立方差公式)【合作探究】 探究一 公式法【例1】分解因式：(1) 34381a b b - (2) 76a ab -归纳总结：【练习1】把下列各式分解因式： (1) 34xy x +(2) 33n n x x y +-(3) 2232(2)y x x y -+探究二 提取公因式法与分组分解法【例2-1】把22x y ax ay -++分解因式．【例2-2】分解因式：（1）()()255a b a b -+-； （2）32933x x x +++．【例2-3】分解因式： （1）32933x x x +++；（2）222456x xy y x y +--+-．【例2-4】把2222428x xy y z ++-分解因式．【练习2】分解因式（1）27()5()2a b a b +-+-(2)22(67)25x x --探究三 十字相乘法【例3-1】把下列各式因式分解：(1) 276x x -+(2) 21336x x ++ (3) 226x xy y +-归纳总结：【例3-2】把下列各式因式分解：(1) 21252x x --(2) 22568x xy y +-归纳总结：【练习3-1】把下列各式因式分解： (1) 2524x x +-(2) 2215x x -- (3) 222()8()12x x x x +-++探究四 拆、添项法【例4】分解因式3234x x -+归纳总结：【课后作业】1．把下列各式分解因式： (1)327a +(2) 38m -(3)3278x -+(4)3311864p q --(5)3318125x y -(6) 3331121627x y c+2．把下列各式分解因式： (1) 34xy x +(2)33n n x x y +-(3) 2323()a m n a b +-(4) 2232(2)y x x y -+3．把下列各式分解因式： (1) 232x x -+ (2) 23736x x ++(3)21126x x +-(4) 2627x x --(5) 2245m mn n --(6) 2()11()28a b a b -+-+4．把下列各式分解因式： (1) 5431016ax ax ax -+ (2) 2126n n n a a b a b +++- (3)22(2)9x x --(4)42718x x --(5)2673x x --(6) 2282615x xy y +-5．把下列各式分解因式： (1) 233ax ay xy y -+- (2) 328421x x x +-- (3)251526x x xy y -+-(4) 224202536a ab b -+- (5) 22414xy x y +-- (6) 432224a b a b a b ab +--(7)66321x y x --+(8) 2(1)()x x y xy x +-+第3讲 根式与根式的运算【基础知识回顾】知识点1 二次根式的概念0)a ≥的代数式叫做二次根式. 知识点2 二次根式性质(1)2(0)a a =≥(2) ||a =(3)0,0)a b =≥≥(4)0,0)a b =>≥a ==,0,,0.a a a a ≥⎧⎨-<⎩ 【合作探究】探究一 根式的简化【例1-1】将下列式子化为最简二次根式：（1（20)x <．(3) +归纳总结：【练习1-1】 化简下列各式：（10)a ≥；(2)1)x +≥【例1-2】（1(x =-x 的取值范围是 ；（2=成立的条件是（ ） A.2x ≠ B.0x > C.2x > D.02x <<归纳总结：【练习1-2】（1）= ；（2）若b =，求a b +的值．探究三有理化因式和分母有理化【例3-1】．【例3-2】化简：20162017⋅．【例3-3】化简：（1；（21)x<<．【例3-4】已知x y==22353x xy y-+的值．归纳总结：【练习3】（1＝；（2）若x==．【课后作业】1a =-成立的条件是( )A ．0a >B ．0a <C ．0a ≤D ．a 是任意实数2．若3x <|6|x -的值是( )A ．－3B ．3C ．－9D ．93．化简(下列a 的取值范围均使根式有意义)：(1)(2)a(3)(4)+-4．化简：(1) 102m(2)0)x y >>5．设x y ==，求代数式22x xy y x y +++的值．6．设x =，求4221x x x ++-的值．7．化简或计算：(1) 3+÷(2)+(3)-第4讲 分式运算【基础知识回顾】知识点1 分式的意义与性质形如A B 的式子，若B 中含有字母，且0B ≠，则称AB 为分式．当M ≠0时，分式AB 具有下列性质：A A MB B M ⨯=⨯； A A M B B M ÷=÷．知识点2 繁分式像abc d +，2m n p m n p +++这样，分子或分母中又含有分式的分式叫做繁分式．【合作探究】探究一 解分的化简与求值 【例1-1】代数式1111++x 有意义，则x 需要满足的条件是_________.【例1-2】若54(2)2x A Bx x x x +=+++，求常数,A B 的值．归纳总结：【练习1】化简：2112111x x x x x +--++-探究二 列项相消【例2】（1）试证：111(1)1n n n n=-++（其中n是正整数）；（2）计算：111 1223910+++⨯⨯⨯；（3）证明：对任意大于1的正整数n，有1111 2334(1)2n n+++<⨯⨯+．归纳总结：【练习2】（1）证明：1111()(21)(21)22121n n n n=--+-+（其中n是正整数）；（2）证明：对任意大于1的正整数n，有1111 1335(21)(21)2n n+++<⨯⨯-+．探究三分式的应用【例3】设cea=，且e＞1，2c2－5ac＋2a2＝0，求e的值．归纳总结：【练习3】设cea=，且e＞1，3c2－10ac＋3a2＝0，求e的值．探究四多项式除以多项式【例4】计算)3()3(2 4xxx-÷-归纳总结：【练习4】计算（1）)32()2713103(223-+÷-++xxxxx（2）)1()22(232-÷-+xxx【课后作业】1．对任意的正整数n，1(2)n n=+(112n n-+)；2．若223x yx y-=+，则xy＝（）（A）１（B）54（C）45（D）653．正数,x y满足222x y xy-=，求x yx y-+的值．4．计算1111... 12233499100 ++++⨯⨯⨯⨯．5．已知1453,211221923234+--=-+--=xxxBxxxxA，求：22BA÷6．填空：（1）12a=，13b=，则2223352a aba ab b-=+-；（2）若2220x xy y+-=，则22223x xy yx y++=+；7．计算：1111 132435911 ++++⨯⨯⨯⨯．8．试证：对任意的正整数n，有111123234(1)(2)n n n+++⨯⨯⨯⨯++＜14．第5讲绝对值和绝对值不等式的解法【基础知识回顾】知识点1 绝对值的代数意义正数的绝对值是它的本身，负数的绝对值是它的相反数，零的绝对值仍是零．即,0,||0,0,,0.a a a a a a >⎧⎪==⎨⎪-<⎩知识点2 绝对值的几何意义一个数的绝对值，是数轴上表示它的点到原点的距离． 知识点3 两个数的差的绝对值的几何意义b a -表示在数轴上，数a 和数b 之间的距离．【合作探究】探究一 绝对值的性质【例1-1】到数轴原点的距离是2的点表示的数是（ ） A ．±2 B ．2 C ．-2 D ．4【例1-2】已知|x |=5，|y |=2，且xy ＞0，则x -y 的值等于（ ）A ．7或-7B ．7或3C ．3或-3D ．-7或-3【例1-3】已知：abc ≠0，且M =a b c a b c ++，当a ，b ，c 取不同值时，M 有 ____种不同可能．归纳总结：【练习1】已知a b c，，是非零整数，且0a b c ++=，求a b c abca b c abc+++的值探究二 绝对值的应用【例2】若42a b -=-+，则_______a b +=．归纳总结：【练习2-1】练习1：()2120a b ++-=， a =________；b =__________【练习2-2】若7322102m n p ++-+-=，则23_______p n m +=＋．探究三零点分段法去绝对值【例3】化简代数式24 x x++-归纳总结：【练习3】化简代数式122 y x x=-+-探究四绝对值函数【例4-1】画出1y x=-的图像【例4-2】画出122y x x=-+-的图象【例4-3】画出函数223y x x=-++的图像【例4-4】画出函数232y x x=-+的图像归纳总结：探究五解绝对值不等式【例5-1】解不等式1 x<．归纳总结：【练习5-1】解不等式：（1）3x<；（2）3x>（3）2x≤【例5-2】解不等式21 x-<．归纳总结：【练习5-2】解不等式：（1）103x-<；（2）252x->；（3）325x-≤；【例5-3】解不等式组240 5132xx⎧--≤⎪⎨-+>⎪⎩．【练习5-3】解不等式1215x≤-<．【例5-4】解不等式：4321 x x->+归纳总结：【练习5-4】解不等式：431x x -≤+．【例5-5】解不等式：215x x ++-<【练习5-5】解不等式：13x x -+-＞4．1．35-=________；3π-=________；3.1415π-=_____；2．2215x y -+-=，4x =，则y =__________．3．若a a +=，那么a 一定是（ ）A ．正数B ．负数C ．非正数D ．非负数 4．若x x>，那么x 是________数．5．如图，化简22a b b c a c +------=_____________6．已知2(2)210x y -+-=，则2x y +=_______．7．化简12x x +++，并画出12y x x =+++的图象8．化简523x x ++-． 9.画出23y x =+的图像10.画出223y x x =-++的图像1.已知6a <-，化简6( )A. 6a -B. 6a --C. 6a +D. 6a -2.不等式23x +<的解是 ，不等式1211<-x 的解是______________.3.不等式830x -≤的解是______________.4.根据数轴表示,,a b c 三数的点的位置，化简a b a c b c +++--=___ .5.解不等式329x ≤-<6.解不等式124x x ++-<7.解下列关于x 的不等式：1235x ≤-<8.解不等式3412x x->+9．解不等式：122x x x -+-<+第6讲 一元二次方程根与系数的关系【基础知识回顾】知识点1 一元二次方程的根的判断式ab c一元二次方程20 (0)ax bx c a ++=≠，用配方法将其变形为：2224()24b b ac x a a -+= (1) 当240b ac ->时，右端是正数，方程有两个不相等的实数根：2b x a -±=(2) 当240b ac -=时，右端是零．因此，方程有两个相等的实数根：1,22bx a =-(3) 当240b ac -<时，右端是负数．因此，方程没有实数根．由于可以用24b ac -的取值情况来判定一元二次方程的根的情况．因此，把24b ac -叫做一元二次方程20 (0)ax bx c a ++=≠的根的判别式，表示为：24b ac ∆=- 知识点2 一元二次方程的根与系数的关系一元二次方程20 (0)ax bx c a ++=≠的两个根为：22b b x x a a -+--==所以：1222b b bx x a a a -+--+=+=-，12244ac cx x a a⋅====韦达定理：如果一元二次方程20 (0)ax bx c a ++=≠的两个根为12,x x ，那么： 1212,b c x x x x a a +=-=【合作探究】探究一 ∆与根个数之间的关系【例1】不解方程，判断下列方程的实数根的个数：(1) 22310x x -+=(2)24912y y +=(3)25(3)60x x +-=归纳总结：【练习1-1】已知关于x 的一元二次方程2320x x k -+=，根据下列条件，分别求出k 的范围： (1) 方程有两个不相等的实数根； (2) 方程有两个相等的实数根 (3)方程有实数根； (4) 方程无实数根．【练习1-2】已知实数x 、y 满足22210x y xy x y +-+-+=，试求x 、y 的值．探究二 一元二次方程的根与系数的关系【例2-1】若12,x x 是方程2220070x x +-=的两个根，试求下列各式的值：(1) 2212x x +； (2) 1211x x +； (3)12(5)(5)x x --；(4)12||x x -．归纳总结：【练习2】若x 1和x 2分别是一元二次方程2x 2＋5x －3＝0的两根． （1）求| x 1－x 2|的值； （2）求221211x x +的值；（3）x 13＋x 23．【例2-2】已知两个数的和为4，积为－12，求这两个数．【例2-2】关于x 的方程221(1)104x k x k -+++=，根据下列条件，分别求出k 的值．(1) 方程两实根的积为5； (2) 方程的两实根12,x x 满足12||x x =．探究三 一元二次方程的根的范围【例3-1】若关于x 的一元二次方程x 2－x ＋a －4＝0的一根大于零、另一根小于零，求实数a 的取值范围．【例3-2】一元二次方程有两个实根，一个比3大，一个比3小，求的取值范围。

高斯九年级（初三）暑假班（教师版）最新讲义高斯教育九年级（初三）暑假辅导讲义学员姓名：刘小米年级：辅导科目：小学思维学科教师：五块石1 上课时间2019-06-25 14:00-16:00授课主题第10讲_一元二次方程的应用一元二次方程的应用一．列一元二次方程解应用题的一般步骤1．找出题中的等量关系；2．设未知数；3．根据找出的等量关系列出方程；4．解一元二次方程；5．将方程的解代入原方程检验，回到实际问题中检验；6．作答结论．注意：列方程解应用题的关键是将实际问题中内在、本质的联系抽象为数学问题，进而建立方程模型，解决问题．一．考点：一元二次方程的应用．知识图谱错题回顾知识精讲三点剖析二．重难点：列一元二次方程解应用题．三．易错点：建立一元二次方程解决实际问题时一定要注意检验是否符合实际意义．题模一：面积问题例1.1.1某校准备修建一个面积为180平方米的矩形活动场地，它的长比宽多11米，设场地的宽为x 米，则可列方程为（ ）A ．x （x ﹣11）=180B ．2x+2（x ﹣11）=180C ．x （x+11）=180D ．2x+2（x+11）=180【答案】C【解析】设宽为x 米，则长为（x+11）米，根据题意得：x （x+11）=180．例1.1.2如图是一无盖长方体铁盒的平面展开图，若铁盒的容积为3m 3，则根据图中的条件，可列出方程：_____________-．【答案】x （x+1）=3【解析】长方体的高是1，宽x ，长是x+1，根据题意得x （x+1）=3．例1.1.3如图，某中学准备在校园里利用围墙的一段，再砌三面墙，围成一个矩形花园ABCD （围墙MN 最长可利用25m ），现在已备足可以砌50m 长的墙的材料，恰好用完，试求AB 的长，使矩形花园的面积为300m 2．【答案】15米【解析】该题考查的是列方程解应用题． 设m AB x =，则()502m BC x =-．…………1分根据题意可得，()502300x x -=，………… 3分解得：110x =，215x =，…………4分题模精讲当110x=，5010103025BC=--=>，故110x=（不合题意舍去），…………5分答：AB的长为15米．………… 6分题模二：经济问题例1.2.1某种衬衣的价格经过连续两次降价后，由每件150元降至96元，平均每次降价的百分率是（）A．10%B．20%C．30%D．40%【答案】B【解析】设平均每次降价的百分率为x，由题意得150×（1﹣x）2=96，解得：x1=0.2，x2=1.8（不符合题意，舍去）．答：平均每次降价的百分率是20%．故选：B．例1.2.2某商场服装部销售一种名牌衬衫，平均每天可售出40件，每件盈利50元．为了扩大销售，减少库存，商场决定降价销售，经调查，每件降价1元时，平均每天可多卖出2件．（1）若商场要求该服装部每天盈利2400元，尽量减少库存，每件衬衫应降价多少元？（2）试说明每件衬衫降价多少元时，商场服装部每天盈利最多．【答案】（1）每件衬衫应降价20元（2）每件衬衫降价15元时，商场服装部每天盈利最多【解析】（1）设每件衬衫应降价x元，由题意得：（50﹣x）（40+2x）=2400，解得：x1=10，x2=20，因为尽量减少库存，x1=10舍去．答：每件衬衫应降价20元．（2）设每天盈利为W元，则W=（50﹣x）（40+2x）=﹣2（x﹣15）2+2450，当x=15时，W最大为2450．答：每件衬衫降价15元时，商场服装部每天盈利最多．题模三：其他问题例1.3.1有x支球队参加篮球比赛，共比赛了45场，每两队之间都比赛一场，则下列方程中符合题意的是（）A．x（x﹣1）=45B．x（x+1）=45C．x（x﹣1）=45D．x（x+1）=45【答案】A【解析】∵有x支球队参加篮球比赛，每两队之间都比赛一场，∴共比赛场数为x（x﹣1），∴共比赛了45场，∴x（x﹣1）=45，例 1.3.2假如一人患红眼病，经过两轮传染共有144人染上了红眼病，按这样的传播速度，若有两人患了红眼病，经过第一轮传染后患红眼病的人数共有__________人【答案】24【解析】设假如一人患红眼病，第一轮传染给x 人，由题意得1(1)144x x x +++=，解得x=11，故若有两人患病，经过第一轮传染后患病的人数共有2+11+11=24人．随练1.1有一块长方形铁皮，长100cm ，宽50cm ，在它的四周各切去一个同样的正方形，然后将四周突出部分折起，就能制作一个无盖方盒．如果要制作的无盖方盒的底面积为3600cm 2，设铁皮各角应切去的正方形边长为xcm ，则下面所列方程正确的是（ ）A ．4x 2=3600B ．100×50﹣4x 2=3600C ．（100﹣x ）（50﹣x ）=3600D ．（100﹣2x ）（50﹣2x ）=3600【答案】D【解析】设切去的小正方形的边长为x ．根据题意得（100﹣2x ）（50﹣2x ）=3600．随练1.2如图，在一块长为22米、宽为17米的矩形地面上，要修建同样宽的两条互相垂直的道路（两条道路各与矩形的一条边平行），剩余部分种上草坪，使草坪面积为300平方米．若设道路宽为x 米，则根据题意可列出方程为 ．【答案】300【解析】设道路的宽应为x 米，由题意有（22﹣x ）（17﹣x ）=300，随练1.3如图，要建一个面积为40平方米的矩形花园ABCD ，为了节约材料，花园的一边AD 靠着原有的一面墙，墙长为8米（8AD <），另三边用栅栏围成，已知栅栏总长为24米，求花园一边AB 的长．【答案】10米【解析】该题考查的是一元二次方程的应用．设AB 的长度为x 米，则BC 的长度为()242x -米． 随堂练习DC B A 8米根据题意：()24240x x -=．解得：2x =或者10x =，当2x =时，BC 的长度为20，大于8米，不合题意．∴AB 边长为10米．答：AB 的长为10米．随练1.4某县政府2011年投资0.5亿元用于保障性房建设，计划到2013年投资保障性房建设的资金为0.98亿元．如果从2011年到2013年投资此项目资金的年增长率相同，那么年增长率是（ ）A ．30%B ．40%C ．50%D ．60%【答案】B【解析】设这两年中投入资金的平均年增长率是x ，由题意得：0.5（1+x ）2=0.98，解得：x 1=40% x 2=-2.4（不合题意舍去）．答：这两年中投入资金的平均年增长率约是40%．故选：B ．随练1.5山西特产专卖店销售核桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每降低2元，则平均每天的销售可增加20千克，若该专卖店销售这种核桃要想平均每天获利2240元，请回答：（1）每千克核桃应降价多少元？（2）在平均每天获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的几折出售？【答案】（1）4元或6元（2）九折【解析】（1）设每千克核桃应降价x 元． …1分根据题意，得 （60-x -40）（100+2x ×20）=2240． …4分 化简，得 x 2-10x+24=0 解得x 1=4，x 2=6．…6分答：每千克核桃应降价4元或6元． …7分（2）由（1）可知每千克核桃可降价4元或6元．因为要尽可能让利于顾客，所以每千克核桃应降价6元．此时，售价为：60-6=54（元），5460×100%=90%． …9分 答：该店应按原售价的九折出售． …10分随练 1.6参加一次商品交易会的每两家公司之间都签订了一份合同，所有公司共签订了45份合同．设共有x 家公司参加商品交易会，则x 满足的关系式为（ ） A ．x （x+1）=45B ．x （x ﹣1）=45C ．x （x+1）=45D ．x （x ﹣1）=45【答案】B【解析】设有x家公司参加，依题意，得x（x﹣1）=45，故选B．随练1.7有一人患了流感，经过两轮传染后共有64人患了流感．（1）求每轮传染中平均一个人传染了几个人？（2）如果不及时控制，第三轮将又有多少人被传染？【答案】（1）7个人（2）448人【解析】本题考查了一元二次方程的应用，先求出每轮传染中平均每人传染了多少人数是解题关键．（1）设每轮传染中平均每人传染了x人，根据经过两轮传染后共有64人患了流感，可求出x，（2）进而求出第三轮过后，又被感染的人数．（1）设每轮传染中平均每人传染了x人，1+x+x（x+1）=64x=7或x=-9（舍去）．答：每轮传染中平均一个人传染了7个人；（2）64×7=448（人）．答：第三轮将又有448人被传染．自我总结课后作业作业1如图，要利用一面墙（墙长为25米）建羊圈，用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈，求羊圈的边长AB ，BC 各为多少米？【答案】20AB =，20BC = 【解析】本题考查了一元二次方程的应用．解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．设AB 的长度为x ，则BC 的长度为（100-4x ）米；然后根据矩形的面积公式列出方程．根据题意得 （100-4x ）x=400，解得 x 1=20，x 2=5．则100-4x=20或100-4x=80．∵80＞25，∵x 2=5舍去．即AB=20，BC=20．答：羊圈的边长AB ，BC 分别是20米、20米．作业2小萍要在一幅长90厘米，宽40厘米的风景画的四周外围，镶上一条宽度相同的金色纸边，制成一幅挂图，使风景画的面积是整个挂图面积的54%，设金色纸边的宽为x 厘米，根据题意所列方程为（ ）A ．()()904054%9040x x ++⨯=⨯B ．()()90240254%9040x x ++⨯=⨯C ．()()9040254%9040x x ++⨯=⨯D ．()()9024054%9040x x ++⨯=⨯【答案】B【解析】由题意可得，()()90240254%9040x x ++⨯=⨯，故答案为B 选项．作业3为响应市委市政府提出的建设“绿色襄阳”的号召，我市某单位准备将院内一块长30m ，宽20m 的长方形空地，建成一个矩形花园，要求在花园中修两条纵向平行和一条横向弯折的小道，剩余的地方种植花草．如图所示，要使种植花草的面积为532m 2，那么小道进出口的宽度应为____米．（注：所有小道进出口的宽度相等，且每段小道均为平行四边形）【答案】1 【解析】本题考查了一元二次方程的应用，解题的关键是找到正确的等量关系并列出方程． 设小道进出口的宽度为x 米，然后利用其种植花草的面积为532平方米列出方程求解即可． 设小道进出口的宽度为x 米，依题意得（30-2x ）（20-x ）=532．整理，得x2-35x+34=0．解得，x1=1，x2=34．∵34＞20（不合题意，舍去），∵x=1．答：小道进出口的宽度应为1米．作业4一件产品原来每件的成本是100元，在市场售价不变的情况下，由于连续两次降低成本，现在利润每件增加了19元，则平均每次降低成本的（）A．8.5%B．9%C．9.5%D．10%【答案】D【解析】设平均每次降低成本x，根据题意得100﹣100（1﹣x）2=19，即（1﹣x）2=0.81，解得x1=0.1，x2=1.9（舍去），所以平均每次降低成本10%．作业5某商店购进600个旅游纪念品，进价为每个6元，第一周以每个10元的价格售出200个，第二周若按每个10元的价格销售仍可售出200个，但商店为了适当增加销量，决定降价销售（根据市场调查，单价每降低1元，可多售出50个，但售价不得低于进价），单价降低x元销售，销售一周后，商店对剩余旅游纪念品清仓处理，以每个4元的价格全部售出，如果这批旅游纪念品共获利1250元，问第二周每个旅游纪念品的销售价格为多少元？【答案】9【解析】由题意得出：200×（10-6）+（10-x-6）（200+50x）+（4-6）[（600-200）-（200+50x）]=1250，即800+（4-x）（200+50x）-2（200-50x）=1250，整理得：x2-2x+1=0，解得：x1=x2=1，∵10-1=9．答：第二周的销售价格为9元．作业6近年来某市加大了对教育经费的投入，2013年投入2500万元，2015年将投入3600万元，该市投入教育经费的年平均增长率为x，根据题意列方程，则下列方程正确的是（）A．2500x2=3600B．2500（1+x）2=3600C．2500（1+x%）2=3600D．2500（1+x）+2500（1+x）2=3600【答案】B【解析】设该市投入教育经费的年平均增长率为x，根据题意，可列方程：2500（1+x）2=3600，故选：B．作业7某种电脑病毒传播速度非常快，如果一台电脑被感染，经过两轮感染后就会有81台电脑被感染，请你用学过的知识分析，每轮感染中平均每台电脑会感染几台电脑？若病毒得不到有效控制，3轮感染后，被感染的电脑会不会超过700台？【答案】每轮感染中平均每台电脑会感染8台电脑；3轮感染后，被感染的电脑会超过700台【解析】设每轮感染中平均每一台电脑会感染x 台电脑，则()1181x x x +++=，解得18x =，210x =-（舍去）；()()33118729700x +=+=>，故3轮感染后，被感染的电脑会超过700台。

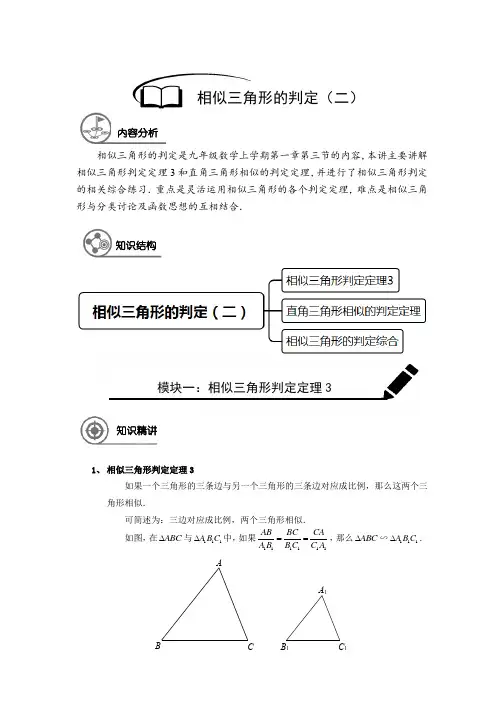
ABCA 1B 1C 1相似三角形的判定是九年级数学上学期第一章第三节的内容，本讲主要讲解相似三角形判定定理3和直角三角形相似的判定定理，并进行了相似三角形判定的相关综合练习．重点是灵活运用相似三角形的各个判定定理，难点是相似三角形与分类讨论及函数思想的互相结合．1、 相似三角形判定定理3如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似．可简述为：三边对应成比例，两个三角形相似．如图，在ABC ∆与111A B C ∆中，如果111111AB BC CAA B B C C A ==，那么ABC ∆∽111A B C ∆．相似三角形的判定（二）内容分析知识结构模块一：相似三角形判定定理3知识精讲2 / 17ABCDEFABCDE F【例1】 根据下列条件判定ABC ∆与DEF ∆是否相似，如果是，那么用符号表示出来．（1）2AB cm =，3BC cm =，4CA cm =，10DE cm =，15EF cm =，20FD cm = （2）1AB cm =，2BC cm =， 1.5CA cm =，6DE cm =，4EF cm =，8FD cm =．【例2】 如图，在边长为1个单位的方格纸上，有ABC ∆与DEF ∆．求证：ABC ∆∽FDE ∆．【例3】 如图，D 、E 、F 分别是ABC ∆的边BC 、CA 、AB 的中点．求证：DEF ∆∽ABC ∆．【例4】 ABC ∆的边长分别为a 、b 、c ，111A B C ∆的边长分别为a 、b 、c ，则ABC∆与111A B C ∆（选填“一定”、“不一定”或“一定不”）相似．例题解析ABCD E FABCDEA BCDE ABCD【例5】 如图，点D 为ABC ∆内一点，点E 为ABC ∆外一点，且满足AB BC ACAD DE AE==． 求证：ABD ∆∽ACE ∆．【例6】 如图，在ABC ∆中，90ABC ∠=︒，30ACB ∠=︒，2AC =，23CD =，4AD =． 求证：ABC ∆∽ACD ∆【例7】 已知：如图，在t R ABC ∆中，90ACB ∠=︒，2AC =，4BC =，点D 在BC 边上，且CAD B ∠=∠． （1）求AD 的长；（2）取AD 、AB 的中点E 、F ，联结CE 、CF 、EF ．求证：CEF ∆∽ADB ∆．【例8】 如图，在梯形ABCD 中，AB // CD ，90A ∠=︒，2AB =，3BC =，1CD =，点E 是AD 的中点．（1）求证：CDE ∆∽EAB ∆；（2）CDE ∆与CEB ∆有可能相似吗？若相似，请证明；若不相似，请说明理由．4 / 171、 直角三角形相似的判定定理如果一个直角三角形的斜边及一条直角边与另一个直角三角形的斜边及一条直角边对应成比例，那么这两个直角三角形相似．可简述为：斜边和直角边对应成比例，两个直角三角形相似．如图，在Rt ABC ∆和111Rt A B C ∆中，如果190C C ∠=∠=︒，1111AB BCA B B C =，那么ABC ∆∽111A B C ∆．【例9】 在Rt ABC ∆和Rt DEF ∆中，90C F ∠=∠=︒．依据下列各组条件判定这两个三角形是否相似，并说明理由． （1）55A ∠=︒，35D ∠=︒；（2）9AC =，12BC =，6DF =，8EF =； （3）3AC =，4BC =，6DF =，8DE =； （4）10AB =，8AC =，15DE =，9EF =．模块二：直角三角形相似的判定定理知识精讲例题解析ABCA 1B 1C 1ABC DA 1B 1C 1D 1AB CDABCD AB CDF G【例10】 如图，在ABC ∆和111A B C ∆中，AD BC ⊥，1111A D B C ⊥，垂足为D 和1D ，且111111AC AB ADAC A B A D ==． 求证：ABC ∆∽111A B C ∆．【例11】 如图，四边形ABCD 中，90BAC ADC ∠=∠=︒，AD a =，BC b =，AC ab求证：DC BC ⊥．【例12】 如图，AB AD ⊥，BD DC ⊥，且2BD AB BC =．求证：ABD DBC ∠=∠．【例13】 如图，在ABC ∆中，CD AB ⊥于D ，DF AC ⊥于F ，DG BC ⊥于G ．求证：CF CA CG CB =．6 / 17ABCDE FA B CDEFMABCD EF【例14】 已知直角三角形斜边上的高为12，并且斜边上的高把斜边分成3:4两段，则斜边上的中线长是．【例15】 如图，直角梯形ABCD 中，90BCD ∠=︒，AD // BC ，BC CD =，E 为梯形内一点，且90BEC ∠=︒．将BEC ∆绕点C 旋转90°使BC 与DC 重合，得到DCF ∆，连接EF 交CD 于点M ．已知5BC =，3CF =，求:DM MC 的值．【例16】 如图，在ABC ∆中，CD AB ⊥于D ，DE AC ⊥于E ，DF BC ⊥于F ，求证：CEF ∆∽CBA ∆．【例17】 在Rt ABC ∆中，90ACB ∠=︒，CD AB ⊥于点D ，E 是AC 边上的一个动点（不与A 、C 重合），CF BE ⊥于点F ，连接DF ． （1）求证：2CB BF BE =； （2）求证：BF AE FD BA =．BCDE FGABCDEF【例18】 求证：如果一个三角形的两边和第三边的高与另一个三角形的对应线段成比例，那么这两个三角形相似．【例19】 如图，在Rt BDC ∆中，点E 在CD 上，DF BC ⊥于F ，DG BE ⊥于G ．求证：FG BC CE BG =．【例20】 如图，90CAB ∠=︒，AD CB ⊥，ACE ∆、ABF ∆是正三角形．求证：DE DF ⊥．8 / 17ABC DEPAB CD1、 相似三角形判定定理1：两角对应相等，两个三角形相似．2、 相似三角形判定定理2：两边对应成比例且夹角相等，两个三角形相似．3、 相似三角形判定定理3：三边对应成比例，两个三角形相似．4、 直角三角形相似的判定定理：斜边和直角边对应成比例，两个直角三角形相似．【例21】 根据下列条件，能判定ABC ∆和DEF ∆相似的个数是（）．（1）35ABC ∠=︒，75ACB ∠=︒，80EDF ∠=︒，35DEF ∠=︒； （2）3AB =，2BC =，30ABC ∠=︒，6DE =，4EF =，30EDF ∠=︒；（3）2AB =，3BC =，4AC =，12DE =，13EF =，14DF =；（4）6AB =，2CB =，2AC =，3DE =，1EF =，2DF =． （A ）1个（B ）2个（C ）3个（D ）4个【例22】 如图，四边形ABCD 是正方形，E 是CD 的中点，P 是BC 边上的一点，下列条件中，不能推出ABP ∆与ECP ∆相似的是（ ）． （A ）APB EPC ∠=∠ （B ）90APE ∠=︒ （C ）P 是BC 的中点 （D ）:2:3BP BC =【例23】 已知ABC ∆中，AB AC =，36A ∠=︒，BD 是角平分线，求证：ABC ∆∽BCD ∆．模块三：相似三角形的判定综合知识精讲例题解析ABCDEFGH1 23ABCD EABCDENM【例24】 在ABC ∆中，12AB =，15AC =，D 为AB 上一点，3ABBD=，在AC 上取一点E ，得到ADE ∆，若ADE ∆与ABC ∆相似，则AE =．【例25】 如图，四边形ABDC 、CDFE 、EFGH 是三个正方形，则123∠+∠+∠的值为多少？【例26】 如图，正方形ABCD 的边长为2，AE EB =，1MN =，线段MN 的两端在CB 、CD 上滑动，当CM 为何值时，AED ∆与以M 、N 、C 为顶点的三角形相似．【例27】 如图，AB AC =，2AC AD AE =，求证：BC 平分DBE ∠．10 / 17AB C DE FAB CDEF A B CMACDEM【例28】 如图，在ABC ∆中，M 在AB 上，且8MB =，12AB =，16AC =，在AC 上求作一点N ，使AMN ∆与原三角形相似，并求AN 的长．【例29】 如图，EM AM ⊥，CE DE =．求证：2ED DM AD CD =．【例30】 如图，在ABC ∆和DEF ∆中，90A D ∠=∠=︒，3AB DE ==，24AC DF ==．（1）判断这两个三角形是否相似，并说明为什么；（2）能否分别过点A 、D 在这两个三角形中各作一条辅助线，使ABC ∆分割成的两个三角形与DEF ∆分割成的两个三角形分别对应相似？证明你的结论．【例31】 如图，在ABC ∆中，3AB AC ==，2BC =，点D 、E 、F 分别在AC 、AB 、BC边上，BEF ∆沿着直线EF 翻折后与DEF ∆重合，设CD x =，BF y =．试问DFC ∆是否有可能与ABC ∆相似，如有可能，求出CD 的长；如不可能，说明理由．ABCD EF【例32】 如图，ABC ∆是等边三角形，D 是AC 上的一点，BD 的垂直平分线交AB 于E ，交BC 于F ．（1）当点D 在边AC 上移动时，DEF ∆中哪一个角的大小始终保持不变？并求出它的度数；（2）当点D 在边AC 上移动时，ADE ∆与哪一个三角形始终相似？并写出证明过程．又问：当点D 移动到什么位置时，这两个三角形的相似比为1？ （3）若等边三角形ABC 的边长为6，2AD =，试求:BE BF 的值．12 / 17A BCD E FGHK AB CDEF【习题1】如图，网格里面有许多三角形．在下列所列出的各三角形之中，不能够与ABC ∆相似的是（）（A ）BCD ∆ （B ）BDE ∆ （C ）BFG ∆（D ）FGH ∆【习题2】下列命题中，说法正确的个数是（ ）（1）有一个锐角相等的两个直角三角形一定相似；（2）斜边和一条直角边对应相等的两个直角三角形一定相似；（3）两个等腰三角形腰上的高和腰对应成比例，则这两个三角形必相似； （4）两边对应成比例的两个三角形相似． （A ）1个（B ）2个（C ）3个（D ）4个【习题3】如图，AC BD ⊥，DE AB ⊥，AC 与ED 交于点F ，3BC =，1FC =，5BD =，则AC =．【习题4】在ABC ∆中，点G 为重心，若BC 边上的高为6，求点G 到BC 的距离．随堂检测ABCDEF ABCDEA BCDEOA BCPQ【习题5】 如图，在ABC ∆中，90ACB ∠=︒，CD AB ⊥于D ，E 为AC 上一点，CF BE⊥于F ，联结DF ． 求证：BD DFBE AE=．【习题6】已知梯形ABCD 中，AB // CD ，90B ∠=︒，3AB =，6CD =，12BC =，点E 在BC 边上自B 点向C 点移动，求使得ABE ∆与ECD ∆相似的BE 的值．【习题7】如图，梯形ABCD 中，AD //BC ，AC 与BD 相交于点O ，过点B 作BE //CD交CA 的延长线于点E ，求证：2OC OA OE =．【习题8】如图，在ABC ∆中，90C ∠=︒，8BC cm =，6AC cm =，点P 从B 出发，沿BC 方向以2cm/s 的速度移动到C 点，点Q 从C 出发，沿CA 方向以1cm/s 的速度移动到A 点．若点P 、Q 分别同时从B 、C 出发，经过多少时间CPQ ∆与CBA ∆相似？14 / 17ABCDEOABCPQN【习题9】如图，ABC ∆中，90C ∠=︒，2AC BC ==，O 是AB 的中点，将45°角的顶点置于点O ，并绕点O 旋转，使角的两边分别交边AC 、BC 于点D 、E ，连接点D 、E ．（1）观察图形，在旋转过程中有无一定相似的三角形？若有，请找出，并证明； （2）设AD x =，BE y =，求y 关于x 的函数关系式，并写出它的定义域； （3）当x 为何值时，ODE ∆是等腰三角形？【习题10】 在ABC ∆中，90ACB ∠=︒，CQ 是斜边AB 上的中线，6AC =，10AB =，点P 是BC 边上的一个动点（与B 、C 不重合），经过点P 、Q 的直线与直线AC 交于点N ，若PNC ∆与ABC ∆相似，求BP 的值．ABCDEFAB CD EF【作业1】如图，ABC ∆与DEF ∆在边长为1个单位的方格纸中，它们的顶点在小正方形的顶点位置，试判定ABC ∆与DEF ∆是否相似，为什么？【作业2】下列每组中的两个三角形，相似的是（） （A ）ABC ∆中，35A ∠=︒，50B ∠=︒；'''A B C ∆中，'35A ∠=︒，'105B ∠=︒ （B ）ABC ∆中， 1.5AB =， 1.25BC =，38B ∠=︒；'''A B C ∆中，''2A B =，'' 1.5B C =，'38B ∠=︒（C ）ABC ∆中，12AB =，15BC =，26CA =；'''A B C ∆中，''20A B =，''25B C =，''40C A =（D ）Rt ABC ∆中，斜边5AB =，直角边3BC =；'''Rt A B C ∆中，斜边''15A B =，直角边''12A C =【作业3】如图，AD BC ⊥于点D ，CE AB ⊥于点E ，交AD 于点F ，则图中相似三角形的对数是（）． （A ）3对（B ）4对（C ）5对（D ）6对课后作业16 / 17ABCDE FGABCDE FABCDEFG【作业4】如图，在ABC ∆中，CD 垂直平分AB ，点E 在CD 上，DF AC ⊥于F ，DG BE ⊥于G ．求证：AF AC BG BE =．【作业5】如图，D 是AC 上的点，BE 平行于AC ，BE AD =，AE 分别交BD 、BC于点F 、G ，CAE CBD ∠=∠． 求证：BF 是FG 和EF 的比例中项．【作业6】已知，E 、F 分别是正方形ABCD 的边AB 和AD 上的点，且13EB AF AB AD ==，求证：AEF FBD ∠=∠．ABCDEFABP QR12ABCDPQ 【作业7】 如图，正方形ABCD 中，2AB =，P 是BC 边上与B 、C 不重合的任意点，DQ AP ⊥于Q ．（1）求证：DQA ∆∽ABP ∆；（2）当点P 在BC 上变化时，线段DQ 也随之变化．设PA x =，DQ y =，求y 与x 之间的函数关系式，并写出x 的取值范围．【作业8】如图，在Rt ABC ∆中，90ACB ∠=︒，CD AB ⊥于D ，DE AC ⊥于E ，DF BC ⊥于F ． 求证：33AE AC BF BC =．【作业9】如图，A 是等边PQR ∆的边RQ 的延长线上的点，B 是QR 延长线上的点．（1）若1260∠+∠=︒，求证：2QR AQ BR =；（2）若12AQ QR =，当RB 与QR 满足什么条件时，BRP ∆∽PQA ∆？（3）BPQ ∆有可能与PQA ∆相似吗？若可能相似，说明应满足什么条件；若不可能相似，请说明理由．。

第24讲诱导公式1．借助单位圆的对称性，利用定义推导出诱导公式；2．能够熟练地运用诱导公式，将任意角的三角函数化归为锐角的三角函数，进行求值、化简和证明。

3．通过三角函数诱导公式的学习，体验“把未知转化为已知”这种重要的化归思想。

一、诱导公式1、诱导公式二：角πα+与角α的终边关于原点对称sin()sin παα+=-，cos()cos παα+=-，tan()tan παα+=，其中k Z∈2、诱导公式三：角α-与角α的终边关于x 轴对称sin()sin αα-=-，cos()cos αα-=，tan()tan αα-=-，其中k Z∈3、诱导公式四：角πα-与角α的终边关于y 轴对称sin()sin παα-=，cos()cos παα-=-，tan()tan παα-=-，其中k Z∈4、诱导公式五：sin cos 2παα⎛⎫-= ⎪⎝⎭，cos sin 2παα⎛⎫-= ⎪⎝⎭，其中k Z ∈诱导公式六：sin cos 2παα⎛⎫+=⎪⎝⎭，cos sin 2παα⎛⎫+=- ⎪⎝⎭，其中k Z ∈5、诱导公式口诀：“奇变偶不变，符号看象限”，意思是说角90k α⋅±(k 为常整数)的三角函数值：当k 为奇数时，正弦变余弦，余弦变正弦；当k 为偶数时，函数名不变，然后α的三角函数值前面加上当视α为锐角时原函数值的符号.二、用诱导公式进行化简时的注意点：（1）化简后项数尽可能的少；（2）函数的种类尽可能的少；（3）分母不含三角函数的符号；（4）能求值的一定要求值；（5）含有较高次数的三角函数式，多用因式分解、约分等．三、利用诱导公式求任意角三角函数值的步骤1、“负化正”：用公式一或三来转化．2、“大化小”：用公式一将角化为0°到360°间的角．3、“角化锐”：用公式二或四将大于90°的角转化为锐角．4、“锐求值”：得到锐角的三角函数后求值．四、利用诱导公式求值与求解解题策略1、条件求值问题的策略（1）条件求值问题，首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间的差异及联系．（2）将已知式进行变形向所求式转化，或将所求式进行变形向已知式转化．2、给值求角问题，先通过化简已给的式子得出某个角的某种三角函数值，再结合特殊角的三角函数值逆向求角．3、观察互余、互补关系：如π3－α与π6＋α，π3＋α与π6－α，π4－α与π4＋α等互余，π3＋θ与2π3－θ，π4＋θ与3π4－θ等互补，遇到此类问题，不妨考虑两个角的和，要善于利用角的变换来解决问题．考点一：利用诱导公式给角求值例1．35πsin 6=（）A ．12B ．12-C D ．【变式训练1】计算：5π7ππ2sin2cos tan 663⎛⎫+--= ⎪⎝⎭______.【变式训练2】计算：1417sincos tan 336πππ+-=___________.例2．若()4sin ,5πα+=-且α是第二象限角，则cos α=（）A ．45-B ．35-C ．35D ．45【变式训练1】设02πα⎛⎫∈ ⎪⎝⎭，，若3sin ,5α=则cos 2πα⎛⎫+= ⎪⎝⎭（）A ．35B ．45C ．35-D ．45-【变式训练2】设sin 25a ︒=，则sin 65cos115tan 205︒︒︒=（）A 2B ．2C ．2a -D ．2a 考点三：互余互补关系的应用例3．已知π3cos 35α⎛⎫-= ⎪⎝⎭，则πsin 6α⎛⎫+= ⎪⎝⎭（）A ．45±B ．45C ．45-D ．35【变式训练1】已知π1sin 43α⎛⎫+= ⎪⎝⎭，则πcos 4α⎛⎫- ⎪⎝⎭的值为（）A ．13B ．223C ．13-D ．3-【变式训练2】已知cos 6πθ⎛⎫- ⎪⎝⎭＝a (|a |≤1)，则cos 56πθ⎛⎫+⎪⎝⎭＋sin 23πθ⎛⎫- ⎪⎝⎭的值是________.考点四：利用诱导公式化简求值例4）A ．sin 4cos4-B ．sin 4cos 4--C ．cos 4sin 4-D ．sin 4cos 4+【变式训练】（多选）已知角α满足sin cos 0αα⋅≠，则()()()sin πcos πsin cos k k k αααα+++∈Z 的取值可能为（）A ．2-B ．1-C ．2D ．0例5．已知A 、B 、C 为ABC 的三个内角，求证：ππsin cos 2424A B C +⎛⎫⎛⎫+=- ⎪⎪⎝⎭⎝⎭【变式训练】求证：232sin()cos()12212sin ()ππθθπθ-+--+＝tan(9)1tan()1πθπθ+++-．考点六：诱导公式综合应用例6．已知()()()()()3sin cos tan cos 222sin 2tan sin f πππααπαααπααππα⎛⎫⎛⎫⎛⎫+--+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=---+.（1）化简()f α；（2）若31cos 25πα⎛⎫-=- ⎪⎝⎭，求()f α的值.【变式训练】（1）化简：222cos(4)cos ()sin (3)sin(4)sin(5)cos ()θπθπθπθππθθπ+++-+--（2）已知()sin3n f n π=（n ∈Z ），求(1)f ＋(2)f ＋(3)f ＋…＋(2012)f 的值.1．4πcos 3=（）A ．12BC ．12-D．2．已知3πsin 23α⎛⎫-= ⎪⎝⎭，且α为第三象限角，则tan α=（）A．BC ．22D3．已知()cos 3π3θ+=-，那么7πsin 2θ⎛⎫+= ⎪⎝⎭（）A ．13-B ．13C．3-D ．2234．已知π,π2α⎛⎫∈ ⎪⎝⎭，且π12sin 313α⎛⎫+= ⎪⎝⎭，则πsin 6α⎛⎫-= ⎪⎝⎭（）A ．1213-B ．1213C ．513-D ．5135．若()5tan 3π2θ-=，则()()sin πcos πππsin 2cos 22θθθθ++-=⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭（）A ．712-B ．38-C ．78-D ．14-6．已知π5cos 513α⎛⎫-= ⎪⎝⎭，则7πsin 10α⎛⎫-= ⎪⎝⎭（）A ．513-B ．513C ．-1213D ．12137．（多选）已知3πsin 2α⎛⎫+= ⎪⎝⎭，则角α的终边可能在（）A ．第一象限B ．第二象限C ．第三象限D ．x 轴的负半轴上8．求证()()31sin 1801sin()1tan cos 360cos(540)ααααα︒︒︒-+-=+--9．计算下列两个小题（1）计算25π10π13πsincos tan 634⎛⎫-+- ⎪⎝⎭；（2）已知角α终边上有一点12P ⎛⎫- ⎪⎝⎭，求()()()ππsin cos tan π22tan πsin πααααα⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭++的值．10．已知函数()()()3πsin 3πcos 4πsin 2π7πsin sin 22x x x f x x x ⎛⎫-++ ⎪⎝⎭=⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭.（1）化简函数()f x 的解析式；（2）若π53f x ⎛⎫+=- ⎪⎝⎭，()0,πx ∈，求3πsin 10x ⎛⎫- ⎪⎝⎭的值.1．若tan 3,2π0x x =-<<，则角x 等于（）A ．π3或2π3B ．2π3或4π3C ．4π3或5π3D ．2π3或5π32．若()2sin π3α-=-，且π(,0)2∈-α，则()cos πα+的值为（）A ．5B 5C ．53D ．233．已知s 5π3sin 42α⎛⎫+= ⎪⎝⎭，则3πsin 4α⎛⎫- ⎪⎝⎭的值为（）A ．12B ．－12C 3D 3412sin(π2)cos(π2)+-⋅-）A ．sin 2cos 2+B ．cos 2sin 2-C ．sin 2cos 2-D ．()cos 2sin 2±-5．（多选）下列三角函数式的值与πsin3的值相同的是（）A ．3πsin 2π,Z4n n ⎛⎫+∈ ⎪⎝⎭B ．πcos 2π,Z6n n ⎛⎫-∈ ⎪⎝⎭C ．πsin 2π,Z3n n ⎛⎫+∈ ⎪⎝⎭D ．()πcos 21π,Z6n n ⎡⎤+-∈⎢⎥⎣⎦6．()()()()()tan 150cos 570cos 1140tan 210sin 690-︒⋅-︒⋅-︒=-︒⋅-︒_________．7．化简：()()()()()()sin πcos 3πtan πcot 2πtan 4πsin 5παααααα----=--+________．8．设Z k ∈，化简：()()()()sin πcos πsin 1πcos 1πk k k k αααα-+++++-⎡⎤⎡⎤⎣⎦⎣⎦9．求下列各式的值:（1）cos25π3+tan 15π4⎛⎫- ⎪⎝⎭;（2）sin 810°+tan 765°+tan 1125°+cos 360°.10．已知函数()π5π10πcos 2cos 2tan 26334π4πtan 2sin 233x x x f x x x ⎛⎫⎛⎫⎛⎫--+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=⎛⎫⎛⎫+-- ⎪ ⎪⎝⎭⎝⎭.（1）化简()f x ；（2）若()0310f x =，求00π2πsin 2cos 263x x ⎛⎫⎛⎫-+-⎪ ⎪⎝⎭⎝⎭的值.。

二次函数的应用内容分析二次函数在实际生活中的应用主要包括以下几个方面：（1）二次函数与经济问题，主要用于求解利润最大化；（2）二次函数与面积问题，涉及到实际图形面积关系式的表达、面积最值的求解等；（3）二次函数与拱桥问题，二次函数的图像与拱桥横截面的形状都是抛物线状，所以利用二次函数求解拱桥问题在实际生活中很常见；（4）二次函数与物体的运动轨迹：在实际生活中，由于只受重力的作用，掷出的铅球、踢出的足球、投出的篮球等物体的运动轨迹一定是抛物线形状，则可以利用二次函数的图像性质求解相关的问题．当然二次函数也会与其他的知识点相结合，例如二次函数与一次函数、二次函数与一元二次方程、二次函数与不等式等的代数综合，以及二次函数与相似三角形、二次函数与圆、二次函数与动点等的几何综合，这些内容我们会在秋季班的课程中深入地学习．知识结构步同级年九模块一：二次函数与利润最大化知识精讲1、知识点名称求解二次函数与利润最大化的问题，主要是根据题意列出相关的二次函数解析式，再通过配方的方式求解最大值．这是一种实际应用的题型，需根据自变量的实际意义确定函数的定义域，在求解最大值时，也需注意自变量的取值范围．例题解析【例1】某商品进价为90元/个，按100一个出售，能售出500个，如果这种商品每涨价1 元，其销售量就减少10个，为了获得最大利润，单价应定为__________．【例2】某商店以120元每件的成本购进一批新产品，在试销阶段，每件产品的销售价x（元）与产品的日销售量y（台）之间的关系如下表所示：x 130 150 165y 70 50 35（1）若日销售量y是销售价x的一次函数，求这个一次函数；（2）每件产品的销售价定为多少元时，日销售利润最大，最大利润为多少元？2/ 14【例3】某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量y（件）与销售单价x（元）符合一次函数y = kx + b，且x = 65时，y = 55；x =75时，y = 45．（1）求一次函数y = kx + b的表达式；（2）若该商场获得利润为W元，试写出利润W与销售单价x之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？（3）若该商场获得利润不低于500元，试确定销售单价x的范围．【例4】某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施．调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．（1）假设每台冰箱降价x元，商场每天销售这种冰箱的利润y元，请写出y与x之间的函数关系式；（2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？（3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？步同级年九4 / 14例题解析1、知识点名称求解二次函数与面积结合的问题时，基本方法上与利润最大化是相同的，也是通过配方的方式求解相关面积的最值，当然也需要注意自变量的取值范围．而与利润最大化问题不同的是，面积问题中可能会涉及到三角形、四边形或者圆等图形，也可能会出现动点与面积相结合的类型，变化较多．【例7】在半径为4厘米的圆面上，从中挖去一个半径为x 厘米的同心圆面，剩下一个圆环 的面积为y 平方厘米，则y 关于x 的函数关系式为（ ） A ．24y x π=-B ．()22y x π=- C ．()24y x π=-+D ．216y x ππ=-+【例8】一长方体的长和宽相等，高比长多0.5米，若长方体的长和宽用x （米）表示，则 长方体的表面积S （平方米）关于x 的函数关系式为________________．【例9】如图，正方形ABCD 的边长为4，P 是BC 上的一动点，若QP AP ⊥，交DC 于Q ，模块二：二次函数与面积问题知识精讲ABCD设PB = x ，ADQ ∆的面积为y ，y 与x 的函数关系式为_________________．【例10】小智用总长为8厘米的铁丝围成矩形，则矩形的最大面积是（ ）平方厘米A ．4B ．8C ．16D ．32【例11】如图所示，矩形花圃ABCD 的一边利用足够长的墙，另三边用总长为32米的篱笆 围成．设AB 边的长为x 米，矩形ABCD 的面积为S 平方米． （1）求S 与x 之间的函数关系式（不要求写出自变量x 的取值范围）； （2）当x 为何值时，S 有最大值？并求出最大值．【例12】如图，在Rt ABC ∆中，90C ∠=︒，AC = 40 cm ，BC = 30 cm ，在Rt ABC ∆内部作一ABC DPQ步同级年九6/ 14A BCDEFNM GH个矩形DEFG，其中点D和点G分别在AC、BC上，点E、F在AB上．设矩形的一边EF = x cm，设矩形的面积为y cm2．（1）写出y关于x的函数关系式及定义域；（2）求当x = 25 cm时，矩形DEFG的面积．【例13】抛物线的对称轴是直线x = 1，它与x轴交于点A、B两点，与y轴交于C点，点A、C的坐标分别是（1-，0）、（0，32）．（1）求此抛物线对应的函数的解析式；（2）若点P是抛物线上位于x轴上方的一个动点，求ABP∆面积的最大值．【例14】如图，E、F分别是边长为4的正方形ABCD的边BC、CD上的点，CE = 1，CF = 43，直线EF交AB的延长线于G，过线段FG上的一个动点H作HM⊥AG，HN⊥AD，垂足分别为M、N，设HM = x，矩形AMHN的面积为y．（1）求y与x之间的函数关系式；（2）当x为何值时，矩形AMHN的面积最大，最大面积为多少？ABCD EFG模块三：二次函数与拱桥问题例题解析1、知识点名称二次函数与拱桥问题的解题，依赖于合理的平面直角坐标系的建立，继而在平面直角坐标系中，利用二次函数的图像性质解答相关的问题．【例16】如图，河上有一座抛物线形状的桥洞，已知桥下的水面离桥拱顶部4米时，水面 宽AB 为12米，如图建立直角坐标系． （1）求抛物线的函数解析式；（2）当水位上升1米时，水面宽为多少米？（答案保留整数，其中3 1.7 ）【例17】有一个横截面为抛物线形的拱形桥洞，桥洞离水面的最大高度为4 m ，跨度为10 m ， 则把它的横截面的图形放在如图所示的直角坐标系中时：（1）抛物线的顶点坐标为________，这条抛物线所对应的函数解析式为________________； （2）如图，在对称轴右边3 m 处，桥洞离水面的高度为______ m ．知识精讲【例18】某农业合作社的蔬菜大棚的横截面为抛物线，尺寸如图所示： （1）根据图中的平面直角坐标系求该抛物线的解析式；（2）若菜农身高为1.6米，则在他不弯腰的情况下，在棚内的横向活动范围有几米？（精 确到0.01米）【例19】一条隧道的截面由抛物线和矩形构成，矩形的长OC 为8米，宽OA 为2米，隧道 最高点P 位于AB 的中央且距地面6米，建立如图所示的坐标系． （1）求抛物线的解析式；（2）一辆货车高4米，宽2米，能否从该隧道内通过？请说明理由； （3）如果隧道内设双行道，那么这辆货车是否可以顺利通过？请说明理由．【例20】某工厂要赶制一批蒙古包．如图，蒙古包横截面的形状是由矩形和抛物线的一部 分组成的，矩形长为12 m ，抛物线拱高为5.6 m ． （1）在如图所示的平面直角坐标系中，求抛物线的表达式；（2）现需在抛物线AOB 的区域内安装几扇窗户，窗户的底边在AB 上，每扇窗户宽1.5 m ， 高1.6 m ，相邻窗户之间的间距均为0.8 m ，左右两边窗户的窗角所在的点到抛物线的 水平距离至少为0.8 m ．请计算最多可安装几扇这样的窗户？1、知识点名称与拱桥问题相同，也需要借助建立平面直角坐标系，利用二次函数的图像性质解答二次函数与运行轨迹的问题．【例23】若物体运动的路程s （米）与时间t （秒）的关系式为232y t t =+，则t = 5秒时， 该物体所经过的路程为________．【例24】如图，是一个运动员投掷铅球的抛物线图，解析式为21251233y x x =-++（单位：米），其中点A 为出手点，点C 为铅球运行中的最高点，点B 为铅球落地点，求： （1）出手点A 离地面的高度； （2）最高点C 离地面的高度； （3）该运动员的成绩是多少米？模块四：二次函数与运行轨迹知识精讲例题解析OA BCxy步同级年九10 / 14【例25】在距离地面2米高的某处把一物体以初速度v 0（米/秒）竖直向上抛出，在不计空气阻力的情况下，其上升高度h （米）与抛出的时间t （秒）满足2012h v t gt =-（其中g是常数，取g = 10 米/秒2）．若v 0 = 10 米/秒，则该物体在运动过程中，最高点距离地 面______米．【例26】顽皮的小明，从10米高的窗口A 用水枪向外喷水，喷出的水流呈抛物线状（抛物线所在平面与墙面垂直）．如果抛物线的最高点M 离墙1米，离地面403米，则水流落地点B 离墙的距离OB 是（ ） A ．2米 B ．3米 C ．4米 D ．5米【习题1】军事演习中，一门迫击炮发射的一发炮弹飞行的高度y （m ）与飞行时间x （s ）的关系满足21104y x x =-+．经过______秒时间炮弹到达它的最高点，最高点的高度是______米，经过______秒时间，炮弹落到地上爆炸（假设地面是平坦的）．随堂检测A BC 【习题2】如图，点C 是线段AB 上的一个动点，AB = 1，分别以AC 、CB 为边作正方形， 用S 表示这两个正方形的面积之和，下列判断正确的是（ ）A ．当C 是AB 的中点时，S 最小B ．当C 是AB 的中点时，S 最大C ．当C 为AB 的三等分点时，S 最小D ．当C 为AB 的三等分点时，S 最大【习题3】某民俗旅游村为了接待游客的需要开设了有100张床位的旅馆，当每张床位每天收费10元时，床位可以全部租出，若每张床位每天收费提高2元，则相应地减少了10 张床位租出，如果每张床位每天以2元为单位提高收费，为使租出的床位少且租金高， 那么每张床位每天最合适的收费是多少？【习题4】如图所示，有长24米的篱笆，一面利用墙（墙的最大长度为10米），围成中间 隔有一道篱笆的长方形花圃．设花圃的边AB 的长为x ，花圃的面积为S 平方米．（1）请求出S 与x 的函数关系式．（2）按照题中要求，所围的花圃面积能否是48 m 2．若能，求出的x 值；若不能，请说明理 由．【习题5】已知一隧道的截面是抛物线，且抛物线的解析式为211584y x =-+，一辆卡车高3米，宽4米，该车__________（选填“能”或“不能”）通过隧道．【习题6】一男生在校运会的比赛中推铅球，铅球的行进高度y（m）与水平距离x（m）之间的关系用如图所示的二次函数图象表示．（铅球从A点被推出，实线部分表示铅球所经过的路线）．（1）求y与x之间的函数关系式；（2）求出铅球被推出的距离；（3）若铅球到达的最大高度的位置为点B，落地点为C，求四边形OABC的面积．课后作业【作业1】某商品的进货单价为40元，售价为60元时，能售出100个，如果这种商品涨价1元，其销售量就减少3个，则销售量y与售价x的关系式为___________，利润W与售价x的关系式为____________，x的取值范围为__________．【作业2】一场足球比赛，一球员在球门正前方10米处将球踢起射向球门，当球飞行的水平距离是6米时，球到达最高点，此时球高3米，若球门高2.44米，则______（填“能”或“不能”）射中球门．【作业3】用12米长的木条做一个如图所示的矩形窗子，为使透进的光线最多，则窗子的长为______米，宽为______米．【作业4】如图，某隧道口的横截面是抛物线形，已知路宽AB为6米，最高点离地面的距离OC为5米．以最高点O为坐标原点，抛物线的对称轴为y轴，1米为数轴的单位长度，建立平面直角坐标系．求：（1）以这一部分抛物线为图像的函数解析式，并写出x的取值范围；（2）有一辆宽2.8米，高4米的货车能否通过此隧道？yxOA B【作业5】某宾馆有50个房间供游客住宿，当每个房间的房价为每天180元时，房间会全部住满．当每个房间每天的房价每增加10元时，就会有一个房间空闲．宾馆需对游客居住的每个房间每天支出20元的各种费用．根据规定，每个房间每天的房价不得高于340元．设每个房间的房价每天增加x元（x为10的正整数倍）．（1）设一天订出的房间数为y，直接写出y与x的函数关系式及自变量x的取值范围；（2）设宾馆一天的利润为W元，求W与x的函数关系式；（3）一天订出多少个房间，宾馆的利润最大？最大利润是多少元？。

《圆》第1讲 圆的认识（1）1、说出几个与圆有关的成语和生活中与圆有关的物体.思考：车轮为什么做成圆形？2、爱好运动的小华、小强、小兵三人相邀搞一次掷飞镖比赛.他们把靶子钉在一面土墙上，规则是谁掷出落点离红心越近，谁就胜.如下图中A 、B 、C 三点分别是他们三人某一轮掷镖的落点，你认为这一轮中谁的成绩好？学习内容：1、圆的定义：_______________ （运动的观点）2、画圆并体会确定一个圆的两个要素是 和3、点和圆的位置关系 量一量（1）利用圆规画一个⊙O ，使⊙O 的半径r=3cm. （2）在平面内任意取一点P ，点与圆有哪几种位置关系？若⊙O 的半径为r ，点P 到圆心O 的距离为d ，那么：点P 在圆 d r点P 在圆 d r点P 在圆 d r4、圆的集合定义（集合的观点）（1）思考：平面上的一个圆把平面上的点分成哪几部分？（2）圆是到定点距离 定长的点的集合.圆的内部是到 的点的集合；圆的外部是 的点的集合 .（3）想一想：角的平分线可以看成是哪些点的集合？线段的垂直平分线呢？ 尝试与交流已知点P 、Q ，且PQ=4cm ，⑴画出下列图形：到点P 的距离等于2cm 的点的集合；到点Q 的距离等于3cm 的点的集合.⑵在所画图中，到点P 的距离等于2cm ，且到点Q 的距离等于3cm 的点有几个？请在图中将它们表示出来.⑶在所画图中，到点P 的距离小于或等于2cm ，且到点Q 的距离大于或等于3cm 的点的集合是怎样的图形？把它画出来.知识梳理1、圆的定义.2、点与圆的位置关系.达标测试1、正方形ABCD 的边长为2cm ，以A 为圆心2cm 为半径作⊙A ，则点B 在⊙A ；点C 在⊙A ；点D 在⊙A .2、已知⊙O 的半径为5cm.(1)若OP=3cm ，那么点P 与⊙O 的位置关系是：点P 在⊙O ；(2)若OQ= cm ，那么点Q 与⊙O 的位置关系是：点Q 在⊙O 上；(3)若OR=7cm ，那么点R 与⊙O 的位置关系是：点R 在⊙O .3、⊙O 的半径10cm ，A 、B 、C 三点到圆心的距离分别为8cm 、10cm 、12cm ，则点A 、B 、C 与⊙O 的位置关系是：点A 在 ；点B 在 ；点C 在4、⊙O 的半径6cm ，当OP=6时，点A 在 ；当OP 时点P 在圆内；当OP 时，点P 不在圆外.5、到点P 的距离等于6厘米的点的集合是________________________________________6、已知AB 为⊙O 的直径P 为⊙O 上任意一点，则点关于AB 的对称点P ′与⊙O 的位置为( ) (A)在⊙O 内 (B)在⊙O 外 (C)在⊙O 上 (D)不能确定6、如图已知矩形ABCD 的边AB=3厘米，AD=4厘米（直接写出答案）（1）以点A 为圆心，3厘米为半径作圆A ，则点B 、C 、D 与圆A 的位置关系如何？（2）以点A 为圆心，4厘米为半径作圆A ，则点B 、C 、D 与圆A 的位置关系如何？（3）以点A 为圆心，5厘米为半径作圆A ，则点B 、C 、D 与圆A 的位置关系如何？ ⇔⇔⇔7、如图，在直角三角形ABCD中，角C为直角，AC=4，BC=3，E，F分别为AB，AC的中点.以B为圆心，BC为半径画圆，试判断点A，C，E，F与圆B的位置关系.8、已知：如图，BD、CE是△ABC的高，M为BC的中点．试说明点B、C、D、E在以点M为圆心的同一个圆上．第2讲圆的认识（2）知识梳理与圆有关概念(1)请在图上画出弦CD，直径AB.并说明___________________________叫做弦；_________________________________叫做直径.(2)弧、半圆、优弧与劣弧的概念及表示方法.弧：___ _半圆：_________________________ 优弧：________________ _ 表示方法：__劣弧：______________________________ _,表示方法：______(3)借助图形理解圆心角、同心圆、等圆.圆心角:______________________________同心圆: __________________ _ _等圆: __________________________ _.(4) 同圆或等圆的半径_______.等弧: _______________________典型例题例1、如图点A、B和点C、D分别在两个同心圆上,且∠AOB=∠COD. ∠C与∠D相等吗?为什么?2如图，AB是⊙O的弦（非直径），C、D是AB上的两点，并且AC=BD.求证：OC=OD.达标检测一、判断：（1）直径是弦，弦是直径. （）（2）半圆是弧，弧是半圆. （）（3）周长相等的两个圆是等圆. （）（4）长度相等的两条弧是等弧. （）（5）同一条弦所对的两条弧是等弧. （）（6）在同圆中，优弧一定比劣弧长. （）二、解答1、如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,求∠A的度数.2、如图，AB是⊙O的直径，AC是弦，D是AC的中点，若OD=4，求BC.3、如图, AB是⊙O的直径,点C在⊙O上, CD⊥AB, 垂足为D, 已知CD=4, OD=3, 求AB的长.3. 如图, AB是⊙O的直径, 点C在⊙O上, ∠A=350, 求∠B的度数.第3讲 圆的对称性（1）学习内容：1、按照下列步骤进行小组活动：⑴在两张透明纸片上，分别作半径相等的⊙O 和⊙O '⑵在⊙O 和⊙O '中,分别作相等的圆心角∠AOB 、∠'''B O A ，连接AB 、''B A⑶将两张纸片叠在一起，使⊙O 与⊙O '重合（如图）⑷固定圆心，将其中一个圆旋转某个角度，使得OA 与OA '重合在操作的过程中，你有什么发现，请与小组同学交流_______________________________________________2、上面的命题反映了在同圆或等圆中，圆心角、弧、弦的关系，对于这三个量之间的关系，你还有什么思考？请与小组同学交流.你能够用文字语言把你的发现表达出来吗?3、圆心角、弧、弦之间的关系：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等4、试一试：如图，已知⊙O 、⊙O '半径相等，AB 、CD 分别是⊙O 、⊙O '的两条弦填空：（1）若AB=CD，则 ， （2）若AB= CD，则 ， （3）若∠AOB=∠CO 'D ，则 ，5、在圆心角、弧、弦这三个量中，角的大小可以用度数刻画，弦的大小可以用长度刻画，那么如何来刻画弧的大小呢？弧的大小：圆心角的度数与它所对的弧的度数相等例1、如图，AB 、AC 、BC 都是⊙O 的弦，∠AOC=∠BOC ∠ABC 与∠BAC 相等吗？为什么？例题2、已知：如图，AB 是⊙O 的直径，点C 、D 在⊙O 上，CE ⊥AB 于E ，DF ⊥AB 于F ，且AE=BF ，AC 与BD 相等吗？为什么？知识梳理：1、在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等；2、圆心角的度数与它所对的弧的度数相等.达标检测：1、画一个圆和圆的一些弦，使得所画图形满足下列条件：（1）是中心对称图形，但不是轴对称图形；︵ ︵（2）既是轴对称图形，又是中心对称图形. 2、如图,在⊙O 中, ,∠1=30°,则∠2=__________3、一条弦把圆分成1：3两部分，则劣弧所对的圆心角为________.4、⊙O 中，直径AB ∥CD 弦，，则∠BOD=______.5、在⊙O 中，弦AB 的长恰好等于半径，弦AB 所对的圆心角为6、如图，AB 是直径，BC ︵＝CD ︵＝DE ︵，∠BOC ＝40°，∠AOE 的度数是 .7.已知，如图，AB 是⊙O 的直径，M,N 分别为AO,BO 的中点，CM ⊥AB,DN ⊥AB,垂足分别为M,N.求证：AC=BD第4讲 圆的对称性（2）知识准备：1、如果一个图形沿着一条直线折叠，直线的两旁的部分能够互相重合，那么这个图形叫做__________________，这条直线叫做_______________.2、圆是中心对称图形，_________是它的对称中心；圆具有_________性.学习内容：提出问题：“圆”是不是轴对称图形？它的对称轴是什么？操作：①在圆形纸片上任画一条直径；②沿直径将圆形纸片折叠，你发现了什么？ 结论：圆是轴对称图形，经过圆心的任意一条直线都是它的对称轴.练习：1、判断下列图形是否具有对称性？如果是中心对称图形，指出它的对称中心；如果是轴对称图形，指出它的对称轴.2、将第二个图中的直径AB 改为怎样的一条弦，它将变成轴对称图形？探索活动：1、如图，CD 是⊙O 的弦，画直径AB ⊥CD ，垂足为P ，将圆形纸片沿AB 对折，你发现了什么？2、你能给出几何证明吗？（写出已知、求证并证明）3、得出垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的弧.4、注意：①条件中的“弦”可以是直径；②结论中的“平分弧”指平分弦所对的劣弧、优弧.5、给出几何语言︒=⋂60度数AC AC = BD例 1 如图，以O 为圆心的两个同心圆中，大圆的弦AB 交小圆于点C 、D ，AC 与BD 相等吗？为什么？例 2 如图，已知：在⊙O 中，弦AB 的长为8，圆心O 到AB 的距离为3.⑴求的半径； ⑵若点P 是AB 上的一动点，试求OP 的范围.知识梳理：1、垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧.2、垂径定理的推论，如：平分弦（非直径）的直径垂直于这条弦，且平分弦所对的弧等. 达标检测：1、如图，∠C=90°，⊙C 与AB 相交于点D ，AC=5，CB=12，则AD=_____2、已知，如图 ，⊙O 的直径AB 与弦CD 相交于点E,AE=1,BE=5, AEC =45°,求CD 的长.3、如图,在⊙O 中，CD 是直径，AB 是弦，CD ⊥AB ，垂足为M ．则有AM=_____， _____= ，____= ．4.过⊙O 内一点P 作一条弦AB ，使P 为AB 的中点.5.⊙O 中，直径AB ⊥弦CD 于点P ，AB=10cm,CD=8cm ，则OP 的长为 CM.6.如图，已知在⊙O 中，弦AB 的长为8cm ，圆心O 到AB 的距离为3cm ，求⊙O 的半径．7. ⊙O 的弦 AB 为5cm ，所对的圆心角为120°，则圆心O 到这条弦AB 的距离为___8.圆内一弦与直径相交成30°且分直径为1cm 和5cm ，则圆心到这条弦的距离为 CM9.在半径为5的圆中,弦AB ∥CD,AB=6,CD=8,试求AB 和CD 的距离.10. 一跨河桥，桥拱是圆弧形，跨度(AB)为16米，拱高(CD)为4米，求：⑴桥拱半径⑵若大雨过后，桥下河面宽度(EF)为12米，求水面涨高了多少？11、“圆材埋壁”是我国古代著名数学家著作《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”此问题的实质是解决下面的问题：“如图，CD为⊙O的直径，弦AB⊥CD于点E，CE=1，AB=10，求CD的长．”根据题意可得CD的长为。

目录本次培训具体计划如下，以供参考：第一讲如何做几何证明题第二讲平行四边形（一）第三讲平行四边形（二）第四讲梯形第五讲中位线及其应用第六讲一元二次方程的解法第七讲一元二次方程的判别式第八讲一元二次方程的根与系数的关系第九讲一元二次方程的应用第十讲专题复习一：因式分解、二次根式、分式第十一讲专题复习二：代数式的恒等变形第十二讲专题复习三：相似三角形第十三讲结业考试（未装订在内，另发）第十四讲试卷讲评第一讲：如何做几何证明题【知识梳理】1、几何证明是平面几何中的一个重要问题，它对培养学生逻辑思维能力有着很大作用。

几何证明有两种基本类型：一是平面图形的数量关系；二是有关平面图形的位置关系。

这两类问题常常可以相互转化，如证明平行关系可转化为证明角等或角互补的问题。

2、掌握分析、证明几何问题的常用方法：（1）综合法（由因导果），从已知条件出发，通过有关定义、定理、公理的应用，逐步向前推进，直到问题的解决；（2）分析法（执果索因）从命题的结论考虑，推敲使其成立需要具备的条件，然后再把所需的条件看成要证的结论继续推敲，如此逐步往上逆求，直到已知事实为止；（3）两头凑法：将分析与综合法合并使用，比较起来，分析法利于思考，综合法易于表达，因此，在实际思考问题时，可合并使用，灵活处理，以利于缩短题设与结论的距离，最后达到证明目的。

3、掌握构造基本图形的方法：复杂的图形都是由基本图形组成的，因此要善于将复杂图形分解成基本图形。

在更多时候需要构造基本图形，在构造基本图形时往往需要添加辅助线，以达到集中条件、转化问题的目的。

【例题精讲】【专题一】证明线段相等或角相等两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系。

很多其它问题最后都可化归为此类问题来证。

证明两条线段或两角相等最常用的方法是利用全等三角形的性质，其它如线段中垂线的性质、角平分线的性质、等腰三角形的判定与性质等也经常用到。

【例1】已知：如图所示，∆A B C 中，∠=︒===C AC BC AD DB AE CF 90，，，。

卖花进行中漫画释义满分晋级3函数13级 二次函数的基本解析式与图象变换函数14级 二次函数 实际应用 函数15级 二次函数 图象综合应用暑期班 第二讲暑期班 第三讲秋季班第三讲二次函数实际应用中考内容中考要求A B C二次函数了解二次函数的意义；会用描点法画出二次函数的图象能通过分析实际问题的情境确定二次函数的解析式；能从图象上认识二次函数的性质；会根据二次函数的解析式求其图象与坐标轴的交点坐标，会确定图象的顶点、开口方向和对称轴；会利用二次函数的图象求一元二次方程的近似解能用二次函数解决简单的实际问题；能解决二次函数与其他知识综合的有关问题二次函数在北京中考中属于必考考点，并且都以压轴题形式出现，是中考的难点，也是同学们失分最高的一部分。

这部分内容要求学生们⑴能用数形结合、归纳等数学思想，根据二次函数的表达式确定二次函数的开口方向、对称轴和顶点坐标；⑵综合运用方程、几何、函数等知识解决实际问题。

年份2010年2011年2012年题号24 7，8，23 8，23分值8分11分11分考点确定抛物线的解析式，二次函数与等腰直角三角形综合抛物线顶点坐标；函数图象；二次函数和一次函数解析式（函数图象与坐标轴交点、函数图象交点坐标），二次函数与一元二次方程（判别式、求根）函数图象；二次函数的对称性；二次函数和一次函数解析式（函数图象与坐标轴交点、函数图象交点坐标）；二次函数图象平移，利用函数图象求取值范围中考考点分析中考内容与要求知识互联网实际应用问题主要考查涨降价、面积等问题，讲解时要明确等量关系．【例1】 如图，线段AB 的长为2，C 为AB 上一个动点，分别以AC 、BC 为斜边在AB 的同侧作两个等腰直角三角形△ACD 和△BCE ，则求DE 长的最小值．（2012扬州）EDB C A EDBC A【解析】 如图，连接DE ．设x AC =则x BC -=2，∵△ACD 和△BCE 分别是等腰直角三角形，∴∠DCA ＝45°，∠ECB ＝45°，DC ＝x 22，CE ＝()x -222， ∴∠DCE ＝90°， 故()()1122221212222222+-=+-=-+=+=x x x x x CE DC DE ， 当1=x 时，2DE 取得最小值，DE 也取得最小值，最小值为1． 故答案为：1．夯实基础模块一 实际应用问题知识导航【例2】 某商品的进价为每件50元，售价为每件60元，每个月可卖出200件。

初升高暑假数学衔接教材第一部分，如何做好高、初中数学的衔接●第一讲如何学好高中数学●初中生经过中考的奋力拼搏，刚跨入高中，都有十足的信心、旺盛的求知欲，都有把高中课程学好的愿望。

但经过一段时间，他们普遍感觉高中数学并非想象中那么简单易学，而是太枯燥、乏味、抽象、晦涩，有些章节如听天书。

在做习题、课外练习时，又是磕磕碰碰、跌跌撞撞，常常感到茫然一片，不知从何下手。

相当部分学生进入数学学习的“困难期”，数学成绩出现严重的滑坡现象。

渐渐地他们认为数学神秘莫测，从而产生畏惧感，动摇了学好数学的信心，甚至失去了学习数学的兴趣。

造成这种现象的原因是多方面的，但最主要的根源还在于初、高中数学教学上的衔接问题。

下面就对造成这种现象的一些原因加以分析、总结。

希望同学们认真吸取前人的经验教训，搞好自己的数学学习。

一高中数学与初中数学特点的变化1 数学语言在抽象程度上突变。

不少学生反映，集合、映射等概念难以理解，觉得离生活很远，似乎很“玄”。

确实，初、高中的数学语言有着显著的区别。

初中的数学主要是以形象、通俗的语言方式进行表达。

而高一数学一下子就触及抽象的集合语言、逻辑运算语言以及以后要学习到的函数语言、空间立体几何等。

2 思维方法向理性层次跃迁。

高中数学思维方法与初中阶段大不相同。

初中阶段，很多老师为学生将各种题建立了统一的思维模式，如解分式方程分几步；因式分解先看什么，再看什么。

即使是思维非常灵活的平面几何问题，也对线段相等、角相等,分别确定了各自的思维套路。

因此，初中学习中习惯于这种机械的、便于操作的定势方式。

高中数学在思维形式上产生了很大的变化，数学语言的抽象化对思维能力提出了高要求。

当然，能力的发展是渐进的，不是一朝一夕的。

这种能力要求的突变使很多高一新生感到不适应，故而导致成绩下降。

高一新生一定要能从经验型抽象思维向理论型抽象思维过渡，最后还需初步形成辩证型思维。

3 知识内容的整体数量剧增。

高中数学在知识内容的“量”上急剧增加了。

第三讲解一元二次方程——公式法用配方法解一元二次方程ax2＋bx＋c=0(a≠0)ax2＋bx=－cx2+bax=−cax2+bax+b24a2=−ca+b24a2(x+b2a)2=b2−4ac4a2（1）当b2－4ac＞0时，x+b2a =±√b2−4ac2a，一元二次方程ax2＋bx＋c=0(a≠0)有两个不相等的实数根：x1=−b+√b2−4ac2a,x2=−b−√b2−4ac2a（2）当b2－4ac=0时，一元二次方程ax2＋bx＋c=0(a≠0)有两个相等的实数根：x1= x2=−b2a；（3）当b2－4ac＜0时，一元二次方程ax2＋bx＋c=0(a≠0)无实数根．1、一元二次方程根的判别式我们称b2－4ac为一元二次方程ax2＋bx＋c=0(a≠0)根的判别式，通常用希腊字母△表示，即△=b2－4ac．判别式△与方程根的关系如下：（1）△＞0⇒方程有两个不相等的实数根；（2）△=0⇒方程有两个相等的实数根；（3）△＜0⇒方程没有实数根．2、运用公式法解一元二次方程当△≥0时，一元二次方程ax2＋bx＋c=0(a≠0)的求根公式是：x=−b±√b 2−4ac2a总结：用公式法解一元二次方程的一般步骤：例1、不解方程，判定下列一元二次方程根的情况．(1)x2＋4=4x； (2)5(x2＋1)－7x=0；(3)2x2＋3x－2=0； (4)x2－2mx＋4(m－1)＝0．例2、用公式法解一元二次方程：(1)2x2－x－6=0； (2)2y2−3y+178=0； (3)4x2－3x－1﹦x－2．例4、已知关于x的方程x2＋mx＋m－2=0．(1)若此方程的一个根为1，求m的值；(2)求证：不论m取何实数，此方程都有两个不相等的实数根．1、一元二次方程x2－2x－3＝0的解是( )A．x1＝－1，x2＝3 B．x1＝1，x2＝－3C．x1＝－1，x2＝－3 D．x1＝1，x2＝32、下列一元二次方程有实数根的是（）A．x2＋1＝0 B．x2＋x＋1＝0C．x2－x＋1＝0 D．x2－x－1＝03、用公式法解下列方程：（1）x2＝6x＋1；（2）3x(x－3)＝2(x＋1)(x－1)．4、已知关于x的方程x2－(4k＋1)x＋4k2－2=0，根据下列情况，求k的取值范围．(1)方程有两个相等的实数根；(2)方程有两个不相等的实数根；(3)方程没有实数根．。

初高中数学衔接课程（1）目 录第一讲 数与式的运算 第二讲 因式分解第三讲 一元二次方程根与系数的关系 第四讲 不 等 式第五讲 二次函数的最值问题 第六讲 简单的二元二次方程组 第七讲 分式方程和无理方程的解法 第八讲 直线、平面与常见立体图形第一讲 数与式的运算1.１绝对值绝对值的代数意义：正数的绝对值是它的本身，负数的绝对值是它的相反数，零的绝对值仍是零。

即,0,||0,0,,0.a a a a a a >⎧⎪==⎨⎪-<⎩或⎪⎩⎪⎨⎧≤-≥=）（）（0a a 0a a a绝对值的几何意义：一个数的绝对值，是数轴上表示它的点到原点的距离。

两个数的差的绝对值的几何意义：b a -表示在数轴上，数a 和数b 之间的距离。

练 习 1．填空：（1）若4-=x ，则x =_________；（2）如果5=+b a ，且1-=a ，则b ＝________； （3）若21=-c ，则c ＝________。

2．选择题：下列叙述正确的是（ ）A 、若a b =，则a b =B 、若a b >，则a b >C 、若a b <，则a b <D 、若a b =，则a b =±3．化简：|x －5|－|2x －13|（6x 5<<）。

4、解答题：已知0)5(4232=++-+-c b a ，求 c b a ++的值。

1.2、乘法公式【公式1】ca bc ab c b a c b a 222)(2222+++++=++ 证明：2222)(2)(])[()(c c b a b a c b a c b a ++++=++=++Θca bc ab c b a c bc ac b ab a 222222222222+++++=+++++=∴等式成立【例1】计算：说明：多项式乘法的结果一般是按某个字母的降幂或升幂排列。

【公式2】3322))((b a b ab a b a +=+-+(立方和公式) 证明: 3332222322))((b a b ab b a ab b a a b ab a b a +=+-++-=+-+ 【例2】计算：))((22b ab a b a ++-【公式3】3322))((b a b ab a b a -=++-(立方差公式)1.3、根式式子(0)a a ≥叫做二次根式，其性质如下：二次根式2a 的意义：2a a ==,0,,0.a a a a ≥⎧⎨-<⎩(1) 2()(0)a a a =≥(2) 2||a a =(3) (0,0)ab a b a b =⋅≥≥ (4)(0,0)bb a b aa=>≥22)312(+-x x例1 将下列式子化为最简二次根式：（1）12b ； （2）2(0)a b a ≥；（3）64(0)x y x <。