e第五章流动的转捩和稳定性5#
- 格式:doc
- 大小:1.97 MB
- 文档页数:12

流体力学张兆顺课后答案【篇一:流体力学知识点大全】书籍:《全美经典-流体动力学》《流体力学》张兆顺、崔桂香《流体力学》吴望一《一维不定常流》《流体力学》课件清华大学王亮主讲目录:第一章绪论第二章流体静力学第三章流体运动的数学模型第四章量纲分析和相似性第五章粘性流体和边界层流动第六章不可压缩势流第七章一维可压缩流动第八章二维可压缩流动气体动力学第九章不可压缩湍流流动第十章高超声速边界层流动第十一章磁流体动力学第十二章非牛顿流体第十三章波动和稳定性第一章绪论1、牛顿流体:剪应力和速度梯度之间的关系式称为牛顿关系式,遵守牛顿关系式的流体是牛顿流体。
2没有内摩擦,也就没有内耗散和损失。
层流:纯粘性流体,流体分层,流速比较小;湍流:随着流速增加,流线摆动,称过渡流,流速再增加,出现漩涡,混合。
因为流速增加导致层流出现不稳定性。
定常流:在空间的任何点,流动中的速度分量和热力学参量都不随时间改变,3、欧拉描述:空间点的坐标;拉格朗日:质点的坐标;4、流体的粘性引起剪切力,进而导致耗散。
5、无黏流体—无摩擦—流动不分离—无尾迹。
6、流体的特性:连续性、易流动性、压缩性不可压缩流体:d??0dtconst是针对流体中的同一质点在不同时刻保持不变,即不可压缩流体的密度在任何时刻都保持不变。
是一个过程方程。
7、流体的几种线流线:是速度场的向量线,是指在欧拉速度场的描述;同一时刻、不同质点连接起来的速度场向量线;dr?u?x,tdr?u?0迹线:流体质点的运动轨迹,是流体质点运动的几何描述;同一质点在不同时刻的位移曲线;涡线:涡量场的向量线,u,dr???x,t??dr???0涡线的切线和当地的涡量或准刚体角速度重合,所以,涡线是流体微团准刚体转动方向的连线,形象的说:涡线像一根柔性轴把微团穿在一起。
第二章流体静力学1、压强:p?lim?fdf??a?0?ada静止流场中一点的应力状态只有压力。
2、流体的平衡状态:1)、流体的每个质点都处于静止状态,==整个系统无加速度;2)、质点相互之间都没有相对运动,==整个系统都可以有加速度;由于流体质点之间都没有相对运动,导致剪应力处处为零,故只有:体积力(重力、磁场力)和表面力(压强和剪切力)存在。






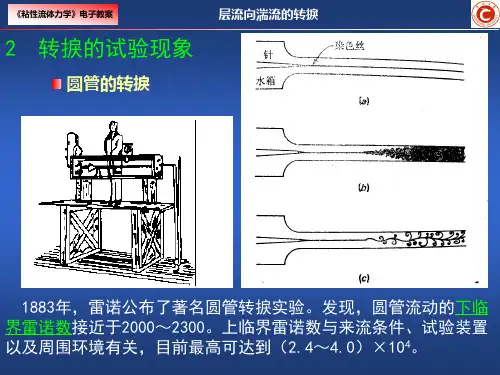
第五章流动的转捩和稳定性1883年,O.Reynolds的圆管流动染色实验揭示出有两种典型流态:层流和湍流。
实验表明,流速达到一定值,流动由层流转变为湍流,见图5.1。
流动由层流转变为湍流的过程,被称为流动转捩。
影响流动转捩的因素,除流速外还有很多,例如,流体的粘性和惯性,管道的截面形状和尺寸,管道入口流动条件等等。
从转捩现象发现至今,大量的实验研究表明,转捩过程,内容丰富而复杂,有许多问题尚需要进一步的研究。
在实验研究的同时,人们试图建立理论来解释或理解流动转捩。
借助固体动力学的稳定性概念,逐渐提出并形成了流动稳定性理论。
其基本观点是,流动参数在一定范围,层流是不稳定的,在外界扰动作用下流动偏离原层流状态而演化成一个新的流动状态,进而最终演化成湍流。
不过,直到现在,流动稳定性理论尚不能完全解释层流到湍流的转捩机理。
尽管如此,在其自身发展过程中,流动稳定性理论献出了不少研究问题的思想、方法和理论,其意义和作用并非只限于流动转捩问题的研究。
在自然界和工程技术中,许多问题和现象本身就涉及流动稳定性,或者能用到流动稳定性理论中的一些概念和方法。
因此,关于流动稳定性的研究,早已不是纯理论、纯学术问题,对理解某些自然现象和解决某些工程实际问题可起到重要的促进作用。
本章的主要内容有,流动稳定性的一些基本概念,线性稳定性理论大意,层流边界层稳定性分析的一些经典结果,边界层转捩的基本现象和影响转图5.1 管流染色实验示意图捩的因素及其影响趋势。
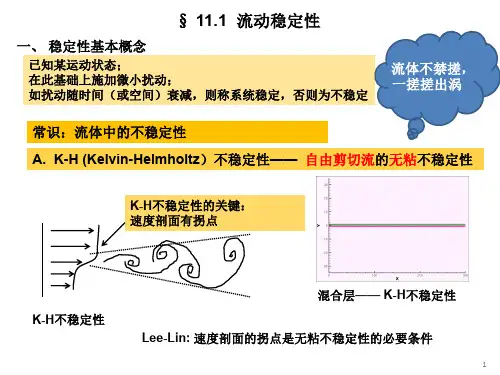
§5.1 稳定性的概念和数学提法设一个系统处于某一状态(称为原始状态)。
这里我们讲该系统的稳定与否,是针对系统的状态而言。
意思如下:由于外界的作用(该作用常称为对系统的干扰或扰动),系统偏离原来所处的状态、而进入一个新状态;当干扰或扰动去除后,如果系统能从新状态回复到原来的状态,那么系统所处状态对这个干扰是稳定的;否则,是不稳定的。
换言之,外界作用去除后,如果系统的新状态与原来状态间的差异——干扰的结果——趋于消失,系统受扰前所处状态对这个干扰是稳定的。


第五章流动的转捩和稳定性1883年,O.Reynolds的圆管流动染色实验揭示出有两种典型流态:层流和湍流。
实验表明,流速达到一定值,流动由层流转变为湍流,见图5.1。
流动由层流转变为湍流的过程,被称为流动转捩。
影响流动转捩的因素,除流速外还有很多,例如,流体的粘性和惯性,管道的截面形状和尺寸,管道入口流动条件等等。
从转捩现象发现至今,大量的实验研究表明,转捩过程,内容丰富而复杂,有许多问题尚需要进一步的研究。
在实验研究的同时,人们试图建立理论来解释或理解流动转捩。
借助固体动力学的稳定性概念,逐渐提出并形成了流动稳定性理论。
其基本观点是,流动参数在一定范围,层流是不稳定的,在外界扰动作用下流动偏离原层流状态而演化成一个新的流动状态,进而最终演化成湍流。
不过,直到现在,流动稳定性理论尚不能完全解释层流到湍流的转捩机理。
尽管如此,在其自身发展过程中,流动稳定性理论献出了不少研究问题的思想、方法和理论,其意义和作用并非只限于流动转捩问题的研究。
在自然界和工程技术中,许多问题和现象本身就涉及流动稳定性,或者能用到流动稳定性理论中的一些概念和方法。
因此,关于流动稳定性的研究,早已不是纯理论、纯学术问题,对理解某些自然现象和解决某些工程实际问题可起到重要的促进作用。
本章的主要内容有,流动稳定性的一些基本概念,线性稳定性理论大意,层流边界层稳定性分析的一些经典结果,边界层转捩的基本现象和影响转图5.1 管流染色实验示意图捩的因素及其影响趋势。
§5.1 稳定性的概念和数学提法设一个系统处于某一状态(称为原始状态)。
这里我们讲该系统的稳定与否,是针对系统的状态而言。
意思如下:由于外界的作用(该作用常称为对系统的干扰或扰动),系统偏离原来所处的状态、而进入一个新状态;当干扰或扰动去除后,如果系统能从新状态回复到原来的状态,那么系统所处状态对这个干扰是稳定的;否则,是不稳定的。
换言之,外界作用去除后,如果系统的新状态与原来状态间的差异——干扰的结果——趋于消失,系统受扰前所处状态对这个干扰是稳定的。
讲到系统稳定性时,应该明确指出系统的某个状态对具体的扰动是稳定或不稳定。
图5.2给出静止小球所处的各种状态稳定性的可能情况:(a)对大扰动和小扰动都稳定;(b)对任意扰动都不稳定;(c)这是中间情形,差异既不消失也不增长,而是保持;(d)对某些较小的扰动是稳定的,当扰动较大时不稳定的,或说失去稳定。
图5.2 静止小球的稳定性示意图依上述含义,对流动系统,其稳定性的数学提法可以如下:设NS(·) = 0、BC(·) = 0分别代表流动基本方程组和定解条件,那么流体系统的状态,可以认为是这样的Φ:⎭⎬⎫=Φ=Φ0)(0)(BC NS (5.1)设系统的原来所处状态为Φ0 ,受扰后所处的新状态为Φ1 ,那么它们都是(5.1)的解,即,⎭⎬⎫=Φ=Φ0)(0)(00BC NS (5.1a )⎭⎬⎫=Φ=Φ0)(0)(11BC NS (5.1b )而且差异(或扰动量)就是01Φ-Φ=φ (5.1c )它的时空演化由下面的方程组和定解条件控制,⎭⎬⎫=Φ-Φ+≡Φ=Φ-Φ+≡Φ0)()();(0)()();(000000BC BC dBC NS NS dNS φφφφ (5.2)简单讲,如对任意的φ都有0→φ,则系统状态 Φ0 是稳定的。
这就是稳定性问题的基本数学提法。
一般而言,稳定性方程(5.2)很难分析求解。
许多问题的稳定性分析,属于所谓的线性稳定性分析范畴。
其中,只考虑干扰量φ很小的情形,即1/0<<Φφ。
此时稳定性分析方程(5.2)可以线性化近似。
由此得出的分析结论:对一切小扰动都稳定,就是线性稳定的;只要对一个小扰动不稳定,就是线性不稳定。
这种分析判定,在实际中很有用。
本章,就限定在线性稳定性分析范围内。
下面一节,简要介绍最简单的稳定性理论——平行流(速度剖面)线性稳定性分析作。
§5.2 平行流线性稳定性理论5.2.1 O-S 方程及色散关系式以平面二维、不可压、平行流动状态为例,并只考虑二维扰动情形。
用U 、V 、W 、P 表示流动原来状态的流速、压强,受扰后的新状态相应的量由小写字母u 、v 、w 、p 表示,而扰动量(差异量)均带有撇“'”,则p P p w w W w v V v u U u y x P P W V y U U '+==''+='+='+=====,)0(,,),(,0,)( 。
扰动量满足的线性方程为⎪⎪⎪⎭⎪⎪⎪⎬⎫=∂'∂+∂'∂'∇=∂'∂+∂'∂+∂'∂'∇=∂'∂+'+∂'∂+∂'∂01122y v x u v y p x v U t v u x p dy dU v x u U t u νρνρ (5.3) 为减少分析变量,引入扰动流函数),,(t y x ψ:y u ∂∂='ψ, x v ∂∂-='ψ 。
显然,流函数适合分解成关于x 、t 的Fourier 级数。
其中任一项可以写为,)](exp[)(),,(t x i y t y x ωαϕψ-⋅= (5.4) 这是行波形式,常称为扰动波。
(5.4)式中 ϕ(y ) 是复值函数,包含波幅和初相位;α、ω一般可为复数,分别是复波数和复频率,ir ir i i ωωωααα+=+= 。
它们的实部,就是波的波数和频率,虚部为增长因子。
如果设0=i ω,即复频率 ω 为实数,稳定性分析称为空间模式。
此时,如有复波数的虚部0<i α,则扰动量将随空间 x 而增长,流动空间不稳定;如果设0=i α,即复波数 α 为实数,稳定性分析称为时间模式。
此时,如有复频率的虚部0>i ω,则扰动量将随时间 t 而增长,流动时间不稳定。
线性稳定性分析中,在判别稳定与否时,通常采用时间模式。
关于更一般的时空模式在本节最后再作介绍。
下面以时间模式为例,导出线性稳定性分析中有名O-S 方程和所谓的色散关系。
引入复波速(相速度)(注意α = αr 为实数)i r i r iC C i C +=⋅+==αωαωαω (5.5)则扰动波(5.4)化为,)](exp[)exp()(),,(t C x i t C y t y x r i -⋅⋅=ααϕψ (5.6)显然,0=i C 对应中性稳定;0>i C ,不稳定。
选定特征尺寸L 、特征流速V 0 ,引入如下无量纲化:0V U U =,0V C C =,L αα=,L y y =,和雷诺数νL V 0Re = 。
将扰动(5.6)代入扰动演化方程组(5.3),并消除扰动压力p ',可得如下无量纲扰动方程,)2(Re))((422ϕαϕαϕαϕϕαϕ+''-''''-=''--''-iU C U (5.7) 这就是平行流线性稳定性分析理论的Orr-Sommerfeld 方程,称为O-S 方程。
O-S 方程的通解,可表示成其四个线性无关解)4:1(=i i ϕ的线性组合,即44332211ϕϕϕϕϕA A A A +++= (5.8)在齐次边界条件(这仅仅是泛泛而论,具体问题有具体的条件)⎭⎬⎫='==='==0)(,0)(:0)(,0)(:222111y y y y y y y y ϕϕϕϕ (5.9)约束下,(5.8)必须满足⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡''''''''0000)()()()()()()()()()()()()()()()(432124232221242322211413121114131211A A A A y y y y y y y y y y y y y y y y ϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ (5.10) 显然,(5.10)有非平凡解的充要条件是,其4×4系数矩阵的行列式为零。
于是,导出下列结果,0),,(Re,=i r C C D α (5.11)(5.11)关系式,就是色散关系式。
它是扰动波的波数和频率必须满足的,其中还包含有流动参数(Re )。
满足该式的C ,α,称为由(5.7)及(5.9)构成的稳定性分析的特征值,与这些特征之相应的 ϕ(y) 成为特征解。
通常,色散关系没有解析表达式。
而是在α-Re 平面上,给出r i C C ,的等值曲线,以此表达色散关系。
其中0=i C 的等值曲线称为中性(稳定)曲线(见例图5.3)。
5.2.2 O-S 方程的一般性质当∞→Re α时,O-S 方程退化为瑞利(Rayleigh )方程,0))((2=''--''-ϕϕαϕU C U (5.12)以此来分析流速剖面稳定性的理论是一种无粘线性稳定性理论。
关于它,前人已有若干重要结论。
例如,(1)不稳定的必要条件是速度剖面有一个拐点[Rayleigh,1880];(2)边界层速度剖面不稳定的充分条件是速度分布有一个拐点[Tollmien,1929];(3)不稳定进一步的必要条件是,涡量︱U ′︱的数值在拐点上有最大值[Fj φrtoft,1950];(4)若U(y)在y=y c有一个拐点,则存在一中性扰动,其相速度C r=U(y s) [林家翘,1945];(5)一个放大的扰动的相速度,始终是在U(y)的最小值和最大值之间[Rayleigh,1880]。
速度分布会出现拐点的例子有,逆压梯度下的边界层,扩张管道内的流动平行流之间的剪切层,射流和尾流。
这些流速剖面均是不稳定的。
对粘性的作用,林家翘(1955)指出过,粘性的存在,即使粘度值值很小,也将保证阻尼衰减到另外的无粘扰动。
因此,许多人自然认为,无拐点的流速分布(如顺压梯度下的管流和边界层),是线性稳定的,粘性就是有助于稳定的。
尽管Rayleigh无粘理论使人们了解了有拐点速度分布的不稳定性,但对无拐点的流速分布稳定与否并不清楚。
而Prantdtl (1921)以为,对某些波数和有限的雷诺数,粘性作用实际上将减弱稳定性,因为实验清楚地表明,所有形式的层流速度分布在有限雷诺数上都变得不稳定。
Tollmien(1929),对无拐点的Blasius速度剖面的有粘(有限雷诺数)稳定性分析计算,即完全的O-S方程的计算,第一个从数学上预示了有限雷诺数上的不稳定,支持了的Prantdtl看法。
随后又有Schlichting(1932-35)等许多人的计算分析结果,都支持了的Prantdtl看法。