高中数学 4.1.2函数的极值同步练习(含解析)北师大版选修11

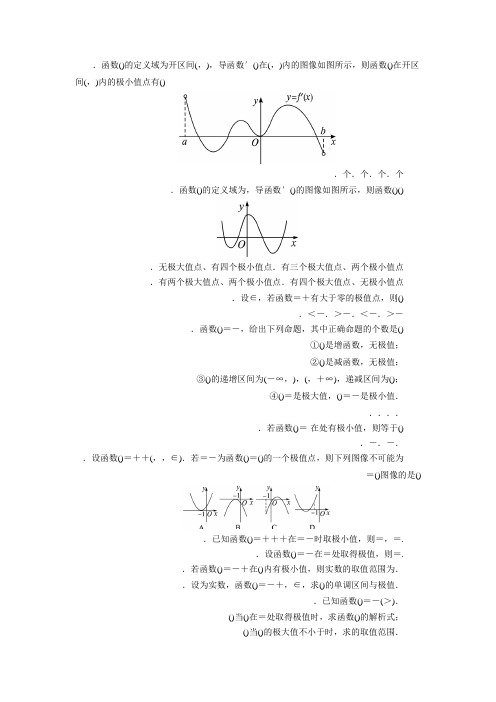
．函数()的定义域为开区间(，)，导函数′()在(，)内的图像如图所示，则函数()在开区间(，)内的极小值点有()．个．个．个．个．函数()的定义域为，导函数′()的图像如图所示，则函数()()．无极大值点、有四个极小值点．有三个极大值点、两个极小值点．有两个极大值点、两个极小值点．有四个极大值点、无极小值点．设∈，若函数＝＋有大于零的极值点，则()．＜－．＞－．＜－．＞－．函数()＝－，给出下列命题，其中正确命题的个数是()①()是增函数，无极值；②()是减函数，无极值；③()的递增区间为(－∞，)，(，＋∞)，递减区间为()；④()＝是极大值，()＝－是极小值．．．．．．若函数()＝·在处有极小值，则等于()．－．－．．设函数()＝＋＋(，，∈)．若＝－为函数()＝()的一个极值点，则下列图像不可能为＝()图像的是()．已知函数()＝＋＋＋在＝－时取极小值，则＝，＝.．设函数()＝－在＝处取得极值，则＝.．若函数()＝－＋在()内有极小值，则实数的取值范围为．．设为实数，函数()＝－＋，∈，求()的单调区间与极值．．已知函数()＝－(＞)．()当()在＝处取得极值时，求函数()的解析式；()当()的极大值不小于时，求的取值范围．参考答案.答案：.解析：设′()与轴的个交点，从左至右依次记为，，，.当＜时，′()＞，()在(－∞，)上为增加的；当＜＜时，′()＜，()在(，)上为减少的，则＝为极大值点．同理，＝为极大值点，＝，＝为极小值点．故选.答案：.解析：′＝＋.函数有极值点，则令＋＝，得＝－.又＞，则＞，故＜－.答案：.解析：′()＝－＝(－)．由′()＞，得＜或＞，由′ ()＜，得＜＜.故③④正确．答案：.解析：′＝··＋＝(·＋)．令′＝，解得＝－.答案：.解析：′()＝[′()＋()]．因为＝－是()的一个极值点，所以′(－)＝，得出′(－)＋(－)＝，在选项中，由图像观察得到(－)＞，′(－)＞，所以(－)＋′(－)＞与′(－)＋(－)＝矛盾．故选.答案：.解析：′()＝＋＋，∴′(－)＝－＋＝.①又(－)＝－＋－＋＝，②联立①②，解得(\\(＝，＝，))或(\\(＝，＝.))但当＝，＝时，′()＝(＋)≥，即＝－不是极值点，舍去．∴＝，＝.答案：.解析：′()＝－－．由题意，得′＝，∴－×－×＝.∴＝－.答案：－.解析：′()＝－，∵()在()内有极小值，∴′()＝在()内有零点．又′()＝－在()上为增加的，∴(\\(′()<，′()>.))解得＜＜.。

（新课标）2017-2018学年北师大版高中数学选修1-1第4章 1.2 函数的极值一、选择题(每小题5分，共20分) 1．下列结论中，正确的是( ) A ．导数为零的点一定是极值点B ．如果在x 0附近的左侧f ′(x)>0，右侧f ′(x)<0，那么，f(x 0)是极大值C ．如果在x 0附近的左侧f ′(x)>0，右侧f ′(x)<0，那么，f(x 0)是极小值D ．如果在x 0附近的左侧f ′(x)<0，右侧f ′(x)>0，那么，f(x 0)是极大值解析： 导数为零的点不一定是极值点，“左正右负”有极大值，“左负右正”有极小值．故A ，C ，D 项错．答案： B2．函数y ＝sin ⎝ ⎛⎭⎪⎫x ＋π2＋π在区间[－π，π]上取极大值时x 的值为( )A.π2 B ．0C ．－πD ．π解析： y ＝sin ⎝ ⎛⎭⎪⎫x ＋π2＋π＝cosx ＋π，y ′＝－sinx ，令y ′>0，则－π<x<0，因此在区间[－π，π]上，当x ∈[－π，0]时，函数为增函数，当x ∈[0，π]时，函数为减函数，根据极值定义，当x ＝0时函数在区间[－π，π]取得极大值．答案： B3．下面对于函数y ＝x 3－3x 2－9x(－2<x<2)的判断正确的是( ) A ．极大值为5，极小值为－27 B ．极大值为5，极小值为－11 C ．极大值为5，无极小值D ．极小值为－27，无极大值解析： y ′＝3x 2－6x －9＝3(x 2－2x －3)，令y ′＝0，可得x ＝3或x ＝－1.当－2<x<－1时，y ′>0；当－1<x<2时，y ′<0，故当x ＝－1时y 取得极大值． 答案： C4．若函数f(x)＝x ·2x 在x 0处有极小值，则x 0等于( ) A.1ln2 B ．－1ln2C ．－ln2D ．ln2解析： ∵y ＝x ·2x ，∴y ′＝2x ＋x ·2x ·ln2＝2x ·(1＋x ·ln2)．令y ′＝0可得：x ＝－1ln2.当x ∈⎝ ⎛⎭⎪⎫－∞，－1ln2时，y ′<0，当x ∈⎝ ⎛⎭⎪⎫－1ln2，＋∞时，y ′>0.∴x ＝－1ln2为极小值点．故选B.答案： B二、填空题(每小题5分，共10分)5．函数y ＝2x 3－15x 2＋36x －24的极大值为__________，极小值为________． 解析： y ′＝6x 2－30x ＋36，即y ′＝6(x －2)(x －3)， 令y ′＝0得x ＝2或x ＝3.经判断有极大值为f(2)＝4，极小值f(3)＝3. 答案： 4 36．函数f(x)＝x 3－3a 2x ＋a(a>0)的极大值为正数，极小值为负数，则a 的取值范围是________．解析： f ′(x)＝3x 2－3a 2＝3(x ＋a)(x －a)， 由f ′(x)<0，得－a<x<a ，∴f(x)在(－∞，－a)内递增，在(－a ，a)内递减，在(a ，＋∞)内递增， 极大值为f(－a)＝2a 3＋a ＝a(2a 2＋1)>0，极小值为f(a)＝a(1－2a 2)<0，由此解得a>22.答案： ⎝ ⎛⎭⎪⎪⎫22，＋∞三、解答题(每小题10分，共20分) 7．求函数f(x)＝x 2e －x 的极值． 解析： 函数的定义域为R ，f ′(x)＝2xe －x ＋x 2·⎝ ⎛⎭⎪⎫1e x ′＝2xe －x －x 2e －x＝x(2－x)e －x ， 令f ′(x)＝0， 得x ＝0或x ＝2，当x 变化时，f ′(x)，f(x)的变化情况如下表：x (－∞，0) 0 (0,2) 2 (2，＋∞) f ′(x) －0 ＋0 －f(x)4e －2由上表可以看出，当x ＝0时，函数有极小值，且f(0)＝0. 当x ＝2时，函数有极大值，且f(2)＝4e －2.8．已知函数y ＝ax 3＋bx 2，当x ＝1时函数有极大值3. (1)求a ，b 的值； (2)求函数y 的极小值．解析： (1)y ′＝3ax 2＋2bx ，当x ＝1时， y ′＝3a ＋2b ＝0，又y ＝a ＋b ＝3，即⎩⎪⎨⎪⎧ 3a ＋2b ＝0，a ＋b ＝3，解得⎩⎪⎨⎪⎧a ＝－6，b ＝9.(2)y ＝－6x 3＋9x 2，y ′＝－18x 2＋18x ， 令y ′＝0，得x ＝0或x ＝1.∴当x ＝0时，函数y 取得极小值0.尖子生题库☆☆☆9．(10分)已知函数f(x)＝x 3＋ax 2＋bx ＋a 2在x ＝1处取极值10，求f(2)的值． 解析： f ′(x)＝3x 2＋2ax ＋b.由题意，得⎩⎪⎨⎪⎧ f (1)＝10，f ′(1)＝0，即⎩⎪⎨⎪⎧a 2＋a ＋b ＋1＝10，2a ＋b ＋3＝0.解得⎩⎪⎨⎪⎧ a ＝4，b ＝－11，或⎩⎪⎨⎪⎧a ＝－3，b ＝3.当a ＝4，b ＝－11时，令f ′(x)＝0，得x 1＝1，x 2＝－113.当x 变化时，f(x)、f ′(x)的变化情况列表如下：x⎝⎛⎭⎪⎫－∞，－113－113⎝ ⎛⎭⎪⎫－113，1 1 (1，＋∞)f ′(x) ＋0 －0 ＋f(x)极大值极小值显然函数f(x)在x ＝1处取极小值，符合题意，此时f(2)＝18. 当a ＝－3，b ＝3时，f ′(x)＝3x 2－6x ＋3＝3(x －1)2≥0， ∴f(x)在x ＝1处没有极值，不合题意．综上可知f(2)＝18.。

【课堂新坐标】（教师用书）2013-2014学年高中数学 4.1.2 函数的极值课时训练 北师大版选修1-1一、选择题1 .函数f (x )的定义域为开区间(a ，b )，导函数f ′(x )在(a ，b )内的图像如图所示，则函数f (x )在开区间(a ，b )内有极小值点( )图4－1－4A ．1个B ．2个C ．3个D ．4个【解析】 函数在极小值点附近的图像应有先减后增的特点，因此应该在导函数的图像上找从x 轴下方变为x 轴上方的点，这样的点只有1个，所以函数f (x )在开区间(a ，b )内只有1个极小值点．【答案】 A2 .函数f (x )＝1－x ＋x 2的极小值为( ) A ．1 B.34 C. 14D.12【解析】 按求极值的步骤求解．f ′(x )＝－1＋2x ＝2(x －12)，令f ′(x )＝0，得x ＝12.当x 变化时，f ′(x )，f (x )的变化情况如下表：当x ＝12时，f (x )有极小值f (12)＝34.故选B.【答案】 B3 .函数y ＝x 3－3x 2－9x (－2<x <2)有( )A．极大值5，极小值－27 B．极大值5，极小值－11C．极大值5，无极小值D．极小值－27，无极大值【解析】由y′＝3x2－6x－9＝0，得x＝－1或x＝3，当x<－1或x>3时，y′>0.当－1<x<3时，y′<0.故当x＝－1时，函数有极大值5；x取不到3，故无极小值．【答案】 C4 .若函数f(x)＝x·2x在x0处有极小值，则x0等于( )A.1ln 2B．－1ln 2C．－ln 2 D．ln 2【解析】f′(x)＝2x＋x·2x ln 2＝2x(1＋x ln 2)，由已知f′(x0)＝0得2x0(1＋x0ln 2)＝0，即1＋x0ln 2＝0，∴x0＝－1ln 2.【答案】 B5 .已知函数f(x)＝x3＋ax2＋(a＋6)x＋1有极大值和极小值，则实数a的取值范围是( )A．－1<a<2 B．－3<a<6C．a<－3或a>6 D．a<－1或a>2【解析】f′(x)＝3x2＋2ax＋(a＋6)由题设知f′(x)有两个零点，令f′(x)＝0，则Δ＝(2a)2－4×3(a＋6)>0，解得a<－3或a>6.【答案】 C二、填空题6 .已知函数f(x)＝x3＋3ax2＋3(a＋2)x＋1既有极大值又有极小值，则实数a的取值范围是________．【解析】f′(x)＝3x2＋6ax＋3(a＋2)，因为原函数既有极大值又有极小值，所以方程f′(x)＝0有两个不同实根，即(6a)2－4×3×3(a＋2)>0，解得a>2或a<－1.【答案】a>2或a<－17 .(2012·杭州高二检测)若函数y＝－x3＋6x2＋m的极大值为13，则实数m等于________．【解析】y′＝－3x2＋12x，由y′＝0，得x＝0或x＝4，易知当x＝4是函数取极大值，所以－43＋6×42＋m＝13，解得m＝－19.【答案】－198 .已知函数f(x)＝ax3＋bx2＋cx，其导函数y＝f′(x)的图像如图所示，则下列说法中不正确的是________．①当x ＝32时，函数取得极小值；②函数有两个极值点；③当x ＝2时，函数取得极小值；图4－1－5④当x ＝1时，函数取得极大值． 【解析】 从图像上可以看到： 当x ∈(－∞，1)时，f ′(x )>0；当x ∈(1，2)时，f ′(x )<0；当x ∈(2，＋∞)时，f ′(x )>0时，所以f (x )有两个极值点1和2，且当x ＝2时，函数取得极小值；当x ＝1时，函数取得极大值．只有①不正确． 【答案】 ① 三、解答题9 .求函数y ＝13x 3－12x 2－1的极值．【解】 y ′＝x 2－x ，令y ′＝0，得x 1＝0，x 2＝1.将x 、y 及在相应区间上y ′的符号关系列表如下：所以当x ＝0时，函数有极大值－1；当x ＝1时，函数有极小值－76.10 .设f (x )＝e x1＋ax 2，其中a 为正实数．当a ＝43时，求f (x )的极值点．【解】 f ′(x )＝e x1＋ax 2－2ax（1＋ax 2）2.①当a ＝43时，若f ′(x )＝0，则4x 2－8x ＋3＝0，解得x 1＝32，x 2＝12.结合①，可知：所以x 1＝32是极小值点，x 2＝12是极大值点．11 .(2012·重庆高考)已知函数f (x )＝ax 3＋bx ＋c 在点x ＝2处取得极值c －16，求a ，b 的值．【解】 由f (x )在点x ＝2处取得极值c －16，得⎩⎪⎨⎪⎧f ′（2）＝0，f （2）＝c －16，即⎩⎪⎨⎪⎧12a ＋b ＝0，8a ＋2b ＋c ＝c －16，解得⎩⎪⎨⎪⎧a ＝1，b ＝－12. 故a ，b 的值分别为1，－12.。

1.2 函数的极值课时目标 1.了解函数在某点取得极值的必要条件和充分条件.2.会用导数求函数的极大值、极小值(其中多项式函数一般不超过三次)．1．函数的极大值点和极大值 在包含x 0的一个区间(a ，b )内，函数y ＝f (x )在任何一点的函数值都小于x 0点的函数值，称点x 0为________________，其函数值f (x 0)为函数的________________________． 2．函数的极小值点和极小值在包含x 0的一个区间(a ，b )内，函数y ＝f (x )在任何一点的函数值都_________，称点x 0为函数y ＝f (x )的极小值点，其函数值f (x 0)为函数的__________． 3．极值和极值点极大值与极小值统称为________，极大值点与极小值点统称为__________． 极值是函数在一个适当区间内的局部性质．一、选择题 1.函数f (x )的定义域为R ，导函数f ′(x )的图像如图，则函数f (x )( ) A ．无极大值点，有四个极小值点 B ．有三个极大值点，两个极小值点 C ．有两个极大值点，两个极小值点 D ．有四个极大值点，无极小值点2．已知函数f (x )，x ∈R ，且在x ＝1处，f (x )存在极小值，则( ) A ．当x ∈(－∞，1)时，f ′(x )>0； 当x ∈(1，＋∞)时，f ′(x )<0B ．当x ∈(－∞，1)时，f ′(x )>0； 当x ∈(1，＋∞)时，f ′(x )>0C ．当x ∈(－∞，1)时，f ′(x )<0； 当x ∈(1，＋∞)时，f ′(x )>0D ．当x ∈(－∞，1)时，f ′(x )<0； 当x ∈(1，＋∞)时，f ′(x )<03．函数f (x )＝x ＋1x在x >0时有( )A ．极小值B ．极大值C ．既有极大值又有极小值D ．极值不存在 4．函数f (x )的定义域为(a ，b )，导函数f ′(x )在(a ，b )内的图像如图所示，则函数f (x )在开区间(a ，b )内有极小值点( )A ． 1个B ．2个C ．3个D ．4个5．函数f (x )＝x 3－3bx ＋3b 在(0,1)内有且只有一个极小值，则( ) A ．0<b <1 B ．b <1C ．b >0D ．b <126．已知f (x )＝x 3＋ax 2＋(a ＋6)x ＋1有极大值和极小值，则a 的取值范围为( ) A ．－1<a <2 B ．－3<a <2 C ．a <－1或a二、填空题7．若函数f (x )＝x 2＋ax ＋1在x ＝1处取极值，则a ＝______.8．函数f (x )＝ax 3＋bx 在x ＝1处有极值－2，则a 、b 的值分别为________、________.9．函数f (x )＝x 3－3a 2x ＋a (a >0)的极大值为正数，极小值为负数，则a 的取值范围是__________． 三、解答题10．求下列函数的极值．(1)f (x )＝x 3－12x ；(2)f (x )＝x e －x.11．设函数f (x )＝x 3－92x 2＋6x －a .(1)对于任意实数x ，f ′(x )≥m 恒成立，求m 的最大值； (2)若方程f (x )＝0有且仅有一个实根，求a 的取值范围．能力提升12．已知函数f (x )＝(x －a )2(x －b )(a ，b ∈R ，a <b )．(1)当a ＝1，b ＝2时，求曲线y ＝f (x )在点(2，f (2))处的切线方程；(2)设x 1，x 2是f (x )的两个极值点，x 3是f (x )的一个零点，且x 3≠x 1，x 3≠x 2.证明：存在实数x 4，使得x 1，x 2，x 3，x 4按某种顺序排列后构成等差数列，并求x 4.1．求函数的极值问题要考虑极值取到的条件，极值点两侧的导数值异号．2．极值问题的综合应用主要涉及到极值的正用和逆用，以及与单调性问题的综合，利用极值可以解决一些函数解析式以及求字母范围的问题．1.2 函数的极值知识梳理1．函数y ＝f (x )的极大值点 极大值 2．大于x 0点的函数值 极小值 3．极值 极值点 作业设计 1．C2．C [∵f (x )在x ＝1处存在极小值， ∴x <1时，f ′(x )<0，x >1时，f ′(x )>0.]3．A [∵f ′(x )＝1－1x2，由f ′(x )>0，得x >1或x <－1，又∵x >0，∴x >1. 由⎩⎪⎨⎪⎧f x ，x >0.得0<x <1，即在(0,1)内f ′(x )<0， 在(1，＋∞)内f ′(x )>0，∴f (x )在 (0，＋∞)上有极小值．]4．A [f (x )的极小值点左边有f ′(x )<0，极小值点右边有f ′(x )>0，因此由f ′(x )的图像知只有1个极小值点．]5．A [f ′(x )＝3x 2－3b ，要使f (x )在(0,1)内有极小值，则⎩⎪⎨⎪⎧ff ，即⎩⎪⎨⎪⎧－3b <03－3b >0，解得0<b <1.]6．D [∵f ′(x )＝3x 2＋2ax ＋a ＋6，∴f ′(x )的图像是开口向上的抛物线，只有当Δ＝4a 2－12(a ＋6)>0时，图像与x 轴的左交点两侧f ′(x )的值分别大于零、小于零，右交点左右两侧f ′(x )的值分别小于零、大于零．所以才会有极大值和极小值．∴4a 2－12(a ＋6)>0得a >6或a <－3.] 7．3解析 f ′(x )＝2x x ＋1－x 2＋a x ＋12＝x 2＋2x －ax ＋12.∵f ′(1)＝0，∴1＋2－a4＝0，∴a ＝3.8．1 －3解析 因为f ′(x )＝3ax 2＋b ， 所以f ′(1)＝3a ＋b ＝0.①又x ＝1时有极值－2，所以a ＋b ＝－2.② 由①②解得a ＝1，b ＝－3. 9.⎝ ⎛⎭⎪⎫22，＋∞ 解析 ∵f ′(x )＝3x 2－3a 2(a >0)，∴f ′(x )>0时得：x >a 或x <－a ，f ′(x )<0时，得－a <x <a .∴当x ＝a 时，f (x )有极小值，x ＝－a 时，f (x )有极大值．由题意得：⎩⎪⎨⎪⎧a 3－3a 3＋a <0，－a 3＋3a 3＋a >0.a >0解得a >22. 10．解 (1)函数f (x )的定义域为R . f ′(x )＝3x 2－12＝3(x ＋2)(x －2)． 令f ′(x )＝0，得x ＝－2或x ＝2.当x 变化时，f ′(x )，f (x )的变化情况如下表：从表中可以看出，当x ＝－2时，函数f (x )有极大值，且f (－2)＝(－2)3－12×(－2)＝16； 当x ＝2时，函数f (x )有极小值，且f (2)＝23－12×2＝－16.(2)f ′(x )＝(1－x )e －x.令f ′(x )＝0，解得x ＝1. 当x 变化时，f ′(x )，f (x )的变化情况如下表：函数f (x )在x ＝1处取得极大值f (1)，且f (1)＝1e.11．解 (1)f ′(x )＝3x 2－9x ＋6. 因为x ∈(－∞，＋∞)，f ′ (x )≥m ，即3x 2－9x ＋(6－m )≥0恒成立，所以Δ＝81－12(6－m )≤0，解得m ≤－34，即m 的最大值为－34.(2)因为当x <1时，f ′(x )>0； 当1<x <2时，f ′(x )<0； 当x >2时，f ′(x )>0.所以当x ＝1时，f (x )取极大值f (1)＝52－a ；当x ＝2时，f (x )取极小值f (2)＝2－a ，故当f (2)>0或f (1)<0时，f (x )＝0仅有一个实根．解得a <2或a >52.12．(1)解 当a ＝1，b ＝2时，f (x )＝(x －1)2(x －2)， 因为f ′(x )＝(x －1)(3x －5)， 故f ′(2)＝1，又f (2)＝0，所以f (x )在点(2,0)处的切线方程为y ＝x －2.(2)证明 因为f ′(x )＝3(x －a )(x －a ＋2b3)，由于a <b ，故a <a ＋2b3，所以f (x )的两个极值点为x ＝a ，x ＝a ＋2b3.不妨设x 1＝a ，x 2＝a ＋2b3，因为x 3≠x 1，x 3≠x 2，且x 3是f (x )的零点， 故x 3＝b .又因为a ＋2b 3－a ＝2(b －a ＋2b 3)，x 4＝12(a ＋a ＋2b 3)＝2a ＋b 3，此时a ，2a ＋b 3，a ＋2b3，b 依次成等差数列，所以存在实数x 4满足题意，且x 4＝2a ＋b3.。

2016-2017学年高中数学第四章导数应用4.1.2函数的极值学业分层测评含解析北师大版选修1-120170704114D不变号零点不是极值点，∴f(x)在开区间(a，b)内有3个极值点．【答案】 C2．函数f(x)＝1＋3x－x3( )A．有极小值，无极大值B．无极小值，有极大值C．无极小值，无极大值D．有极小值，有极大值【解析】∵f′(x)＝－3x2＋3，由f′(x)＝0得x＝±1.当x∈(－1,1)时f′(x)>0，∴f(x)的单调递增区间为(－1,1)；同理，f(x)的单调递减区间为(－∞，－1)和(1，＋∞)．∴当x＝－1时，函数有极小值－1，当x＝1时，函数有极大值3.【答案】 D3．已知函数f(x)＝x3＋ax2＋(a＋6)x＋1没有极值，则实数a的取值范围是( )A．(－3,6) B．[－3,6]C．(－∞，－3)∪(6，＋∞) D．(－∞，－3]∪[6，＋∞)【解析】f′(x)＝3x2＋2ax＋a＋6，由题意可知f′(x)＝0没有实根或有两个相等实根，故Δ＝4a2－12(a＋6)≤0，解得－3≤a≤6，故选B.【答案】 B4．函数f(x)＝ax3＋bx2＋cx的图像如图4­1­6所示，且f(x)在x＝x0与x＝2处取得极值，则f(1)＋f(－1)的值一定( )图4­1­6A．等于0 B．大于0C．小于0 D．小于或等于0【解析】f′(x)＝3ax2＋2bx＋c，由题意知，x＝x0与x＝2是方程3ax2＋2bx＋c＝0的两根，由图像知，a＞0且x0＋2＜0，∴－2b6a＜0，∴b＞0.又f(1)＋f(－1)＝2b，∴f(1)＋f(－1)＞0.【答案】 B5．三次函数当x＝1时有极大值4，当x＝3时有极小值0，则此函数的解析式是( ) A．y＝x3＋6x2＋9x B．y＝x3－6x2＋9xC．y＝x3－6x2－9x D．y＝x3＋6x2－9x【解析】设f(x)＝ax3＋bx2＋cx＋d(a≠0)，则f(x)＝3ax2＋2bx＋c，由题意得f′(1)＝f′(3)＝0，f(1)＝4，f(3)＝0，即⎩⎪⎨⎪⎧3a ＋2b ＋c ＝0，27a ＋6b ＋c ＝0，a ＋b ＋c ＋d ＝4，27a ＋9b ＋3c ＋d ＝0，解得：a ＝1，b ＝－6，c ＝9，d ＝0. 【答案】 B 二、填空题6．(2016·湛江高二检测)函数f (x )＝x 3－3x 2＋1在x ＝________处取得极小值．【解析】 f ′(x )＝3x 2－6x ＝3x (x －2)，令f ′(x )＝0，得x ＝0或x ＝2；由f ′(x )＞0，得x ＜0或x ＞2；由f ′(x )＜0，得0＜x ＜2，∴f (x )在x ＝2处取得极小值．【答案】 27．函数f (x )＝2x 3－3x 2＋a 的极大值为6，那么a ＝________.【解析】 由f ′(x )＝6x 2－6x ，知函数f (x )的单调递增区间为(－∞，0)和(1，＋∞)，单调递减区间为(0,1)，故f(x)在x＝0处取得极大值6，故a＝6.【答案】 68．已知函数f(x)＝－12x2＋4x－3ln x在[t，t＋1]上不单调，则t的取值范围是________．【解析】由题意知f′(x)＝－x＋4－3x ＝－x2＋4x－3x ＝－x－1x－3x，由f′(x)＝0得函数f(x)的两个极值点为1,3，则只要这两个极值点有一个在区间(t，t＋1)内，函数f(x)在区间[t，t＋1]上就不单调，由t<1<t＋1或t<3<t＋1，得0<t<1或2<t<3.【答案】(0,1)∪(2,3)三、解答题9．求下列函数的极值： (1)f (x )＝x 3－2x 2＋x ＋1； (2)f (x )＝x2ex .【解】 (1)函数的定义域为R ，f ′(x )＝3x 2－4x ＋1＝3(x －1)⎝⎛⎭⎪⎫x －13.令f ′(0)>0，可得x >1或x <13；令f ′(x )<0，可得13<x <1.∴函数f (x )＝x 3－2x 2＋x ＋1的单调递增区间为⎝ ⎛⎭⎪⎫－∞，13和(1，＋∞)，单调递减区间为⎝ ⎛⎭⎪⎫13，1. ∴当x ＝13时，函数有极大值，且为f ⎝ ⎛⎭⎪⎫13＝4327，当x ＝1时，函数有极小值，且为f (1)＝1，(2)函数的定义域为R，f′(x)＝2x e－x－x2e－x＝x(2－x)e－x，令f′(x)＝0，得x＝0或x＝2.当x变化时，f′(x)，f(x)的变化情况如下表：由上表可以看出，当＝0时，函数有极小值，且为f(0)＝0；当x＝2时，函数有极大值，且为f(2)＝4e －2.10．是否存在实数a，使函数f(x)＝13x3＋x2＋ax＋1在x＝1处取极值？若存在，求出a的值，并判断f(1)是极大值还是极小值；若不存在，请说明理由．【解】假设存在实数a使函数f(x)＝1 3 x3＋x2＋ax＋1在x＝1处取极值．又f′(x)＝x2＋2x＋a，∴f′(1)＝0，即1＋2＋a＝0，∴a＝－3当a＝－3时，f′(x)＝x2＋2x－3，令f′(x)＝0得x＝1或x＝－3.当x>1时，f′(x)>0，当－3<x<1时，f′(x)<0，故函数f(x)在x＝1处取极小值．故存在实数a＝－3使函数f(x)＝13x3＋x2＋ax＋1在x＝1处取极小值．[能力提升]1．设函数f(x)在R上可导，其导函数为f′(x)，且函数f(x)在x＝－2处取得极小值，则函数y＝xf′(x)的图像可能是( )【解析】∵f(x)在x＝－2处取得极小值，∴当x＜－2时，f(x)单调递减，即f′(x)＜0；当x＞－2时，f(x)单调递增，即f′(x)＞0.∴当x＜－2时，y＝xf′(x)＞0；当x＝－2时，y＝xf′(x)＝0；当－2＜x＜0时，y＝xf′(x)＜0；当x＝0时，y＝xf′(x)＝0；当x＞0时，y＝xf′(x)＞0.结合选项中图像知，选C.【答案】 C2．已知e为自然对数的底数，设函数f(x)＝(e x－1)·(x－1)k(k＝1,2)，则( ) A．当k＝1时，f(x)在x＝1处取到极小值B．当k＝1时，f(x)在x＝1处取到极大值C．当k＝2时，f(x)在x＝1处取到极小值D．当k＝2时，f(x)在x＝1处取到极大值【解析】当k＝1时，f′(x)＝e x·x－1，f′(1)≠0.∴x＝1不是f(x)的极值点．当k＝2时，f′(x)＝(x－1)(x e x＋e x－2)显然f′(1)＝0，且x在1的左边附近f′(x)<0，x在1的右边附近f′(x)>0，∴f(x)在x＝1处取到极小值．故选C.【答案】 C3．设函数f(x)＝x3－92x2＋6x－a.(1)对于任意实数x，f′(x)≥m恒成立，求m的最大值；(2)若方程f(x)＝0有且仅有一个实根，求a的取值范围．【解】(1)f′(x)＝3x2－9x＋6.∵x∈(－∞，＋∞)，f′(x)≥m恒成立，即3x2－9x＋(6－m)≥0恒成立，∴Δ＝81－12(6－m)≤0，得m≤－34 .即m的最大值为－34 .(2)∵当x<1时，f′(x)>0；当1<x<2时，f′(x)<0；当x>2时，f′(x)>0；∴当x＝1时，f(x)取极大值f(1)＝52－a；当x＝2时，f(x)取极小值f(2)＝2－a. 故当f(2)>0或f(1)<0时，方程f(x)＝0仅5 2.有一个实根，解得a<2或a>。

4-1.2函数的极值(本栏目内容，在学生用书中以活页形式分册装订！)一、选择题(每小题5分，共20分) 1．下列结论中，正确的是( ) A ．导数为零的点一定是极值点B ．如果在x 0附近的左侧f ′(x )>0，右侧f ′(x )<0，那么，f (x 0)是极大值C ．如果在x 0附近的左侧f ′(x )>0，右侧f ′(x )<0，那么，f (x 0)是极小值D ．如果在x 0附近的左侧f ′(x )<0，右侧f ′(x )>0，那么，f (x 0)是极大值解析： 导数为零的点不一定是极值点，“左正右负”有极大值，“左负右正”有极小值．故A ，C ，D 项错．答案： B2．函数y ＝sin ⎝⎛⎭⎫x ＋π2＋π在区间[－π，π]上取极大值时x 的值为( ) A.π2 B ．0 C ．－πD ．π解析： y ＝sin ⎝⎛⎭⎫x ＋π2＋π＝cos x ＋π，y ′＝－sin x ，令y ′>0， 则－π<x <0，因此在区间[－π，π]上，当x ∈[－π，0]时，函数为增函数，当x ∈[0，π]时，函数为减函数，根据极值定义，当x ＝0时函数在区间[－π，π]取得极大值．答案： B3．下面对于函数y ＝x 3－3x 2－9x (－2<x <2)的判断正确的是( ) A ．极大值为5，极小值为－27 B ．极大值为5，极小值为－11 C ．极大值为5，无极小值D ．极小值为－27，无极大值解析： y ′＝3x 2－6x －9＝3(x 2－2x －3)，令y ′＝0，可得x ＝3或x ＝－1.当－2<x <－1时，y ′>0；当－1<x <2时，y ′<0，故当x ＝－1时y 取得极大值． 答案： C4．若函数f (x )＝x ·2x 在x 0处有极小值，则x 0等于( ) A.1ln2 B ．－1ln2C ．－ln2D ．ln2解析： ∵y ＝x ·2x ，∴y ′＝2x ＋x ·2x ·ln2＝2x ·(1＋x ·ln2)． 令y ′＝0可得：x ＝－1ln2.当x ∈⎝⎛⎭⎫－∞，－1ln2时，y ′<0，当x ∈⎝⎛⎭⎫－1ln2，＋∞时，y ′>0. ∴x ＝－1ln2为极小值点．故选B.答案： B二、填空题(每小题5分，共10分)5．函数y ＝2x 3－15x 2＋36x －24的极大值为__________，极小值为________． 解析： y ′＝6x 2－30x ＋36，即y ′＝6(x －2)(x －3)， 令y ′＝0得x ＝2或x ＝3.经判断有极大值为f (2)＝4，极小值f (3)＝3. 答案： 4 36．函数f (x )＝x 3－3a 2x ＋a (a >0)的极大值为正数，极小值为负数，则a 的取值范围是________．解析： f ′(x )＝3x 2－3a 2＝3(x ＋a )(x －a )， 由f ′(x )<0，得－a <x <a ，∴f (x )在(－∞，－a )内递增，在(－a ，a )内递减，在(a ，＋∞)内递增， 极大值为f (－a )＝2a 3＋a ＝a (2a 2＋1)>0， 极小值为f (a )＝a (1－2a 2)<0，由此解得a >22. 答案： ⎝⎛⎭⎫22，＋∞三、解答题(每小题10分，共20分) 7．求函数f (x )＝x 2e －x 的极值． 解析： 函数的定义域为R ，f ′(x )＝2x e －x ＋x 2·⎝⎛⎭⎫1e x ′ ＝2x e －x －x 2e －x ＝x (2－x )e －x ，令f ′(x )＝0， 得x ＝0或x ＝2，当x 变化时，f ′(x )，f (x )的变化情况如下表：x (－∞，0)0 (0,2) 2 (2，＋∞)f ′(x ) －0 ＋0 －f (x )4e －2当x ＝0时，函数有极小值，且f (0)＝0. 当x ＝2时，函数有极大值，且f (2)＝4e －2.8．已知函数y ＝ax 3＋bx 2，当x ＝1时函数有极大值3. (1)求a ，b 的值； (2)求函数y 的极小值．解析： (1)y ′＝3ax 2＋2bx ，当x ＝1时， y ′＝3a ＋2b ＝0，又y ＝a ＋b ＝3，即⎩⎪⎨⎪⎧ 3a ＋2b ＝0，a ＋b ＝3，解得⎩⎪⎨⎪⎧a ＝－6，b ＝9.(2)y ＝－6x 3＋9x 2，y ′＝－18x 2＋18x ， 令y ′＝0，得x ＝0或x ＝1. ∴当x ＝0时，函数y 取得极小值0.9．(10分)已知函数f (x )＝x 3＋ax 2＋bx ＋a 2在x ＝1处取极值10，求f (2)的值． 解析： f ′(x )＝3x 2＋2ax ＋b .由题意，得⎩⎪⎨⎪⎧ f (1)＝10，f ′(1)＝0，即⎩⎪⎨⎪⎧a 2＋a ＋b ＋1＝10，2a ＋b ＋3＝0.解得⎩⎪⎨⎪⎧ a ＝4，b ＝－11，或⎩⎪⎨⎪⎧a ＝－3，b ＝3.当a ＝4，b ＝－11时，令f ′(x )＝0，得x 1＝1，x 2＝－113.当x 变化时，f (x )、f ′(x )的变化情况列表如下：x ⎝⎛⎭⎫－∞，－113－113 ⎝⎛⎭⎫－113，1 1 (1，＋∞)f ′(x ) ＋0 －0 ＋f (x )极大值极小值当a ＝－3，b ＝3时，f ′(x )＝3x 2－6x ＋3＝3(x －1)2≥0， ∴f (x )在x ＝1处没有极值，不合题意．综上可知f (2)＝18.。

课时跟踪训练(十一) 函数的极值．函数＝－的极值情况为( )．在＝处取得极大值，但无极小值．在＝处取得极小值－，但无极大值．在＝处取得极大值，在＝处取得极小值－．以上都不对．函数＝＋(－)在＝时取极值，则的值为( )．．．－．不存在．函数()＝－＋在()内有极值，则( )．<．<<．<．>．设三次函数()的导函数为′()，函数＝′()的图像的一部分如图所示，则正确的是()．()的极大值为()，极小值为(－)．()的极大值为(－)，极小值为()．()的极大值为(－)，极小值为()．()的极大值为()，极小值为(－)．若函数()＝在＝处取得极值，则＝.．已知函数()＝＋＋，其导函数＝′()的图像经过点()，()，如图所示，则下列说法中正确的是．①当＝时函数取得极小值；②()有两个极值点；③当＝时函数取得极小值；④当＝时函数取得极大值．．求下列函数的极值．()()＝－－＋；()()＝.．已知函数()＝－＋－，其中≠，求()的极值．答案．选因为＝－，所以′＝－＝(－)．令′＝，解得＝或＝.令＝()，当变化时，′()，()的变化情况如下表：当＝时，函数＝－取得极小值－.．选′＝＋＝(<)，由题意得＝时′＝，即＝.检验：当＝时′＝，当<时′>，当<<时′<，符合题意．．选′()＝－.因()在()内有极值，所以′()＝有解，∴＝±，∴<<，∴<<.．选由题图可知，当∈(－∞，－)时，′()>，即′()<；当∈(－)时，′()<，即′()>；当∈()时，′()>，即′()>；当∈(，＋∞)时，′()<，即′()<.故函数()在＝－处取得极小值，在＝处取得极大值．．解析：′()＝＝，由题意得′()＝＝，解得＝.经检验，＝符合题意．答案：．解析：由图像可知，当∈(－∞，)时，′()>；当∈()时，′()<；。

1.函数f(x)的定义域为开区间(a，b)，导函数f′(x)在(a，b)内的图像如图所示，则函数f(x)在开区间(a，b)内有极小值点()A．1个B．2个C．3个D．4个解析：函数在极小值点附近的图像应有先减后增的特点，因此根据导函数的图像，应该在导函数的图像上找从x轴下方变为x轴上方的点，这样的点只有1个，所以函数只有1个极小值点．[]答案：A2．若函数f(x)＝x·2x在x0处有极小值，则x0等于()A.1ln 2B．－1 ln 2C．－ln 2 D．ln 2 解析：f′(x)＝2x＋x·2x ln 2，令f′(x)＝0，得x＝－1ln 2.当x<－1ln 2时f′(x)<0，当x>－1ln 2时，f′(x)>0，∴当x＝－1ln 2时，函数f(x)取极小值．答案：B3．(2012·陕西高考)设函数f(x)＝x e x，则()A．x＝1为f(x)的极大值点B．x＝1为f(x)的极小值点C．x＝－1为f(x)的极大值点D．x＝－1为f(x)的极小值点解析：求导得f′(x)＝e x＋x e x＝e x(x＋1)，令f′(x)＝e x(x＋1)＝0，解得x＝－1，易知x ＝－1是函数f(x)的极小值点．答案：D4．三次函数当x＝1时有极大值4，当x＝3时有极小值0，则此函数的解析式是() A．y＝x3＋6x2＋9x B．y＝x3－6x2＋9xC．y＝x3－6x2－9x D．y＝x3＋6x2－9x解析：设f (x )＝ax 3＋bx 2＋cx ＋d (a ≠0)，则f ′(x )＝3ax 2＋2bx ＋c ，由题意得f ′(1)＝f ′(3)＝0，f (1)＝4，f (3)＝0，即⎩⎪⎨⎪⎧ 3a ＋2b ＋c ＝0，27a ＋6b ＋c ＝0，a ＋b ＋c ＋d ＝4，27a ＋9b ＋3c ＋d ＝0，解得：a ＝1，b ＝－6，c ＝9，d ＝0.答案：B 5．函数y ＝x 3＋x 2－x ＋1在x ＝________处取极大值．解析：y ′＝3x 2＋2x －1＝(3x －1)(x ＋1)．当－1<x <13时，y ′<0；当x >13或x <－1时，y ′>0. ∴函数在x ＝－1处取极大值．答案：－16．若函数f (x )＝x 2＋a x ＋1在x ＝1处取极值，则a ＝________. 解析：∵f ′(x )＝⎝ ⎛⎭⎪⎫x 2＋a x ＋1′ ＝(x 2＋a )′·(x ＋1)－(x 2＋a )(x ＋1)′(x ＋1)2＝x 2＋2x －a (x ＋1)2. 又∵x ＝1为函数的极值点，∴有f ′(1)＝0.∴1＋2×1－a ＝0，即a ＝3.答案：37．已知f (x )＝x 3＋3ax 2＋bx ＋a 2在x ＝－1时有极值0，求a 、b 的值． 解：∵f (x )在x ＝－1时有极值0，且f ′(x )＝3x 2＋6ax ＋b ，∴⎩⎪⎨⎪⎧ f ′(－1)＝0，f (－1)＝0，即⎩⎪⎨⎪⎧ 3－6a ＋b ＝0，－1＋3a －b ＋a 2＝0，解得⎩⎪⎨⎪⎧ a ＝1，b ＝3，或⎩⎪⎨⎪⎧a ＝2，b ＝9.当a ＝1，b ＝3时，f ′(x )＝3x 2＋6x ＋3＝3 (x ＋1)2≥0，所以f (x )在R 上是增加的，无极值，故舍去．当a ＝2，b ＝9时，f ′(x )＝3x 2＋12x ＋9＝3(x ＋1)(x ＋3)．当x ∈(－∞，－3)时，f (x )为增加的；当x ∈(－3，－1)时，f (x )为减少的；当x ∈(－1，＋∞)时，f (x )为增加的．所以f (x )在x ＝－1时取得极小值，因此a ＝2，b ＝9.8．设函数f (x )＝x 3－3ax ＋b (a ≠0)．(1)若曲线y ＝f (x )在点(2，f (2))处与直线y ＝8相切，求a ，b 的值；(2)求函数f (x )的单调区间与极值点．解：(1)f ′(x )＝3x 2－3a .因为曲线y ＝f (x )在点(2，f (2))处与直线y ＝8相切， 所以⎩⎪⎨⎪⎧ f ′(2)＝0，f (2)＝8.即⎩⎪⎨⎪⎧3(4－a )＝0，8－6a ＋b ＝8.解得a ＝4，b ＝24. (2)f ′(x )＝3(x 2－a )(a ≠0)．当a <0时，f ′(x )>0，函数f (x )的单调递增区间为(－∞，＋∞)；此时函数f (x )没有极值点．当a >0时，由f ′(x )＝0得x ＝±a .当x ∈(－∞，－a )时，f ′(x )>0；当x ∈(－a ，a )时，f ′(x )<0；当x ∈(a ，＋∞)时，f ′(x )>0.函数的单调递增区间为(－∞，－a )，(a ，＋∞)，递减区间为(－a ，a )．此时x＝－a是f(x)的极大值点，x＝a是f(x)的极小值点．。

高中数学学习材料鼎尚图文*整理制作1函数的单调性与极值（北师大版选修1-1） 建议用时实际用时 满分 实际得分 45分钟一、选择题（每小题5分）1. 关于函数的极值，下列说法正确的是（ ）A.导数为0的点一定是函数的极值点B.函数的极小值一定小于它的极大值C.在定义域内最多只能有一个极大值，一个极小值D.若在内有极值，则在内不是单调函数2.函数的极值点个数为( ) A ．2 B ．1C ．0D ．由a 确定 3.已知是R 上的单调增函数,则b 的取值范围是( )A. {b|b-1或b2}B. {b|b-1或b2}C. {b|-2b1}D. {b|-1b2}4.函数f(x)＝，已知f(x)有两个极值点，则等于( )A ．9B ．－9C ．1D ．－1二、填空题（每小题5分）5.函数的极值点个数为 .6.若函数f (x )＝a －3x 在(－1,1)上单调递减，则实数a 的取值范围是 .7.已知f(x)＝+1在R 上是减函数，求实数a 的取值范围 .三、解答题（共55分）8.(10分)设1x =和2x =是函数3()f x ax =+261bx x ++的两个极值点. (1)求a ，b 的值(2)求()f x 的单调区间.9.(12分)已知函数323()(32af x x x a =-++1)1x +其中a 为实数. （1）已知函数()f x 在1x =处取得极值，求a 的值；（2）已知不等式2()1f x x x a '--+＞对任意(0,)a ∈+∞都成立，求实数x 的取值范围.10.(10分) 设函数，其中≠0．证明：当时，函数没有极值点；当时，函数有且只有一个极值点，并求出极值．11.（8分）已知函数讨论函数f(x)的单调性12.(15分)已知函数()ln f x ax x =+()a ∈R .(1)若2a =，求曲线()y f x =在1x =处切线的 斜率；(2)求()f x 的单调区间；(3)设2()22g x x x =-+，若对任意1(0,)x ∈+∞，均存在[]20,1x ∈，使得12()()f x g x <，求a 的取值范围1.D 解析：函数在处取得极值⇔，且，故A 不正确；极值是函数的局部性质，极大值与极小值之间，一般来说没有大小关系，故B 不正确； 函数在定义域内可能有多个极大值和多个极小值，故C 不正确；若在内有极值，则在内不是单调函数，正确.故选D ．2.C 解析：因为恒成立，所以f(x)无极值.3.D 解析：因为是R 上的单调增函数，所以对x ∈R 恒成立，即解得.4.C 解析：，由，得的两个解，则＝1.5.0 解析：因为恒成立，所以f(x)无极值.6.a ≤1 解析：f ′(x )＝3a －3，由题意知f ′(x )≤0在 (－1,1)上恒成立．若a ≤0，显然有f ′(x )＜0；若a ＞0，由f ′(x )≤0，得－≤x ≤，于是≥1，∴ 0＜a ≤1.综上知a ≤1.7.(] 解析：已知当时，f(x)是减函数.所以，(1)当时，由，知在R 上是减函数；(2)当时，，由函数在R 上的单调性，可知当时，在R 上是减函数；(3)当时，在R 上存在一个区间，其上有所以，当时，函数在R 上不是减函数.综上，所求a 的取值范围是.8.解：（1）2()326f x ax bx '=++，由已知可得(1)3260f a b '=++=，2(2)322260f a b '=⨯+⨯+=.解得91,.2a b ==- (2)由（1）知22'()3963(32)3(1)(2).f x x x x x x x =-+=-+=-- 当(,1)(2,)x ∈-∞+∞∪时，()0f x '>； 当(1,2)x ∈时，()0f x '<. 因此()f x 的单调增区间是(,1),(2,),-∞+∞ ()f x 的单调减区间是(1,2).9.解：(1) 2()3(1)f x ax x a '=-++.由于函数()f x 在1x =处取得极值，所以有(1)0f '=，即3101a a a -++=⇒=.（2）由题设知：223(1)1ax x a x x a -++>--+对任意(0,)a ∈+∞都成立， 即22(2)20a x x x +-->对任意(0,)a ∈+∞都成立.于是2222x x a x +>+对任意(0,)a ∈+∞都成立，即22202x x x +≤+.20x ∴-≤≤. 从而实数x 的取值范围为20x -≤≤.10. 证明：因为，，所以的定义域为（0，+∞）,．当时，如果＞0，＞0，，在（0，+∞）上单调递增；如果＜0，＜0，＜0，在（0，+∞）上单调递减．所以当＞0，函数没有极值点．当＜0时，.令，得（舍去），，当＞0，＜0时，，随的变化情况如下表：从上表可看出，函数有且只有一个极小值点，极小值为.当＜0，＞0时，，随的变化情况如下表：从上表可看出，函数有且只有一个极大值点，极大值为.综上所述，当＞0时，函数没有极值点；当＜0时，若＞0，＜0时，函数有且只有一个极小值点，极小值为若＜0，＞0时，函数有且只有一个极大值点，极大值为.11.解：当（2）当时，函数上单调递增，最大值为12.解：(1)由已知1()2(0)f x x x'=+>，(1)213f '=+=. 故曲线()y f x =在1x =处切线的斜率为3.(2)11'()(0)ax f x a x x x+=+=>. ①当0a ≥时，由于0x >，故10ax +>，'()0f x >，所以函数()f x 的单调递增区间为.②当0a <时，由'()0f x =，得1x a=-. 在区间1(0,)a -内，()0f x '>；在区间1(,)a-+∞内，()0f x '<， 所以函数()f x 的单调递增区间为1(0,-)a ，单调递减区间为1(-,)a+∞. (3)由已知，转化为max max ()()f x g x <，max ()2g x =. 由(2)知，当0a ≥时，函数()f x 在(0,)+∞上单调递增，值域为R ，故不符合题意. (或者举出反例：存在33(e )e 32f a =+>，故不符合题意.) 当0a <时，函数()f x 在)1,0(a -上单调递增，在),1(+∞-a上单调递减， 故()f x 的极大值即为最大值，11()1ln()1ln()f a a a-=-+=----， 所以21ln()a >---，解得31e a <-。