平面设计缓和曲线

收稿日期:20040524作者简介:王厚雄(1938—),男,研究员,1959年毕业于唐山铁道学院选线设计及铁路航空勘察专业。

线路圆曲线半径、缓和曲线长度和线间距标准制定依据的介绍王厚雄(铁道科学研究院铁道建筑研究所　北京　100081) 摘　要:着重介绍《新建时速200公里客货共线铁路设计暂行规定》(以下简称《暂规》)中3个主要线路平面设计标准的拟定原则,计算方法和参数选择的思路。

《暂规》期望,这些思路有助于提高线路平面质量,使线路有可能达到“少维修”的水平,从而满足新建时速200km 客货共线铁路安全、舒适和不间断运营的要求。

关键词:时速200km 铁路;客货共线铁路;线路圆曲线半径;线间距;缓和曲线长度 中图分类号:U412134 文献标识码:C 文章编号:10042954(2004)07003304 《新建时速200公里客货共线铁路设计暂行规定》基于我国铁路设计和运营实践多年经验教训,对线路主要平面设计标准的拟定原则、计算方法及参数选择方法,作了不同于99版国标《铁路线路设计规范》(以下简称《线规》)的一些改动。

这些改动与前苏联铁路设计规范(СНИПⅡ3976)和欧盟国家铁路设计思路基本接轨[1]。

编制者期望,由这些改动得出的相关设计标准,配合线路、轨道、路基和桥梁等设计标准,有助于提高时速200km 铁路的线路设计质量,在符合安全适用、技术先进、经济合理的前提下,有可能使线路达到“少维修”水平,从而满足新建时速200km 客货共线铁路安全、舒适和不间断的运营要求。

国外多年运营实践表明,“少维修”是时速200km 以上高速铁路所必需具备的基本条件之一。

由于新建时速200km 客货共线铁路在我国属开创性工程,既无试验数据可以利用,也无运营实践经验可遵循,故本次编制的相关规定只能是暂时性的,有待今后深入研究、实践观测和修订完善。

1　线路圆曲线半径111　圆曲线半径的划分及选用原则(1)推荐半径在定线选择圆曲线半径时,应优先选用推荐半径。

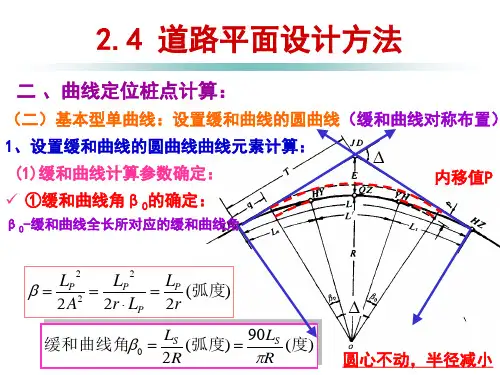
平面设计-缓和曲线、平面线形组合设计缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间，由较大圆曲线向较小圆曲线过渡的线形，是道路平面线形要素之一。

缓和曲线的主要特征是曲率均匀变化。

一、设置缓和曲线的目的和条件（一）设置缓和曲线的条件《公路工程技术标准》规定：直线与小于不设超高的圆曲线最小半径相衔接处，应设置缓和曲线（回旋线）；四级公路的直线与小于不设超高的圆曲线最小半径相衔接处，可不设置缓和曲线（回旋线），用超高、加宽缓和段径相连接。

（二）设置缓和曲线的目的1．有利于驾驶员操纵方向盘2．消除离心力的突变，提高舒适性3．完成超高和加宽的过渡4．与圆曲线配合得当，增加线形美观二、缓和曲线的性质（一）汽车转弯时行驶的理论轨迹方程图2—4 汽车进入曲线行驶轨迹图假定汽车是等速行驶，驾驶员匀速转动方向盘，当方向盘转动角度为φ 时，前轮相应转动角度为φ，通过理论推导得出弧长和曲率半径的关系有:=式中：K为小于1的系数；ω—方向盘转动的角速度（rad /s）；t —行驶时间（s）； d —汽车前后轴轮距；－汽车匀速行驶的速度（m/s）。

鉴于、d 、K、ω均为常数，可令C= ，则有：= ；此为汽车车轮行驶的轨迹方程。

式中：—汽车自直线终点进入曲线经t 时间后行驶的弧长，m；ρ—汽车行驶经t 时间后行驶的弧长处相对应的曲率半径，m；C—常数（二）回旋线作为缓和曲线根据回旋线的数学定义：其曲率半径随曲线上某一点至该曲线起点之距离成反比。

即：ρ=A2式中A为曲率与曲线长度的比例常数；若令，通过对汽车行驶理论方程与回旋线基本方程的比较可知，它们的形式是相符的，因此《标准》规定缓和曲线采用回旋线。

回旋线参数A 的确定：R LS = A2 A=式中：R—圆曲线半径 m ；LS—缓和曲线长度m ；三、缓和曲线最小长度缓和曲线最小长度应满足：（1）使汽车平顺地由直线段过渡到到圆曲线段，并对离心力的增长有一定的限制；（2）驾驶员操纵方向盘所需的必要时间以利驾驶员顺适地操纵放向盘；（3）满足道路设置超高与加宽过渡的要求。

浅析路线设计缓和曲线合理长度取值范围0 引言缓和曲线是公路平面线形设计中采用的最常用的线形之一。

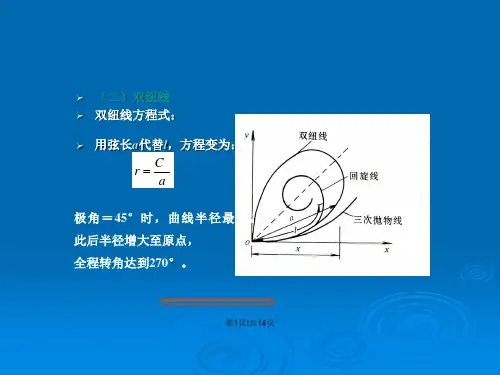
缓和曲线是在直线和圆曲线之间插入一段曲率半径由+∞逐步渐变为R的回旋线，不仅符合汽车转弯时的行车轨迹，而且使公路的平面线形顺适美观，具有良好的视觉效果和心理作用感。

在缓和曲线设计中，缓和曲线缓和段长度的取值是影响道路平面线形视觉质量的重要因素之一。

如果缓和曲线缓和段长度取值太短，不仅不能起到曲率渐变的作用，而且缓和段与剩余圆曲线的衔接和搭配极不协调，行车视觉效果比较差；如果缓和曲线缓和段长度取值太长，无论从线形组合效果还是弯道超高和加宽设计方面都存在着较大的不足。

因此，合理确定和设计缓和曲线缓和段的长度，是平面缓和曲线线形设计需要解决的重要问题之一。

目前无论是专业参考资料，还是公路线形设计使用的设计软件中，都没有给出合理确定缓和段长度的计算方法，只是按照《公路工程技术标准》（以下简称《标准》）的设计要求，取大于或等于缓和曲线最小缓和段长度即可，而没有考虑不同平曲线半径条件下缓和曲线缓和段长度的合理取值。

缓和段长度对平面线形质量的影响分析在平面缓和曲线设计中，缓和曲线缓和段长度的取值将直接影响到平面线形的视觉质量和行车效果。

道路平面线形由由直线和曲线组合而成，曲线又分为曲率半径为常数的圆曲线和曲率半径为变数的缓和曲线两种。

对于缓和曲线的取值范围，公路相关规范中均只有最小值的界定，而对于最大值，规范并没有明确，本文根据驾驶员反应操作3s行程、离心加速度变化、考虑超高缓和率所需长度、考虑视觉和线形美学所需长度及公路路线设计规范及平纵组合等原则进行最值拟定，为公路设计提供一定的理论价值。

1 缓和曲线的设置设置缓和曲线的目的在于通过曲率的逐渐变化，适应汽车转向操作的行使轨迹及路线的顺畅，缓和行车方向的突变和离心力的突然产生；使离心加速度逐渐变化，不致产生侧向冲击，并缓和超高，作为超高变化的过渡段，来减少行车震荡。

第三节竖曲线纵断面上两个坡段的转折处，为方便行车，用一段曲线来缓和，称为竖曲线。

可采用抛物线或圆曲线。

一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时，是凹曲线；ω为负，是凸曲线。

1.二次抛物线基本方程：或ω：坡度差（%）；L：竖曲线长度；R：竖曲线半径2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: （前提：ω很小）L=Rω竖曲线切线长：T=L/2=Rω/2竖曲线上任一点竖距h：竖曲线外距：二、竖曲线最小半径（三个因素）1.缓和冲击对离心加速度加以控制。

ν(m/s)根据经验，a=0.5~0.7m/s2比较合适。

我国取a=0.278,则Rmin=V2/3.6 或Lmin=V2ω/3.62.行驶时间不过短 3s的行程Lmin=V.t/3.6=V/1.23.满足视距的要求分别对凸凹曲线计算。

(一)凸形竖曲线最小半径和最小长度按视距满足要求计算1.当L<ST时，Lmin = 2ST - 4/ω2.当L≥ST时，ST为停车视距。

以上两个公式，第二个公式计算值大，作为有效控制。

按缓和冲击、时间行程和视距要求（视距为最不利情况）计算各行车速度时的最小半径和最小长度，见表4-13。

表中：（1）一般最小半径为极限最小半径的1.5~2倍；（2）竖曲线最小长度为3s行程的长度。

（二）凹曲线最小半径和长度1.夜间行车前灯照射距离要求：1）L<ST2) L≥STL<ST Lmin = 2ST - 26.92/ω (4-14)L≥STω /26.92 (4-15)3s时间行程为有效控制。

例：设ω＝2%=0.02;则L＝ωＲ竖曲线最小长度Ｌ＝Ｖ/1.2速度Ｖ=120km/h V=40km/h 一般最小半径Ｒ凸17000 700一般最小半径Ｒ凹6000 700 L凸340 14Ｌ凹120 14 例题4-3ω=-0.09 凸形；L=Rω=2000*0.09=180mT=L/2=90mE=T2/2R=2.03m起点桩号＝k5+030 - T =K4+940起始高程＝427.68 - 5%*90=423.18m桩号k5+000处：x1=k5+000-k4+940=60m切线高程＝423.18+60*0.05=426.18m h1=x21/2R=602/2*2000=0.90m设计高程＝426.18 - 0.90=425.28m 桩号k5+100处：x２=k5+100-k4+940=160m切线高程＝423.18+160*0.05=431.18m h2=x22/2R=1602/2*2000=6.40m设计高程＝431.18 - 6.40=424.78m第一节平面线形概述一、路线路线指路的中心线；路线在水平面上的投影叫路线的平面；路线设计：确定路线空间位置和各部分几何尺寸的工作；可分为平面设计、纵断面设计、横断面设计。

一、道路平面线型概述一、路线道路：路基、路面、桥梁、涵洞、隧道和沿线设施构成的三维实体。

路线：是指道路中线的空间位置。

平面图：路线在水平面上的投影。

纵断面图：沿道路中线的竖向剖面图，再行展开。

横断面图：道路中线上任意一点的法向切面。

路线设计：确定路线空间位置和各部分几何尺寸。

分解成三步：路线平面设计：研究道路的基本走向及线形的过程。

路线纵断面设计：研究道路纵坡及坡长的过程。

路线横断面设计：研究路基断面形状与组成的过程。

二、汽车行驶轨迹与道路平面线形（一）汽车行驶轨迹行驶中汽车的轨迹的几何特征：（1）轨迹连续：连续和圆滑的，不出现错头和折转；（2）曲率连续：即轨迹上任一点不出现两个曲率的值。

（3）曲率变化连续：即轨迹上任一点不出现两个曲率变化率的值。

（二）平面线形要素行驶中汽车的导向轮与车身纵轴的关系：现代道路平面线形正是由上述三种基本线形构成的，称为平面线形三要素。

二、直线一、直线的特点1、优点：①距离短，直捷，通视条件好。

②汽车行驶受力简单，方向明确，驾驶操作简易。

③便于测设。

2、缺点①线形难于与地形相协调②过长的直线易使驾驶人感到单调、疲倦，难以目测车间距离。

③易超速二、最大直线长度问题：《标准》规定：直线的最大与最小长度应有所限制。

德国：20V（m）。

美国：3mile（4.38km）我国：暂无强制规定景观有变化≧20V；<3KM景观单调≦ 20V公路线形设计不是在平面线形上尽量多采用直线，或者是必须由连续的曲线所构成，而是必须采用与自然地形相协调的线形。

采用长的直线应注意的问题：公路线形应与地形相适应，与景观相协调，直线的最大长度应有所限制，当采用长的直线线形时，为弥补景观单调的缺陷，应结合具体情况采取相应的技术措施。

（1）直线上纵坡不宜过大，易导致高速度。

（2）长直线尽头的平曲线，设置标志、增加路面抗滑性能（3）直线应与大半径凹竖曲线组合，视觉缓和。

（4）植树或设置一定建筑物、雕塑等改善景观。

2-1汽车行驶轨迹有哪些特征？道路平面线形由哪些要素组成? 【答】汽车行驶轨迹的特性有：①连续而且圆滑的，②曲率是连续的，③曲率变化率是连续的。

道路平面线形要素有直线、园曲线和缓和曲线三要素。

2-2 为何要限制直线的长度？答；在道路平面线形设计，一般应根据沿线地形、地物条件，驾驶员的视觉、心理感受以及保证行车安全等因素，合理布设直线路段，对直线的最大长度和最小长度应有所限制。

2-3.公路最小圆曲线半径有几种？分别在何情况下使用？答：三种。

分别是极限最小半径；一般最小半径；不设超高最小半径。

极限最小半径：是路线设计中的极限值，是在特殊困难条件下不得已才使用的，一般不轻易采用。

一般最小半径：是在通常情况下推荐采用的最小半径。

一是考虑汽车在这种圆曲线上以设计速度或以接近设计速度行驶时，旅客有充分的舒适感；二是考虑在地形比较复杂的情况下不会过多增加工程量。

不设超高最小半径：当圆曲线半径比较大时，离心力影响较小，路面摩擦阻力可保证汽车有足够的稳定性，这时可不设超高，设置于直线段上相同的双向横坡路拱形式。

因此，不设超高最小半径是指不必设置超高就能满足行驶稳定性的圆曲线最小半径。

2-4.缓和曲线的作用是什么？确定其长度应考虑哪些因素？答：作用：1、曲率连续变化，便于车辆遵循2、离心加速度逐渐变化，旅客感觉舒服3、超高及加宽逐渐变化，行车更加平稳4、与圆曲线配合，增加线形美观」因素：1、旅客感觉舒适2、超高渐变率适中3、行驶时间不过短2-5.设某二级公路设计速度为80km/h，路拱横坡为2%。

(1)试求不设超高的平曲线半径及设置超高( i h = 8%)的极限最小半径(分别取0.035和0.15) o(2) ( 2)当采用极限最小半径时，缓和曲线长度应为多少(路面宽B=9m，超高渐变率取1/150 )？解：(1)不设超高时(反超高，ih=—2%):2 2R min = v/127 ( p+i h)= 80 /[127 (0.035 —0.02)] = 3359.58 m，规范中取3350m。

45道路工程习题课 第2章道路平面设计一. 含缓和曲线的平曲线几何要素计算公式1.已知平原区某二级公路有一弯道，偏角α右=13°38′42″=13.645°，半径R=800m ，JD=K5+136.53。

假的缓和曲线长度为70，计算曲线主点里程桩号。

或者试计算 ： 1）平曲线要素2）主点ZH ，HY ，QZ ，YH ，HZ 点的桩号解：（1）计算平曲线的几何要素：=（800+0.255）*0.1196+34.998=95.710+34.998=130.708J=2T-L=2×130.708-260.514=0.902（2）主点里程桩号计算：以交点里程桩号为起算点：JD=K5+136.53ZH = JD – T = K5+136.53 -130.708 = K5+5.822HY = ZH + Ls = K5+5.822 +70 = K5+75.822QZ = ZH + L/2= K5+5.822 +260.514/2 =K5+136.079HZ = ZH + L = K5+5.822 +260.514=K5+266.336YH = HZ – Ls = K5+266.336–70=K5+196.336[公式提示] 有缓和曲线的平曲线几何要素计算公式q=L S /2－ L S 3/(240R 2)22700.2552424800Ls p R ===⨯3322707034.99822402240800Ls Ls q R =-=-=⨯13.64580070260.514180180L R Ls ππα=+=⨯⨯+=()sec (8000.255)sec 800 5.85722E R p R αα=+-=+-=()tan 130.7082T R P q α=++=p=L S 2/24R —L S 4/(2688R 3）= L S 2/24R β0=28.6479L S /R T=(R ＋P)tg a/2＋qL=(a －2β0)πR/180＋2L S= 180L R Ls πα=+E=(R ＋P)sec a/2－RJ=2T －L2.圆曲线几何要素计算公式（不含缓和曲线） 曲线主点里程桩号计算计算基点为交点里程桩号，记为JD ，ZY=JD-TYZ=ZY+LQZ=ZY+L/2JD=QZ+D/2 （桩号计算校核）2.某二级公路设计速度为60km/小时，已知JD4交点桩号为K0+750.00, 偏角α右=13°30′,该处的平面线形为单圆曲线，圆曲线半径为600m,试计算该圆曲线的几何元素及曲线主点桩的桩号？解： 圆曲线几何要素计算：已知R=600m, α右=13°30′=13.5°, 则 T=Rtan(a/2)=600×tan(13.5/2)=71.015(m)ππ13.5600L αR=141.372()180180m ⨯⨯==α13.5E R(sec 1)=600(sec 1)=4.188(m)22=-⨯- D=2T-L =2×71.015-141.372=0.658(m)曲线主点桩号计算：ZY=JD-T= K0+750.000-71.015= K0+678.985YZ=ZY+L= K0+678.985 +141.372= K0+820.357QZ=ZY+L/2= K0+678.985+70.866= K0+749.671桩号计算校核 JD 桩号=QZ+D/2= K0+749.671+（0.658/2）= K0+750.00= JD 桩号αT Rtg2πL αR=0.01745αR 180αE R(sec 1)22T L D ===-=-3.与横向力计算公式与因素根据汽车行驶在曲线上力的平衡式计算曲线半径：当设超高时： 式中：V ——计算行车速度，（km/h ）；μ——横向力系数；i h ——超高横坡度；i 1——路面横坡度。