项目三 轴向拉压杆习题

问题解析问题1、什么是强度？什么是强度条件？强度是指构件抵抗破坏的能力。

房屋结构的每一个构件承受荷载后都不允许发生破坏。

如屋架、立柱、吊车梁、基础梁、承重墙等都不允许发生断裂。

这就要求每一个构件应具有足够的抵抗破坏的能力，这种能力称为强度。

强度条件公式为：[]max N A σσ=≤，要注意式中的max σ与[]σ的区别。

max N A σ=表示的是在荷载作用下构件的工作应力，这个值只与内力（由外力引起的）和截面尺寸有关，与材料无关。

[]N Aσ≤是强度条件，是构件能安全承载的依据。

式中的[]σ，表示的是所用材料本身的性质，是由实验测定的，不是工作时外力引起的内力。

问题2、2. 图示砖柱。

24=a cm ，37=b cm ，31=l m ，42=l m ，501=P kN ，902=P kN 。

略去砖柱自重。

求砖柱各段的轴力及应力，并绘制轴力图。

解：砖柱受轴向荷载作用，是轴向压缩。

（1）计算柱各段轴力AB 段： kN P N 5011-=-=（压力）BC 段： 212P P N --=1409050-=--=kN （压力）（2）画柱的轴力图（b ）。

（3）计算柱各段的应力AB 段：1－1横截面上的轴力为压力，501-=N kN ， 横截面面积241mm 1076.5240240⨯=⨯=A ， 则 MPa A N 868.01076.5105043111-=⨯⨯-==σ （压应力） BC 段：2－2横截面上的轴力为压力 1402-=N kN 横截面面积421069.13370370⨯=⨯=A mm 2 则 MPa A N 02.11069.131014043222-=⨯⨯-==σ（压应力）。

【开始】单选题（分值=2分；答案=C；难度=基本题）在其他条件不变时，若受轴向拉伸的杆件横截面面积增加一倍，则杆件横截面上的正应力（）。

A、4倍B、2倍C、1/2倍D、1/4倍【结束】【开始】单选题（分值=2分；答案=C；难度=水平题）在其他条件不变时，若受轴向拉伸的杆件杆长增加一倍，则杆件纵向线应变（）。

A、增大B、减小C、不变D、不能确定【结束】【开始】单选题（分值=2分；答案=B；难度=基本题）弹性模量E与（）有关。

A、应力和应变B、杆件的材料C、外力大小D、泊松比μ【结束】【开始】单选题（分值=2分；答案=B；难度=水平题）横截面面积不同的两根杆件，受到大小相同的轴向外力作用时，则（）。

A、轴力相同，应力也相同B、轴力相同，应力不同C、轴力不同，应力也不同D、轴力不同，应力不同【结束】【开始】单选题（分值=2分；答案=A；难度=基本题）材料在轴向拉伸时，在比例极限内，线应变与（）成正比。

A、正应力B、弹性模量EC、泊松比μD、都切应力【结束】【开始】单选题（分值=2分；答案=D；难度=基本题）危险截面的确定，对于杆件对象的工程设计是非常重要的，若杆件的材料相同，轴向拉伸杆件危险截面发生在（）的截面上。

A、轴力最大、横截面面积最大B、轴力最小、横截面面积最小C、轴力最小、横截面面积最大D、轴力最大、横截面面积最小【结束】【开始】单选题（分值=2分；答案=D；难度=基本题）下列关于内力的说法中错误的是（）。

A、由外力引起的杆件内各部分间的相互作用力B、内力随外力的改变而改变C、内力可由截面法求得D、内力不仅与外力有关，还与杆件的截面形状和尺寸有关【结束】【开始】单选题（分值=2分；答案=B；难度=基本题）对于塑性材料取（）作为材料的极限应力。

A、弹性极限B、屈服极限C、比例极限D、强度极限【结束】【开始】单选题（分值=2分；答案=B；难度=基本题）轴向拉压杆的应力与杆件的（）有关。

A、外力B、外力、截面面积和形状C、外力、截面面积和形状、材料D、外力、截面面积和形状、材料、杆长【结束】【开始】单选题（分值=2分；答案=D；难度=基本题）轴向拉压杆的纵向线应变与杆件的（）有关。

项目三轴向拉伸与压缩一、填空题：1、内力是由引起的杆件内个部分间的。

2、求内力的基本方法是。

3、直杆的作用内力称。

其正负号规定为：当杆件受拉而伸长时为正，其方向截面。

4、截面法就轴力的步骤为：、、。

5、轴力图用来表达，画轴力图时用的坐标表示横截面位置，坐标表示横截面上的轴力。

6、轴力图中，正轴力表示拉力，画在轴的。

7、轴力的大小与外力有关。

与杆件截面尺寸、材料（有关、无关）。

8、应力是，反应了内力的分布集度。

单位，简称。

9、1pa= N/mm2 = N/m2。

1Mpa= pa。

10、直杆受轴力作用时的变形满足假设，根据这个假设，应力在横截面上分布，计算公式为。

11、正应力是指。

12、在荷载作用下生产的应力叫。

发生破坏是的应力叫。

许用应力是工作应力的；三者分别用符号、、表示。

13、当保证杆件轴向拉压时的安全，工作应力与许用应力应满足关系式：。

14、等截面直杆，受轴向拉压力作用时，危险截面发生在处。

而变截面杆，强度计算应分别进行检验。

15、轴向拉压杆的破坏往往从开始。

16、杆件在轴向力作用下长度的改变量叫，用表示。

17、胡克定律表明在范围内，杆件的纵向变形与及，与杆件的成正比。

18、材料的抗拉、压弹性模量用表示，反映材料的能力。

19、EA称作材料的，它反映了材料制成一定截面尺寸后的杆件的抗拉、压能力。

EA越大，变形越。

20、ε叫作，指单位长度的变形。

21、泊松比又叫，ν= ，应用范围为弹性受力范围。

二、计算题：1、试计算轴向拉压杆指定截面的轴力。

2、绘制图示杆件的轴力图。

3、求图示结构中各杆的轴力。

4、用绳索起吊管子如图所示。

若构件重W=10KN ，绳索的直径d=40mm ，许用应力[30 20KNB 45C 455、图示支架中，荷载P=100KN。

杆1为圆形截面钢杆，其许用应力[σ]=150MPa，拉=4MPa。

试确定钢杆的直径d和木杆杆2位正方形截面木杆，其许用应力[σ]压截面的边长c。

C6、钢杆长ｌ=2m，截面面积A=200 mm2，受到拉力P=32KN的作用，钢杆的弹性模量E=2.0×105MPa，试计算此钢杆的伸长量Δｌ。

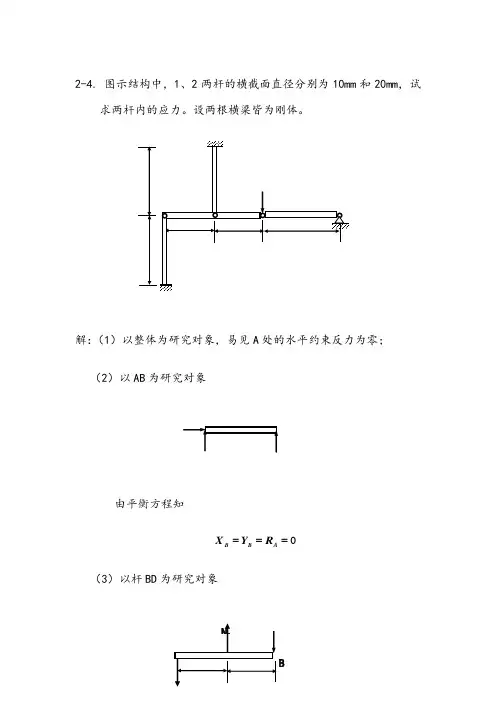
2-4. 图示结构中，1、2两杆的横截面直径分别为10mm 和20mm ，试求两杆内的应力。

设两根横梁皆为刚体。

解：（1）以整体为研究对象，易见A 处的水平约束反力为零； （2）以AB 为研究对象由平衡方程知0===A B B R Y X（3）以杆BD 为研究对象由平衡方程求得KNN N NY KNN N mC20010 01001101 021211==--===⨯-⨯=∑∑（4）杆内的应力为MPa A N MPa A N 7.63204102012710410102322223111=⨯⨯⨯===⨯⨯⨯==πσπσ2-19. 在图示结构中，设AB 和CD 为刚杆，重量不计。

铝杆EF 的l 1=1m ，A 1=500mm 2，E 1=70GPa 。

钢杆AC 的l 2=，A 2=300mm 2，E 2=200GPa 。

若载荷作用点G 的垂直位移不得超过。

试求P 的数值。

解：（1）由平衡条件求出EF 和AC 杆的内力P N N N P N N AC EF AC4332 2112=====（2）求G 处的位移22221111212243)ΔΔ23(21)ΔΔ(21Δ21ΔA E l N A E l N l l l l l l A C G +=+=+== （3）由题意kNP P P A E Pl A E Pl mml G 1125.2300102001500500107010009212143435.233222111≤∴≤⨯⨯⨯+⨯⨯⨯⨯=⨯⨯+⨯⨯≤ 2-27. 在图示简单杆系中，设AB 和AC 分别是直径 为20mm 和24mm的圆截面杆，E=200GPa ，P=5kN ，试求A 点的垂直位移。

解：（1）以铰A 为研究对象，计算杆AB 和杆AC 的受力kN N kN N AC AB 66.3 48.4==（2）两杆的变形为()伸长mm πEA l N l ABAB AB AB201.04201020045cos 20001048.42303=⨯⨯⨯⨯⨯==Δ ()缩短mm πEA l N l ACAC AC AC 0934.04241020030cos 20001066.32303=⨯⨯⨯⨯⨯==Δ （3）如图，A 点受力后将位移至A ’,所以A 点的垂直位移为AA ’’mmctg A A l A A AA A A mmA A ctg A A ctg A A A mm AA AA AA AA A A A A l l AB A AB AC 249.00355.0284.0 4545sin /Δ 035.0 4530A 0972.030sin /45sin /AΔΔAA ΔAA 00330043010243434321=-='''-=''-=''=∴='''∴'''+'''==-=-='==δ 又中在图中2-36. 在图示结构中，设AC 梁为刚杆，杆件1、2、3的横截面面积相等，材料相同。

第2章 轴向拉伸和压缩主要知识点：（1）轴向拉伸（压缩）时杆的内力和应力；（2）轴向拉伸（压缩）时杆的变形；（3）材料在轴向拉伸和压缩时的力学性能；（4）轴向拉压杆的强度计算；（5）简单拉压超静定问题。

轴向拉伸（压缩）时杆的变形4. 一钢制阶梯杆如图所示。

已知沿轴线方向外力F 1=50kN ，F 2=20kN ，各段杆长l 1=100mm ，l 2=l 3=80mm ，横截面面积A 1=A 2=400mm 2，A 3=250mm 2，钢的弹性模量E=200GP a ，试求各段杆的纵向变形、杆的总变形量及各段杆的线应变。

解：（1）首先作出轴力图如图4-11所示，由图知kN F N 301-=，kN F F N N 2032==。

（2）计算各段杆的纵向变形m m EA l F l N 5693311111075.31040010200101001030---⨯-=⨯⨯⨯⨯⨯⨯-==∆ m m EA l F l N 569332222100.2104001020010801020---⨯=⨯⨯⨯⨯⨯⨯==∆(3)杆的总变形量m l l l l 53211045.1-⨯=∆+∆+∆=∆。

(4)计算各段杆的线应变 451111075.310.01075.3--⨯-=⨯-=∆=l l ε 45222105.208.0100.2--⨯=⨯=∆=l l ε 45333100.408.0102.3--⨯=⨯=∆=l l ε材料在轴向拉伸和压缩时的力学性能5. 试述低碳钢拉伸试验中的四个阶段，其应力—应变图上四个特征点的物理意义是什么？答：低碳钢拉伸试验中的四个阶段为弹性阶段、屈服阶段、强化阶段和颈缩阶段。

在弹性阶段，当应力小于比例极限σp 时，材料服从虎克定律；当应力小于弹性极限σe 时，材料的变形仍是弹性变形。

屈服阶段的最低点对应的应力称为屈服极限，以σs 表示。

强化阶段最高点所对应的应力称为材料的强度极限，以σb 表示，它是材料所能承受的最大应力。

第二章轴向拉伸与压缩练习题一．单项选择题1、在轴向拉伸或压缩杆件上正应力为零的截面是（）A、横截面B、与轴线成必定交角的斜截面C、沿轴线的截面D、不存在的2、一圆杆受拉，在其弹性变形范围内，将直径增添一倍，则杆的相对变形将变为原来的（）倍。

11A、4；B、2；C、1；D、23、由两杆铰接而成的三角架（如下图），杆的横截面面积为 A，弹性模量为E，当在节点 C 处遇到铅垂载荷 P 作用时，铅垂杆 AC 和斜杆 BC的变形应分别为（）Pl4Pl Pl Pl Pl PlA、EA,3EA；B、0,EA；C、2EA,3EA D、EA,04、几何尺寸同样的两根杆件，其弹性模量分别为 E1=180Gpa,E2=60 Gpa,在弹性1变形的范围内二者的轴力同样，这时产生的应变的比值 2 应力为（）1A、3B、 1；C、 2；D、 35、全部脆性资料，它与塑性资料对比，其拉伸力学性能的最大特色是（）。

A、强度低，对应力集中不敏感；B、同样拉力作用下变形小；C、断裂前几乎没有塑性变形；D、应力 -应变关系严格按照胡克定律6、构件拥有足够的抵挡损坏的能力，我们就说构件拥有足够的()A、刚度，B、稳固性，C、硬度，D、强度。

7、构件拥有足够的抵挡变形的能力，我们就说构件拥有足够的()A、强度，B、稳固性，C、刚度，D、硬度。

8、单位面积上的内力称之为()A、正应力，B、应力，C、拉应力，D、压应力。

9、与截面垂直的应力称之为()A、正应力，B、拉应力，C、压应力，D、切应力。

10、轴向拉伸和压缩时，杆件横截面上产生的应力为()A、正应力，B、拉应力，C、压应力，D、切应力。

二、填空题1、杆件轴向拉伸或压缩时，其受力特色是：作用于杆件外力的协力的作用线与杆件轴线相 ________。

2、轴向拉伸或压缩杆件的轴力垂直于杆件横截面，并经过截面________。

3、杆件轴向拉伸或压缩时 ,其横截面上的正应力是________散布的。

轴向拉伸与压缩习题及解答轴向拉伸与压缩习题及解答⼀、判断改错1、构件内⼒的⼤⼩不但与外⼒⼤⼩有关，还与材料的截⾯形状有关。

答：错。

静定构件内⼒的⼤⼩之与外⼒的⼤⼩有关，与材料的截⾯⽆关。

2、杆件的某横截⾯上，若各点的正应⼒均为零，则该截⾯上的轴⼒为零。

答：对。

3、两根材料、长度都相同的等直柱⼦，⼀根的横截⾯积为1A ，另⼀根为2A ，且21A A >。

如图所⽰。

两杆都受⾃重作⽤。

则两杆最⼤压应⼒相等，最⼤压缩量也相等。

答：对。

⾃重作⽤时，最⼤压应⼒在两杆底端，即max max N All A Aνσν=== 也就是说，最⼤应⼒与⾯积⽆关，只与杆长有关。

所以两者的最⼤压应⼒相等。

最⼤压缩量为 2max max22N Al l l l A EA Eνν??===即最⼤压缩量与⾯积⽆关，只与杆长有关。

所以两杆的最⼤压缩量也相等。

4、受集中⼒轴向拉伸的等直杆，在变形中任意两个横截⾯⼀定保持平⾏。

所以宗乡纤维的伸长量都相等，从⽽在横截⾯上的内⼒是均匀分布的。

答：错。

在变形中，离开荷载作⽤处较远的两个横截⾯才保持平⾏，在荷载作⽤处，横截⾯不再保持平⾯，纵向纤维伸长不相等，应⼒分布复杂，不是均匀分布的。

5、若受⼒物体内某电测得x 和y ⽅向都有线应变x ε和y ε，则x 和y ⽅向肯定有正应⼒x σ和y σ。

答：错，不⼀定。

由于横向效应作⽤，轴在x ⽅向受拉（压），则有x σ；y ⽅向不受⼒，但横向效应使y ⽅向产⽣线应变，y x εενε'==-。

A 1(a) (b)⼆、填空题1、轴向拉伸的等直杆，杆内的任⼀点处最⼤剪应⼒的⽅向与轴线成（45o）2、受轴向拉伸的等直杆，在变形后其体积将（增⼤）3、低碳钢经过冷做硬化处理后，它的（⽐例）极限得到了明显的提⾼。

4、⼯程上通常把延伸率δ>（5%）的材料成为塑性材料。

5、⼀空⼼圆截⾯直杆，其内、外径之⽐为0.8，两端承受⼒⼒作⽤，如将内外径增加⼀倍，则其抗拉刚度将是原来的（4）倍。

第三章练习之三轴向拉、压的变形
班级姓名学号2009-9-15
一、填空
1、杆件在外力作用下发生变形，随外力取消即随之消失的变形叫。

2、杆件在轴向力作用下杆的长度发生变化，杆件长度的改变量叫。

3、胡克定理表明在弹性范围内，杆件的纵向变形与成正比，与成反比。

4、E被称为是材料的。

它反映了某种材料的
能力，它常用的单位是。

5、EA被称为是，它反映了某种材料制成的杆件
抵抗的能力。

6、胡克定理的表达式为。

应用胡克定理计算变形的前提条件
是，。

7、单位长度的变形叫。

8、胡克定理（应力与应变）的表达式可写成，它表明在弹性范围内。

二、名词解释
1、塑性变形
2、横向变形
三、计算
1、杆件的长为4m，截面积为250mm2 ，受到拉力32KN，杆件的弹性模
量E=2.0×105Mpa，试计算杆件的伸长量
2、已知杆件的线应变为0.001，试计算当杆长为5米时杆件的变形量
3、试计算A、B、C三点的位移，A1=120×120 mm2 A2=240×240mm2
A3=370×370mm2，材料的弹性模量为E=1.5×104Mpa
3。

拉伸压缩一、填空题（共11题，53分）1、在轴向拉压杆中,只有一种沿杆轴作用的内力,这种内力称为(__)。

正确答案：第1空:轴力解析：具体解析2、杆件截面上某点处分布内力的集度称为该点处的(__)。

正确答案：第1空:应力解析：具体解析3、材料力学主要研究 (__)的构件,称为杆件,简称为杆。

正确答案：第1空:长度大于横截面尺寸解析：具体解析4、工程上通常按延伸率的大小把材料分成两大类,δ大于(__)的材料称为塑性材料。

正确答案：第1空:5%解析：具体解析5、图示钢杆在轴向拉力作用下,横截面上的正应力σ超过子材料的屈服极限,此时轴向线应力ε1,现开始卸载,轴向拉力全部卸掉后,轴向残余应应变ε2,则该钢材的弹性模量= (__)。

正确答案：第1空:6/(ε1-ε2)解析：具体解析6、低碳钢拉伸经过冷作硬化后,其得到提高的指标是(__)。

正确答案：第1空:比例极限解析：具体解析7、在低碳钢拉伸曲线中,其变形破坏全过程可分为4个变形阶段,它们依次是(__)、(__)、(__)和(__)。

正确答案：第1空:弹性阶段第2空:屈服阶段第3空:强化阶段第4空:颈缩阶段解析：具体解析8、已知一轴上所受拉力为F,变形前长度为l,弹性模量为E,截面积为A,则其抗拉刚度为(__)。

正确答案：第1空:EA解析：具体解析9、如图所示低碳钢拉伸时的δ-ε曲线,在B点试件被拉断,作BO1平行于OA,则线段OO1表示试件拉断时的(__)应变,也即是材料的塑性指标(__),线段O1O2表示试件拉断时的(__)应变。

正确答案：第1空:塑性应变第2空:延伸率第3空:弹性应变解析：具体解析10、关于应力的符号,一般规定为(__)为正(__)为负。

正确答案：第1空:拉应力第2空:压应力解析：具体解析11、构件的强度是指构件抵抗(__)的能力;刚度是指构件抵抗(__)的能力;稳定性是指构件维持原有(__)的能力。

正确答案：第1空:破坏第2空:变形第3空:平衡状态解析：具体解析二、计算题（共10题，47分）1、一等直杆所受外力如图所示,试求各段截面上的轴力,并作杆的轴力图。

轴向拉伸与压缩习题一、填空题1.在工程设计中，构件不仅要满足、和稳定性的要求，同时还必须符合经济方面的要求。

2、在式σ=eε中，比例系数e称作材料的拉压_______，相同材料的e值相同；它充分反映某种材料抵抗变形的能力，在其他条件相同时，ea越大，杆件的变形__________。

3、构件工作应力的最高极限叫做__________。

材料能承受的最大应力叫做材料__________。

4、材料抵抗弹性变形能力的指标就是____和_______。

5.在低碳钢的拉伸试验中，材料的应力变化不大而变形显著增加的现象称为。

二、选择题1.轴向弯曲或放大时，直杆横截面上的内力称作轴力，则表示为：()a.fnb.fsfqc.d.fjy2.材料的塑性指标有：()a.σu和δb.σs和ψc.σb和δd.δ和ψ3.截面上的内力大大，()a.与截面的尺寸和形状无关b.与截面的尺寸有关，但与截面的形状无关c.与截面的尺寸无关，但与截面的形状有关d.与截面的尺寸和形状都有关4.等横截面直杆在两个外力的促进作用下出现轴向放大变形时，这对外力所具有的特点一定就是等值、()。

a逆向、共线b反向，过截面形心c方向相对，促进作用线与杆轴线重合d方向相对，沿同一直线促进作用5.一阶梯形杆件受拉力ｐ的作用，其截面1-1，2-2，3-3上的内力分别为n1，n2和n3，三者的关系为()。

an1≠n2n2≠n3bn1＝n2n2＝n3cn1＝n2n2＞n3dn1＝n2n2＜n36.图示阶梯形杆，cd段为铝，横截面面积为a；bc和de段为钢，横截面面积均为2a。

设1-1、2-2、3-3截面上的正应力分别为σ1、σ2、σ3，则其大小次序为()。

aσ1＞σ2＞σ3bσ2＞σ3＞σ1cσ3＞σ1＞σ2dσ2＞σ1＞σ37.轴向拉伸杆，正应力最大的截面和剪应力最大的截面()a分别是横截面、450斜截面b都是横截面c分别是450斜截面、横截面d都是450斜截面10.由变形公式δl＝pl/ea即e＝pl/aδl可知，弹性模量()a与载荷、杆长、横截面面积毫无关系b与载荷成正比c与杆长成正比d与横截面面积成正比11.在以下观点，()就是恰当的。