材料力学轴向拉压题目答案详解
- 格式:doc
- 大小:172.50 KB
- 文档页数:8


第二章轴向拉压一、选择题1.图1所示拉杆的外表面上有一斜线,当拉杆变形时,斜线将( D)A.平动B.转动C.不动D.平动加转动2.轴向拉伸细长杆件如图2所示,其中1-1面靠近集中力作用的左端面,则正确的说法应是( C)A.1-1、2-2面上应力皆均匀分布B.1-1、2-2面上应力皆非均匀分布C.1-1面上应力非均匀分布,2-2面上应力均匀分布D.1-1面上应力均匀分布,2-2面上应力非均匀分布(图1)(图2)3.有A、B、C三种材料,其拉伸应力—应变实验曲线如图3所示,曲线( B)材料的弹性模量E大,曲线( A )材料的强度高,曲线( C)材料的塑性好。
4.材料经过冷作硬化后,其( D)。
A.弹性模量提高,塑性降低B.弹性模量降低,塑性提高C.比例极限提高,塑性提高D.比例极限提高,塑性降低5.现有钢、铸铁两种杆材,其直径相同。
从承载能力与经济效益两个方面考虑,图4所示结构中两种合理选择方案是( A)。
A.1杆为钢,2杆为铸铁B.1杆为铸铁,2杆为钢C.2杆均为钢D.2杆均为铸铁(图3)(图4)(图5)6.在低碳钢的拉伸试验中,材料的应力变化不大而变形显著增加的是(B)。
A. 弹性阶段;B.屈服阶段;C.强化阶段;D.局部变形阶段。
7.铸铁试件压缩破坏(B)。
A. 断口与轴线垂直;B. 断口为与轴线大致呈450~550倾角的斜面;C. 断口呈螺旋面;D. 以上皆有可能。
8.为使材料有一定的强度储备,安全系数取值应( A )。
A .大于1; B. 等于1; C.小于1; D. 都有可能。
9. 等截面直杆在两个外力的作用下发生轴向压缩变形时,这对外力所具备的特点一定是等值、( C )。
A 反向、共线B 反向,过截面形心C 方向相对,作用线与杆轴线重合D 方向相对,沿同一直线作用10. 图6所示一阶梯形杆件受拉力P的作用,其截面1-1,2-2,3-3上的内力分别为N 1,N 2和N 3,三者的关系为( B )。


第2章 轴向拉伸和压缩主要知识点:(1)轴向拉伸(压缩)时杆的内力和应力;(2)轴向拉伸(压缩)时杆的变形;(3)材料在轴向拉伸和压缩时的力学性能;(4)轴向拉压杆的强度计算;(5)简单拉压超静定问题。
轴向拉伸(压缩)时杆的变形4. 一钢制阶梯杆如图所示。
已知沿轴线方向外力F 1=50kN ,F 2=20kN ,各段杆长l 1=100mm ,l 2=l 3=80mm ,横截面面积A 1=A 2=400mm 2,A 3=250mm 2,钢的弹性模量E=200GP a ,试求各段杆的纵向变形、杆的总变形量及各段杆的线应变。
解:(1)首先作出轴力图如图4-11所示,由图知kN F N 301-=,kN F F N N 2032==。
(2)计算各段杆的纵向变形m m EA l F l N 5693311111075.31040010200101001030---⨯-=⨯⨯⨯⨯⨯⨯-==∆ m m EA l F l N 569332222100.2104001020010801020---⨯=⨯⨯⨯⨯⨯⨯==∆(3)杆的总变形量m l l l l 53211045.1-⨯=∆+∆+∆=∆。
(4)计算各段杆的线应变 451111075.310.01075.3--⨯-=⨯-=∆=l l ε 45222105.208.0100.2--⨯=⨯=∆=l l ε 45333100.408.0102.3--⨯=⨯=∆=l l ε材料在轴向拉伸和压缩时的力学性能5. 试述低碳钢拉伸试验中的四个阶段,其应力—应变图上四个特征点的物理意义是什么?答:低碳钢拉伸试验中的四个阶段为弹性阶段、屈服阶段、强化阶段和颈缩阶段。
在弹性阶段,当应力小于比例极限σp 时,材料服从虎克定律;当应力小于弹性极限σe 时,材料的变形仍是弹性变形。
屈服阶段的最低点对应的应力称为屈服极限,以σs 表示。
强化阶段最高点所对应的应力称为材料的强度极限,以σb 表示,它是材料所能承受的最大应力。
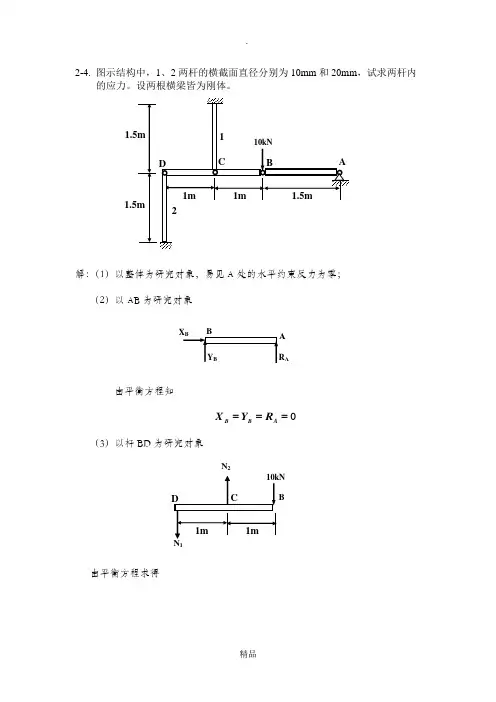
2-4. 图示结构中,1、2两杆的横截面直径分别为10mm 和20mm ,试求两杆内的应力。
设两根横梁皆为刚体。
解:(1)以整体为研究对象,易见A 处的水平约束反力为零; (2)以AB 为研究对象由平衡方程知0===A B B R Y X(3)以杆BD 为研究对象由平衡方程求得1KNN N NY KNN N mC20010 01001101 021211==--===⨯-⨯=∑∑(4)杆内的应力为MPa A N MPa A N 7.63204102012710410102322223111=⨯⨯⨯===⨯⨯⨯==πσπσ2-19. 在图示结构中,设AB 和CD 为刚杆,重量不计。
铝杆EF 的l 1=1m ,A 1=500mm 2,E 1=70GPa 。
钢杆AC 的l 2=1.5m ,A 2=300mm 2,E 2=200GPa 。
若载荷作用点G 的垂直位移不得超过2.5mm 。
试求P 的数值。
解:(1)由平衡条件求出EF 和AC 杆的内力P N N N P N N AC EF AC4332 2112=====(2)求G 处的位移22221111212243)ΔΔ23(21)ΔΔ(21Δ21ΔA E l N A E l N l l l l l l A C G +=+=+==(3)由题意kNP P P A E Pl A E Pl mml G 1125.2300102001500500107010009212143435.233222111≤∴≤⨯⨯⨯+⨯⨯⨯⨯=⨯⨯+⨯⨯≤ 2-27. 在图示简单杆系中,设AB 和AC 分别是直径 为20mm 和24mm 的圆截面杆,E=200GPa ,P=5kN ,试求A 点的垂直位移。
解:(1)以铰A 为研究对象,计算杆AB 和杆AC 的受力kN N kN N AC AB 66.3 48.4==(2)两杆的变形为()伸长mm πEA l N l ABABAB AB 201.04201020045cos 20001048.42303=⨯⨯⨯⨯⨯==Δ ()缩短mm πEA l N l ACAC AC AC 0934.04241020030cos 20001066.32303=⨯⨯⨯⨯⨯==Δ(3)如图,A点受力后将位移至A’,所以A点的垂直位移为AA’’mmctg A A l A A AA A A mmA A ctg A A ctg A A A mm AA AA AA AA A A A A l l AB A AB AC 249.00355.0284.0 4545sin /Δ 035.04530A 0972.030sin /45sin /AΔΔAA ΔAA 00330043010243434321=-='''-=''-=''=∴='''∴'''+'''==-=-='==δ 又中在图中2-36. 在图示结构中,设AC 梁为刚杆,杆件1、2、3的横截面面积相等,材料相同。
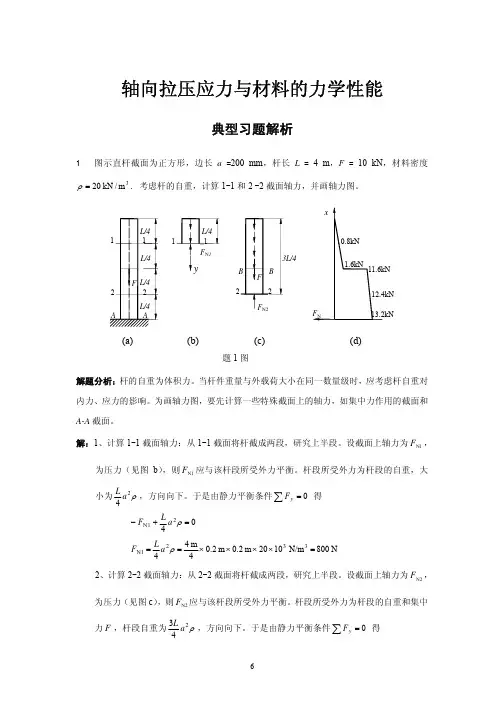

第二章轴向拉(压)变形[习题2-1] 试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a )解:(1)求指定截面上的轴力 FN =-11FF F N -=+-=-222(2)作轴力图轴力图如图所示。
(b )解:(1)求指定截面上的轴力 FN 211=-2222=+-=-F F N (2)作轴力图FF F F N =+-=-2233 轴力图如图所示。
(c )解:(1)求指定截面上的轴力 FN 211=-FF F N =+-=-222(2)作轴力图FF F F N 32233=+-=- 轴力图如图所示。
(d )解:(1)求指定截面上的轴力 FN =-11F F a aFF F qa F N 22222-=+⋅--=+--=-(2)作轴力图 中间段的轴力方程为: x aFF x N ⋅-=)(]0,(a x ∈轴力图如图所示。
[习题2-2] 试求图示等直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
2400mm A =解:(1)求指定截面上的轴力kNN 2011-=- )(10201022kN N -=-=-)(1020102033kN N =-+=-(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力MPa mm N A N 504001*********-=⨯-==--σMPa mm N A N 254001010232222-=⨯-==--σMPamm N A N 254001010233333=⨯==--σ[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
21200mm A =22300mm A =23400mm A =解:(1)求指定截面上的轴力kNN 2011-=-)(10201022kN N -=-=-)(1020102033kN N =-+=-(2)作轴力图轴力图如图所示。
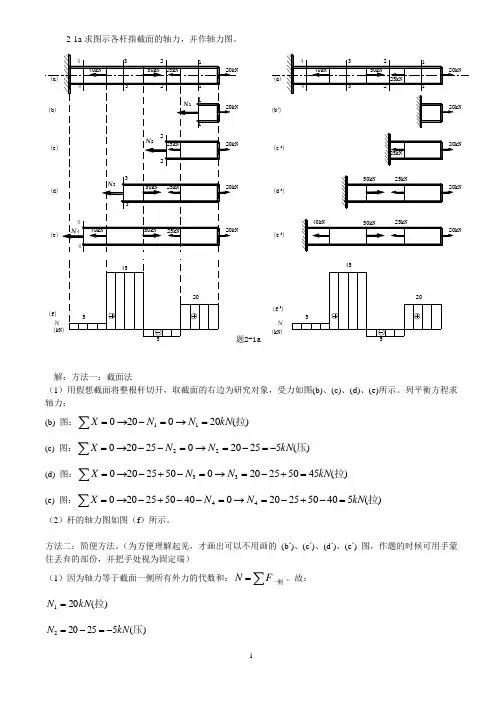
2-1a 求图示各杆指截面的轴力,并作轴力图。
(c ')(e ')(d ')N (kN)205455(f ')解:方法一:截面法(1)用假想截面将整根杆切开,取截面的右边为研究对象,受力如图(b)、(c)、(d)、(e)所示。
列平衡方程求轴力: (b) 图:)(20020011拉kN N NX =→=-→=∑(c) 图:)(5252002520022压kN N NX -=-=→=--→=∑(d) 图:)(455025200502520033拉kN N NX =+-=→=-+-→=∑(e) 图:)(540502520040502520044拉kN N NX =-+-=→=--+-→=∑(2)杆的轴力图如图(f )所示。
方法二:简便方法。
(为方便理解起见,才画出可以不用画的 (b ‘)、(c ‘)、(d ‘)、(e ‘) 图,作题的时候可用手蒙住丢弃的部份,并把手处视为固定端)(1)因为轴力等于截面一侧所有外力的代数和:∑=一侧FN 。
故:)(201拉kN N =)(525202压kN N -=-=)(455025203拉kN N =+-=)(5405025204拉kN N =-+-=(2)杆的轴力图如图(f ‘)所示。
2-2b 作图示杆的轴力图。
(c)图:(b)图:(3)杆的轴力图如图(d )所示。
2-5 图示两根截面为100mm ⅹ100mm 的木柱,分别受到由横梁传来的外力作用。
试计算两柱上、中、下三段的应力。
(b)(c)(d)(f)题2-5-N图(kN)6108.5N图(kN)326.5-解:(1)梁与柱之间通过中间铰,可视中间铰为理想的光滑约束。
将各梁视为简支梁或外伸梁,柱可视为悬臂梁,受力如图所示。
列各梁、柱的平衡方程,可求中间铰对各梁、柱的约束反力,计算结果见上图。
(2)作柱的轴力图,如(e)、(f)所示。
(3)求柱各段的应力。
解:(1)用1-1截面将整个杆切开,取左边部分为研究对象;再用x -x 截面整个杆切开,取右边部分为研究对象,两脱离体受力如图(b)、(c),建立图示坐标。

轴向拉伸与压缩习题及解答一、判断改错1、构件力的大小不但与外力大小有关,还与材料的截面形状有关。
答:错。
静定构件力的大小之与外力的大小有关,与材料的截面无关。
2、杆件的某横截面上,假设各点的正应力均为零,那么该截面上的轴力为零。
答:对。
3、两根材料、长度都一样的等直柱子,一根的横截面积为1A ,另一根为2A ,且21A A >。
如下图。
两杆都受自重作用。
那么两杆最大压应力相等,最大压缩量也相等。
答:对。
自重作用时,最大压应力在两杆底端,即max max N All A Aνσν=== 也就是说,最大应力与面积无关,只与杆长有关。
所以两者的最大压应力相等。
最大压缩量为 2max max22N Al l l l A EA Eνν⋅∆===即最大压缩量与面积无关,只与杆长有关。
所以两杆的最大压缩量也相等。
4、受集中力轴向拉伸的等直杆,在变形中任意两个横截面一定保持平行。
所以宗乡纤维的伸长量都相等,从而在横截面上的力是均匀分布的。
答:错 。
在变形中,离开荷载作用处较远的两个横截面才保持平行,在荷载作用处,横截面不再保持平面,纵向纤维伸长不相等,应力分布复杂,不是均匀分布的。
5、假设受力物体某电测得x 和y 方向都有线应变x ε和y ε,那么x 和y 方向肯定有正应力x σ和y σ。
答:错, 不一定。
由于横向效应作用,轴在x 方向受拉〔压〕,那么有x σ;y 方向不受力,但横向效应使y 方向产生线应变,y x εενε'==-。
A 1(a) (b)二、填空题1、轴向拉伸的等直杆,杆的任一点处最大剪应力的方向与轴线成〔45〕2、受轴向拉伸的等直杆,在变形后其体积将〔增大〕3、低碳钢经过冷做硬化处理后,它的〔比例〕极限得到了明显的提高。
4、工程上通常把延伸率δ>〔5%〕的材料成为塑性材料。
5、 一空心圆截面直杆,其、外径之比为0.8,两端承受力力作用,如将外径增加一倍,那么其抗拉刚度将是原来的〔4〕倍。
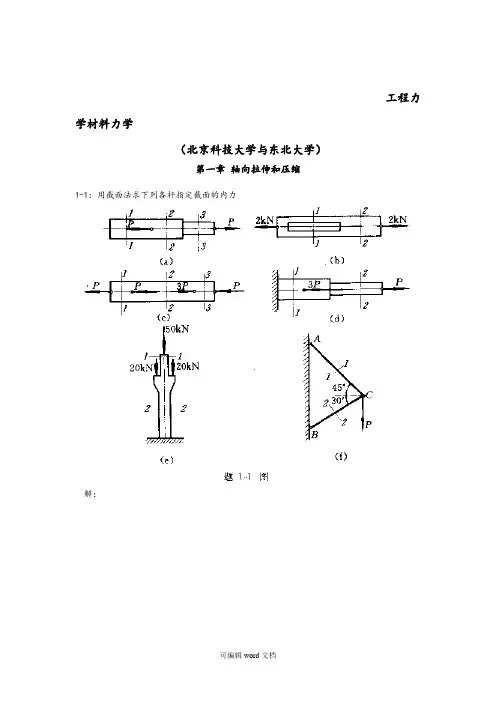
工程力学材料力学(北京科技大学与东北大学)第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力解:(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注(轴向拉伸为正,压缩为负)1-2:高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN,试计算大钟拉杆的最大静应力。
解:σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3:试计算图a所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN,吊杆的尺寸如图b所示。
解:下端螺孔截面:σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面:σ2=2P S =8.72MPa上端双螺孔截面:σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4:一桅杆起重机如图所示,起重杆AB为一钢管,其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。
已知起重量P=2000N,试计算起重机杆和钢丝绳的应力。
解:受力分析得:F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5:图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知 材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC AC LNL EA EA σε===1.59*104,CB CB CB LNL EA EA σε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa. 解:NllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9:用一板状试样进行拉伸试验,在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
第二章轴向拉(压变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(b)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(c)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(d)解:(1)求指定截面上的轴力(2)作轴力图中间段的轴力方程为:轴力图如图所示。
[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力[习题2-4] 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EC横截面上的应力。
解:(1)求支座反力由结构的对称性可知:(2)求AE和EG杆的轴力①用假想的垂直截面把C铰和EG杆同时切断,取左部分为研究对象,其受力图如图所示。
由平衡条件可知:②以C节点为研究对象,其受力图如图所示。
由平平衡条件可得:(3)求拉杆AE和EG横截面上的应力查型钢表得单个等边角钢的面积为:[习题2-5] 石砌桥墩的墩身高,其横截面面尺寸如图所示。
荷载,材料的密度,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:墩身底面积:因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
[习题2-6]图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当时各斜截面上的正应力和切应力,并用图表示其方向。
解:斜截面上的正应力与切应力的公式为:式中,,把的数值代入以上二式得:轴向拉/压杆斜截面上的应力计算题目编号10000 100 0 100 100.0 0.0 习题2-6100 30 100 75.0 43.310000100 45 100 50.0 50.010000100 60 100 25.0 43.310000100 90 100 0.0 0.010000[习题2-7]一根等直杆受力如图所示。
cos sin 3AyF F Fθθ轴向拉伸与压缩习题及解答计算题1:利用截面法,求图2. 1所示简支梁m — m 面的内力分量。
解:(1)将外力F 分解为两个分量,垂直于梁轴线的分量F sin θ,沿梁轴线的分量F cos θ. (2)求支座A 的约束反力:xF∑=0,AxF∑=cos F θB M ∑=0, Ay F L=sin 3L F θAy F =sin 3Fθ (3)切开m — m ,抛去右半部分,右半部分对左半部分的作用力N F ,S F 合力偶M 代替 (图1.12 )。
图 2.1 图2.1(a) 以左半段为研究对象,由平衡条件可以得到xF∑=0, N F =—Ax F =—cos F θ(负号表示与假设方向相反)y F ∑=0, s F =Ay F =sin 3Fθ 左半段所有力对截面m-m 德形心C 的合力距为零sin θC M ∑=0, M=AyF 2L =6FL sin θ 讨论 对平面问题,杆件截面上的内力分量只有三个:和截面外法线重合的内力称为轴力,矢量与外法线垂直的力偶距称为弯矩。
这些内力分量根据截面法很容易求得。
在材料力学课程中主要讨论平面问题。
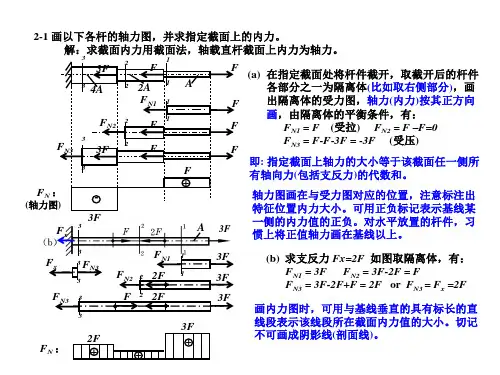
计算题2:试求题2-2图所示的各杆1-1和2-2横截面上的轴力,并作轴力图。
解 (a )如图(a )所示,解除约束,代之以约束反力,作受力图,如题2-2图(1a )所示。
利用静力学平衡条件,确定约束反力的大小和方向,并标示在题2-2图(1a )中。
作杆左端面的外法线n ,将受力图中各力标以正负号,凡与外法线指向一致的力标以正号,反之标以负号,轴力图是平行于杆轴线的直线。
轴力图在有轴力作用处,要发生突变,突变量等与该处轴力的数值,对于正的外力,轴力图向上突变,对于负的外力,轴力图向下突变,如题2-2图(2a )所示,截面1和截面2上的轴力分别为1N F =F 和2N F =—F 。
(b)解题步骤与题2-2(a )相同,杆受力图和轴力图如题2-2(1b )、(2b )所示。
习 题2-1 一木柱受力如图示,柱的横截面为边长20cm 的正方形,材料服从虎克定律,其弹性模量51010.0⨯=E MPa .如不计柱自重,试求:(1) 作轴力图;(2) 各段柱横截面上的应力;(3) 各段柱的纵向线应变;(4) 柱的总变形.解:(1) 轴力图(2) AC 段应力a a MP P σ5.2105.22.010100623-=⨯-=⨯-=CB 段应力a a MP P σ5.6105.62.010260623-=⨯-=⨯-=(3) AC 段线应变45105.2101.05.2-⨯-=⨯-==E σε CB 段线应变45105.6101.05.6-⨯-=⨯-==E σε(4) 总变形 m 3441035.15.1105.65.1105.2---⨯=⨯⨯-⨯⨯-=AB ∆2-2 图(a)所示铆接件,板件的受力情况如图(b)所示.已知:F =7 kN ,t =0.15cm ,b 1=0.4cm ,b 2=0.5cm ,b 3=0.6cml 。
试绘板件的轴力图,并计算板内的最大拉应力。
解:(2)a MP σ4.194101024.015.0767311=⨯⨯⨯⨯⨯=-a MP σ1.311101025.015.0767322=⨯⨯⨯⨯⨯=- a MP σ9.388101026.015.07673=⨯⨯⨯⨯=- 最大拉应力a MP σσ9.3883max ==2-3 直径为1cm 的圆杆,在拉力F =10 kN 的作用下,试求杆内最大剪应力,以及与横截面夹角为α=30o 的斜截面上的正应力与剪应力。
轴力图 (1)轴力图解:(1) 最大剪应力76max 22141210101063.66221F a d στππ-⨯===⨯⨯=MP ⨯ (2) ︒=30α界面上的应力()a MP ασσα49.952366.632cos 12=⨯=+= a MP αστα13.5530sin 66.632sin 2=⨯=⨯=︒2-4 图示结构中ABC 与CD 均为刚性梁,C 与D 均为铰接,铅垂力F =20kN 作用在C 铰,若(1)杆的直径d 1=1cm ,(2)杆的直径d 2=2cm ,两杆的材料相同,E =200Gpa ,其他尺寸如图示,试求(1)两杆的应力;(2)C 点的位移。
第四章轴向拉伸和压缩、填空题1、杆件轴向拉伸或压缩时,其受力特点是:作用于杆件外力的合力的作用线与杆件轴线相_________ .2、轴向拉伸或压缩杆件的轴力垂直于杆件横截面,并通过截面_____________ .4、杆件轴向拉伸或压缩时,其横截面上的正应力是___________ 分布的.7、在轴向拉,压斜截面上,有正应力也有剪应力,在正应力为最大的截面上剪应力为________ .8杆件轴向拉伸或压缩时,其斜截面上剪应力随截面方位不同而不同,而剪应力的最大值发生在与轴线间的夹角为________ 的斜截面上.矚慫润厲钐瘗睞枥庑赖。
9、杆件轴向拉伸或压缩时,在平行于杆件轴线的纵向截面上,其应力值为_______ .10、胡克定律的应力适用范围若更精确地讲则就是应力不超过材料的________ 极限.11、杆件的弹必模量E表征了杆件材料抵抗弹性变形的能力,这说明杆件材料的弹性模量E值越大,其变形就越 ________ 聞創沟燴鐺險爱氇谴净。
12、在国际单位制中,弹性模量E的单位为________ .13、在应力不超过材料比例极限的范围内,若杆的抗拉(或抗压)刚度越_________ ,则变形就越小.15、低碳钢试样据拉伸时,在初始阶段应力和应变成___________ 关系,变形是弹性的,而这种弹性变形在卸载后能完全消失的特征一直要维持到应力为__________ 极限的时候.残骛楼諍锩瀨濟溆塹籟。
16、在低碳钢的应力一应变图上,开始的一段直线与横坐标夹角为a,由此可知其正切tg a在数值上相当于低碳钢的值.酽锕极額閉镇桧猪訣锥。
17、金属拉伸试样在屈服时会表现出明显的__________ 变形,如果金属零件有了这种变形就必然会影响机器正常工作.彈贸摄尔霁毙攬砖卤庑。
18、金属拉伸试样在进入屈服阶段后,其光滑表面将出现与轴线成_______ 角的系统条纹,此条纹称为__________ .謀养抟箧飆鐸怼类蒋薔。
第二章轴向拉伸与压缩2-1 试求图示直杆横截面1-1、2-2、3-3上的轴力,并画出轴力图。
F1=18kN (b)F3=25kN 3力。
解:2-2 图示中部对称开槽直杆,试求横截面1-1和2-2上的正应1 .轴力M1I2- , --------------------------------------------------------- 4kN* -------------- —------------------------------------- r .------------- *—1 2201 F2=3kNF4=10kN2 31518F N F14kN2.应力F N141031 1MPa175MPaA1 1204F N141032 2MPa350A2 22010 4由截面法可求得,杆各横截面上的轴力为2-3 图示桅杆起重机,起重杆 AB 的横截面是外径为 20mm 、 径为18 mm 的圆环,钢丝绳 BC 的横截面面积为 BC 横截面上的应力。
AB 和钢丝绳 o 10mm 2。
试求起重杆解:1 .轴力 取节点 F x 0 :B 为研究对象,受力如图所示, F NBC F NAB cos30 F cos 45 2-4 图示由铜和钢两种材料组成的等直杆,铜和钢的弹性模量分别为 E 1100 GPa 和 E 2210 GPa 。
若杆的总伸长为A l 0.126mm ,试求载荷F 和杆横截面上的应力。
2铜1钢/ /F140 . -400600解:1•横截面上的应力由题意有I 1Fh FI 2 l 2E 1AE 2A由此得到杆横截面上的应力为l h I 2 E 1 E 2 h E 1l 2E 20.126 600 400 100 103 210 103 MPa 15.9MPaF y 0 : 由此解得: 2 .应力 起重杆横截面上的应力为F NABABF NAB sin 30 F sin 45 F NAB 2.83kN , 2.83 103 A AB ____ 2。
工程力学材料力学(北京科技大学与东北大学)第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力解:(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注(轴向拉伸为正,压缩为负)1-2:高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN,试计算大钟拉杆的最大静应力。
解:σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3:试计算图a所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN,吊杆的尺寸如图b所示。
解:下端螺孔截面:σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面:σ2=2P S =8.72MPa 上端双螺孔截面:σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4:一桅杆起重机如图所示,起重杆AB为一钢管,其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。
已知起重量P=2000N,试计算起重机杆和钢丝绳的应力。
解:受力分析得:F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5:图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变.解:31.8127ACACCBCBPMPaSPMPaSσσ====ACACACLNLEA EAσε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:QNllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9:用一板状试样进行拉伸试验,在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
2-4. 图示结构中,1、2两杆的横截面直径分别为10mm 和20mm ,试求两杆内
的应力。
设两根横梁皆为刚体。
解:(1)以整体为研究对象,易见A 处的水平约束反力为零; (2)以AB 为研究对象
由平衡方程知
0===A B B R Y X
(3)以杆BD
由平衡方程求得
KN
N N N
Y KN
N N m
C
200
10 01001101 0212
11==--===⨯-⨯=∑∑
(4)杆内的应力为
1
MPa A N MPa A N 7.6320
41020127104101023
2222
3111=⨯⨯⨯==
=⨯⨯⨯==πσπσ
2-19. 在图示结构中,设AB 和CD 为刚杆,重量不计。
铝杆EF 的l 1=1m ,
A
1=500mm 2,E 1=70GPa 。
钢杆AC 的l 2=1.5m ,A 2=300mm 2,E 2=200GPa 。
若载荷作用点G 的垂直位移不得超过2.5mm 。
试求P 的数值。
解:(1)由平衡条件求出EF 和AC 杆的内力
P N N N P N N AC EF AC
4
3
32 2112=====
(2)求G 处的位移
2
2221111212243)ΔΔ23
(21)ΔΔ(21Δ21ΔA E l N A E l N l l l l l l A C G +
=+=+== (3)由题意
kN
P P P A E Pl A E Pl mm
l G 1125.2300
102001500500107010009212143435.23
3222111≤∴≤⨯⨯⨯+⨯⨯⨯⨯=⨯⨯+⨯⨯≤ 2-27. 在图示简单杆系中,设AB 和AC 分别是直径 为20mm 和24mm 的圆截面
杆,E=200GPa ,P=5kN ,试求A 点的垂直位移。
解:(1)以铰A 为研究对象,计算杆AB 和杆AC 的受力
kN N kN N AC AB 66.3 48.4==
(2)两杆的变形为
()伸长mm πEA l N l AB
AB
AB AB 201.0420
1020045cos 2000
1048.4230
3=⨯⨯
⨯⨯
⨯==
Δ ()缩短mm πEA l N l AC
AC AC AC 0934.0424
1020030cos 2000
1066.3230
3=⨯⨯
⨯⨯
⨯==
Δ (3)如图,A 点受力后将位移至A ’,所以A 点的垂直位移为AA ’’
mm
ctg A A l A A AA A A mm
A A ctg A A ctg A A A mm AA AA AA AA A A A A l l A
B A AB A
C 249.00355.0284.0 4545sin /Δ 035.0 4530A 0972.030sin /45sin /A
ΔΔAA ΔAA 00330043010243434321=-='''-=''-=''=∴='''∴'''+'''==-=-='==δ 又中在图中
2-36. 在图示结构中,设AC 梁为刚杆,杆件1、2、3的横截面面积相等,材料
相同。
试求三杆的轴力。
解:(1)以刚杆AC 为研究对象,其受力和变形情况如图所示
(2)由平衡方程
2 0)(0
03
2
3
2
1
=+==-++=∑∑a N a N F m P N N N Y A
(3)由变形协调条件
Δ2ΔΔ 231l l l =+
(4)由物理关系
Δ Δ Δ332211EA
l N l EA l
N l EA l N l ===
(5)联立求解得
P N P N P N 6
1 31 65321-===
2-38. 图示支架的三根杆的材料相同,杆1的横截面面积为200mm 2,杆2为
300mm 2,杆3为400mm 2。
若P=30kN ,试求各杆内的应力。
解:(1)铰A 的受力及变形如图所示
(2)由平衡方程
30sin )( 0 030cos 30cos 00
310
1
032=-+==-+=∑∑P N N Y N N N X
(3)由变形几何关系
N1
2
310
21
0232
1310
1
40
21Δ3ΔΔ30sin 30cos ΔΔ30cos ΔΔ30sin 30cos Δl l l l l l l A A A A AA AA l AA +=∴⋅-=+
===
(4)由物理关系
2
313
3332222111130cos Δ Δ Δl l l EA l N l EA l
N l EA l N l =
====
(5)得补充方程
022321=--N N N
(6)解联立方程得
)(64.34 )(04.8 )(36.25321受压受拉受拉KN N KN N KN N ===
(7)计算各杆应力
MPa A N MPa A N MPa A N 6.86 8.26 1273
3322
2111-======σσσ
2-40. 阶梯形钢杆的两端在t 1=5o C 时被固定,杆件的A 1=500mm 2,A 2=1000mm 2。
当温度升高到t 2=25o C 时,试求杆内各部分的应力。
设钢的E=200GPa ,α=12.5×10-6/o C 。
解:阶梯杆的受力如图所示,由平衡条件可得 由平衡条件可得
21R R =
由温度升高引起的阶梯杆伸长为
a t t tl l t 2)(ΔΔ12-==αα
由两端反力引起的阶梯杆缩短为
2
211ΔEA a
R EA a R l +
=
由变形关系
0ΔΔ=-t l l
求得约束力
KN R R 3.3321==
计算应力
KN A R MPA A R 3.33 7.662
1
2111-=-=-=-=σσ
2-42. 在图示结构中,1、2两杆的抗拉刚度同为E 1A 1,3杆为E 3A 3。
3杆的长度
为l +δ,其中δ为加工误差。
试求将3杆装入AC 位置后,1、2、3杆的内力。
解:3杆装入后,三杆的铰接点为A 1,此时3杆将缩短,而1杆和2杆将伸长,
A 1受力分析
N3
由平衡方程
00 0X 321
12=-+==-=∑∑N N N
Y N N
由变形谐调条件
αδcos )Δ(Δ31l l -=
由物理关系
α
cos
Δ Δ Δ3
213
3333112
2211111l l l A E l N l A E l N l A E l N l =
====
得补充方程
αδcos )(3
33111
1A E l N A E l N -= 联立求解三根杆的内力
)
cos 2(cos 2)cos 2(cos 332112
33113332112331121A E A E l A E A E N A E A E l A E A E N N +=
+=
=ααδααδ。