231直线与平面垂直的判定

直线与平面垂直的判定[新知初探]1．直线与平面垂直的定义(1)自然语言：如果直线l与平面α内的任意一条直线都垂直，就说直线l与平面α互相垂直，记作l⊥α.直线l叫做平面α的垂线，平面α叫做直线l的垂面．直线与平面垂直时，它们惟一的公共点P叫做垂足．(2)图形语言：如图．画直线l与平面α垂直时，通常把直线画成与表示平面的平行四边形的一边垂直．(3)符号语言：任意a⊂α，都有l⊥a⇒l⊥α.[点睛](1)直线与平面垂直是直线与平面相交的特殊情形．(2)注意定义中“任意一条直线”与“所有直线”等同但不可说成“无数条直线”．2．直线与平面垂直的判定定理(1)自然语言：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直．(2)图形语言：如图所示．(3)符号语言：a⊂α，b⊂α，a∩b＝P，l⊥a，l⊥b⇒l⊥α.[点睛]判定定理条件中的“两条相交直线”是关键性词语，此处强调“相交”，若两条直线平行，则直线与平面不一定垂直．3．直线与平面所成的角(1)定义：平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角．如图，∠PAO就是斜线AP与平面α所成的角．(2)当直线AP与平面垂直时，它们所成的角是90°.(3)当直线与平面平行或在平面内时，它们所成的角是0°.(4)线面角θ的范围：0°≤θ≤90°.[点睛]把握定义应注意两点：①斜线上不同于斜足的点P的选取是任意的；②斜线在平面上的射影是过斜足和垂足的一条直线而不是线段．[小试身手]1．判断下列命题是否正确．(正确的打“√”，错误的打“×”)(1)若直线l垂直于平面α，则l与平面α内的直线可能相交，可能异面，也可能平行()(2)若a∥b，a⊂α，l⊥α，则l⊥b()(3)若a⊥b，b⊥α，则a∥α()答案：(1)×(2)√(3)×2．直线l与平面α内的两条直线都垂直，则直线l与平面α的位置关系是()A．平行B．垂直C．在平面α内D．无法确定解析：选D3.如图，∠BCA＝90°，PC⊥平面ABC，则在△ABC，△PAC的边所在的直线中：(1)与PC垂直的直线有________________________________________________________________________；(2)与AP垂直的直线有________________________________________________________________________．答案：(1)AB，AC，BC(2)BC对直线与平面垂直的判定定理的理解[典例]下列说法正确的有________(填序号)．①垂直于同一条直线的两条直线平行；②如果一条直线与一个平面内的一条直线不垂直，那么这条直线就一定不与这个平面垂直；③如果一条直线垂直于平面内的两条直线，那么这条直线与这个平面垂直；④若l与平面α不垂直，则平面α内一定没有直线与l垂直．[答案]②(1)对于线面垂直的定义要注意“直线垂直于平面内的所有直线”说法与“直线垂直于平面内无数条直线”不是一回事，后者说法是不正确的，它可以使直线与平面斜交．(2)判定定理中要注意必须是平面内两相交直线．[活学活用]1．若三条直线OA，OB，OC两两垂直，则直线OA垂直于()A．平面OAB B．平面OACC．平面OBC D．平面ABC解析：选C2．如果一条直线垂直于一个平面内的：①三角形的两边；②梯形的两边；③圆的两条直径；④正五边形的两边．能保证该直线与平面垂直的是________(填序号)．答案：①③④线面垂直的判定[典例]如图，在三棱锥S-ABC中，∠ABC＝90°，D是AC的中点，且SA＝SB＝SC.(1)求证：SD⊥平面ABC；(2)若AB＝BC，求证：BD⊥平面SAC.[证明](1)因为SA＝SC，D是AC的中点，所以SD⊥AC.在Rt△ABC中，AD＝BD，由已知SA＝SB，所以△ADS≌△BDS，所以SD⊥BD.又AC∩BD＝D，所以SD⊥平面ABC.(2)因为AB＝BC，D为AC的中点，所以BD⊥AC.由(1)知SD⊥BD.又因为SD∩AC＝D，所以BD⊥平面SAC.利用线面垂直的判定定理证明线面垂直的步骤(1)在这个平面内找两条直线，使它和这条直线垂直；(2)确定这个平面内的两条直线是相交的直线；(3)根据判定定理得出结论．[活学活用]如图，AB为⊙O的直径，PA垂直于⊙O所在的平面，M为圆周上任意一点，AN⊥PM，N为垂足．(1)求证：AN⊥平面PBM.(2)若AQ ⊥PB ，垂足为Q ，求证：NQ ⊥PB . 证明：(1)∵AB 为⊙O 的直径， ∴AM ⊥BM .又PA ⊥平面ABM ，∴PA ⊥BM . 又∵PA ∩AM ＝A ，∴BM ⊥平面PAM . 又AN ⊂平面PAM ，∴BM ⊥AN . 又AN ⊥PM ，且BM ∩PM ＝M ， ∴AN ⊥平面PBM .(2)由(1)知AN ⊥平面PBM ， PB ⊂平面PBM ，∴AN ⊥PB . 又∵AQ ⊥PB ，AN ∩AQ ＝A ， ∴PB ⊥平面ANQ .又NQ ⊂平面ANQ ，∴PB ⊥NQ .直线与平面所成角[典例] 三棱锥S -ABC 的所有棱长都相等且为所成角的余弦值． [解] 如图，过S 作SO ⊥平面ABC 于点O ，连接AO ，BO ，CO .则SO ⊥AO ，SO ⊥BO ，SO ⊥CO .∵SA ＝SB ＝SC ＝a ， ∴△SOA ≌△SOB ≌△SOC ， ∴AO ＝BO ＝CO ， ∴O 为△ABC 的外心． ∵△ABC 为正三角形， ∴O 为△ABC 的中心． ∵SO ⊥平面ABC ，∴∠SAO 即为SA 与平面ABC 所成的角． 在Rt △SAO 中，SA ＝a ，AO ＝23×32a ＝33a ，∴cos ∠SAO ＝AO SA ＝33，∴SA 与底面ABC 所成角的余弦值为33.求斜线与平面所成的角的步骤(1)作角：作(或找)出斜线在平面上的射影，将空间角(斜线与平面所成的角)转化为平面角(两条相交直线所成的锐角)，作射影要过斜线上一点作平面的垂线，再过垂足和斜足(有时可以是两垂足)作直线，注意斜线上点的选取以及垂足的位置要与问题中已知量有关，才能便于计算．(2)证明：证明某平面角就是斜线与平面所成的角．(3)计算：通常在垂线段、斜线和射影所组成的直角三角形中计算．在正方体ABCD-A1B1C1D1中，(1)直线A1B与平面ABCD所成的角的大小为________；(2)直线A1B与平面ABC1D1所成的角的大小为________；(3)直线A1B与平面AB1C1D所成的角的大小为________．解析：(1)由线面角定义知，∠A1BA为A1B与平面ABCD所成的角，∠A1BA＝45°.(2)如图，连接A1D，设A1D∩AD1＝O，连接BO，则易证A1D⊥平面ABC1D1，∴A1B在平面ABC1D1内的射影为OB，∴A1B与平面ABC1D1所成的角为∠A1BO.∵A1O＝12A1B，∴∠A1BO＝30°.(3)∵A1B⊥AB1，A1B⊥B1C1，∴A1B⊥平面AB1C1D，即A1B与平面AB1C1D所成的角的大小为90°.答案：(1)45°(2)30°(3)90°层级一学业水平达标1．已知m和n是两条不同的直线，α和β是两个不重合的平面，那么下面给出的条件中，一定能推出m⊥β的是()A．α∥β，且m⊂αB．m∥n，且n⊥βC．m⊥n，且n⊂βD．m⊥n，且n∥β解析：选B2．若两条不同的直线与同一平面所成的角相等，则这两条直线()A．平行B．相交C．异面D．以上皆有可能解析：选D.3．下列四个命题中，正确的是()①若一条直线垂直于一个平面内的无数条直线，则这条直线与这个平面垂直；②若一条直线平行于一个平面，则垂直于这条直线的直线必垂直于这个平面；③若一条直线平行于一个平面，另一条直线垂直于这个平面，则这两条直线互相垂直；④若两条直线垂直，则过其中一条直线有惟一一个平面与另一条直线垂直．A．①②B．②③C．②④D．③④解析：选D①②不正确．4.如图，α∩β＝l，点A，C∈α，点B∈β，且BA⊥α，BC⊥β，那么直线l与直线AC的关系是()A．异面B．平行C．垂直D．不确定解析：选C5.如图所示，若斜线段AB是它在平面α上的射影BO的2倍，则AB与平面α所成的角是()A．60°B．45°C．30°D．120°解析：选A6．已知直线l，a，b，平面α，若要得到结论l⊥α，则需要在条件a⊂α，b⊂α，l⊥a，l⊥b中另外添加的一个条件是________．答案：a，b相交7.如图所示，三棱锥P-ABC中，PA⊥平面ABC，PA＝AB，则直线PB与平面ABC所成的角等于________．答案：45°8．已知PA垂直于平行四边形ABCD所在的平面，若PC⊥BD，则平行四边形ABCD 一定是________．答案：菱形9.如图，在四面体A-BCD中，∠BDC＝90°，AC＝BD＝2，E，F分别为AD，BC的中点，且EF＝ 2.求证：BD⊥平面ACD.证明：取CD的中点为G，连接EG，FG.又∵E，F分别为AD，BC的中点，∴FG∥BD，EG∥AC.∵AC ＝BD ＝2，则EG ＝FG ＝1.∵EF ＝2，∴EF 2＝EG 2＋FG 2，∴EG ⊥FG ， ∴BD ⊥EG .∵∠BDC ＝90°，∴BD ⊥CD . 又EG ∩CD ＝G ，∴BD ⊥平面ACD .10.在棱长为1的正方体ABCD -A 1B 1C 1D 1中，E 是A 1B 1的中点，求直线AE 与平面ABC 1D 1所成的角的正弦值．解：如图，取CD 的中点F ，连接EF 交平面ABC 1D 1于O ，连接AO ，B 1C .由ABCD -A 1B 1C 1D 1为正方体，易得B 1C ⊥BC 1，B 1C ⊥D 1C 1，BC 1∩D 1C 1＝C 1，BC 1⊂平面ABC 1D 1，D 1C 1⊂平面ABC 1D 1，∴B 1C ⊥平面ABC 1D 1.∵E ，F 分别为A 1B 1，CD 的中点，∴EF ∥B 1C ，∴EF ⊥平面AC 1，即∠EAO 为直线AE 与平面ABC 1D 1所成的角．在Rt △EOA 中，EO ＝12EF ＝12B 1C ＝22，AE ＝A 1E 2＋AA 21＝ ⎝⎛⎭⎫122＋12＝52， ∴sin ∠EAO ＝EO AE ＝105. ∴直线AE 与平面ABC 1D 1所成的角的正弦值为105. 层级二 应试能力达标1．在正方体ABCD -A 1B 1C 1D 1中，与AD 1垂直的平面是 ( ) A ．平面DD 1C 1C B ．平面A 1DB 1 C ．平面A 1B 1C 1D 1 D ．平面A 1DB答案：B2．下面四个命题：①过一点和一条直线垂直的直线有且只有一条； ②过一点和一个平面垂直的直线有且只有一条； ③过一点和一条直线垂直的平面有且只有一个； ④过一点和一个平面垂直的平面有且只有一个． 其中正确的是( ) A ．①④ B ．②③ C ．①②D ．③④解析：选B过一点和一条直线垂直的直线有无数条，故①不正确；过一点和一个平面垂直的平面有无数个，故④不正确；易知②③均正确．故选B.3．设l，m是两条不同的直线，α是一个平面，则下列命题正确的是()A．若l⊥m，m⊂α，则l⊥αB．若l⊥α，l∥m，则m⊥αC．若l∥α，m⊂α，则l∥m D．若l∥α，m∥α，则l∥m解析：选B根据两条平行线中的一条直线垂直于一个平面，则另一条直线也垂直于这个平面，知选项B正确．4.如图，四棱锥S-ABCD的底面为正方形，SD⊥底面ABCD，则下列结论中不正确的是()A．AC⊥SBB．AB∥平面SCDC．SA与平面SBD所成的角等于SC与平面SBD所成的角D．AB与SC所成的角等于DC与SA所成的角解析：选D选项A正确，因为SD垂直于平面ABCD，而AC在平面ABCD内，所以AC垂直于SD；再由ABCD为正方形，所以AC垂直于BD，而BD与SD相交，所以AC垂直于平面SBD，进而垂直于SB.选项B正确，因为AB平行于CD，而CD在平面SCD内，AB不在平面SCD内，所以AB平行于平面SCD.选项C正确，设AC与BD的交点为O，连接SO，则SA与平面SBD所成的角就是∠ASO，SC与平面SBD所成的角就是∠CSO，易知这两个角相等．选项D错误，AB与SC所成的角等于∠SCD，而DC与SA所成的角是∠SAB，这两个角不相等．5.如图，在棱长为2的正方体ABCD-A1B1C1D1中，E是AD的中点，F是BB1的中点，则直线EF与平面ABCD所成角的正切值为________．解析：连接EB，由BB1⊥平面ABCD，知∠FEB即直线EF与平面ABCD所成的角．在Rt△FBE中，BF＝1，BE＝5，则tan∠FEB＝55.答案：5 56.如图所示，将平面四边形ABCD 沿对角线AC 折成空间四边形，当平面四边形ABCD 满足________时，空间四边形中的两条对角线互相垂直．(填上你认为正确的一种条件即可，不必考虑所有可能情况)解析：在平面四边形中，设AC 与BD 交于E ，假设AC ⊥BD ，则AC ⊥DE ，AC ⊥BE . 折叠后，AC 与DE ，AC 与BE 依然垂直，所以AC ⊥平面BDE ，所以AC ⊥BD .若四边形ABCD 为菱形或正方形，因为它们的对角线互相垂直，同上可证AC ⊥BD .答案：AC ⊥BD (或四边形ABCD 为菱形、正方形等)7．如图，在直三棱柱ABC -A 1B 1C 1中，∠BAC ＝90°，AB ＝AC ＝AA 1. (1)求证：AB 1⊥平面A 1BC 1.(2)若D 为B 1C 1的中点，求AD 与平面A 1B 1C 1所成角的正弦值． 解：(1)证明：由题意知四边形AA 1B 1B 是正方形， ∴AB 1⊥BA 1.由AA 1⊥平面A 1B 1C 1得AA 1⊥A 1C 1. 又∵A 1C 1⊥A 1B 1，AA 1∩A 1B 1＝A 1， ∴A 1C 1⊥平面AA 1B 1B ， 又∵AB 1⊂平面AA 1B 1B ， ∴A 1C 1⊥AB 1.又∵BA 1∩A 1C 1＝A 1，∴AB 1⊥平面A 1BC 1. (2)连接A 1D .设AB ＝AC ＝AA 1＝1， ∵AA 1⊥平面A 1B 1C 1，∴∠A 1DA 是AD 与平面A 1B 1C 1所成的角． 在等腰直角三角形A 1B 1C 1中，D 为斜边的中点， ∴A 1D ＝12×B 1C 1＝22.在Rt △A 1DA 中，AD ＝A 1D 2＋A 1A 2＝62. ∴sin ∠A 1DA ＝A 1A AD ＝63，即AD 与平面A 1B 1C 1所成角的正弦值为63.8.如图，直三棱柱ABC -A 1B 1C 1中，AC ＝BC ＝1，∠ACB ＝90°，AA 1＝2，D 是A 1B 1的中点．(1)求证C1D⊥平面AA1B1B；(2)当点F在BB1上的什么位置时，会使得AB1⊥平面C1DF？并证明你的结论．证明：(1)∵ABC-A1B1C1是直三棱柱，∴A1C1＝B1C1＝1，且∠A1C1B1＝90°.又D是A1B1的中点，∴C1D⊥A1B1.∵AA1⊥平面A1B1C1，C1D⊂平面A1B1C1，∴AA1⊥C1D，又A1B1∩C1D＝D，∴C1D⊥平面AA1B1B.(2)作DE⊥AB1交AB1于E，延长DE交BB1于F，连接C1F，则AB1⊥平面C1DF，点F为所求．∵C1D⊥平面AA1B1B，AB1⊂平面AA1B1B，∴C1D⊥AB1.又AB1⊥DF，DF∩C1D＝D，∴AB1⊥平面C1DF.∵AA1＝A1B1＝2，∴四边形AA1B1B为正方形．又D为A1B1的中点，DF⊥AB1，∴F为BB1的中点，。

2.3.1直线与平面垂直的判定知识点1．直线与平面垂直的有关概念(1)定义：如果直线l与平面α内的任意一条直线都垂直，我们就说直线l与平面α互相垂直，记作l⊥α．(2)相关概念：若直线l与平面α垂直，则直线l叫做平面α的垂线，平面α叫做直线l的垂面．直线与平面垂直时，它们唯一的公共点P叫做垂足．(3)画法：画直线与平面垂直时，通常把直线画成与表示平面的平行四边形的一边垂直．如图：(4)符号语言：任意a⊂α，都有l⊥a⇒l⊥α.其中“任意直线”等同于“所有直线”．2．直线与平面垂直的判定定理(1)文字语言：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直．(2)图形语言：如图所示．(3)符号语言：a⊂α，b⊂α，a∩b＝A，l⊥a，l⊥b⇒l⊥α.3．直线和平面所成的角平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角．一条直线垂直于平面，我们说它们所成的角是直角；一条直线和平面平行，或在平面内，我们说它们所成的角是0°的角．线面垂直的判定定理的应用已知a∥b，a⊥α，求证：b⊥α.1．过△ABC所在平面α外一点P，作PO⊥α，垂足为O，连接PA，PB，PC．(1)若P A＝PB＝P C，∠C＝90°，则点O是AB边的________点；(2)若P A＝PB＝P C，则点O是△ABC的________心．直线与平面所成的角如图，正方体ABCD-A1B1C1D1中，求直线A1B和平面A1B1CD所成的角．2．如图，在正方体ABCD-A1B1C1D1中，(1)A1C1与平面ABCD所成的角为________；(2)A1C1与平面BB1D1D所成的角为________．如图，已知P是△ABC所在平面外一点，P A，P B，P C两两互相垂直，H是△ABC的垂心．求证：PH⊥平面ABC．已知P为△ABC所在平面外一点，P A，PB，PC两两垂直，P A＝PB＝PC＝a，求点P 到平面ABC的距离．A组训练1．直线l⊥平面α，直线m⊂α，则l与m不可能()A．平行B．相交C．异面D．垂直2．线段AB的长等于它在平面α内的射影长的2倍，则AB所在直线与平面α所成的角为() A．30°B．45°C．60°D．120°3．如图，如果MC⊥菱形ABCD所在的平面，那么MA与BD的位置关系是()A．平行B．垂直相交C．垂直异面D．相交但不垂直4．如图，在长方体ABCD-A1B1C1D1中，AB＝BC＝2，AA1＝1，则AC1与平面A1B1C1D1所成角的正弦值为()A.223B.23C.24D.135．已知P为△ABC所在平面外一点，且PA，PB，PC两两垂直，则下列结论：①P A⊥BC；②PB⊥AC；③PC⊥AB；④AB⊥BC.其中正确的是()A．①②③B．①②④C．②③④D．①②③④6．如图，直三棱柱ABC-A1B1C1中，∠ABC＝90°，M为线段BB1上的一动点，则直线AM 与直线BC的位置关系为________．7．在正方体ABCD-A1B1C1D1中，直线AB1与平面ABCD所成的角等于________．8．如图，四棱锥S-ABCD的底面ABCD为正方形，SD⊥底面ABCD，则下列结论中正确的有________个．①AC⊥SB；②AB∥平面SCD；③SA与平面ABCD所成的角是∠SAD；④AB与SC所成的角等于DC与SC所成的角．9．如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP＝AB＝2，BC＝22，E，F分别是AD，PC的中点．证明：PC⊥平面BEF.10．如图所示，三棱锥A-SBC中，∠BSC＝90°，∠ASB＝∠ASC＝60°，SA＝SB＝SC.求直线AS与平面SBC所成的角．B组训练1. 如图，三棱锥V-ABC中，VO⊥平面ABC，O∈CD，VA＝VB，AD＝BD，则下列结论中不一定成立的是()A．AB＝BCB．VC⊥VDC．AB⊥VCD．S△VCD·AB＝S△ABC·VO2．如图所示，在矩形ABCD中，AB＝1，BC＝a(a>0)，PA⊥平面AC，且P A＝1，若BC边上存在点Q，使得PQ⊥QD，则a的取值范围是________．3．如图，在四棱锥P-ABCD中，PD⊥平面ABCD，AD⊥CD，且DB平分∠ADC，E为PC 的中点，AD＝CD＝1，DB＝2 2.(1)证明P A∥平面BDE；(2)证明AC⊥平面PBD；(3)求直线BC与平面PBD所成的角的正切值．4. 某个实心零部件的形状是如图所示的几何体，其下部是底面均为正方形，侧面是全等的等腰梯形的四棱台A1B1C1D1-ABCD，上部是一个底面与四棱台的上底面重合，侧面是全等的矩形的四棱柱ABCD-A2B2C2D2.(1)证明：直线B1D1⊥平面ACC2A2；(2)现需要对该零部件表面进行防腐处理，已知AB＝10，A1B1＝20，AA2＝30，AA1＝13(单位：cm)，每平方厘米的加工处理费为0.20元，需加工处理费多少元？2.3.1直线与平面垂直的判定参考答案知识点1．直线与平面垂直的有关概念(1)定义：如果直线l与平面α内的任意一条直线都垂直，我们就说直线l与平面α互相垂直，记作l⊥α．(2)相关概念：若直线l与平面α垂直，则直线l叫做平面α的垂线，平面α叫做直线l的垂面．直线与平面垂直时，它们唯一的公共点P叫做垂足．(3)画法：画直线与平面垂直时，通常把直线画成与表示平面的平行四边形的一边垂直．如图：(4)符号语言：任意a⊂α，都有l⊥a⇒l⊥α.其中“任意直线”等同于“所有直线”．2．直线与平面垂直的判定定理(1)文字语言：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直．(2)图形语言：如图所示．(3)符号语言：a⊂α，b⊂α，a∩b＝A，l⊥a，l⊥b⇒l⊥α.3．直线和平面所成的角平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角．一条直线垂直于平面，我们说它们所成的角是直角；一条直线和平面平行，或在平面内，我们说它们所成的角是0°的角．线面垂直的判定定理的应用已知a∥b，a⊥α，求证：b⊥α.[证明]如图，在平面α内作两条相交直线m，n.因为直线a⊥α，根据直线与平面垂直的定义知a⊥m，a⊥n.又因为b∥a，所以b⊥m，b⊥n.又因为m⊂α，n⊂α，m，n是两条相交直线，所以b⊥α.1．过△ABC所在平面α外一点P，作PO⊥α，垂足为O，连接PA，PB，PC．(1)若P A＝PB＝P C，∠C＝90°，则点O是AB边的________点；(2)若P A＝PB＝P C，则点O是△ABC的________心．解析：(1)∵PA＝P B＝P C，∴O A＝OB＝O C．又∵∠C＝90°，∴O点是AB边的中点．(2)∵PA＝PB＝PC，则OA＝OB＝OC，∴O 是△ABC 的外心． 答案：(1)中 (2)外 直线与平面所成的角如图，正方体ABCD -A 1B 1C 1D 1中，求直线A 1B 和平面A 1B 1CD 所成的角．(链接教材P 66例2) [解]如图，连接BC 1交B 1C 于点O ，连接A 1O .设正方体的棱长为a ，因为A 1B 1⊥B 1C 1，A 1B 1⊥B 1B ，所以A 1B 1⊥平面BCC 1B 1，所以A 1B 1⊥BC 1.又因为BC 1⊥B 1C ，所以BC 1⊥平面A 1B 1CD ．所以A 1O 为斜线A 1B 在平面A 1B 1CD 内的射影，∠BA 1O 为A 1B 与平面A 1B 1CD 所成的角．在R t △A 1BO 中，A 1B ＝2a ，BO ＝22a ，所以BO ＝12A 1B ，∠BA 1O ＝30°.因此，直线A 1B 和平面A 1B 1CD 所成的角为30°. 2．如图，在正方体ABCD -A 1B 1C 1D 1中， (1)A 1C 1与平面ABCD 所成的角为________； (2)A 1C 1与平面BB 1D 1D 所成的角为________．解析：(1)因为A 1C 1∥平面ABCD ， 所以A 1C 1与平面ABCD 所成的角为0°. (2)因为ABCD -A 1B 1C 1D 1是正方体， 所以BB 1⊥平面A 1B 1C 1D 1. 又因为A 1C 1⊂平面A 1B 1C 1D 1， 所以BB 1⊥A 1C 1.又四边形A 1B 1C 1D 1是正方形，所以A 1C 1⊥B 1D 1.又B 1D 1⊂平面BB 1D 1D ，BB 1⊂平面BB 1D 1D ，BB 1∩B 1D 1＝B 1， 所以A 1C 1⊥平面BB 1D 1D ，所以A 1C 1与平面BB 1D 1D 所成的角为90°. 答案：(1)0° (2)90°如图，已知P是△ABC所在平面外一点，P A，P B，P C两两互相垂直，H是△ABC的垂心．求证：PH⊥平面ABC．[证明]如图所示，∵P C⊥AP，P C⊥BP，AP∩BP＝P，A P⊂平面APB，BP⊂平面APB，∴PC⊥平面APB．3分∵AB⊂平面APB，∴P C⊥AB．5分连接CH，∵H为△ABC的垂心，∴CH⊥AB．7分∵PC∩CH＝C，PC⊂平面PHC，C H⊂平面PHC，∴AB⊥平面PHC．∵PH⊂平面PHC，∴AB⊥PH.9分同理可证PH⊥BC．10分∵AB⊂平面ABC，BC⊂平面ABC且AB∩BC＝B，∴PH⊥平面ABC．12分已知P为△ABC所在平面外一点，P A，PB，PC两两垂直，P A＝PB＝PC＝a，求点P 到平面ABC的距离．[解]法一：过P作PO⊥平面ABC于点O，连接AO，BO，CO，则PO⊥OA，PO⊥OB，PO⊥OC．因为PA＝PB＝PC＝a，所以△PAO≌△PBO≌△PCO，所以OA＝OB＝OC，所以O为△ABC的外心．因为PA，PB，PC两两垂直，所以AB＝BC＝CA＝2a，所以△ABC为正三角形，所以OA＝33AB＝63a，所以PO＝PA2－OA2＝33 A．故点P到平面ABC的距离为33 A．法二：因为PC⊥PA，PC⊥PB，P A∩PB＝P，所以PC⊥平面P AB，CP是点C到平面P AB的距离．又PA⊥PB，P A＝PB＝PC，所以AB＝2a，△ABC为正三角形，所以V P -ABC ＝13h P S △ABC ．又V C-P AB ＝13C P ·S △P AB ，由V P -ABC ＝V C-P AB 得，13h P 34(2a )2＝13a ·12a 2，所以h P ＝33A ．A 组训练1．直线l ⊥平面α，直线m ⊂α，则l 与m 不可能( ) A ．平行 B ．相交 C ．异面 D ．垂直解析：选A.因为l ⊥平面α，m ⊂α，所以l ⊥m ，l 与m 的位置关系是相交或异面，不可能出现平行． 2．线段AB 的长等于它在平面α内的射影长的2倍，则AB 所在直线与平面α所成的角为( ) A ．30° B ．45° C ．60° D ．120° 解析：选C.如图，AC ⊥α，AB ∩α＝B ，则BC 是AB 在平面α内的射影，则BC ＝12AB ，所以∠ABC ＝60°，它是AB 与平面α所成的角．3．如图，如果MC ⊥菱形ABCD 所在的平面，那么MA 与BD 的位置关系是( )A ．平行B ．垂直相交C ．垂直异面D ．相交但不垂直 解析：选C.因为MC ⊥菱形ABCD 所在平面，BD ⊂平面ABCD ， 所以MC ⊥BD . 又BD ⊥AC ，AC ∩MC ＝C 且AC ，MC 在平面ACM 内， 所以BD ⊥平面ACM . 又AM ⊂平面ACM ，所以BD ⊥MA ，但BD 与MA 不相交． 4．如图，在长方体ABCD -A 1B 1C 1D 1中，AB ＝BC ＝2，AA 1＝1，则AC 1与平面A 1B 1C 1D 1所成角的正弦值为( )A.223 B.23 C.24 D.13 解析：选D.连接A 1C 1(图略)．又AA 1⊥平面A 1B 1C 1D 1，所以∠AC 1A 1就是AC 1与平面A 1B 1C 1D 1所成角，所以sin∠AC1A1＝AA1 A1C1＝122＋22＋1＝13.5．已知P为△ABC所在平面外一点，且PA，PB，PC两两垂直，则下列结论：①P A⊥BC；②PB⊥AC；③PC⊥AB；④AB⊥BC.其中正确的是()A．①②③B．①②④C．②③④D．①②③④解析：选A.如图，∵PA⊥PB，PA⊥PC，PB∩PC＝P，且PB⊂平面PBC，PC⊂平面PBC，∴PA⊥平面PBC，又BC⊂平面PBC，∴PA⊥BC.同理可得PB⊥AC，PC⊥AB.故①②③正确．6．如图，直三棱柱ABC-A1B1C1中，∠ABC＝90°，M为线段BB1上的一动点，则直线AM 与直线BC的位置关系为________．解析：∵三棱柱ABC-A1B1C1为直三棱柱，∴BB1⊥平面ABC.又BC⊂平面ABC，∴BB1⊥BC.又AB⊥BC，且AB∩BB1＝B，AB，BB1在平面ABB1A1内，∴BC⊥平面ABB1A1.又AM⊂平面ABB1A1，∴BC⊥AM.答案：垂直7．在正方体ABCD-A1B1C1D1中，直线AB1与平面ABCD所成的角等于________．解析：在正方体ABCD-A1B1C1D1中，B1B⊥平面ABCD，所以AB即为AB1在平面ABCD中的射影，∠B1AB即为直线AB1与平面ABCD所成的角，所以∠B1AB＝45°.答案：45°8．如图，四棱锥S-ABCD的底面ABCD为正方形，SD⊥底面ABCD，则下列结论中正确的有________个．①AC⊥SB；②AB∥平面SCD；③SA与平面ABCD所成的角是∠SAD；④AB与SC所成的角等于DC与SC所成的角．解析：①∵SD⊥平面ABCD，AC⊂平面ABCD，∴SD⊥AC.又AC⊥BD，且SD∩BD＝D，SD，BD⊂平面SDB∴AC⊥平面SBD.又SB⊂平面SBD，∴AC⊥SB.②∵AB∥DC，DC⊂平面SCD，AB⊄平面SCD，∴AB∥平面SCD.③∵SD⊥平面ABCD，∴∠SAD就是SA与平面ABCD所成的角，④∵AB∥CD，∴AB与SC所成的角为∠SCD，综上，4个都正确．答案：49．如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP＝AB＝2，BC＝22，E，F分别是AD，PC的中点．证明：PC⊥平面BEF.证明：如图，连接PE，EC.在Rt△P AE和Rt△CDE中，PA＝AB＝CD，AE＝DE，∴PE＝CE，即△PEC是等腰三角形．又F是PC的中点，∴EF⊥PC.又BP＝AP2＋AB2＝22＝BC，F是PC的中点，∴BF⊥PC.又BF∩EF＝F，∴PC⊥平面BEF.10．如图所示，三棱锥A-SBC中，∠BSC＝90°，∠ASB＝∠ASC＝60°，SA＝SB＝SC.求直线AS与平面SBC所成的角．解：因为∠ASB＝∠ASC＝60°，SA＝SB＝SC，所以△ASB与△SAC都是等边三角形．因此AB＝AC.如图所示，取BC的中点D，连接AD，SD，则AD⊥BC.设SA＝a，则在Rt△SBC中，BC ＝2a ，CD ＝SD ＝22a . 在Rt △ADC 中，AD ＝AC 2－CD 2＝22a . 则AD 2＋SD 2＝SA 2，所以AD ⊥SD . 又BC ∩SD ＝D ，所以AD ⊥平面SBC .因此∠ASD 即为直线AS 与平面SBC 所成的角．在Rt △ASD 中，SD ＝AD ＝22a ，所以∠ASD ＝45°，即直线AS 与平面SBC 所成的角为45°.B 组训练1. 如图，三棱锥V -ABC 中，VO ⊥平面ABC ，O ∈CD ，VA ＝VB ，AD ＝BD ，则下列结论中不一定成立的是( )A ．AB ＝BC B ．VC ⊥VD C ．AB ⊥VC D ．S △VCD ·AB ＝S △ABC ·VO解析：选B.因为VA ＝VB ，AD ＝BD ，所以VD ⊥AB . 因为VO ⊥平面ABC ，AB ⊂平面ABC ，所以VO ⊥AB .又VO ∩VD ＝V ，VO ⊂平面VCD ，VD ⊂平面VCD ， 所以AB ⊥平面VCD .又CD ⊂平面VCD ，VC ⊂平面VCD ，所以AB ⊥VC ，AB ⊥CD . 又AD ＝BD ，所以AC ＝BC (线段垂直平分线的性质)．因为VO ⊥平面ABC ，所以V V -ABC ＝13S △ABC ·VO . 因为AB ⊥平面VCD ，所以V V -ABC ＝V B -VCD ＋V A -VCD ＝13S △VCD ·BD ＋13S △VCD ·AD ＝13S △VCD ·(BD ＋AD )＝13S △VCD ·AB ，所以13S △ABC ·VO ＝13S △VCD ·AB ，即S △VCD ·AB ＝S △ABC ·VO . 综上知，A ，C ，D 正确．2．如图所示，在矩形ABCD 中，AB ＝1，BC ＝a (a >0)，PA ⊥平面AC ，且P A ＝1，若BC 边上存在点Q ，使得PQ ⊥QD ，则a 的取值范围是________．解析：因为PA ⊥平面AC ，QD ⊂平面AC ，所以P A ⊥QD .又因为PQ ⊥QD ，PA ∩PQ ＝P ， 所以QD ⊥平面PAQ ，所以AQ ⊥QD .①当0<a <2时，由四边形ABCD 是矩形且AB ＝1知，以AD 为直径的圆与BC 无交点，即对BC 上任一点Q ，都有∠AQD <90°，此时BC 边上不存在点Q ，使PQ ⊥QD ； ②当a ＝2时，以AD 为直径的圆与BC 相切于BC 的中点Q ，此时∠AQD ＝90°，所以BC 边上存在一点Q ，使PQ ⊥QD ；③当a >2时，以AD 为直径的圆与BC 相交于点Q 1，Q 2，此时∠AQ 1D ＝∠AQ 2D ＝90°，故BC 边上存在两点Q (即Q 1与Q 2)，使PQ ⊥QD . 答案：[2，＋∞)3．如图，在四棱锥P -ABCD 中，PD ⊥平面ABCD ，AD ⊥CD ，且DB 平分∠ADC ，E 为PC的中点，AD ＝CD ＝1，DB ＝2 2.(1)证明P A ∥平面BDE ； (2)证明AC ⊥平面PBD ；(3)求直线BC 与平面PBD 所成的角的正切值． 解：(1)证明：设AC ∩BD ＝H ，连接EH . 在△ADC 中，因为AD ＝CD ，且DB 平分∠ADC ，所以H 为AC 的中点．又因为E 为PC 的中点，故EH ∥PA . 又HE ⊂平面BDE ，PA ⊄平面BDE ， 所以PA ∥平面BDE .(2)证明：因为PD ⊥平面ABCD ， AC ⊂平面ABCD ，所以PD ⊥AC . 由(1)知，BD ⊥AC ，PD ∩BD ＝D ， 故AC ⊥平面PBD .(3)由AC ⊥平面PBD 可知，BH 为BC 在平面PBD 内的射影，所以∠CBH 为直线BC 与平面PBD 所成的角． 由AD ⊥CD ，AD ＝CD ＝1，DB ＝22，可得DH ＝CH ＝22，BH ＝322.在Rt △BHC 中，tan ∠CBH ＝CH BH ＝13，所以直线BC 与平面PBD 所成的角的正切值为13.4. 某个实心零部件的形状是如图所示的几何体，其下部是底面均为正方形，侧面是全等的等腰梯形的四棱台A 1B 1C 1D 1-ABCD ，上部是一个底面与四棱台的上底面重合，侧面是全等的矩形的四棱柱ABCD -A 2B 2C 2D 2.(1)证明：直线B 1D 1⊥平面ACC 2A 2；(2)现需要对该零部件表面进行防腐处理，已知AB ＝10，A 1B 1＝20，AA 2＝30，AA 1＝13(单位：cm)，每平方厘米的加工处理费为0.20元，需加工处理费多少元？ 解：(1)证明：因为四棱柱ABCD -A 2B 2C 2D 2的侧面是全等的矩形，所以AA 2⊥AB ，AA 2⊥AD .又AB ∩AD ＝A ，所以AA 2⊥平面ABCD .连接BD (图略)，因为BD ⊂平面ABCD ，所以AA 2⊥BD . 根据棱台的定义知，BD 与B 1D 1共面．又已知平面ABCD ∥平面A 1B 1C 1D 1，且平面ABCD ∩平面BB 1D 1D ＝BD ，平面BB 1D 1D ∩平面A 1B 1C 1D 1＝B 1D 1，所以BD ∥B 1D 1，于是由AA 2⊥BD ，AC ⊥BD ，BD ∥B 1D 1，可得AA 2⊥B 1D 1，AC ⊥B 1D 1. 又AA 2∩AC ＝A ，所以直线B 1D 1⊥平面ACC 2A 2. (2)由于四棱柱ABCD -A 2B 2C 2D 2的底面是正方形，侧面是全等的矩形，所以S 1＝S 四棱柱ABCD -A 2B 2C 2D 2上底面＋S 四棱柱ABCD -A 2B 2C 2D 2的侧面＝(A 2B 2)2＋4AB ·AA 2＝102＋4×10×30＝1 300(cm 2)． 又四棱台A 1B 1C 1D 1-ABCD 的下底面是正方形，侧面是全等的等腰梯形，设四棱台侧面的高为h ，所以S 2＝S 四棱台A 1B 1C 1D 1-ABCD 的下底面＋S 四棱台A 1B 1C 1D 1-ABCD 的侧面＝(A 1B 1)2＋4(AB ＋A 1B 1)h ÷2＝202＋2(10＋20) 132－[12×（20－10）]2＝1 120(cm 2)．所以S ＝S 1＋S 2＝2 420(cm 2)． 故需加工处理费2 420×0.2＝484(元)．。

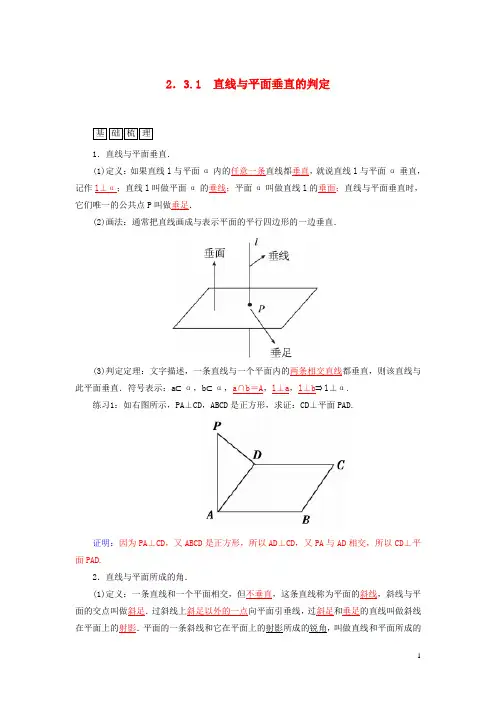
2．3.1 直线与平面垂直的判定基础梳理1．直线与平面垂直．(1)定义：如果直线l与平面α内的任意一条直线都垂直，就说直线l与平面α垂直，记作l⊥α；直线l叫做平面α的垂线；平面α叫做直线l的垂面；直线与平面垂直时，它们唯一的公共点P叫做垂足．(2)画法：通常把直线画成与表示平面的平行四边形的一边垂直．(3)判定定理：文字描述，一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直．符号表示：a⊂α，b⊂α，a∩b＝A，l⊥a，l⊥b⇒l⊥α.练习1：如右图所示，PA⊥CD，ABCD是正方形，求证：CD⊥平面PAD.证明：因为PA⊥CD，又ABCD是正方形，所以AD⊥CD，又PA与AD相交，所以CD⊥平面PAD.2．直线与平面所成的角．(1)定义：一条直线和一个平面相交，但不垂直，这条直线称为平面的斜线，斜线与平面的交点叫做斜足．过斜线上斜足以外的一点向平面引垂线，过斜足和垂足的直线叫做斜线在平面上的射影．平面的一条斜线和它在平面上的射影所成的锐角，叫做直线和平面所成的角，如图，∠PAO就是斜线AP与平面α所成的角．(2)特别的，当直线AP与平面α垂直时，它们所成的角是90°；当直线与平面平行，或在平面内时，它们所成的角是0°．(3)直线和平面所成角θ的范围[0°，90°]．练习2：直线与平面不垂直时，能否在平面内找到两条直线与这条直线垂直？答案：能练习3：两条直线垂直就一定相交吗？答案：错►思考应用1．“两条平行直线能确定一个平面，一条直线垂直于平面内的两条平行直线，则这条直线也垂直于这个平面．”这个结论对吗？解析：不正确．实际上，由公理4可知，平行具有“传递性”，因此一条直线与平面内的一条直线垂直，那么它与这个平面内的平行于这条直线的所有直线都垂直，但不能保证与其他直线垂直．2．异面直线所成的角的定义及范围是什么？解析：异面直线所成的角是通过作平行线得到的，即异面直线a与b所成的角，在空间中任取一点O，过O作a′∥a，b′∥b，则a′与b′的夹角就是a与b所成的角，其范围为(0°，90°]．自测自评1．如果一条直线垂直于一个平面内的：①三角形的两边；②梯形的两边；③圆的两条直径；④正六边形的两条边，则能保证该直线与平面垂直的是(A)A．①③B．②C．②④D．①②④解析：①③能保证这条直线垂直于该平面内的两条相交直线，②④中的两直线有可能平行．2．若斜线段AB是它在平面α上的射影的长的2倍，则AB与平面α所成的角是(A) A．60°B．45°C．30°D．120°解析：AB与平面α所成的角，即AB与其在平面α射影所成的角，由已知得为60°.3．如果直线l和平面α内的两条平行线垂直，那么下列结论正确的是(D)A．l⊂αB．l与α相交C．l∥αD．都有可能4．已知a，b是异面直线，下列结论不正确的是(D)A．存在无数个平面与a，b都平行B．存在一个平面与a，b等距离C．存在无数条直线与a，b都垂直D．存在一个平面与a，b都垂直5．三条直线两两垂直，下列四个命题：①三条直线必共点；②其中必有两条直线是异面直线；③三条直线不可能在同一平面内；④其中必有两条直线在同一平面内．其中真命题的序号是③．解析：两条直线垂直不一定相交，只有③正确．基础达标1．下列说法中错误的是(D)①如果一条直线和平面内的一条直线垂直，该直线与这个平面必相交；②如果一条直线和平面的一条平行线垂直，该直线必在这个平面内；③如果一条直线和平面的一条垂线垂直，该直线必定在这个平面内；④如果一条直线和一个平面垂直，该直线垂直于平面内的任何直线．A．①②B．②③④C．①②④D．①②③解析：由线面垂直的判定定理可得①②③错误．2．一条直线和平面所成角为θ，那么θ的取值范围是(B)A ．(0°，90°)B ．[0°，90°]C ．[0°，180°]D ．[0°，180°)3．如图，在四棱锥P －ABCD 中，底面ABCD 为矩形，侧棱PA⊥底面ABCD ，AB ＝3，BC ＝1，PA ＝2，E 为PD 的中点，则直线BE 与平面ABCD 所成角的正切值为________．解析：取AD 的中点F ，连接EF 、BF ，则EF∥PA，由侧棱PA⊥底面ABCD ，∴EF ⊥底面ABCD ，则∠EBF 为BE 与平面ABCD 所成角．答案：21313 4．设O 为平行四边形ABCD 对角线的交点，P 为平面AC 外一点且有PA ＝PC ，PB ＝PD ，则PO 与平面ABCD 的关系是________．答案：垂直5．给出下列命题：①若直线a⊥平面α，且直线a⊥直线b ，则b⊥平面α；②如果一条直线垂直于平面内的无数条直线，那么这条直线和这个平面垂直；③如果一条直线与一个平面内的某一条直线不垂直，那么这条直线就一定不与这个平面垂直．其中正确命题的序号是________．解析：解答此类问题的关键是正确理解和掌握好直线与平面垂直的定义，对不正确的命题，可通过举反例说明．①b 与平面α可以平行或者b ⊂α.②直线垂直于平面α内的无数条平行直线时，直线与平面不一定垂直．③由反证法可知正确．答案：③6．已知PA 垂直于平行四边形ABCD 所在平面，若PC ⊥BD ，则平行四边形一定是________． 解析：由于PA⊥平面ABCD ，BD ⊂平面ABCD ，所以PA⊥BD.又PC⊥BD，所以BD⊥平面PAC.又AC ⊂平面PAC ，所以BD⊥AC.又四边形ABCD 是平行四边形，所以四边形ABCD 是菱形．答案：菱形 巩固提升7．已知三条相交于一点的线段PA ，PB ，PC 两两垂直，P 在平面ABC 外，PH ⊥平面ABC 于H ，则垂足H 是△ABC 的(D )A ．内心B ．外心C ．重心D ．垂心解析：连接AH 并延长交BC 于D ，如图所示．由于PH⊥平面ABC ，则BC ⊥PH ，又PA⊥PB，PA ⊥PC ，则PA⊥平面PBC ，所以BC⊥PA.所以BC⊥平面PAD ，又AH ⊂平面PAD ，所以AH⊥BC.同理可证BH⊥AC，CH ⊥AB ，所以垂足H 是△ABC 的垂心． 8．如图，在四棱锥PABCD 中，AB ⊥平面PAD ，AB ∥CD ，PD ＝AD ，E 是PB 的中点，F 是DC 上的点，且DF ＝12AB ，PH 为△PAD 中AD 边上的高． (1)证明：PH⊥平面ABCD ；(2)证明：EF⊥平面PAB.证明：(1)∵PH 为△PAD 中的高，∴PH ⊥AD.又AB⊥平面PAD ，PH ⊂平面PAD ，∴PH ⊥AB ，AB ∩AD ＝A.∴PH ⊥平面ABCD.(2)取PA 的中点Q ，连接EQ ，DQ ，∵E 是PB 的中点，∴EQ ∥AB 且EQ ＝12AB. 又DF ＝12AB 且DF∥AB， ∴EQ 綊DF ，∴四边形EQDF 是平行四边形．∴EF ∥DQ.由(1)知AB⊥平面PAD ，∴AB ⊥DQ.又∵PD＝AD ，∴DQ ⊥PA.∵PA ∩AB ＝A ，∴DQ ⊥平面PAB.∵EF ∥DQ ，∴EF ⊥平面PAB.9．如图，正方形ABCD 所在平面与三角形CDE 所在平面相交于CD ，AE ⊥平面CDE ，且AE ＝3，AB ＝6.(1)求证：AB⊥平面ADE；(2)求凸多面体ABCDE的体积．(1)证明：∵AE⊥平面CDE，CD⊂平面CDE，∴AE⊥CD.在正方形ABCD中，CD⊥AD，∵AD∩AE＝A，∴CD⊥平面ADE.∵AB∥CD，∴AB⊥平面ADE.(2)解析：在Rt△ADE中，AE＝3，AD＝6，∴DE＝AD2－AE2＝3 3.如图，过点E作EF⊥AD于点F，∵AB⊥平面ADE，EF⊂平面ADE，∴EF⊥AB.∵AD∩AB＝A，∴EF⊥平面ABCD.∵AD·EF＝AE·DE，∴EF ＝AE ·DE AD ＝3×336＝332. 又正方形ABCD 的面积S 正方形ABCD ＝36，∴V 多面体ABCDE ＝V EABCD ＝13S 正方形ABCD ·EF ＝13×36×332＝18 3. 故所求凸多面体ABCDE 的体积为18 3.1．直线和平面垂直的判定定理可简化为“线线垂直，则线面垂直”．这里的“线线”指的是“一条直线和平面内的两条相交直线”，“线面”则是指这条直线和两条相交直线所在的平面．判定定理告诉我们，要证明直线和平面垂直，只需在这个平面内找出两条相交直线都与已知直线垂直，这是关键．2．判定线面垂直的两种方法：(1)线面垂直的定义；(2)线面垂直的判定定理．。

2．3 直线、平面垂直的判定及其性质2．3.1 直线与平面垂直的判定 2．3.2 平面与平面垂直的判定1．直线与平面垂直(1)定义：如果直线l 与平面α内的所有直线都垂直，就说直线l 与平面α互相垂直.记法 垂线 垂面 垂足 l ⊥αlα唯一公共点P(2)判定定理文字表述：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直．符号表述：⎭⎪⎬⎪⎫l ⊥a l ⊥ba ⊂α，b ⊂αa ∩b ＝A ⇒l ⊥α.2．直线与平面所成的角(1)定义：平面的一条斜线和它在平面上的射影所成的角，叫做这条直线和这个平面所成的角．如图，∠P AO 就是斜线AP 与平面α所成的角． (2)当直线AP 与平面垂直时，它们所成的角是90°. (3)当直线与平面平行或在平面内时，它们所成的角是0°. (4)线面角θ的范围：[0°，90°]． 3．两个平面垂直(1)二面角：从一条直线出发的两半平面所组成的图形叫做二面角．直线叫做二面角的棱．两半平面叫做二面角的面．如图(1)，记作：α-l -β或P -l -Q 或P -AB -Q .(2)二面角的平面角 如图(2)：二面角α-l -β若有①O ∈l ；②OA ⊂α，OB ⊂β； ③OA ⊥l ，OB ⊥l .则∠AOB 就叫做二面角α-l -β的平面角． (3)平面与平面的垂直①定义：如果两个平面相交，且它们所成的二面角是直角，就说这两个平面互相垂直．②画法：记作：α⊥β.③面面垂直的判定定理文字语言：一个平面过另一个平面的垂线，则这两个平面垂直． 符号表示：⎭⎪⎬⎪⎫a ⊥βa ⊂α⇒α⊥β1．下列表述正确的个数为( )①若直线a ∥平面α，直线a ⊥b ，则b ⊥α； ②若直线a ⊄平面α，b ⊂α，且a ⊥b ，则a ⊥α； ③若直线a 平行于平面α内的两条直线，则a ∥α； ④若直线a 垂直于平面α内的两条直线，则a ⊥α. A ．0 B ．1 C ．2 D ．3答案：A2．若斜线段AB 是它在平面α内的射影长的2倍，则AB 与α所成的角为( ) A ．60° B ．45° C ．30°D ．120° 解析：选A.斜线段AB ，设斜足为B ，A 在平面α上的射影为H ，∴BH 为AB 在平面α上的射影． ∴∠ABH 为斜线段AB 与α所成的角． ∵sin ∠ABH ＝AH AB ，又∵ABBH ＝2，∴sin ∠ABH ＝32， ∵∠ABH 为锐角，∴∠ABH ＝60°. 3．下列结论中错误的是( )A ．如果平面α⊥平面β，那么α内所有直线都垂直于平面βB ．如果平面α⊥平面β，那么α内一定存在直线平行于平面βC ．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面βD ．如果平面α⊥平面γ，平面β⊥平面γ，α∩β＝l ，那么l ⊥γ 答案：A4．把等腰直角△ABC 沿斜边BC 上的高线AD 折成一个二面角，此时∠BAC ＝60°，那么此二面角的大小是________．解析：如图，设AD ＝a ，∴AB ＝AC ＝2a ，又∠BAC ＝60°，∴BC ＝2a ， 又BD ＝DC ＝AD ＝a ， ∴∠BDC ＝90°.又∵AD ⊥DB ，AD ⊥DC ，∴∠BDC 为二面角B -AD -C 的平面角． 故所求二面角大小为90°. 答案：90°5．如图，二面角α-l -β的大小是60°，线段AB ⊂α，B ∈l ，AB 与l 所成的角为30°，则AB 与平面β所成的角的正弦值是________． 解析：如图，作AC ⊥β于C ，作CD ⊥l 于D ，连接AD . 在Rt △ABD 中，∠ABD ＝30°，设AB ＝2a ，则AD ＝a ，在Rt △ACD 中，∠ADC 为二面角α-l -β的平面角，∠ADC ＝60°，所以AC ＝32a .又AB 与β所成的角为∠ABC ， sin ∠ABC ＝AC AB ＝34.答案：34类型一 线面垂直的判定例1►如图，已知空间四边形ABDC 的边BC ＝AC ，AD ＝BD ，过B 作BE ⊥CD ，E 为垂足，作AH ⊥BE 于H ，求证：AH ⊥平面BCD . 【证明】 取AB 中点F ，连接CF ，DF ， ∵AC ＝BC ，∴CF ⊥AB .又∵AD ＝BD ，∴DF ⊥AB ， ∴AB ⊥平面CDF ，∴AB ⊥CD . 又BE ⊥CD ， 且AB ∩BE ＝B ，根据直线与平面垂直的判定定理， 直线CD ⊥平面ABE .∴CD ⊥AH .而AH ⊥BE ，CD ∩BE ＝E ， ∴AH ⊥平面BCD .【点评】 利用直线与平面垂直的判定定理判定直线与平面垂直的步骤是：①在这个平面内找两条直线，使它和这两条直线垂直；②确定这个平面内的两条直线是相交的直线；③根据判定定理得出结论．1.P为△ABC所在平面外一点，P A⊥平面ABC，∠ABC＝90°，AE⊥PB交于E，AF⊥PC 交于F，求证：(1)BC⊥平面P AB；(2)AE⊥平面PBC；(3)PC⊥平面AEF.证明：(1)P A⊥平面ABC，BC⊂平面ABC，∴P A⊥BC.∵AB⊥BC，AB∩P A＝A，∴BC⊥平面P AB.(2)BC⊥平面P AB，AE⊂平面P AB，∴BC⊥AE.∵PB⊥AE，BC∩PB＝B，∴AE⊥平面PBC.(3)AE⊥平面PBC，PC⊂平面PBC.∴AE⊥PC，∵AF⊥PC，AE∩AF＝A，∴PC⊥平面AEF.类型二求线面角例2►如图所示，正方体ABCD-EFGH的棱长为a，点P在AC上，Q在BG上，AP＝BQ＝a，求直线PQ与平面ABCD所成角的正切值．【解】过点P作PM∥AB交BC于M，连接QM，则MPAB＝CPCA＝CMCB，即MPa＝(2－1)a2a＝CMa，所以CM＝MP＝⎝⎛⎭⎫1－22a，所以BMBC＝22，又BQBG＝a2a＝22，所以BMBC＝BQBG，所以QM∥CG，即QM⊥平面ABCD ，∠QPM 即为PQ 与平面ABCD 所成的角．易知，QM ＝22a ，又MP ＝⎝⎛⎭⎫1－22a ， 所以，在Rt △PQM 中， tan ∠QPM ＝QMMP＝2＋1，即直线PQ 与平面ABCD 所成角的正切值为2＋1. 【点评】 求斜线与平面所成角的步骤 2.如图所示，已知正四面体A -BCD 的棱长为a ，E 为AD 的中点，连接CE . (1)求AD 与平面BCD 所成角的余弦值； (2)求CE 与平面BCD 所成角的正弦值．解：(1)如图所示，过点A 作AO ⊥底面BCD ，垂足为O 点，连接OB ，OC ，OD .则OB ，OC ，OD 分别是AB ，AC ，AD 在平面BCD 上的射影． ∴∠ADO 为直线AD 与平面BCD 所成的角． 又∵AB ＝AC ＝AD ，∴OB ＝OC ＝OD . ∴O 为△BCD 的外心．∵△BCD 为正三角形，∴点O 为重心． 又正四面体棱长为a ，∴OD ＝32a ×23＝33a ， ∴cos ∠ADO ＝OD AD ＝33，∴AD 与平面BCD 所成角的余弦值为33. (2)取OD 的中点F ，连接EF ，CF .∵E ，F 分别为△DAO 的边AD ，OD 的中点， ∴EF 为△DAO 的中位线． ∴EF ∥AO .又AO ⊥平面BCD ， ∴EF ⊥平面BCD .∴FC 为EC 在平面BCD 上的射影． ∴∠ECF 为CE 与平面BCD 所成的角．在Rt △EFC 中，EF ＝12AO .而AO ＝AD 2－OD 2＝a 2－⎝⎛⎭⎫33a 2＝63a ， ∴EF ＝66a . ∵E 为AD 的中点，∴CE ＝32AD ＝32a . ∴sin ∠ECF ＝EF CE ＝66a32a ＝23.∴CE 与平面BCD 所成角的正弦值为23. 类型三 面面垂直的判定例3►如图在正方体ABCD -A 1B 1C 1D 1中，E 为BB 1的中点，F 为CD 的中点，G 为AB 的中点．求证：平面ADE ⊥平面A 1FG .【证明】 ∵G 、F 分别为AB 、CD 的中点，∴GF 綊A 1D 1， 又∵ABCD -A 1B 1C 1D 1为正方体， ∴A 1D 1⊥平面ABB 1A 1， ∴A 1D 1⊥AE . ∵E 为BB 1的中点，在Rt △ABE 与Rt △A 1AG 中， AB ＝A 1A ，BE ＝AG ， ∴△ABE ≌△A 1AG ， ∴∠AEB ＝∠A 1GA ， 又∵∠AEB ＋∠EAB ＝90°， 设AE ∩A 1G ＝M ，∴∠AGM＋∠MAG＝90°，∴∠AMG＝90°，∴AE⊥A1G.由AE⊥A1G，AE⊥A1D1且A1D1∩A1G＝A1，A1D1，A1G⊂平面A1GFD1，∴AE⊥平面A1GF.又∵AE⊂平面ADE，∴平面ADE⊥平面A1FG.【点评】证明平面与平面垂直的方法根据面面垂直的定义判定两平面垂直实质上是把问题转化成了求二面角的平面角，通常情况下利用判定定理要比定义简单些，是证明面面垂直的常用方法，即要证面面垂直，只要转证线面垂直，其关键与难点是在其中一个平面内寻找一直线与另一平面垂直．3.如图△ABC为正三角形，EC⊥平面ABC，BD∥CE，且CE＝CA＝2BD，M是EA的中点，求证：(1)DE＝DA；(2)平面BDM⊥平面ECA；(3)平面DEA⊥平面ECA.证明：(1)如图，取EC的中点F，连接DF.因为EC⊥平面ABC，BC⊂平面ABC，所以EC⊥BC.因为CE＝2BD所以CF＝BD，又CF ∥BD ，所以四边形BCFD 为平行四边形， 所以DF ∥BC ，所以DF ⊥EC . 在Rt △EFD 和Rt △DBA 中． 因为EF ＝12EC ＝BD ，FD ＝BC ＝AB ，所以Rt △EFD ≌Rt △DBA ，故DE ＝DA .(2)取CA 的中点N ，连接MN ，BN ，则MN ∥EC ，所以MN ∥BD ，所以N 点在平面BDM 内．因为EC ⊥平面ABC ，所以EC ⊥BN . 又△ABC 为正三角形，所以CA ⊥BN ， 又EC ∩CA ＝C ，所以BN ⊥平面ECA .因为BN 在平面MNBD 内，所以平面MNBD ⊥平面ECA ，即平面BDM ⊥平面ECA . (3)因为BD ∥EC ，且BD ＝12EC ，MN ∥EC ，且MN ＝12EC ，所以MN ∥BD ，且MN ＝BD ，所以四边形MNBD 为平行四边形，所以DM ∥BN .因为BN ⊥平面ECA ，所以DM ⊥平面ECA ，又DM ⊂平面DEA ，所以平面DEA ⊥平面ECA . 类型四 求二面角例4►如图，在四棱锥P -ABCD 中，底面是边长为a 的正方形，侧棱PD ＝a ，P A ＝PC ＝2a ，(1)求证：PD ⊥平面ABCD ； (2)求证：平面P AC ⊥平面PBD ； (3)求二面角P -BC -D 的大小．【解】 (1)证明：∵PD ＝a ，DC ＝a ，PC ＝2a ， ∴PC 2＝PD 2＋DC 2，∴PD ⊥DC .同理可证PD ⊥AD ，又AD ∩DC ＝D ， ∴PD ⊥平面ABCD .(2)证明：由(1)知PD ⊥平面ABCD ， ∴PD ⊥AC ，而四边形ABCD 是正方形，∴AC⊥BD，又BD∩PD＝D，∴AC⊥平面PDB.AC⊂平面P AC，∴平面P AC⊥平面PBD.(3)由(1)知PD⊥BC，又BC⊥DC，∴BC⊥平面PDC，∴BC⊥PC.∴∠PCD为二面角P-BC-D的平面角．在直角△PCD中，PD＝CD＝a，∴∠PCD＝45°.∴二面角P-BC-D的平面角为45°.【点评】(1)证明垂直关系时，注意线面垂直与线线垂直的相互转化．(2)求二面角的大小的关键是作出二面角的平面角，这就需要紧扣它的三个条件．即这个角的顶点是否在棱上；角的两边是否分别在两个平面内；这两边是否都与棱垂直．在具体作图时，还要注意掌握一些作二面角的平面角的方法技巧．如：线面的垂直，图形的对称性，与棱垂直的面等．4．如图所示，四边形ABCD是正方形，P A⊥平面ABCD，且P A＝AB.(1)求二面角A-PD-C的平面角的度数；(2)求二面角B-P A-D的平面角的度数；(3)求二面角B-P A-C的平面角的度数．解：(1)∵P A⊥平面ABCD，∴P A⊥CD，∵四边形ABCD为正方形，∴CD⊥AD，∵P A∩AD＝A，∴CD⊥平面P AD，又CD⊂平面PCD，∴平面P AD⊥平面PCD.∴二面角A-PD-C的平面角的度数为90°.(2)∵P A⊥平面ABCD，∴AB⊥P A，AD⊥P A.∴∠BAD为二面角B-P A-D的平面角．由题意知∠BAD＝90°，∴二面角B-P A-D的平面角的度数为90°.(3)∵P A⊥平面ABCD，∴AB⊥P A，AC⊥P A.∴∠BAC为二面角B-P A-C的平面角．∵四边形ABCD为正方形，∴∠BAC＝45°.即二面角B-P A-C的平面角的度数为45°.1．如果一条直线垂直于一个平面内的：①三角形的两边；②梯形的两边；③圆的两条直径；④正六边形的两条边．则能保证该直线与平面垂直的是()A．①③B．②C．②④D．①②④解析：选A.①③能保证这条直线垂直于该平面内的两条相交直线，②④中的两条直线有可能是平行的．2．设m，n是两条不同的直线，α，β是两个不同的平面．()A．若m⊥n，n∥α，则m⊥αB．若m∥β，β⊥α，则m⊥αC．若m⊥β，n⊥β，n⊥α，则m⊥αD．若m⊥n，n⊥β，β⊥α，则m⊥α解析：选C.根据条件确定相应的位置关系，再对照选项确定答案．A中，由m⊥n，n ∥α可得m∥α或m与α相交或m⊂α，错误；B中，由m∥β，β⊥α可得m∥α或m与α相交或m⊂α，错误；C中，由m⊥β，n⊥β可得m∥n，又n⊥α，所以m⊥α，正确；D中，由m⊥n，n⊥β，β⊥α可得m∥α或m与α相交或m⊂α，错误．3．如图，BC是Rt△ABC的斜边，过A作△ABC所在平面α的垂线AP，连PB、PC，过A作AD⊥BC于D，连接PD，那么图中直角三角形的个数是()A．5 B．6C．7 D．8解析：选D.题图中直角三角形有△ABC，△ADC，△ADB，△P AD，△P AC，△P AB，△PDC，△PDB.4．下列结论中①两个相交平面组成的图形叫做二面角；②异面直线a、b分别和一个二面角的两个面垂直，则a、b组成的角与这个二面角的平面角相等或互补；③二面角的平面角是从棱上一点出发，分别在两个面内作射线所成角的最小角；④二面角的大小与其平面角的顶点在棱上的位置没有关系．其中正确的是()A．①③B．②④C．③④D．①②解析：选 B.由二面角的定义：从一条直线出发的两个半平面所组成的图形叫做二面角，所以①不对，实质上它共有四个二面角；由a、b垂直于两个面，则a、b都垂直于二面角的棱，故②正确；③中所作的射线不一定垂直于二面角的棱，故③不对；由定义知④正确，故选B.5.如图，在三棱锥P-ABC中，已知PC⊥BC，PC⊥AC，点E，F，G分别是所在棱的中点，则下面结论中错误的是()A．平面EFG∥平面PBCB．平面EFG⊥平面ABCC．∠BPC是直线EF与直线PC所成的角D．∠FEG是平面P AB与平面ABC所成二面角的平面角解析：选D.A正确，∵GF∥PC，GE∥CB，GF∩GE＝G，PC∩CB＝C，∴平面EFG ∥平面PBC；B正确，∵PC⊥BC，PC⊥AC，PC∥GF，∴GF⊥BC，GF⊥AC，又BC∩AC＝C，∴GF⊥平面ABC，∴平面EFG⊥平面ABC；C正确，易知EF∥BP，∴∠BPC是直线EF与直线PC所成的角；D错误，∵GE与AB不垂直，∴∠FEG不是平面P AB与平面ABC所成二面角的平面角．6．设平面α外两点A和B在α上的射影是A1和B1，已知AA1＝1，BB1＝2，A1B1＝3，则直线AB与平面α所成的角为________．解析：如图(1)，A、B在平面α的同侧tan∠BAC＝13＝33，∴∠BAC＝30°.如图(2)，A、B在平面α的两侧tan∠ACA1＝tan ∠ABA″＝133＝3，∠ACA1＝60°.答案：30°或60°7．如图所示，在四棱锥P -ABCD 中，P A ⊥平面ABCD ，四边形ABCD 是正方形，且P A ＝2AD ，二面角P -CD -A 的平面角为θ，则tan θ＝________.解析：∵P A ⊥平面ABCD ，CD ⊂平面ABCD .∴P A ⊥CD ，又CD ⊥AD ，AD ∩P A ＝A .∴CD ⊥平面P AD ，又PD ⊂平面P AD .∴CD ⊥PD ，故∠PDA 为二面角P -CD -A 的平面角θ.在Rt △P AD 中，tan θ＝P A AD ＝2AD AD＝2. 答案：28．P A 、PB 、PC 是从P 点出发的三条射线，每两条射线的夹角均为60°，那么直线PC 与平面P AB 所成的角的余弦值是________．解析：如图，设所求角为θ，由题意知，C 在平面P AB 内的射影O 应在∠APB 的平分线上，过O 作OM ⊥P A .在Rt △PMO 中，∠OPM ＝30°，设OM ＝a ，则PO ＝2a ，PM ＝3a .在Rt △PMC 中，∠APC ＝60°，则PC ＝23a .在Rt △POC 中，cos θ＝OP PC ＝2a 23a ＝33. 答案：339．如图，三棱柱ABC -A 1B 1C 1的底面是边长为a 的正三角形，侧棱长为22a ，点D 在棱A 1C 1上．(1)若A 1D ＝DC 1，求证：直线BC 1∥平面AB 1D ；(2)是否存在D ，使平面AB 1D ⊥平面ABB 1A 1？若存在，请确定点D 的位置；若不存在，说明理由．解：(1)证明：如图，连接A 1B 交AB 1于点E ，连接DE ，在平行四边形ABB 1A 1中，有A 1E ＝BE ，又A 1D ＝DC 1，∴DE 是△A 1BC 1的中位线，从而DE ∥BC 1，又DE ⊂平面AB 1D .BC 1⊄平面AB 1D ，∴直线BC 1∥平面AB 1D .(2)由题意：假设存在点D ，使平面AB 1D ⊥平面ABB 1A 1，过点D 作DN ⊥AB 1于点N ，则DN ⊥平面ABB 1A 1.又过点D 作DM ⊥A 1B 1于点M ，则DM ⊥平面ABB 1A 1，而过平面外一点有且仅有一条直线与已知平面垂直，故M 、N 应重合于点B 1，此时应有DB 1⊥A 1B 1，故∠A 1B 1D ＝90°.又点D 在棱A 1C 1上，故∠A 1B 1D ≤∠A 1B 1C 1＝60°，显然矛盾，故不存在这样的点D ， 使平面AB 1D ⊥平面ABB 1A 1.10.如图所示，在四棱锥P -ABCD 中，底面ABCD 是矩形，侧棱P A 垂直于底面，E 、F 分别是AB 、PC 的中点，P A ＝AD .求证：(1)CD ⊥PD ；(2)EF ⊥平面PCD .证明：(1)∵P A ⊥底面ABCD ，∴CD ⊥P A .又矩形ABCD 中，CD ⊥AD ，且AD ∩P A ＝A ，∴CD ⊥平面P AD ，又PD ⊂平面P AD ，∴CD ⊥PD .(2)取PD 的中点G ，连接AG ，FG .又∵G 、F 分别是PD 、PC 的中点，∴GF 綊12CD ，∴GF 綊AE ， ∴四边形AEFG 是平行四边形，∴AG ∥EF .∵P A ＝AD ，G 是PD 的中点，∴AG ⊥PD ，∴EF ⊥PD ，∵CD ⊥平面P AD ，AG ⊂平面P AD .∴CD ⊥AG ，∴EF ⊥CD .∵PD ∩CD ＝D ，∴EF ⊥平面PCD .。

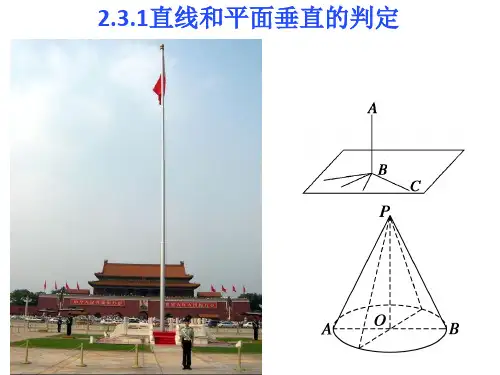
§2.3.1直线与平面垂直的判定—、课标要求（1）掌握直线与屏幕垂直的定义及判定定理；（2）能灵活应用直线与平面垂直的判定定理证明直线与平面垂直；（3）知道百线与平面所成角的概念，并能解决简单的线面角问题。

二、教学重、难点重点：直线与平面垂直的定义；难点：直线与平面垂直的判定定理的探究。

三、设计思路肓线与平面垂肓问题是肓线与平面的重要内容，也是高考考杳的重点。

求解的关键是根据线与曲之间的互化关系，借助创设辅助线与面，找出符号语言与图形语言之间的关系把问题解决。

通过对有关概念和定力的概括、证明和应用，使学生体会“转化”的观点，提高学而思的空间想彖力和逻辑推理能力。

四、教学过程（一）情境设置问题1：如果一条直线垂直于平面内的无数条直线，那么这条直线是否与这个平面垂直？答：不一定，当平面内的无数条直线都相互平行时，该直线与平面的位置关系可能是平行，相交，垂直。

设计意图：归纳总线与平而垂直的定义，强调定义中的“任意性”。

问题2：如何判断一条直线是否与一个平而垂直？能不能像判定直线与平面平行那样，利用直线与平血内的一条直线垂直来判定在线与平面垂在呢？答：直线I垂直于平面以内的直线m,但1不垂直于平面久。

如图：问题3：—条直线不行，那么又能不能像判断平面与平而平行那样，利用直线与平而内两条直线都垂直来判定直线与平面垂直呢？答：当平面内的两条直线互相平行时，结论是否定的，如图：肓线1垂肓于平面a内的直线m、n, m//n,但1不垂肓于平而a .设计总图：通过探索，归纳出直线与平面垂直的判定定理，强调定理的关键是：找到两条相交直线与己知直线垂直。

同时，定理体现了线而垂直与线线垂直互相转化的思想。

（二）讲授新课1.直线与平面垂直的定义：如果直线/与平面Q内的任意一条直线都垂直，则直线/与平而Q互相垂直, 记作/丄Q2.直线与平而垂直的判定定理：文字语言：一-条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直图形语言:I丄b符号语言：aaa I丄ab u aa cb = P三推一：线线垂直（证明）；线在而内，线线相交（说明）n线而垂直3.直线与平面所成的角（1）定义：平面的一条斜线和它在平面上的射影所成的锐也（2）线面角e e [0°,90°]（三）即吋体验例1.如图，点P是平行四边形ABCD所在平而外一点，0是对角线AC与BD的交点，且PA=PC, PB二PD。