高一数学《2.3.2平面与平面垂直的判定》

2.3.2平面和平面垂直的判定和性质一、教学目标（一）核心素养（1）通过本节教学，提高学生空间想象能力．（2）通过问题解决，提高等价转化思想渗透的意识．（3）进一步提高学生分析问题、解决问题的能力．（二）学习目标（1）两个平面互相垂直的判定．（2）两个平面互相垂直的性质．（三）学习重点两个平面垂直的判定、性质．（四）学习难点（1）两个平面垂直的判定定理、性质定理运用．（2）正确作出符合题意的空间图形．二、教学设计（一）课前设计1．预习任务（1）读一读：阅读教材第67页到第69页，填空：二面角的定义：平面内的一条直线把平面分为两部分,其中的每一部分都叫做半平面,从一条直线出发的两个半平面所组成的图形叫做二面角；以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角．（2）平面与平面垂直的定义两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直．（3）判定定理与性质定理文字语言图形语言符号语言判定定理如果一个平面经过另一个平面的一条垂线，则这两个平面互相垂直⎭⎬⎫l⊥αl⊂β⇒α⊥β性质定理如果两个平面互相垂直，则在一个平面内垂直于它们交线的直线垂直于另一个平面⎭⎬⎫α⊥βα∩β＝al⊥al⊂β⇒l⊥α1．直线a⊥直线b，a⊥平面β，则b与β的位置关系是（）A．b⊥βB．b∥βC．b⊂βD．b⊂β或b∥β【解题过程】由垂直和平行的有关性质可知b⊂β或b∥β，故选D.【答案】D2.设平面α与平面β相交于直线m，直线a在平面α内，直线b在平面β内，且b⊥m，则“α⊥β”是“a⊥b”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【解题过程】若α⊥β，因为α∩β＝m，b⊂β，b⊥m，所以根据两个平面垂直的性质定理可得b⊥α，又a⊂α，所以a⊥b；反过来，当a∥m时，因为b⊥m，且a，m共面，一定有b⊥a，但不能保证b⊥α，所以不能推出α⊥β.故选A.【答案】A3．设m、n是两条不同的直线，α、β是两个不同的平面（）A．若m⊥n，n∥α，则m⊥α.B．若m∥β，β⊥α，则m⊥α.C．若m⊥β，n⊥β，n⊥α，则m⊥α.D．若m⊥n，n⊥β，β⊥α，则m⊥α.【解题过程】A中，由m⊥n，n∥α可得m∥α或m与α相交或m⊂α，错误；B中，由m∥β，β⊥α可得m∥α或m与α相交或m⊂α，错误；C中，由m⊥β，n⊥β可得m∥n，又n⊥α，所以m⊥α，正确；D中，由m⊥n，n⊥β，β⊥α可得m∥α或m与α相交或m⊂α，错误．【答案】C(二)课堂设计1．知识回顾（1）直线和平面垂直的判定定理文字语言图形语言符号语言判定定理如果一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直⎭⎪⎬⎪⎫l⊥al⊥ba∩b＝Oa⊂αb⊂α⇒l⊥α（2）直线和平面垂直的判定的另外一种判定方法文字语言图形语言符号语言判定方法如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于同一个平面．ba//，α⊥a．则α⊥b（3）直线和平面垂直的性质定理性质定理如果两条直线垂直于同一个平面，那么这两条直线平行⎭⎬⎫a⊥αb⊥α⇒a∥b2．问题探究探究一实例引领，认识平面和平面垂直的概念★●活动①简单类比，引出定义两个平面互相垂直是两个平面相交的特殊情形．教室的墙面与地面、一个正方体中每相邻的两个面、课桌的侧面与地面都是互相垂直的．两个平面互相垂直的概念和平面几何里两条直线互相垂直的概念类似，也是用它们所成的角为直角来定义的．请同学思考两个平面互相垂直的定义.两个平面互相垂直的定义可表述为：如果两个相交平面所成的二面角为直二面角，那么这两个平面互相垂直．那么两个互相垂直的平面画其直观图时，应把直立平面的边画成和水平平面的横边垂直，如下图．平面α和β垂直，记作α⊥β．●活动②实例引领，思维激活实例：如图,检查工件的相邻两个平面是否垂直时,只要用曲尺的一边紧靠在工件的一个面上,另一边在工件的另一个面上转动,观察尺边是否和这个面密合就可以了,这是为什么?曲尺的一边在一面内转动即为形成一个平面,而另一边与此平面垂直,且又紧靠在另一平面上,即垂线在另一平面内．所以我们得到面面垂直的判定定理．如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直．）下面我们一起给出分析，证明：已知：AB⊥β，AB∩β＝B，AB⊂α．【解题过程】要证α⊥β，需证α 和β 构成的二面角是直二面角，而要证明一个二面角是直二面角，需找到其一个平面角，并证明这个二面角的平面角是直角．证明：设α∩β＝CD，则由AB⊂α知，AB、CD共面．∵AB⊥β，CD⊂β，∴AB⊥CD，垂足为点B．在平面β内过点B作直线BE⊥CD．则∠ABE是二面角α-CD-β的平面角．又AB⊥BE，即二面角α-CD-β是直二面角．∴α⊥β．现在同学们明确了面面垂直的判定定理，请思考：建筑工人在砌墙时，常用一段系有铅锤的线来检查所砌墙面是否和水平面垂直，依据是什么？［学生］依据是两个平面垂直的判定定理，一面经过另一面的一条垂线．［老师］从转化的角度来看，两个平面垂直的判定定理可简述为：线面垂直⇒面面垂直请同学们接着思考如下问题：在所给正方体中，下式是否正确：①平面ADD1A1⊥平面ABCD；②D1A⊥AB；③D1A⊥面ABCD．［学生］①∵AB⊥面ADD1A1，AB⊂面ABCD．∴平面ABCD⊥平面ADD1A1．②∵AB⊥面ADD1A1，D1A⊂面ADD1A1∴AB⊥D1A③∵AA1⊥面ABCD，∴AD1与平面ABCD不垂直．平面ADD1A1⊥面ABCD，平面ADD1A1∩平面ABCD＝AD，A是平面ADD1A1内一点．过点A可以在平面ADD1A1内作无数条直线，而这些直线满足什么条件就可以使之与平面垂直？判定定理解决两个平面如何垂直，性质定理可以解决上述线面垂直．从转化的角度可表述为：面面垂直，则线面垂直．也给了我们以后证明问题的一种思想方法．下面我们一起来完成证明.证明过程如下：已知：α⊥β、α∩β＝a，AB⊂α，AB⊥a于B．【解题过程】：在平面β内作BE⊥a垂足为B，则∠ABE就是二面角α-a-β的平面角．由α⊥β可知，AB⊥BE．又AB⊥a，BE与a是β内两条相交直线，∴AB⊥β．证明的难点在于“作BE⊥a”．为什么要做这一步？主要是由两面垂直的关系，去找其二面角的平面角来决定的.【设计意图】构造二面角的平面角过程可以体现学生的创新精神、转化能力．【答案】见解题过程.探究二层层深化，掌握平面和平面垂直的判定定理和性质定理．●活动①互动交流，初步实践例1 求证：（1）如果一个平面与另一个平面的垂线平行，那么这两个平面互相垂直；（2）如果一个平面与另一个平面的垂面平行，那么这两个平面互相垂直．【知识点】平面和平面垂直的判定.【数学思想】化归思想.【解题过程】（1）已知：l∥α，l⊥β，求证：α⊥β.证明：在平面α内任取一点P．∵l ∥α，∴P ∉l ．P 、l 可确定一平面γ．设α∩γ＝l ′则l ∥l ′．⎪⎭⎪⎬⎫⊂'⊥'⇒⎭⎬⎫'⊥αββl l l l l //⇒α⊥β［该题目难在构造既符合题，又能使问题得证的立体图形．］ (2)已知：α⊥β，β∥γ．求证：α⊥γ证明：过β 内一点P 作直线l ，使l ⊥α则l ⊂β． l 与γ内任一点Q 确定平面δ，设δ∩γ＝l ′，则l ∥l ′． l ′⊥α，因此γ⊥α．【思路点拨】题目较抽象，构造图形，创造条件，使问题转化为可利用已有定理来解决．由此我们又多了两个判断面面垂直的结论. 【答案】见解题过程. ●活动②巩固基础，检查反馈例2 如图，AB 是⊙O 的直径，P A 垂直于⊙O 所在的平面，C 是圆周上异于A 、B 的任意一点，求证：平面P AC ⊥平面PBC ．【知识点】平面和平面垂直的判定 【数学思想】化归思想【解题过程】证明：因为AB 是⊙O 的直径，C 是圆周上的点，所以有BC ⊥AC ①．因为P A ⊥平面ABC ，BC ⊂平面ABC ，则P A ⊥BC ②． 由①②及AC ∩PA ＝A ，得BC ⊥平面P AC ．因为BC⊂平面PBC，有平面P AC⊥平面PBC．【思路点拨】低一级的垂直关系是判定高一级垂直关系的依据，根据条件，由线线垂直⇒线面垂直⇒面面垂直．通过这个例题展示了空间直线与平面的位置关系的内在联系，垂直关系的判定和性质共同构成了一个完整的知识体系．【答案】见解题过程.例3 如图，P是△ABC所在平面外的一点，且P A⊥平面ABC，平面P AC⊥平面PBC，求证：BC⊥AC．【知识点】平面和平面垂直的判断和性质.【数学思想】转化思想.【解题过程】证明：在平面P AC内作AD⊥PC，交PC于D．因为平面P AC⊥平面PBC于PC，AD⊂平面P AC，且AD⊥PC，所以AD⊥平面PBC．又因为BC⊂平面PBC，于是有AD⊥BC①．另外P A⊥平面ABC，BC⊂平面ABC，所以P A ⊥BC．由①②及AC∩PA＝A，可知BC⊥平面P AC．因为AC⊂平面P AC，所以BC⊥AC．【思路点拨】在空间图形中，高一级的垂直关系中蕴含着低一级的垂直关系，通过本题可以看到，面面垂直⇒线面垂直⇒线线垂直．本题是利用直线和平面垂直的定义及判定定理等知识来解答的问题．解答此类问题必须作到：概念清楚、问题理解透彻、相关知识能灵活运用．【答案】见解题过程.例4 P为120°角α-a-β内一点，P到α和β的距离均为10，求点P到棱a的距离．【知识点】二面角的概念，距离.【数学思想】化归思想.【解题过程】如图，过点P 作P A ⊥α于A ，PB ⊥β于B ，设相交直线P A 、PB 确定的平面为γ，a ∩γ＝O ，则α∩γ＝OA ，β∩γ＝OB 连结PO ，则AP =BP =10∵P A ⊥α，PB ⊥β，∴a ⊥γ，而PO ⊂平面γ，∴a ⊥PO ， ∴PO 的长即为点P 到直线a 的距离． 又∵a ⊥γ，γ⊂OA ，γ⊂OB∴∠AOB 是二面角α-a -β的平面角，即∠AOB =120°．而四边形AOBP 为一圆内接四边形，且PO 为该四边形的外接圆直径． ∵四边形AOBP 的外接圆半径等于由A 、B 、O 、P 中任意三点确定的三角形的外接圆半径，因此求PO 的长可利用△APB ． 在△APB 中，AP =BP =10，∠APB =60°，∴AB =10． 由正弦定理：332060sin 2=︒==AB R PO ． 【思路点拨】(1)该题寻找120°的二面角的平面角，所采取的方法即为垂面法，由此可见，若题目可找到与棱垂直的平面，用“垂面法”确定二面角的平面角也是一种可取的方法．（2）充分借助于四边形P AOB 为一圆内接四边形，∵P A ⊥OA ，PB ⊥OB ，∵PO 即为其外接圆直径，然后借助于四边形的外接圆直径等于其中任一三角形的外接圆直径进行转移，由正弦定理帮助解决了问题．【答案】.3320活动③ 强化提升，灵活应用例5.过点S 引三条不共面的直线SA 、SB 、SC ，如图，∠BSC =90°，∠ASC =∠ASB =60°，若截取SA =SB =SC =a .(1)求证：平面ABC ⊥平面BSC ； (2)求S 到平面ABC 的距离．【知识点】面面垂直的证明，距离. 【数学思想】化归思想【解题过程】(1)证明：∵SA =SB =SC =a ， 又∠ASC =∠ASB =60°，∴△ASB 和△ASC 都是等边三角形，∴AB =AC =a ， 取BC 的中点H ，连结AH ，∴AH ⊥BC ． 在Rt △BSC 中，BS =CS =a ， ∴SH ⊥BC ，a BC 2=，∴2)22(222222a a a CH AC AH =-=-=，∴222a SH =． 在△SHA 中，∴222a AH =，222a SH =，22a SA =， ∴222HA SH SA +=，∴AH ⊥SH ，∴AH ⊥平面SBC ．∵AH ⊂平面ABC ，∴平面ABC ⊥平面BSC ． 或：∵SA =AC =AB ，∴顶点A 在平面BSC 内的射影H 为△BSC 的外心， 又△BSC 为Rt △，∴H 在斜边BC 上，又△BSC 为等腰直角三角形，∴H 为BC 的中点，∴AH ⊥平面BSC ． ∵AH ⊂平面ABC ，∴平面ABC ⊥平面BSC ．(2)由前所证：SH ⊥AH ，SH ⊥BC ，∴SH ⊥平面ABC ，∴SH 的长即为点S 到平面ABC 的距离，a BC SH 222==，∴点S到平面ABC的距离为a22．【思路点拨】（1）要证明平面ABC⊥平面BSC，根据面面垂直的判定定理，须在平面ABC或平面BSC内找到一条与另一个平面垂直的直线；（2）外心为三角形外接圆的圆心，即三条中垂线的交点.【答案】（1）见解题过程；（2）a22．同类训练如图，在三棱台ABC－DEF中，CF⊥平面DEF，AB⊥B C.(1)设平面ACE∩平面DEF＝a，求证：DF∥a；(2)若EF＝CF＝2BC，试问在线段BE上是否存在点G，使得平面DFG⊥平面CDE？若存在，请确定G点的位置；若不存在，请说明理由．【知识点】线面平行的判定，面面垂直的证明.【解题过程】(1)证明：在三棱台ABC－DEF中，AC∥DF，AC⊂平面ACE，DF 平面ACE，∴DF∥平面ACE.又∵DF⊂平面DEF，平面ACE∩平面DEF＝a，∴DF∥a.(2)线段BE上存在点G，且BG＝13BE，使得平面DFG⊥平面CDE.证明如下：取CE的中点O，连接FO并延长交BE于点G，连接GD、GF，∵CF＝EF，∴GF⊥CE.在三棱台ABC－DEF中，AB⊥BC⇒DE⊥EF.由CF⊥平面DEF⇒CF⊥DE.又CF ∩EF ＝F ，∴DE ⊥平面BEF ，∴DE ⊥GF .GF CE GF DE GF CDE CE DE E ⎫⎪⇒⎬⎪⎭⊥⊥⊥平面＝.又GF ⊂平面DFG ，∴平面DFG ⊥平面CDE .此时，如平面图所示，∵O 为CE 的中点，EF ＝CF ＝2BC ，由平面几何知识易证△HOC ≌△FOE ，∴HB ＝BC ＝12EF .由△HGB ∽△FGE 可知12BG GE =，即13BG BE =. 【思路点拨】“探索性问题”的规律方法：一般是先探求点的位置，多为线段的中点或某个三等分点，然后给出符合要求的证明．【答案】（1）见解题过程；（2）线段BE 上存在点G ，且13BG BE =，使得平面DFG ⊥平面CDE .3. 课堂总结知识梳理（1）证明面面垂直的方法（2）重难点归纳空间中直线与直线垂直、直线与平面垂直、平面与平面垂直三者之间可以相互转化，每一种垂直的判定都是从某种垂直开始转向另一种垂直最终达到目的，其转化关系为在证明两平面垂直时一般先从现有的直线中寻找平面的垂线，若这样的直线图中不存在，则可通过作辅助线来解决．（三）课后作业基础型 自主突破一、选择题1．已知平面α⊥平面β，α∩β＝l，点A∈α，A∉l，直线AB∥l，直线AC⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是（）A．AB∥mB．AC⊥mC．AB∥βD．AC⊥β【知识点】线面平行的判定，面面垂直的证明.【解题过程】如图所示，AB∥l∥m；AC⊥l，m∥l⇒AC⊥m；AB∥l⇒AB∥β，只有D不一定成立，故选D.【思路点拨】由题意，画出满足条件的图形，依据面面垂直的性质以及线面平行的性质等知识解答.【答案】D.2．设a是空间中的一条直线，α是空间中的一个平面，则下列说法正确的是（）A．过a一定存在平面β，使得β∥αB．过a一定存在平面β，使得β⊥αC．在平面α内一定不存在直线b，使得a⊥bD．在平面α内一定不存在直线b，使得a∥b【知识点】线面平行的判定，面面垂直的证明.【解题过程】当a与α相交时，不存在过a的平面β，使得β∥α，故A错误；直线a与其在平面α内的投影所确定的平面β满足β⊥α，故选B；平面α内的直线b只要垂直于直线a在平面α内的投影，则就必然垂直于直线a，故C错误；当a与α平行时，在平面α内存在直线b，使得a∥b，故D错误．【思路点拨】A.根据面面平行的定义和性质判断；B.利用面面垂直的性质和定义判断；C.根据线面垂直的性质判断；D.根据线面平行的性质判断.【答案】B．3.设直线l⊥平面α，直线m⊂平面β，（）A．若m∥α，则l∥m B．若α∥β，则l⊥mC．若l⊥m，则α∥β D．若α⊥β，则l∥m【知识点】线面平行的判定，面面垂直的证明.【解题过程】A中直线l与m互相垂直，不正确；B中根据两个平面平行的性质知是正确的；C中的α与β也可能相交；D中l与m也可能异面，也可能相交，故选B.【思路点拨】通过线面平行的性质定理和线面垂直的性质定理即可判断A；由一直线垂直于两个平行平面中的一个，也垂直于另一个，结合线面垂直的性质定理即可判断B；举反例，由线面垂直的性质定理即可判断C；举反例，结合线面垂直和面面垂直的性质定理即可判断D.【答案】B.4．设a、b是两条不同的直线，α、β是两个不同的平面，则能得出a⊥b的是() A．a⊥α，b∥β，α⊥βB．a⊥α，b⊥β，α∥βC．a⊂α，b⊥β，α∥βD．a⊂α，b∥β，α⊥β【知识点】线面平行的判定，面面垂直的证明.【解题过程】A中，两直线可以平行、相交或异面，故不正确；B中，两直线平行，故不正确；C中，由α∥β，a⊂α可得a∥β，又b⊥β，得a⊥b，故正确；D 中，两直线可以平行，相交或异面，故不正确．【思路点拨】通过线面垂直的性质定理判断A；通过面面平行的性质和线面垂直的性质判断B；通过面面平行的性质和线面垂直的定义判断C；由线面平行的性质和面面垂直的性质判断D.【答案】C.5.如图，在四面体D－ABC中，若AB＝CB，AD＝CD，E是AC的中点，则下列正确的是（）A ．平面ABC ⊥平面ABDB ．平面ABD ⊥平面BDCC ．平面ABC ⊥平面BDE ，且平面ADC ⊥平面BDED ．平面ABC ⊥平面ADC ，且平面ADC ⊥平面BDE【知识点】面面垂直的判定.【解题过程】因为AB ＝CB ，且E 是AC 的中点，所以BE ⊥AC ，同理有DE ⊥AC ，于是AC ⊥平面BDE .因为AC ⊂平面ABC ，所以平面ABC ⊥平面BDE .又由于AC ⊂平面ACD ，所以平面ACD ⊥平面BDE ，所以选C.【思路点拨】缺少【答案】C.6.在平面几何里，有勾股定理：“设△ABC 的两边AB 、AC 互相垂直，则AB 2＋AC 2＝BC 2．”拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面面积与底面面积间的关系，可以得出正确结论是：“设三棱锥A -BCD 的三个侧面ABC 、ACD 、ADB 两两相互垂直”，则______．【解题过程】此题是突破以往高考命题模式的又一典范，丰富的想象和联想是增强创新意识的利器，本题如果能联想构造一长方体，用一平面去截长方体易得满足条件的棱锥A -BCD ，进而易证结论：“2222ABC ACD ADB BCD SS S S ++=．” 【答案】2222ABC ACD ADB BCD S S S S ++=．7.如图，在四棱锥P －ABCD 中，P A ⊥底面ABCD ，且底面各边都相等，M 是PC 上的一动点，当点M 满足________时，平面MBD ⊥平面PCD (只要填写一个你认为正确的条件即可)．【知识点】线面平行的判定，面面垂直的证明.【解题过程】∵PC在底面ABCD上的射影为AC，且AC⊥BD，∴BD⊥P C.∴当DM⊥PC(或BM⊥PC)时，即有PC⊥平面MBD，而PC⊂平面PCD，∴平面MBD ⊥平面PC D.【答案】DM⊥PC(或BM⊥PC)8.如图所示，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD ＝DE＝2AB，F为CD的中点．求证：(1)AF∥平面BCE；(2)平面BCE⊥平面CDE.【知识点】线面平行的判定，面面垂直的证明。

2.3.2 平面与平面垂直的判定【学习目标】1、掌握二面角及面面垂直的定义及判定定理；2、能够应用判定定理证明面面垂直；3、解决简单的求二面角问题.【重点】面面垂直的判定定理的应用【难点】求二面角【基础内容】1、二面角从一条直线出发的 所组成的图形，叫做二面角.这条直线叫做 ，这两个半平面叫做 .如图的二面角可以记作 或 或.2、二面角的平面角在二面角α-l-β的棱l 上人去一点O ，以点O 为垂足，在半平面α，β内分别作 的射线OA 和OB ，则构成的∠AOB 叫做二面角的平面角.平面角是直角的二面角叫做 .思考：二面角的平面角θ的取值范围是 .3、两平面垂直的定义一般地，两个平面相交，如果他们所成的二面角是 （二面角大小是 ），就说这两个平面互相垂直.4、两个平面垂直的判定定理一个平面过另一个平面的 ，则这两个平面垂直.【前置作业】1、已知平面α ,β ,γ ,且β ∩γ = l ，l || α ，直线m α⊆，m ⊥γ，则必有（ ）A. α⊥γ ，且l ⊥m .B. α⊥γ ，且m || βC. m || β ，且l ⊥m .D. α⊥β ，且m ⊥β.2、对于直线a ，b ，c 和平面α ,β ,已知,,a b c αβγ⊆⊆⊆，,a b a c ⊥⊥，则α 与β的位置关系是（ ）A.αβ⊥B. αβC. l αβ=D.不确定【研讨探究】探究一：面面垂直的判定（线面垂直．．．．（面面垂直判定））．．．．（线面垂直判定）→面面垂直例1 如图，AB是⊙O的直径，P A垂直于⊙O所在的平面，C是圆周上不同于A，B的任意一点，求证：平面P AC⊥平面PBC.1、如图，四棱锥P-ABCD的底面是边长为a的正方形，PB⊥平面ABCD.求证：平面P AD ⊥平面P AB.探究二：求二面角的大小（找到对应二面角．．．．．．．．．（交线上的一个点引出两条垂直射线）→构造三角形．．．．）．．．→余弦定理思考：四边形ABCD是正方形，P A⊥平面ABCD，且P A=AB。

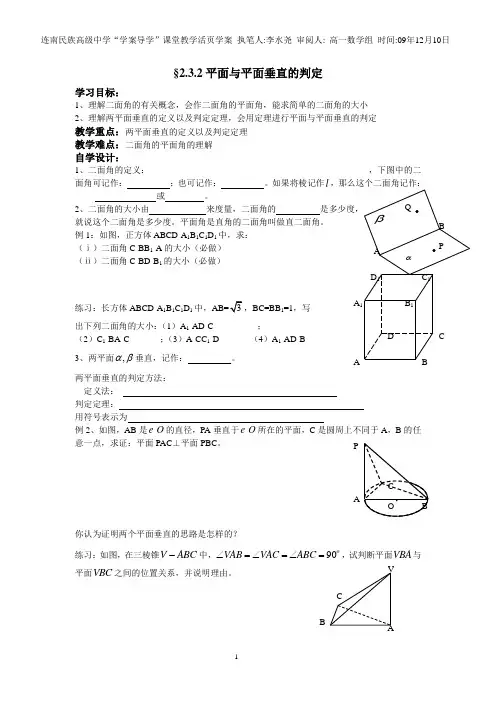
§2.3.2平面与平面垂直的判定学习目标：1、理解二面角的有关概念，会作二面角的平面角，能求简单的二面角的大小2、理解两平面垂直的定义以及判定定理，会用定理进行平面与平面垂直的判定教学重点：两平面垂直的定义以及判定定理 教学难点：二面角的平面角的理解 自学设计：1、二面角的定义：__________________________________________________，下图中的二面角可记作： ；也可记作： 。

如果将棱记作l ，那么这个二面角记作：或 。

2、二面角的大小由 来度量，二面角的是多少度，就说这个二面角是多少度。

平面角是直角的二面角叫做直二面角。

例1：如图，正方体ABCD-A 1B 1C 1D 1中，求： （ⅰ）二面角C-BB 1-A 的大小（必做）（ⅱ）二面角C-BD-B 1的大小（必做）练习：长方体ABCD-A 1B 1C 1D 1中，AB=，BC=BB 1=1，写 出下列二面角的大小：（1）A 1-AD-C__________；（2）C 1-BA-C_______；（3）A-CC 1-D_______（4）A 1-AD-B_______ 3、两平面,αβ垂直，记作： 。

两平面垂直的判定方法：定义法：判定定理：用符号表示为例2、如图，AB 是O 的直径，PA 垂直于O 所在的平面，C 是圆周上不同于A ，B 的任意一点，求证：平面PAC ⊥平面PBC 。

你认为证明两个平面垂直的思路是怎样的？________________________________________练习：如图，在三棱锥V A B C -中，90oVAB VAC ABC ∠=∠=∠=，试判断平面V B A 与平面V B C 之间的位置关系，并说明理由。

VABC A达标练习：1、如图所示：在正方体ABCD-A 1B 1C 1D 1中：（1）二面角A 1-AB-D 的大小为： （必做） （2）二面角D 1-AB-D 的大小为： （必做） （3）二面角D 1-BC-D 的大小为2、已知四面体P A B C -中，P A ⊥平面,90o ABC ABC ∠=，则四面体中互相垂直的面有 对，分别是： 3、若一个二面角的两个面所在的平面分别平行于另一个二面角的两个面所在的平面，则这两个二面角的关系为 （ ）A 、相等B 、互补C 、相等或互补D 、无法确定 4、在四面体A B C D中，,BD AB AD C B C D AC a ======。

班级____________ 姓名_____________ ______月______日星期____2.3.2平面与平面垂直的判定【学习目标】1.（重点）正确理解和掌握二面角和“两个平面互相垂直”的概念.2.（难点）“二面角的平面角”的理解和求解.【知识梳理】（1）二面角.①定义：从一条直线出发的两个所组成的图形叫做二面角，这条直线叫，这两个半平面叫 .②画法：看图自己画一画直立式：平卧式：③记法：如图，棱为AB，面为α、β的二面角，记作二面角.或二面角.如果棱为l，则这个二面角还可记作或（2）二面角的平面角.①二面角的平面角定义：在二面角α-l-β的棱上任取点O，以O为垂足，在半平面α和β内分别作垂直于棱的射线OA和OB，则射线OA和OB组成∠AOB.叫做.②直二面角定义：二面角的大小可以用它的平面角来度量，二面角的平面角是多少度，就说二面角是多少度. 平面角是的二面角叫做直二面角.③二面角的大小：二面角的大小是用平面角来度量的，其范围是（3）两个平面互相垂直①定义：如果两个相交平面所成的二面角为直二面角，那么这两个平面②判定定理: 一个平面过另一个平面的，则这两个平面垂直。

图形语言: 符号语言:③思考：判定两个平面互相垂直的关键找什么？思想：线线垂直线面垂直面面垂直【例题探究】例1、已知直线PA垂直于圆O所在的平面，AB为圆O的直径，C是圆周上异于A、B的一点。

求证：平面PAC 平面PBC练1、如图，在正方体ABCD —A 'B 'C 'D '中，求证：平面BB 'D 'D ⊥平面A 'BC '．练2、如图，四棱锥P ABCD -的底面是边长为a 的正方形，PA ⊥底面ABCD ，E 为AB 的中点，且 PA AB =，求证：平面PCE ⊥平面PCD【课堂小结】【课后作业】1.下面说法正确的个数是 （ ）①如果一条直线垂直于一个平面内的无数条直线，那么这条直线和这个平面垂直②过空间一定点有且只有一个平面和已知平面垂直③垂直于同一个平面的两个平面面互相平行④经过一个平面的垂线的平面与这个平面垂直。

高中数学必修21高中数学必修二2.3.2《平面与平面垂直的判定》导学导练给出下列命题：①a ∥考点二．两平面垂直的证明例2：如图，AB 是⊙O 的直径，PA 垂直⊙O 所在的平面，C 是圆周上不同于A ，B 的任意一点，求证：平面PAC ⊥平面PBC 。

【针对练习】1、如图，在三棱锥P-ABC 中，已知PA ⊥PB ，PB ⊥PC ，PC ⊥PA ，求证：平面PAB ⊥平面PBC ，平面PBC ⊥平面PCA ，平面PCA ⊥平面PAB 。

2、如图，在三棱锥P-ABC 中，已知PA ⊥平面ABC ，AB ⊥BC ，D 、E分别是点A 在PB ，PC 上的射影，求证： （1）平面PBC ⊥平面PAB 。

（2）AD ⊥平面PBC 。

（3）平面ADE ⊥平面PAC 。

3、S 是△ABC 所在平面外一点，SA=SB=SC ，∠ASC=90︒，∠ASB=∠BSC=60︒， 求证：平面ASC ⊥平面ABC.个人原创，版权所有，翻印必究，如需借用，QQ 索取密码 第2页 解密佛山吉红勇老师扣扣：一0七669八114．已知：如图，在△ABC 中，AB=AC ，AD⊥平面ABC ，EC⊥平面ABC ，且CE=2AD.求证：平面BDE⊥平面BCE.考点三．二面角大小的求法例3：如图四面体ABCD 的棱BD 长为2，其余各棱长均为2，求二面角A-BD-C 的大小。

【针对练习】1、如图三棱锥 P-ABC 中，PC ⊥平面ABC ，PC =32 ，D 是 BC 的中点，且△ADC是边长为 2的正三角形，则二面角 P-AB －C 的大小为考点四．综合考查线线、线面、面面垂直和平行例4：已知直四棱柱1111ABCD A BC D -的底面是菱形，且160AA AD ,DAB =︒=∠，F 为棱1BB 的中点，M 为线段1AC 的中点. （1）求证：直线MF//平面ABCD ； （2）求证：平面1AFC ⊥平面11ACC A ；（3）求平面1AFC 与平面ABCD 所成二面角的大小.【针对练习】 2、直线a⊥平面α，α//b ，则a 与b 的关系为（ ）A.b a ⊥，且a 与b 相交B.b a ⊥，且a 与b 不相交C. b a ⊥D.a 与b 不一定垂直3、若三条直线OC ,OB ,OA 两两垂直，则直线OA 垂直于（ ） A.平面OAB B.平面OAC C.平面OBC D.平面ABC4、给出下列四个命题：①.若一条直线垂直于平面内的任意一条直线，则这条直线垂直于这个平面②.若一条直线垂直于平面内的两条直线，则这条直线垂直于这个平面③.若两条平行线中的一条垂直于一个平面，则另一条直线也垂直于这个平面④.若两条直线垂直于同一个平面，则这两条直线互相平行 其中正确的命题的个数是（ ）A.1个B.2个C.3个D.4个5、下列命题正确的是（ ）A.平行于同一个平面的两条直线必定平行B.垂直于同一条直线的两个平面必定平行C.过一点有且只有一条直线与已知直线垂直D.与两条异面直线都相交的两条直线是异面直线 6、已知四棱锥P-ABCD 的底面为直角梯形，AB∥DC，⊥=∠PA DAB ,90 底面ABCD ，且PA=AD=DC=21AB=1，M 是PB 的中点.（1）证明：平面PAD⊥平面PCD ； （2）求AC 与PB 所成的角的余弦值；（3）求平面AMC 与平面BMC 所成二面角的余弦值.高中数学必修23【课后练习】1．已知PD⊥矩形ABCD 所在的平面，图中相互垂直的平面有（ ） A.1对 B.2对 C.3对 D.5对2．下列命题中错误的是（ ）A.若//,,m n n m βα⊥⊂，则αβ⊥B.若αβ⊥，a⊂α，则αβ⊥C.若γα⊥，γβ⊥，l αβ=，则γ⊥D.若αβ⊥，βα⋂=AB ，a //α，a ⊥AB ，则β⊥a3．如图，已知矩形ABCD 中，AB =1，BC =a ，PA ⊥平面ABCD ，若在BC 上只有一点Q 满足PQ ⊥DQ ，则a 的值等于4．对四面体ABCD ，给出下列四个命题：①若AB=AC ，BD=CD ，则BC⊥AD ②若AB=CD ，AC=BD ，则BC⊥AD ③若AB⊥AC，BD⊥CD，则BC⊥AD④若AB⊥CD，BD⊥AC，则BC⊥AD 其中真命题的序号是________（写出所有真命题的序号） 5、如图，三棱锥ABC P -中，⊥PB 底面ABC ，︒=∠90BCA ，CA BC PB ==，E 为PC 的中点，指出图中有哪四对互相垂直的平面.5、如图，在三棱锥V ABC -中，VA=VC ，AB=BC ，求证：VB ⊥AC.6、如图，已知PA O ⊥e 所在的平面，AB 是O e 的直径，C 是O e 上异于点A ，B 的任意一点，过点A 作AE PC ⊥于点E ，求证：AE ⊥平面PBC .7．如图，ABCD 是正方形，O 是正方形的中心，PO ⊥底面ABCD ，E是PC 的中点。