造桥选址问题 PPT课件

造桥选址问题乐乐课堂（最新版）目录1.造桥选址的重要性2.造桥选址的考虑因素3.造桥选址的方法和工具4.案例：乐乐课堂的造桥选址实践5.总结正文1.造桥选址的重要性造桥是一项极其重要的基础设施建设，它能够有效地连接两个地方，促进交通运输、经济发展和人口流动。

然而，如何选择一个合适的地点来建造桥梁，却是一项充满挑战的任务。

如果选址不当，可能会导致桥梁建设成本过高、使用率低、维护困难等问题，甚至会威胁到人们的生命安全。

因此，造桥选址问题必须得到足够的重视。

2.造桥选址的考虑因素在进行造桥选址时，需要综合考虑多种因素，包括地理环境、社会经济、交通需求等。

具体来说，需要考虑以下因素：（1）地理环境：包括地形、地质、气候、水文等条件，这些都会直接影响到桥梁的建设和运营。

（2）社会经济：包括人口密度、经济发展水平、土地利用情况等，这些都会影响到桥梁的使用和维护。

（3）交通需求：包括交通流量、运输需求、线路规划等，这些都是决定桥梁建设必要性和经济效益的关键因素。

3.造桥选址的方法和工具随着科技的发展，现在有许多方法和工具可以用于造桥选址，包括地理信息系统（GIS）、遥感技术、数据挖掘等。

这些方法和工具可以帮助工程师们更全面、更准确地了解选址地的各种情况，从而做出更科学、更合理的决策。

4.案例：乐乐课堂的造桥选址实践乐乐课堂是一家专注于在线教育的企业，他们在进行造桥选址时，充分考虑了以上所有因素，并且运用了先进的科技手段。

他们首先通过 GIS 系统，综合分析了各种地理、社会、经济数据，初步确定了选址范围。

然后，他们利用遥感技术，对选址地进行了详细的地形、地质、气候等调查，进一步确定了桥梁的具体位置。

最后，他们通过数据挖掘，分析了该地区的交通需求和运输情况，最终确定了桥梁的规模和设计。

5.总结造桥选址是一项复杂而重要的任务，需要综合考虑多种因素，并运用先进的科技手段。

造桥选址问题乐乐课堂
（实用版）
目录
1.造桥选址问题的背景和重要性
2.造桥选址问题的解决方案
3.乐乐课堂的作用和应用
4.结论
正文
1.造桥选址问题的背景和重要性
造桥选址问题一直是桥梁工程中的重要环节，选址的合理性直接影响到桥梁的建设成本、通行效率以及周边环境的影响。

因此，如何科学、合理地选择桥梁的建设位置，是桥梁工程领域长期以来研究的问题。

2.造桥选址问题的解决方案
随着科技的发展，造桥选址问题的解决方案也在不断更新和完善。

目前，常见的造桥选址方法包括：地理信息系统（GIS）辅助选址、人工神经网络选址、遗传算法选址等。

这些方法各有优缺点，需要根据实际情况选择最合适的方法。

3.乐乐课堂的作用和应用
乐乐课堂是一款面向中小学生的在线学习平台，提供了丰富的课程资源和学习工具。

在造桥选址问题的学习中，乐乐课堂可以提供相关的学习视频、练习题和模拟测试，帮助学生深入理解造桥选址的原理和方法。

4.结论
造桥选址问题是桥梁工程中的关键环节，合理的选址可以降低建设成本、提高通行效率和减少环境影响。

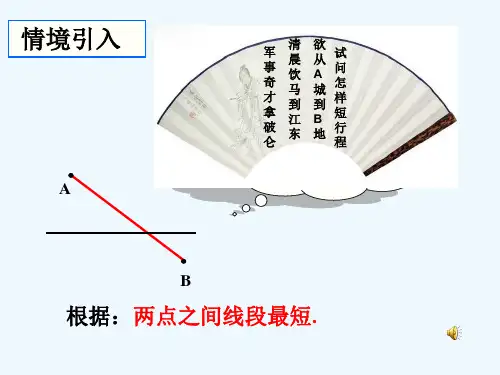
课例造桥选址问题中图分类号：G623.5 文献标识码：A 文章编号：1002-7661（2016）19-0112-02造桥选址问题在现实生活中有着广泛的应用，在一条河上造桥，利用桥的长度始终保持不变，通过平移桥到河的岸边，再利用两点之间线段最短，从而达到最佳的建造一座桥选址的问题，有了在一条河道上建一座桥的基础，可以得到在两条河道、三条河道、直到在n条河道分别建造两座桥、三座桥、n座桥的方法。

利用平移变换进行造桥选址问题，是平移变换的一个重要应用，体现了数学源于生活，同时用运用于生活。

从而达到平移知识的迁移在实际生活中的具体应用。

一、背景介绍本节内容是我校实施的省级科研课题：“初中数学“课题学习”校本化实施与评价的行动研究”研究实施方案的研讨内容之一。

本节内容经过了几位教师的执教与研讨，本文展示的是笔者的实践设计与实录。

（一）内容与学情分析“造桥选址问题”是人教版《数学》八年级上册第十三章“轴对称”的最后一节“课题学习”的第二节内容。

比“将军饮马”问题较难，本节内容的解决主要是平移知识的综合应用。

是对学生动手操作能力的一个考查，本节的难点在于如何把问题转化为“两点之间，线段最短的问题”，在解决的过程中渗透了化归的思想。

（二）目标与目标解析1.能利用轴对称、平移解决简单的最短路径问题.2.体会图形的变化在解决最值问题中的作用；3.能通过逻辑推理证明所求距离最短，感悟转化思想，体会利用作图解决最短路径问题。

达成目标的标志是：能够将实际问题中的“河”的两岸抽象为数学中的“平行线”，把实际问题抽象为线段和最小问题。

通过学生独立思考、合作讨论、教师点拨等方式；能利用平移将线段的最小问题转化为“两点之间，线段最短”问题；能通过逻辑推理证明所求路径最短；在探索最短路径的过程中，体会平移的“桥梁”作用，感悟化归的转化思想，（三）教学思路与理念本节教学的重点是利用平移变换解决造桥选址问题并利用“两点之间，线段最短”公理进行证明，难点是体会利用平移作图将最短路径问题转化为线段和最小问题。

造桥选址问题乐乐课堂摘要：I.引言- 造桥选址问题背景- 乐乐课堂介绍II.造桥选址问题的基本概念- 选址的重要性- 影响选址的主要因素III.造桥选址问题的解决方法- 定性分析法- 定量分析法- 综合评价法IV.案例分析- 案例一：某地区桥梁选址分析- 案例二：某地区桥梁选址分析V.结论- 造桥选址问题解决的意义- 乐乐课堂在造桥选址问题中的贡献正文：I.引言在我国，桥梁建设是交通基础设施的重要组成部分，对于地方经济发展和社会进步具有深远影响。

因此，选址问题成为桥梁建设中的关键环节。

乐乐课堂作为一家专注于知识普及的教育机构，旨在为广大青少年提供科学、有趣的课程，助力我国桥梁建设事业。

本文将结合乐乐课堂，探讨造桥选址问题。

II.造桥选址问题的基本概念造桥选址问题是指在桥梁建设过程中，根据一定的标准和原则，选择一个适合修建桥梁的具体位置。

选址是否合理，将对桥梁的使用寿命、安全性能、经济效益等方面产生重要影响。

选址时需要考虑的主要因素包括：地质条件、地形地貌、气候环境、水文条件、交通需求等。

III.造桥选址问题的解决方法为了解决造桥选址问题，我们可以采用以下方法：1.定性分析法：通过对影响选址的因素进行定性分析，初步筛选出适合修建桥梁的位置。

2.定量分析法：在定性分析的基础上，采用数学模型和计算方法，对选址进行定量分析，进一步优化选址方案。

3.综合评价法：结合定性分析和定量分析的结果，对各个选址方案进行综合评价，最终确定最佳选址。

IV.案例分析为了更直观地展示造桥选址问题的解决过程，我们以两个实际案例进行分析：案例一：某地区桥梁选址分析在某地区，由于经济发展和交通需求的不断增长，新建一座桥梁成为当务之急。

通过定性分析和定量分析，我们初步筛选出两个选址方案。

经过综合评价，最终确定了一个最适合的选址。

该选址不仅符合各项建设标准，而且能够最大限度地满足当地居民的出行需求。

案例二：某地区桥梁选址分析在某地区，由于地理环境和气候条件的限制，桥梁选址成为一大难题。