最短路径问题

最短路径问题介绍全文共四篇示例，供读者参考第一篇示例：最短路径问题是指在一个带有边权的图中，寻找连接图中两个特定节点的最短路径的问题。

在实际生活中，最短路径问题广泛应用于交通运输、通信网络、物流配送等领域。

通过解决最短路径问题，可以使得资源的利用更加高效，节约时间和成本，提高运输效率，并且在紧急情况下可以迅速找到应急通道。

最短路径问题属于图论中的基础问题，通常通过图的表示方法可以简单地描述出这样一个问题。

图是由节点和边组成的集合，节点表示不同的位置或者对象，边表示节点之间的连接关系。

在最短路径问题中，每条边都有一个权重或者距离，表示从一个节点到另一个节点移动的代价。

最短路径即是在图中找到一条路径，使得该路径上的边权和最小。

在解决最短路径问题的过程中，存在着多种算法可以应用。

最著名的算法之一是Dijkstra算法，该算法由荷兰计算机科学家Edsger W. Dijkstra于1956年提出。

Dijkstra算法是一种贪心算法，用于解决单源最短路径问题，即从一个给定的起点到图中所有其他节点的最短路径。

该算法通过维护一个距离数组和一个集合来不断更新节点之间的最短距离，直到找到目标节点为止。

除了Dijkstra算法和Floyd-Warshall算法外，还有一些其他与最短路径问题相关的算法和技术。

例如A*算法是一种启发式搜索算法，结合了BFS和Dijkstra算法的特点，对图中的节点进行评估和排序，以加速搜索过程。

Bellman-Ford算法是一种解决含有负权边的最短路径问题的算法，通过多次迭代来找到最短路径。

一些基于图神经网络的深度学习方法也被应用于最短路径问题的解决中，可以获得更快速和精确的路径搜索结果。

在实际应用中，最短路径问题可以通过计算机程序来实现，利用各种算法和数据结构来求解。

利用图的邻接矩阵或者邻接表来表示图的连接关系，再结合Dijkstra或者Floyd-Warshall算法来计算最短路径。

最短路径问题及其变形
最短路径问题是指给定一个图和起点、终点，求出起点到终点的路径中具有最小权重和的路径的问题。

可以通过一些经典算法来解决，如Dijkstra算法、Bellman-Ford算法和Floyd-Warshall算法。

最短路径问题的变形可以有很多种，下面介绍几个常见的变形：
1. 单源最短路径问题：给定一个图和一个起点，求出起点到图中所有其他节点的最短路径。

这个问题可以通过Dijkstra算法
或Bellman-Ford算法求解。

2. 多源最短路径问题：给定一个图和多个起点，求出每个起点到图中所有其他节点的最短路径。

这个问题可以通过多次运行Dijkstra算法或Floyd-Warshall算法求解。

3. 含有负权边的最短路径问题：给定一个图，其中可能存在负权边，求出起点到终点的最短路径。

如果图中不存在负权回路，可以使用Bellman-Ford算法求解，如果存在负权回路，则无
法找到最短路径。

4. 最长路径问题：与最短路径问题相反，求出起点到终点的路径中具有最大权重和的路径。

可以通过将图中的权重取反来将最长路径问题转化为最短路径问题求解。

5. 限制路径中经过的节点或边数的最短路径问题：给定一个图和一个限制条件，如经过的节点数或经过的边数等，求出满足
限制条件的最短路径。

可以通过修改Dijkstra算法或Floyd-Warshall算法，增加限制条件来求解。

以上仅为最短路径问题的一些常见变形，实际问题可能还有其他的变形。

解决这些变形问题的关键是根据具体情况修改或选择合适的算法，以及定义适当的权重和限制条件。

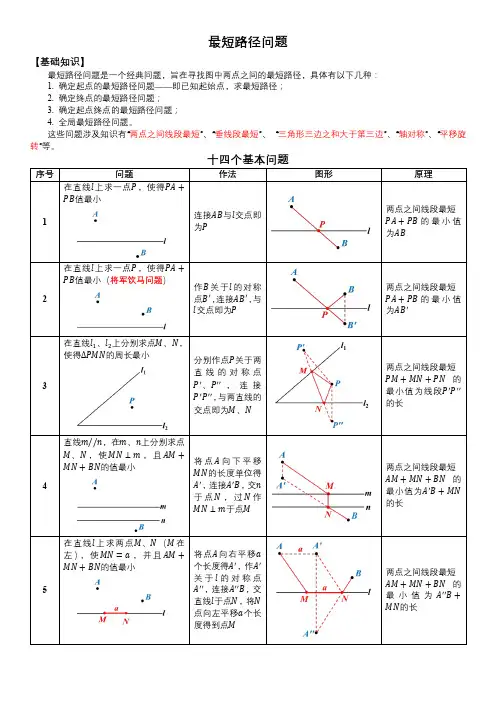
最短路径问题【基础知识】最短路径问题是一个经典问题，旨在寻找图中两点之间的最短路径，具体有以下几种：1. 确定起点的最短路径问题——即已知起始点，求最短路径；2. 确定终点的最短路径问题；3. 确定起点终点的最短路径问题；4. 全局最短路径问题。

这些问题涉及知识有“两点之间线段最短”、“垂线段最短”、“三角形三边之和大于第三边”、“轴对称”、“平移旋转”等。

问题图形在直线l上求一点P，使得PA+PB值最小在直线l上求一点P，使得PA+PB值最小（将军饮马问题）在直线l1、l2上分别求点M、N，使得∆PMN的周长最小直线m//n，在m、n上分别求点M、N，使MN⊥m，且AM+MN+BN的值最小在直线l上求两点M、N（M在左），使MN=a，并且AM+MN+BN的值最小在直线l1、l2上分别求点M、N，使得四边形PQMN的周长最小在直线l1上求点A，在l2上求点B，使PA+PB最小点A、B分别为直线l1、l2上定点，在l1、l2上分别求点N、M，使AM+MN+NB在直线l上求一点P，使|PA−PB|的值最小在直线l上求一点P，使|PA−PB|的值最大在直线l上求一点P，使|PA−PB|的值最大若∆ABC中每一个内角都小于120°，在∆ABC内求一点P，使得PA+PB+PC的值最小）如图，在△ABC 中，AB ＝AC ＝10，tanA ＝2，BE ⊥AC 于点E ，D 是线段BE 上的一个动点，则CD+√55BD 的最小值是 .如图，半圆的半径为1，AB 为直径，AC 、BD 为切线，AC ＝1，BD ＝2，点P 为弧AB 上一动点，求的最小值.。

运筹学最短路径问题
在运筹学中，最短路径问题是指寻找图中两个节点之间的最短路径。

最短路径可以通过一系列边连接起来，使得路径上的累计权值总和最小。

最短路径问题是运筹学中的经典问题，有广泛的应用领域，如交通网络规划、物流路径优化等。

常见的最短路径算法包括迪杰斯特拉算法和弗洛伊德算法。

迪杰斯特拉算法是用于解决单源最短路径问题的一种算法。

它从起点开始，通过不断更新节点的最短路径估计值和前驱节点，逐步扩展到其他节点，直到找到目标节点或所有节点都被处理。

弗洛伊德算法是用于解决全源最短路径问题的一种算法。

它通过动态规划的方式，对所有节点之间的最短路径进行逐步计算和更新，最终得到所有节点之间的最短路径。

除了迪杰斯特拉算法和弗洛伊德算法，还有其他一些算法可以用于解决最短路径问题，如贝尔曼-福特算法和A*算法等。

总之，最短路径问题在运筹学中具有重要的实际应用价值，可以通过不同的算法来求解。

这些算法在实践中可以根据具体的问题特点和需求选择合适的算法进行求解。

最短路径12种类型例题最短路径问题是图论中的一个重要问题。

它通常指从一个点到另一个点的最短距离或最短路径。

解决此类问题需要选择一个恰当的算法和数据结构。

本文将介绍12种最短路径类型的例题，并逐步解决它们。

1.单源最短路径单源最短路径指从一个源点到其他所有点的最短距离。

使用Dijkstra算法或Bellman-Ford算法来解决。

2.最短路径树最短路径树是从一个源点到所有其他节点的最短路径构成的一棵树。

使用Dijkstra算法或Bellman-Ford算法来解决。

3.多源最短路径多源最短路径指从所有源点到所有其他点的最短距离。

使用Floyd-Warshall算法来解决。

4.任意两点之间的最短路径任意两点之间的最短路径指从一个点出发，到达另一个点的最短距离。

使用Johnson算法来解决。

5.负权边的最短路径负权边的最短路径指当图中存在负权边时，求取从一个源点到其他所有节点的最短距离。

使用Bellman-Ford算法来解决。

6.负权环的最短路径负权环的最短路径指当图中存在负权环时，求取从一个源点到其他所有节点的最短距离。

使用Bellman-Ford算法来解决。

7.非全源点的最短路径非全源点的最短路径指从集合S中的任意一个节点到集合T中的任意一个节点的最短距离。

使用Dijkstra算法和A*算法来解决。

8.带优先级的最短路径带优先级的最短路径指在一张具有边权和点权的图中，到达终点时要满足某些特殊条件，如使路径上没有超过限定时间的边。

使用A*算法来解决。

9.带障碍的最短路径带障碍的最短路径指在一张具有障碍物的图中，找到穿过障碍物的最短路径。

使用A*算法来解决。

10.可走斜向的最短路径可走斜向的最短路径指在一个八方向图中，找到从起点到终点的最短路径。

使用A*算法来解决。

11.带环的最短路径带环的最短路径指在一个含有环的图中，找到从起点到终点的最短路径。

使用Bellman-Ford算法来解决。

12.非最短路径非最短路径是指除最短路径以外的路径。

行程问题7大经典题型行程问题是在现代计算机科学中研究的重要研究领域之一，也称为旅行商问题。

根据具体的应用，行程问题可分为七类经典题型：一、最短路径问题最短路径问题是指使行程开销最小化的最优路径问题，即在有权网（即有距离弧权值的有向图）中求出从起点到终点的最短路径问题。

最短路径问题的特点是将多条路径的值做比较，选择最优的路径。

最短路径问题的解法一般有迪杰斯特拉算法和贝尔曼-福德算法。

二、最小生成树问题最小生成树问题是指在连通图中求最小代价覆盖图（最小生成树）的问题。

求最小生成树也可以用迪杰斯特拉算法、贝尔曼-福德算法、克鲁斯卡尔算法等求解。

三、拓扑排序问题拓扑排序问题是指要解决有向图中的局部拓扑排序问题，让用户能够处理有向图的排序操作。

例如，拓扑排序可以用来求解项目管理中的生产流程排序，求解最长路径问题，用来求解运输问题。

某些拓扑排序问题常用拓扑排序法来解决，它的优点是举例简单，容易解决，但是在处理较大的网络可能不太方便。

四、负责度限制约束最小生成树问题负责度限制约束最小生成树问题是指当有负责度限制或边限制时，求出最小生成树的问题。

负责度限制最小生成树问题与最小生成树问题相似，但限制要求不同，使其可以求最小生成树但不需要所有节点出现。

解决负责度限制最小生成树问题的常见算法有Prim，Kruskal算法，单源最短路径算法等。

五、旅行商问题旅行商问题是指将一个实体从一个位置出发，访问所有位置，最后返回原位置，要尽可能使得整个行程之和最小的问题。

旅行商问题与最短路径问题之间存在着一定的联系，但是它更加复杂，可能有多个路径都是最优的，旅行商问题最优解的求解方法有穷举法、贪心法、遗传算法等。

六、交通网络问题交通网络问题是指涉及多晶体的旅行问题，在该问题中，客户的行程将跨越多个晶体构成的网络，以最小的费用或最短的时间从起点到终点运输物品或人员。

交通网络问题可以使用模拟退火法、遗传算法、混合算法等解决。

七、联通子图覆盖问题联通子图覆盖问题是指求解一个图G是否存在一个联通子图T，满足T中所有顶点和G中的全部顶点是相同的，最小顶点覆盖问题是联通子图覆盖问题的一个特殊情况，该问题的解法一般有贪心法和回溯法。

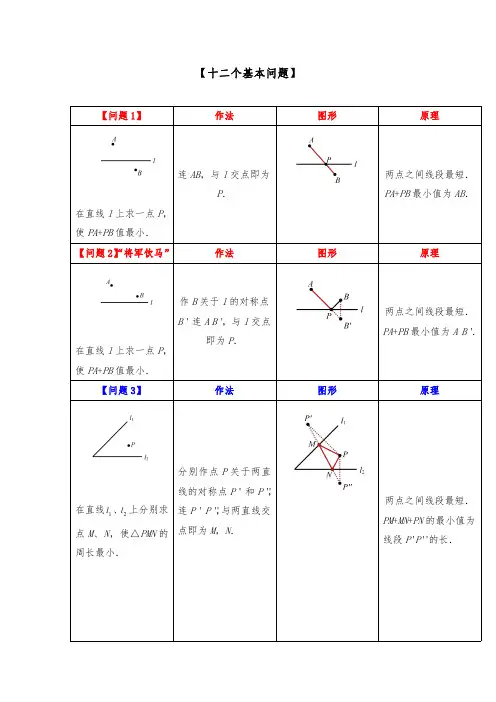
最短路径问题
2.3.1最短路径的定义
最短路径问题是运动规划的一个主要的课题。

运动规划问题由二部分组成，分别是最短路径和轨迹规划，其中路径问题归结起来就是连接起点和终点的一条曲线，而与之相匹配的路径规划问题就是形成这样一种路径的策略。

最短路径问题在生活生产的方方面面都会遇到，已经在很多领域都有着充分的运用。

比如现在中国最前端的领域就有涉及，比如：机器人在行动的时候必须做到自主无碰；无人机在飞行的时候必须做到避障突防；巡航导弹在飞行的时候必须做到躲避雷达的范围性探知；在我们的现实生活之中有：全球定位系统导航；各个城市内部不同的道路网规划等。

2.3.2最短路径的一般步骤
最短路径问题总结起来一般有下面三个步骤：
（1）环境建模。

其中，环境建模可以说是最短路径的一个不容忽视的一步，环境建模的目的是建立在实际上可以让计算机来操作进一步来最短路径的环境模型，也就是把现实之中的物理空间转化成算法从而可以形成抽象空间，实现相互间的映射。

（2）路径搜索。

路径搜索就是在环境模型已经完成了之后，运用之前已经建立好的算法，进而去寻找一条最优的的路径，使得我们所建立目标函数能够获得我们所期望的最优值。

（3）路径平滑。

通过之前已经建立好的算法，找到的最优的的路径在实际情况之中，并不一定实际上可行路径，需要后期继续作进一步处理，并且进行平滑的操作，才能使之前找到的最优的的路径成为一条在现实之中可以行走的路径。

最短路径问题和解法最短路径问题是计算一个图中从一个源点到目标点的最短路径问题，是图论中的重要问题之一。

该问题的解法可以划分为两种：单源最短路径问题和全源最短路径问题。

一、单源最短路径问题单源最短路径问题是指从一个源点出发，计算该源点到其他所有点的最短路径的问题。

解法有两种：Dijkstra算法和Bellman-Ford算法。

1. Dijkstra算法Dijkstra算法是一种贪心算法，每次将到源点距离最短的点加入已求出最短路径的点集。

虽然Dijkstra算法只适用于边权值均为正的带权有向图或者无向图，但是它的时间复杂度相比Bellman-Ford算法更优秀，为O(n^2)。

2. Bellman-Ford算法Bellman-Ford算法是一种较为通用的算法，不需要图的属性满足任何特殊要求，但是时间复杂度为O(n^3)，不适用于大规模的图。

算法原理是进行n次松弛操作，查找从源点到其他点的最短路径，其中进行松弛的过程是比较消耗时间的。

二、全源最短路径问题全源最短路径问题是指求解所有点之间的最短路径问题。

解法有两种：Floyd算法和Johnson算法。

3. Floyd算法Floyd算法是一种动态规划算法，算法将所有点对之间的最短路径逐步推进，通过枚举中间点，得到更加精细的状态转移方程和最短路径。

时间复杂度为O(n^3)，因此带来的计算负担较大。

4. Johnson算法Johnson算法目前是解决稠密图最短路径问题的最好算法之一。

Johnson算法先通过引入虚拟点，将原图转化为一个没有负权边的新图，再对新图使用Dijkstra算法进行求解。

该算法的时间复杂度为O(mnlogn)，其中m为边的条数，n为点的个数。

综上所述，最短路径问题是图论中的重要问题之一。

对于单源最短路径问题，Dijkstra算法和Bellman-Ford算法是常用的解法；全源最短路径问题，Floyd算法和Johnson算法是较为常用的解法。

最短路径问题最短路径问题是图论中一个重要的研究领域，即求解两个节点之间的最短路径。

在实际生活中，最短路径问题有着广泛的应用，例如导航系统、交通规划以及网络通信等领域。

本文将介绍最短路径问题的定义、常见算法以及应用实例。

一、定义最短路径问题可以用来求解从一个节点到另一个节点的最短路径。

在图论中，最短路径通常指的是路径上的边的权重之和最小。

图可以由节点和边组成，边可以有权重，表示两个节点之间的距离或成本。

最短路径问题的目标是找到两个节点之间的路径，使得路径上的边的权重之和最小。

二、算法1. Dijkstra算法Dijkstra算法是解决最短路径问题的经典算法之一。

该算法采用贪心策略，逐步确定起点到其他节点的最短路径。

具体步骤如下：（1）初始化距离数组，起点到起点的距离为0，所有其他节点的距离为无穷大。

（2）选择一个未被访问过的节点，标记为当前节点。

（3）对于当前节点的所有邻居节点，更新其距离为当前节点距离加上边的权重，并更新最短路径。

（4）继续选择未被访问过的节点中最短路径最小的节点，标记为当前节点，重复步骤（3）。

（5）重复步骤（3）和（4），直到所有节点都被访问过。

Dijkstra算法的时间复杂度为O(V^2)，其中V为节点的数量。

2. Bellman-Ford算法Bellman-Ford算法是另一种解决最短路径问题的算法。

与Dijkstra 算法不同，Bellman-Ford算法可以处理带有负权边的图。

该算法通过迭代更新距离数组，逐步确定最短路径。

具体步骤如下：（1）初始化距离数组，起点到起点的距离为0，其他节点的距离为无穷大。

（2）对于图中的每条边，重复以下步骤：a. 从边的起点到终点的距离是否可以通过起点到起点的距离加上边的权重来达到更小值。

b. 如果是，则更新终点的距离为该更小值。

（3）重复步骤（2）|V|-1次，其中V为节点的数量。

Bellman-Ford算法的时间复杂度为O(VE)，其中V为节点的数量，E为边的数量。

最短路径问题（珍藏版）【问题概述】最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由结点和路径组成的）中两结点之间的最短路径．算法具体的形式包括：①确定起点的最短路径问题-即已知起始结点，求最短路径的问题．②确定终点的最短路径问题-与确定起点的问题相反，该问题是已知终结结点，求最短路径的问题．③确定起点终点的最短路径问题-即已知起点和终点，求两结点之间的最短路径．④全局最短路径问题-求图中所有的最短路径．【问题原型】“将军饮马”，“造桥选址”，“费马点”．【涉及知识】“两点之间线段最短”，“垂线段最短”，“三角形三边关系”，“轴对称”，“平移”．【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等．【解题思路】找对称点实现“折”转“直”，近两年出现“三折线”转“直”等变式问题考查．【十二个基本问题】【问题1】作法图形原理在直线l上求一点P ，使PA +PB 值最小．连AB ，与l 交点即为P ．两点之间线段最短．PA +PB 最小值为AB ．【问题2】“将军饮马”作法图形原理在直线l 上求一点P ，使PA +PB 值最小．作B 关于l 的对称点B ＇连A B ＇，与l 交点即为P ．两点之间线段最短．PA +PB 最小值为A B ＇．【问题3】作法图形原理在直线1l 、2l 上分别求点M 、N ，使△PMN 的周长最小．分别作点P 关于两直线的对称点P ＇和P ＇＇，连P ＇P ＇＇，与两直线交点即为M ，N ．两点之间线段最短．PM +MN +PN 的最小值为线段P ＇P ＇＇的长．【问题4】作法图形原理在直线1l 、2l 上分别求点M 、N ，使四边形PQMN 的周长最小．分别作点Q 、P 关于直线1l 、2l 的对称点Q ＇和P ＇连Q ＇P ＇，与两直线交点即为M ，N ．两点之间线段最短．四边形PQMN 周长的最小值为线段P ＇P ＇＇的长．直线m∥n，在m、n上分别求点M、N，使MNm，且AM+MN+BN值最小．【问题6】图形在直线l上求两点M、N（MN=，并使在左），使a+MN+NB的值最小．【问题7】图形上求点A，在2l上求1B，使PA+AB值最小．【问题8】图形为1l上一定点，B为2l上一定点，在2l上求点M，在1l上求点N，使AM+MN+NB的值最小．【问题9】图形在直线l上求一点P，使P A-的值最小．PB【问题10】作法图形原理在直线l上求一点P，使PBP A-的值最大．作直线AB，与直线l的交点即为P．三角形任意两边之差小于第三边．PBP A-≤AB．PBP A-的最大值＝AB．【问题11】作法图形原理在直线l上求一点P，使PBP A-的值最大．作B关于l的对称点B＇作直线A B＇，与l交点即为P．三角形任意两边之差小于第三边．PBP A-≤AB＇．PBP A-最大值＝AB＇．【问题12】“费马点”作法图形原理△ABC中每一内角都小于120°，在△ABC内求一点P，使PA+PB+PC值最小．所求点为“费马点”，即满足∠APB＝∠BPC＝∠APC＝120°．以AB、AC为边向外作等边△ABD、△ACE，连CD、BE相交于P，点P即为所求．两点之间线段最短．PA+PB+PC最小值＝CD．【精品练习】1．如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（）A．B．C．3D2．如图，在边长为2的菱形ABCD中，∠ABC＝60°，若将△ACD绕点A旋转，当AC′、AD′分别与BC、CD 交于点E、F，则△CEF的周长的最小值为（）A．2B．32C．32+D．4A DEPB C3．四边形ABCD 中，∠B ＝∠D ＝90°，∠C ＝70°，在BC 、CD 上分别找一点M 、N ，使△AMN 的周长最小时，∠AMN +∠ANM 的度数为（）A ．120°B ．130°C ．110°D ．140°4．如图，在锐角△ABC 中，AB ＝42，∠BAC ＝45°，∠BAC 的平分线交BC 于点D ，M 、N 分别是AD 和AB 上的动点，则BM +MN 的最小值是．5．如图，Rt △ABC 中，∠C ＝90°，∠B ＝30°，AB ＝6，点E 在AB 边上，点D 在BC 边上（不与点B 、C 重合），且ED ＝AE ，则线段AE 的取值范围是．6．如图，∠AOB ＝30°，点M 、N 分别在边OA 、OB 上，且OM ＝1，ON ＝3，点P 、Q 分别在边OB 、OA 上，则MP ＋PQ ＋QN 的最小值是_________．（注“勾股定理”：直角三角形中两直角边的平方和等于斜边的平方，即Rt △ABC 中，∠C ＝90°，则有222AB BC AC =+）7．如图，三角形△ABC 中，∠OAB ＝∠AOB ＝15°，点B 在x 轴的正半轴，坐标为B (36，0)．OC 平分∠AOB ，点M 在OC 的延长线上，点N 为边OA 上的点，则MA ＋MN 的最小值是______．8．已知A（2，4）、B（4，2）．C在y轴上，D在x轴上，则四边形ABCD的周长最小值为，此时C、D两点的坐标分别为．9．已知A（1，1）、B（4，2）．（1）P为x轴上一动点，求PA+PB的最小值和此时P点的坐标；P A 的值最大时P点的坐标；（2）P为x轴上一动点，求PB（3）CD为x轴上一条动线段，D在C点右边且CD＝1，求当AC+CD+DB的最小值和此时C点的坐标；10．点C为∠AOB内一点．（1）在OA求作点D，OB上求作点E，使△CDE的周长最小，请画出图形；（2）在（1）的条件下，若∠AOB＝30°，OC＝10，求△CDE周长的最小值和此时∠DCE的度数．11．（1）如图①，△ABD和△ACE均为等边三角形，BE、CE交于F，连AF，求证：AF+BF+CF＝CD；（2）在△ABC中，∠ABC＝30°，AB＝6，BC＝8，∠A，∠C均小于120°，求作一点P，使PA+PB+PC的值最小，试求出最小值并说明理由．。