第7章-图
- 格式:doc
- 大小:542.00 KB
- 文档页数:11




第7章 《图》习题参考答案一、单选题(每题1分,共16分)( C )1. 在一个图中,所有顶点的度数之和等于图的边数的 倍。
A .1/2 B. 1 C. 2 D. 4 (B )2. 在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的 倍。
A .1/2 B. 1 C. 2 D. 4 ( B )3. 有8个结点的无向图最多有 条边。
A .14 B. 28 C. 56 D. 112 ( C )4. 有8个结点的无向连通图最少有 条边。
A .5 B. 6 C. 7 D. 8 ( C )5. 有8个结点的有向完全图有 条边。
A .14 B. 28 C. 56 D. 112 (B )6. 用邻接表表示图进行广度优先遍历时,通常是采用 来实现算法的。
A .栈 B. 队列 C. 树 D. 图 ( A )7. 用邻接表表示图进行深度优先遍历时,通常是采用 来实现算法的。
A .栈 B. 队列 C. 树 D. 图 ()8. 已知图的邻接矩阵,根据算法思想,则从顶点0出发按深度优先遍历的结点序列是( D )9. 已知图的邻接矩阵同上题8,根据算法,则从顶点0出发,按深度优先遍历的结点序列是A . 0 2 4 3 1 5 6 B. 0 1 3 5 6 4 2C. 0 4 2 3 1 6 5D. 0 1 2 34 6 5 ( D )10. 已知图的邻接表如下所示,根据算法,则从顶点0出发按深度优先遍历的结点序列是( A )11. 已知图的邻接表如下所示,根据算法,则从顶点0出发按广度优先遍历的结点序列是A .0 2 4 3 1 5 6B. 0 1 3 6 5 4 2C. 0 1 3 4 2 5 6D. 0 3 6 1 5 4 2⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡0100011101100001011010110011001000110010011011110A .0 1 3 2 B. 0 2 3 1 C. 0 3 2 1 D. 0 1 2 3(A)12. 深度优先遍历类似于二叉树的A.先序遍历 B. 中序遍历 C. 后序遍历 D. 层次遍历(D)13. 广度优先遍历类似于二叉树的A.先序遍历 B. 中序遍历 C. 后序遍历 D. 层次遍历(A)14. 任何一个无向连通图的最小生成树A.只有一棵 B. 一棵或多棵 C. 一定有多棵 D. 可能不存在(注,生成树不唯一,但最小生成树唯一,即边权之和或树权最小的情况唯一)二、填空题(每空1分,共20分)1. 图有邻接矩阵、邻接表等存储结构,遍历图有深度优先遍历、广度优先遍历等方法。
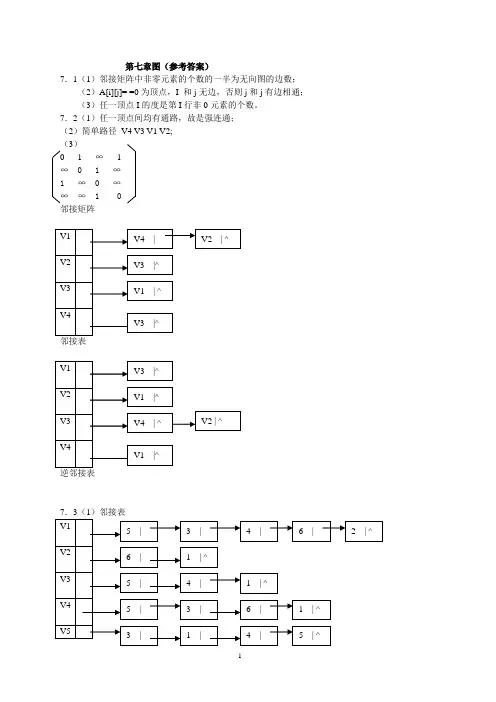
第七章图(参考答案)7.1(1)邻接矩阵中非零元素的个数的一半为无向图的边数;(2)A[i][j]= =0为顶点,I 和j无边,否则j和j有边相通;(3)任一顶点I的度是第I行非0元素的个数。
7.2(1)任一顶点间均有通路,故是强连通;(2)简单路径V4 V3 V1 V2;(3)0 1 ∞ 1∞ 0 1 ∞1 ∞ 0 ∞∞∞ 1 0邻接矩阵邻接表(2)从顶点4开始的DFS序列:V5,V3,V4,V6,V2,V1(3)从顶点4开始的BFS序列:V4,V5,V3,V6,V1,V27.4(1)①adjlisttp g; vtxptr i,j; //全程变量② void dfs(vtxptr x)//从顶点x开始深度优先遍历图g。
在遍历中若发现顶点j,则说明顶点i和j间有路径。
{ visited[x]=1; //置访问标记if (y= =j){ found=1;exit(0);}//有通路,退出else { p=g[x].firstarc;//找x的第一邻接点while (p!=null){ k=p->adjvex;if (!visited[k])dfs(k);p=p->nextarc;//下一邻接点}}③ void connect_DFS (adjlisttp g)//基于图的深度优先遍历策略,本算法判断一邻接表为存储结构的图g种,是否存在顶点i //到顶点j的路径。
设 1<=i ,j<=n,i<>j.{ visited[1..n]=0;found=0;scanf (&i,&j);dfs (i);if (found) printf (” 顶点”,i,”和顶点”,j,”有路径”);else printf (” 顶点”,i,”和顶点”,j,”无路径”);}// void connect_DFS(2)宽度优先遍历全程变量,调用函数与(1)相同,下面仅写宽度优先遍历部分。
![第7章 图论 [离散数学离散数学(第四版)清华出版社]](https://uimg.taocdn.com/58b7923143323968011c9244.webp)
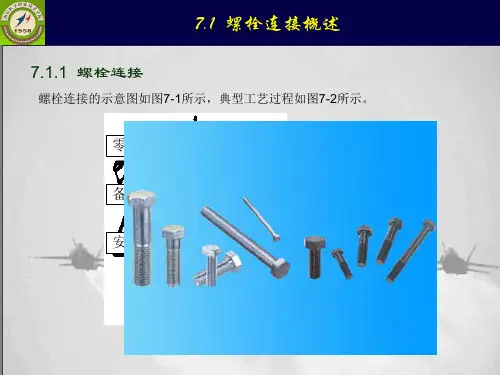
7.1.1 螺栓连接螺栓连接的示意图如图7-1所示,典型工艺过程如图7-2所示。
图7-1 螺栓连接零件夹紧确定孔位制 孔备 件倒角倒圆制 窝安 装定 力防 松涂 漆图7-2 螺栓连接的典型工艺过程7.1.2 托板螺母连接(如图7-3所示)典型工艺过程与螺栓连接的区别在于在制孔和制窝之间增加铆接托板螺母工序,而无定力和防松工序。
工作步骤如下:在固定构件上制螺栓孔铆接托板螺母将活动构件定位安装在固定构件上在活动构件上制螺栓孔固定活动构件图7-3 托板螺母连接7.1.3 高锁螺栓连接(如图7-4所示)典型工艺过程与螺栓连接的区别在于无定力和防松工序,对于双六角型高锁螺母安装后按需要再次拧紧定力。
(a)(b)图7-4 高锁螺栓连接7.1.4 锥型螺栓连接(如图7-5所示)典型工艺过程与螺栓连接的区别在于无定力工序,制孔与制窝同时进行。
(a)(b)图7-5 锥型螺栓连接7.2 零件的定位及夹紧7.2.1 螺栓连接(见表7-1)7.2.2 孔位的技术要求确定螺栓孔位螺栓孔边距、间距和排距的极限偏差螺栓孔的最小边距7.3.1 孔的技术要求常见螺栓孔的技术要求见表7-2高锁螺栓孔的技术要求与普通螺栓孔的技术要求相同锥形螺栓孔的技术要求孔应垂直于工件表面孔锥度极限偏差孔表面粗糙度孔与锥形螺栓光杆接触的面积孔表面允许的轻微划伤、孔的外观质量7.3.2 孔加工方法的选择孔的公差等级选择孔加工方法时主要考虑孔直径孔的深度被加工的材料结构的开敞性各种孔加工方法见表7-3 钻孔用扩孔钻扩孔手铰风钻铰孔拉孔自动进给钻制孔自动铆机制孔7.4.1 制孔前的准备工作明确加工孔的孔径和公差检查工件间隙、孔边矩检查要用的钻机、刀具和量具等是否合格及适用在试件上进行试加工7.4.2 钻孔和扩孔的技术要点注意孔的垂直度(见图7-6)手工钻制初孔的直径确定钻孔工具的工作转速选用带前导杆的扩孔钻用自动进给钻钻孔时的过程自动进给钻的轴转速恒定不变的情况下,钻头反复进入孔和完全撤离孔固定在钻模上(如图7-7所示)建议使用润滑剂7.4.2 钻孔和扩孔的技术要点图7-6 保证钻孔垂直度的方法(a)按垂直钻套钻孔(b)按直角尺钻孔(c)按钻模钻孔图7-7 自动进给钻钻孔示意图用带前、后引导的扩孔钻扩孔(如图7-8所示)由相同材料组成时,从较厚面进刀由不同材料组成时,从较硬面进刀图7-8 空心零件的扩孔7.4.3 手工铰孔方法及操作要点手工铰孔操作过程将铰刀沾上润滑液后插入初孔用角度尺检查铰刀是否垂直于工件表面(如图7-9所示)用大拇指轻推铰刀尾部,旋转铰杠或棘轮扳手铰深孔时,要常退刀排屑检查孔的精度、粗糙度和孔的垂直度手工铰孔操作要点工件装配夹紧要正确手铰过程中,两手用力要平衡注意变换铰刀每次停歇的位置旋转铰杠进刀时,不要猛力压铰杠图7-9 用90°角尺检查铰刀垂直度7.4.3 手工铰孔方法及操作要点手工铰孔操作要点若铰刀被卡住,应将铰刀取出,清除切屑铰刀绝不可倒转当使用风钻铰孔时,一定要掌握好进刀方向根据所加工材料,合理选择转速和进给量7.4.4锥形孔的加工(a)扩孔钻(b)铰刀图7-10 沉头锥形螺栓孔用的加工刀具以螺纹直径为锥形螺栓的基本直径选择专用锥形铰刀(见图7-10)光整孔壁取出铰刀清除切屑扩孔钻初孔7.4.5 可调铰刀的使用在刀体上开有六条斜底直槽,具有同样斜度的刀条嵌在槽里利用前后两只螺母压紧刀条的两端,调节两端的螺母可使刀条沿斜槽移动,即能改变铰刀的直径7.4.6 切削用量的选择扩孔切削用量(见表7-4)手铰和风钻铰孔在铰孔过程中的切屑用量(见表7-5)7.4.7 扩、铰孔过程中切削液的选择(见表7-6)7.4.8 铰孔中常见的缺陷和解决措施(见表7-7)7.5.1 锪窝锪窝包括锪沉头螺栓的沉头窝和端面窝(见图7-12)正锪和反锪(如图7-13或图7-14所示)锪窝操作要点图7-12 沉头窝和端面窝(a)沉头螺栓的沉头窝(b)六角头或圆柱头螺栓的沉头窝(c)螺栓端面窝(a)正锪(b)反锪图7-14 锪端面窝锪窝速度锪钻装夹牢固加机油润滑留余量带球面导杆锪窝钻(见图7-15)锪钻应先接触被锪面并拉紧风钻,再开动扳机锪窝限定器(见图7-17)图7-15带球面形导杆的窝锪钻带阶梯的导杆锪窝钻(如图7-16所示)图7-16 带台阶导杆的窝锪钻图7-17 用锪窝深度限制衬套锪窝涂防腐保护层7.5.2 倒角与倒圆技术要求倒角与倒圆的工艺方法孔与沉头窝交接处的倒角形状(见图7-19)安装凸头锥形螺栓的孔,在靠锥形螺栓头的一侧应倒角安装沉头锥形螺栓用的孔在与沉头窝的交接处(简称沉头窝底)制倒角倒角与倒圆形状(见图7-18),尺寸(见表7-8)图7-18 倒角与倒圆(a)倒角(b)倒圆图7-19 孔与沉头窝交接处的倒角倒圆一般采用倒圆锪钻倒圆。


《离散数学》第七章图的基本概念讲稿7.1 ⽆向图及有向图⼀、本节主要内容⽆向图与有向图顶点的度数握⼿定理简单图完全图⼦图补图⼆、教学内容⽆序对: 两个元素组成的⼆元组(没有顺序),即⽆论a,b是否相同,(a,b )=(b, a )⽆序积: A与B 为两个集合,A&B={(x,y) |x∈A∧y∈B}例A={a1, a2}, B={b1, b2}A&B={(a1 , b1 ), (a1 , b2 ) ,(a2 , b1 ) ,(a2 , b2 )}A&A={(a1 , a1 ), (a1 , a2 ) ,(a2 , a2 )}多重集合: 元素可以重复出现的集合⽆向图与有向图定义⽆向图G=, 其中(1) V?≠为顶点集,元素称为顶点(2) E为V&V的多重⼦集,其元素称为⽆向边,简称边.例如, G=如图所⽰,其中V={v1, v2, …,v5},E={(v1,v1), (v1,v2), (v2,v3), (v2,v3), (v2,v5), (v1,v5), (v4,v5)}定义⽆向图G=, 其中(1) V≠?为顶点集,元素称为顶点(2) E为V&V的多重⼦集,其元素称为⽆向边,简称边.例如, G=如图所⽰,其中V={v1, v2, …,v5},E={(v1,v1), (v1,v2), (v2,v3), (v2,v3), (v2,v5), (v1,v5), (v4,v5)} ⽆向图与有向图(续)定义有向图D=, 其中(1) V同⽆向图的顶点集, 元素也称为顶点(2) E为V?V的多重⼦集,其元素称为有向边,简称边.⽤⽆向边代替D的所有有向边所得到的⽆向图称作D的基图右图是有向图,试写出它的V和E⽆向图与有向图(续)通常⽤G表⽰⽆向图, D表⽰有向图,也常⽤G泛指⽆向图和有向图,⽤ek表⽰⽆向边或有向边.V(G), E(G), V(D), E(D): G和D的顶点集, 边集.n 阶图: n个顶点的图有限图: V, E都是有穷集合的图零图: E=?平凡图: 1 阶零图顶点和边的关联与相邻定义设ek=(vi, vj)是⽆向图G=的⼀条边, 称vi, vj为ek的端点, ek与vi ( vj)关联.若vi ≠ vj, 则称ek与vi ( vj)的关联次数为1;若vi = vj, 则称ek为环, 此时称ek与vi 的关联次数为2;若vi不是ek端点, 则称ek与vi 的关联次数为0.⽆边关联的顶点称作孤⽴点.定义设⽆向图G=, vi,vj∈V,ek,el∈E,若(vi,vj) ∈E, 则称vi,vj相邻;若ek,el⾄少有⼀个公共端点, 则称ek,el相邻.对有向图有类似定义. 设ek=?vi,vj?是有向图的⼀条边, vi,vj是ek端点,⼜称vi 是ek的始点, vj是ek的终点,vi邻接到vj, vj邻接于vi.邻域和关联集设⽆向图G , v ∈V(G)v 的邻域 N(v)={u|u ∈V(G)∧(u,v)∈E(G)∧u ≠v} v 的闭邻域 = N(v)∪{v} v 的关联集 I(v)={e|e ∈E(G)∧e 与v 关联} 设有向图D, v ∈V(D)v 的后继元集 ={u|u ∈V(D)∧∈E(G)∧u ≠v}v 的先驱元集 ={u|u ∈V(D)∧∈E(G)∧u ≠v}v 的邻域v 的闭邻域顶点的度数设G=为⽆向图, v ∈V,v 的度数(度) d(v): v 作为边的端点的次数之和悬挂顶点: 度数为1的顶点悬挂边: 与悬挂顶点关联的边 G 的最⼤度?(G)=max{d(v)| v ∈V} G 的最⼩度δ(G)=min{d(v)| v ∈V} 例如 d(v5)=3, d(v2)=4, d(v1)=4, ?(G)=4, δ(G)=1,v4是悬挂顶点, e7是悬挂边, e1是环顶点的度数(续)设D=为有向图, v ∈V,v 的出度d+(v): v 作为边的始点的次数之和 v 的⼊度d -(v): v 作为边的终点的次数之和 v 的度数(度) d(v): v 作为边的端点次数之和 d(v)= d+(v)+ d-(v)D 的最⼤出度?+(D), 最⼩出度δ+(D) 最⼤⼊度?-(D), 最⼩⼊度δ-(D) 最⼤度?(D), 最⼩度δ(D) 例如 d+(a)=4, d-(a)=1, d(a)=5, d+(b)=0, d-(b)=3, d(b)=3,+(D)=4, δ+(D)=0, ?-(D)=3, δ-(D)=1, ?(D)=5, δ(D)=3. 图论基本定理——握⼿定理定理任意⽆向图和有向图的所有顶点度数之和都等于边数的2倍, 并且有向图的所有顶点⼊度之和等于出度之和等于边数.)(v N )(v D +Γ)(v D -Γ)()()(v v v N D D D -+ΓΓ= }{)()(v v N v N D D =证 G 中每条边(包括环)均有两个端点,所以在计算G 中各顶点度数之和时,每条边均提供2度,m 条边共提供2m 度.有向图的每条边提供⼀个⼊度和⼀个出度, 故所有顶点⼊度之和等于出度之和等于边数. 握⼿定理(续)推论在任何⽆向图和有向图中,度为奇数的顶点个数必为偶数. 证设G=为任意图,令 V1={v | v ∈V ∧d(v)为奇数} V2={v | v ∈V ∧d(v)为偶数}则V1∪V2=V, V1∩V2=?,由握⼿定理可知∑∑∑∈∈∈+==21)()()(2V v V v Vv v d v d v d m由于2m,∑∈2)(V v v d 均为偶数,所以 ∑∈1)(V v v d 也为偶数, 但因为V1中顶点度数都为奇数,所以|V1|必为偶数.图的度数列设⽆向图G 的顶点集V={v1, v2, …, vn} G 的度数序列: d(v1), d(v2), …, d(vn) 如右图度数序列:4,4,2,1,3设有向图D 的顶点集V={v1, v2, …, vn} D 的度数序列: d(v1), d(v2), …, d(vn) D 的出度序列: d+(v1), d+(v2), …, d+(vn) D 的⼊度序列: d -(v1), d -(v2), …, d -(vn) 如右图度数序列:5,3,3,3出度序列:4,0,2,1 ⼊度序列:1,3,1,2 握⼿定理的应⽤例1 (3,3,3,4), (2,3,4,6,8)能成为图的度数序列吗? 解不可能. 它们都有奇数个奇数.例2 已知图G 有10条边, 4个3度顶点, 其余顶点的度数均⼩于等于2, 问G ⾄少有多少个顶点? 解设G 有n 个顶点. 由握⼿定理, 4?3+2?(n-4)≥2?10 解得 n ≥8握⼿定理的应⽤(续)例3 给定下列各序列,哪组可以构成⽆向图的度数序列 (2,2,2,2,2) (1,1,2,2,3) (1,1,2,2,2) (1,3,4,4,5)多重图与简单图定义(1) 在⽆向图中,如果有2条或2条以上的边关联同⼀对顶点, 则称这些边为平⾏边, 平⾏边的条数称为重数.(2)在有向图中,如果有2条或2条以上的边具有相同的始点和终点, 则称这些边为有向平⾏边, 简称平⾏边, 平⾏边的条数称为重数.(3) 含平⾏边的图称为多重图.(4) 既⽆平⾏边也⽆环的图称为简单图.注意:简单图是极其重要的概念多重图与简单图(续)例如e5和e6 是平⾏边重数为2不是简单图e2和e3 是平⾏边,重数为2 e6和e7不是平⾏边不是简单图图的同构定义设G1=, G2=为两个⽆向图(有向图), 若存在双射函数f: V1→V2, 使得对于任意的vi,vj∈V1,(vi,vj)∈E1(∈E1)当且仅当(f(vi),f(vj))∈E2(∈E2),并且,(vi,vj)()与(f(vi),f(vj))()的重数相同,则称G1与G2是同构的,记作G1?G2.图的同构(续)⼏点说明:图之间的同构关系具有⾃反性、对称性和传递性.能找到多条同构的必要条件, 但它们都不是充分条件:①边数相同,顶点数相同②度数列相同(不计度数的顺序)③对应顶点的关联集及邻域的元素个数相同,等等若破坏必要条件,则两图不同构图的同构(续)例1 试画出4阶3条边的所有⾮同构的⽆向简单图例2 判断下述每⼀对图是否同构:(1)度数列不同不同构例2 (续)(2)不同构⼊(出)度列不同度数列相同但不同构为什么?完全图与正则图n阶⽆向完全图Kn: 每个顶点都与其余顶点相邻的n阶⽆向简单图.简单性质: 边数m=n(n-1)/2, ?=δ=n-1n阶有向完全图: 每对顶点之间均有两条⽅向相反的有向边的n阶有向简单图.简单性质: 边数m=n(n-1), ?=δ=2(n-1),+=δ+=?-=δ-=n-1n阶k正则图: ?=δ=k 的n阶⽆向简单图简单性质: 边数m=nk/2完全图与正则图(续)(1) 为5阶⽆向完全图K5(2) 为3阶有向完全图(3) 为彼得森图, 它是3 正则图⼦图定义设G=, G '=是2个图(1) 若V '?V且E '?E, 则称G '为G的⼦图, G为G '的母图, 记作G '?G(2)若G '?G且G '≠ G(即V '?V 或E '?E),称G '为G的真⼦图(3) 若G '?G 且V '=V,则称G '为G的⽣成⼦图(4) 设V '?V 且V '≠?, 以V '为顶点集, 以两端点都在V '中的所有边为边集的G的⼦图称作V '的导出⼦图,记作G[V '](5) 设E '?E且E '≠?, 以E '为边集, 以E '中边关联的所有顶点为顶点集的G的⼦图称作E '的导出⼦图, 记作G[E ']⼦图(续)例画出K4的所有⾮同构的⽣成⼦图补图定义设G=为n阶⽆向简单图,以V为顶点集,所有使G成为完全图Kn的添加边组成的集合为边集的图,称为G的补图,记作G?G.若G ? G , 则称G 是⾃补图.例画出5阶7条边的所有⾮同构的⽆向简单图⾸先,画出5阶3条边的所有⾮同构的⽆向简单图然后,画出各⾃的补图7.2 通路、回路与图的连通性⼀、本节主要内容简单通(回)路, 初级通(回)路, 复杂通(回)路⽆向连通图, 连通分⽀弱连通图, 单向连通图, 强连通图点割集与割点边割集与割边(桥) ⼆、教学内容通路与回路定义给定图G=(⽆向或有向的),设G 中顶点与边的交替序列Γ=v0e1v1e2…elvl ,(1) 若?i(1≤i ≤l), vi -1 和 vi 是ei 的端点(对于有向图, 要求vi -1是始点, vi 是终点), 则称Γ为通路, v0是通路的起点, vl 是通路的终点, l 为通路的长度. ⼜若v0=vl ,则称Γ为回路. (2) 若通路(回路)中所有顶点(对于回路, 除v0=vl)各异,则称为初级通路(初级回路).初级通路⼜称作路径, 初级回路⼜称作圈.(3) 若通路(回路)中所有边各异, 则称为简单通路(简单回路), 否则称为复杂通路(复杂回路). 通路与回路(续) 说明:在⽆向图中,环是长度为1的圈, 两条平⾏边构成长度为2的圈. 在有向图中,环是长度为1的圈, 两条⽅向相反边构成长度为2的圈. 在⽆向简单图中, 所有圈的长度≥3; 在有向简单图中, 所有圈的长度≥2. 通路与回路(续)定理在n 阶图G 中,若从顶点vi 到vj (vi ≠vj )存在通路,则从vi 到vj 存在长度⼩于等于n -1的通路.推论在n 阶图G 中,若从顶点vi 到vj (vi ≠vj )存在通121212G G G G G G ??例设与均为⽆向简单图,当且仅当路,则从vi到vj存在长度⼩于等于n-1的初级通路.定理在⼀个n阶图G中,若存在vi到⾃⾝的回路,则⼀定存在vi到⾃⾝长度⼩于等于n的回路.推论在⼀个n阶图G中,若存在vi到⾃⾝的简单回路,则⼀定存在长度⼩于等于n的初级回路.⽆向图的连通性设⽆向图G=,u与v连通: 若u与v之间有通路. 规定u与⾃⾝总连通.连通关系R={| u,v ∈V且u~v}是V上的等价关系连通图: 平凡图, 或者任意两点都连通的图连通分⽀: V关于R的等价类的导出⼦图设V/R={V1,V2,…,Vk}, G[V1], G[V2], …,G[Vk]是G的连通分⽀, 其个数记作p(G)=k.G是连通图? p(G)=1u与v之间的短程线: u与v之间长度最短的通路(u与v连通)u与v之间的距离d(u,v): u与v之间短程线的长度若u与v不连通, 规定d(u,v)=∞.性质:d(u,v)≥0, 且d(u,v)=0 ? u=vd(u,v)=d(v,u)(对称性)d(u,v)+d(v,w)≥d(u,w) (三⾓不等式)点割集记G-v: 从G中删除v及关联的边G-V': 从G中删除V'中所有的顶点及关联的边G-e : 从G中删除eG-E': 从G中删除E'中所有边定义设⽆向图G=, 如果存在顶点⼦集V'?V, 使p(G-V')>p(G),⽽且删除V'的任何真⼦集V''后(? V''?V'),p(G-V'')=p(G), 则称V'为G的点割集. 若{v}为点割集, 则称v为割点.点割集(续)例{v1,v4}, {v6}是点割集, v6是割点.{v2,v5}是点割集吗?边割集定义设⽆向图G=, E'?E, 若p(G-E')>p(G)且?E''?E',p(G-E'')=p(G), 则称E'为G的边割集. 若{e}为边割集, 则称e为割边或桥.在上⼀页的图中,{e1,e2},{e1,e3,e5,e6},{e8}等是边割集,e8是桥,{e7,e9,e5,e6}是边割集吗?⼏点说明:Kn⽆点割集n阶零图既⽆点割集,也⽆边割集.若G连通,E'为边割集,则p(G-E')=2若G连通,V'为点割集,则p(G-V')≥2有向图的连通性设有向图D=u可达v: u到v有通路. 规定u到⾃⾝总是可达的.可达具有⾃反性和传递性D弱连通(连通): 基图为⽆向连通图D单向连通: ?u,v∈V,u可达v 或v可达uD强连通: ?u,v∈V,u与v相互可达强连通?单向连通?弱连通有向图的连通性(续)例下图(1)强连通, (2)单连通, (3) 弱连通有向图的短程线与距离u到v的短程线: u到v长度最短的通路(u可达v)u与v之间的距离d: u到v的短程线的长度若u不可达v, 规定d=∞.性质:d+d ≥d注意: 没有对称性7.3 图的矩阵表⽰⼀、本节主要内容⽆向图的关联矩阵有向图的关联矩阵有向图的邻接矩阵有向图的可达矩阵⼆、教学内容⽆向图的关联矩阵定义设⽆向图G=, V={v1, v2, …, vn}, E={e1, e2, …, em}, 令mij为vi与ej的关联次数,称(mij)n?m为G的关联矩阵,记为M(G).定义设⽆向图G=, V={v1, v2, …, vn}, E={e1, e2, …, em}, 令mij为vi与ej的关联次数,称(mij)n?m为G的关联矩阵,记为M(G).性质关联次数为可能取值为0,1,2有向图的关联矩阵定义设⽆环有向图D=, V={v1, v2, …, vn}, E={e1, e2, …, em}, 令则称(mij)n ?m 为D 的关联矩阵,记为M(D). 性质:有向图的邻接矩阵定义设有向图D=, V={v1, v2, …, vn}, E={e1, e2, …, em}, 令 )1(ij a 为顶点vi 邻接到顶点vj 边的条数,称()1(ij a )n ?n 为D 的邻接矩阵, 记作A(D), 简记为A. 1110001110()1001200000M G=1100010111()0000101110M D ---?=-??-??平⾏边的列相同)4(2)3(),...,2,1()()2(),...,2,1(2)1(,11mm n i v d m m j m ji ijimj ijni ij =====∑∑∑==(1)1(1)1(1)(),1,2,...,(2)(),1,2,...,nij i j n ij ji a d vi n a d v j n+=-=====∑∑性质D 中的通路及回路数定理设A 为n 阶有向图D 的邻接矩阵, 则Al(l ≥1)中元素)(l ij a 为D 中vi 到vj 长度为 l 的通路数, )(l ii a 为vi 到⾃⾝长度为 l 的回路数,∑∑==n i nj l ija11)( 为D 中长度为 l 的通路总数,∑=ni l iia1)( 为D 中长度为 l 的回路总数.D 中的通路及回路数(续)推论设Bl=A+A2+…+Al(l ≥1), 则Bl 中元素为D 中长度⼩于或等于l 的通路数,为D 中长度⼩于或等于l 的回路数. 例有向图D 如图所⽰, 求A, A2, A3, A4, 并回答问题:(1) D 中长度为1, 2, 3, 4的通路各有多少条?其中回路分别为多少条? (2) D 中长度⼩于或等于4的通路为多少条?其中有多少条回路?12100010()00010010A D=有向图的可达矩阵定义设D=为有向图, V={v1, v2, …, vn}, 令称(pij)n ?n 为D 的可达矩阵, 记作P(D), 简记为P. 性质:P(D)主对⾓线上的元素全为1.D 强连通当且仅当P(D)的元素全为1. 有向图的可达矩阵(续)例右图所⽰的有向图D 的可达矩阵为7.4 最短路径及关键路径⼀、本节主要内容最短路关键路线⼆、教学内容对于有向图或⽆向图G 的每条边,附加⼀个实数w(e),则称w(e)为边e 上的权. G 连同附加在各边上的实数,称为带权图.设带权图G=,G 中每条边的权都⼤于等于0.u,v 为G 中任意两个顶点,从u 到v 的所有通=1101110111110001P路中带权最⼩的通路称为u 到v 的最短路径.求给定两个顶点之间的最短路径,称为最短路径问题. 算法:Dijkstra(标号法){}()*()*1()*()()1()*1.2./5.i r r i i i i ir i r r j j j j j r i r v l v v v l v r p l l v v v l v r l v v p r T V r ∞==-j ij r r 如果顶点与v 不相邻,则w =为顶点到顶点最短路径的权,如果顶点获得了标号,则称顶点在第步获得了标号(永久性标号)3.为顶点到顶点最短路径的权的上界,如果顶点获得了标号,则称顶点在第步获得了t 标号(临时性标号)4.P 已经获得标号为第步通过集P 为第步未通过集例:求图中v0与v5的最短路径(0)*000(0)0(1)*(0)(1)*1010100,{},T {},1,2,3,4,5{},min {},T T {}(2)T j jj i j i v T l P l w j l l l P P t ∈=======?=-0012345j i i i i 第步(r=0):v 获得p 标号v v ,v ,v ,v ,v ,v 获得t 标号第1步(r=1):(1)求下⼀个p 标号的顶点,将标在顶点v 处,表明顶点v 获得p 标号.修改通过集和未通过集:v v 修改中各顶点的标1(1)(0)(1)*(2)*(1)(2)*2121(2)(1)(2)*2min{,}{},min {},T T {}(2)T min{,}j jj iij i j iv T j j iij ll lw l l l P P t l l l w ∈=+==?=-=+i i i i 号:第2步(r=2):(1)求下⼀个p 标号的顶点,将标在顶点v 处,表明顶点v 获得p 标号.修改通过集和未通过集:v v 修改中各顶点的标号:2.关键路径问题,(){/,}(){/,}D D D V E v V v x x V v x E v v x x V x v E v +=<>∈Γ=∈∧<>∈Γ=∈∧<>∈-设为⼀个有向图,,则为的后继元集为的先继元集定义:PERT 图设D=是n 阶有向带权图1. D 是简单图2. D 中⽆环路3. 有⼀个顶点出度为0,称为发点;有⼀个顶点⼊度为0,称为收点4. 记边的权为wij,它常常表⽰时间1. 最早完成时间:⾃发点v1开始,沿最长路径(权)到达vi 所需时间,称为vi 的最早完成时间,记为TE (vi ),i=1,2,…,nj 1i i j ij v ()234567TE(v )=0,v (1)TE(v )={(v )+w },1,2,,max TE(v )=max{0+1}=1;TE(v )=max{0+2,1+0}=2;TE(v )=max{0+3,2+2}=4;TE(v )=max{1+3,4+4}=8;TE(v )=max{2+4,8+1}=9;TE(v )=max{1+4,2+D i v i TE i n -∈Γ≠=显然的最早完成时间按如下公式计算:813784}=6;TE(v )=max{6+6,9+1}=12;v v v v 关键路径:从发点到收点的⼀条最长路径,2. 最晚完成时间:在保证收点vn 的最早完成时间不增加的条件下,⾃发点v1最迟到达vi 所需时间,称为vi 的最晚完成时间,记为TL (vi ).j n n i i j ij v ()876543TL(v )=TL(v ),v ()TL(v )={(v )-w },1,2,,min TL(v )=12;TL(v )=min{12-6}=6;TL(v )=min{12-1}=11;TL(v )=min{11-1}=10;TL(v )=min{10-4}=6;TL(v )=min{6-2,11-4,6-4}=2;TL(D i v i n TL i n∈Γ≠=+显然的最晚完成时间按如下公式计算:21v )=min{2-0,10-3,6-4}=2;TL(v )=min{2-1,2-2,6-3}=0;3. 缓冲时间:TS(vi)=TL(vi)- TE(vi) TS(v1)= TS(v3)= TS(v7)= TS(v8)=0 TS(v2)=2-1=1; TS(v4)=6-4=2; TS(v5)=10-8=2; TS(v6)=11-9=2。
第7章-图-CAL-FENGHAI.-(YICAI)-Company One1第7章图实验图的基本操作及应用一、实验目的1、熟悉图的基本概念,理解图的各种类型2、掌握图的邻接矩阵、邻接表的表示方法3、掌握图的两种遍历方法4、加深理解图的最小生成树的基本思想。
5、掌握图的最小生成树的生成方法和实现算法6、加深对图的理解,熟悉图的实际应用二、实验内容(一)验证实验1、图的邻接矩阵表示(二)设计实验1、图的遍历问题案例描述:已知8个城市的交通路线图如下图1所示,从沈阳出发,要到其他7个城市推销产品。
给出到达每一个城市的一组城市顺序。
图1:8个城市的交通路线图设计方案:图的遍历有深度优先遍历和广度优先遍历两种算法。
在这里我们利用数据结构中图的邻接矩阵存储方式以及图的深度优先遍历的算法来解决该问题。
结构定义:typedef char vextype[LEN];typedef int edgetype;typedef struct{ vexntype vex[LEN];edgetype arc[VEXN][VEXN];int vexn,arcn;}Mgraph;2、某公司拟建一个局域网,需要连接6栋楼(0,1,2,3,4,5),其地理分布如下图2所示,各边上的权值代表楼宇间距离。
设计要求:根据下图中的楼宇分布,设计出布线造价最小的局域网络图,要求连接所有的顶点,并且总的布线费用最低。
实验提示:要想布线造价最小,可将图中各顶点间的距离看作其费用。
这样就可以用Prim算法构造一棵最小生成树来解决问题。
图2 图2的邻接矩阵运行时输入数据及运行结果显示如下:Input vexnum,arcnum:6,10V1,v2,w=0,1,6V1,v2,w=0,2,5V1,v2,w=0,5,1V1,v2,w=1,5,5V1,v2,w=1,3,3V1,v2,w=2,5,5V1,v2,w=2,4,2V1,v2,w=3,5,6V1,v2,w=3,4,6V1,v2,w=4,5,4输出最小生成树中的边及其权值如下:(0,5)1(5,4)4(4,2)2(5,1)5(1,3)3参考程序:(一)验证实验1、图的邻接矩阵表示实验程序:#include "Stdio.h"#include "Conio.h"#include"stdio.h"#define MaxNum 50 //图的最大顶点数设为50typedef char VexType[7]; //图的顶点类型设为字符数组,2个字符长度typedef int EdgeType; //弧(边)的权值设为整型typedef struct {VexType V[MaxNum]; //一维数组存储顶点信息EdgeType E[MaxNum][MaxNum]; //二维数组表示邻接矩阵,存储边的信息int n,e; //顶点数和边数}MGraph; //图类型定义int Locate(MGraph *G,char vex[]) //确定顶点在图G中的位置,即在G->V中的序{int i;for(i=0;i<G->n;i++)if(strcmp(G->V[i],vex)==0)return i;}void CreateGraph(MGraph *G){int i,j,k;char vex1[3],vex2[3];//保存输入的顶点printf("\n输入图的顶点数和边数(用逗号分隔):");scanf("%d,%d",&(G->n),&(G->e));//输入顶点数和边数printf("输入图的顶点信息(最长2个字符):");for (i=0;i<G->n;i++){/*G->V[i][0]=G->V[i][1]=0;*/scanf("\n%s",G->V[i]); //输入n个顶点的标识信息,建立顶点数组}for (i=0;i<G->n;i++)for (j=0;j<G->n;j++)G->E[i][j]=0; //对邻接矩阵元素进行初始化printf("\n输入图中每条边所依附的两个顶点的标识信息:");for (k=0;k<G->e;k++) //输入e条边{printf("\n输入第%d条边的第1个顶点:",k+1);scanf("%s",vex1);printf("输入第%d条边的第2个顶点:",k+1);scanf("%s",vex2);// scanf("%s\n%s",vex1,vex2);i=Locate(G,vex1);j=Locate(G,vex2);// scanf("\n%d,%d",&i,&j); //输入每条边所依附的顶点在二维数组中的下标,建立邻接矩阵G->E[i][j]=1; //如果同时输入G->E[j][i]=1;,则是建立无向图的邻接矩阵}}void PrintGraph(MGraph *G)//打印图的顶点和边的信息{int i,j;printf("\n图中顶点个数为:%d",G->n);printf("\n图中边数为:%d",G->e);printf("\n图中顶点为:");for (i=0;i<G->n;i++)printf("%c%c ",G->V[i][0],G->V[i][1]);printf("\n图中边为:");for(i=0;i<G->n;i++)for(j=0;j<G->n;j++)if(G->E[i][j])printf("[%c%c,%c%c] ",G->V[i][0], G->V[i][1], G->V[j][0], G->V[j][1]);}main(){MGraph mg;CreateGraph(&mg);PrintGraph(&mg);}(二)设计实验1、图的遍历问题案例描述:已知8个城市的交通路线图如下图1所示,从沈阳出发,要到其他7个城市推销产品。
给出到达每一个城市的一组城市顺序。
#define NULL 0#define VEXN 30 //顶点的最大个数#define LEN 10 //城市名称的最大长度#include <stdio.h>typedef char vexntype[LEN]; //顶点数据类型typedef int edgetype; //边数据类型typedef struct{vexntype vex[VEXN];edgetype arc[VEXN][VEXN];int vexn,arcn; //顶点个数和边数}Mgraph; //图的邻接矩阵表示结构int visit[VEXN]; //遍历标志数组Mgraph City_Graph(){int i,j,k;Mgraph G;printf("\n input vex number");scanf("%d",&G.vexn); //输入顶点数目printf("input edge numbef:");scanf("%d",&G.arcn); //输入总边数printf("input %d vex information such as Shenyang Beijing and soon:\n",G.vexn);for(i=0;i<G.vexn;i++)scanf("%s",&G.vex[i]);for(i=0;i<G.vexn;i++)for(j=0;j<G.vexn;j++)G.arc[i][j]=0;for(k=0;k<G.arcn;k++) //输入各顶点距离{printf("input edge %d such as i,j:",k+1);scanf("%d,%d",&i,&j);while(i<1||i>G.vexn||j<1||j>G.vexn) //输入各顶点距离{printf("Error vexn Number,input(i,j)again:");scanf("%d,%d",&i,&j);}G.arc[i-1][j-1]=1;G.arc[j-1][i-1]=1;}return G;}void DFS_G(Mgraph G,int i) //输出深度优先遍历序列{int j;printf("%s,",G.vex[i]);visit[i]=1;for(j=0;j<G.vexn;j++)if((G.arc[i][j]==1)&&(!visit[j]))DFS_G(G,j);}main(){Mgraph G;G=City_Graph(); //调用输入顶点和边的函数printf("\nDFS:\n"); //调用查询最短路径函数DFS_G(G,0);}运行测试:<输入>Input vex number:8Input edge number:9Input 8 vex information such as Shenyang Beijing and so on:沈阳北京天津大连营口鞍山抚顺丹东(输入:每一个顶点回车)Input edge1 such as i,j:1,2(在英文状态下输入)Input edge1 such as i,j:1,3Input edge1 such as i,j:2,3Input edge1 such as i,j:4,5Input edge1 such as i,j:5,6Input edge1 such as i,j:6,7Input edge1 such as i,j:7,8Input edge1 such as i,j:1,6Input edge1 such as i,j:1,7<输出>DFS:沈阳北京天津鞍山营口大连抚顺丹东2、某公司拟建一个局域网,需要连接6栋楼(0,1,2,3,4,5),其地理分布如下图2所示,各边上的权值代表楼宇间距离。