8-5范氏方程

如何理解范德华方程式的概念范德华方程式是描述系统间分子间作用力的一个数学公式，在化学和物理学领域有着广泛的应用。

它由荷兰物理学家约翰·范德华在1873年提出，至今已经发展成为一种强大的理论工具，成为了许多分子间作用力研究的基础。

在分子间相互作用力的研究中，范德华方程式是必须的一项工具。

这个方程式的特点是简单明了，容易使用。

通过范德华方程式，我们可以描述分子间的相互作用力，进而推导出各种物理性质。

这些物理性质包括分子之间的吸引和斥力，热力学性质和其他重要参数。

通过对范德华方程式的分析和研究，我们能够更好地理解分子的特性以及它们之间的相互作用。

在范德华方程式中，两个分子之间的相互作用能量取决于它们之间的距离和分子的极性。

具体来说，如果相互作用分子的极性不同，则相互作用能量为吸引作用；如果相互作用分子极性相同，则相互作用能量为斥力作用。

在范德华方程式中，分子之间的相互作用能够量化，表现为一个数值，拥有非常高的准确度。

范德华方程式在实践应用中经常遇到的问题是需要考虑分子间的相互作用力和吸附现象。

在工业生产和化学实验中，分子之间的相互作用力和吸附现象往往是必须考虑的重要因素。

通过范德华方程式的研究可以得出这些物理现象的量化数据，这些数据可以帮助科学家更好地理解分子间作用和现象，并为他们的实验和生产提供指导。

除了应用方面，范德华方程式在基础物理学的发展中也占据着重要的地位。

在试图理解分子间相互作用力和物理现象的基本特征、规律的过程中，范德华方程式提供了一个理论框架，使得物理学家能够将它们的观察结果跟理论分析相联系起来。

范德华方程式可以帮助我们更好地理解分子的物理性质，并为我们进一步探索微观世界的规律提供支持。

总之，范德华方程式是描述分子间相互作用力的重要数学公式，具有广泛的实际应用价值和理论价值。

范德华方程式不仅可以为我们理解分子间作用力以及各种物理现象提供指导，同时也对我们探索微观世界的规律具有重要的意义。

范德华方程的名词解释在物理学中，范德华方程（van der Waals equation）是描述气体行为的方程之一。

它由荷兰物理学家约翰内斯·迪德里克·范德华于1873年提出，对于理解气体的物理特性和态变行为具有重要意义。

范德华方程包含了两个关键参数：气体的修正压缩因子和修正过程体积。

首先，让我们来了解范德华方程中的修正压缩因子。

在理想气体模型中，气体分子之间没有相互作用力，因此理想气体满足理想气体状态方程。

然而，在实际情况下，气体分子之间存在范德华力，这种吸引力会导致气体分子之间间距的减小。

因此，为了考虑这些相互作用，范德华引入了修正压缩因子（修正因子）b。

修正因子在范德华方程中起到了减少气体分子体积的作用，从而使方程更适用于实际气体的描述。

其次，我们来讨论范德华方程中的修正过程体积。

在理想气体模型中，气体分子被认为是点状物体，占据的体积可以忽略。

然而，气体分子的实际体积对气体行为有重要影响。

范德华方程通过引入修正过程体积（修正因子）a来考虑这一点，修正过程体积是气体分子之间的斥力引起的。

范德华方程的数学形式如下：[P + a(n/V)^2] [V - nb] = nRT其中，P表示气体的压强，V表示气体的体积，n表示气体的物质的量，R表示理想气体常数（值为8.314 J/(mol·K)），T表示气体的温度。

范德华方程中的a 和b表示气体的特性常数，不同气体具有不同的数值。

范德华方程提供了对气体行为更准确的描述，特别是在高压和低温情况下，对实际气体的描述更加准确。

它能够解释气体的液化和气体的临界点等现象，在工程和科学研究中具有广泛的应用。

除了范德华方程，还有其他描述气体的方程和模型，如理想气体状态方程、范德瓦尔斯方程等。

这些方程模型在不同的条件下具有不同的适用性。

范德华方程对于描述气体的非理想性质是一种重要的改进，并在相关领域中为理解气体的特性和行为提供了宝贵的工具。

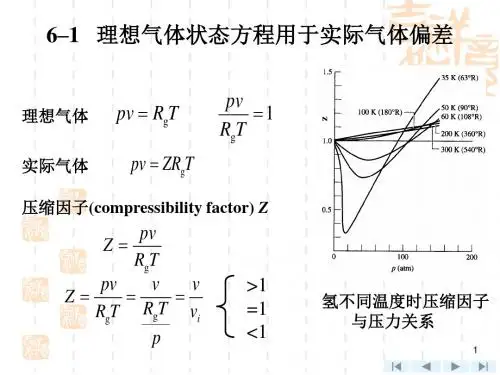
理想气体状态方程（又称理想气体定律、普适气体定律）是描述理想气体在处于平衡态时，压强、体积、物质的量、温度间关系的状态方程。

它建立在波义耳定律、查理定律、盖-吕萨克定律等经验定律上。

其方程为pV = nRT[1]。

这个方程有4个变量：p是指理想气体的压力，V为理想气体的体积，n表示气体物质的量，而T则表示理想气体的热力学温度；还有一个常量：R为理想气体常数。

可以看出，此方程的变量很多。

因此此方程以其变量多、适用范围广而著称，对常温常压下的空气也近似地适用。

[编辑] 应用一定量处于平衡态的气体，其状态由p、V和T刻划，表达这几个量之间的关系的方程称之为气体的状态方程，不同的气体有不同的状态方程。

但真实气体的方程通常十分复杂，而理想气体的状态方程具有非常简单的形式。

虽然完全理想的气体并不可能存在，但许多实际气体，特别是那些不容易液化、凝华的气体（如氦、氢气、氧气、氮气等，由于氦气不但体积小[2]、互相之间作用力小、也是所有气体中最难液化的[3]，因此它是所有气体中最接近理想气体的气体。

）在常温常压下的性质已经十分接近于理想气体。

此外，有时只需要粗略估算一些数据，使用这个方程会使计算变得方便很多。

[编辑] 计算气体的压强、体积、温度或其所含物质的量从数学上说，当一个方程中只含有1个未知量时，就可以计算出这个未知量。

因此，在压强、体积、温度和所含物质的量这4个量中，只要知道其中的3个量即可算出第四个量。

这个方程根据需要计算的目标不同，可以转换为下面4个等效的公式：求压力：求体积：求所含物质的量：求温度：[编辑] 化学平衡问题根据理想气体状态方程可以用于计算气体反应的化学平衡问题。

根据理想气体状态方程可以得到如下推论：温度、体积恒定时，气体压强之比与所含物质的量的比相同，即可得Ρ平/P始＝n平/n始温度、压力恒定时，气体体积比与气体所含物质的量的比相同，即V平/V始=n平/n始通过结合化学反应的方程，很容易得到化学反应达到平衡状态后制定物质的转化率。

几种常见的气态方程及适用条件作者：王子佳来源：《科学之友》2009年第30期摘要:本文阐述了几种常见的气态方程及其适用条件,并进行了实例计算。

关键词:常见气态方程;适用条件;实例计算中图分类号:O414.12 文献标识码:A 文章编号:1000-8136(2009)30-0003-021前言世界上许多物理学家都致力于气体的性质和规律的研究,并建立了多种反映气体的性质和规律的气态方程。

本文将把笔者知道的、了解的几种常见气态方程及其适用条件作简要的阐述。

2几种常见的气态方程及适用条件2.1理想气态方程及适用条件理想气态方程可写为:P理=式中,P理:理想气态方程计算的瓦斯压强,Pa;N:容器在中的瓦斯量,mol;R:摩尔气体恒量,8.31 Jmol-1k-1;T:瓦斯的热力学温度,K;T=273+t,t为瓦斯的摄氏温度,°C;V:贮存瓦斯容器的容积,m3。

理想气态方程的适用条件是:瓦斯分子压强和瓦斯分子体积压强相互平衡的情况。

实例计算:今有一个容器V为2 m3的容器,容器中贮存的瓦斯量N为25 108 mol,瓦斯温度T=300 K,(1)问瓦斯分子引力压强P引和瓦斯分子体积压强P体各是多少?(2)能否用理想气态方程来计算瓦斯的压强?(3)如果能,试用范氏气态方程来验证其计算结果的准确性。

解:(1)瓦斯分子引力压强P引为:P引= =35 618 000 Pa=35.618 MPa瓦斯分子体积压强P体为:P体==35 618 000 Pa=35.618 MPa(2)由计算结果可见,P引和P体相等,互相平衡,因此,可用理想气态方程来计算瓦斯的压强。

(3)理想气态方程计算的瓦斯压强P理为:P理=范氏气态方程计算的瓦斯压强P范为:P范==31 297 000 Pa=31.297 MPa由计算结果可见,P理与P范相等,所以,P理准确。

2.2引力压强方程及适用条件引力压强方程为:PK=式中,PK:引力压强方程计算的瓦斯压强,Pa;a:瓦斯分子引力常量,226×10-3 Nm4mol-2;K:引力压强系数,0≤KK的具体数值由下式确定:(1)式中,b:瓦斯分子体积常量,42.4×10-6 m3mol-1;其余的符号意义同前。

1.2 证明任何一种具有两个独立参量,T p 的物质，其物态方程可由实验测得的体胀系数α及等温压缩系数κT ，根据下述积分求得：()ln T V =αdT κdp -⎰ 如果11,T T pακ==，试求物态方程。

解：以,T p 为自变量，物质的物态方程为(),,V V T p =其全微分为.p TV V dV dT dp T p ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭ （1） 全式除以V ，有11.p TdV V V dT dp V V T V p ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭ 根据体胀系数α和等温压缩系数T κ的定义，可将上式改写为.T dV dT dp Vακ=- （2） 上式是以,T p 为自变量的完整微分，沿一任意的积分路线积分，有()ln .T V dT dp ακ=-⎰ （3） 若11,T T pακ==，式（3）可表为11ln .V dT dp T p ⎛⎫=- ⎪⎝⎭⎰ （4） 选择图示的积分路线，从00(,)T p 积分到()0,T p ，再积分到（,T p ），相应地体积由0V 最终变到V ，有000ln =ln ln ,V T p V T p - 即000p V pV C T T ==（常量）， 或.p V C T =（5） 式（5）就是由所给11,T T p ακ==求得的物态方程。

确定常量C 需要进一步的实验数据。

1.10 声波在气体中的传播速度为s p αρ⎛⎫∂= ⎪∂⎝⎭ 假设气体是理想气体，其定压和定容热容量是常量，试证明气体单位质量的内能u 和焓h 可由声速及γ给出：()21a a u u h h γγγ=+=+-200,-1 其中00,u h 为常量。

解：根据式（1.8.9），声速a 的平方为2v,a p γ= （1）其中v 是单位质量的气体体积。

理想气体的物态方程可表为,m pV RT m+= 式中m 是气体的质量，m +是气体的摩尔质量。

对于单位质量的气体，有 1v ,p RT m +=（2） 代入式（1）得2.a RT m γ+= （3）以,u h 表示理想气体的比内能和比焓（单位质量的内能和焓）。

⼭师物电热统答案——第⼆章2.1 已知在体积保持不变时，⼀⽓体的压强正⽐于其热⼒学温度. 试证明在温度保质不变时，该⽓体的熵随体积⽽增加.解：根据题设，⽓体的压强可表为(),p f V T = （1）式中()f V 是体积V 的函数. 由⾃由能的全微分 dF SdT pdV =--得麦⽒关系.T VS p V T = ? ? （2）将式（1）代⼊，有().T VS p p f V V T T=== ? ??????? （3）由于0,0p T >>，故有0TS V>. 这意味着，在温度保持不变时，该⽓体的熵随体积⽽增加.2.2 设⼀物质的物态⽅程具有以下形式：(),p f V T =试证明其内能与体积⽆关.解：根据题设，物质的物态⽅程具有以下形式：(),p f V T = （1）故有().Vp f V T= （2）但根据式（2.2.7），有,T VU p T p V T=- ? ??????? （3）所以()0.TU Tf V p V =-= ? （4）这就是说，如果物质具有形式为（1）的物态⽅程，则物质的内能与体积⽆关，只是温度T 的函数.2.3 求证： ()0;H S a p ??< ()0.US bV> 解：焓的全微分为.dH TdS Vdp =+ （1）令0dH =，得0.HS Vp T =-< ?（2）内能的全微分为.dU TdS pdV =- （3）令0dU =，得0.US p V T=> （4）2.4 已知0T UV= ，求证0.TU p ??=解：对复合函数(,)(,(,))U T P U T V T p = （1）求偏导数，有.T T TU U V p V p= ? ? （2）如果0TU V=，即有0.TU p = ? （3）式（2）也可以⽤雅可⽐⾏列式证明：(,)(,)(,)(,)(,)(,)T U U T p p T U T V T V T p T = ?=.T TU V V p =（2）2.5 试证明⼀个均匀物体的在准静态等压过程中熵随体积的增减取决于等压下温度随体积的增减.解：热⼒学⽤偏导数pS V描述等压过程中的熵随体积的变化率，⽤pT V描述等压下温度随体积的变化率. 为求出这两个偏导数的关系，对复合函数(,)(,(,))S S p V S p T p V == （1）求偏导数，有.p p p p pC S S T T V T V T V== ? ? ? ? （2）因为0,0p C T >>，所以p S V的正负取决于pT V的正负. 式（2）也可以⽤雅可经⾏列式证明：(,)(,)(,)(,)(,)(,)P S S p V V p S p T p T p V p= ?=P PS T T V = ? ? （2）2.6 试证明在相同的压强降落下，⽓体在准静态绝热膨胀中的温度降落⼤于在节流过程中的温度降落.解：⽓体在准静态绝热膨胀过程和节流过程中的温度降落分别由偏导数S T p和HT p ??描述. 熵函数(,)S T p 的全微分为 .P TS S dS dT dp T p=+ ? ?在可逆绝热过程中0dS =，故有.TP p SS V T p T T S p C T=-=???? （1）最后⼀步⽤了麦⽒关系式（2.2.4）和式（2.2.8）.焓(,)H T p 的全微分为.P TH H dH dT dp T p=+ ? ?在节流过程中0dH =，故有.T PpH PH V T V p T T H p C T- ? ??????????=-= ??????? ???? （2）最后⼀步⽤了式（2.2.10）和式（1.6.6）. 将式（1）和式（2）相减，得0.pSH T T Vp p C -=> ? ?（3）所以在相同的压强降落下，⽓体在绝热膨胀中的温度降落⼤于节流过程中的温度降落. 这两个过程都被⽤来冷却和液化⽓体.由于绝热膨胀过程中使⽤的膨胀机有移动的部分，低温下移动部分的润滑技术是⼗分困难的问题，实际上节流过程更为常⽤.但是⽤节流过程降温，⽓体的初温必须低于反转温度. 卡⽪查（1934年）将绝热膨胀和节流过程结合起来，先⽤绝热膨胀过程使氦降温到反转温度以下，再⽤节流过程将氦液化.2.7 实验发现，⼀⽓体的压强p 与体积V 的乘积以及内能U 都只是温度的函数，即(),().pV f T U U T ==试根据热⼒学理论，讨论该⽓体的物态⽅程可能具有什么形式.解：根据题设，⽓体具有下述特性：(),pV f T = （1）().U U T = （2）由式（2.2.7）和式（2），有0.T VU p T p V T =-= ? ? （3）⽽由式（1）可得.Vp T df T T V dT= （4）将式（4）代⼊式（3），有Tf dT= 或.df dT f T= （5）积分得ln ln ln ,f T C =+或,pV CT = （6）式中C 是常量. 因此，如果⽓体具有式（1），（2）所表达的特性，由热⼒学理论知其物态⽅程必具有式（6）的形式. 确定常量C 需要进⼀步的实验结果.00000000000000002222,V T VC S S S T T T V V T T V T===0000000000 2.9 证明范⽒⽓体的定容热容量只是温度T 的函数，与⽐体积⽆关.解：根据习题2.8式（2）22,V T VC p T V T= ? ??????? （1）范⽒⽅程（式（1.3.12））可以表为22.nRT n a p V nb V =-- （2）由于在V 不变时范⽒⽅程的p 是T 的线性函数，所以范⽒⽓体的定容热容量只是T 的函数，与⽐体积⽆关.不仅如此，根据2.8题式（3）0202(,)(,),VV V V Vp C T V C T V T dV T ??=+ （3）我们知道，V →∞时范⽒⽓体趋于理想⽓体. 令上式的0V →∞，式中的0(,)V C T V 就是理想⽓体的热容量. 由此可知，范⽒⽓体和理想⽓体的定容热容量是相同的.顺便提及，在压强不变时范⽒⽅程的体积V 与温度T 不呈线性关系. 根据2.8题式（5）22,V T VC p V T = ? ? （2）这意味着范⽒⽓体的定压热容量是,T p 的函数.2.15 计算热辐射在等温过程中体积由1V 变到2V 时所吸收的热量.解：根据式（1.14.3），在可逆等温过程中系统吸收的热量为.Q T S =? （1）式（2.6.4）给出了热辐射的熵函数表达式3S aT V =（2）所以热辐射在可逆等温过程中体积由1V 变到2V 时所吸收的热量为()4214.3Q aT V V =- （3）2.16 试讨论以平衡辐射为⼯作物质的卡诺循环，计算其效率. 解：根据式（2.6.1）和（2.6.3），平衡辐射的压强可表为41,3p aT = （1）因此对于平衡辐射等温过程也是等压过程. 式（2.6.5）给出了平衡辐射在可逆绝热过程（等熵过程）中温度T 与体积V 的关系3().T V C =常量（2）将式（1）与式（2）联⽴，消去温度T ，可得平衡辐射在可逆绝热过程中压强p 与体积V 的关系43pV C '=（常量）. （3）下图是平衡辐射可逆卡诺循环的p V -图，其中等温线和绝热线的⽅程分别为式（1）和式（3）.下图是相应的T S -图. 计算效率时应⽤T S -图更为⽅便.在由状态A 等温（温度为1T ）膨胀⾄状态B 的过程中，平衡辐射吸收的热量为()1121.Q T S S =- （4）在由状态C 等温（温度为2T ）压缩为状态D 的过程中，平衡辐射放出的热量为()2221.Q T S S =- （5）循环过程的效率为()()2212211211111.T S S Q T Q T S S T η-=-=-=-- 2.19 已知顺磁物质遵从居⾥定律：().CM H T=居⾥定律若维物质的温度不变，使磁场由0增⾄H ，求磁化热.解：式（1.14.3）给出，系统在可逆等温过程中吸收的热量Q 与其在过程中的熵增加值?S 满⾜.Q T S =? （1）在可逆等温过程中磁介质的熵随磁场的变化率为（式（2.7.7））0.T HS m H T µ= ? ??????? （2）如果磁介质遵从居⾥定律(),CVm H C T=是常量（3）易知2Hm CV H T T =- ?, （4）所以0.TCV H S H T µ=- 2（5）在可逆等温过程中磁场由0增⾄H 时，磁介质的熵变为202.2HTCV H S S dH H T µ==-（6）吸收的热量为20.2CV H Q T S Tµ=?=-20.下⾯回到本题的求解. 由式（3）知，在超导体内部恒有,M H =- （16）这是超导体独特的磁物态⽅程. 通常的磁物态⽅程(,,)0f H M T =对超导体约化为式（16）.根据式（16），有0,0.HMM T H T = ?= ? （17）（a ）考虑单位体积的超导体. 式（2.7.2）给出准静态过程中的微功为0?.W HdM µ= （18）与简单系统的微功?W pdV =-⽐较知在代换0,p H V M µ→→下，简单系统得到的热⼒学关系同样适⽤于超导体. 2.9题式（2）给出22.V T VC p T V T = ? ? 超导体相应的热⼒学关系为2020.M T MC H T ΜT µ=-= ? ??????? （19）最后⼀步⽤了式（17）. 由式（19）可知，M C 与M ⽆关，只是T 的函数.（b ）相应于简单系统的（2.2.7）式,T VU p T p V T=- ? ??????? 超导体有000,T MU ΗT H M ΜT µµµ=-+=- ? ? （20）其中第⼆步⽤了式（17）.以,T M 为⾃变量，内能的全微分为0.M TM U U dU dT dMT M C dT MdM µ=+ ? ???????=- 积分得超导体内能的积分表达式为200.2M M U C dT U µ=-+? （21）第⼀项是不存在磁场时超导体的内能，第⼆项代表外磁场使超导体表⾯感⽣超导电流的能量. 第⼆项是负的，这是式（16）的结果，因此处在外磁场中超导体的内能低于⽆磁场时的内能. （c ）相应于简单系统的（2.4.5）式0,V V C p S dT dV S T T=++超导体有00M MC ΗS dT dM S T T µ=-+ ??0,MC dT S T=+?（22）第⼆步⽤了式（17）. 这意味着，处在外磁场中超导体表⾯的感⽣超导电流对熵（⽆序度）没有贡献.。

范德华方程范德华方程范德华方程是范德瓦耳斯方程的另一种翻译，简称范氏方程，是荷兰物理学家范德瓦耳斯（van der Waals，又译“范德华”、“凡德瓦耳”）于1873年提出的一种实际气体状态方程。

1范德华方程范德华方程是范德瓦耳斯方程的另一种翻译，简称范氏方程，是荷兰物理学家范德瓦耳斯（van der Waals，又译“范德华”、“凡德瓦耳”）于1873年提出的一种实际气体状态方程。

范氏方程是对理想气体状态方程的一种改进，特点在于将被理想气体模型所忽略的的气体分子自身大小和分子之间的相互作用力考虑进来，以便更好地描述气体的宏观物理性质。

2适用范围范氏方程对气-液临界温度以上流体性质的描写优于理想气体方程。

对温度稍低于临界温度的液体和低压气体也有较合理的描述。

但是，当描述对象处于状态参量空间(P,V,T)中气液相变区（即正在发生气液转变）时，对于固定的温度，气相的压强恒为所在温度下的饱和蒸气压，即不再随体积V（严格地说应该是单位质量气体占用的体积，即比容）变化而变化，所以这种情况下范氏方程不再适用。

3与理想气体方程模拟结果的比较3.1低压状况在气体压强不太高的情况下，以下事实成立：排斥体积b 的影响相对V 而言极小，可以忽略；以二氧化碳（CO2）为例，在标准状况（0°C，1标准大气压）下，一摩尔CO2体积V 为22414 cm³，而相应的b= 43 cm³，比V 小3个数量级；分子间的距离足够大，a/V² 项完全可以视为0；譬如在一大气压下二氧化碳气体的a/V² 值只有7‰。

所以此时理想气体方程是范氏方程（也是对实际气体行为的）的一个良好近似。

分别用理想气体方程和范德瓦耳斯方程模拟的二氧化碳气体70°C时的p-V等温线3.2中高压状况随着气体压力的增加，范氏方程和理想气体方程结果的差别会变得十分明显（左图为CO2分别用理想气体方程和范德瓦耳斯方程模拟的p-V等温线，温度70°C）：在压强为5000~15000kPa（50~150标准大气压）的中压区，由于体积被“压小”导致分子间距靠近，分子间的引力（表现为a/V² 项）变得不可忽略。

范德华(J.D.vanderwaals1837—1923)荷兰物理学家。

青年时代家境贫寒，无力入学读书。

在工作之余，刻若钻研，自学成才，1874年他的论文“论液态和气态的连续性”引起了学术界的关注。

并获得了莱顿大学的博士学位。

经过研究，他认识到如果假定气体分子不占有体积，而且分子之间不存在引力，则可从气体分子运动论得出理想气体的状态方程，但是，这两项假定不符合事实。

1881年，他给这个方程引入两个参量，分别表示分子的大小和引力，得出一个更准确的方程即范德华方程。

他还研究了毛细作用，对附着力进行了计算。

他在研究物质三态(气、液、固)相互转化的条件时，推导出临界点的计算公式，计算结果与实验结果相符。

1877—1910年任阿姆斯特丹大学教授。

1910年因研究气态和液态方程获诺贝尔物理学奖。

原子间和分子间的吸引力被命名为范德华力。

1873年他最先假设了这种力，以研究关于真实气体的理论范德华方程范德华方程是范德瓦耳斯方程的另一种翻译，简称范氏方程，是荷兰物理学家范德瓦耳斯（van der Waals，又译“范德华”、“凡德瓦耳”）于1873年提出的一种实际气体状态方程。

范氏方程是对理想气体状态方程的一种改进，特点在于将被理想气体模型所忽略的的气体分子自身大小和分子之间的相互作用力考虑进来，以便更好地描述气体的宏观物理性质。

范德华方程式具体形式为更常用的形式为(N=摩尔数)式中p为气体的压强a'为度量分子间重力的唯象参数b'为单个分子本身包含的体积v为每个分子平均占有的空间大小（即气体的体积除以总分子数量）; k为波兹曼常数T绝对温度在第二个方程式里V为总体积a为度量分子间重力的参数b为1摩尔分子本身包含的体积之和b= NAb', R为普适气体常数NA为阿伏加德罗常数. 下表列出了部分气体的a，b的值范德华方程常用的形式(N=摩尔数)在一般形式的范氏方程中，常数a和b 因气体/流体种类而异，但我们可以通过改变方程的形式，得到一种适用于所有气体/流体的普适形式。

范德华方程常数范德华方程常数是描述非理想气体行为的重要参数之一。

它是根据实验数据拟合得到的，可以用来衡量气体分子间的相互作用程度。

范德华方程常数包括范德华吸引常数（a）和范德华斥力常数（b），它们对应了气体分子间的吸引力和斥力。

范德华方程常数的引入是为了修正理想气体方程，使其更加适用于实际气体的行为。

理想气体方程假设气体分子之间没有相互作用，而实际气体分子之间存在吸引力和斥力，因此需要引入修正项。

范德华方程可以写为：P = (nRT)/(V - nb) - a(n/V)^2其中，P表示气体的压强，n表示气体的物质的量，R表示气体常数，T表示气体的温度，V表示气体的体积。

范德华方程常数a和b可以根据实验数据进行拟合得到。

范德华吸引常数a表示气体分子之间的吸引力，它的值越大，吸引力越强。

范德华斥力常数b表示气体分子之间的斥力，它的值越大，斥力越强。

范德华方程常数的值与气体的性质有关。

不同气体的分子间相互作用不同，因此它们的范德华方程常数也不同。

例如，极性分子之间的相互作用较强，其范德华方程常数的值较大；而非极性分子之间的相互作用较弱，其范德华方程常数的值较小。

范德华方程常数的应用非常广泛。

在化学工程领域，它常被用来描述气体的物理性质，如压力、密度、温度等。

在化学反应工程中，范德华方程常数的值可以用来预测气体的行为，从而优化反应条件和改进工艺。

范德华方程常数还可以用来计算气体的偏差因子（压缩因子），从而更准确地描述气体的行为。

偏差因子是实际气体与理想气体之间的差异，它的值与范德华方程常数密切相关。

范德华方程常数是描述气体分子间相互作用的重要参数。

通过引入范德华方程常数，可以修正理想气体方程，使其更适用于实际气体的行为。

范德华方程常数的值与气体的性质有关，不同气体的范德华方程常数不同。

范德华方程常数在化学工程和化学反应工程中有着广泛的应用，可以用来描述气体的物理性质，预测气体的行为，以及计算偏差因子等。