高中物理 范德瓦尔斯方程与真实气体状态研究

气体状态方程的推导与应用气体状态方程是描述气体在不同条件下的状态的数学表达式。

它是理解气体行为和性质的基础，在物理、化学以及工程领域有着广泛的应用。

本文将对气体状态方程的推导和应用进行探讨。

一、气体状态方程的推导气体状态方程是通过实验观测和理论推导建立起来的。

它主要有三个常见形式：理想气体状态方程、范德瓦尔斯状态方程和实际气体状态方程。

1. 理想气体状态方程理想气体状态方程是描述理想气体行为的基本方程。

理想气体指的是分子间相互作用力可以忽略不计的气体。

根据气体动力学理论，其推导可由以下步骤得到：首先，假设气体分子为点状，分子间碰撞是完全弹性的。

其次，根据动量守恒定律和实验观测，推导出理想气体的压强与温度、体积之间的关系。

最终得到理想气体状态方程为：PV = nRT。

其中，P为气体的压强，V为气体的体积，n为气体的摩尔数，R为气体常数，T为气体的温度。

2. 范德瓦尔斯状态方程理想气体状态方程假设了气体分子间相互作用力可以忽略不计，但在某些情况下，气体分子之间存在相互吸引或斥力，这时需要使用范德瓦尔斯状态方程。

范德瓦尔斯状态方程是对理想气体状态方程的修正。

它考虑了气体分子之间的相互作用力，通过引入修正因子a和b得到。

范德瓦尔斯状态方程为：（P + a/V^2）(V - b) = nRT。

其中，a和b是由实验数据拟合得到的常数。

3. 实际气体状态方程实际气体状态方程是对实际气体行为进行描述的方程。

实际气体指的是存在分子间相互作用力的气体。

由于实际气体的分子间相互作用复杂，无法通过简单的理论推导得到精确的状态方程。

常用的实际气体状态方程有范德瓦尔斯状态方程、特征方程等。

这些方程都是通过实验数据和统计方法获得的近似表达式，可以较好地描述实际气体的状态行为。

二、气体状态方程的应用气体状态方程在科学研究和工程实践中有着广泛的应用。

以下列举其中的一些应用：1. 研究气体性质：通过气体状态方程可以计算气体的物理性质，如压强、体积、温度等。

气体状态方程气体是一种具有一定体积的物质，其分子之间的距离相对较大，分子之间存在较弱的相互作用力。

为了研究气体的性质和行为，科学家们提出了气体状态方程，用来描述气体的状态和性质。

本文将介绍三种常见的气体状态方程：理想气体状态方程、范德瓦尔斯气体状态方程和普朗克气体状态方程。

一、理想理想气体状态方程是最简单也是最常用的气体状态方程。

根据理想气体状态方程，气体的体积、温度和压强之间有简单的数学关系，表达式为：PV = nRT其中，P表示气体的压强，V表示气体的体积，n表示气体的物质的量，R表示气体常数，T表示气体的温度。

理想气体状态方程的推导基于以下两个假设：气体分子之间无相互作用力，气体分子的体积可以忽略不计。

在满足这两个假设的情况下，理想气体状态方程适用于大多数实际气体，在低压和高温下更加可靠。

二、范德瓦尔斯范德瓦尔斯气体状态方程是对理想气体状态方程的修正和拓展。

范德瓦尔斯方程考虑了气体分子之间的相互作用力和气体分子的体积，表达式为：(P + a * (n / V)^2) * (V - nb) = nRT,其中，P表示气体的压强，V表示气体的体积，n表示气体的物质的量，R表示气体常数，T表示气体的温度，a和b分别为范德瓦尔斯常数。

范德瓦尔斯方程中的a项代表吸引力，b项代表体积校正。

范德瓦尔斯方程更适用于高压和低温下的气体，可以更准确地预测实际气体的行为。

三、普朗克普朗克气体状态方程是对高度离子化的气体（如等离子体）状态的描述。

普朗克方程使用以下表达式：PV = aT^(3/2) * exp(b / T),其中，P表示气体的压强，V表示气体的体积，T表示气体的温度，a和b为普朗克常数。

普朗克方程适用于高温下离子化气体的状态描述，可以更好地解释等离子体的性质和行为。

小结气体状态方程是描述气体状态和性质的数学表达式。

理想气体状态方程是最常用的气体状态方程，适用于大多数实际气体。

范德瓦尔斯方程修正了理想气体状态方程的不足，并适用于高压和低温下的气体。

气体状态方程与实际气体行为的修正气体状态方程是描述气体性质和行为的一组等式，其中最常见的是理想气体状态方程。

然而，理想气体状态方程只适用于低压、高温条件下的气体，而不适用于实际气体的行为。

为了更准确地描述实际气体的性质和行为，科学家提出了多种修正的气体状态方程。

修正一：范德瓦尔斯方程范德瓦尔斯方程是最早用于修正理想气体状态方程的方程之一。

它考虑了气体分子之间的吸引力和排斥力，并添加了修正因子。

范德瓦尔斯方程的形式如下：（P + a(n/V)²)(V - nb) = nRT其中，P是气体的压强，V是气体的体积，n是气体的摩尔数，R是气体常数，T是气体的温度。

a和b是与气体性质有关的常数。

修正二：本塞方程本塞方程是对理想气体状态方程的另一种修正。

它考虑了气体分子之间的相互作用和非理想性。

本塞方程的形式如下：P = nRT/(V - nb) - a(n/V)²与范德瓦尔斯方程类似，本塞方程也包含了修正因子a和b，以调整理想气体状态方程的不准确之处。

修正三：压缩因子压缩因子是描述气体行为的一个重要参数，用Z表示。

对于理想气体来说，其压缩因子始终为1。

然而，对于实际气体，压缩因子通常不是恒定的，而是与温度、压强和摩尔体积有关。

实际气体的压缩因子可以通过实验或计算得到。

当压缩因子大于1时，表示气体分子之间的相互作用较强，其体积大于理想气体预测值；当压缩因子小于1时，则表示气体分子之间的相互作用较弱，其体积小于理想气体预测值。

修正四：德拜方程德拜方程是一种修正范德瓦尔斯方程的模型，它对气体的非理想性进行了更加精确的描述。

德拜方程的形式如下：P(V - b) = RT + (a/√T)(V + β)其中，β是与气体分子之间相互作用有关的常数。

德拜方程考虑了气体分子的运动和相互碰撞对气体性质的影响，使得在高压和低温条件下，德拜方程能更好地描述实际气体的行为。

总结：气体状态方程是描述气体行为的基本方程，然而由于理想气体状态方程的局限性，科学家对其进行了多种修正。

理想气体(范德瓦尔斯方程)实验报告范文大物实验报告一、实验名称：利用Mathcad对范德瓦尔斯方程进行分析二、实验内容和目的：学会使用Mathcad，分析范德瓦尔斯理想气体状态方程三、实验原理：(1)研究实际气体性质首先要求得出精确的状态方程式。

对实际气体状态方程己作了百余年的研究，得到了许多不同形式的方程。

得出状态方程有两种方法：一是直接利用由实验得到的各种热系数数据，按热力学关系组成状态方程。

二是从理论分析出发，考虑气体分子运动的行为而对理想气体状态方程引入一些常数加以修正，得出方程的形式，引入常数的值则根据实验数据确定。

(2)1873年范德瓦尔斯针对理想气体模型的两个假定（分子自身不占有体积；分子之间不存在相互作用力），考虑了分子自身占有的体积和分子间的相互作用力，对理想气体状态方程进行了修正。

分子自身占有的体积使其自由活动空间减小，在相同温度下分子撞击容器壁的频率增加，因而压力相应增大。

如果用Vmb表示每摩尔气体分子自由活动的空间，参照理想气体状态方程，气体压力应为pRT。

另一方面，分子间的相互吸引力使分子撞击容器壁面的力量减弱，从而使气体Vmb压力减小。

压力减小量与一定体积内撞击器壁的分子数成正比，又与吸引它们的分子数成正比，这两个分子数都与气体的密度成正比。

因此，压力减小量应与密度的平方成正比，也就是与摩尔体积的平方成反比，用a表示。

可以导出方程2vm(pa)(Vmb)RT2Vm这就是范德瓦尔斯导出的状态方程式，称为范德瓦尔斯状态方程式。

它在理想气体状态方程的基础上又引入两个常数a(mPa/mol)、b(m/mol)做范德瓦尔斯常数，对原方程进行修正。

(3)范德瓦尔斯方程的引出，是从理论分析出发导出气体状态方程的一个典型例子。

范德63瓦尔斯方程只不过是用两个常数很粗略地考虑了气体内分子运动的行为，所以还不能精确地表述气体的pvt关系。

但是，它为用理论方法研究状态方程开拓了道路。

特别是它在定性上能反映出物质气—液相变的性质。

对范德瓦耳斯气体的热力学函数及热容量的研究范德瓦耳斯气体是一种理想气体的延伸，它在描述实际气体的热力学性质方面更准确。

本文将对范德瓦耳斯气体的热力学函数及热容量进行研究，并探讨范德瓦耳斯方程的应用。

1.范德瓦耳斯气体的热力学函数：范德瓦耳斯气体可以用以下方程描述：P(V-b)=nRT其中，P为气体的压强，V为气体的体积，n为气体的物质的量，R为气体常数，T为气体的温度，b为修正系数。

从这个方程中可以得到范德瓦耳斯气体的热力学函数。

首先，我们可以计算出范德瓦耳斯方程的状态方程：PV=nRT/(V-b)然后，根据理想气体的状态方程，可以知道热力学函数U与范德瓦耳斯方程的关系：dU = C_vdT = TdS - PdV其中，C_v为定容热容量，T为温度，S为熵，dU表示内能的微分。

将前面推导的范德瓦耳斯方程代入上述等式，可以得到范德瓦耳斯气体的热力学函数：dU = C_vdT = TdS - (nRT)/(V - b)dV2.范德瓦耳斯气体的热容量：根据上一节的推导，范德瓦耳斯气体的定容热容量C_v可以表示为：C_v=T(∂S/∂T)V现在来计算这个偏导数。

假设范德瓦耳斯气体满足简单的状态方程：P = nkT其中，k为玻尔兹曼常数。

由于S与V无关，我们可以得到：dS=(∂S/∂T)VdT将以上两式代入定容热容量的表达式中：C_v = T(dS/dT)V = T(1/T)kndT从而可以化简为：C_v = kn即范德瓦耳斯气体的定容热容量与物质的量成正比。

3.范德瓦耳斯方程的应用：范德瓦耳斯方程可以广泛应用于研究气体的行为和性质，特别是高压下的气体。

它可以用于计算气体的物质的量、压强、温度和体积之间的关系。

通过范德瓦耳斯方程，我们可以定量地描述气体的压力、体积和温度之间的关系。

例如，在常温常压下，我们可以计算气体的物质的量。

另外，范德瓦耳斯方程还可以用于计算气体的体积在不同压力和温度下的变化。

总结：本文对范德瓦耳斯气体的热力学函数及热容量进行了研究。

气体状态方程气体的状态可以通过气体状态方程来描述和计算。

气体状态方程是研究气体性质和行为的基础，它描述了气体的压力、体积和温度之间的关系。

在本文中，我将详细介绍三种常见的气体状态方程：理想气体状态方程、范德瓦尔斯气体状态方程和实际气体状态方程。

一、理想理想气体状态方程是最简单的气体状态方程，适用于低密度、高温、常压条件下的气体。

根据理想气体状态方程，气体的压力与体积成反比，与温度成正比。

其数学表达式为：PV = nRT其中，P代表气体的压力，V代表气体的体积，n代表气体的物质量，R代表气体常数，T代表气体的温度（绝对温度）。

理想气体状态方程揭示了气体状态之间的定量关系，可以用于计算气体的各项性质。

然而，理想气体状态方程只适用于理想气体，不考虑气体分子之间的相互作用和体积以及温度的变化对气体行为的影响。

二、范德瓦尔斯范德瓦尔斯气体状态方程是对理想气体状态方程的修正和拓展。

范德瓦尔斯气体状态方程考虑了气体分子之间的相互作用和气体分子的体积，并引入了修正因子。

其数学表达式为：(P + a/V^2)(V - b) = nRT其中，a和b为修正常数，与气体的性质有关。

范德瓦尔斯气体状态方程能够更准确地描述气体的行为，特别适用于高密度、低温、高压条件下的气体。

三、实际实际气体状态方程是更加精确地描述气体性质和行为的数学模型。

实际气体状态方程基于统计力学和热力学原理，考虑了气体分子之间的相互作用、体积的可压缩性以及温度对气体性质的影响。

常见的实际气体状态方程包括范德瓦尔斯方程的修正版本（如范德瓦尔斯-柯克伍德方程）和其他复杂的方程模型（如德拜-亥伯和魏兰德方程）。

这些方程模型在不同条件下对气体性质的计算更加准确，但由于其复杂性，通常只在科学研究和工程应用中使用。

总结气体状态方程是描述气体性质和行为的重要工具。

理想气体状态方程适用于低密度、高温、常压条件下的气体；范德瓦尔斯气体状态方程对气体分子相互作用和体积进行修正；而实际气体状态方程更加精确地描述了气体性质和行为。

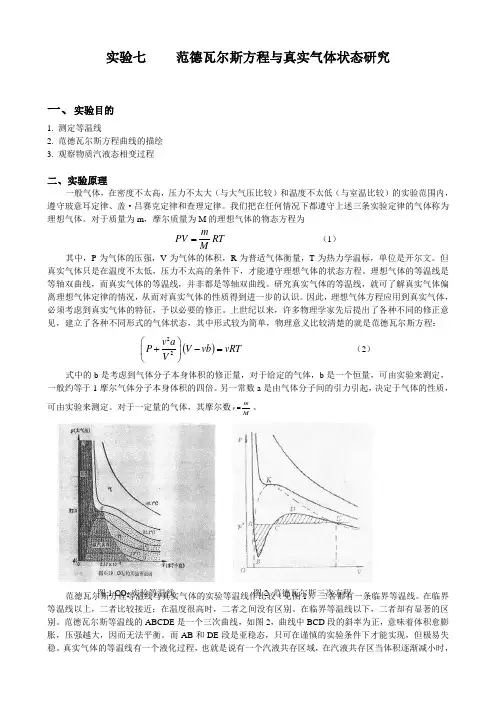
实验七范德瓦尔斯方程与真实气体状态研究一、实验目的1. 测定等温线2. 范德瓦尔斯方程曲线的描绘3. 观察物质汽液态相变过程二、实验原理一般气体，在密度不太高，压力不太大（与大气压比较）和温度不太低（与室温比较）的实验范围内，遵守玻意耳定律、盖·吕赛克定律和查理定律。

我们把在任何情况下都遵守上述三条实验定律的气体称为理想气体。

对于质量为m ，摩尔质量为M 的理想气体的物态方程为m PV RT M= （1） 其中，P 为气体的压强，V 为气体的体积，R 为普适气体衡量，T 为热力学温标，单位是开尔文。

但真实气体只是在温度不太低，压力不太高的条件下，才能遵守理想气体的状态方程。

理想气体的等温线是等轴双曲线，而真实气体的等温线，并非都是等轴双曲线。

研究真实气体的等温线，就可了解真实气体偏离理想气体定律的情况，从而对真实气体的性质得到进一步的认识。

因此，理想气体方程应用到真实气体，必须考虑到真实气体的特征，予以必要的修正。

上世纪以来，许多物理学家先后提出了各种不同的修正意见，建立了各种不同形式的气体状态，其中形式较为简单，物理意义比较清楚的就是范德瓦尔斯方程：()22v a P V vb vRT V ⎛⎫+-= ⎪⎝⎭ （2） 式中的b 是考虑到气体分子本身体积的修正量，对于给定的气体，b 是一个恒量，可由实验来测定，一般约等于1摩尔气体分子本身体积的四倍。

另一常数a 是由气体分子间的引力引起，决定于气体的性质，可由实验来测定。

对于一定量的气体，其摩尔数M mv =。

范德瓦尔斯方程等温线与真实气体的实验等温线作比较（见图1），二者都有一条临界等温线。

在临界等温线以上，二者比较接近；在温度很高时，二者之间没有区别。

在临界等温线以下，二者却有显著的区别。

范德瓦尔斯等温线的ABCDE 是一个三次曲线，如图2，曲线中BCD 段的斜率为正，意味着体积愈膨胀，压强越大，因而无法平衡。

而AB 和DE 段是亚稳态，只可在谨慎的实验条件下才能实现，但极易失图1 CO 2实验等温线 图2 范德瓦尔斯三次方程稳。

范德瓦耳斯方程的气体动理论推导荷兰物理学家范德瓦耳斯（Johannes Diderik Van der Waals，1837—1923）改进了气体的状态方程，把分子间的作用力和分子的有限体积放进方程中去。

他论证了，分子间距离较远时，它们间必定存在吸引力，这一作用附加到容器壁施加的压强上去。

他进一步提供论据，假设附加产生的压强反比于气体比容的平方。

还有，由于分子占有体积，它们可利用的空间必须减少，或者说得更明白些，减少的总体积就正比于分子在相互接触时所占有的体积。

于是一摩尔真实气体的状态方程变成(p+an2/V2)(V-nb)=RT。

这简单方程包含两个常数，即a和b，对于每一种物质它们可由实验确定。

R是普适气体数学。

1873 年在博士论文《论气态和液态的连续性》中考虑了分子体积和分子间吸力的影响，推出了著名的物态方程：(p+a/V2)（V－b）＝RT 后来人们称之为范德瓦耳斯方程。

他还导出了b 是分子体积的4 倍。

这个方程不仅能解释安德纽斯的实验结果及J．汤姆生的见解，而且能从常数a、b 值计算出临界参数，这对“永久气体”液化的理论起了指导作用。

下面以理想气体状态方程为基础，推导范氏方程。

若把气体视为由体积无限小、相互之间无作用力的分子组成，这种模型便是理想气体模型，与其相对应的状态方程是：p=kT/V.若抛弃前一个的假设，把组成气体的分子视为有一定大小的刚性球（其半径称为范德瓦尔斯半径），用b 表示这些“球”的体积，上面的方程便改写为：p=kT/(V-b).在这里，每个分子的“占有体积”v 被所谓“排斥体积”v - b 代替，反映了分子在空间中不能重叠。

若气体被压缩至体积接近分子体积之和（即分子间空隙v - b 趋向于0），那么其压强将趋于无穷大。

下一步，我们考虑原子对之间的引力。

引力的存在会使分子的平均亥姆霍兹自由能下降，减少量正比于流体的密度。

但压强的大小满足热力学关系。

综述：范德瓦耳斯方程的产生是这样的：先由范德瓦耳斯提出假设，再通过计算证明假设的成立，因此当初方程的产生并不是由于数学推导，而是一种经验性的假设，通过计算，符合事实，便成为一个结论。

物态方程与实际气体与范德瓦尔斯方程物态方程是描述物质在不同状态下的性质和相互关系的数学等式。

它对于研究气体特性以及工程应用非常重要。

范德瓦尔斯方程是一种修正的物态方程，可以更准确地描述理想气体与实际气体之间的差异。

一、理想气体与实际气体理想气体是指在一定温度和压力下，分子之间的相互作用可以忽略的气体。

对于理想气体，物态方程可简化为PV = nRT（其中P为压力，V为体积，n为分子的摩尔数，R为气体常数，T为温度）。

然而，实际气体在高压和低温条件下，分子之间的吸引力和排斥力会显著影响其行为，导致物态方程不能完全适用。

二、范德瓦尔斯方程的提出为了更准确地描述实际气体的性质，荷兰物理学家约翰内斯·迪德里克·范德瓦尔斯于19世纪末提出了范德瓦尔斯方程。

范德瓦尔斯方程修正了理想气体方程中的假设，引入了修正因子来考虑真实气体分子之间的吸引力和排斥力。

范德瓦尔斯方程的一般形式为（P + a/V^2）(V - b) = nRT，其中a和b为范德瓦尔斯常数，与气体的性质有关。

a/V^2表示吸引力的修正，b表示分子体积的修正。

三、范德瓦尔斯方程的应用范德瓦尔斯方程的引入使得我们能够更准确地预测实际气体的行为，特别是在高压和低温条件下。

这对于工程应用尤其重要，例如在化学工业中对气体混合物的分离和精馏过程中，准确描述气体的性质可以提高工艺效率并降低能源消耗。

范德瓦尔斯方程也被用于研究气体的相变现象。

相变是指物质从一种物态转变为另一种物态的过程，例如液化、升华和冷凝等。

通过范德瓦尔斯方程，我们可以计算出气体在不同温度和压力下的相变点，从而深入了解气体在不同条件下的行为。

除了范德瓦尔斯方程，还有其他物态方程被用于描述实际气体的行为，例如德拜方程和贝尔方程等。

这些方程都是在理想气体方程的基础上，引入了修正因子来考虑实际气体的性质。

总结：物态方程对于研究气体的性质和行为具有重要意义。

范德瓦尔斯方程是一种修正的物态方程，可以更准确地预测实际气体的行为。

气体的状态方程气体是一种物质的状态，具有松散的分子排列和高度的运动性质。

为了描述气体在不同条件下的行为和性质，科学家们提出了一系列的状态方程。

本文将从理想气体状态方程、范德瓦尔斯方程和诸多实际气体状态方程等多个角度进行探讨。

一、理想气体状态方程理想气体状态方程（也称作理想气体定律）是描述理想气体在一定条件下的状态的数学表达式。

它以压强（P）、体积（V）、摩尔数量（n）和绝对温度（T）为变量，可表示为以下形式：PV = nRT其中，R为气体常数，其值与单位选择有关。

在国际单位制中，R 的值为8.31 J/(mol·K)。

理想气体状态方程的适用范围有限，适用于低密度、高温度条件下的气体。

在一般情况下，气体分子之间相互吸引、体积占据、碰撞等因素对气体性质会产生影响。

因此，为了更准确地描述实际气体的状态，科学家们提出了其他更为复杂的气体状态方程。

二、范德瓦尔斯方程范德瓦尔斯方程是对理想气体状态方程的修正，考虑了气体分子之间的相互吸引和体积占据等因素。

它的数学表达式如下：(P + an^2/V^2)(V - nb) = nRT其中，a和b为范德瓦尔斯常数，与不同气体的性质有关。

范德瓦尔斯方程适用于较高密度、较低温度的气体，较好地描述了实际气体的状态。

三、实际气体状态方程除了理想气体状态方程和范德瓦尔斯方程外，还存在着许多用于描述实际气体状态的方程。

其中比较常见的有柯西方程、安德鲁斯方程、本齐曼方程等。

这些状态方程根据实验数据和物理原理进行构建，适用于特定范围的气体。

以柯西方程为例，它是描述气体在近临界条件下行为的状态方程。

其数学表达式为：P(V - b) = RT / (V - a)这个方程修正了范德瓦尔斯方程在高压缩情况下的不足，适用于近临界状态下的气体。

总结本文简要介绍了气体的状态方程，包括理想气体状态方程、范德瓦尔斯方程和一些实际气体状态方程。

这些方程通过数学表达式描述气体在不同条件下的行为和性质，有助于我们深入了解气体的特性。

范德华方程与真实气体研究
范德华方程与真实气体研究
首先说明，描述真实气体p、V、T之间数值关系的方程称为真实气体状态方程。

从理论上描述真实气体压力、体积、温度的困难性
1.由于分子间作用力不仅与分子间的距离有关，还与分子的取向有关，所以分子之间的相
互作用力非常复杂；
2.分子外围是电子云，分子的边界无法确定，因而分子的体积也就无得而知；
3.分子是在不断运动着的，分子相互间的位置也不断变化，我们就只能统计地讨论它们对
时间的平均位置，以及分子间相互作用力的平均值。

因此，理论上严格地描述气体p、V、T关系是极其困难的，它涉及到当今科学界许多仍待解决的课题。

迄今，真实气体状态方程都是通过实验人总结出来的。

范德华方程
迄今为止，人们已经提出200多个真实气体状态方程。

其中，范德华方程较具有代表性。

（p+a/Vm2）(Vm-b)=RT
式中：a近似代表气体分子间的相互作用力，b相当于1mol气体分子本身具有的体积。

因而，范德华方程对理想气体状态方程进行了“引力校正”、“体积校正”，较好的弥补了理想气体状态方程最主要的2点不足。

但是，范德华方程也不是普遍使用于所有气体的，符合它的气体称为范德华气体，如CO2等。

范德瓦尔斯实际气体状态方程范德瓦尔斯实际气体状态方程，也被称为范德瓦尔斯方程，是描述气体行为的重要方程之一。

它是由荷兰物理学家约翰·范德瓦尔斯于1873年提出的，通过将理想气体方程修正，考虑分子之间的相互作用而得到。

范德瓦尔斯实际气体状态方程的一般形式为：(P + a/Vm^2)(Vm - b) = RT其中，P表示气体的压强，V表示气体的体积，Vm表示气体的摩尔体积，a和b分别是实际气体的修正参数，R为气体常数，T为气体的温度。

范德瓦尔斯方程的修正主要考虑了两个因素：分子之间的吸引力和分子体积。

在高压和低温条件下，分子之间的吸引力作用会使气体分子聚集，导致实际气体的压强低于理想气体。

而分子体积的考虑则是因为气体分子并非质点，而是具有体积的实体，因此在高密度情况下，分子体积的占据也会影响气体的性质。

范德瓦尔斯方程的修正参数a和b可以通过实验数据进行测定。

实验观测到的气体体积、压强和温度数据可以代入范德瓦尔斯方程，通过曲线拟合等方法计算出修正参数的数值。

范德瓦尔斯方程在化学和工程领域中有广泛的应用。

它可以用于计算气体的物理性质，如压强、体积、温度等。

在工程实践中，范德瓦尔斯方程可以用于设计和优化化工过程，如气体压缩、液化和分离等。

范德瓦尔斯方程还可以用于研究气体的相变行为。

当气体接近临界点时，范德瓦尔斯方程描述的实际气体行为与理想气体有明显差异，此时分子之间的相互作用会导致气体出现液体相和气体相的共存现象，称为临界点。

范德瓦尔斯方程的提出和应用，对于研究气体行为和理解物质的性质有着重要的意义。

它在化学、物理学及工程领域的应用使得我们能够更加准确地描述和预测气体的行为，为工业生产和科学研究提供了有力的工具。

范德瓦尔斯实际气体状态方程是一种修正了理想气体方程的描述气体行为的方程。

它通过考虑分子之间的相互作用和分子体积，更准确地描述了实际气体的性质。

范德瓦尔斯方程在化学、物理学及工程领域的应用广泛，为科学研究和工业生产提供了重要的理论基础和实际工具。

气体的状态方程及研究自古以来，人类对于物质的研究一直是科学进步的重要组成部分。

在这个领域中，气体的状态方程一直扮演着举足轻重的角色。

通过研究气体的状态方程，我们可以更好地了解气体的性质和行为，进而为工业生产、能源利用、环境保护等问题提供指导和解决方案。

一、理想气体状态方程理想气体状态方程是描述理想气体性质的基本公式，也是研究气体的起点。

根据理想气体状态方程，我们可以得出如下公式：PV = nRT其中，P代表气体的压强，V代表气体的体积，n代表气体的摩尔数，R代表气体常数，T代表气体的绝对温度。

这个方程表明，在一定条件下，气体的压强和体积是呈线性关系的。

二、真实气体状态方程尽管理想气体状态方程在大多数情况下能够很好地描述气体的性质，但是对于高压、低温下的气体，理想气体状态方程失效。

为了更准确地描述气体在各种条件下的行为，科学家们提出了多种修正后的气体状态方程。

1. 范德瓦尔斯方程范德瓦尔斯方程是最早被提出的修正后的气体状态方程之一。

在这个方程中，引入了修正因子，用来考虑分子之间的相互作用。

(P + a/V^2)(V - b) = nRT其中，a和b分别代表修正因子。

通过引入这些修正因子，范德瓦尔斯方程使得气体在高压和低温下的状态更符合实际。

2. 牛顿-克劳修斯方程牛顿-克劳修斯方程是另一种修正后的气体状态方程。

在这个方程中，引入了更多的修正因子，用来考虑气体分子的体积和分子之间的相互作用。

(P + an^2/V^2)(V - nb) = nRT牛顿-克劳修斯方程的引入增强了对气体性质的描述能力，使得我们更好地了解气体在不同条件下的行为。

三、气体状态方程的研究进展气体状态方程一直是热门的研究方向之一。

随着科学技术的进步，科学家们通过实验和理论计算，不断提出新的气体状态方程和修正模型，以更全面、更准确地描述气体的性质。

除了修正后的气体状态方程，研究人员还通过引入量子力学理论、统计力学等方法，对气体的性质进行更深入的研究。