尺寸链基础

机械设计基础如何进行尺寸链设计尺寸链设计是机械设计中非常重要的一环，它关系到产品的精确度和功能的实现。

在机械设计过程中，合理的尺寸链设计可以确保产品的稳定性、运动的平滑性以及工作效率的提高。

本文将介绍机械设计基础中的尺寸链设计，包括尺寸链的定义、尺寸链设计的步骤以及一些实际应用案例。

一、尺寸链的定义尺寸链是指在机械设计中，通过连接不同零部件之间的尺寸关系，形成一个相对稳定的尺寸链条。

在设计过程中，尺寸链需要考虑整体结构的稳定性和运动的平滑性。

一个好的尺寸链设计可以提高产品的精确度，降低故障率，并且方便制造和维修。

二、尺寸链设计的步骤1. 确定产品的功能要求：在进行尺寸链设计之前，首先需要明确产品的功能要求。

根据产品的功能要求，确定各个零部件之间的相对位置和运动方式。

2. 确定尺寸链的起点和终点：根据产品的功能要求，确定尺寸链的起点和终点，即起始尺寸和终止尺寸。

起点和终点之间的所有零部件需要通过合适的尺寸关系相互连接起来。

3. 确定尺寸链的传递方式：根据产品的功能需求，确定尺寸链的传递方式。

尺寸链的传递方式可以是直接传递、间接传递或者复合传递。

在传递方式的选择上，需要考虑产品结构的复杂程度和工作效率的要求。

4. 绘制尺寸链图：在尺寸链设计的过程中，需要将尺寸链的各个零部件和尺寸关系进行绘制。

通过绘制尺寸链图，可以直观地了解尺寸链的结构和尺寸关系，有助于后续的设计和制造工作。

5. 优化尺寸链的设计：在完成初步尺寸链设计之后，需要对尺寸链进行优化。

优化的目标是提高产品的精确度和稳定性，同时降低制造和维修的成本。

在优化的过程中，可以采用各种工具和方法，如CAD软件和有限元分析等。

三、实际应用案例1. 汽车发动机的尺寸链设计：在汽车发动机的设计过程中，尺寸链设计起到关键的作用。

通过合理的尺寸链设计，可以提高发动机的工作效率和可靠性。

例如，通过控制活塞的尺寸和连杆的长度，实现活塞运动的平滑性和发动机的动力输出。

尺寸链基础一、尺寸链的基本术语1.尺寸链——在机器装配或零件加工过程中，由相互连接的尺寸形成封闭的尺寸组，称为尺寸链。

如下图间隙A0与其它五个尺寸连接成的封闭尺寸组，形成尺寸链。

2.环——列入尺寸链中的每一个尺寸称为环。

如上图中的A0、A1、A2、A3、A4、A5都是环。

长度环用大写斜体拉丁字母A，B，C……表示；角度环用小写斜体希腊字母α，β等表示。

3.封闭环——尺寸链中在装配过程或加工过程后自然形成的一尺寸，称为封闭环。

如上图中A0。

封闭环的下角标“0”表示。

4.组成环——尺寸链中对封闭环有影响的全部尺寸，称为组成环。

如上图中A1、A2、A3、A4、A5。

组成环的下角标用阿拉伯数字表示。

5.增环——尺寸链中某一类组成环，由于该类组成环的变动引起封闭环同向变动，该组成环为增环。

如上图中的A36.减环——尺寸链中某一类组成环，由于该类组成环的变动引起封闭环的反向变动，该类组成环为减环。

如上图中的A1、A2、A4、A5。

7.补偿环——尺寸链中预先选定某一组成环，可以通过改变其大小或位置，使封闭环达到规定的要求，该组成环为补偿环。

如下图中的L2。

二、尺寸链的形成为分析与计算尺寸链的方便，通常按尺寸链的几何特征，功能要求，误差性质及环的相互关系与相互位置等不同观点，对尺寸链加以分类，得出尺寸链的不同形式。

1.长度尺寸链与角度尺寸链①长度尺寸链——全部环为长度尺寸的尺寸链，如图1②角度尺寸链——全部环为角度尺寸的尺寸链，如图32.装配尺寸链，零件尺寸链与工艺尺寸链①装配尺寸链——全部组成环为不同零件设计尺寸所形成的尺寸链，如图4②零件尺寸链——全部组成环为同一零件设计尺寸所形成的尺寸链，如图5③工艺尺寸链——全部组成环为同一零件工艺尺寸所形成的尺寸链，如图6。

工艺尺寸指工艺尺寸，定位尺寸与基准尺寸等。

装配尺寸链与零件尺寸链统称为设计尺寸链。

3.基本尺寸链与派生尺寸链①基本尺寸链——全部组成环皆直接影响封闭环的尺寸链，如图7中尺寸链β。

一、尺寸链的概念图5-1: 尺寸链示例二、尺寸链的基本术语及分类（一）尺寸链的基本术语1.环：尺寸链中每个尺寸2.封闭环：在加工或装配过程中最后形成的一环，它的大小是由组成环间接保证的ＡＯ3.组成环：对封闭环有影响的其它各环。

增环：引起封闭环同向变动减环：引起封闭环反向变动（二）尺寸链的分类1.按尺寸链的功能要求分：1）工艺尺寸链2）装配尺寸链2.尺寸链间相互联系分：1）独立尺寸链2）并联尺寸链图5-2:并联尺寸链3.按环的几何特征分1.长度尺寸链2.角度尺寸链图5-3:角度尺寸链3.组合形式4.按环的空间位置分1.直线尺寸链2.平面尺寸链图5-4:平面尺寸链3.空间尺寸链三、尺寸链的计算公式（一）极值法计算公式1.基本尺寸计算2.极限尺寸的计算3.上、下偏差的计算4.环公差的计算5.各环平均公差计算6.平均尺寸及对称偏差计算法二、概率法计算公式k 0、ki为各环的相对分布系数，影响k的因素为二个方面：一是合格率，在公差带范围内即（3σ内）全部合格，认为k'=1不作另外考虑，一般与实际中的情况符合，否则要考虑置信水平P二是分布规律：当分布规律为正态分布时k n=1,否则要考虑分布特性K″获得,在3σ区间内（公差带内）全部合格推导：一、工艺尺寸链的建立和增环、减环判别（一）、尺寸链的建立1.确定封闭环装配尺寸链中，装配精度就是封闭环；（设计）尺寸链中，未标尺寸（环）就是封闭环。

工艺尺寸链：间接获得的，不是直接保证的尺寸。

2.查组成环加工中直接获得且对封闭环有影响的尺寸3.画出尺寸链注意：使组成环环数达到最少（二）、增坏，减环的判别1、回路法：与封闭环反向的为增环，与封闭环同向的为减环。

2、直观法：与封闭环串联的是减环，与封闭环共基线并联的是增环。

串联的组成环性质相同，共基线并联的组成环性质相反。

3、分析法：假定其它组成环均为定值，分析某一组成环，其增大使封闭环增大为增环，反之为减环。

二、工艺基准与设计基准不重合时，工序尺寸及其公差的确定例、图5-5：测量基准与设计基准不重合的尺寸换算轴承碗问题，测量基准与设计基准不重合1、设计要求保证10-0.10及40-0.20孔深任意设计尺寸链，封闭环---总长X0X0=10+40=50, ES(x0)=0, EI0=-0.2-0.1=-0.3封闭环X0=50-00.32、测量问题----如何保证40-0.2？测量基准与设计基准不重合尺寸换算40-0.2尺寸的设计基准为B，无法直接测量改为A, 40-0.2是封闭环，由10-0.1及尺寸X1间接保证A.初检T0=ΣT i？否则调整公差B．判别增减环C．选用公式3、假废品问题，若测量结果为50? 49.75？合格否？需重测Ａ１4、如何提高测量----加工的可能性-----设计工艺装备，保证设计尺寸。

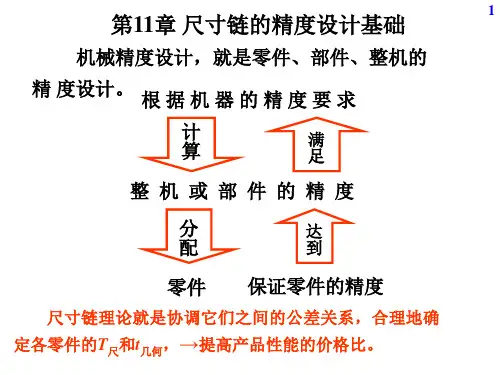
尺寸链基础一、基本概念为了保证机器或仪器能顺利的进行装配，并达到预定的工作要求。

要在设计与生产过程中，正确分析和确定各零部件尺寸关系，合理确定构成各有关零部件的几何精度（尺寸公差、形状和位置公差），它们之间的关系需用尺寸链来计算和处理。

1.尺寸链的基本术语与定义尺寸链的定义：在零件加工或机器装配过程中，由相互连接的尺寸形成封闭的尺寸组，称为尺寸链。

尺寸链图可见下图。

图1如图1所示零件，其轴向尺寸A0、A1、A2之间也具有封闭性，所组成的尺寸链叫工艺尺寸链。

当尺寸A1、A2一旦确定了，尺寸A0也就得到了，所以A0是加工后间接得到的。

尺寸A0的大小受尺寸A1、A2大小的影响图2如图2所示为轴和孔的装配，间隙S0与孔尺寸S1和轴的尺寸S2也组成封闭图形。

其中S1和S2是直接获得的尺寸，S0是装配后间接获得的尺寸，因此它们构成一个装配尺寸链。

从以上分析，我们可以看出尺寸链具有以下三个特点：1、封闭性：尺寸链必须是由一系列相互连接的尺寸组成的封闭图形。

（至少由三环尺寸组成）。

2、相关性（函数性）：尺寸链中的间接尺寸要受到直接获得尺寸的影响，它们彼此关联，互相制约。

3、唯一性：尺寸链中只有一个间接获得的尺寸（即一个封闭环）。

构成尺寸链的各个尺寸称为环。

环封闭环:加工或装配过程中最后自然形成的那个尺寸。

如上图中的A0和S0。

组成环:尺寸链中除封闭环以外的其他环。

根据它们对封闭环影响的不同，又分为增环和减环。

增环：与封闭环同向变动的组成环称为增环，即当该组成环尺寸增大（或减小）而其它组成环不变时，封闭环也随之增大（或减小），如上图中的A1和S1；减环：与封闭环反向变动的组成环称为减环，即当该组成环尺寸增大（或减小）而其他组成环不变时，封闭环的尺寸却随之减小（或增大），如上图中中的A2和S2。

箭头法判断增减环封闭环A0上面按任意指向画一箭头，见下图，沿已定箭头方向在每个组成环符号A1、A2、A3上各画一箭头，使所画各箭头依次彼此头尾相连，组成环中箭头与封闭环箭头方向相同者为减环，相反者为增环。

尺寸链介绍2010年5月目录尺寸链概述 尺寸链计算案例分析内容提要尺寸链计算软件介绍 尺寸链计算软件演示交流尺寸链概述本部分主要介绍尺寸链中的基本概念、名 词定义、基本方法、原理、目的以及相关 的理论基础等。

尺寸链计算目的• • • • • 验证设计是否能达到质量要求 提高产品合格率 预防生产过程中的重复工作和延工现象 降低产品的返修率 实现产品的无修锉、大批量生产降低成本、缩短周期、提高质量尺寸链计算与研发成本关系尺寸链基本概念在零件的加工或机器的装配中决定各个几何要素(点、线、 面)间相互位置的尺寸通常都是彼此相联系的、按一定顺 序排列的、一个封闭的尺寸系统，这个尺寸系统就称为尺 寸链尺寸链主要特征封闭性：尺寸链必须是一组相关尺寸按 顺序首尾相接而形成的封闭轮廓，其中应 包含一个间接保证的尺寸和若干个与之有 关的直接获得的尺寸 关联性：尺寸链内间接保证的尺寸的大 小和变化范围(即精度)，是受该链内直接 获得的尺寸大小和变化范围所制约的，彼 此间具有特定的函数关系尺寸链的组成单元——环构成尺寸链的每一个尺寸都称为“环”，一条尺寸链中必包含两种环。

封闭环：尺寸链中最终被间接保证的那个尺寸称为封闭环，它是在加工或装配之后形成的。

组成环：除封闭以外尺寸链中其它所有的环皆称为组成环。

组成环按其对封闭环的影响性质又可划分为增环和减环。

尺寸链的组成单元——闭环对于单个零件的加工而言，封闭环通常是零件设计图上未标注的尺寸即最不重要的尺寸。

对于若干零部件的装配而言，封闭环通常是对有关要素间的联系所提出的技术要求，如位置精度、距离精度、间隙过盈等。

注意，不要错误的认为需要求的环就是闭环。

尺寸工程、尺寸链计算、公差分析关系尺寸工程尺寸链计算数据检测统计分析…公差分析公差分析公差分配公差分配（（设计设计））公差分配公差分配（（设计设计））尺寸链的分类——各环尺寸所处的空间位置线性尺寸链：尺寸链各环位于同一平面内，且互相平行平面尺寸链：尺寸链各环位于同一平面内，但其中有些环彼此不平行(存在一定的夹角关系)。

尺寸链计算正态分布尺寸链计算是一种用于估算产品质量控制的统计方法，它基于正态分布（也称为高斯分布）的假设。

正态分布是统计学中最重要的概率分布之一，也是尺寸链计算的重要理论基础。

正态分布是一种连续概率分布，它的图形呈钟形曲线，对称分布于均值的左右两侧。

正态分布的图像由两个参数决定：均值（μ）和标准差（σ），其中均值确定图像的位置，标准差决定图像的宽度。

在尺寸链计算中，正态分布被用来描述产品尺寸的变异性。

假设产品尺寸服从正态分布，那么尺寸链中的每一个环节都可以通过正态分布的参数来计算。

具体而言，尺寸链计算包括以下几个步骤：1. 收集样本数据：首先，需要收集关于产品尺寸的样本数据。

这些样本可以是从生产线上随机选择的，确保代表了整个产品群体的尺寸分布。

2. 计算统计量：使用收集到的样本数据，可以计算出各个统计量，比如均值和标准差。

均值表示了尺寸的平均水平，标准差则衡量了尺寸的变异程度。

3. 绘制正态分布图像：根据计算得到的均值和标准差，可以绘制出产品尺寸的正态分布图像。

这个图像反映了产品尺寸在整个尺寸空间内的分布情况。

4. 分析尺寸链：根据正态分布的性质，可以利用统计学方法来分析尺寸链的各个环节。

比如，可以计算出某个环节的概率，即产品在该环节的尺寸变异能力达到一定程度的概率。

尺寸链计算的关键在于正态分布的应用。

正态分布具有许多重要的性质，例如68-95-99.7原则。

根据这一原则，约有68%的观测值落在均值的一倍标准差范围内，约有95%的观测值落在均值的两倍标准差范围内，约有99.7%的观测值落在均值的三倍标准差范围内。

通过利用这些性质，可以更好地了解和控制产品尺寸的变异性。

总结起来，尺寸链计算是一种基于正态分布的统计方法，用于估算产品尺寸的变异性。

通过收集样本数据、计算统计量、绘制正态分布图像和分析尺寸链，可以更好地理解和控制产品尺寸的分布情况。

正态分布的性质和统计学方法为我们提供了有效的工具和理论基础，帮助我们进行尺寸链计算。

机械设计基础中的尺寸链与公差分析尺寸链与公差分析在机械设计基础中，尺寸链和公差分析是两个重要的概念，它们对于确保产品的质量和性能起着关键作用。

本文将从尺寸链的概念、尺寸链分析的方法以及公差分析的意义等方面进行阐述。

1. 尺寸链的概念尺寸链是指在机械装配过程中，各个关键部件的尺寸之间的相互关系。

在一个机械系统中，各个部件的尺寸必须满足一定的要求，以确保装配的正确性和工作的稳定性。

尺寸链的建立需要考虑到装配的顺序、尺寸的限制以及功能与效能等因素。

2. 尺寸链分析方法尺寸链分析是为了确定装配过程中各个部件尺寸的控制范围，以保证装配的质量和可靠性。

常用的尺寸链分析方法有以下几种：(1) 结构法：通过建立各部件之间的结构关系，确定各个部件之间的尺寸要求和公差范围。

(2) 功能法：根据产品的功能要求，确定各个部件的尺寸限值，使其满足产品的使用要求。

(3) 统计法：通过对一组相同部件的尺寸进行统计分析，确定其尺寸的均值、极限和公差。

(4) 经验法：根据设计师的实际经验和相关标准规范，确定各个部件的尺寸链。

通过以上方法的综合运用，可以建立合理的尺寸链分析模型，从而确保产品的尺寸控制和装配质量。

3. 公差分析的意义公差分析是为了确定机械系统各个部件的公差，以确保装配的精度和性能。

公差是指在设计和制造过程中，由于种种原因所引起的尺寸和形状上的误差。

公差分析的主要目的是通过确定合适的公差限制，控制装配过程中的误差，从而提高产品的精度和性能。

公差分析的意义主要表现在以下几个方面：(1) 可靠性：通过合理的公差分析，可以减少装配过程中的配合和间隙问题，提高产品的可靠性和稳定性。

(2) 成本控制：合理的公差分析可以避免不必要的尺寸测量和调整，减少生产成本。

(3) 产品质量：公差分析有助于控制产品的尺寸精度，实现产品的一致性和稳定性，提高产品的质量。

(4) 工艺优化：公差分析可以为工艺优化提供依据，有助于改进制造工艺，提高生产效率。