Pspice模型参数

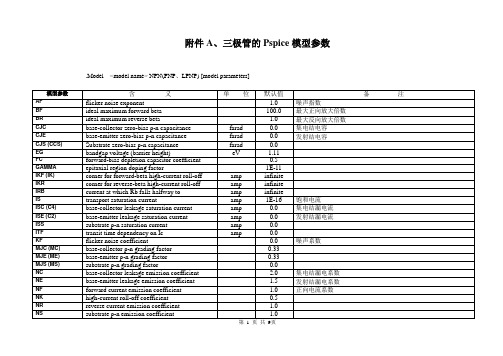
附件A、三极管的Pspice模型参数.Model <model name> NPN(PNP、LPNP) [model parameters]第 1 页共9页第 2 页共9页附件B、PSpice Goal Function第 3 页共9页附件CModeling voltage-controlled and temperature-dependent resistorsAnalog Behavioral Modeling (ABM) can be used to model a nonlinear resistor through use of Ohm抯 law and tables and expressions which describe resistance. Here are some examples.Voltage-controlled resistorIf a Resistance vs. Voltage curve is available, a look-up table can be used in the ABM expression. This table contains (Voltage, Resistance) pairs picked from points on the curve. The voltage input is nonlinearly mapped from the voltage values in the table to the resistance values. Linear interpolation is used between table values.Let抯 say that points picked from a Resistance vs. Voltage curve are:Voltage ResistanceThe ABM expression for this is shown in Figure 1.第 4 页共9页Figure 1 - Voltage controlled resistor using look-up tableTemperature-dependent resistorA temperature-dependent resistor (or thermistor) can be modeled with a look-up table, or an expression can be used to describe how the resistance varies with temperature. The denominator in the expression in Figure 2 is used to describe common thermistors. The TEMP variable in the expression is the simulation temperature, in Celsius. This is then converted to Kelvin by adding 273.15. This step is necessary to avoid a divide by zero problem in the denominator, when T=0 C.NOTE: TEMP can only be used in ABM expressions (E, G devices).Figure 3 shows the results of a DC sweep of temperature from -40 to 60 C. The y-axis shows the resistance or V(I1:-)/1A.Figure 2 - Temperature controlled resistor第 5 页共9页Figure 3 - PSpice plot of Resistance vs. Temperature (current=1A)Variable Q RLC networkIn most circuits the value of a resistor is fixed during a simulation. While the value can be made to change for a set of simulations by using a Parametric Sweep to move through a fixed sequence of values, a voltage-controlled resistor can be made to change dynamically during a simulation. This is illustrated by the circuit shown in Figure 5, which employs a voltage-controlled resistor.第 6 页共9页Figure 4 - Parameter sweep of control voltageThis circuit employs an external reference component that is sensed. The output impedance equals the value of the control voltage times the reference. Here, we will use Rref, a 50 ohm resistor as our reference. As a result, the output impedance is seen by the circuit as a floating resistor equal to the value of V(Control) times the resistance value of Rref. In our circuit, the control voltage value is stepped from 0.5 volt to 2 volts in 0.5 volt steps, therefore, the resistance between nodes 3 and 0 varies from 25 ohms to 100 ohms in 25 ohm-steps.第7 页共9页Figure 5 - Variable Q RLC circuitA transient analysis of this circuit using a 0.5 ms wide pulse will show how the ringing differs as the Q is varied.Using Probe, we can observe how the ringing varies as the resistance changes. Figure 6 shows the input pulse and the voltage across the capacitor C1. Comparing the four output waveforms, we can see the most pronounced ringing occurs when the resistor has the lowest value and the Q is greatest. Any signal source can be used to drive the voltage-controlled resistance. If we had used a sinusoidal control source instead of a staircase, the resistance would have varied dynamically during the simulation.第8 页共9页Figure 6 - Output waveforms of variable Q RLC circuit通过几天来的补习,我认为IS只是等于Icb0;而VAF才是VCE0就是最高管耐压;而IKF才是ICE0最大管电流;BF是放大倍数没错了,不知各位师傅有没有别的看法呢?.MODEL MOD1 NPN IS=1E-6 BF=50 RB=100 V AF=160 CJC=3P 3DG201第9 页共9页。

元器件模型参数的优化提取微电子学院贾新章(2013. 11 )PSpice中的模型和模型参数库一、概述：为元器件建立模型参数的步骤二、采用Model Editor分组提取模型参数三、基于器件物理原理计算部分模型参数四、建立适用于高级分析的元器件模型参数描述五、元器件模型参数的综合优化提取。

六、为元器件模型描述建立元器件符号七、将新建模型设置为PSpice仿真可以调用的库文件一、概述：为元器件建立模型参数的步骤第一步：优化提取模型参数1、采用Model Editor分组提取模型参数；2、基于器件物理原理，计算部分模型参数；3、为元器件建立适用于高级分析的模型参数描述；4、采用PSpice/Optimizer进行一次综合优化提取。

（采用前面结果作为优化提取模型参数的最佳初值）第二步：建立供Capture绘制电路图调用的元器件符号第三步：将新建模型设置为PSpice仿真可以调用的库文件。

下面将分别介绍每一部分的操作方法。

PSpice中的模型和模型参数库一、概述：为元器件建立模型参数的步骤二、采用Model Editor分组提取模型参数三、基于器件物理原理计算部分模型参数四、建立适用于高级分析的元器件模型参数描述五、元器件模型参数的综合优化提取。

六、为元器件模型描述建立元器件符号七、将新建模型设置为PSpice仿真可以调用的库文件二、采用Model Editor分组提取模型参数Model Editor模块可以对其支持的几种元器件，依据元器件的各种端特性数据，分组优化提取相应当模型参数数据。

(1) 调用MODEL EDITOR模块；(2) 选择执行Model/New命令，从对话框中设置模型类型。

下面以提取双极型晶体管模型参数为例(3)完成设置之后，点击OK，窗口就会更新为参数提取界面，不同的模型类型所对应的界面不相同，但界面的结构形式是一样的，分为三个子窗口。

特性数据输入窗口模型列表窗口参数列表窗口(4) 分组提取各组模型参数：将测试得到的器件外部端特性数据分别输入相应的特性窗口，分组进行参数提取。

PSpice中的模型和模型参数库一．PSpice中的模型参数库二．模型描述格式半导体器件模型描述格式子电路模型描述格式三．以已有模型为基础新建模型描述四．为实际元器件提取模型参数、建立模型描述3．模型类别（按照建模方式划分）(1) 元器件物理模型(2) 子电路宏模型(3) 黑匣子宏模型4. 目前研究的问题(1) 提高模型精度。

(2) 建立新器件的模型。

(3) 提高模型参数提取精度。

5．PSpice中的模型参数库(1) PSpice软件数据库中提供有三万多个元器件的模型参数；分别存放在一百多个模型参数库文件（扩展名为LIB）；一．PSpice中的模型参数库5．PSpice中的模型参数库(1) PSpice软件数据库中提供有三万多个元器件的模型参数；分别存放在一百多个模型参数库文件（扩展名为LIB）；每个模型参数库文件都对应有一个元器件符号库文件(以OLB为扩展名)，存放不同元器件的符号图。

一．PSpice中的模型参数库5．PSpice中的模型参数库(1) PSpice软件数据库中提供有三万多个元器件的模型参数；分别存放在一百多个模型参数库文件（扩展名为LIB）；每个模型参数库文件都对应有一个元器件符号库文件(以OLB为扩展名)，存放不同元器件的符号图。

注意：这两类库文件存放的子目录不相同。

元器件符号库文件所在的路径元器件模型参数库文件所在的路径注意：只有上述库文件中的元器件符号才配置有模型参数一．PSpice中的模型参数库5．PSpice中的模型参数库(1) PSpice软件数据库中提供有三万多个元器件的模型参数；分别存放在一百多个模型参数库文件（扩展名为LIB）；每个模型参数库文件都对应有一个元器件符号库文件(以OLB为扩展名)，存放不同元器件的符号图。

注意：这两类库文件存放的子目录不相同。

(2) 用户绘制电路图时实际调用的是元器件符号库中的元器件符号图。

调用PSpice进行模拟仿真时软件自动从对应的模型参数库中调用相应的模型参数。

SPICE模型、命令介绍SPICE模型、命令介绍下⾯列出常⽤SPICE器件的模型描述。

{ }中的参数是必须的，[ ]中的参数可选，{ }*中的参数需要重复。

此外，每个SPICE模型提供商可能会有其他的参数或命令。

DEVICE：1、C device - Capacitor.C{name} {+node} {-node} [{model}] {value} [IC={initial}]Examples:CLOAD 15 0 20pFCFDBK 3 33 CMOD 10pF IC=1.5v2、D device - Diode.D{name} {+node} {-node} {model} [area]Examples:DCLAMP 14 0 DMOD3、I device - Current Source.I{name} {+node} {-node} [[DC] {value}] [AC {mag} [{phase}]]Examples:IBIAS 13 0 2.3mAIAC 2 3 AC .001IPULSE 1 0 PULSE(-1mA 1mA 2ns 2ns 2ns 50ns 100ns)I3 26 77 AC 1 SIN(.002 .002 1.5MEG)4、J device - Junction FET.J{name} {d} {g} {s} {model} [{area]}Examples:JIN 100 1 0 JFAST5、K device - Inductor Coupling.K{name} L{name} { L{name} }* {coupling}Examples:KTUNED L3OUT L4IN .8KXFR1 LPRIM LSEC .996、L device - Inductor.L{name} {+node} {-node} [model] {value} [IC={initial}]Examples:LLOAD 15 0 20mHL2 1 2 .2e-6LSENSE 5 12 2uH IC=2mA7、M device - MOSFET.M{name} {d} {g} {s} {sub} {mdl} [L={value}] [W={value}] + [AD={value}] [AS={value}] + [PD={value}] [PS={value}]+ [NRD={value}] [NRS={value}]Examples:M1 14 2 13 0 PNOM L=25u W=12uM13 15 3 0 0 PSTRONG8、Q device - Bipolar Transistor.Q{name} {c} {b} {e} [{subs}] {model} [{area}]Examples:Q1 14 2 13 PNPNOMQ13 15 3 0 1 NPNSTRONG 1.59、R device - Resistor.R{name} {+node} {-node} [{model}] {value}Examples:RLOAD 15 0 2k10、S device - Voltage-Controlled Switch.S{name} {+node} {-node} {+control} {-control} {model}Examples:S12 13 17 2 0 SMOD11、T device - Transmission Line.T{name} {A+} {A-} {B+} {B-} Z0={value}[TD={val} | F={val}[NL={val}]]Examples:T1 1 2 3 4 Z0=220 TD=115nsT2 1 2 3 4 Z0=50 F=5MEG NL=0.512、V device - Voltage Source.V{name} {+node} {-node} [[DC] {value}] [AC {mag} [{phase}]]Examples:VBIAS 13 0 2.3mVV AC 2 3 AC .001VPULSE 1 0 PULSE(-1mV 1mV 2ns 2ns 2ns 50ns 100ns)V3 26 77 AC 1 SIN(.002 .002 1.5MEG)13、X device - Subcircuit Call.X{name} [{node}]* {subcircuit name}Examples:X12 100 101 200 201 DIFFAMPCONTROLLED SOURCES14、E device - Voltage Controlled V oltage Source VCVS.E{name} {+node} {-node} {+cntrl} {-cntrl} {gain}E{name} {+node} {-node} POL Y({value}) {{+cntrl} {-cntrl}}* {{coeff}}* Examples: EBUFF 1 2 10 11 1.0EAMP 13 0 POL Y(1) 26 0 50015、F device - Current Controlled Current Source CCCS.F{name} {+node} {-node} {vsource name} {gain}Examples:FSENSE 1 2 VSENSE 10.016、G device - Voltage Controlled Current Source VCCS.G{name} {+node} {-node} {+control} {-control} {gain}Examples:GBUFF 1 2 10 11 1.017、H device - Current Controlled V oltage Source CCVS.H{name} {+node} {-node} {vsource name} {gain}H{name} {+node} {-node} POL Y({value}) { {vsource name} }* {{coeff}}* Examples: HSENSE 1 2 VSENSE 10.0HAMP 13 0 POL Y(1) VIN 500INPUT SOURCES18、EXPONENTIALEXP( {v1} {v2} {trise_delay} {tau_rise} {tfall_delay} {tau_fall) )19、PULSEPULSE( {v1} {v2} {tdelay} {trise} {tfall} {width} {period} )20、PIECE WISE LINEARPWL( {time1} {v1} {time2} {v2} ... {time3} {v3} )21、SINGLE FREQUENCY FMSFFM( {voffset} {vpeak} {fcarrier} {mod_index} {fsignal} )22、SINE WA VESIN( {voffset} {vpeak} {freq} {tdelay} {damp_factor} {phase} )ANALOG BEHA VIORAL MODELING23、V ALUEE|G{name} {+node} {-node} V ALUE {expression}Examples:GMULT 1 0 V ALUE = { V(3)*V(5,6)*100 }ERES 1 3 VALUE = { I(VSENSE)*10K }24、TABLEE|G{name} {+node} {-node} TABLE {expression} = (invalue, outvalue)* Examples: ECOMP 3 0 TABLE {V(1,2)} = (-1MV 0V) (1MV, 10V)25、LAPLACEE|G{name} {+node} {-node} LAPLACE {expression} {s expression} Examples:ELOPASS 4 0 LAPLACE {V(1)} {10 / (s/6800 + 1)}26、FREQE|G{name} {+node} {-node} FREQ {expression} (freq, gain, phase)* Examples:EAMP 5 0 FREQ {V(1)} (1KZ, 10DB, 0DEG) (10KHZ, 0DB, -90DEG)27、POL YE|G{name} {+node} {-node} POL Y(dim) {inputs X} {coeff k0,k1,...} [IC=value] Examples:EAMP 3 0 POL Y(1) (2,0) 0 500EMULT2 3 0 POL Y(2) (1,0) (2,0) 0 0 0 0 1ESUM3 6 0 POL Y(3) (3,0) (4,0) (5,0) 0 1.2 0.5 1.2COEFFICIENTS28、POL Y(1)y = k0 + k1?X1 + k2?X1?X1 + k3?X1?X1?X1 + ...29、POL Y(2)y = k0 + k1?X1+ k2?X2 + k3?X1?X1+ k4?X2?X1 + k5?X2?X2+ k6?X1?X1?X1 + k7?X2?X1?X1 + k8?X2?X2?X1+ k9?X2? X2?X2 + ...30、POL Y(3)y = k0 + k1?X1 + k2?X2 + k3?X3 + k4?X1?X1 + k5?X2?X1 + k6?X3?X1+ k7?X2?X2+ k8?X2?X3 + k9?X3?X3 + ...STATEMENTS31、.AC - AC Analysis..AC [LIN][OCT][DEC] {points} {start} {end}Examples:.AC LIN 101 10Hz 200Hz.AC DEC 20 1MEG 100MEG32、.DC - DC Analysis..DC [LIN] {varname} {start} {end} {incr}.DC [OCT][DEC] {varname} {start} {end} {points}Examples:.DC VIN -.25 .25 .05.DC LIN I2 5mA -2mA 0.1mA VCE 10V 15V 1V 33、.FOUR - Fourier Analysis..FOUR {freq} {output var}*Examples:.FOUR 10KHz v(5) v(6,7)34、.IC - Initial Transient Conditions..IC { {vnode} = {value} }*Examples:.IC V(2)=3.4 V(102)=035、.MODEL – Device Model..MODEL {name} {type}Typename Devname DevtypeCAP Cxxx capacitorIND Lxxx inductorRES Rxxx resistorD Dxxx diodeNPN Qxxx NPN bipolarPNP Qxxx PNP bipolarNJF Jxxx N-channel JFETPJF Jxxx P-channel JFETNMOS Mxxx N-channel MOSFETPMOS Mxxx P-channel MOSFETVSWITCH Sxxx voltage controlled switch Examples:.MODEL RMAX RES (R=1.5 TC=.02 TC2=.005).MODEL QDRIV NPN (IS=1e-7 BF=30)36、.NODESET – Initial bias point guess..NODESET { {node}={value} }*Examples:.NODESET V(2)=3.4 V(3)=-1V37、.NOISE - Noise Analysis..NOISE {output variable} {name} [{print interval}] Examples:.NOISE V(5) VIN38、.PLOT – Plot Output..PLOT [DC][AC][NOISE][TRAN] [ [{output variable}*] Examples: .PLOT DC V(3) V(2,3) V(R1) I(VIN).PLOT AC VM(2) VP(2) VG(2)39、.PRINT – Print Output..PRINT [DC][AC][NOISE][TRAN] [{output variable}*] Examples: .PRINT DC V(3) V(2,3) V(R1) IB(Q13).PRINT AC VM(2) VP(2) VG(5) II(7)40、.PROBE – Save simulation output PSPICE COMMAND. .PROBE [output variable]*Examples:.PROBE.PROBE V(3) VM(2) I(VIN)41、.SENS - Sensitivity Analysis..SENS {output variable}*Examples:.SENS V(9) V(4,3) I(VCC)42、.SUBCKT - Subcircuit Definition..SUBCKT {name} [{node}*]Examples:.SUBCKT OPAMP 1 2 101 10243、.TEMP – Temperature Analysis..TEMP {value}*Examples:.TEMP 0 27 12544、.TF – DC Transfer Function..TF {output variable} {input source name}Examples:.TF V(5) VIN45、.TRAN - Transient Analysis..TRAN {print step value} {final time} [{no print time} [{step ceiling value}]] [UIC] Examples:.TRAN 5NS 100NS。

关于PSPICE仿真软件中如何使用PARAMETERS参数分析教程利用PARAMETERS进行参数分析，能够很好的分析参数变化所引起的波形变化，从而迅速观察出所需参数的范围值。

掌握此方法能够帮助我们高效率的完成工作。

接下来让我们看一下PARAMETERS参数分析使用的具体方法。

我们以一个TL431的分路稳压器的电路我为基础了解如何运用参数分析功能。

首先建立一个简单的原理图。

如上图所示，利用TL431的可编程性，调整R1,R2的比例关系，我们可以得到一个≤36V的输出电压，即Vout=Vvef（1+R2/R1）。

接下来我们看下此点路的波形，在原理图上我们添加两个电压探针。

仿真波形如下图所示：从波形中我们可以看出，Vref=2.4912V ，Vout=4.9845V。

从而验证了Vout=Vref（1+R2/R1），从例子中我们看出仿真软件给我们带来的便利。

接下来我们进入主题，学习如何运用PARAMETERS进行参数分析。

首先我们如下图搜索PARAM，选定PARAM/SPECIAL放在原理图上。

接下来我们就针对上图中的PARAMETERS进行相关的设置，设置之前要明确我们的目的，就是通过改变R2的值，来观察输出曲线的变化。

所以我们要做的工作就是把PARAMETERS进行关联。

1、双击PARAMETERS进行Property Editor设定。

2、在新打开的窗口中点击New Column…设置相关参数，var为任意起的一个名字，1k为R2现在的阻值。

3、双击R2的值1k进行关联设置。

此处的Value要与PARAM设置相互关联，此处我设置为｛var｝4、接下来我们进行仿真的相关设置。

设置参数如下图，注意全局变量Parameter name的设置。

5、点击仿真按钮，我们会看到如下对话框，点击OK。

6、我们可以观察到的仿真图形如下：参考电压不变，输出电压根据我们的设定显示出了不同的值。

方便我们对参数选取。

功能的实现基本就介绍到这里，如有疑问请联系我！hanjping@Hanjping at OPPLE2011.2.18。

附件A、三极管的Pspice模型参数.Model <model name> NPN(PNP、LPNP) [model parameters]第 1 页共9页第 2 页共9页附件B、PSpice Goal Function第 3 页共9页附件CModeling voltage-controlled and temperature-dependent resistorsAnalog Behavioral Modeling (ABM) can be used to model a nonlinear resistor through use of Ohm抯 law and tables and expressions which describe resistance. Here are some examples.Voltage-controlled resistorIf a Resistance vs. Voltage curve is available, a look-up table can be used in the ABM expression. This table contains (Voltage, Resistance) pairs picked from points on the curve. The voltage input is nonlinearly mapped from the voltage values in the table to the resistance values. Linear interpolation is used between table values.Let抯 say that points picked from a Resistance vs. Voltage curve are:Voltage ResistanceThe ABM expression for this is shown in Figure 1.第 4 页共9页Figure 1 - Voltage controlled resistor using look-up tableTemperature-dependent resistorA temperature-dependent resistor (or thermistor) can be modeled with a look-up table, or an expression can be used to describe how the resistance varies with temperature. The denominator in the expression in Figure 2 is used to describe common thermistors. The TEMP variable in the expression is the simulation temperature, in Celsius. This is then converted to Kelvin by adding 273.15. This step is necessary to avoid a divide by zero problem in the denominator, when T=0 C.NOTE: TEMP can only be used in ABM expressions (E, G devices).Figure 3 shows the results of a DC sweep of temperature from -40 to 60 C. The y-axis shows the resistance or V(I1:-)/1A.Figure 2 - Temperature controlled resistor第 5 页共9页Figure 3 - PSpice plot of Resistance vs. Temperature (current=1A)Variable Q RLC networkIn most circuits the value of a resistor is fixed during a simulation. While the value can be made to change for a set of simulations by using a Parametric Sweep to move through a fixed sequence of values, a voltage-controlled resistor can be made to change dynamically during a simulation. This is illustrated by the circuit shown in Figure 5, which employs a voltage-controlled resistor.第 6 页共9页Figure 4 - Parameter sweep of control voltageThis circuit employs an external reference component that is sensed. The output impedance equals the value of the control voltage times the reference. Here, we will use Rref, a 50 ohm resistor as our reference. As a result, the output impedance is seen by the circuit as a floating resistor equal to the value of V(Control) times the resistance value of Rref. In our circuit, the control voltage value is stepped from 0.5 volt to 2 volts in 0.5 volt steps, therefore, the resistance between nodes 3 and 0 varies from 25 ohms to 100 ohms in 25 ohm-steps.第7 页共9页Figure 5 - Variable Q RLC circuitA transient analysis of this circuit using a 0.5 ms wide pulse will show how the ringing differs as the Q is varied.Using Probe, we can observe how the ringing varies as the resistance changes. Figure 6 shows the input pulse and the voltage across the capacitor C1. Comparing the four output waveforms, we can see the most pronounced ringing occurs when the resistor has the lowest value and the Q is greatest. Any signal source can be used to drive the voltage-controlled resistance. If we had used a sinusoidal control source instead of a staircase, the resistance would have varied dynamically during the simulation.第8 页共9页Figure 6 - Output waveforms of variable Q RLC circuit第9 页共9页。