圆锥的侧面展开后是一个扇形

圆锥的体积公式是什么
圆锥的体积公式为：V=1/3sh，其中s为圆锥底面面积，h为圆锥的高。

1圆锥的具体构成
圆锥的高：圆锥的顶点到圆锥的底面圆心之间的最短距离叫做圆锥的高；
圆锥母线：圆锥的侧面展开形成的扇形的半径、底面圆周上任意一点到顶点的距离。

圆锥的侧面积：将圆锥的侧面沿母线展开，是一个扇形,这个扇形的弧长等于圆锥底面的周长,而扇形的半径等于圆锥的母线的长.圆锥的侧面积就是弧长为圆锥底面的周长×母线/2；没展开时是一个曲面。

圆锥有一个底面、一个侧面、一个顶点、一条高、无数条母线，且底面展开图为一圆形，侧面展开图是扇形。

2圆锥体的展开图
圆锥体展开图由一个扇形（圆锥的侧面）和一个圆（圆锥的底面）组成。

(如下图）。

在绘制指定圆锥的展开图时，一般知道a（母线长）和d（底面直径）
∵弧AB=⊙O的周长
∴弧AB=πd
∵弧AB=2πa(∠1/360°)
∴2πa(∠1/360°)=πd
∴2a(∠1/360°)=d
将a,d带入2a(∠1/360°)=d得到∠1的值。

这样绘制展开图的所有所需数据都求出来了。

根据数据即可画出圆锥的展开图。

母线长等于底面圆直径的圆锥，展开的扇形就是半圆。

所有圆锥展开的扇形角度等于（底面直径÷母线）×180度。

青岛版六年级下册《第2章圆柱和圆锥》小学数学-有答案-单元测试卷（5）一、填一填．（22分，每空1分）1. 一般情况下，圆柱侧面展开后是一个________，圆锥侧面展开后是一个________．一个圆柱的侧面展开后是一个正方形，说明它的________和________相等。

2. 一个圆柱底面半径是3厘米，高5厘米，侧面积是________平方厘米，表面积是________平方厘米，体积是________立方厘米，与它等底等高的圆锥的体积是________立方厘米。

3. 一个圆锥的体积是24立方厘米，底面积是8平方厘米，它的高是________．4. 一个圆柱和一个圆锥等底等高，它们的体积之和是48立方米，那么圆锥体积是________立方分米。

5. 一个圆柱的底面半径是5cm，高是10cm，它的底面积是78.5cm2，侧面积是314 cm2，体积是785cm3．6. 用一张长4.5分米，宽1.2分米的长方形铁皮制成一个圆柱，这个圆柱的侧面积最多是________平方分米。

（接口处不计）7. 一个圆锥和一个圆柱等底等高，圆锥的体积是75cm3，圆柱的体积是________cm3．8. 一个圆柱半径是2分米，高是10分米，把圆柱沿水平方向切成两段，表面积增加了________．9. 42个铁圆锥可以熔铸成________个等底等高的圆柱体。

10. 一个圆柱底面直径是4厘米，高是10厘米，它的侧面积是________，表面积是________．11. 把一根长6米圆柱形的木料截成3段，表面积增加了25.12平方米，这个圆柱的体积是________立方米。

12. 把一个圆柱沿底面半径切开，等分后再拼成一个近似长方体，这个长方体长12.56厘米，高10厘米，这个圆柱的体积是________立方厘米。

13. 如图，工人师傅用薄铝板裁减下了2个相同的圆和一个长方形，用它们刚好能焊接成一个圆柱，已知圆的直径是4分米，则焊接成的圆柱的容积是________立方分米。

圆锥面积的推导过程
圆锥是一种常见的几何体，它由一个圆形的底部和一个顶点连
接起来的侧面组成。

圆锥的表面积是指其底部圆的面积加上其侧面
的面积。

下面我们来推导一下圆锥的表面积公式。

首先，我们来计算圆锥的底部圆的面积。

底部圆的面积公式为，A = πr^2，其中r为圆的半径，π为圆周率。

接下来，我们来计算圆锥的侧面积。

我们可以将圆锥的侧面展
开成一个扇形，然后计算其面积。

首先，我们需要计算圆锥的斜高（l）和生成线（s）。

斜高是指从圆锥顶点到底部圆周上的点的距离，生成线是指从圆锥顶点到底部圆心的距离。

根据勾股定理，我
们可以得到斜高和生成线的关系，l^2 = r^2 + h^2，其中h为圆锥
的高度。

然后，我们可以计算扇形的面积公式为，A = 1/2 r l θ，
其中θ为扇形的圆心角。

根据圆周率的定义，我们知道θ/360°
= l/2πr，因此θ = 2πl/r。

将θ代入扇形的面积公式中，我们
可以得到圆锥侧面积的公式，A = 1/2 r l (2πl/r) = πrl。

最后，我们将底部圆的面积和侧面积相加，即可得到圆锥的表面积公式，S = A + πrl = πr^2 + πrl。

通过以上推导过程，我们得到了圆锥的表面积公式，这个公式可以帮助我们计算圆锥的表面积，从而更好地理解和应用圆锥的几何性质。

圆锥的侧面展开图问题解决圆锥问题的关键是明确圆锥的侧面展开图各元素与圆锥各元素的关系——圆锥的侧面展开图是扇形，扇形的半径是圆锥的母线，弧长是圆锥的底面圆的周长．问题往往涉及圆锥的母线长、圆锥的高以及底面半径之间的关系，勾股定理则是架起三元素间的桥梁．如图1，设圆锥的底面半径为r ，母线AB 的长为l ，高为h ，则r 2+h 2=l 2，圆锥的侧面展开图是扇形ACD ，该扇形的半径为l ，设扇形ACD 的圆心角是θ，则扇形的弧CD 的长=2πr =180l θπ，圆锥的侧面积为S 侧=12×2πr ×l =πrl ．一、计算圆锥的侧面积例1 （邵阳）如图2所示的圆锥主视图是一个等边三角形，边长为2，则这外圆锥的侧面积为______（结果保留π）．分析：依题意，圆锥主视图是一个等边三角形，所以圆锥的母线长为2，底面半径为1，可以直接代入公式求得．解：依题意，r=1，l =2，所以S 侧=π×1×2=2π．二、求圆锥的母线长例2 （桂林）已知圆锥的侧面积为8πcm 2, 侧面展开图的圆心角为45°，则该圆锥的母线长为（ ）．（A ）64cm （B ）8cm （C ）22cm （D ）2cm 分析：圆锥的侧面积即其侧面展开图扇形的面积，由扇形的面积公式可求出圆锥的母线长（侧面展开图扇形的半径即为圆锥的母线长）．解：由2360n l S π=扇形，即2360n l π＝8π，解得l ＝8（cm ）．故应选（B ）． 三、计算圆锥的底面半径例3 （日照）将直径为60cm 的圆形铁皮，做成三个相同的圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），那么每个圆锥容器的底面半径为（ ）．（A ）10cm （B ）30cm （C ）40cm （D ）300cm分析：依题意，将直径为60cm 的圆形铁皮分割成三个大小相等的扇形，这三个扇形即三个相同的圆锥容器的侧面展开图．根据“侧面展开图扇形的弧长是圆锥的底面圆的周长”可求每个圆锥容器的底面半径．解：直径为60cm 的圆形铁皮的周长为60πcm ，故将该铁皮分割成三个大小相等的扇形的弧长为20πcm ．图1 图2设圆锥的底面半径为r ，则2πr ＝20π，解得r ＝10．故应选（A ）．四、计算圆锥的高例4 （鸡西）如图3，小明想用图中所示的扇形纸片围成一个圆锥，已知扇形的半径为5cm ，弧长是6πcm ，那么围成的圆锥的高度是 cm ． 分析：借助图1分析，知在r 2+h 2=l 2中，欲求h ，需知道r ，l ，显然这里l ＝5 cm ，故只需再求出r ．解：设圆锥的底面半径为r ，则2πr ＝6π，解得r ＝3．所以h 2=l 2－ r 2＝52－32，所以h ＝4（cm ）．五、计算侧面展开图中扇形圆心角的度数 例5 （成都）若一个圆锥的底面圆的周长是4πcm ，母线长是6cm ，则该圆锥的侧面展开图的圆心角的度数是（ ）．（A ）40° （B ）80° （C ）120° （D ）150°分析：设圆锥展开图的圆心角为n °，根据弧长公式可求出侧面展开图扇形的弧长为180n l π，再根据“侧面展开图扇形的弧长是圆锥的底面圆的周长”列方程可解． 解：设圆锥展开图的圆心角为n °，则4π=6180n πg ． 解得n ＝120．所以选（C ）．六、最短路径问题例6 （青岛）如图4是一个用来盛爆米花的圆锥形纸杯，纸杯开口圆的直径EF 长为10cm ．母线OE （OF ）长为10cm ．在母线OF 上的点A 处有一块爆米花残渣，且FA ＝2cm ，一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点．则此蚂蚁爬行的最短距离为 cm ．分析：由于小蚂蚁只能在圆锥侧面上爬行，所以我们可考虑把圆锥侧面展开，将问题转化为平面图形解决.将圆锥沿母线OE 剪开，如图7所示的展开图，根据“两点之间线段最短”，知EA 即为最短路径．解：设圆锥侧面展开后扇形的圆心角为n °，因为底面的周长等于展开后扇形的弧长，所以180n OE π⋅＝π E F ，即10180n π⋅＝10π，解得n °＝180°． 此圆锥的侧面展开图为扇形（如图5），在Rt △AEO 中， OA ＝OF －AF ＝8（cm ），O B A 图3 5cm 图5 Ａ Ｆ Ｅ Ｏ 图4。

圆锥的特征答案典题探究例1．一个圆柱有无数条高，一个圆锥也有无数条高．×（判断对错）考点：圆锥的特征；圆柱的特征．专题：立体图形的认识与计算．分析：根据圆柱的特征：圆柱的上下面是完全相同的两个圆，侧面是曲面，上下面之间的距离叫做圆柱的高，圆柱有无数条高，再根据圆锥高的定义，从圆锥的顶点到底面圆心的距离叫做圆锥的高，它只有1条高．据此判断．解答：解：圆柱下面之间的距离叫做圆柱的高，圆柱有无数条高；从圆锥的顶点到底面圆心的距离叫做圆锥的高，它只有1条高．因此，一个圆柱有无数条高，一个圆锥也有无数条高．这种说法是错误的．故答案为：×．点评：此题考查的目的是理解掌握圆柱、圆锥的特征，掌握圆柱、圆锥高的定义．例2．圆锥的侧面展开后是一个等腰三角形．×．（判断对错）考点：圆锥的特征．专题：图形与变换．分析：因为用一个扇形和一个圆可以制作一个圆锥，扇形是圆锥的侧面，圆是底面，由此得出结论．解答：解：圆锥的侧面展开后是一个扇形，不是等腰三角形；故答案为：×．点评：此题主要回顾圆锥的特征和制作过程，以此做出判断．例3．把圆锥的侧面展开，得到的是一个长方形．×．（判断对错）考点：圆锥的特征．分析：根据圆锥的侧面展开图可以判断．解答：解：根据圆锥的侧面展开后为一个扇形，如下图所示：所以上面的说法是错误的．故答案为：×．点评：此题考查了圆锥的侧面展开图的形状．例4．一个直角三角板的两条直角边分别为a、b，以b为轴旋转一周，在你眼前出现一个圆锥体，a 是它的底面半径，b是它的高．考点：圆锥的特征．分析：根据圆锥的特征进行解答即可．解答：解：一个直角三角板的两条直角边分别为a、b，以b为轴旋转一周，在你眼前出现一个圆锥体，a 是它的底面半径，b是它的高；故答案为：圆锥，底面半径，高．点评：此题考查的是对圆锥特征的理解，平时要注意对基础知识的积累．演练方阵A档（巩固专练）一．选择题（共15小题）1．一个圆锥的侧面展开图形是半径为8cm，圆心角为120°的扇形，则此圆锥的底面半径为（）A．cm B．cmC．3cm D．cm考点：圆锥的特征．专题：立体图形的认识与计算．分析：利用弧长公式L=和圆的周长公式C=2πr求解．解答：解：设此圆锥的底面半径为r，根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得：2πr=，r=cm．故选：A．点评：圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．本题就是把的扇形的弧长等于圆锥底面周长作为相等关系，列方程求解．2．以一个直角三角形的一条直角边为轴旋转一周，就可以得到一个（）A．长方形B．正方形C．圆柱体D．圆锥体考点：圆锥的特征．分析：根据圆锥的特征：为轴的那条直角边是旋转后的圆锥的高，另一条直角边是旋转后的圆锥的底面半径；进而得出结论．解答：解：如果以直角三角形的一条直角边为轴旋转一周，可以得到一圆锥体；故选：D．点评：解答此题的关键：根据圆锥的特征进行解答即可．3．圆锥体侧面展开图是（）A．扇形B．三角形C．梯形D．正方形考点：圆锥的特征．专题：立体图形的认识与计算．分析：根据圆锥的特征：圆锥的侧面展开后是一个扇形，据此选择即可．解答：解：根据圆锥的特征可知：圆锥的侧面展开后是一个扇形；故选：A．点评：此题考查了圆锥的侧面展开图，是对圆锥基础知识的掌握情况的了解，应注意平时基础知识的积累．4．下面几何体中，是圆锥体的是（）A．B．C．D．考点：圆锥的特征．分析：圆锥体由两部分组成，底面是个圆形，侧面是个曲面，圆锥的侧面展开后是一个扇形；据此选择即可．解答：解：A、是圆柱，不符合题意．B、是圆锥，符合题意．C、是圆台，不符合题意．D、是立方体，不符合题意；故选：B．点评：此题主要考查了对立体图形的认识，熟悉各种常见立体图形的性质即可轻松解答．5．把圆锥的侧面展开，会得到一个（）A．三角形B．长方形C．圆形D．扇形考点：圆锥的特征．专题：立体图形的认识与计算．分析：根据圆锥的特征：圆锥的侧面展开后是一个扇形，据此选择即可．解答：解：根据圆锥的特征可知：圆锥的侧面展开后是一个扇形；故选：D．点评：此题考查了圆锥的侧面展开图，是对圆锥基础知识的掌握情况的了解，应注意平时基础知识的积累．6．有一条高的立体图形（）A．圆柱B．长方体C．圆锥考点：圆锥的特征．分析：要选出有一条高的立体图形是哪种图形，要对给出的答案进行依次分析，进而得出答案．解答：解：A，圆柱有无数条高，即不符合；B，长方体有4条高，不符合题意；C，圆锥只有一条高，符合条件；故选：C．点评：此题应结合圆柱、长方体和圆锥的特征进行分析，比较，进而得出正确选项．7．圆锥的侧面展开可以得到一个（）A．圆B．长方形C．三角形D．扇形考点：圆锥的特征．专题：立体图形的认识与计算．分析：根据圆锥的特征：圆锥的侧面展开后是一个扇形，据此选择即可．解答：解：根据圆锥的特征可知：圆锥的侧面展开后是一个扇形；故选：D．点评：此题考查了圆锥的侧面展开图，是对圆锥基础知识的掌握情况的了解，应注意平时基础知识的积累．8．（2003•龙湖区）如果以直角三角形的一条直角边为轴旋转一周，可以得到一个（）A．圆柱体B．圆锥体C．长方体考点：圆锥的特征．专题：压轴题．分析：根据圆锥的认识：为轴的那条直角边是旋转后的圆锥的高，另一条直角边是旋转后的圆锥的底面半径；进而得出结论．解答：解：如果以直角三角形的一条直角边为轴旋转一周，可以得到一圆锥体；故选：B．点评：解答此题的关键：根据圆锥的特征进行解答即可．9．（•建华区）下面的平面图形，旋转一周可能形成圆锥的是（）A．长方形B．正方形C．直角三角形考点：圆锥的特征．专题：立体图形的认识与计算．分析：抓住圆锥图形的特征，即可选择正确答案．解答：解：根据圆锥的特征可得：直角三角形沿一条直角边旋转一周后得到圆锥，所给图形是直角三角形的是C选项．故选：C．点评：此题考查了旋转的性质及圆锥的展开图的特点．10．（•富源县）圆锥的侧面展开后是（）A．长方形B．扇形C．圆形考点：圆锥的特征．专题：压轴题；立体图形的认识与计算．分析：根据圆锥的特征：圆锥的侧面展开后是一个扇形，据此选择即可．解答：解：根据圆锥的特征可知：圆锥的侧面展开后是一个扇形；故选：B．点评：此题考查了圆锥的侧面展开图，是对圆锥基础知识的掌握情况的了解，应注意平时基础知识的积累．11．（•岑巩县）一个圆锥有（）条高．A．一B．二C．三D．无数考点：圆锥的特征．分析：紧扣圆锥的特征：从圆锥的顶点到底面圆心的距离是圆锥的高；即可解决问题．解答：解：根据圆锥的高的定义可知：圆锥只有一条高；故选：A．点评：此题考查了圆锥的特征，应注意基础知识的积累．12．（•安仁县）圆锥的侧面展开是一个（）A．三角形B．长方形C．扇形考点：圆锥的特征．专题：立体图形的认识与计算．分析：根据圆锥的特征：圆锥的侧面展开后是一个扇形，据此选择即可．解答：解：根据圆锥的特征可知：圆锥的侧面展开后是一个扇形；故选：C．点评：此题考查了圆锥的侧面展开图，是对圆锥基础知识的掌握情况的了解，应注意平时基础知识的积累．13．（•天河区）将一个圆锥体沿着它的高平均切成两块，切面一定是一个（）A．扇形B．长方形C．等腰三角形D．梯形考点：圆锥的特征．专题：立体图形的认识与计算．分析：根据圆锥的定义：以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的面所围成的旋转体叫做圆锥．因此将圆锥沿着它的高平均切成两半，截面是一个等腰三角形．解答：解：根据圆锥的定义，将圆锥沿着它的高平均切成两半，截面是一个等腰三角形．故选：C．点评：此题主要考查圆锥的认识，考查目的是让学生牢固掌握圆锥的特征．14．（•法库县模拟）圆锥的侧面展开后是一个（）A．圆B．扇形C．三角形D．梯形考点：圆锥的特征．分析：根据圆锥的特征：圆锥的侧面展开后是一个扇形，据此选择即可．解答：解：根据圆锥的特征可知：圆锥的侧面展开后是一个扇形；故选：B．点评：此题考查了圆锥的侧面展开图，是对圆锥基础知识的掌握情况的了解，应注意平时基础知识的积累．15．（•麻城市模拟）下面图形中，只有一条高的是（）A．三角形B．梯形C．圆柱D．圆锥考点：圆锥的特征．专题：立体图形的认识与计算．分析：根据圆锥的特征和高的意义，圆锥的底面是一个圆，侧面是一个曲面；从圆锥的顶点到底面圆心的距离叫做圆锥的高；由此解答．解答：解：三角形有3条高，梯形有无数条高，圆柱有无数条高，只有圆锥有1条高；故选：D．点评：此题要根据圆锥的特征和高的意义来进行分析判断．二．填空题（共2小题）16．从圆锥顶点到底面圆心的距离是圆锥的高，圆锥有无数条高．×（判断对错）考点：圆锥的特征．专题：立体图形的认识与计算．分析：根据圆锥的高的含义：从圆锥的顶点到底面圆心的距离是圆锥的高，圆锥有一条高；据此进行判断．解答：解：由分析可知：从圆锥顶点到底面圆心的距离是圆锥的高，圆锥有一条高；故答案为：×．点评：明确圆锥的高的含义，是解答此题的关键．17．一个三角形绕着它的一条边旋转，能得到一个圆锥．×．（判断对错）考点：圆锥的特征．专题：立体图形的认识与计算．分析：如果是直角三角形，绕直角边旋转一周可以得到一个圆锥，如果不是直角三形旋转一周不可以得到一个圆锥，据此即可判断．解答：解：如果是直角三角形，旋转一周，可以得到一个圆锥，否则不可能得到一个圆锥．故答案为：×．点评：注意只有是直角三角形绕直角边旋转一周，可得到圆锥．B档（提升精练）一．选择题（共15小题）1．一个图形的侧面展开是一个扇形，这个图形是（）A．圆柱B．圆锥C．圆考点：圆锥的特征．专题：立体图形的认识与计算．分析：因为圆锥的侧面展开图是扇形，所以一个图形的侧面展开是一个扇形，这个图是圆锥；据此选择即可．解答：解：根据圆锥的特征可知，侧面展开图是扇形的是圆锥．故选：B．点评：解题时勿忘记圆锥的特征及圆锥展开图的情形．2．圆锥有（）条高．A．1B．2C．无数考点：圆锥的特征．分析：紧扣圆锥的特征：从圆锥的顶点到底面圆心的距离是圆锥的高；即可解决问题．解答：解：根据圆锥的高的定义可知：圆锥只有一条高；故选：A．点评：此题考查了圆锥的特征，应注意基础知识的积累．3．如图，以直线AB为轴旋转后会形成图形（）A．B．C．考点：圆锥的特征；圆柱的特征．专题：立体图形的认识与计算．分析：以直线AB为轴旋转后，得到的是立体图形上在是圆锥体，下面是圆柱体；据此解答．解答：解：以直线AB为轴旋转后，得到的是立体图形上在是圆锥体，下面是圆柱体；故选：A．点评：此题考查了点、线、面、体，重在体现面动成体，考查学生立体图形的空间想象能力及分析问题、解决问题的能力．4．把一个底面半径10分米，高5分米的圆锥形木料，如果沿着高垂直切成相等的两半，表面积增加了（）平方分米．A．20B．100C．5D．无法计算考点：圆锥的特征．专题：立体图形的认识与计算．分析：圆锥沿直径切开，则表面积比原圆锥表面积增加了两个以底面直径为底，以圆锥的高为高的三角形面的面积，由此利用三角形的面积公式即可解答．解答：解：2×10×5÷2×2，=100÷2×2，=100（平方分米），答：表面积增加了100平方分米．故选：B．点评：解答此题要明确：增加的面积是两个以圆锥的底面直径和高分别为底和高的三角形面的面积．5．圆锥的高有（）条．A．无数B．0C．1考点：圆锥的特征．专题：立体图形的认识与计算．分析：紧扣圆锥的特征：从圆锥的顶点到底面圆心的距离是圆锥的高；即可解决问题．解答：解：根据圆锥的高的定义可知：圆锥只有一条高；故选：C．点评：此题考查了圆锥的特征，应注意基础知识的积累．6．圆锥的高（）A．仅有1条B．仅有2条C．有3条D．无数条考点：圆锥的特征．专题：立体图形的认识与计算．分析：根据圆锥高的定义，从圆锥的顶点到底面圆心的距离叫做圆锥的高，圆锥的高只有1条．据此解答．解答：解：从圆锥的顶点到底面圆心的距离叫做圆锥的高，圆锥的高只有1条．故选：A．点评：此题考查的目的是理解掌握圆锥的特征以及圆锥高的定义．7．一个直角三角形，以它的一条直角边为轴旋转一周，得到一个（）A．圆柱体B．圆锥体C．扇形考点：圆锥的特征．专题：立体图形的认识与计算．分析：根据圆锥的认识：为轴的那条直角边是旋转后的圆锥的高，另一条直角边是旋转后的圆锥的底面半径；进而得出结论．解答：解：如果以直角三角形的一条直角边为轴旋转一周，可以得到一圆锥体．故选：B．点评：解答此题的关键：根据圆锥的特征进行解答即可．8．下图是三位同学测量圆锥高的方法，你认为（）的方法正确．A．B．C．考点：圆锥的特征；长度的测量方法．专题：立体图形的认识与计算．分析：根据圆锥高的含义：从圆锥的顶点到底面圆心的距离是圆锥的高，并结合选项进行解答即可．解答：解：根据圆锥的高的测量方法可得：选项中C的方法正确；故选：C．点评：明确圆锥高的测量方法，是解答此题的关键．9．把一个底面直径为12厘米，高为9厘米的圆锥形铁块从中间切开，分成两个完全一样的小铁块，表面积比原来增加了（）平方厘米．A．54B．108C．226.08D．552.16考点：圆锥的特征．专题：立体图形的认识与计算．分析：把一个底面直径为12厘米，高为9厘米的圆锥形铁块从中间切开，分成两个完全一样的小铁块，表面积比原来增加了两个切面的面积，两个切面均是底为12厘米，高为9厘米的三角形，求出两个三角形的面积即可．解答：解：根据分析，表面积比原来增加了两个切面的面积，两个切面均是底为12厘米，高为9厘米的三角形，所以表面积比原来增加了：12×9÷2×2=108÷2×2=108（平方厘米）故选：B．点评：解答此题的关键是分析出增加的表面积即两个切面均是底为12厘米，高为9厘米的三角形的面积．10．以直角三角形的一条直角边为轴，旋转180°，就可以得到一个（）A．圆锥B．圆柱C．半圆锥考点：圆锥的特征．专题：立体图形的认识与计算．分析：根据圆锥的定义，以直角三角形的一条直角边为轴旋转一周得到的图形是圆锥，因此以直角三角形的一条直角边为轴，旋转180°，就可以得到一个半圆锥．据此解答． 解答： 解：由分析得：以直角三角形的一条直角边为轴，旋转180°，就可以得到一个半圆锥．故选：C ．点评： 此题考查的目的是理解掌握圆锥的特征．11．以一个正三角形的一条高为轴，旋转一周得到一个（ ）A ． 圆锥B ． 圆柱C ． 正方体D ． 长方体考点： 圆锥的特征；作旋转一定角度后的图形．专题： 立体图形的认识与计算．分析： 根据圆锥的特征，圆锥的底面是一个圆，侧面是一个曲面，顶点到底面圆心的距离叫做圆锥的高．因此，以一个正三角形的一条高为轴，旋转一周得到一个圆锥．解答： 解：由圆锥的特征可知：以一个正三角形的一条高为轴，旋转一周得到一个圆锥．故选：A ．点评： 此题考查的目的是理解掌握圆锥的特征．12．从圆锥顶点向底面作垂直切割，所得到的横截面是（ ）A ． 等腰三角形B ． 圆形C ． 扇形考点： 圆锥的特征．专题： 立体图形的认识与计算．分析： 从圆锥的顶点向底面作垂直切割，得到的是一个以底面直径为底，以圆锥的高为高的等腰三角形，由此解答即可．解答： 解：从圆锥的顶点向底面作垂直切割，得到的是一个以底面直径为底，以圆锥的高为高线的等腰三角形，故选：A ．点评： 抓住圆锥的切割特点，得出切割面是以底面直径为底以圆锥的高为底边高线的等腰三角形，是解决本题的关键．13．将如右图所示的圆心角为90°的扇形纸片AOB 围成圆锥形纸帽，使扇形的两条半径OA 与OB 重合（接缝粘贴部分忽略不计），则围成的圆锥形纸帽是（ ）A ．B ．C ．D ．考点： 圆锥的特征．分析： 圆锥的侧面展开后是扇形，由图可知：A 、B 一定重合，与A 、B相邻的两个阴影一定在A所在的母线重合，而另一端一定与圆锥的底面相交，即靠近A、B两点的两个空白部分无法围成环并且紧贴底面；据此解答．解答：解：由分析知：如右图所示的圆心角为90°的扇形纸片AOB围成圆锥形纸帽，使扇形的两条半径OA与OB重合（接缝粘贴部分忽略不计），则围成的圆锥形纸帽是第二种；故选：B．点评：解答此题应认真观察，根据圆锥的特征，进行分析，进而得出结论．14．（•合肥）下面说法正确的是（）A．圆锥的侧面展开图是一个等腰三角形B．小华身高1.2米，她在平均水深是1米的水池中游泳是绝对安全的C．圆的面积和半径成正比例D．如果ab=cd（a、b、c、d均不为0），那么a：c=d：b考点：圆锥的特征；比例的意义和基本性质；辨识成正比例的量与成反比例的量；平均数的含义及求平均数的方法．分析：根据题意，对各选项进行认真分析、进而得出结论．解答：解：A、圆锥的侧面展开图是一个等腰三角形，说法错误，应为扇形；B、小华身高1.2米，她在平均水深是1米的水池中游泳是绝对安全的，说法错误，因为平均水深是1米，并不代表所有的地方的水深都是1米；C、圆的面积和半径成正比例，说法错误，因为：=π（一定），圆的面积应和半径的平方成正比例；D、如果ab=cd（a、b、c、d均不为0），根据比例的基本性质可知：如果a是外项，那么b是外项，即c和d为内项，那么a：c=d：b，说法正确；故选：D．点评：解答此题用到的知识点：（1）圆锥的特征；（2）平均数的含义；（3）比例的基本性质；（4）判断成正反比例关系的量的方法．15．（•东城区）如图扇形的圆心角是120°，半径是r．请你想像，用这个扇形围成一个高为h的圆锥（接缝处不计），圆锥的高h与扇形的半径r之间的关系是（）A．h＞r B．h=r C．h＜r考点：圆锥的特征．专题：立体图形的认识与计算．分析：把该扇形围成圆锥后，扇形的半径即围成后圆锥的母线，圆锥的高与底面半径、圆锥母线构成直角三角形的三边，根据三角形中，斜边最长，所以扇形的高小于圆锥的母线（即扇形的半径r）；据此判断即可．解答：解：由分析知：用这个扇形围成一个高为h的圆锥（接缝处不计），圆锥的高h与扇形的半径r之间的关系：h＜r；故选：C．点评：解答此题应明确：圆锥的侧面展开图是一个扇形，此扇形的半径等于圆锥的母线长，圆锥的高与底面半径、圆锥母线构成直角三角形的三边．二．填空题（共12小题）16．（•杭州模拟）一个直角三角形沿一条直角边旋转一周，就会得到一个圆锥体．正确．考点：圆锥的特征．分析：根据圆锥的特征：一个直角三角形沿一条直角边旋转一周，就会得到一个圆锥体，为轴的那条直角边是旋转后的圆锥的高，另一条直角边是旋转后的圆锥的底面半径；进而得出结论．解答：解：根据圆锥的特征可知：一个直角三角形沿一条直角边旋转一周，就会得到一个圆锥体；故答案为：正确．点评：解答此题的关键：根据圆锥的特征进行解答即可．17．（•楚州区）如图一个半径为10厘米的半圆形铁皮，再配上一个面积是78.5平方厘米的圆形铁皮刚好可以制成一个圆锥体（不考虑损耗）．考点：圆锥的特征．专题：立体图形的认识与计算．分析：根据半径求圆周长的一半，圆周长的一半就是母线长，母线长就是底面圆的周长，根据底面圆的周长可以求出底面圆的半径，从而求出底面圆的面积．解答：解：半径为10厘米，则圆周长的一半=10π（厘米），底面半径r=10π÷2π=5（厘米），底面面积=25π=78.5（平方厘米）；故答案为：78.5．点评：本题利用了圆的面积公式，圆的周长公式和圆锥的特征进行求解．18．（•扬州）一个圆锥的底面半径扩大3倍，底面周长扩大6倍，底面积扩大9倍．错误．考点：圆锥的特征．分析：此题利用C=2πr，S=πr2即可计算解决．解答：解：已知C=2πr，S=πr2，根据积的变化规律可得：半径扩大3倍，那么周长就扩大3倍，底面积就扩大3×3=9倍，所以原题说法错误，故答案为：错误．点评：此题考查了积的变化规律在公式中的应用．19．（•慈利县）从圆锥顶点到底面圆心的距离就是圆锥的高．考点：圆锥的特征．分析：根据圆锥的高的含义：从圆锥顶点到底面圆心的距离就是圆锥的高；进行解答即可．解答：解：从圆锥顶点到底面圆心的距离就是圆锥的高；故答案为：底面圆心．点评：解答此题应根据圆锥的高的意义进行解答即可（这里所指的圆锥都是直圆锥）．20．（•普定县模拟）将圆锥沿着它的高平均切成两半，截面是一个等腰三角形．正确．考点：圆锥的特征．专题：立体图形的认识与计算．分析：根据圆锥的定义：以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的面所围成的旋转体叫做圆锥．因此将圆锥沿着它的高平均切成两半，截面是一个等腰三角形．解答：解：根据圆锥的定义，将圆锥沿着它的高平均切成两半，截面是一个等腰三角形．此说法正确．故答案为：正确．点评：此题主要考查圆锥的认识，考查目的是让学生牢固掌握圆锥的特征．21．（•广州模拟）从圆锥的顶点到底面圆心的距离是圆锥的高，圆锥有一条高．考点：圆锥的特征．分析：直接利用圆锥高的意义解答即可．解答：解：从圆锥的顶点到底面圆心的距离是圆锥的高，圆锥有一条高；故答案为：顶点，底面圆心，一．点评：解答有关特征题时，强记圆锥特征的四个一：一个顶点，一条高，一个侧面，一个圆．22．（•桐梓县模拟）冬冬说：“把圆锥的侧面展开，得到的是一个等腰三角形．”错误．考点：圆锥的特征．分析：根据圆锥的特征：圆锥的侧面展开后是扇形；进行判断即可．解答：解：因为圆锥的侧面展开后是扇形，所以冬冬说：“把圆锥的侧面展开，得到的是一个等腰三角形”说法错误；故答案为：错误．点评：解答此题应明确：圆锥的侧面展开后是一个扇形．23．（•泗县模拟）圆锥的底面是圆形，圆锥的侧面是一个曲面．考点：圆锥的特征．专题：立体图形的认识与计算．分析：根据圆锥的特征：圆锥的底面是一个圆，侧面是一个曲面，从顶点到底面圆心的距离叫做圆锥的高．解答：解：圆锥的底面是圆，侧面是一个曲面．。

人教版六年级下册数学第3单元《圆锥》强化训练题一．选择题（共9小题，满分45分，每小题5分）1．（5分）圆锥有（）条高．A．1B．2C．32．（5分）圆锥的侧面展开后是一个（）A．圆B．扇形C．三角形D．梯形3．（5分）将如图的图形绕虚线旋转一周后会得到的立体图形是（）A．B．C．D．4．（5分）如图图形以虚线为轴快速旋转后形成的图形是（）A．三角形B．圆锥C．圆柱5．（5分）在下面的图形中，以直线为轴旋转，可以得到圆锥的是（）A．B．C．D．6．（5分）下列哪一个不是圆锥（）A．B．C．D．7．（5分）如图所示，圆锥的高（）A．大于5cm B．等于5cm C．小于5cm 8．（5分）下面（）图形旋转就会形成圆锥．A．B．C．9．（5分）下面图形中，只有一条高的是（）A．三角形B．梯形C．圆柱D．圆锥二．填空题（共4小题，满分20分，每小题5分）10．（5分）如图中，以直线为轴旋转一周，形成圆柱的是，形成圆锥的是．11．（5分）以一个等腰直角三角形的一条直角边为轴，旋转一周生成的图形是．如果这个等腰直角三角形的一条直角边的长是10厘米，那么生成图形的高是厘米，底面积是平方厘米．12．（5分）圆锥的侧面展开图是一个，将圆锥沿高展开，所得到的横截面是一个．13．（5分）（单位：cm）以直角三角形的长直角边为轴旋转一周（如图）得到几何体是，体积是cm3．三．判断题（共5小题，满分25分，每小题5分）14．（5分）直角三角形绕着一条直角边旋转一周，得到的图形是圆锥．．（判断对错）15．（5分）冬冬说：“把圆锥的侧面展开，得到的是一个等腰三角形．”（判断对错）16．（5分）从圆锥的顶点到底面周长上任一点的距离是圆锥的高．．（判断对错）17．（5分）从圆锥的顶点到底面周长任意一点的连线都是圆锥的高．．（判断对错）18．（5分）圆锥的高有无数条．．（判断对错）四．解答题（共2小题，满分10分，每小题5分）19．（5分）标出下面圆锥的顶点、高、底面半径．20．（5分）一个圆锥的底面周长是15.7厘米，高是3厘米．从圆锥的顶点沿着高将它切成两半后，表面积之和比原圆锥的表面积增加了多少平方厘米？参考答案与试题解析一．选择题（共9小题，满分45分，每小题5分）1．【考点】圆锥的特征．【专题】立体图形的认识与计算．【分析】紧扣圆锥的特征：从圆锥的顶点到底面圆心的距离是圆锥的高；即可解决问题．【解答】解：根据圆锥的高的定义可知：圆锥只有一条高．故选：A．【点评】此题考查了圆锥的特征，应注意基础知识的积累．2．【考点】圆锥的特征．【分析】根据圆锥的特征：圆锥的侧面展开后是一个扇形，据此选择即可．【解答】解：根据圆锥的特征可知：圆锥的侧面展开后是一个扇形；故选：B．【点评】此题考查了圆锥的侧面展开图，是对圆锥基础知识的掌握情况的了解，应注意平时基础知识的积累．3．【考点】圆锥的特征．【专题】立体图形的认识与计算；几何直观．【分析】一个直角三角形围绕一条直角边为中心对称轴旋转一周形成一个圆锥体，据此选择即可．【解答】解：一个直角三角形围绕一条直角边为中心对称轴旋转一周形成一个圆锥体，故选：C．【点评】解决本题的关键是掌握圆锥体的特征．4．【考点】圆锥的特征．【专题】立体图形的认识与计算；几何直观．【分析】根据圆锥的特征及直角三角形的特征，直角三角形绕一条直角边旋转一周后会得到一个以旋转轴为高，另一直角边为底面半径的一个圆锥；由此解答即可．【解答】解：如图图形以虚线为轴快速旋转后形成的图形是圆锥；故选：B．【点评】本题是考查学生的空间想象力，关键是抓住圆锥的特征及直角三角形的特征．5．【考点】圆锥的特征．【专题】立体图形的认识与计算．【分析】一个直角三角形以一条直角边为轴，旋转一周，得到的图形是圆锥，据此解答．【解答】解：在下面的图形中，以直线为轴旋转，可以得到圆锥的是．故选：C．【点评】灵活掌握圆锥的特点，是解答此题的关键．6．【考点】圆锥的特征．【专题】立体图形的认识与计算；几何直观．【分析】圆锥是由一个底面和一个侧面两部分组成的，它的底面是一个圆，侧面是一个曲面．据此解答即可．【解答】解：不是圆锥，而是圆柱．故选：D．【点评】此题考查了圆锥的特征，要熟练掌握．7．【考点】圆锥的特征．【专题】立体图形的认识与计算；空间观念；应用意识．【分析】根据圆锥高的意义，从圆锥的顶点到底面圆心的距离叫做圆锥的高．再根据直角三角形的特征，在直角三角形中直角边一定小于斜边．所以这个圆锥的高小于5厘米．据此解答．【解答】解：从圆锥的顶点到底面圆心的距离叫做圆锥的高．因为在直角三角形中直角边一定小于斜边，所以这个圆锥的高小于5厘米．故选：C．【点评】此题考查的目的是理解掌握圆锥的特征，以及圆锥高的意义．8．【考点】圆锥的特征．【专题】立体图形的认识与计算；几何直观．【分析】长方形或正方形的对边相等，长方形或正方形以它的一边为轴旋转一周，它的上、下两个面就是以半径相等的两个圆面，与轴平行的一边形成一个曲面，这个长方形或正方形就成为一个圆柱．一个直角三角形，以它的一条直角边为轴，旋转一周，它的一面就是一个以另一条直角边为半径的一个圆面，直角三角形的斜边形成一个曲斜面，由于直角三角形的另一点在轴上，旋转后还是一点，这个直角三角形就形成一个圆锥．等腰三角形以它的底为轴，旋转一周，形成的是两个圆锥的组合体．【解答】解：图形旋转就会形成圆锥．故选：B．【点评】本题考主要考查面动成体，培养学生的空间观念．9．【考点】圆锥的特征．【专题】立体图形的认识与计算．【分析】根据圆锥的特征和高的意义，圆锥的底面是一个圆，侧面是一个曲面；从圆锥的顶点到底面圆心的距离叫做圆锥的高；由此解答．【解答】解：三角形有3条高，梯形有无数条高，圆柱有无数条高，只有圆锥有1条高；故选：D．【点评】此题要根据圆锥的特征和高的意义来进行分析判断．二．填空题（共4小题，满分20分，每小题5分）10．【考点】圆锥的特征；圆柱的展开图．【分析】根据旋转的性质和圆柱、圆台、圆锥的展开图的特点，逐项分析即可解答．【解答】解：A、长方形沿一条边旋转一周，得到的是圆柱体；B、半圆形沿直径所在的直线转一周形成一个球体；C、直角梯形沿直角腰旋转一周，得到的是圆台；D、直角三角形沿一条直角边旋转一周，得到的是圆锥体；所以，以直线为轴旋转一周，形成圆柱的是A，形成圆锥的是D．故答案为：A、D．【点评】此题考查了旋转的性质及圆锥、圆柱的展开图的特点．11．【考点】圆锥的特征．【专题】立体图形的认识与计算．【分析】如果以这个等腰直角三角形的直角边为轴，旋转后组成的图形是一个底面半径为10cm，高为10cm的一个圆锥；根据圆锥的底面积公式S＝π×r×r，即可求出圆锥的底面积，据此解答即可．【解答】解：圆锥底面半径10厘米，高10厘米3.14×10×10＝3.14×100＝314（平方厘米）答：以一个等腰直角三角形的一条直角边为轴，旋转一周生成的图形是圆锥．如果这个等腰直角三角形的一条直角边的长是10厘米，那么生成图形的高是10厘米，底面积是314平方厘米．故答案为：圆锥，10，314．【点评】本题考查了将一个简单图形绕一轴旋转一周所组成的图形是什么图形，以及圆锥的底面积计算和特征．12．【考点】圆锥的特征．【专题】综合填空题；立体图形的认识与计算．【分析】根据圆锥的特征：圆锥的底面是个圆面，把圆锥的侧面展开后是一个扇形；把圆锥沿底面直径和高切成两半，得到的每个截面是一个以底面直径为底，以圆锥的高为高的等腰三角形，据此解答即可．【解答】解：圆锥的底面是个圆面，圆锥的侧面是一个曲面，展开后是一个扇形，把圆锥沿底面直径和高切成两半，得到的每个截面是一个以底面直径为底，以圆锥的高为高的等腰三角形；故答案为：扇形，等腰三角形．【点评】此题考查了圆锥的侧面展开图、切割面的特点，是对圆锥基础知识的掌握情况的了解，应注意平时基础知识的积累．13．【考点】圆锥的特征．【专题】综合填空题；立体图形的认识与计算．【分析】（1）如图，以4cm的直角边为轴旋转一周，可以得到一个高是4厘米，底面半径是3厘米的圆锥．（2）根据圆锥的体积公式V＝πr2h即可求出这个圆锥的体积．【解答】解：（1）以4cm的直角边为轴旋转一周，可以得到一个立体图形，这个立体图形是圆锥体；（2）×3.14×32×4＝3.14×3×4＝37.68（立方厘米）故答案为：圆锥体，37.68．【点评】本题一是考查将一个简单图形绕一轴旋转一周所组成的图形是什么图形，二是考查圆锥的体积计算．三．判断题（共5小题，满分25分，每小题5分）14．【考点】圆锥的特征【专题】立体图形的认识与计算．【分析】根据圆锥的定义：以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的面所围成的旋转体叫做圆锥．由此解答．【解答】解：根据圆锥的定义，直角三角形绕着一条直角边旋转一周，得到的图形是圆锥．此说法正确．故答案为：√．【点评】此题考查的目的是使学生掌握圆锥的特征．15．【考点】圆锥的特征．【分析】根据圆锥的特征：圆锥的侧面展开后是扇形；进行判断即可．【解答】解：因为圆锥的侧面展开后是扇形，所以冬冬说：“把圆锥的侧面展开，得到的是一个等腰三角形”说法错误；故答案为：×．【点评】解答此题应明确：圆锥的侧面展开后是一个扇形．16．【考点】圆锥的特征．【专题】立体图形的认识与计算．【分析】根据圆锥的高的含义：从圆锥的顶点到底面圆心的距离是圆锥的高，进而判断即可【解答】解：从圆锥的顶点到底面周长上任一点的距离是圆锥的高，说法错误；故答案为：×．【点评】此题主要考查了圆锥的高的含义，应注意基础知识的积累．17．（【考点】圆锥的特征．【专题】立体图形的认识与计算．【分析】根据圆锥的特征，圆锥的底面是一个圆，侧面是曲面，侧面展开是一个扇形，从圆锥的顶点到底面圆心的距离叫做圆锥的高．据此判断．【解答】解：从圆锥的顶点到底面圆心的距离叫做圆锥的高．因此，从圆锥的顶点到底面周长任意一点的连线都是圆锥的高．这种说法是错误的．故答案为：×．【点评】此题考查的目的是理解掌握圆锥的特征，以及圆锥高的意义．18．【考点】圆锥的特征．【专题】立体图形的认识与计算．【分析】紧扣圆锥的特征：从圆锥的顶点到底面圆心的距离是圆锥的高；可知：圆锥只有一条高；据此判断即可．【解答】解：由圆锥高的含义可知：圆锥的高有无数条，说法错误；故答案为：×．【点评】此题考查了圆锥的特征，应注意基础知识的积累．四．解答题（共2小题，满分10分，每小题5分）19．【考点】圆锥的特征．【专题】立体图形的认识与计算；空间观念；应用意识．【分析】根据圆锥的特征，圆锥的底面是一个圆，侧面是一个曲面，从顶点到底面圆心的距离叫做圆锥的高。

2020年湖北省中考数学各地区模拟试题分类（武汉市专版）（二）——《圆》一．选择题1．（2020•江岸区校级模拟）已知⊙O的半径为4，点O到直线m的距离为3，则直线m与⊙O的位置关系是（）A．相离B．相交C．相切D．不确定2．（2020•武汉模拟）如图，AB是⊙O的直径，AB＝a，点P在半径OA上，AP＝b，过P 作PC⊥AB交⊙O于点C，在半径OB上取点Q，使得OQ＝CP，DQ⊥AB交⊙O于点D，点C，D位于AB两侧，则弧AC与弧BD的弧长之和为（）A．B．C．D．3．（2020•武汉模拟）在⊙O中内接四边形ABCD，其中A，C为定点，AC＝8，B在⊙O 上运动，BD⊥AC，过O作AD的垂线，若⊙O的直径为10，则OE的最大值接近于（）A．B．C．4 D．5 4．（2020•武昌区模拟）如图，正方形ABCD的边长为1，点E是AB边上的一点，将△BCE 沿着CE折叠得△FCE．若CF，CE恰好都与正方形ABCD的中心O为圆心的⊙O相切，则折痕CE的长为（）A．2B．C．D．5．（2020•武汉模拟）如图，在等腰直角△ABC中，斜边AB的长度为8，以AC为直径作圆，点P为半圆上的动点，连接BP，取BP的中点M，则CM的最小值为（）A．3B．2﹣C．﹣D．3﹣6．（2020•武汉模拟）如图，PA、PB为⊙O的切线，直线MN切⊙O且MN⊥PA．若PM ＝5，PN＝4，则OM的长为（）A．2 B．C．D．7．（2020•青山区模拟）如图，A，B，C，D为一直线上4个点，BC＝3，△BCE为等边三角形，⊙O过A，D，E三点，且∠AOD＝120°，设AB＝x，CD＝y，则y与x的函数关系式是（）A．y＝B．y＝x C．y＝3x+3 D．y＝8．（2020•硚口区模拟）平面直角坐标系中，M点坐标为（﹣2，3），以2为半径画⊙M，则以下结论正确的是（）A．⊙M与x轴相交，与y轴相切B．⊙M与x轴相切，与y轴相离C．⊙M与x轴相离，与y轴相交D．⊙M与x轴相离，与y轴相切9．（2020•武汉模拟）如图，在⊙O中，AB是直径，且AB＝10，点D是⊙O上一点，点C 是的中点，CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CE、CB于点P、Q，连接AC，OP，CO．关于下列结论：①∠BAD＝∠ABC；②GP ＝GD；③点P是△ACQ的外心；④点P是△AOC的内心；⑤若CB∥GD，则OP＝．正确的个数有（）A．2 B．3 C．4 D．0 10．（2020•武汉模拟）如图，BC为⊙O直径，弦AC＝2，弦AB＝4，D为⊙O上一点，I 为AD上一点，且DC＝DB＝DI，AI长为（）A．B．C．D．二．填空题11．（2020•武汉模拟）如图，在⊙O中，弦AB＝4，点C是上的动点（不为A，B），且∠ACB＝120°，则CA+CB的最大值为．12．（2020•武汉模拟）如图，正方形的边长为8，剪去四个角后成为一个正八边形，则这个正八边形的面积为．13．（2020•武汉模拟）圆锥的侧面展开图是一个扇形，扇形的弧长为10πcm，扇形面积为65πcm2，则圆锥的高为．14．（2020•武汉模拟）正八边形半径为2，则正八边形的面积为．15．（2020•武汉模拟）如图，正方形ABCD中，AB＝4，E，F分别是边AB，AD上的动点，AE＝DF，连接DE，CF交于点P，过点P作PK∥BC，且PK＝2，若∠CBK的度数最大时，则BK长为．16．（2020•武汉模拟）已知一个圆锥的高为6cm，半径为8cm，则这个圆锥的侧面积为．17．（2020•武汉模拟）正n边形内接于半径为R的圆，这个n边形的面积为3R2，则n等于．18．（2020•武汉模拟）如图，PA，PB分别与⊙O相切于A，B两点，∠P＝70°，点C在劣弧AB上，则∠C＝．19．（2020•武汉模拟）我国魏晋时期的数学家刘徽首创“割圆术”，利用圆的内接正多边形逐步逼近圆来近似计算圆的周长，进而确定圆周率．某圆的半径为R，其内接正十二边形的周长为C．若R＝，则C＝，≈（结果精确到0.01，参考数据：≈2.449，≈1.414）．三．解答题20．（2020•武汉模拟）如图，AB是⊙O的直径，CD与⊙O相切于D，作CH⊥AB于H，交⊙O于E，交AD于F，若AE∥CD．（1）求证：AE＝EF；（2）若cos C＝，AB＝，求AF的长．21．（2020•青山区模拟）已知，⊙O过矩形ABCD的顶点D，且与AB相切于点E，⊙O 分别交BC，CD于H，F，G三点．（1）如图1，求证：BE﹣AE＝CG；（2）如图2，连接DF，DE．若AE＝3，AD＝9，tan∠EDF＝，求FC的值．22．（2020•武汉模拟）如图，在△ABC中，∠C＝90°，∠BAC的平分线交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC、AB于点E．F．（1）试判断直线BC与⊙O的位置关系，并说明理由；（2）若BD＝2，BF＝2，求⊙O的半径．23．（2020•硚口区二模）如图，在Rt△ABC中，∠ACB＝90°，以AB上的一点O为圆心，OA为半径作圆O，与BC相切于点D，交AB于点E，交AC于点F．（1）求证：DE＝DF；（2）若CF：BE＝4：5，求tan∠BDE的值．24．（2020•洛江区一模）如图①，AB为⊙O的直径，C为⊙O上一点，D为BC延长线一点，且BC＝CD，直线CE与⊙O相切于点C，与AD相交于点E．（1）求证：CE⊥AD；（2）如图②，设BE与⊙O交于点F，AF的延长线与CE交于点P．①求证：∠PCF＝∠CBF；②若PF＝6，tan∠PEF＝，求PC的长．参考答案一．选择题1．解：∵d＝3＜半径＝4，∴直线与圆相交，故选：B．2．解：连接OC、OD，如图，∵CP⊥OA，DQ⊥OB，∴∠OPC＝∠OQD＝90°，在Rt△OPC和Rt△DQO中，∴Rt△OPC≌Rt△DQO（HL），∴∠POC＝∠ODQ，而∠ODQ+∠DOQ＝90°，∴∠POC+∠DOQ＝90°，∴弧AC与弧BD的弧长之和＝＝aπ．故选：B．3．解：如图，当点B与A重合时，连接CD．∵BD⊥AC，∴∠DAC＝90°，∴CD是直径，∵OE⊥AD，∴AE＝ED，∵OC＝OD，∴OE＝AC＝4，此时OE的值最大，最大值为4∴OE的最大值为4，故选：C．4．解：连接OC，∵O为正方形ABCD的中心，∴∠DCO＝∠BCO，∵CF与CE都为⊙O的切线，∴CO平分∠ECF，即∠FCO＝∠ECO，∴∠DCO﹣∠FCO＝∠BCO﹣∠ECO，即∠DCF＝∠BCE，∵△BCE沿着CE折叠至△FCE，∴∠BCE＝∠ECF，∴∠BCE＝∠ECF＝∠DCF＝∠BCD＝30°，在Rt△BEC中，cos∠ECB＝，∴CE＝＝＝，故选：B．5．解：如图，连接PA、PC，取AB、BC的中点E、F，连接EF、EM、FM，取EF的中点O，连接OM，OC，CM．∵AC是直径，∴∠APC＝90°，∵BE＝EA，BM＝MP，∴EM∥PA，同理FM∥PC，∴∠BME＝∠BPA，∠BMF＝∠BPC，∴∠BME+∠BMF＝∠BPA+∠BPC＝90°，∴∠EMF＝90°，∴点M的轨迹是，（EF为直径的半圆，图中红线部分）∵BC＝AC，∠ACB＝90°，AB＝8，∴AC＝BC＝4，∵AE＝EB，BF＝CF＝2，∴EF＝AC＝2，EF∥AC，∴∠EFB＝∠EFC＝∠ACB＝90°，OE＝OF＝OM＝，∴OC＝＝＝，∵CM≥OC﹣OM，∴CM≥﹣故选：C．6．解：∵PA、PB为⊙O的切线，直线MN切⊙O于C，∴MB＝MC，PA＝PB，连接OC，OA，则四边形AOCN是正方形，设NC＝OC＝OA＝AN＝r，∵MN⊥PA，PM＝5，PN＝4，∴MN＝3，∴CM＝BM＝3﹣r，∴5+3﹣r＝4+r，解得：r＝2，∴OC＝2，CM＝1，∴OM＝＝，故选：D．7．解：连接AE，DE，∵∠AOD＝120°，∴为240°，∴∠AED＝120°，∵△BCE为等边三角形，∴∠BEC＝60°；∴∠AEB+∠CED＝60°；又∵∠EAB+∠AEB＝∠EBC＝60°，∴∠EAB＝∠CED，∵∠ABE＝∠ECD＝120°；∴△ABE∽△ECD，∴＝，即＝，∴y＝（0＜x＜6）．8．解：∵M点坐标为（﹣2，3），∴点M到x轴的距离为3，到y轴的距离为2，∵⊙P的半径为2，∴圆心M到x轴的距离大于半径，到y轴的距离等于半径，故⊙M与x轴相离，与y轴相切，故选：D．9．解：不妨设∠BAD＝∠ABC，则＝，∵＝，∴＝＝，这个显然不符合题意，故①错误，连接OD，∵GD是⊙O的切线，∴OD⊥DG，∴∠ODG＝90°，∴∠GDP+∠ODA＝90°，∵GE⊥AB，∴∠AEP＝90°，∴∠PAE+∠APE＝90°，∵OA＝OD，∴∠OAD＝∠ODA，∵∠APE＝∠GPD，∴∠GDP＝∠GPD，∴GP＝GD，故②正确，∵AB是直径，∴∠ACB＝90°，∵∠ACP+∠BCE＝90°，∠BCE+∠ABC＝90°，∴∠ACE＝∠ABC，∵＝，∴∠CAP＝∠ABC，∴∠PAC＝∠PCA，∵∠AQC+∠CAP＝90°，∠ACP+∠PCQ＝90°，∴∠PCQ＝∠PQC，∴PC＝PQ，∴PA＝PQ，∵∠ACQ＝90°，∴点P是△ACQ的外接圆的圆心，故③正确，∵与不一定相等，∴∠CAP与∠DAB不一定相等，∴点P不一定是△AOC的内心，故④错误，∵DG∥BC，OD⊥DG，∴OD⊥BC，∴＝，∵＝，∴＝＝，∴∠AOC＝∠COD＝∠DOB＝60°，∠CAD＝∠DAB＝30°∵OA＝OC，∴△OAC是等边三角形，∵CE⊥OA，∴∠ACE＝∠OCE，∴点P是△AOC的外心，∴OP＝AP＝PC＝＝＝，故⑤错误，故选：A．10．解：如图，连接IC，作IE⊥AC于E，IF⊥AB于F，IG⊥BC于G．∵DB＝DC，∴＝，∠DBC＝∠DCB，∴∠BAD＝∠CAD，∵DI＝DC，∴∠DIC＝∠DCI，∵∠DIC＝∠DAC+∠ACI，∠DCI＝∠DCB+∠ICB，∠DBC＝∠DAC，∴∠ICA＝∠ICB，∴点I为△ABC内心，∴IE＝IF＝IG，∵BC是直径，∴∠BAC＝90°，∴BC＝＝＝2，∵S△ABC＝•AB•AC＝•IE•（AB+AC+BC），∴IE＝3﹣，∵∠IAE＝∠AIE＝45°，∴AI＝IE＝3﹣，故选：D．二．填空题（共9小题）11．解：取优弧AB中点P，连接PC，PA，PB，延长CA至M，使MA＝CB，连接PM．∵＝，∴PA＝PB，∵∠APB+∠ACB＝180°，∠ACB＝120°，∴∠APB＝60°，∴△APB是等边三角形，∴∠ACP＝∠ABP＝60°，∵∠PAM+∠PAC＝180°，∠PAC+∠PBC＝180°，∴∠PAM＝∠PBC，∵AM＝BC，AP＝BP，∴△MAP≌△CBP（SAS），∴PM＝PC，∵∠PCM＝60°∴△MPC为等边三角形，∴PC＝CM．∴CA+CB＝PC，过点P作PD⊥AB连接OB，∵△PAB是等边三角形，∴PD过圆心O，∠BPD＝30°，∴BD＝AB＝2，在Rt△BDP中，DP＝6，在Rt△BDO中，根据勾股定理得，（6﹣OB）2+（2）2＝OB2∴OB＝4，当PC为圆的直径时，CA+CB的最大值为8．故答案为8．12．解：设剪掉的等腰直角三角形的直角边为x，则由2x+x＝8，解得x＝4（2﹣），∴S＝64﹣2（8﹣4）2＝128﹣128，故答案为：128﹣128．13．解：设母线长为R，由题意得：65π＝×10π×R，解得R＝13cm．设圆锥的底面半径为r，则10π＝2πr，解得：r＝5，故圆锥的高为：＝12故答案为：12．14．解：连接OA，OB，作AC⊥BO于点C，∵⊙O的半径为2，则⊙O的内接正八边形的中心角为：＝45°，∴AC＝CO＝2，∴S△ABO＝OB•AC＝×2×2＝2，∴S正八边形＝8S△ABO＝16，故答案为：16．15．解：∵正方形ABCD中，AD＝CD，∠A＝∠CDA＝90°，∵AE＝DF，∴△ADE≌△DCF（SAS），∴∠ADE＝∠DCF，∵∠ADE+∠CDE＝90°，∴∠DCF+∠CDE＝90°，∴∠CPD＝90°，∴点P在以CD为直径的半圆上运动，取CD的中点O，过O作OM⊥CD，且点M在CD的右侧，MO＝2，连接OP，KM，∵PK∥BC，BC⊥CD，∴PK⊥CD，∴PK∥OM，PK＝OM＝2，∴四边形POMK是平行四边形，∵CD＝AB＝4，∴OP＝CD＝2，∴OP＝OM，∴四边形POMK是菱形，∴点K在以M为圆心，半径＝2的半圆上运动，当BK与⊙M相切时，∠CBK最大，∴∠BKM＝90°，∵BM＝＝2，∴BK＝＝6，故答案为：6．16．解：这个圆锥的母线长为＝10，所以这个圆锥的侧面积＝×2π×8×10＝80π（cm2）．故答案为80πcm2．17．解：根据正n边形内接于半径为R的圆，则可将其分割成n个全等的等腰三角形，其中等腰三角形的腰长为圆的半径R，顶角为，∵n边形的面积为3R2，∴n××R×R×sin＝3R2n sin＝6解得n＝12．故答案为12．18．解：连结OA、OB，D为优弧AB上一点，∠ADB为弧AB所对的圆周角，如图，∵PA，PB分别与⊙O相切于A，B两点，∴OA⊥PA，OB⊥PB，∴∠OAP＝∠OBP＝90°，∴∠AOB+∠P＝180°，∴∠AOB＝180°﹣70°＝110°，∴∠D＝∠AOB＝55°，∴∠ACB＝180°﹣∠D＝125°．故答案为：125°．19．解：如图，△AOB中，∠AOB＝30°，OA＝OB＝+，作AH⊥OB于H．则AH＝OA＝，OH＝AH＝，∴BH＝OB﹣OH＝，∴AB＝＝＝2，∴正十二边形的周长C＝12×2＝24，∴＝≈3.11，故答案我为24，3.11．三．解答题（共5小题）20．（1）证明：连接OD，如图1，∵CD与⊙O相切于D，∴OD⊥DC，∴∠ODA+∠ADC＝90°，∵OA＝OD，∴∠ODA＝∠OAD，∴∠OAD+∠ADC＝90°，又∵CH⊥AB，∴∠AHC＝90°，∴∠OAD+∠AFH＝90°，∴∠ADC＝∠AFH，∵AE∥CD，∴∠ADC＝∠EAF，∴∠EAF＝∠AFH，∴AE＝EF；（2）解：∵AE∥CD，∴∠C＝∠E，∴cos∠C＝cos∠E＝，设EH＝4x，AE＝5x，则AH＝3x，连接OE，如图2，∵AB＝，∴OA＝OE＝，∵EH2+OH2＝OE2，∴，解得x＝1，∴AE＝EF＝5，EH＝4，AH＝3，∴HF＝1，∴AF＝＝．21．解：（1）连接OE，延长EO与CD交于点M，∵⊙O与AB相切于点E，∴OE⊥AB，∵四边形ABCD是矩形，∴∠A＝∠B＝∠C＝∠D＝90°，AB∥CD，∴EM⊥CD，∴∠EMD＝∠EMC＝90°，DM＝GM，∴四边形AEMD和四边形BEMC都是矩形，∴AE＝DM，BE＝CM，∵CM﹣CG＝GM，∴BE﹣AE＝CG；（2）连接EO，延长EO交⊙O于点N，交CD于点M，连接OD，EF，FN，过点N作NH⊥BC，与BC的延长线交于点H，如图2，由（1）知，四边形AEMD为矩形，∴AE＝DM＝MG＝3，AD＝EM＝9，设⊙O的半径为r，则OD＝r，OM＝9﹣r，∵OD2﹣OM2＝DM2，∴r2﹣（9﹣r）2＝32，解得，r＝5，∴BH＝EN＝2r＝10，∴CH＝BH﹣BC＝BH﹣AD＝1，∵EN为⊙O的直径，∴∠EFN＝90°，∵∠ENF＝∠EDF，tan∠EDF＝，∴tan∠ENF＝，设EF＝4x，则FN＝3x，∵EF2+FN2＝EN2，∴16x2+9x2＝100，解得，x＝2，或x＝﹣2（舍），∴EF＝8，FN＝6，设CF＝y，BE＝HN＝z，则BF＝9﹣y，FH＝y+1，∵∠EFN＝90°，∠B＝∠H＝90°，∴∠BFE+∠HFN＝∠BFE+∠BEF＝90°，∴∠BEF＝∠HFN，∴△BEF∽△HFN，∴，即，解得，y＝，即CF＝．22．解：（1）线BC与⊙O的位置关系是相切，理由是：连接OD，∵OA＝OD，∴∠OAD＝∠ODA，∵AD平分∠CAB，∴∠OAD＝∠CAD，∴∠ODA＝∠CAD，∴OD∥AC，∵∠C＝90°，∴∠ODB＝90°，即OD⊥BC，∵OD为半径，∴线BC与⊙O的位置关系是相切；（2）设⊙O的半径为R，则OD＝OF＝R，在Rt△BDO中，由勾股定理得：OB2＝BD2+OD2，即（R+2）2＝（2）2+R2，解得：R＝4，即⊙O的半径是4．23．（1）证明：连接OD、EF交于点M，∵AE是⊙O的直径，∴∠AFE＝∠90°＝∠ACB，∴EF∥BC，又∵BC切⊙O于D，∴∠ODB＝90°，∴∠OME＝∠ODB＝90°，即OD⊥EF，∴＝，∴DE＝DF；（2）解：∵EF∥BC，∴＝，∴可设AF＝8k，AE＝10k，∴OA＝OE＝OD＝5k，∵∠AFE＝90°，∴EF＝＝6k，又∵OD⊥EF，∴EM＝FM＝3k，∵OD⊥EF，∴OM＝＝4k，∴DM＝OD﹣OM＝k，∵EF∥BC，∴∠BDE＝∠FED，∴tan∠BDE＝tan∠FED＝＝＝．24．（1）证明：如图①，连结OC．∵直线CE与⊙O相切于点C，∴OC⊥CE，即∠OCE＝90°．∵OA＝OB，BC＝CD，∴OC是△BDA的中位线．∴OC∥AD．∴∠CED＝∠OCE＝90°，即OC⊥AD；（2）①证明：如图②，作直径CG，连结FG，连结CF，∵CG是直径，点F在圆上，∴∠CFG＝90°．∴∠G+∠FCG＝90°．由（1）可知∠OCE＝∠PCF+∠FCG＝90°，∴∠G＝∠PCF．又∵∠G＝∠CBF，∴∠PCF＝∠CBF；②如图②，连结AC．∵AB是直径，点F在圆上，∴∠AFB＝∠PFE＝90°＝∠CEA．又∵∠EPF＝∠APE，∴△PEF∽△PAE．∴＝，即PE2＝PF•PA．在直角△PEF中，tan∠PEF＝＝，又∵PF＝6，∴EF＝8，由勾股定理，可求得PE＝10．∵∠FBC＝∠PCF＝∠CAF，∠CPF＝∠APC ∴△PCF∽△PAC．∴＝，即PC2＝PF×PA．∴PC2＝PE2，则PC＝PE＝10．。

圆锥侧面展开图是什么图形
圆锥的侧面展开图为扇形。

扇形的半径为圆锥的母线，扇形的弧长为圆锥的底面周长。

面积公式：圆锥侧面展开图S侧=πrl=（nπl^2）/360
拓展资料：
以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的面所围成的旋转体叫做圆锥。

该直角边叫圆锥的轴。

（1）以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的面所（2）圆锥由一个顶点，一个侧面和一个底面组成，从顶点到底面圆心的距离是圆锥的高。

(3)圆锥有两个面，底面是圆形，侧面是曲面。

(4)让圆锥沿母线展开，是一个扇形。

圆柱的体积等于和它等底等高的圆锥的体积的三倍是叫圆锥形。

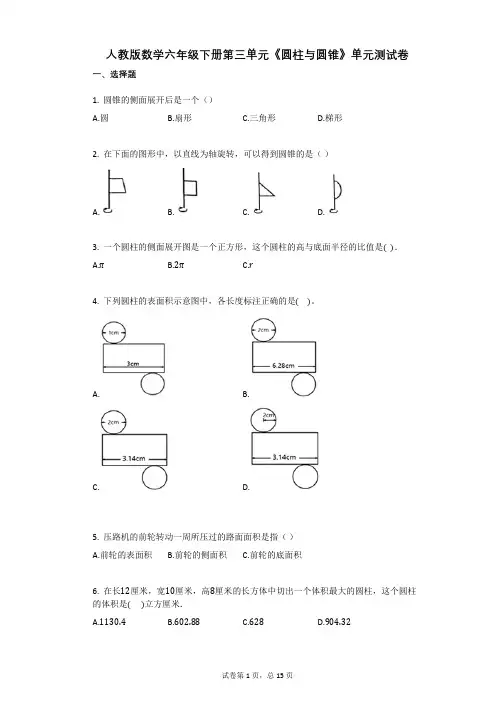
人教版数学六年级下册第三单元《圆柱与圆锥》单元测试卷一、选择题1. 圆锥的侧面展开后是一个（）A.圆B.扇形C.三角形D.梯形2. 在下面的图形中，以直线为轴旋转，可以得到圆锥的是（）A. B. C. D.3. 一个圆柱的侧面展开图是一个正方形，这个圆柱的高与底面半径的比值是()．A.πB.2πC.r4. 下列圆柱的表面积示意图中，各长度标注正确的是()。

A. B.C. D.5. 压路机的前轮转动一周所压过的路面面积是指（）A.前轮的表面积B.前轮的侧面积C.前轮的底面积6. 在长12厘米，宽10厘米，高8厘米的长方体中切出一个体积最大的圆柱，这个圆柱的体积是()立方厘米．A.1130.4B.602.88C.628D.904.327. 一个圆柱的底面直径与一个圆锥的底面半径都是10厘米，如果它们的体积也相等，圆柱的高是圆锥的（）A. B. C.8. 用24个铁圆锥，可以熔铸成（）个等底等高的铁圆柱．A.12B.8C.6D.4二、填空题用一张边长是12.56分米的正方形纸，围成一个圆柱体，这个圆柱体的底面直径是________分米．当圆柱的底面周长与它的高相等时，沿着高将圆柱的侧面展开，得到一个________．一个圆锥体积是12cm³，底面积是1.2cm²，高是(________)cm．把一个圆柱的侧面展开是一个正方形，这个圆柱的底面直径是4厘米，圆柱的高是(________)厘米。

(π取3.14)一根长1米的圆柱形木棒，锯成3段后，表面积增加了64平方分米，这根木棒的体积是________．一个直角三角形的三条边长分别是3cm、4cm和5cm，若以直角边为轴旋转一圈，旋转一圈形成的图形体积是(________)立方厘米。

(π取3.14)以直角三角形的长直角边为轴旋转一周（如图）得到几何体是________，体积是________cm3．（单位：cm）圆锥的侧面展开图是一个(________)，将圆锥沿高展开，所得到的横截面是一个(________)。

2021学年北师大版六年级数学下册《第一单元圆柱与圆锥》单元测试题一．选择题（共8小题）1．把圆锥的侧面展开得到的图形是（）A．圆B．扇形C．正方形2．一个圆柱，底面直径和高都是2分米，这个圆柱的表面积是（）平方分米．A．6πB．5πC．4πD．2π3．在学习圆柱的体积计算公式时，是把圆柱转化为（）推导出来的．A．正方体B．长方体C．长方形4．一个圆柱的底面直径扩大3倍，高不变，体积扩大（）A．3倍B．9倍C．27倍5．一个圆柱体的侧面展开是一个正方形，这个圆柱体的底面半径是5厘米，这个圆柱体的高是（）厘米．A．5B．10C．15.7D．31.46．如图的转盘上，当老鼠转到狮子的位置上时，蜗牛转到了（）的位置上．A．老鼠B．狮子C．猫D．熊猫7．一个圆柱形纸筒，它的底面半径是0.5分米，高是3.14分米，它沿高展开后的侧面是一个（）A．正方形B．长方形C．扇形D．圆形8．图中的正方体、圆柱和圆锥底面积相等，高也相等．下面是（）正确的．A．圆柱的体积比正方体的体积小一些B．圆锥的体积和正方体体积相等C．圆柱体积与正方体体积相等D．无法比较二．填空题（共10小题）9．一个圆柱的侧面积是188.4平方分米，底面半径是2分米．它的高是分米．10．把一根长是2米，底面直径是4分米的圆柱形木料锯成3段后，表面积增加了．11．大风车的转动是现象．12．等腰三角形沿着它的对称轴旋转一周得到的是一个．13．一个圆锥体和一个圆柱体等底等高，它们体积之差是60cm3，这个圆柱的体积是cm3．14．一个棱长为6cm的正方体钢坯，要熔铸成一个高为24cm的圆锥形模具．这个模具的底面积是cm2．15．一根长20分米的圆柱形圆木，锯成两段后表面积增加了4平方分米，它原来的体积是立方分米．16．把高1m的圆柱锯成两段小圆柱，表面积增加了14m2，原来这个圆柱的体积是m3．17．如果把圆柱的侧面展开得到一个边长为9cm的正方形，那么圆柱的高是．18．一个圆柱形油桶的侧面展开图是一个正方形．已知这个油桶的底面半径是45厘米，那么油桶的高是厘米．三．判断题（共5小题）19．一根圆木的长一定，它的体积和横截面积成正比例．（判断对错）20．钟表的分针从“1”到“3”是按顺时针方向旋转了60°．（判断对错）21．两个圆柱的侧面积相等，它们的高一定相等．（判断对错）22．一个圆柱形容器的容积等于它的体积。

数学圆锥试题1.把28.26立方米的沙子堆成高是3米的圆锥形沙堆，沙堆的底面积是（）平方米．A．6.28B．28.26C．12.56D．9.42【答案】B【解析】根据圆锥的体积公式：V=sh可计算出圆锥的底面积，即用沙子的体积除以再除以高即可得到答案．解：28.26÷÷3=28.26（平方米），答：沙堆的底面积是28.26平方米．故选：B．点评：此题主要考查的是圆锥体积公式的应用．2.已知：一个圆锥的侧面积与表面积的比为2：3．求这圆锥的锥角．【答案】60°【解析】设圆锥的底面半径为r，母线长为l，则由题意可得：πrl：πr（l+r）=2：3，从而可得：l=2r，因此可知：锥角的一半为30°，则锥角为60°，据此解答即可．解：设圆锥的底半径为r，母线长为l．则由已知条件得：πrl：πr（l+r）=2：3．由此得l=2r．这就知道锥角的一半为30°，所以锥角为60°．答：这个圆锥的锥角是60°．点评：此题主要考查圆锥侧面积="πLR" （L是圆锥的侧长，R是圆锥半径）以及圆锥底面积=πR2的计算方法的灵活应用．3.圆锥的底面积是25平方厘米，它的体积是50立方厘米，求圆锥的高．【答案】6厘米【解析】根据圆锥的体积公式：v=sh，得h=v÷÷s，由此列式解答．解：50÷÷25，=50×3÷25，=150÷25，=6（厘米）；答：高是6厘米．点评：此题主要根据圆锥的体积计算方法，推导出圆锥的高等于体积除以除以底面积．由此解决问题．4.求圆锥的体积：底面积9.42平方分米，高2分米．【答案】6.28立方分米【解析】圆锥的体积=×底面积×高，底面积和高已知．代入公式即可求解．解：圆锥的体积：×9.42×2=6.28（立方分米）；答：圆锥的体积是6.28立方分米．点评：此题主要考查圆锥的体积的计算方法：V=Sh．5.一个圆锥体和一个圆柱的高相等，它们的底面积比是3：2，那么圆锥体积和圆柱体积的比是多少？【答案】1：2【解析】设一个圆柱和圆锥的高都是h，圆锥的底面积为s，圆柱的底面积为S，根据圆柱和圆锥体积公式用字母表示出来，即圆柱的体积是：V圆柱=Sh，圆锥的体积是：V圆锥=sh，然后利用已知它们底面积比是3：2，化简求出最简比．解：设一个圆柱和圆锥的高都是h，圆锥的底面积为s，圆柱的底面积为S，圆柱的体积是：V圆柱=Sh，圆锥的体积是：V圆锥=sh，圆锥与圆柱的体积之比是=sh：Sh=s：S，因为s：S=3：2，所以s：S=1：2，答：圆锥体积和圆柱体积的比是1：2．点评：本题主要利用圆柱和圆锥的体积公式，用字母表示出各自的体积，然后求比即可．6.观察填空．a．b．（1）请在上图的括号中填上各面（或量）名称，在横线上填上图形的名称．（2）图a外表的面是曲面，相等的两个面是形；图b外表的面也是曲面，将它展开可得到一个形，这种立体图形有条高，个底面．【答案】（1）见解析（2）侧面，圆，侧面，扇，一，一．【解析】圆柱体的上下底面是完全相同的两个圆，侧面是一个曲面，侧面展开是一个长方形；圆锥的侧面是一个曲面，侧面展开是一个扇形，底面是圆，顶点到底面圆心的距离叫做圆锥的高．解：（1）（2）图a外表的侧面面是曲面，相等的两个面是圆形；图b外表的侧面面也是曲面，将它展开可得到一个扇形，这种立体图形有一条高，一个底面．故答案为：侧面，圆，侧面，扇，一，一．点评：此题主要考查圆柱体和圆锥体的特征以及各部分的名称．7.一个底面周长18.84米，高3米的圆锥形沙堆的体积是多少？【答案】28.26立方米【解析】沙堆的形状是圆锥形的，利用圆锥的体积计算公式求得体积，问题得解．解：×3.14×（18.84÷3.14÷2）2×3，=×3.14×32×3，=3.14×9，=28.26（立方米）；答：这个圆锥沙堆的体积是28.26立方米．点评：此题主要考查圆锥的体积计算公式V=πr2h，运用公式计算时不要漏乘．8.计算下面物体的体积【答案】47.1（cm3）；706.5（cm3）．【解析】观察图形可知，此题就是求出底面半径为3厘米，高5厘米的圆锥的体积和底面半径为5厘米，高9厘米的圆柱的体积，由此代入公式即可解答．解：（1）×3.14×32×5，=3.14×3×5，=47.1（cm3）；（2）3.14×52×9，=3.14×25×9，=706.5（cm3）．点评：此题考查了圆柱与圆锥的体积公式的计算应用，要求学生熟记公式即可解答．9.有一圆柱体容器，它的底面半径为3分米，高18分米，容器里装有14分米高的水，现将一个底面半径为2分米的圆锥放入其中（全部侵在水中），这时容器里的水位高度是16分米，这个圆锥的高是多少分米？【答案】13.5分米【解析】根据“容器里装有14分米高的水”和“圆锥放入其中（全部侵在水中），这时容器里的水位高度是16分米”说明容器内水面上升了2分米，则圆锥的体积就等于容器内上升2分米的水的体积，由此利用圆柱的体积公式先求出容器中上升部分的水的体积，即得出圆锥的体积，再利用圆锥的高=3×体积÷圆锥的底面积即可解决问题．解：上升部分水的体积即圆锥的体积是：3.14×32×（16﹣14），=3.14×9×2，=3.14×18，=56.52（立方分米），圆锥的高是：56.52×3÷（3.14×22），=169.56÷12.56，=13.5（分米），答：圆锥的高是13.5分米．点评：此题考查了圆柱与圆锥的体积公式的灵活应用，此题关键是根据水的体积得出圆锥的体积．10.一个圆锥底面直径是6厘米，高是12厘米．它的体积是多少立方厘米？【答案】113.04立方厘米【解析】圆锥的体积=πr2h，由此先求出这个圆锥的底面半径，再代入数据即可求出圆锥的体积．解：6÷2=3（厘米），×3.14×32×12，=3.14×9×4，=113.04（立方厘米），答：圆锥的体积是113.04立方厘米．点评：此题考查了圆锥体积的计算应用．11.一个圆柱体侧面展开后是一个长6.28厘米，宽3.14厘米的长方形，底面直径是多少厘米？如果把它削成一个最大的圆锥，削去部分的体积是多少？【答案】6.57立方厘米【解析】由圆柱的侧面展开图的特点可知：圆柱的侧面展开得到的是一个长方形，长方形的长等于圆柱底面周长，宽等于圆柱的高；由此根据圆的周长公式，求出这个圆柱体的底面直径．根据圆柱的体积公式：v=sh，把数据代入公式解答；如果把它削成一个最大的圆锥，这个圆锥与圆柱等底等高，因为等底等高的圆锥的体积是圆柱体积的，所以削去部分的体积是圆柱体积的（1），然后根据一个数乘分数的意义解答．解：底面直径是：6.28÷3.14=2（厘米）；3.14×（）2×3.14×（1），=3.14×1×3.14×，=9.8596×，=，≈6.57（立方厘米）；答：圆柱的底面直径是2厘米，削去部分的体积约是6.57立方厘米．点评：此题考查的目的是掌握圆柱的侧面展开的特点，以及圆柱体积的计算．12.将一块长宽高分别为：8分米、2分米、1.2分米的长方体钢锭，可以铸成高为6分米的圆锥体，求圆锥体的底面积．【答案】9.6平方分米【解析】熔铸前后的体积不变，所以先根据长方体的体积公式求出这个钢锭的体积，再利用圆锥的体积公式即可求出它的底面积．解：8×2×1.2×3÷6，=57.6÷6，=9.6（平方分米），答：圆锥的底面积是9.6平方分米．点评：此题考查长方体和圆锥的体积公式的综合应用，抓住熔铸前后的体积不变进行解答．13.如图直角三角形ABC，以BC为轴旋转一周，得到一个立体图形，求这个立体图形的体积．【答案】50.24立方厘米【解析】由题意可知：以BC为轴旋转一周，旋转后组成的图形是一个底面半径为4cm，高为3cm的一个圆锥；根据圆锥的体积公式V=πr2h即可求出圆锥的体积．解：×3.14×42×3，=3.14×16，=50.24（立方厘米）；答：这个立体图形的体积是50.24立方厘米．点评：本题一是考查将一个简单图形绕一轴旋转一周所组成的图形是什么图形，二是考查圆锥的体积计算．14.将一个三角形的小旗绕旗杆旋转一周，可以形成一个形体．这个形体的体积是多少立方厘米？（单位：厘米）【答案】37.68立方厘米【解析】由题意可知：组成的图形是一个底面半径为3厘米，高为4厘米的一个圆锥，根据圆锥的体积公式V=πr2h即可求出圆锥的体积．解：×3.14×32×4，=×3.14×9×4，=37.68（立方厘米）；答：体积是37.68立方厘米．点评：本题一是考查将一个简单图形绕一轴旋转一周所组成的图形是什么图形，二是考查圆锥的体积计算．15.把一块长10cm，宽5cm，高4cm的长方体钢材，锻造成一个底面积是25cm2的圆锥体，这个圆锥体的高是多少厘米？【答案】24厘米【解析】根据题意可知，把长方体的钢材锻造成圆锥体，只是形状改变了，但是体积不变，因此，首先根据长方体的体积公式v=abh，求出长方体钢材的体积，再根据圆锥的体积公式v=sh，用体积除以除以圆锥的底面积即可．解：10×，=200×3÷25，=600÷25，=24（厘米），答：这个圆锥体的高是24厘米．点评：此题主要考查长方体的体积公式、圆锥的体积公式的灵活运用．16.如图ABCD是直角梯形，以AB为轴将梯形旋转一周，得到一个旋转体，它的体积是多少立方厘米？若以CD为轴旋转一周，也得到一个旋转体，哪个旋转体的体积大一些？（单位：厘米）【答案】以AB为轴旋转后的图形的体积是113.04立方厘米．以CD为轴旋转后的图形的体积是141.39立方厘米，以CD为轴旋转得到的图形体积较大【解析】观察图形可知：（1）这个梯形以AB为轴旋转一周后上半部分得到的是一个底面半径为3厘米、高为6﹣3=3厘米的圆锥，下半部分是底面半径为3厘米，高为3厘米的圆柱，旋转后的图形的体积，就是这个圆锥与圆柱的体积之和；（2）以CD为轴旋转一周，下部是一个底面半径为3厘米，高为3厘米的圆柱，上部是一个底面半径为3厘米、高为6﹣3=3厘米的圆柱的（1﹣），（上部是一个圆柱减去中间与它等底等高的圆锥）解：（1）×3.14×32×3+3.14×32×3，=28.26+84.78，=113.04（立方厘米），（2）（1﹣）×3.14×32×3+3.14×32×3，=56.52+84.87，=141.39（立方厘米），答：以AB为轴旋转后的图形的体积是113.04立方厘米．以CD为轴旋转后的图形的体积是141.39立方厘米，以CD为轴旋转得到的图形体积较大．点评：此题考查了圆柱与圆锥的体积公式的计算应用，抓住圆锥与圆柱的侧面展开图，得出旋转后的图形形状是解决本题的关键．17.半径是10，圆心角216°的扇形围成一个圆锥体，圆锥体的体积是多少？【答案】301.44【解析】由已知利用弧长公式先求出这个圆弧长，圆弧长就是围成的圆锥的底面周长，由此可以求出圆锥的底面半径为及高，代入圆锥体积公式，即可得到答案．解：圆心角216°的圆弧长为：=37.68；则圆锥体的底面周长为37.68，则圆锥的底面半径为：37.68÷3.14÷2=6；因为母线长是10，所以：设圆柱的高为h，则：h2=102﹣62=100﹣36=64，因为8×8=64，所以h=8；所以圆锥的体积为：×3.14×62×8=301.44；答：圆锥的体积是301.44．点评：本题考查的知识点是圆锥的体积公式，其中根据已知计算出圆锥的底面半径为及高，是解答本题的关键．18.（2012•陆良县模拟）打谷场上有一堆圆锥形的稻谷，底面周长18.84米，高1.5米，把这堆稻谷装入一个内直径6米的圆柱形粮囤内，稻谷堆的高度是多少米？【答案】0.5米【解析】根据底面周长18.84米，可以求出底面的半径，再根据圆锥的体积公式，即可求出圆锥形稻谷的体积，由于稻谷的体积不变，所以再根据圆柱的体积公式，即可求出稻谷堆的高度．解：半径是：18.84÷3.14÷2=3（米），×1.5×3.14×32=9.42×1.5，=14.13（立方米），14.13÷[3.14×（6÷2）2]，=14.13÷[3.14×9]，=14.13÷28.26，=0.5（米）；答：稻谷堆的高度是0.5米．点评：解答此题的关键是，弄清思路，找出数量关系，确定运算顺序，列式解答即可．19.一个底面积为40cm2，高6cm的圆锥体容器，装满水后全部倒入一个棱长为5cm的正方体容器里，水深多少厘米？【答案】3.2厘米【解析】根据题意可知，把圆锥容器中的水倒入正方体容器中，虽然形状改变了，但是水的体积没变．根据圆锥的体积公式：v=sh，正方体的体积公式：v=sh，求出容器中水的体积，再用水的体积除以正方体的底面积就是水的深（高）．由此解答．解：40×6×÷（5×5），=80÷25，=3.2（厘米）．答：水深为3.2厘米．点评：此题主要根据圆锥和正方体的体积公式解决问题．20.一个圆锥体积是12.56立方分米，底面半径1分米，则高是；和它等底等高的长方体体积是立方分米．【答案】12分米，37.68【解析】已知圆锥的底面半径，先求出它的底面积，用体积除以底面积再除以，即可求出它的高．等底等高的长方体的体积是圆锥的体积的3倍，由此列式解答．解：12.56÷（3.14×12），=12.56÷3.14×3=12（分米）；12.56×3=37.68（立方分米）；答：圆锥的高是12分米，和它等底等高的长方体体积是37.68立方分米．故答案为：12分米，37.68．点评：解答此题主要明确等底等高的长方体的体积是圆锥体积的3倍．21.一个圆柱和一个圆锥体积相等，圆柱的底面半径是圆锥底面半径的，那么圆锥的高与圆柱的高的比是．【答案】4：3【解析】圆柱的体积=Sh，圆锥的体积=Sh，设圆柱的底面半径为2r，圆柱的高为h，圆锥的高为H，则圆锥的底面半径为3r，依据体积相等，即可得解．解：根据体积相等得：π（3r）2H=π（2r）2h，H=h，所以H：h=4：3．故答案为：4：3．点评：此题主要考查圆柱和圆锥的体积的计算方法的灵活应用．22.把一个棱长6厘米的正方体切削成一个最大的圆锥体，切削部分的体积的是平方厘米．【答案】159.48【解析】正方体内最大的圆锥体的底面直径和高都等于正方体的棱长，削去部分的体积等于正方体的体积减去圆锥的体积，由此利用正方体和圆锥的体积公式即可列式计算．解：6×6×6﹣×3.14××6，=216﹣56.52，=159.48（立方厘米），答：切去部分的体积是159.48立方厘米．故答案为：159.48．点评：此题考查了正方体和圆锥的体积公式的计算应用，这里也主要考查了正方体内最大圆锥的特点．23.一个圆柱的体积是18m3，与它等底等高的圆锥的体积是m3．【答案】6【解析】根据等底等高的圆锥的体积是圆柱体积的，已，知圆柱的体积，求与它等底等高的圆锥的体积，根据一个数乘分数的意义，用乘法解答即可．解：18×=6（立方厘米）；答：与它等底等高的圆锥的体积是6立方厘米；故答案为：6．点评：明确等底等高的圆锥的体积是圆柱体积的，是解答此题的关键；用到知识点：一个数乘分数的意义．24.一个圆柱削去48立方厘米后，正好形成和一个圆柱等底等高的圆锥，这个圆锥的体积是．【答案】24立方厘米【解析】根据等底等高的圆柱的体积是圆锥的体积的3倍，所以把圆锥的体积看作1份，圆柱的体积是3份，则相差（3﹣1）=2份，即2份是48立方厘米，由此求出1份，即求出圆锥的体积．解：48÷（3﹣1），=48÷2，=24（立方厘米）；答：这个圆锥的体积是24立方厘米．故答案为：24立方厘米．点评：关键是利用等底等高的圆柱与圆锥的体积的关系，找准48立方厘米对应的份数，求出一份，进而求出答案．25.一个圆柱的体积是180cm3，与它等底等高的圆锥体积是cm3；如果一个圆锥的体积是180cm3，与它等底等高的圆柱的体积比它大cm3．【答案】60、360【解析】等底等高的圆锥的体积是圆柱的体积的，则圆锥比圆柱的体积少，由此即可解答．解：180×=60（立方厘米），180÷×（1﹣），=540×，=360（立方厘米）；故答案为：60、360．点评：此题考查了等底等高的圆柱与圆锥的体积的倍数关系的灵活应用．26.把圆锥的侧面展开可以得到一个．【答案】扇形【解析】根据圆锥的特征：圆锥的侧面展开后是一个扇形，据此解答即可．解：根据圆锥的特征可知：圆锥的侧面展开后是一个扇形；故答案为：扇形．点评：此题考查了圆锥的侧面展开图，是对圆锥基础知识的掌握情况的了解，应注意平时基础知识的积累．27.一个圆柱体和一个圆锥体的底面积和体积都相等，如果圆锥体的高是a厘米，那么圆柱体的高是a厘米．【答案】a【解析】根据圆柱的体积公式V=sh及圆锥的体积公式V=sh，知道当圆柱和圆锥的底面积和体积相等时，圆柱的高与圆锥的高的比是1：3，再根据圆锥的高是3厘米，由此即可求出圆柱的高．解：因为圆柱的体积公式是：V=sh，圆锥的体积公式是：V=sh，所以当圆柱和圆锥的底面积和体积相等时，圆柱的高与圆锥的高的比是1：3，即圆柱的高是圆锥的高的，所以圆柱的高是：a×=a（厘米），答：圆柱体的高是a厘米．故答案为：a．点评：解答此题的关键是，根据圆柱和圆锥的体积公式，得出圆柱和圆锥的高的关系．28.一个圆锥与一个圆柱等底等高，圆锥的体积是圆柱的；圆柱的体积是圆锥的．【答案】；3倍【解析】根据等底等高的圆锥体积与圆柱体积的关系：等底等高的圆柱体积是圆锥体积的3倍，即可解答问题．解：因为等底等高的圆柱和圆锥，圆柱的体积是圆锥的3倍，则圆锥的体积是圆柱的体积的，答：一个圆锥与一个圆柱等底等高，圆锥的体积是圆柱的；圆柱的体积是圆锥的3倍．故答案为：；3倍．点评：此题是考查圆柱、圆锥的关系，要注意圆柱和圆锥在等底等高的条件下有3倍或的关系．29.一段圆柱体的钢材，切削成一个最大的圆锥体，切去部分是圆锥体积的2倍．．【答案】√【解析】根据把“一段圆柱体切削成一个最大的圆锥”，实际是把一段圆柱体切削成一个和它等底等高的圆锥；根据等底等高的圆锥体是圆柱体的，得出削去部分的体积是圆柱的，即切去部分是圆锥体积的2倍．解：由分析可知：一段圆柱体的钢材，切削成一个最大的圆锥体，切去部分是圆锥体积的2倍；故答案为：√．点评：解答此题的关键是，知道如何把一段圆柱体切削成一个最大的圆锥，得出削成的圆锥与圆柱的关系，进而得出削去部分的体积与圆柱的关系．30.从圆锥的顶点到底面圆上的线段是圆锥的高．．（判断对错）【答案】×【解析】根据圆锥的高的含义：从圆锥的顶点到底面圆心的距离叫做圆锥的高；进行判断即可．解：根据圆锥的高的含义可知：从圆锥的顶点到底面直径上任意一点的线段叫做圆锥的高，说法错误．故答案为：×．点评：此题考查了圆锥的高的含义．31.等底等高的圆柱和圆锥，体积相差16dm3，那么圆柱的体积是dm3，圆锥的体积是dm3．【答案】24，8【解析】等底等高的圆柱和圆锥，圆柱的体积与圆锥体积的比是3：1，所以我们运用差比问题进行解答，求出圆柱的体积，再用圆柱的体积除以3就是圆锥的体积．解：圆柱的体积：16÷（3﹣1）×3，=8×3，=24（立方分米）；圆锥的体积：24÷3=8（立方分米）；答：圆柱的体积是24立方分米，圆锥的体积是8立方分米．故答案为：24，8．点评：本题考查了等底等高的圆柱和圆锥的体积问题，运用差比问题的解决方法进行解答即可．32.把一个圆柱切削成一个最大的圆锥，圆柱的体积被切，若将这个圆柱铸造成一个和它等底等高的圆锥可铸造个．【答案】，3【解析】（1）圆柱内削出的最大的圆锥，与原来圆柱是等底等高的，所以削出的圆锥的体积是圆柱的体积的，则圆柱的体积被切掉了，（2）因为圆柱的体积是与它等底等高的圆锥的体积的3倍，熔铸前后的体积不变，由此即可解答．解：（1）因为圆柱内削出的最大圆锥的体积是圆柱的体积的，则圆柱的体积被切掉了1﹣=；（2）圆柱的体积是与它等底等高的圆锥的体积的3倍，熔铸前后的体积不变，所以若将这个圆柱铸造成一个和它等底等高的圆锥可铸造3个．故答案为：，3．点评：此题考查了圆柱内最大的圆锥的特点以及等底等高的圆柱与圆锥的体积倍数关系的灵活应用．33.用图中三角形3cm的边为轴旋转一周得到了一个体，这个立体图形的体积是．【答案】圆锥；50.24立方厘米【解析】根据圆锥的展开图可得：以三角形3厘米的边为轴旋转一周得到的是一个底面半径为4厘米，高为3厘米的圆锥体，利用圆锥的体积公式即可计算解答．解：以三角形3厘米的边为轴旋转一周得到的是一个底面半径为4厘米，高为3厘米的圆锥体，体积是：×3.14×42×3，=3.14×16，=50.24（立方厘米），答：以三角形3厘米的边为轴旋转一周得到的是一个圆锥体，它的体积是50.24立方厘米．故答案为：圆锥；50.24立方厘米．点评：根据圆锥的展开图特点，得出旋转后的圆锥的底面半径和高是解决此类问题的关键．34.已知一个圆锥的体积是20立方厘米，一个圆柱的底面积和它相等，要使圆柱的体积是30立方厘米，底面积不变，则圆柱的高是圆锥高的．【答案】【解析】根据题干分析，可设圆柱与圆锥的底面积相等是S，则根据圆柱与圆锥的体积可得：圆柱的高是；圆锥的高是：，据此即可解答．解：设圆柱与圆锥的底面积相等是S，则根据圆柱与圆锥的体积可得：圆柱的高÷圆锥的高=÷=，答：圆柱额高是圆锥的高的．故答案为：．点评：此题主要考查圆柱与圆锥的体积公式的灵活应用．35.一个底面半径6厘米的圆锥形容器装满水，倒入和它等高的圆柱形容器，倒了6次才倒满，圆柱的底面积是平方厘米．【答案】226.08【解析】根据题干，设圆柱与圆锥容器的高相等是h，先利用圆锥的体积公式求出倒入圆柱容器的水的体积，根据圆住的体积=底面积×高，用求出的水的体积除以高即可得出底面积．解：设圆柱与圆锥容器的高相等是h，水的体积是：×3.14×62×h×6=226.08h（立方厘米），所以圆柱形容器的高是：226.08h÷h=226.08（平方厘米），答：圆柱的底面积是 226.08平方厘米．故答案为：226.08．点评：此题主要考查圆柱与圆锥的体积公式的灵活应用．36.一个圆柱与一个圆锥的体积与底面直径都相等，圆锥的高是12分米，圆柱的高是分米．【答案】4【解析】底面直径相等，则圆柱的底面积就相等，根据圆柱的体积=底面积×高，圆锥的体积=×底面积×高，可得：当圆柱与圆锥的体积和底面积分别相等时，圆锥的高是圆柱的高的3倍，由此即可解决此类问题．解：底面直径相等，则圆柱的底面积就相等，当圆柱与圆锥的体积和底面积分别相等时，圆锥的高是圆柱的高的3倍，12÷3=4（分米），答：圆柱的高是4分米．故答案为：4．点评：此题可得结论：体积与底面积分别相等时，圆锥的高是圆柱的高的3倍，由此结论即可解决此类问题．37.等底等体积的圆锥与圆柱体，已知圆柱底为4平方厘米，圆锥底为平方厘米．【答案】12【解析】根据圆柱体的体积是和它等底等高的圆锥体的体积的三倍，如果一个圆柱体和一个圆锥体的体积与高都相等，那么圆锥的底面积则是圆柱的底面积的三倍，据此求出即可．解：4×3=12（平方厘米）．答：圆锥的底面积是12平方厘米．故答案为：12．点评：此题考查圆锥的体积，运用圆柱体的体积是和它等底等高的圆锥体的体积的三倍推出并计算．38.一个圆柱和一个圆锥体积相等，高也相等；圆柱的底面积是15cm2；圆锥的底面积是平方厘米．【答案】45【解析】根据圆柱的体积公式V=sh，圆锥的体积公式V=sh，当圆柱和圆锥的体积、高分别相等时，圆锥的底面积是圆柱的底面积的3倍，由此求出圆锥的底面积即可．解：15×3=45（平方厘米），答：圆柱锥的底面积是45平方厘米．故答案为：45．点评：此题主要考查了利用圆柱与圆锥的体积公式，推导出在体积、高分别相等时，圆柱的底面积与圆锥的底面积的关系．39.一个长方体和一个圆锥等底等高，则长方体的体积是圆锥的3倍．．【答案】正确【解析】长方体的体积=底面积×高；圆锥的体积=×底面积×高，由此公式即可得出长方体体积与圆锥的体积的倍数关系．解：长方体的体积=底面积×高；圆锥的体积=×底面积×高，若它们的底面积和高分别相等，则：长方体的体积是圆锥的体积的3倍，所以原题说法正确．故答案为：正确．点评：此题考查了长方体和圆锥的体积公式的灵活应用，得出结论：等底等高的长方体体积是圆锥的体积的3倍．40.一个圆柱形木棒的体积是48立方分米，把它削成一个最大的圆锥，削去部分的体积是立方分米，削去部分体积与原来体积的比是：．【答案】32；2：3【解析】根据题意知，把圆柱形木头削成一个最大的圆锥，如果要削成一个最大的圆锥，那么这。

圆锥面的曲面方程
圆锥面方程式：z=±（√x＾2+y＾2）×cotα。

其中，α是圆锥面的半顶角；x＾2/a＾2+y＾2/a＾2=z＾2。

其中，a=cotα。

组成：
圆锥的高：圆锥的顶点到圆锥的底面圆心之间的最短距离叫做圆锥的高。

圆锥母线：圆锥的侧面展开形成的扇形的半径、底面圆周上任意一点到顶点的距离。

圆锥的侧面积：将圆锥的侧面沿母线展开，是一个扇形,这个扇形的弧长等于圆锥底面的周长,而扇形的半径等于圆锥的母线的长. 圆锥的侧面积就是弧长为圆锥底面的周长×母线/2；没展开时是一个曲面。

圆锥有一个底面、一个侧面、一个顶点、一条高、无数条母线，且底面展开图为一圆形，侧面展开图是扇形。