空间角及其计算

空间角总结什么是空间角？空间角是几何学中的一个重要概念，用来描述两个向量之间的夹角。

空间角通常用希腊字母θ（theta）表示，其单位是弧度（rad）。

空间角的概念可以扩展到三维空间中，帮助我们描述物体之间的方向关系和位置关系。

空间角的特征空间角具有以下几个重要特征：1.空间角是无向角：空间角没有方向之分，只关注两个向量之间夹角的大小，与向量的起点和终点无关。

2.空间角的大小范围：空间角的取值范围是0到π（也就是0到180度）。

3.水平角和垂直角：当两个向量在同一平面内，夹角为水平角；当两个向量互相垂直，夹角为垂直角。

4.空间角的计算方法：可以使用余弦定理或向量的点积来计算空间角的大小。

空间角的计算方法余弦定理余弦定理是计算空间角的常用方法之一。

设有两个向量A和B，它们之间的夹角θ满足以下关系：cos(θ) = (A·B) / (|A| * |B|)其中，A·B表示向量A和向量B的点积，|A|和|B|表示向量A和向量B的模。

通过余弦定理，我们可以根据向量的数值计算出它们之间的夹角。

向量的点积另一种计算空间角的方法是使用向量的点积。

向量A·B的点积可以通过以下公式计算得到：A·B = |A| * |B| * cos(θ)其中，θ表示向量A和向量B的夹角。

通过这个公式，我们可以根据两个向量的点积来计算它们之间的夹角。

球面角与立体角除了空间角之外，还有两个相关概念：球面角和立体角。

球面角球面角是指由球心发出的射线与球面上两个端点所夹的角。

球面角的单位是球面度（sr），1球面度是球面上的一个单位面积所占的立体角。

球面角可以通过球面面积和球半径来计算。

立体角立体角用来描述三维空间中的角度，是由空间中一点发出的射线与空间中的两个向量所夹的角。

立体角的单位是立体度（steradian，sr），1立体度表示空间中的一个单位面积所占的立体角。

立体角可以通过空间角和距离来计算。

核心考点四 空间角及空间距离的计算方向一：点到平面的距离解法突破：求点到平面的距离的常见方法有：（1）定义法：直接作出点到平面的垂线，垂线段的长度就是点到平面的距离（2）转化法：利用等体积法或者线面平行的位置关系进行转化例1、如图所示，在三棱锥ABC P -中，AB BP AP ACB BC AC ===∠==,90,20，AC PC ⊥，求点C 到平面APB 的距离。

变式1、如图所示，正三棱柱111C B A ABC -的所有棱长都为2，D 为1CC 中点，求点C 到平面BD A 1的距离。

⊥OA 底面ABCD ，2=OA ，求点B 到平面OCD 的距离。

例2、如图所示，三棱柱111C B A ABC -中，21====AA AB CB CA ，61=C A ，0160=∠BAA ，求三棱柱111C B A ABC -的体积。

已知6,2===PA PD PB ，若E 为PA 的中点，求三棱锥BCE P -的体积。

变式2、如图所示，在四棱锥ABCD P -中，⊥PA 底面ABCD ，底面ABCD 为正方形，F 为AB 上一点，该四棱锥的侧（左）视图如图所示，求四面体BFC P -的体积。

变式3、如图1所示，在边长为1的等边三角形ABC 中，E D ,分别是AC AB ,上的点，且32==AE AD ，F 是BC 的中点，AF 与DE 交于点G ，将ABF ∆沿AF 折起，得到如图2所示的三棱锥BCF A -，其中22=BC ，求三棱锥DEG F -的体积。

方向二：空间角计算（1）异面直线所成的角解法突破：通过“平移法”将异面直线所成的角转化为共面相交的两直线的夹角来完成，即异面成角问题转化为共面相交成角问题，这是解决异面直线所成角问题的基本思路和方法，其中平移法又包括中位线平移法、选点平移法、补形（体）平移法等具体方法，同时要注意两条一面直线所成的角的范围是]2,0(π。

例3、如图所示，在棱长为2的正方体1111D C B A ABCD -中，点O 是底面ABCD 的中心，F E ,分别是AD CC ,1的中点，求异面直线OE 和1FD 所成角的余弦值。

第65讲 空间的角及计算【考点解读】了解空间三种角的概念，并会求三种角的大小.【知识扫描】1、异面直线,a b 所成的角：范围(0,]2π ① 平移法：过空间上一点（注意取图形中的特殊点）作1//a a 、1//b b ，则1a 与1b 所成的锐角或直角就是异面直线,a b 所成的角；（书写时要分三步：作— 指— 求） ② 证明a b ⊥，则a 与b 的夹角为2π； ③ 向量法：求a < ，b >（[0,]π∈)，再确定异面直线a 与b 所成的角((0,2πα∈)。

2、直线与平面所成的角：范围[0,)π① 定义法：找出直线PA 在平面α内的射影AO （射影AO 怎么找），则锐角PAO ∠就是直线PA 与平面α所成的角；（书写时要分三步：作— 证— 求） ② 证明a α⊥(或//a α)，则直线a 与平面α所成的角2π（或0）； ③ 向量法：求a 与α的法向量n 所成的角,a n <> ，则直线a 与平面α所成的角θ为,2a n π-<>或,2a n π<>- ，总之有||sin |cos ,|||||a n a n a n θ⋅=<>=⨯。

3、二面角① 直接法：直接作出二面角AB αβ--的平面角（书写时要分三步：作—证— 求）；② 向量法：设平面α的法向量1n 与平面β的法向量2n所成的角为θ，则所求的二面角为θ或πθ-（要依图形确定是取θ，还是取θπ-）。

【考计点拨】牛刀小试：1．在正三棱柱ABC-A 1B 1C 1中，若AB=2，A A 1=1，则点A 到平面A 1BC 的距离为（B ）A ．43B ．23 C ．433 D ．32．在正三棱柱ABC-A 1B 1C 1中，若AB=2BB 1,则AB 1与C 1B 所成的角的大小为 （B ）A.60ºB. 90ºC.105ºD. 75º3．正方体ABCD —A 1B 1C 1D 1中，E 、F 分别是AA 1与CC 1的中点，则直线ED 与D 1F 所成角的大小是（A）A ．15B 。

空间几何中的角度与距离计算在空间几何中，角度与距离的计算是非常重要的。

通过正确计算角度和距离，我们能够准确描述和分析物体的位置、运动以及相互关系。

本文将介绍空间几何中常用的角度计算方法和距离计算方法。

一、角度计算在空间几何中，角度是表示物体之间相对方向关系的重要指标。

常见的角度计算方法有以下几种：1. 余弦定理余弦定理是计算三角形内角的常用方法之一。

在空间几何中，如果已知三点的坐标，可以通过余弦定理计算出这三个点所形成的夹角。

余弦定理的公式如下：cos A = (b² + c² - a²) / (2bc)其中，A为夹角的大小，a、b、c为夹角对应的边长。

2. 矢量法矢量法是一种基于向量运算的角度计算方法。

通过将空间中的两个向量进行运算，可以得到它们之间的夹角。

常见的向量法角度计算包括点乘法和叉乘法。

（1）点乘法：两个向量的点乘结果等于它们的模长相乘再乘以它们之间的夹角的余弦值。

可以通过点乘法计算向量之间的夹角。

（2）叉乘法：两个向量的叉乘结果等于它们的模长相乘再乘以它们之间的夹角的正弦值。

可以通过叉乘法计算向量之间的夹角。

3. 三角函数在空间几何中，三角函数也是用于角度计算的常用方法之一。

通过正弦、余弦和正切等三角函数的运算，可以计算出角度的大小。

三角函数的计算方法需要先将坐标系进行转换，然后根据坐标的数值，利用相应的三角函数公式进行计算。

二、距离计算在空间几何中，距离是表示物体之间远近程度的重要指标。

常见的距离计算方法有以下几种：1. 欧几里得距离欧几里得距离是空间几何中最常用的距离计算方法。

对于二维或三维空间中的两个点，欧几里得距离可以通过计算它们在各坐标轴上的差值的平方和再开方的方式得到。

欧几里得距离的公式如下：d = √[(x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)²]其中，d为距离，(x₁, y₁, z₁)和(x₂, y₂, z₂)分别为两个点的坐标。

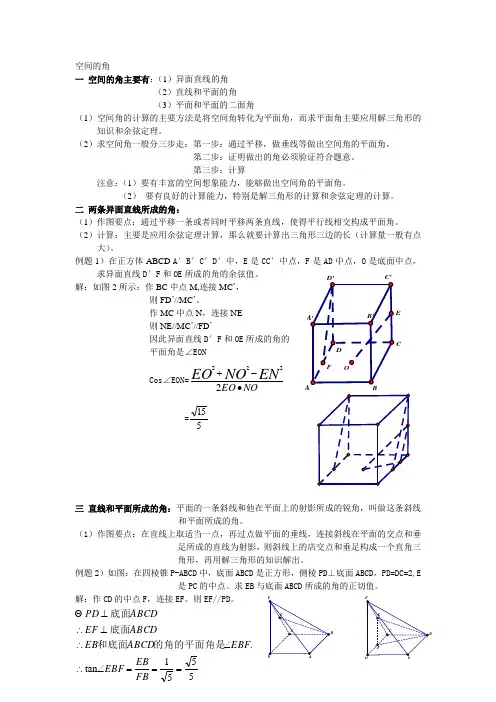
EC5551tan .===∠∴∠∴⊥∴⊥FB EB EBF EBF ABCD EB ABCD EF ABCD PD 的角的平面角是和底面底面底面 空间的角一 空间的角主要有：（1）异面直线的角（2）直线和平面的角（3）平面和平面的二面角（1）空间角的计算的主要方法是将空间角转化为平面角，而求平面角主要应用解三角形的知识和余弦定理。

（2）求空间角一般分三步走：第一步：通过平移，做垂线等做出空间角的平面角。

第二步：证明做出的角必须验证符合题意。

第三步：计算注意：（1）要有丰富的空间想象能力，能够做出空间角的平面角。

（2） 要有良好的计算能力，特别是解三角形的计算和余弦定理的计算。

二 两条异面直线所成的角：（1）作图要点：通过平移一条或者同时平移两条直线，使得平行线相交构成平面角。

（2）计算：主要是应用余弦定理计算，那么就要计算出三角形三边的长（计算量一般有点大）。

例题1）在正方体ABCD-A ′B ′C ′D ′中，E 是CC ′中点，F 是AD 中点，O 是底面中点，求异面直线D ′F 和OE 所成的角的余弦值。

解：如图2所示：作BC 中点M,连接MC ’， 则FD ’//MC ’。

作MC 中点N ，连接NE 则NE//MC ’//FD ’因此异面直线D ′F 和OE 所成的角的 平面角是∠EONCos ∠EON=NO EO ENNO EO ∙-+2222 =515三 直线和平面所成的角：平面的一条斜线和他在平面上的射影所成的锐角，叫做这条斜线和平面所成的角。

（1）作图要点：在直线上取适当一点，再过点做平面的垂线，连接斜线在平面的交点和垂足所成的直线为射影，则斜线上的店交点和垂足构成一个直角三角形，再用解三角形的知识解出。

例题2）如图：在四棱锥P-ABCD 中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD=DC=2,E是PC 的中点。

求EB 与底面ABCD 所成的角的正切值。

解：作CD 的中点F ，连接EF 。

在高中的空间几何学习中，常见的几何形状包括点、线、面、体等，涉及到各种角的计算。

以下是一些常见的角的公式：
1. 平面内的角：
-顶点在圆心的圆心角和半圆角：圆心角等于对应的圆周角，半圆角为180度。

-对顶角：对顶角相等。

-同位角：同位角相等。

-内错角和内错角互补：内错角之和等于180度，内错角互补。

2. 空间内的角：
-平行线与截线：平行线与截线的对应角相等。

-直线与平面：直线与平面的夹角等于其倾斜角。

-平面与平面：两平面的夹角等于它们法向量的夹角。

3. 立体几何中的角：
-直线与立体的交角：直线与平面或立体的夹角等于90度减去它们的夹角余补角。

-两平面之间的夹角：两平面的夹角是它们的法线之间的夹角。

这些公式是空间几何中常见的角度计算原则，通过理解和掌握这些规律，可以更好地解决空间几何题目中涉及到的各种角度问题。

立体角、空间角及发光角计算公式摘要：本文应用数学工具，推导出灯具在两个相互垂直方向上的发光角同立体角之间的关系。

关键词：立体角，发光角。

0引言光强度是照明工程中的一个重要术语，其定义是“光源在给定方向的单位立体角中发射的光通量”，一般以I 表示。

若在某微小立体角d Ω内的光通量为d Φ（ψ，θ），则该方向上的光强为：I （ψ，θ）=d Φ（ψ，θ）/d Ω。

式中，d Ω的单位为sr （球面度），光强的单位为cd （坎德拉，烛光）。

1 cd=1 lm/sr 。

但关于立体角的计算方法，照明教材及各类文献中却没有述及。

这给从事照明工程的专业技术人员带来很大的困惑。

1立体角的定义将弧度表示平面角度大小的定义（弧长除以半径）推广到三维空间中，定义“立体角”为：球面面积与半径平方的比值。

即：Ω=2rA图1平面角（单位：弧度rad ） 图2立体角（单位：球面度sr ）2立体角的计算设灯具在两个相互垂直方向上的发光角为2α和2β，求其所对应的立体角的大小。

设0<2α<π，0<2β<π不失一般性，设球体半径为单位长度1，坐标原点在球心，坐标轴方向如图。

根据定义，只须求出两角所夹球面的面积，即是立体角的大小。

由于对称性，只需求出第一卦限内的面积再乘以4即可。

图3 计算示意图曲面面积计算公式为： A=⎰⎰∂∂+∂∂+Dyz x z 22)()(1dxdy （1） 上半球球面方程为：Z=221y x -- （2）由 x z ∂∂=221yx x --- （3）221yx y y z ---=∂∂ （4） 得 222211)()(1yx y z x z --=∂∂+∂∂+ （5）代入（1）式得： A=⎰⎰--Dyx dxdy 221 (6)利用极坐标，得： A=⎰⎰-Drrdrd 21θ (7)易知，积分区域在xy 平面上的投影是由两条椭圆曲线围成，方程分别为：α22sin x +y 2=1 (8) x 2+β22sin y =1 (9)交点坐标（βαβα22sin sin 1cos sin -,βααβ22sin sin 1cos sin -)φ1=arctg αβtg tg (10)φ2=arctg βαtg tg (11)将x=rcos Φ，y=rsin Φ带入（8）、（9）式，得极坐标表示的边界方程为： α222sin cos sin 11Φ+Φ=r (12)β222sin sin cos 12Φ+Φ=r (13)图4 xy 面投影XY12Dr1r2根据对称性，有：A=4(A1+A2) (14) A1=⎰⎰-ΦΦ102101r r rdr d A2=⎰⎰Φ-Φ2221r rrdrd于是， A1=10121(r r d ⎰Φ--Φ=⎰ΦΦ+Φ--1222sin cos sin 111(α）dΦ=Φ1-⎰ΦΦ+Φ-102222cos sin sin sin 1ααdΦ =Φ1-⎰ΦΦ+Φ-ΦΦ10222sin sin sin 1cos cos ααd设t=sinΦ，则cosΦdΦ=dt A1=Φ1-⎰Φ-1sin 022cos 1cos tdt αα =Φ1-⎰Φ-1sin 022cos /1tdtα =Φ1-arcsin(cos α·t)1sin 0Φ=Φ1-arcsin(cos αsinΦ1) (15) 同理，A2=Φ2-arcsin(cosβsinΦ2) (16)带入（14）式,得出最终结果：A=4(arctgαβtg tg -arcsin(cos αsin(arctg αβtg tg )) +arctg βαtg tg -arcsin(cosβsin(arctg βαtg tg ))) (17)特别地，当α=β时，Φ1=Φ2=π/4， A1=A2=π/4-arcsin(cos α/2)3数值结果参考文献⑴周太明等，电气照明设计，复旦大学出版社，2001，11⑵同济大学数学教研室，高等数学，高等教育出版社，1998，12⑶陈大华等译，光源与照明（第四版），复旦大学出版社，2000，1注：本文发表于《中国照明学会（2005）学术年会论文集》，2005.9·上海。

PCDBA 空间角的求法空间角，能比较集中反映空间想象能力的要求，历来为高考命题者垂青，几乎年年必考。

空间角是异面直线所成的角、直线与平面所成的角及二面角总称。

空间角的计算思想主要是转化：即把空间角转化为平面角，把角的计算转化到三角形边角关系或是转化为空间向量的坐标运算来解。

空间角的求法一般是：一找、二证、三计算。

异面直线所成的角的范围：090θ<≤ （一）平移法【例1】已知四边形ABCD 为直角梯形，//AD BC ，90ABC ∠=，PA ⊥平面AC ，且2BC =，1PA AD AB ===，求异面直线PC 与BD 所成角的余弦值的大小。

【解】过点C 作//CE BD 交AD 的延长线于E ，连结PE，则PC 与BD 所成的角为PCE ∠或它的补角。

CEBD ==PE=∴由余弦定理得 222cos 2PC CE PE PCE PC CE +-∠==⋅∴PC 与BD 所成角的余弦值为63 （二）补形法【变式练习】已知正三棱柱111ABC A B C -的底面边长为8，侧棱长为6，D 为AC 中点。

求异面直线1AB与1BC 所成角的余弦值。

【答案】125A 1C 1CBAB 1 DCP二、直线与平面所成角直线与平面所成角的范围：090θ≤≤ 方法：射影转化法（关键是作垂线，找射影）【例2】如图，在三棱锥P ABC -中，90APB ∠=，60PAB ∠=，AB BC CA ==，点P 在平面ABC内的射影O 在AB 上，求直线PC 与平面ABC 所成的角的大小。

【解】连接OC ，由已知，OCP ∠为直线PC 与平面ABC 所成角设AB 的中点为D ，连接,PD CD 。

AB BC CA ==，所以CD AB ⊥90,60APB PAB ∠=∠=，所以PAD ∆为等边三角形。

不妨设2PA =，则1,3,4OD OP AB ===2223,13CD OC OD CD ∴==+=在Rt OCP ∆中，339tan 13OP OCP OC ∠===【变式练习1】如图，四棱锥S ABCD -中，//AB CD ，BC CD ⊥，侧面SAB 为等边三角形。

高中数学中的立体几何空间角与空间距离计算方法立体几何是数学中的一个分支，其重点研究的是三维空间中点、线、面和体之间的关系。

在立体几何中，空间角和空间距离是非常关键的概念。

本文将详细探讨高中数学中的立体几何空间角与空间距离计算方法。

一、空间角的概念与计算方法1. 空间角的概念空间角指的是由两个非共面向量所张成的角度，在立体几何中具有重要的意义。

空间角的大小是依据两个向量的夹角计算得来的。

2. 空间角的计算方法在计算空间角时，我们首先需要求出两个向量的点积。

设向量a=(a1,a2,a3)和向量b=(b1,b2,b3)，则它们的点积为a*b=a1b1+a2b2+a3b3。

接下来，我们可以利用余弦定理来计算角度，即cosθ=(a*b)/(|a||b|)，其中|a|和|b|分别表示向量a和向量b的模长，θ表示向量a和向量b之间的夹角。

二、空间距离的概念与计算方法1. 空间距离的概念空间距离指的是三维空间中两个点之间的距离，也是立体几何中经常涉及到的一个概念。

2. 空间距离的计算方法我们可以借助勾股定理来计算空间距离。

设点A(x1,y1,z1)和点B(x2,y2,z2)是三维空间中的两个点，它们之间的距离为d，则d=sqrt((x2-x1)^2+(y2-y1)^2+(z2-z1)^2)。

三、空间角和空间距离的应用空间角和空间距离在立体几何中的应用非常广泛，例如在计算棱台的侧面积、计算四面体内切圆半径、求解圆锥截面面积等问题中，我们都需要用到空间角和空间距离的知识。

比如，在计算棱台的侧面积时，我们需要首先求出两条棱所在的平面之间的空间角，然后根据棱长和计算出的角度，就可以快速计算出棱台的侧面积。

在计算四面体内切圆半径时，我们需要先计算出四面体各面的法线向量，然后根据法线向量计算面上的角度，最后用勾股定理求出四面体内切圆的半径。

在求解圆锥截面面积时，我们需要用到空间角和空间距离的知识，以找出圆锥截面的边界和计算截面的面积。

空间角的范围什么是空间角空间角是物体之间相对位置的一种度量，用于描述在三维空间中两个向量之间的夹角。

它是向量的方向性特征的量化表示。

在数学上，空间角可以通过向量的点积和模长来计算。

给定两个向量A和B，它们的空间角θ可以通过以下公式计算：θ = arccos(A·B / |A|·|B|)其中，A·B表示向量A和向量B的点积，|A|和|B|分别表示向量A和向量B的模长。

空间角的范围空间角的范围是从0到π之间的实数。

这是因为点积的值范围是从-1到1之间，而空间角θ的取值范围是从0到π之间。

当两个向量的方向相同时，它们的空间角为0。

当两个向量的方向完全相反时，它们的空间角为π。

当两个向量的方向相互垂直时，它们的空间角为π/2。

在实际应用中，空间角的范围可以用于描述物体之间的相对位置关系。

例如，在机器人技术中，空间角可以用于判断机器人的朝向和目标位置之间的夹角，从而实现精确的导航和定位。

空间角的应用空间角在物理学、工程学和计算机图形学等领域中具有广泛的应用。

在物理学中，空间角被用于描述光线的传播方向和反射方向之间的夹角。

通过测量空间角，可以计算出光线的折射角和反射角，从而研究光的传播规律和光学器件的设计。

在工程学中，空间角被用于描述机械零件之间的相对位置关系。

通过测量空间角，可以确定机械零件的装配方式和运动轨迹，从而实现机械系统的设计和优化。

在计算机图形学中，空间角被用于描述三维模型之间的相对位置关系。

通过计算空间角，可以确定三维模型的旋转角度和投影方向，从而实现计算机图形的渲染和动画效果。

总结空间角是一种用于描述物体之间相对位置的度量，可以通过向量的点积和模长来计算。

空间角的范围是从0到π之间的实数，用于表示两个向量之间的夹角。

空间角在物理学、工程学和计算机图形学等领域中具有广泛的应用，可以用于研究光的传播规律、机械系统的设计和优化，以及计算机图形的渲染和动画效果等方面。

通过深入理解空间角的概念和应用，我们可以更好地理解和应用三维空间中的向量和位置关系。

空间角的概念与计算在几何学中，角是一个基本的概念，用于描述物体之间的相对方向。

而空间角则是在三维空间中描述物体之间方向关系的重要指标。

本文将介绍空间角的概念及其计算方法。

一、空间角的概念空间角是用来描述三维空间中两个矢量之间的夹角关系。

在二维空间中，我们可以通过一条射线和一条直线之间的夹角来描述角度，而在三维空间中，空间角则需要考虑更多的因素。

具体而言，对于任意两个非零矢量a和b，它们之间的空间角被定义为它们的夹角θ，满足0 ≤ θ ≤ π。

其中，θ=0时表示a和b共线，θ=π/2时表示a和b正交，θ=π时表示a和b反向。

二、空间角的计算1. 余弦定理计算空间角余弦定理是空间角计算中常用的方法之一。

对于两个非零矢量a和b，它们之间的空间角θ满足以下关系：cosθ = (a·b) / (|a|·|b|)其中，·表示矢量的点积，|a|和|b|分别表示矢量a和b的模长。

通过求解上式，我们可以得到空间角θ的值。

2. 向量叉积计算空间角另一种常用的空间角计算方法是利用向量的叉积。

对于两个非零矢量a和b，它们之间的空间角θ满足以下关系：sinθ = |a×b| / (|a|·|b|)其中，×表示矢量的叉积。

通过求解上式，我们可以得到空间角θ的正弦值，进而计算出空间角的值。

三、实例演示下面通过一个实例来演示如何计算空间角。

假设有两个矢量a = (1, 2, 3)和b = (4, 5, 6)。

我们希望计算出它们之间的空间角θ。

首先，我们可以通过求解余弦定理来计算空间角的余弦值：cosθ = (1×4 + 2×5 + 3×6) / √(1² + 2² + 3²) × √(4² + 5² + 6²)= (4 + 10 + 18) / √14 × √77= 32 / √1078 ≈ 0.979然后，通过反余弦函数可以求得空间角的弧度值：θ = arccos(0.979) ≈ 0.199 rad最后，将弧度值转换为度数，即可得到空间角的度数表示：θ ≈ 0.199 × (180/π) ≈ 11.4°因此，矢量a和b之间的空间角约为11.4°。

空间中的角度计算与应用角度是空间中一种重要的几何概念，可以用来描述物体之间的相对位置和方向关系。

在工程、物理、建筑、航天等领域中，角度计算和应用都扮演着重要的角色。

本文将介绍空间中角度的计算方法和几个相关应用。

一、空间中的角度计算方法在二维平面中，我们可以使用直尺和量角器等工具来测量角度。

但在空间中，由于有长度、高度和深度三个方向的变化，所以需要使用更高级的工具和方法来计算角度。

1. 三维空间中的角度计算方法在三维空间中，我们通常使用向量来表示方向和位置。

一个向量可以用起点和终点来表示，这两个点在三维坐标系中分别有三个坐标值。

设两个向量A和B，它们的坐标分别为(Ax, Ay, Az)和(Bx, By, Bz)。

我们可以使用向量的点积和模长计算它们之间的夹角θ。

点积的计算公式为：A·B = Ax·Bx + Ay·By + Az·Bz向量的模长计算公式为：|A| = √(Ax^2 + Ay^2 + Az^2)两个向量的夹角θ的余弦值可表示为：cosθ = (A·B) / (|A|·|B|)通过反余弦函数可求得夹角θ的值，即θ = arccos(cosθ)2. 四元数计算法四元数是一种用于表示旋转的数学工具，它可以用一个实部和三个虚部来表示。

四元数既可以描述物体的姿态和旋转角度，也可以用来计算两个物体之间的旋转或夹角。

具体计算步骤如下：1）定义两个四元数q1和q2，分别表示两个物体的姿态；2）求解它们的乘积p = q1 * q2的实部，得到一个新的四元数；3）通过arccos函数计算p的实部的绝对值，得到两个物体之间的夹角。

二、空间中角度的应用在物理和工程领域，空间中的角度计算和应用非常广泛，下面介绍几个常见的应用场景。

1. 机械设计与运动控制在机械设计和运动控制领域，角度的计算和控制是非常重要的。

例如，在机器人运动控制中，需要根据机器人末端执行器的位置和姿态，计算出各个关节的角度，以实现期望的运动轨迹。

空间角的求法方法归纳
空间角的求法方法归纳
在数学和物理学中，空间角是一种非常重要的概念。

物体在空间中的角度关系经常被用到各种计算和分析中。

因此，求解空间角的方法也变得尤为重要。

本文将按类划分，总结空间角的求法方法。

立体角的求法
立体角是三维空间中用来描述四面体的角度大小的量，并且与其各个顶点相对应。

求解四面体的立体角可以通过以下公式进行计算：
V5 = 1/3(arccos(A1) + arccos(A2) + arccos(A3) - π )
其中V5指四面体的立体角，A1、A2、A3为三个向量的夹角余弦，pi 为圆周率。

平面角的求法
平面角是在二维平面中两个射线之间的角度大小，于是端点重合，两条射线叫做角的顶点，并记为O。

平面角的计算公式如下：
cosθ = a·b / |a||b|
其中，a和b分别表示两个向量，|a|和|b|表示向量的模，lala和lblb都为0，则cosθ没有定义。

球面角的求法
球面角是指在球面上相互靠近的两条弧（或线）之间的角度大小。

求解球面角需要先计算其对应的球面扇形的面积，然后进行换算即可，具体公式如下：
S = R²θ
其中R表示球体半径，θ表示对应的球面角。

总结
空间角的求法方法主要包括立体角、平面角和球面角三种。

其中立体角的求解需要根据四面体的三个向量夹角余弦值计算，平面角的计算需要先计算两个向量的点积并除以其模，而球面角的求解则需要先计算出对应的球面扇形面积。

这些空间角的求法方法可以帮助我们更准确地分析并解决各类问题。

空间角公式空间角公式是三维空间中两个向量之间的夹角，也称为向量夹角。

在三维空间中，向量的方向和大小都很重要，因此空间角公式是非常重要的数学工具。

空间角公式可以用余弦定理来表示。

假设有两个向量a和b，它们的夹角为θ，那么它们的余弦值可以表示为：cosθ = (a·b) / (|a|·|b|)其中，a·b表示向量a和向量b的点积，|a|和|b|分别表示向量a和向量b的模长。

这个公式可以用来计算任意两个向量之间的夹角。

空间角公式还可以用向量的坐标表示。

假设有两个向量a和b，它们的坐标分别为(a1, a2, a3)和(b1, b2, b3)，那么它们的夹角可以表示为：cosθ = (a1b1 + a2b2 + a3b3) / (sqrt(a1^2 + a2^2 + a3^2)·sqrt(b1^2 + b2^2 + b3^2))其中，sqrt表示平方根。

这个公式可以用来计算任意两个向量之间的夹角，只需要知道它们的坐标。

空间角公式在三维计算机图形学中有广泛的应用。

例如，在计算机游戏中，需要计算物体之间的碰撞，就需要用到空间角公式来计算它们之间的夹角。

在计算机辅助设计中，也需要用到空间角公式来计算物体之间的相对位置和方向。

除了空间角公式，还有一些其他的向量公式也非常重要。

例如，向量的叉积公式可以用来计算两个向量的垂直向量，向量的投影公式可以用来计算一个向量在另一个向量上的投影长度。

这些公式都是三维空间中向量计算的基础，对于理解和应用三维计算机图形学非常重要。

空间角公式是三维空间中向量计算的重要工具，它可以用来计算任意两个向量之间的夹角。

在三维计算机图形学中，空间角公式是非常重要的数学工具，它可以用来计算物体之间的相对位置和方向，对于计算机游戏和计算机辅助设计等领域都有广泛的应用。

一、求异面直线所成角步骤：（一作、二证、三计算）第一步作角：先固定其中一条直线，在这条直线取一点，过这个点作另一条直线的平行线；或两条同时平移到某个特殊的位置，顶点选在特殊的位置上。

第二步证明作出的角即为所求角。

第三步利用三角形边长关系计算出角。

（思路是把两条异面直线所成的角转化为两条相交直线所成的角）1、正方体ABCD—A1B1C1D1中， C1D和B1C所成角为；C1D 和B1D1所成角为。

2、二、线面角：技巧总结：求直线和平面所成的角时，应注意的问题是：(1)先判断直线和平面的位置关系．(2)当直线和平面斜交时，①作——作出或找到斜线与射影所成的角；②证——论证所作或找到的角为所求的角；③算——常用解三角形的方法求角；④结论——说明斜线和平面所成的角值．1、（概念考察）若斜线段AB 是它在平面α内的射影长的2 倍，则AB与α所成的角为2、在长方体ABCD－A1B1C1D1中，AB＝BC＝2，AA1＝1，则AC1与平面A1B1C1D1所成角的正弦值为3、在正方体ABCD－A1B1C1D1中，求A1B 与平面A1B1CD 所成的角．4、在三棱锥P-ABC中，PC⊥底面ABC，AB⊥BC，D是PB的中点．(1)求证：AB⊥PB；(2)若AB=BC=PC，求直线AD与底面ABC所成角的正弦值.三、二面角的平面角以二面角的棱上任一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角二面角的平面角的三个特征:1.点在棱上 2.线在面内 3.与棱垂直平面角是直角的二面角叫做直二面角。

αβlOAB1、如图，AB 是圆O 的直径，P A 垂直于圆O 所在的平面，C 是圆周上不同于A ,B 的一点，PA=AC,求二面角P-BC-A.2、已知正四棱锥的体积为12，底面对角线的长为2√6，则侧面与底面所成的二面角等于（ ）。

3、在正方体 ABCD －A 1B 1C 1D 1 中，（1）求 二面角D 1 –AB-D 的大小，（2）求 二面角A 1 –AB-D 的大小，PABC•O。