空间角的计算方法与技巧

2023年高考数学----空间角问题规律方法与典型例题讲解【规律方法】1、用综合法求空间角的基本数学思想主要是转化与化归，即把空间角转化为平面角，进而转化为三角形的内角，然后通过解三角形求得．求解的一般步骤为：（1）作图：作出空间角的平面角．（2）证明：证明所给图形是符合题设要求的． （3）计算：在证明的基础上计算得出结果． 简称：一作、二证、三算．2、用定义作异面直线所成角的方法是“平移转化法”，可固定一条，平移另一条；或两条同时平移到某个特殊的位置，顶点选在特殊的位置上．3、求直线与平面所成角的常见方法（1）作角法：作出斜线、垂线、斜线在平面上的射影组成的直角三角形，根据条件求出斜线与射影所成的角即为所求．（2）等积法：公式θ=sin hl，其中θ是斜线与平面所成的角，h 是垂线段的长，是斜线段的长，其中求出垂线段的长（即斜线上的点到面的距离）既是关键又是难点，为此可构造三棱锥，利用等体积法来求垂线段的长．（3）证垂法：通过证明线面垂直得到线面角为90°． 4、作二面角的平面角常有三种方法（1）棱上一点双垂线法：在棱上任取一点，过这点分别在两个面内作垂直于棱的射线，这两条射线所成的角，就是二面角的平面角．（2）面上一点三垂线法：自二面角的一个面上一点向另一面引垂线，再由垂足向棱作垂线得到棱上的点（即垂足），斜足与面上一点连线和斜足与垂足连线所夹的角，即为二面角的平面角．（3）空间一点垂面法：自空间一点作与棱垂直的平面，截二面角得两条射线，这两条射线所成的角就是二面角的平面角．【典型例题】例19．（2022·浙江金华·高三期末）已知正方体1111ABCD A B C D −中，P 为1ACD △内一点，且1113PB D ACD S S =△△，设直线PD 与11AC 所成的角为θ，则cos θ的取值范围为（ ）A ．⎡⎢⎣⎦B ．⎤⎥⎣⎦C ．10,2⎡⎤⎢⎥⎣⎦D ．1,12⎡⎤⎢⎥⎣⎦【答案】C【解析】如图1，设1B D 与平面1ACD 相交于点E ，连接BD 交AC 于点O ，连接11B D ， ∵1BB ⊥平面ABCD ，AC ⊂平面ABCD ，则1BB AC ⊥，AC BD ⊥，1BD BB B ⋂=，1,BD BB ⊂平面11BDD B∴AC ⊥平面11BDD B ，由1B D ⊂平面11BDD B ，则1AC B D ⊥， 同理可证：11AD B D ⊥， 1AD AC A =，1,AD AC ⊂平面1ACD ，∴1B D ⊥平面1ACD ，∵111111AC AD CD AB B D B C =====，由正三棱锥的性质可得：E 为1ACD △的中心， 连接1OD ，∵O 为AC 的中点，∴1OD 交1B D 于点E ，连接PE ，由1B D ⊥平面1ACD ，PE ⊂平面1ACD ，则1B D PE ⊥，即PE 是1PB D 的高，设AB a =，PE d =，则1,B D AC =，且1ACD △的内切圆半径r OE ==，则1112PB D S B D PE =⋅=△，))1212ACD S =⨯=△，∵1113PB DACD S S =△△213=，则13d a r =<， ∴点P 的轨迹是以E 为圆心，13a 为半径的圆.∵1B D ⊥平面1ACD ，1OD ⊂平面1ACD ，则11B D OD ⊥，∴DE ， 故PD 为底面半径为13a，高为=DE 的圆锥的母线，如图2所示，设圆锥的母线与底面所成的角α，则3tan 13a α== 所以π3α=，即直线PD 与平面1ACD 所成的角为π3. 直线AC 在平面1ACD 内，所以直线PD 与直线AC 所成角的取值范围为ππ,32⎡⎤⎢⎥⎣⎦，因为11AC AC ∥，所以直线PD 与直线11AC 所成角的取值范围为ππ,32⎡⎤⎢⎥⎣⎦，即ππ,32θ⎡⎤∈⎢⎥⎣⎦， 所以10cos 2θ≤≤. 故选：C.例20．（2022·浙江·效实中学模拟预测）在等腰梯形ABCD 中，AD BC ∥，12AB AD CD BC ===，AC 交BD 于O 点，ABD △沿着直线BD 翻折成1A BD ，所成二面角1A BD C −−的大小为θ，则下列选项中错误的是（ ）A ．1A BC θ∠≤B ．1AOC θ∠≥ C ．1A DC θ∠≤ D ．11A BC A DC θ∠+∠≥【答案】C【解析】等腰梯形ABCD 中，AD BC ∥，12AB AD CD BC ===,可知：30,ACB ACD BD DC ∠=∠=⊥取BD 中点N ,BC 中点M 连接1,A N NM ,则1A N BD ⊥，NM BC ⊥,所以1A NM ∠为 二面角1A BD C −−的平面角，即1A NM θ∠=设122AB AD CD BC ====，则1111,1,2,2A N MN A B A D ==== 2222211111111cos 1222A N NM A M A M A M A N NM θ+−+−∴===−⋅,2222222111111221cos 122228A B BM A M A M A BC A M A B BM +−+−∴∠===−⋅⨯⨯,因为在[]0,π上余弦函数单调递减，又2211111111cos cos 82A M A M A BC A BC θθ−≥−⇒∠≥⇒∠≤，故A 对. 2222222111111221cos 122228A D DC AC AC A DC AC A D CD +−+−∴∠===−⋅⨯⨯222122221111153cos 2416AC AO OC AC AOC AC AO OC +−+−∴∠===−⋅ 当0θ=时,1A 与M 重合,此时160A DC ∠=,故C 不对. 1A DC ∠在翻折的过程中，角度从120减少到60 1AOC ∠在翻折的过程中，角度从180减少到30BD 选项根据图形特征及空间关系，可知正确.. 故选:C例21．（2022·浙江·湖州中学高三阶段练习）如图，ABC 中，90C ∠=︒，1AC =，BC D 为AB 边上的中点，点M 在线段BD （不含端点）上，将BCM 沿CM 向上折起至'B CM △，设平面'B CM 与平面ACM 所成锐二面角为α，直线'MB 与平面AMC 所成角为β，直线MC 与平面'B CA 所成角为γ，则在翻折过程中，下列三个命题中正确的是（ ）①tan βα，②γβ≤，③γα>. A ．① B ．①② C ．②③ D ．①③【答案】B 【解析】如图，设直线BN 与直线CM 垂直相交于点N ，在折叠图里，线段B T '与平面ACM 垂直相交于点T ，,(0,30)BCM θθ∠=∈，由图像知：;B NT B MT αβ''∠=∠=，B N BN θ=='， ()sin ;/sin 30B T B M θαθθ=*='︒+'，cos NT θα*，()tan 60MN θθ=*︒−，()()2sin 30CM θ=︒+，①tan β==，tan β=≤≤，所以tan βα；② ()Δ1sin 902ACM S CM CA θ=*︒−= 设ACB δ∠'=，则()()()2cos cos cos 90sin sin 90cos cos 0.5sin2δθθθθααθ=*︒−+*︒−=*，Δsin ACB S δ'== 由ΔΔ1133ACM M ACB ACB B T S d S −''**=**'，得M ACB d −'=()sin sin 30sin M ACB d B TMC B M γβθα'−====︒+*''，则()()sin sin 2tan 21sin 2sin 30cos 22sin 30γθθβθθθ=≤=≤︒+︒+， 由sin sin γβ≤得γβ≤； ③sin sin sin γγα=⇒，则sin sin 2tan 2sin 2cos 22γθθαθ≤=<sin γα<，所以sin sin γα<，则γα<.故选：B例22．（2022·浙江·高三专题练习）已知等边ABC ，点,E F 分别是边,AB AC 上的动点，且满足EF BC ∥，将AEF △沿着EF 翻折至P 点处，如图所示，记二面角P EF B −−的平面角为α，二面角P FC B −−的平面角为β，直线PF 与平面EFCB 所成角为γ，则（ ）A ．αβγ≥≥B ．αγβ≥≥C ．βαγ≥≥D ．βγα≥≥【答案】A【解析】在等边ABC 中，取BC 边中点D ，连接AD ，交EF 于O ，连接PO ， 则,EF PO EF DO ⊥⊥，=PO DO O ⋂，PO ⊂平面POD ，DO ⊂平面POD 故EF ⊥平面POD ，又EF ⊂平面EFCB ，则平面POD ⊥平面EFCB 在POD 中，过P 做PM 垂直于OD 于M ，则PM ⊥平面EFCB ，连接MF ， 在等边ABC 中，过M 做MN 垂直于AC 于N ，连接PN.由,EF PO EF DO ⊥⊥，则POM ∠为二面角P EF B −−的平面角即POM α∠=， 由PM ⊥平面EFCB ，MN AC ⊥，则PNM ∠为二面角P FC B −−的平面角即PNM β?由PM ⊥平面EFCB ，则PFM ∠直线PF 与平面EFCB 所成角，即PFM γ?，设AO ，则PO ，=FO a ，sin PM α，cos MO αFM ，)1=cos (1cos )2MN αα+=+， 则有FM OM >，FM NM >由cos MO MN α-(1cos )(cos 1)0αα-+=-<可得MO MN <，则有FM MN OM >>，则111FM MN OM<< 又tan tan ,tan PM PM PMOM NM FMαβγ，=== 故tan tan tan αβγ>>，又0,2παβγ⎛⎫∈ ⎪⎝⎭、、故αβγ>> 故选：A例23．（2022·全国·高三专题练习）设三棱锥V ABC −的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点），记直线PB 与直线AC 所成的角为α，直线PB 与平面ABC 所成的角为β，二面角P AC B −−的平面角是γ则三个角α，β，γ中最小的角是（ ） A ．α B ．β C ．γD ．不能确定【答案】B【解析】如图，取BC 的中点 D ，作VO ⊥平面ABC 于点O ， 由题意知点O 在AD 上，且AO =2OD .作PE //AC ，PE 交VC 于点E ，作PF ⊥AD 于点F ，连接BF ，则PF ⊥平面ABC 取AC 的中点M ，连接BM ，VM ，VM 交 PE 于点H ， 连接BH ，易知BH ⊥PE ， 作于点G ，连接FG ，由PG ⊥AC ，PF ⊥AC ，PG PF =P ，由线面垂直判定定理可得AC ⊥平面PGF ，又FG ⊂平面PGF ∴ FG ⊥AC , 作FN ⊥BM 于点N . ∵ PG ∥VM ，PF ∥VN∴ 平面PGF ∥平面VMB ， 又 PH ∥FN , 四边形PFNH 为平行四边形， 所以PH =FN因此，直线PB 与直线AC 所成的角=BPE α∠， 直线PB 与平面ABC 所成的角PBF β=∠， 二面角P -AC -B 的平面角PGF γ=∠， 又cos cos PH FN BFPB PB PBαβ==<=又,[0,]2παβ∈，∴ αβ> 因为 tan =tan PF PFGF BF γβ>= ,(0,)2πβγ∈∴ γβ>综上所述，,,αβγ中最小角为β，故选 B.。

高三数学空间角与空间距离的计算通用版【本讲主要内容】空间角与空间距离的计算 空间直线与直线、直线与平面、平面与平面所成角的大小，直线与直线、直线与平面、平面与平面间的距离的求解【知识掌握】 【知识点精析】空间的角和距离是空间图形中最基本的数量关系，空间的角主要研究射影以及与射影有关的定理、空间两直线所成的角、直线和平面所成的角、以及二面角和二面角的平面角等．解这类问题的基本思路是把空间问题转化为平面问题去解决． 1. 空间的角的概念及计算方法（1）空间角概念——空间的角，是对由点、直线、平面所组成的空间图形中各种元素间的位置关系进行定量分析的一个重要概念，由它们的定义，可得其取值X 围，如①两异面直线所成的角θ∈（0，2π） ②直线与平面所成的角θ∈[0，2π] ③二面角的大小，可用它们的平面角来度量，其平面角θ∈（0，π）．说明：对于空间角的计算，总是通过一定的手段将其转化为一个平面内的角，并把它置于一个平面图形，而且是一个三角形的内角来解决，而这种转化就是利用直线与平面的平行与垂直来实现的，因此求这些角的过程也是直线、平面的平行与垂直的重要应用．通过空间角的计算和应用进一步提高运算能力、逻辑推理能力及空间想象能力．（2）空间的角的计算方法①求异面直线所成的角常用平移法（转化为相交直线）；②求直线与平面所成的角常利用射影转化为相交直线所成的角； ③求二面角α－l －β的平面角（记作θ）通常有以下几种方法： （ⅰ）根据定义； （ⅱ）过棱l 上任一点O 作棱l 的垂面γ，设γ∩α＝OA ，γ∩β＝OB ，则∠AOB ＝θ（图1）；（ⅲ）利用三垂线定理或逆定理，过一个半平面α内一点A ，分别作另一个平面β的垂线AB （垂足为B ），或棱l 的垂线AC （垂足为C ），连结AC ，则∠ACB ＝θ或∠ACB ＝π－θ（图2）；（ⅳ）设A 为平面α外任一点，AB ⊥α，垂足为B ，AC ⊥β，垂足为C ，则∠BAC ＝θ或∠BAC ＝π－θ（图3）；（ⅴ）利用面积射影定理，设平面α内的平面图形F 的面积为S ，F 在平面β内的射影图形的面积为S ‘，则cos θ＝SS '．2. 空间的距离问题 （1）空间各种距离是对点、线、面组成的空间图形位置关系进行定量分析的重要概念．空间距离是指两点间距离、点线距离、点面距离、线线距离、线面距离以及面面距离等，距离都要转化为两点间距离即线段长来计算，在实际题型中，这六种距离的重点和难点是求点到平面的距离，因线线距离、线面距离和面面距离除用定义能直接计算出结果的外，都要转化为求点到平面的距离进行计算．（2）空间的距离问题主要是：求空间两点之间、点到直线、点到平面、两条异面直线之间（限于给出公垂线段的）、平面和它的平行直线、以及两个平行平面之间的距离．（3）求距离的一般方法和步骤是： 一作——作出表示距离的线段；二证——证明它就是所要求的距离；三算——计算其值． 此外，我们还常用体积法或向量法求点到平面的距离．【解题方法指导】例1. 三棱锥P-ABC 中，∠ABC ＝90，PA ＝1，AB ＝3，AC ＝2，PA ⊥平面ABC.（1）求直线AB 与直线PC 所成的角； （2）求PC 和面ABC 所成的角； （3）求二面角A-PC-B 的大小．PA BC解：（1）作矩形ABCD.∴AB 和PC 所成角即为CD 和PC 所成角，且CD ⊥PD ．CD ＝3，AD ＝1，PD ＝2，tanPCD ＝3632=.故AB 和PC 所成角为arctan 36（2）∵PA ⊥面ABC ，PC 和面ABC 所成角即为∠ACP ，求得tanACP ＝21， ∴∠ACP ＝arctan21 （3）∵PA ⊥面ABC ，∴面PAC ⊥面ABC ，过B 作BG ⊥AC 于G ，则BG ⊥面PAC.过G 作GH ⊥PC 于H ，连接BH ，则BH ⊥PC ． ∴∠BHG 为二面角A-PC-B 的平面角． 在Rt △ABC 与Rt △PBC 中，PB ＝2，BC ＝1，AC ＝2，AB ＝3∴PC ＝5∴BH ＝52，BG ＝23． ∴sinBHG ＝4155223==BH BG ∴∠BHG ＝arcsin 45．故二面角A-PC-B 的大小为arcsin 45．例2. 在正三棱柱111C B A ABC -中，各棱长都等于a ，D 、E 分别是1AC 、1BB 的中点， （1）求证：DE 是异面直线1AC 与1BB 的公垂线段，并求其长度；（2）求二面角C AC E --1的大小； （3）求点1C 到平面AEC 的距离．解：（1）取AC 中点F ，连接DF ．∵ D 是1AC 的中点，F∴DF ∥1CC ，且121CC DF =．又11//CC BB ，E 是1BB 的中点， ∴DF ∥BE ，DF ＝BE ，∴四边形BEDF 是平行四边形， ∴DE ∥BF ，DE ＝BF ．∵1BB ⊥面ABC ，⊂BF 面ABC ，∴1BB ⊥BF ．又∵F 是AC 的中点，△ABC 是正三角形，∴BF ⊥AC ，a BF 23=． ∵1BB ⊥BF ，1BB ∥1CC ，∴BF ⊥1CC ，∴BF ⊥面11A ACC ， 又∵⊂1AC 面11A ACC ，∴BF ⊥1AC ， ∵DE ∥BF ，∴DE ⊥1AC ，DE ⊥1BB ，∴DE 是异面直线1AC 与1BB 的公垂线段，且a DE 23=． （2）∵11//CC BB ，DE ⊥1BB ， ∴DE ⊥1CC ， 又∵为DE ⊥1AC ，∴DE ⊥面11A ACC ． 又⊂DE 面1AEC ，∴面1AEC ⊥面1ACC ， ∴二面角C AC E --1的大小为90°．（3）连接CE ，则三棱锥1CEC A -的底面面积为221a S CEC =∆，高a h 23=．所以32123232311a a a V CEC A ==⋅⋅-．在三棱锥AEC C -1中，底面△AEC 中，a CE AE 25==，则其高为a ，所以22a S AEC =∆．设点1C 到平面AEC 的距离为d ，由AEC C CEC A V V --=11得32123231a a d =⋅， 所以a d 23=，即点1C 到平面AEC 的距离为a 23【考点突破】【考点指要】空间角是立体几何中的一个重要概念．它是空间图形中的一个突出的量化指标，是空间图形位置关系的具体体现，故它以高频率的姿态出现在历届高考试题中，可以在填空题或选择题中出现，更多的在解答题中出现．空间中各种距离都是高考中的重点内容，可以和多种知识相结合，是诸多知识的交汇点，考查题型多以选择题、填空题为主，有时渗透于解答题中，所以复习时应引起重视．【典型例题分析】例1. （2003全国卷文）如图，已知正四棱柱2,1,11111==-AA AB D C B A ABCD ，点E 为1CC 中点，点F 为1BD 中点．（1）证明EF 为BD 1与CC 1的公垂线；（2）求点1D 到平面BDE 的距离．解法1：（1）连结AC 交BD 于点O ，则点O 为BD 中点，连OF ，则可证OCEF 为矩形， 故EF ⊥CC 1 ，EF ∥AC ．又可证AC ⊥平面BD 1 ∴AC ⊥BD 1，∴EF ⊥BD 1， 故 EF 为BD 1与CC 1的公垂线．O（2）连结D 1E ，则有三棱锥D1-DBE 的高d 即为点1D 到平面BDE 的距离． 由已知可证三角形DBE 为边长为2的正三角形，故2331311⋅⋅=⋅⋅=∆-d S d V DBE DBE D ； 又31311111=⋅===∆---DBD DBD C DBD E DBE D S CO V V V∴3123=d ∴332=d ， 即1D 到平面BDE 的距离为332解法2：解（1）以D 为原点，建立如图所示的直角坐标系，则 )0,0,0(D ，)2,0,0(1D)0,1,1(B ，)0,1,0(C ，)2,1,0(1C ，)1,1,0(E ，)1,21,21(F ，∴)0,21,21(-=EF ，)2,1,1(1--=BD ，)2,0,0(1=CC∴01=⋅BD EF ，01=⋅CC EF ；∴1BD EF ⊥，1BD EF ⊥ 又EF 与CC 1、BD 1分别交于E 、F ，故EF 为BD 1与CC 1的公垂线. （2）由（1）)0,1,1(--=BD ，)1,0,1(-=BE ，)2,1,1(1--BD ， 设 平面BDE 的法向量为 ),,(z y x n =，则BD n ⊥，BE n ⊥，∴⎪⎩⎪⎨⎧=⋅=⋅00BE n BD n ， ∴⎩⎨⎧=+-=--00z x y x ， 即 ⎩⎨⎧=-=z x y x ，∴ 不妨设 )1,1,1(-=n ，则点1D 到平面BDE 的距离为33232||1===n n BD d ， 即为所求．例2. （2006全国卷Ⅲ文20）如图，12l l ，是互相垂直的异面直线，MN 是它们的公垂线段．点A B ，在1l 上，C 在2l 上，AM MB MN ==．（Ⅰ）证明AC NB ⊥；（Ⅱ）若60ACB ∠=，求NB 与平面ABC 所成角的余弦值．Ｃ1l2解法一：（Ⅰ）由已知221l MN l l ⊥⊥，，1MNl M =，可得2l ⊥平面ABN ．由已知1MN l AM MB MN ⊥==，，可知AN NB =且AN NB ⊥． 又AN 为AC 在平面ABN 内的射影， AC NB ∴⊥．（Ⅱ）Rt Rt CNA CNB △≌△，AC BC ∴=，又已知60ACB ∠=︒，因此ABC △为正三角形． Rt Rt ANB CNB △≌△，NC NA NB ∴==，因此N 在平面ABC 内的射影H 是正三角形ABC 的中心， 连结BH ，NBH ∠为NB 与平面ABC 所成的角．在Rt NHB △中，cos 3ABHB NBH NB ∠===．N1l l解法二：如图，建立空间直角坐标系M xyz -．1l令1MN =，则有(100)(100)(010)A B N -，，，，，，，，．（Ⅰ）MN 是12l l ，的公垂线，21l l ⊥， 2l ∴⊥平面ABN ．2l ∴平行于z 轴．故可设(01)C m ，，．于是(11)(110)AC m NB ==-，，，，，， ∵0011=+-=⋅NB AC AC NB ∴⊥． （Ⅱ）(11)AC m =，，，(11)BC m =-，，，AC BC ∴=．又已知60ACB ∠=︒，ABC ∴△为正三角形，2AC BC AB ===． 在Rt CNB △中，NB =NC =(0C ． 连结MC ，作NH MC ⊥于H ，设(0)(0)H λλ>，．(012)(01HN MC λλ∴=--=，，，，，．∵021=--=⋅λλMC HN ，∴31=λ1033H ⎛⎫∴ ⎪ ⎪⎝⎭，，，可得2033HN ⎛⎫=- ⎪ ⎪⎝⎭，，， 连结BH ，则1133BH ⎛⎫=- ⎪ ⎪⎝⎭，，，∵092920=-+=⋅BH HN ，HN BH ∴⊥，又MC BH H =， HN ∴⊥平面ABC ，NBH ∠为NB 与平面ABC 所成的角．又(110)BN =-，，， ∴3623234cos =⨯=⋅=∠BN BH BN BH NBH【综合测试】一、选择题1、已知AB 是异面直线a 、b 的公垂线段，AB ＝2，a 与b 成30°，在直线a 上取AP ＝4，则点P 到直线b 的距离是（ ）A 、22B 、25C 、142D 、5 2、将锐角为60°，边长为a 的菱形ABCD 沿较短的对角线BD 折成60°的二面角，则AC 与BD 的距离为（ ）A 、a 43B 、a 43C 、a 23 D 、64a 3、正方体ABCD-A 1B 1C 1D 1中，M 是DD 1的中点，O 为正方形A 1B 1C 1D 1的中心，P 是棱AB 上的垂足，则直线A 1M 与OP 所成的角（ ）．A 、30oB 、45oC 、60oD 、90o 4、二面角α-AB-β大小为θ（0°≤θ≤90°），AC ⊂α，∠CAB ＝45o ，AC 与平面β所成角为30o ，则θ角等于（ ）．A 、30oB 、45oC 、60oD 、90o 5、（2005某某卷文4）如图，正方体ABCD －A 1B 1C 1D 1的棱长为1，E 是A 1B 1的中点，则E 到平面AB C 1D 1的距离为（ ）A 、23 B 、22C 、21 D 、336、已知直线a 及平面α，a 与α间的距离为d ．a 在平面α内的射影为a '，l 为平面α内与a '相交的任一直线，则a 与l 间的距离的取值X 围为（ ）A 、[),d +∞B 、(),d +∞C 、(]0,dD 、{}d二、填空题 7、（2005某某卷理12）如图，PA ⊥平面ABC ，∠ACB ＝90°且PA ＝AC ＝BC ＝a ，则异面直线PB 与AC 所成角的正切值等于____________．8、已知∠60o ，则以OC三、解答题：9. C 点到AB 1ABC DA 1E B 1C10.（2006理17）如图，在底面为平行四边形的四棱锥P ABCD -中，AB AC ⊥，PA ⊥平面ABCD ，且PA AB =，点E 是PD 的中点．（Ⅰ）求证：AC PB ⊥；（Ⅱ）求证：PB ∥平面AEC ； （Ⅲ）求二面角E AC B --的大小．B[参考答案]一、选择题1. 选A 提示：过P 做直线b 的垂线2. 选A 提示：用异面直线距离公式求解3. 选D 提示：过A 1做OP 的平行线4. 选B 提示：过C 做平面β的垂线5. 选B. 提示：转化为求B 1到平面AB C 1D 1的距离6. 选D 提示：转化为a 与α间的距离 二、填空题7.2. 提示：将三角形ABC 补成正方形ACBD. 8. 33- 提示：利用直线与直线所成角的大小求出边长，再求二面角平面角的大小三、解答题：9. 解：由CD ⊥平面A 1B 1BA ∴CD ⊥DE ∵AB 1⊥平面CDE ∴DE ⊥AB 1，∴DE 是异面直线AB 1与CD 的公垂线段∵CE ＝23，AC ＝1 ，∴CD ＝.22∴21)()(22=-=CD CE DEABC DA 1E B 1C 110. 解法一：（Ⅰ）（Ⅱ）（略 解见第45讲【达标测试】第9题）（Ⅲ）过O 作FG AB ∥，交AD 于F ，交BC 于G ，则F 为AD 的中点．CDAB AC ⊥，OG AC ∴⊥． 又由（Ⅰ），（Ⅱ）知，AC PB EO PB ，⊥∥，AC EO ∴⊥． EOG ∴∠是二面角E AC B --的平面角．连接EF ，在EFO △中，1122EF PA FO AB ==，，word11 / 11 又PA AB EF FO =，⊥，45135EOF EOG ∴∠=∠=，，∴二面角E AC B --的大小为135．解法二：（Ⅰ）建立空间直角坐标系A xyz -，如图．y 设AC a PA b ==，，则有(000)(00)(00)(00)A B b C a P b ，，，，，，，，，，，，(00)(0)AC a PB b b ∴==-，，，，，，从而0=⋅PB AC ，AC PB ∴⊥．（Ⅱ）连接BD ，与AC 相交于O ，连接EO ．由已知得(0)D a b -，，，002222ab b a E O ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭，，，，，， 022b b EO ⎛⎫∴=- ⎪⎝⎭，，，又(0)PB b b =-，，， 2PB EO ∴=，PB EO ∴∥，又PB ⊄平面AEC EO ，⊂平面AEC ， PB ∴∥平面AEC ．（Ⅲ）取BC 中点G ．连接OG ，则点G 的坐标为000222a b b OG ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，，，，，， 又0(00)22b b OE AC a ⎛⎫=-= ⎪⎝⎭，，，，，，00=⋅=⋅∴AC OG AC OE ，．OE AC OG AC ∴，⊥⊥．EOG ∴∠是二面角E AC B --的平面角．22cos -=⋅<OGOE OG OE ．135EOG ∴∠=． ∴二面角E AC B --的大小为135．。

nPMdab2图npMdα1图MdP nβα4图MdP nα3图怎样求空间角、 空间距离求空间角、 空间距离高考的重点热点之一，属必考内容，同时也是最重要的得分点。

既是必考，就须反复操练，烂熟于心。

一、求空间距离方法方法一：用定义法做出相应的距离，转化为两点间的距离问题求解（通常转化为解三角形问题，有时也用等面积、等体积法求之）方法二： 向量坐标法 则d=||||n MP n ⋅（公式一）1、点P 到平面α的距离.如图1（M 为α内的点，n 为平面的法向量）2、异面直线a 与b 的距离如图2（P 为a 上一点，M 为b 上一点，n 为与两异面直线都垂直的向量）3、平行于平面α的直线l 到平面α的距离如图3（P 为线上一点，M 为面α内一点，n 为平面的法向量）4、平行平面α 、β间的距离如图4（P 为α内一点，M 为β内一点，n 为平面的法向量）二、求空间角的方法方法一：用定义法作角，转化为相交直线所成的角，然后求解. 1、异面直线a 与b 所成的角θ在一条直线上找一点作另一直线的平行线，构成三角形，或在具体图形中找另一点，过此点作两直线的平行线，构成三角形. 2、直线l 与平面α所成的角ϕ斜线上选点P ，过P 作PM ⊥α于M ，连 AM, ϕ=AMP ∠为所求;利用公式cos θb nam5图mαMPn6图=cos 1θ cos ϕ （θ为斜外角，1θ为面平角）3、二面角ϕ过二面角棱上一点分别在两个半平面内做垂线，从而得到所求的二面角（通常利用特殊图形法 、两垂一连法既三垂线定理去做）也可用射影面积公式求之 S ′=S cos ϕ方法二：向量法利用公式cos θ =||||||n m n m ⋅（公式二）求出θ= arccos||||||n m n m ⋅1、异面直线a 与b 所成的角θ如图5分别求出两条直线a 与b 的方向向量m 、n，利用公式二求出θ= arccos||||||n m n m ⋅2、直线l 与平面α所成的角ϕ如图6求与l 的方向向量m ,再求平面α的法向量n , m 与n 所在直线所成的角为θ，利用公式二求出θ= arccos||||||n m n m ⋅则ϕ＝2π－θ 3、求二面角ϕ如图7、8求两平面的法向量m 与n 或如图9、10找分别与两半平面平行且都垂直于棱的两向量m 与n .利用公式二求出θ= arccos||||||n m n m ⋅，当ϕ为锐角时如图7、9ϕ=θ， 当ϕ为钝角时如图8、10 ϕ= π－θ三.、用向量求角，求距离典型例题分析（对我们而言，不能求出角和距离许多时候是因为我们不能找到或作出角和距离。

高三数学知识点：空间角问题知识点总结下面整理了高三数学知识点：空间角问题，希望大家能把觉得有用的知识点摘抄下来，在空余时间进行复习。

一、直线与直线所成的角①两平行直线所成的角：规定为。

②两条相交直线所成的角：两条直线相交其中不大于直角的角，叫这两条直线所成的角。

③两条异面直线所成的角：过空间任意一点O，分别作与两条异面直线a，b平行的直线，形成两条相交直线，这两条相交直线所成的不大于直角的角叫做两条异面直线所成的角。

二、直线和平面所成的角①平面的平行线与平面所成的角：规定为。

②平面的垂线与平面所成的角：规定为。

③平面的斜线与平面所成的角：平面的一条斜线和它在平面内的射影所成的锐角，叫做这条直线和这个平面所成的角。

求斜线与平面所成角的思路类似于求异面直线所成角：一作，二证，三计算。

在作角时依定义关键作射影，由射影定义知关键在于斜线上一点到面的垂线，三、解题技巧在解题时，注意挖掘题设中两个主要信息(1)斜线上一点到面的垂线;(2)过斜线上的一点或过斜线的平面与已知面垂直，由面面垂直性质易得垂线。

(3)二面角和二面角的平面角①二面角的定义：从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫做二面角的棱，这两个半平面叫做二面角的面。

②二面角的平面角：以二面角的棱上任意一点为顶点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫二面角的平面角。

③直二面角：平面角是直角的二面角叫直二面角。

两相交平面如果所组成的二面角是直二面角，那么这两个平面垂直;反过来，如果两个平面垂直，那么所成的二面角为直二面角④求二面角的方法定义法：在棱上选择有关点，过这个点分别在两个面内作垂直于棱的射线得到平面角垂面法：已知二面角内一点到两个面的垂线时，过两垂线作平面与两个面的交线所成的角为二面角的平面角以上就是高三数学知识点：空间角问题，希望能帮助到大家。

张喜林制[选取日期]高三数学第二轮专题讲座复习：关于求空间的角的问题高考要求空间的角是空间图形的一个要素，在异面直线所成的角、线面角、二面角等知识点上，较好地考查了学生的逻辑推理能力以及化归的数学思想 重难点归纳空间角的计算步骤 一作、二证、三算1 异面直线所成的角 范围 0°＜θ≤90°方法 ①平移法；②补形法2 直线与平面所成的角 范围 0°≤θ≤90° 方法 关键是作垂线，找射影3 二面角方法 ①定义法；②三垂线定理及其逆定理；③垂面法注1 二面角的计算也可利用射影面积公式S ′=S cos θ来计算注2 借助空间向量计算各类角会起到事半功倍的效果 4．三种空间角的向量法计算公式：⑴异面直线,a b 所成的角θ：cos cos ,a b θ=<>；⑵直线a 与平面α(法向量n )所成的角θ：sin cos ,a n θ=<>； ⑶锐二面角θ：cos cos ,m n θ=<>，其中,m n 为两个面的法向量。

典型题例示范讲解例1在棱长为a 的正方体ABCD —A ′B ′C ′D ′中，E 、F 分别是BC 、A ′D ′的中点(1)求证 四边形B ′EDF 是菱形；(2)求直线A ′C 与DE 所成的角；(3)求直线AD 与平面B ′EDF 所成的角；(4)求面B ′EDF 与面ABCD 所成的角命题意图 本题主要考查异面直线所成的角、线面角及二面角的一般求法，综合性较强知识依托 平移法求异面直线所成的角，利用三垂线定理求作二面角的平面角 错解分析 对于第(1)问，若仅由B ′E =ED =DF =FB ′就断定B ′EDF 是菱形是错误的，因为存在着四边相等的空间四边形，必须证明B ′、E 、D 、F 四点共面技巧与方法 求线面角关键是作垂线，找射影，求异面直线所成的角采用平移法 求二面角的大小也可应用面积射影法(1)证明 如上图所示，由勾股定理，得B ′E =ED =DF =FB ′=25a ,下证B ′、E 、D 、F 四点共面，取AD 中点G ，连结A ′G 、EG ，由EG AB A ′B ′知，B ′EGA ′是平行四边形 ∴B ′E ∥A ′G ,又A ′FD G ,∴A ′GDF 为平行四边形∴A ′G ∥FD ，∴B ′、E 、D 、F 四点共面故四边形B ′EDF 是菱形(2)解 如图所示，在平面ABCD 内，过C 作CP ∥DE ，交直线AD 于P ，则∠A ′CP (或补角)为异面直线A ′C 与DE 所成的角在△A ′CP 中， 易得A ′C =3a ，C P =DE =25a ,A ′P =213a 由余弦定理得cos A ′CP =1515 故A ′C 与DE 所成角为另法（向量法） 如图建立坐标系，则(0,0,),(,,0),(0,,0),(,,0)2aA a C a a D a E a '(,,),(,,0)2aA C a a a DE a '⇒=-=-15cos ,15||||A C DE A C DE A C DE ''⇒<>==' 故A ′C 与DE 所成角为 (3)解 ∵∠ADE =∠ADF ,∴AD 在平面B ′EDF 内的射影在∠EDF 的平分线上 如下图所示又∵B ′EDF 为菱形，∴DB ′为∠EDF 的平分线， 故直线AD 与平面B ′EDF 所成的角为∠ADB ′ 在Rt △B ′AD 中，AD =2a ，AB ′=2a ,B ′D =2a则cosADB ′=33故AD 与平面B ′EDF 所成的角是 另法（向量法）∵∠ADE =∠ADF ,∴AD 在平面B ′EDF 内的射影在∠EDF 的平分线上 如下图所示 又∵B ′EDF 为菱形，∴DB ′为∠EDF 的平分线，故直线AD 与平面B ′EDF 所成的角为∠ADB ′， 如图建立坐标系，则 (0,0,0),(,0,),(0,,0)A B a a D a '(0,,0),(,,)DA a DB a a a '⇒=-=-3cos ,3||||DA DB DA DB DA DB ''⇒<>=='，故AD 与平面B ′EDF 所成的角是 (4)解 如图，连结EF 、B ′D ，交于O 点，显然O 为B ′D 的中点，从而O 为正方形ABCD —A ′B ′C ′D 的中心作OH ⊥平面ABCD ，则H 为正方形ABCD 的中心， 再作HM ⊥DE ，垂足为M ，连结OM ，则OM ⊥DE ，B故∠OMH 为二面角B ′—DE ′—A 的平面角在Rt △DOE 中，OE =22a ,OD =23a ,斜边DE =25a , 则由面积关系得OM =1030=⋅DEOEOD a 在Rt △OHM 中，sin OMH =630=OM OH 故面B ′EDF 与面ABCD 所成的角为 另法（向量法） 如图建立坐标系，则(0,0,0),(0,0,),(,0,),(0,,0),(,,0)2aA A aB a a D a E a ''，所以面ABCD 的法向量为(0,0,),m AA a '==下面求面B ′EDF 的法向量n设(1,,)n y z =，由(,,0),(0,,),22a aED a EB a '=-=- 00221002a a y nED y a z nED y az ⎧-+=⎪⎧==⎧⎪⎪⇒⇒⎨⎨⎨==⎩⎪⎪⎩-+=⎪⎩∴(1,2,1)n =∴6cos ,||||6n m n m n m <>==故面B ′EDF 与面ABCD 所成的角为 例2如下图，已知平行六面体ABCD —A 1B 1C 1D 1中，底面ABCD 是边长为a 的正方形，侧棱AA 1长为b ,且AA 1与AB 、AD 的夹角都是120°求 (1)AC 1的长；(2)直线BD 1与AC 所成的角的余弦值技巧与方法 数量积公式及向量、模公式的巧用、变形用21111111222111:(1)||()()()()||||||222AC AC AC AA AC AA AC AA AB AD AA AB AD AA AB AD AA AB AA AD AB AD=⋅=++=++++=+++⋅+⋅+⋅解22222111112221:||,||||,,120,,9011cos120,cos120,0,22||2AA b AB AD aAA AB AA AD AB AD AA AB b aab AA AD b a ab AB AD AC a b ===<>=<>=︒<>=︒∴⋅=⋅︒=-⋅=⋅︒=-⋅=∴=+-由已知得12,||ab AC ∴=1111112211(2),||2,()()AC a AC AB AD BD AD BA AA AD AB AC BD AB AD AA AD AB AB AA AD AA AB AD AD AB ==+=+=+-∴⋅=++-=⋅+⋅+⋅+-依题意得21111122222111||()()||||||2222AB AD ab BD BD BD AA AD AB AA AD AB AA AD AB AA AD AB AD AA AB a b -⋅=-=⋅=+-+-=+++⋅-⋅-⋅=+2212||b a BD +=∴111cos ,||||4BD AC BD AC BD AC ⋅<>==∴BD 1与AC例3如图，l αβ--为60°的二面角，等腰直角三角形MPN 的直角顶点P 在l 上，M ∈α,N ∈β,且MP 与β所成的角等于NP 与α (1)求证 MN 分别与α、β所成角相等； (2)求MN 与β所成角(1)证明 作NA ⊥α于A ，MB ⊥β于B ,连接AM ，再作AC ⊥l 于C ，BD ⊥l 于D ，连接NC 、∵NA ⊥α,MB ⊥β,∴∠MPB 、∠NP A 分别是及NP 与α所成角，∠MNB ，∠NMA 分别是MN 与角，∴∠MPB =∠NP A在Rt △MPB 与Rt △NP A 中，PM =PN ，∠MPB =∠NPA ，∴△MPB ≌△NPA ，∴MB =NA在Rt △MNB 与Rt △NMA 中，MB =NA ，MN 是公共边，∴△MNB ≌△NMA ，∴∠MNB =∠NMA ，即(1)结论成立(2)解 设∠MNB =θ,MN =2a ,则PB =PN =a ,MB =NA =2a sin θ，NB =2a cos θ,∵MB ⊥β,BD ⊥l ,∴MD ⊥l ,∴∠MDB 是二面角α—l —β的平面角，∴∠MDB =60°，同理∠NCA =60°,∴BD =AC =3633=MB a sin θ,CN =DM =63260sin 6=︒MB a sin θ, ∵MB ⊥β，MP ⊥PN ，∴BP ⊥PN∵∠BPN =90°,∠DPB =∠CNP ,∴△BPD ∽△PNC ,∴PBBDPN PC ===整理得，16sin 4θ－16sin 2θ+3=0解得sin 2θ=4341或,sin θ=2321或，当sin θ=23时，CN =632a sin θ= 2a ＞PN 不合理，舍去 ∴sin θ=21,∴MN 与β所成角为30°。

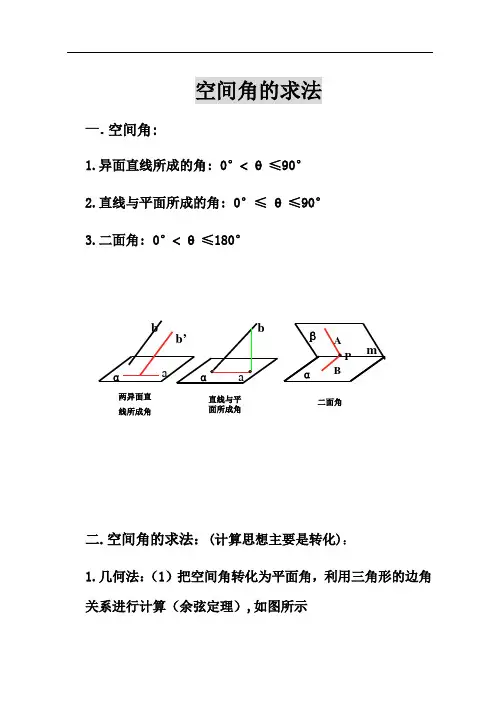
空间角的求法一.空间角:1.异面直线所成的角: 0°<θ≤90°2.直线与平面所成的角: 0°≤θ≤90°3.二面角: 0°<θ≤180°二.空间角的求法：(计算思想主要是转化)：1.几何法：（1）把空间角转化为平面角，利用三角形的边角关系进行计算（余弦定理）,如图所示（2）计算步骤：一作、二证、三点、四算2.向量法：把空间角的计算转化为空间向量的坐标运算来求解（1）异面直线所成的角：把异面直线所成角化为向量的夹角。

一般地，异面直线l1、l2的方向向量夹角的余弦为：cosa ba bβ⋅=⋅，则所求异面直线所成角（范围）与其相等或互补。

（2）直线和平面所成的角:利用斜线和射影的夹角或考虑法向量，设θ为直线l 与平面α所成的角，ϕ为直线l 的方向向量v 与平面α的法向量n 之间的夹角，则有2πϕθ=-或θπϕ+=2,所以sin cos n v n vθϕ⋅==特别地 0=ϕ时，2πθ=，α⊥l ；2πϕ=时，0=θ，α⊆l 或α//l 。

（3）二面角的求法：①从平面的法向量考虑，设 21,n n 分别为平面βα,的法向量，二面角β--αl 的大小为θ，向量21,n n 的夹角为ϕ，则有π=ϕ+θ或 ϕ=θ（图5）,所以1212cos n n n n ϕ⋅=⋅ 。

θωαlvnωθαvln因为二面角的大小有时为锐角、直角，有时也为钝角。

所以在计算之前不妨先依题意判断一下所求二面角的范围，然后根据计算取“相等角”或取“补角”。

②如果AB 、CD 分别是二面角l αβ--的两个面内与棱l 垂直的异面直线，则二面角的大小为,AB CD 〈〉。

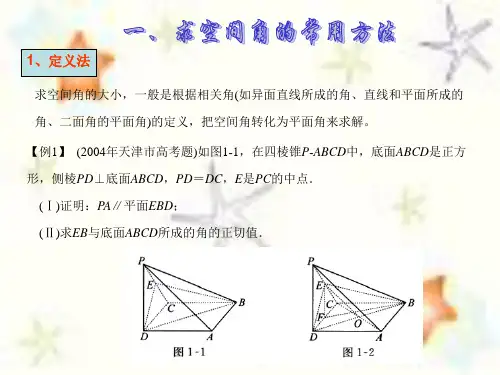
三.例题与练习：例1.如右下图，在长方体1111ABCD A B C D -中，已知4AB =，3AD =，12AA =,E 、F 分别是线段AB 、BC 上的点，且1EB FB == ，求直线1EC 与1FD 所成的角。

空间角的几何求法一、 异面直线所成角（线线角）范围：(0,]2πθ∈先通过其中一条直线或者两条直线的平移，找出这两条异面直线所成的角，然后通过解三角形去求得。

【典例分析】例1. 已知多面体ABCDE 中，AB ⊥平面ACD ，DE ⊥平面ACD ，AC = AD = CD = DE = 2，AB = 1，F 为CD 的中点. （1）求证：AF ⊥平面CDE ； （2）求异面直线AC ，BE 所成角余弦值；【变式】在长方体中，，，则异面直线与所成角的余弦值为。

二、直线与平面所成角（线面角）范围：[0,]2πθ∈【典例分析】例1.如图，已知多面体ABCA 1B 1C 1，A 1A ，B 1B ，C 1C 均垂直于平面ABC ，∠ABC =120°，A 1A =4，C 1C =1，AB =BC =B 1B =2．（1）证明：AB 1⊥平面A 1B 1C 1；（2）求直线AC 1与平面ABB 1所成的角的正弦值．【变式】如图，四边形ABCD 是正方形，PB ⊥平面ABCD ，MA//PB ，PB=AB=2MA ， （1）证明：AC//平面PMD ；（2）求直线BD 与平面PCD 所成的角的大小；1111ABCD A B C D -1AB BC ==13AA =1AD 1DB例2. 如图所示，四棱锥P —ABCD 中，AB ⊥AD ，CD ⊥AD ，PA ⊥底面ABCD ，PA=AD=CD=2AB=2， M 为PC 的中点。

(1)求证：BM∥平面PAD ；(2)在侧面PAD 内找一点N ，使MN ⊥平面PBD ； (3)求直线PC 与平面PBD 所成角的正弦。

【变式】如图，在三棱锥V ABC -中，VC ABC ⊥底面，AC BC ⊥，D 是AB 的中点，且AC BC a ==，π02VDC θθ⎛⎫=<< ⎪⎝⎭∠．（1）求证：平面VAB ⊥平面VCD ；（2）试确定角θ的值，使得直线BC 与平面VAB 所成的角为π6．三、平面与平面所成角（面面角）范围：[0,]θπ∈（1）定义法：当点A 在二面角α- -β的棱 上时，可过A 分别在α、β内作棱 的垂线，AB 、AC ，由定义可知∠BAC 即为二面角α- -β的平面角。

立体几何专题：空间角第一节：异面直线所成的角一、基础知识1.定义： 直线a 、b 是异面直线，经过空间一交o ，分别a ΄//a ，b ΄//b ，相交直线a ΄b ΄所成的锐角（或直角）叫做。

2.范围： ⎥⎦⎤⎝⎛∈2,0πθ3.方法： 平移法、问量法、三线角公式（1）平移法：在图中选一个恰当的点（通常是线段端点或中点）作a 、b 的平行线，构造一个三角形，并解三角形求角。

（2）向量法：可适当选取异面直线上的方向向量，利用公式ba b a b a ⋅=><=,cos cos θ求出来方法1：利用向量计算。

选取一组基向量，分别算出 b a ⋅，a ，b 代入上式 方法2：利用向量坐标计算，建系，确定直线上某两点坐标进而求出方向向量),,(111z y x a =),,(222z y x b =222222212121212121cos z y x z y x z z y y x x ++++++=∴θ（3）三线角公式 用于求线面角和线线角 斜线和平面内的直线与斜线的射影所成角的余弦之积等于斜线和平面内的直线所成角的余弦 即：θθθcos cos cos 21= 二、例题讲练例1、（2007年全国高考）如图，正四棱柱1111ABCD A B C D -中， 12AA AB =，则异面直线1A B 与1AD 所成角的余弦值为 例2、在长方体ABCD-A 1B 1C 1D 1中，已知AB=a ，BC=)(b a b >,AA 1=c ，求异面直线D 1B 和AC 所成的角的余弦值。

方法一：过B 点作 AC 的平行线（补形平移法） 方法二：过AC 的中点作BD1平行线方法三：（向量法）例3、 已知四棱锥P ABCD -的底面为直角梯形，//AB DC ，⊥=∠PA DAB ,90 底面ABCD ，且12PA AD DC ===，1AB =，M 是PB 的中点（Ⅰ）证明：面PAD ⊥面PCD ； （Ⅱ）求AC 与PB 所成的角；例4、 如图，在四棱锥P ABCD -中，底面ABCD 为矩形，侧棱PA ⊥底面ABCD ，3AB =，1BC =，2PA =， E 为PD 的中点求直线AC 与PB 所成角的余弦值；AB1B 1A 1D 1CCDOBB1A1AC1D CD1ϕ2ϕ1c b aθPαO AB1.正方体的12条棱和12条 面对角线中，互相异面的两条线成的角大小构成的集合是。

空间角及其求法张玉洪异面直线所成角直线与平面所成二面角图示定义在空间任取一点o，分别作a，b的平行线，从而形成的的锐（角）叫作异面直线所成角。

斜线与它在平面内的射影所成的锐角。

从一条直线引出的两个半平面所组成的图形叫做二面角。

表示异面直线a、b所成角线a与平面所成角范围备注平移、妙选顶点找射影、二足相连用什么度量？一.用定义求空间角的步骤1.作出所求的空间角<定位>2.证明所作的角符合定义<定性>3.构造三角形并求出所要求角<定量>简言之，空间角的求解步骤为：“一作”、“二证”、“三算”二典例分析例1已知正方体ABCD-A1B1C1D1，M、N分别是棱A1B1和BB1的中点，求直线AM 和CN所成角。

解析：途径一过D1作D1E//AM，作D1F//CN，连接EF，显然为异面直线AM与CN所成角。

通过解△D1EF即可。

途径二过D作D1E//AM，再过N作NG//D1E，显然为异面直线AM与CN所成角。

通过解△ＮＧＣ即可。

方法提炼1求两条异面直线所成的角关键在于妙选点、作平线。

常选中点或线端点，利用中位线的性质或平行四边形的性质等作出符合要求的平行线。

例2.如图棱长是1的正方体，p、Q分别是棱AB、CC1上的内分点，满足.（1）求证：A1p⊥平面AQD；（2）求直线pQ与平面AQD所成角的正弦值.解析：过Q作QR平行AD，交BB1与R，连接AR，易知面ADQR即为面AQD由（1）知A1p ⊥面AQD，设A1p交AR与S，连接SQ即可。

由以上的作法可知即为所求角，只需解三角形SpQ即可。

方法提炼2.求直线和平面所成角要领“找射影，二足相连”。

由于平面的一条斜线在这个平面的射影只有一条，所以关键在于寻该斜线在面上的射影。

例3. 在四棱锥p-ABCD中，已知ABCD为矩形，pA ⊥平面ABCD，设pA=AB=a，BC=2a，求二面角B-pC-D的大小。

解析1.定义法过D作DE ⊥pC于E，过E作EF ⊥pC于F，连接FD，由二面角的平面角的定义可知是所求二面角B-pC-D的平面角。

PCDBA 空间角的求法空间角，能比较集中反映空间想象能力的要求，历来为高考命题者垂青，几乎年年必考。

空间角是异面直线所成的角、直线与平面所成的角及二面角总称。

空间角的计算思想主要是转化：即把空间角转化为平面角，把角的计算转化到三角形边角关系或是转化为空间向量的坐标运算来解。

空间角的求法一般是：一找、二证、三计算。

异面直线所成的角的范围：090θ<≤ （一）平移法【例1】已知四边形ABCD 为直角梯形，//AD BC ，90ABC ∠=，PA ⊥平面AC ，且2BC =，1PA AD AB ===，求异面直线PC 与BD 所成角的余弦值的大小。

【解】过点C 作//CE BD 交AD 的延长线于E ，连结PE，则PC 与BD 所成的角为PCE ∠或它的补角。

CEBD ==PE=∴由余弦定理得 222cos 2PC CE PE PCE PC CE +-∠==⋅∴PC 与BD 所成角的余弦值为63 （二）补形法【变式练习】已知正三棱柱111ABC A B C -的底面边长为8，侧棱长为6，D 为AC 中点。

求异面直线1AB与1BC 所成角的余弦值。

【答案】125A 1C 1CBAB 1 DCP二、直线与平面所成角直线与平面所成角的范围：090θ≤≤ 方法：射影转化法（关键是作垂线，找射影）【例2】如图，在三棱锥P ABC -中，90APB ∠=，60PAB ∠=，AB BC CA ==，点P 在平面ABC内的射影O 在AB 上，求直线PC 与平面ABC 所成的角的大小。

【解】连接OC ，由已知，OCP ∠为直线PC 与平面ABC 所成角设AB 的中点为D ，连接,PD CD 。

AB BC CA ==，所以CD AB ⊥90,60APB PAB ∠=∠=，所以PAD ∆为等边三角形。

不妨设2PA =，则1,3,4OD OP AB ===2223,13CD OC OD CD ∴==+=在Rt OCP ∆中，339tan 13OP OCP OC ∠===【变式练习1】如图，四棱锥S ABCD -中，//AB CD ，BC CD ⊥，侧面SAB 为等边三角形。

高中数学知识专题系列空间角的求法（1）定义法:求解空间角的大小，一般都是根据有关角的定义（如异面直线所成的角、斜线和平面所成的角、二面角的平面角），把空间角转化为平面角来求解的。

例1、如图，在棱长为2的正方体1111D C B A ABCD -中，O 是底面ABCD 的中心，E 、F 分别是1CC 、AD 的中点，那么异面直线OE 和1FD 所成的角的余弦值等于（ ）A 、510 B 、515 C 、54 D 、32解：（方法一）如图2，取11C D 的中点M ，连结MO O 为底面中心，∴O 为BD 中点，从而FO 为DAB ∆的中位线M D AB FO 1//21//∴，∴四边形FOM D 1为平行四边形F D MO 1//∴，故MOE ∠（或其补角）即为异面直线F D 1和OE 所成的角。

在MOE ∆中，2,51221==+==ME F D OMOE 3)2(1222=+=+=OC EC 由余弦定理得：5153522352cos 222=⋅⋅-+=⋅-+=∠OE OM ME OE OM MOE 故选B（方法二）如图3，取C D 1的中点N ，连结NF 、N D 1，易知NF //EO ，FN D 1∠∴（或其补角）即为异面直线F D 1和OE 所成的角。

在FN D 1∆中，3,221,5111=====OE NF C D N D F D ，由余弦定理得： 5153522352cos 1212211=⋅⋅-+=⋅⋅-+=∠NF FD N D NF FD FN D 故选BA 1 图1C A 1图2A 1图3A 1 D 图4高中数学知识专题系列haiPage 2 of 13(方法三) 如图4，设BC 中点为P ，PC 中点为Q ，连结P C 1、EQ 、OQ 、OP ，易知F D P C 11//F D EQ P C EQ 1121//,21//∴OEQ ∠∴（或其补角）即为异面直线F D 1和OE 所成的角。