二阶电路 RLC串联电路零输入响应

实验二二阶电路响应的三种（欠阻尼、过阻尼及临界阻尼）状态轨迹及其特点一、实验目的1、熟练掌握二阶电路微分方程的列写及求解过程；2、掌握RLC 二阶电路零输入响应及电路的过阻尼、临界阻尼和欠阻尼状态；3、学会利用MULTISIM 仿真软件熟练分析电路，尤其是电路中各电压电流的变化波形。

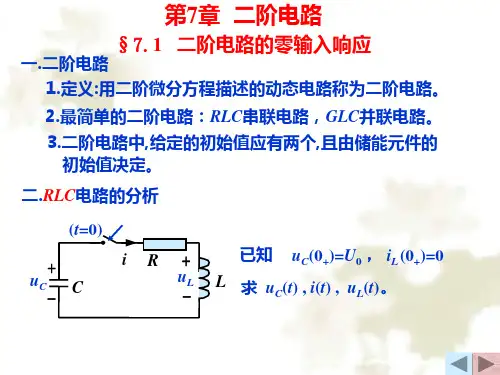
二、实验原理用二阶线性常微分方程描述的电路称为二阶电路，二阶电路中至少含有两个储能元件。

二阶电路微分方程式一个含有二次微分的方程，由二阶微分方程描述的电路称为二阶电路。

分析二阶电路的方法仍然是建立二阶微分方程，并利用初始条件求解得到电路的响应。

二阶方程一般都为齐次方程。

齐次方程的通解一般分为三种情况：（RLC 串联时）1、 21S S ≠ 为两个不等的实根（称过阻尼状态）t S t S h e A e A f 211121+= 此时，CL R 2>，二阶电路为过阻尼状态。

2、 σ==21S S 为相等实根（称临界状态）t h e A A f σ)21+=（ 此时，CL R 2=，二阶电路为临界状态。

3、 ωσj S ±-=21、为共轭复根（称欠阻尼状态）t h e t f σβω-+=)sin( 此时CL R 2<，二阶电路为欠阻尼状态。

这三个状态在二阶电路中式一个重要的数据，它决定了电路中电流电压关系以及电流电压波形。

三、实验内容电路中开关S 闭合已久。

t=0时将S 打开，并测量。

1、欠阻尼状态（R=10Ω,C=10mF,L=50mH ）如图所示，为欠阻尼状态时的二阶电路图。

波形图展示了欠阻尼状态下的C U 和L U 波形(橙色线条为电容电压衰减波形，红色线条为电感电压衰减波形)。

2、临界阻尼（R=10Ω,C=10mF,L=0.25mH ）如图所示，为临界状态的二阶电路图。

图展示了临界状态下的C U 的波形。

波形图展示了临界状态下的C U 和L U 波形。

3、过阻尼状态（R=10Ω,C=1mF,L=1mH ）如图所示，为过阻尼状态下的二阶电路图。

二阶电路分析——LC 震荡的推导如图9.16所示，RLC 串联电路零输入响应的数学分析依KVL ，得 0=-+C L R u u u按图9.16中标定的电压，电流参考方向有 dtdu Ci C-= dtdu RCRi u CC -== 22dtu d LC dt diL u C L -==将以上各式代入KVL 方程，便可以得出以 C u 为响应变量的微分方程，为022=++C CC u dt du RC dt u d LC ()0≥T （9.10）式（9.10）为一常系数二阶线性齐次微分方程，其特征方程为012=++RCp LCp其特征根为20222,1122ωαα-±-=-⎪⎭⎫ ⎝⎛±-=LC L R L R p 式中：L R 2/=α称为衰减系数；LC /10=ω称为固有振荡角频率。

1.几种不同情况的讨论(1)当(R/2L)2>1/LC 时，1p 、2p 为不相等的负实根，称为过阻尼情况。

特征根为2022,1ω-±-=a a p微分方程的通解为()tp t p C e A e A t u 2121+= （9.11）其中待定常数1A 、2A 由初始条件来确定，其方法是：当+=0t 时刻，则由式(9.11) 可得()21A A t u C +=对式(9.12)求导，可得+=0t 时刻()t u C 对t 的导数的初始值为()()()Ci p A p A dt t du u t C C+=+-=+=='+0022110联立求解式(9.12)和式(9.13)，便可以解出1A 、2A 。

根据式(9.11)可知，零输入响应()t u C 是随时间按指 数规律衰减的，为非振荡性质。

()t u C 的波形如图9. 17所示。

（2）.当()LC L R /12/2=时， 1p 、2p 为相等的负实根， 称为临界阻尼情况。

特征根为a p p -==21微分方程的通解为()()at C e t A A t u -+=21其中常数1A 、2A 由初始条件()+0C u 和()+'0C u 来确定。

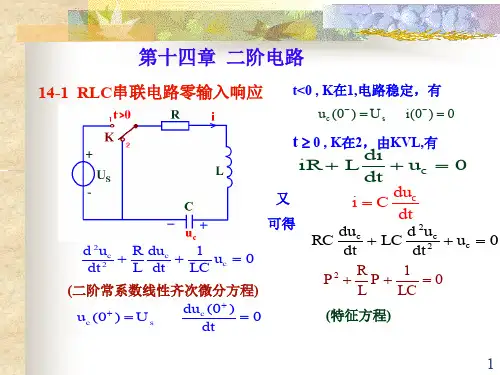
二阶电路分析——LC 震荡的推导如图9.16所示，RLC 串联电路零输入响应的数学分析依KVL ，得 0=-+C L R u u u按图9.16中标定的电压，电流参考方向有 dtdu Ci C-= dtdu RCRi u CC -== 22dtu d LC dt diL u C L -==将以上各式代入KVL 方程，便可以得出以 C u 为响应变量的微分方程，为022=++C CC u dt du RC dt u d LC ()0≥T （9.10）式（9.10）为一常系数二阶线性齐次微分方程，其特征方程为012=++RCp LCp其特征根为20222,1122ωαα-±-=-⎪⎭⎫ ⎝⎛±-=LC L R L R p 式中：L R 2/=α称为衰减系数；LC /10=ω称为固有振荡角频率。

1.几种不同情况的讨论(1)当(R/2L)2>1/LC 时，1p 、2p 为不相等的负实根，称为过阻尼情况。

特征根为2022,1ω-±-=a a p微分方程的通解为()tp t p C e A e A t u 2121+= （9.11）其中待定常数1A 、2A 由初始条件来确定，其方法是：当+=0t 时刻，则由式(9.11) 可得()21A A t u C +=对式(9.12)求导，可得+=0t 时刻()t u C 对t 的导数的初始值为()()()Ci p A p A dt t du u t C C+=+-=+=='+0022110联立求解式(9.12)和式(9.13)，便可以解出1A 、2A 。

根据式(9.11)可知，零输入响应()t u C 是随时间按指 数规律衰减的，为非振荡性质。

()t u C 的波形如图9. 17所示。

（2）.当()LC L R /12/2=时， 1p 、2p 为相等的负实根， 称为临界阻尼情况。

特征根为a p p -==21微分方程的通解为()()at C e t A A t u -+=21其中常数1A 、2A 由初始条件()+0C u 和()+'0C u 来确定。

关于RLC 二阶电路的分析方法——电路的微分方程与初始条件
由两个独立储能元件组成的电路，其过渡过程的特征性用二阶微分方程描述，故称为二阶电路。

RLC 串联电路，是典型的二阶电路。

通过对它的分析来明确二阶电路过渡过程的基本概念和分析方法，着重讨论RLC 串联电路的放电过程，即电路的固有响应也就是零输入响应。

也介绍RLC 串联电路的充电过程，即零状态响应和完全响应。

1．电路的微分方程与初始条件
如图4-5所示RLC 串联二阶电
路，0≥t 时以电容电压C u 为变
量描述动态过程特性的微分方程
是图 4-5 RLC 串联二阶电路 022=++C C C u dt du RC dt u d LC
过渡过程中电容电压C u 随时间变化的规律，就是微分方程的解。

方程的求解，需有如下两个初始条件：
)0(C u
C i dt du u L t C C )
0()0(0=='=
只要知道电路的两个初始状态)0(C u 和)0(L i ，按上式便可得出初始条件)0(C u 和)0(C u '。

于是，RLC 串联电路的放电过程的C u ，就是满足上述初始条件齐次微分方程的解；充电过程的C u ，就是满足初始条件非齐次微分方程的解。

+-
C u。

实验二二阶电路响应的三种（欠阻尼、过阻尼及临界阻尼）状态轨迹及其特点一、实验目的1、熟练掌握二阶电路微分方程的列写及求解过程；2、掌握RLC 二阶电路零输入响应及电路的过阻尼、临界阻尼和欠阻尼状态；3、学会利用MULTISIM 仿真软件熟练分析电路，尤其是电路中各电压电流的变化波形。

二、实验原理用二阶线性常微分方程描述的电路称为二阶电路，二阶电路中至少含有两个储能元件。

二阶电路微分方程式一个含有二次微分的方程，由二阶微分方程描述的电路称为二阶电路。

分析二阶电路的方法仍然是建立二阶微分方程，并利用初始条件求解得到电路的响应。

二阶方程一般都为齐次方程。

齐次方程的通解一般分为三种情况：（RLC 串联时）1、 21S S ≠ 为两个不等的实根（称过阻尼状态）t S t S h e A e A f 211121+= 此时，CL R 2>，二阶电路为过阻尼状态。

2、 σ==21S S 为相等实根（称临界状态）t h e A A f σ)21+=（ 此时，CL R 2=，二阶电路为临界状态。

3、 ωσj S ±-=21、为共轭复根（称欠阻尼状态）t h e t f σβω-+=)sin( 此时CL R 2<，二阶电路为欠阻尼状态。

这三个状态在二阶电路中式一个重要的数据，它决定了电路中电流电压关系以及电流电压波形。

三、实验内容电路中开关S 闭合已久。

t=0时将S 打开，并测量。

1、欠阻尼状态（R=10Ω,C=10mF,L=50mH ）如图所示，为欠阻尼状态时的二阶电路图。

波形图展示了欠阻尼状态下的C U 和L U 波形(橙色线条为电容电压衰减波形，红色线条为电感电压衰减波形)。

2、临界阻尼（R=10Ω,C=10mF,L=0.25mH ）如图所示，为临界状态的二阶电路图。

图展示了临界状态下的C U 的波形。

波形图展示了临界状态下的C U 和L U 波形。

3、过阻尼状态（R=10Ω,C=1mF,L=1mH ）如图所示，为过阻尼状态下的二阶电路图。

RLC串联电路的零输入响应方程和特征根
二阶电路:可用二阶常微分方程描述的电路称为二阶电路。

如图7-15所示RLC串联电路。

选择各元件的电压与电流为关联参考方向的情况下，由KVL得
其中：
即
化简得
上式是二阶常系数线性齐次微分方程，可见RLC串联电路属于二阶电路。

为求解方程，令
称δ为衰减系数，为回路谐振角频率。

则
这样，得到二阶齐次方程的特征方程为
所以，RLC串联电路零输入响应可写成
式中A、B是积分常数，由初始条件确定。

电路的初始条件有三种情况：uc(0-)，iL(0-)都不为零；uc(0-)不为零，iL(0-)为零；uc(0-)为零，iL(0-)不为零。

这三种情况的分析过程是相似
的，这里只分析
的情况。

即充了电的电容器对没有储能的电感线圈放电的情况。

由于δ的取值不同，则会有三种情况：
即。

§5.6 二阶电路的零输入响应5.6.1 二阶电路的初始条件初始条件在二阶电路的分析进程中起着决定性作用，确定初始条件时，必须注意以下几个方面。

第一，在分析电路时，要始终仔细考虑电容两端电压C u 的极性和流过电感电流L i 的方向；第二，电容上的电压总是连续的，即)0()0(-+=C C u u （5-31） 流过电感的电流也总是连续的，即)0()0(-+=L L i u （5-32） 确定初始条件时，首先要用（5-31）和（5-32）式确定没有突变的电路电流，电容电压和电感电流的初始值。

5.6.2 R L C 串联电路的零输入响应如图5-37所示为RLC 串联电路。

开关S 闭合前，电容已经充电，且电容的电压0U u C =，电感中储存有电场能，且初始电流为0I 当0=t 时，开关S 闭合，电容将通过L R 放电，其中一部分被电阻消耗，另一部分被电感以磁场能的形式储存，之后磁场能有通过R 转换成电场能，如此反复；同样，也有可能先是由电感储存的磁场能转换成电场能，并如此反复，当然也可能不存在能量的反复转换。

+-L u C图5-37 RLC 串联电路的零输入响应由图5-37所示参考方向，据KVL 可得0=++-L R C u u u且有dtdu C i C C -=，dt du RC Ri u C R ==，dt u d LC dt di L u CL 2-==。

将其代入上式得022=++C CC u dtdu RC dt u d LC 式（5-33）是RLC 串联电路放电过程以C u 为变量的微分方程，为一 个线性常系数二阶微分方程。

如果以电流i 作为变量，则RLC 串联电路的微分方程为022=++i dtdi RC dt i LC d （5-34）在此，仅以C u 为变量进行分析，令Aeu ptC =，并代入（5-33），得到其对应的特征方程012=++RCp LCp 求解上式，得到特征根为LCL R L R P LC L R L R P 1221222221-⎪⎭⎫⎝⎛--=-⎪⎭⎫ ⎝⎛+-= （5-35）因此，电容电压C u 用两特征根表示如下：t p tp C e A eA u 2121+= （5-36）从式（5-35）可以看出，特征根1p 、2p 仅与电路的参数和结构有关，而与激励和初始储能无关。

二阶电路分析-—LC 震荡的推导如图9。

16所示，RLC 串联电路零输入响应的数学分析依KVL ，得 0=-+C L R u u u按图9.16中标定的电压，电流参考方向有 dtdu Ci C-= dtdu RCRi u CC -== 22dtu d LC dt diL u C L -==将以上各式代入KVL 方程，便可以得出以 C u 为响应变量的微分方程,为022=++C CC u dt du RC dt u d LC ()0≥T （9。

10）式（9.10）为一常系数二阶线性齐次微分方程，其特征方程为012=++RCp LCp其特征根为20222,1122ωαα-±-=-⎪⎭⎫ ⎝⎛±-=LC L R L R p 式中:L R 2/=α称为衰减系数；LC /10=ω称为固有振荡角频率。

1.几种不同情况的讨论(1）当(R/2L)2〉1/LC 时，1p 、2p 为不相等的负实根，称为过阻尼情况。

特征根为2022,1ω-±-=a a p微分方程的通解为()tp t p C e A e A t u 2121+= (9.11）其中待定常数1A 、2A 由初始条件来确定,其方法是：当+=0t 时刻，则由式(9。

11） 可得()21A A t u C +=对式(9.12)求导，可得+=0t 时刻()t u C 对t 的导数的初始值为()()()Ci p A p A dt t du u t C C+=+-=+=='+0022110联立求解式（9。

12)和式（9.13)，便可以解出1A 、2A . 根据式(9.11)可知，零输入响应()t u C 是随时间按指 数规律衰减的，为非振荡性质。

()t u C 的波形如图9。

17所示。

（2）。

当()LC L R /12/2=时， 1p 、2p 为相等的负实根, 称为临界阻尼情况。

特征根为a p p -==21 微分方程的通解为()()at C e t A A t u -+=21其中常数1A 、2A 由初始条件()+0C u 和()+'0C u 来确定。