低通滤波器电路结构仿真图
- 格式:pdf
- 大小:232.31 KB
- 文档页数:4
![微带阶梯阻抗低通滤波器原理图的仿真_物联网:ADS射频电路仿真与实例详解_[共10页]](https://uimg.taocdn.com/d13916b39b6648d7c0c746c5.webp)
║260 物联网:ADS 射频电路仿真与实例详解 5式(11.7)和(11.8)中,L 和C 是低通滤波器原型的元器件值,R S 是滤波器阻抗。
2.阶梯阻抗低通滤波器的设计下面设计微带线阶梯阻抗低通滤波器,设计的详细过程可以参阅人民邮电出版社出版的《射频电路理论与设计》。
要求截止频率为3GHz ,通带内波纹为0.5dB ,在6GHz 处具有不小于30dB 的衰减,系统阻抗为50Ω。
选微带线特性阻抗最大值h Z =120Ω,特性阻抗最小值l Z =15Ω。
设计微带线阶梯阻抗低通滤波器的步骤如下。
(1)根据波纹为0.5dB 切比雪夫滤波器衰减随频率的对应关系,滤波器需为5阶,对应的切比雪夫低通滤波器原型元器件值为111.7058g C ==221.2296g L ==332.5408g C ==441.2296g L ==551.7058g C == (2)利用式(11.7)和(11.8)计算可以得到 1 1.70581518029.350l ⨯=⨯≈︒πβ 2 1.22965018029.4120l ⨯=⨯≈︒πβ 3 2.54081518043.750l ⨯=⨯≈︒πβ 4 1.22965018029.4120l ⨯=⨯≈︒πβ 5 1.70581518029.350l ⨯=⨯≈︒πβ (3)低通滤波器电路的示意图如图11.3所示,其中图11.3(a )为由低通滤波器原型元器件值构成的低通滤波器,图11.3(b )为微带线阶梯阻抗低通滤波器。
图11.3 低通滤波器电路的示意图11.1.2 微带阶梯阻抗低通滤波器原理图的仿真由上面微带线阶梯阻抗低通滤波器的理论基础,我们得到了微带线阶梯阻抗低通滤波器第11章 分布参数低通滤波器的仿真 261║的电路基本结构,本节学习如何利用ADS微带线的计算工具完成微带线的计算,以及如何设计并仿真微带线阶梯阻抗低通滤波器的原理图。
微带线阶梯阻抗低通滤波器的设计指标如下。

目录一题目规定与方案论证........................................................ 错误!未定义书签。
1.1(设计题题目)二阶有源低通滤波器............................................. 错误!未定义书签。
1.1.1题目规定.................................................................................. 错误!未定义书签。
1.1.2 方案论证................................................................................. 错误!未定义书签。
1.2(实训题题目)波形发生器与计数器............................................. 错误!未定义书签。
1.2.1题目规定.................................................................................. 错误!未定义书签。
1.2.2方案论证.................................................................................. 错误!未定义书签。
二电子线路设计与实现........................................................ 错误!未定义书签。
2.1二阶有源低通滤波器........................................................................ 错误!未定义书签。
2.2十位二进制加法计数器电路设计.................................................... 错误!未定义书签。


低通滤波器仿真一、题目:采样时间为1ms,输入信号为0.2Hz正弦信号,其中带有高频为100Hz的正弦信号,用低通滤波器滤掉高频信号设低通滤波器对象传递函数为:G(s)=1/(0.04s+1)二、语法:sysd = c2d(sys,Ts)sysd = c2d(sys,Ts,method)[sysd,G] = c2d(sys,Ts,method)说明:sysd = c2d(sys,Ts) 将连续时间LTI 对象sys 离散化,采样周期为Ts,单位为秒。
对输入采用零阶保持。
sysd = c2d(sys,Ts,method)定义离散化所采用的方法,其中method 可以为以下字符串:’zoh’:零阶保持,假设控制输入在采样周期内为常值;’foh’:一阶保持,假设控制输入在采样周期内为线性;’tustin’:采用双线性(tustin)逼近;’prewarp’:采用改进的tusitin 方法;’matched’:采用SISO 系统的零极点匹配法。
[sysd,G] = c2d(sys,Ts,method)返回矩阵G,将连续初值条件x0和u0映射为对应的离散形式三、程序清单:%Low Pass Filterclear all;close all;ts=0.001;Q=tf([1],[0.04,1]); %Low Freq Signal FilterQz=c2d(Q,ts,'tucsin'); %tucsin为双线性逼近[num,den]=tfdata(Qz,'v');y_1=0;y_2=0;r_1=0;r_2=0;for k=1:1:5000time(k)=k*ts;%Input Signal with disturbanceD(k)=0.10*sin(100*2*pi*k*ts); %Disturbance signal rin(k)=D(k)+0.50*sin(0.2*2*pi*k*ts); %Input Signalyout(k)=-den(2)*y_1+num(1)*rin(k)+num(2)*r_1;y_2=y_1;y_1=yout(k);r_2=r_1;r_1=rin(k);endfigure(1);bode(Q);figure(2);subplot(211);plot(time,rin,'r');xlabel('time(s)');ylabel('rin');subplot(212);plot(time,yout,'b');xlabel('time(s)');ylabel('yout');Bode图:输出图:由上图看出,输入信号通过低通滤波器后,高频正弦信号已经被滤波器滤掉,得到低频的正弦信号。

无源低通滤波器的设计与仿真摘要:无源低通滤波器应用范围十分广泛。
本文分别就无源低通滤波器中RC 滤波器和LC 滤波器的电路结构和传递函数进行分析后,设计出截止角频率为10Krad/s 的无源低通滤波器,并利用Matlab 下的simulink 环境进行仿真,比较滤波器的滤波效果。
关键词:RC 滤波器;LC 滤波器;Matlab0. 引言滤波器是一种用来消除干扰的器件,有能力进行信号处理的装置可以称为滤波器。
无源滤波器具有结构简单、成本低廉、运行可靠性较高等优点,如何合理地设计和优化其参数,对保证电网谐波治理和无功补偿的效果,提高系统的整体性能起着十分重要的作用。
滤波器按所通过信号的频段分为低通、高通、带通和带阻四种。
低通滤波器允许信号中的低频或直流分量通过,抑制高频分量或干扰和噪声;高通滤波器允许信号中的高频分量通过,抑制低频或直流分量;带通滤波器它允许一定频段的信号通过,抑制低于或高于该频段的信号、干扰和噪声;带阻滤波器抑制一定频段内的信号,允许该频段以外的信号通过。
1.无源低通滤波器类型及其特性分析1.1RC 滤波器无源RC 低通滤波器的组成元件为电阻R 与电容C 。
1.1.1 一阶RC 低通滤波器一阶RC 低通滤波器的电路如图1-1所示。
图1-1 一阶RC 低通滤波器由拉普拉斯变换法分析线性电路知该系统传递函数()G S 为:11()1SC G S RCS R SC==++(1-1) 取S j ω=,得:1()1G jw jRC ω=+ 令T=RC,则:幅频特性()A ω=,相频特性()arctan()T ϕωω=-故,当ω很小时,A(ω)→1,信号几乎不衰减;当ω很大时,A(ω)→0,信号几乎完全被衰减,不能通过。
当增益的分贝数下降3dB时,即()A ω==,得到截止频率c ω,此时c T ω=1,1/c RC ω=.令c ω=10Krad/s,R 取100Ω,C 取1F μ,则1()0.00011G S S =+.利用matlab 仿真软件,得到波特图如图1-2所示。
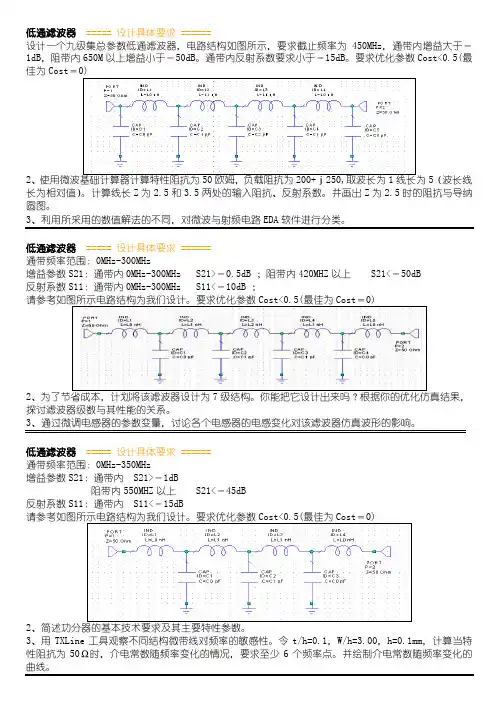
设计一个九级集总参数低通滤波器,电路结构如图所示,要求截止频率为450MHz,通带内增益大于-1dB,阻带内650M以上增益小于-50dB。
通带内反射系数要求小于-15dB。
要求优化参数Cost<0.5(最佳为2、使用微波基础计算器计算特性阻抗为50欧姆,负载阻抗为200+j250,取波长为1线长为5(波长线长为相对值)。
计算线长Z为2.5和3.5两处的输入阻抗、反射系数。
并画出Z为2.5时的阻抗与导纳圆图。
低通滤波器===== 设计具体要求 ======通带频率范围:0MHz-300MHz增益参数S21:通带内0MHz-300MHz S21>-0.5dB ;阻带内420MHZ以上 S21<-50dB反射系数S11:通带内0MHz-300MHz S11<-10dB ;2、为了节省成本,计划将该滤波器设计为7级结构。
你能把它设计出来吗?根据你的优化仿真结果,探讨滤波器级数与其性能的关系。
低通滤波器===== 设计具体要求 ======通带频率范围:0MHz-350MHz增益参数S21:通带内 S21>-1dB阻带内550MHZ以上 S21<-45dB反射系数S11:通带内 S11<-15dB2、简述功分器的基本技术要求及其主要特性参数。
通带频率范围:0MHz-400MHz增益参数S21:通带内0MHz-400MHz S21>-0.2dB阻带内600MHZ以上 S21<-50dB反射系数S11:通带内0MHz-400MHz S11<-10dB要求优化参数2、简述HFSS的特点及其主要应用的范围。
IVCURVEI来测量非线性器件——三极管GBJT3的特性曲线并加入调谐,分析其变化。
高通滤波器===== 设计具体要求 ======通带频率范围:550MHz以上增益参数S21:通带内S21>-2dB ;阻带内0-400MHz,S21<-50dB反射系数S11:通带内S11<-20dB;2、你会添加Marker吗?试在S21曲线上,添加一横坐标为600MHz的Marker。
数字PLC滤波器1 引言PLC是目前在众多领域广泛使用的一种数字控制器。
能够对模拟信号进行处理是PLC的主要功能之一。
在进行信号处理之前,PLC先要采样信号。
由于模拟信号很容易受到干扰,因此在采样信号时,必须进行滤波处理。
数字滤波的方法有很多种,比较经常使用的有算术平均值滤波、中值滤波等方法。
在模拟电路中,经常使用低通滤波器进行滤波,从而去处高频信号对模拟量的影响。
本文详细介绍了低通滤波器的数学模型及其滤波的仿真效果,而后介绍了对其进行数字化的过程,并给出了这种数字滤波器的PLC程序,最后介绍了这种数字滤波器在英德市长湖水电厂水位监测中的应用。
应用实践表明,这种数字滤波的效果是相当好的。
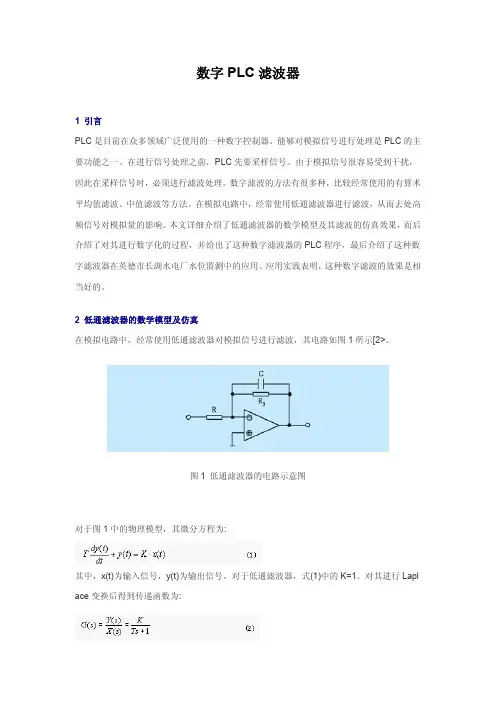
2 低通滤波器的数学模型及仿真在模拟电路中,经常使用低通滤波器对模拟信号进行滤波,其电路如图1所示[2>。
图1 低通滤波器的电路示意图对于图1中的物理模型,其微分方程为:其中,x(t)为输入信号,y(t)为输出信号。
对于低通滤波器,式(1)中的K=1。
对其进行Lapl ace变换后得到传递函数为:其中,K为增益,T为时间常数。
当低通滤波器只进行滤波,不进行信号变换时,则K=1,那么(2)式变为:令时间常数T=4,采用MatLab的SIMULI NK建模[3>,如图2所示:图2 低通滤波器仿真结构框图在图2中有二个示波器,其中“示波器1”用于显示添加了白噪声的阶跃信号,其结果如图3所示;“示波器”用于显示含有高频成分的阶跃信号经过低通滤波之后的结果,如图4所示。
对比图3和图4中可见,低通滤波器的效果良好,对于频率较高的干扰,低通滤波器能够有效抑制其对输出的影响。
图3 添加了白噪声的阶跃信号图4 阶跃信号经过滤波后的结果3 低通滤波器的数字化低通滤波器虽然效果良好,但是在采用PLC的控制系统中通过添加硬件的方式进行滤波,会使得系统的可靠性降低,因此最好采用软件进行滤波,也就是数字滤波。
重写图1的微分方程如下:对式(4)进行离散化,令,其中TS为采样周期,k为采样次数,则把式(5)代入式(4)中,可得:对公式(6)进行整理可得:其中,y(k-1)为上一次滤波器的输出,x(k)本次采样的值,y(k)为本次滤波器的输出,时间常数T可以在程序中设定。

2013级《模拟电子技术》课程设计说明书二阶有源低通滤波器院、部:电气与信息工程学院学生姓名:***指导教师:张松华职称副教授专业:电气工程及其自动化班级:电气本1302完成时间:2015年6月25日摘要滤波器是一种使有用信号通过而同时抑制无用频率信号的电子装置,在信息处理、数据传送和抑制干扰等自动控制、通信及其它电子系统中应用广泛。
滤波一般可分为有源滤波和无源滤波,无源滤波器较有源滤波器无通带增益但设计简单易行。
从滤波器阶数可分为一阶和高阶,阶数越高,幅频特性越陡峭。
高阶滤波器通常可由一阶和二阶滤波器级联而成。
采用集成运放构成的RC有源滤波器具有输入阻抗高,输出阻抗低,可提供一定增益,截止频率可调等特点。
压控电压源型二阶低通滤波电路和无限增益二阶低通滤波器是有源滤波电路的重要两种电路,适合作为多级放大器的级联。
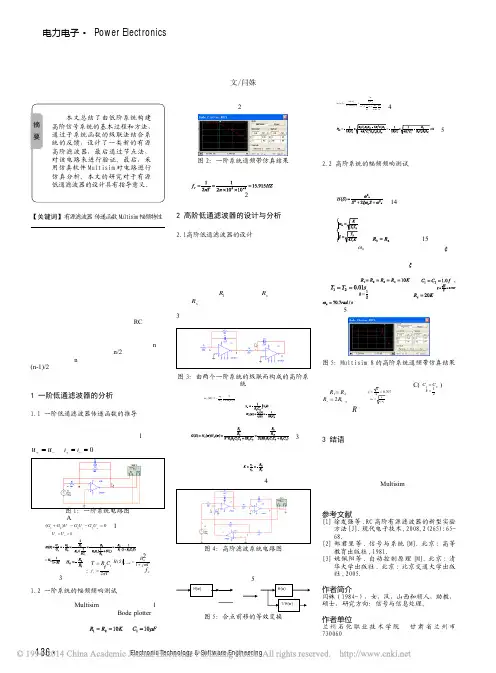
论文先设计了一种压控电压源二阶有源低通滤波电路,其次并利用 Multisim10 仿真软件对电路的频率特性、特征参量等进行了仿真分析,仿真结果满足设计要求之后,用AD绘制电路原理图,再用AD导入原理图以手工布局和布线为铺完成其单面PCB的设计,最后,在PCB 板安装电路并调试,调试数据与仿真数据大致相同,满足设计要求。
关键词:压控电压源型;二阶;有源低通滤波器;Multisim10;AD目录1 绪论 (1)1.1 设计意义及背景 (1)1.2 设计任务 (1)1.3 设计要求 (1)2 方案选择 (2)2.1 一阶有源低通滤波器电路 (2)2.2 压控电压源型二阶有源低通波电路 (2)3 元器件的选择与电路参数计算 (4)3.1 选择运放 (4)3.2 选择电容器 (4)3.3 计算电阻器阻值 (4)3.4 直流稳压源的设计 (6)3.4.1 变压器的选择 (6)3.4.2 整流器的选择 (6)3.4.3 电容的选择 (6)3.4.5 选择三端稳压器 (7)4 电路仿真 (8)4.1 仿真电路图 (8)4.2 仿真结果 (8)5.1 电路的制作 (10)5.2 直流稳压源的调试 (10)5.3 二阶有源低通滤波器电路调试 (11)5.3.1 调试过程 (11)5.3.3 调试数据分析 (14)5.3.4 误差分析 (14)5.3.5 设计体会 (14)结束语 (16)参考文献 (17)致谢 (18)附录A电路原理图 (19)附录B PCB图 (20)附录C电路板实物图 (21)附录D元件清单 (22)1 绪论1.1 设计意义及背景电子技术是当今科技发展的热点,各先进国家无不把它放在优先发展的地位。


电子线路设计(论文)说明书题目:有源低通滤波器的设计院(系):信息与通信学院专业:电子信息工程学生姓名:黄翔学号:1100220514指导教师:王娇职称:讲师2013年11月16日摘要低通滤波器是一个通过低频信号而衰减或抑制高频信号的部件。
理想滤波器电路的频响在通带内应具有一定幅值和线性相移,而在阻带内其幅值应为零。
有源滤波器是指由放大电路及RC网络构成的滤波器电路,它实际上是一种具有特定频率响应的放大器。
滤波器的阶数越高,幅频特性衰减的速率越快,但RC网络节数越多,元件参数计算越繁琐,电路的调试越困难。
关键词:低通;放大器;阶数AbstractLow pass filter allows low frequency signal to pass through and suppresses the high frequency components of signals. Ideal filter circuit should have certain amplitude frequency response in the passband and linear phase shift, and its amplitude should be zero in the stopband. Active filter is one that is composed of RC network and amplifying circuit. It is actually a kind of specific frequency response amplifier. The higher the order number of the filter, the faster the amplitude frequency attenuation rate.But the RC network node number is associated with the components parameter calculation and the debugging of the circuit.Key words: low pass; Amplifier; Order number目录引言 (1)1 原理及设计方案 (1)1.1滤波器的介绍 (1)1.2 有源滤波器的设计 (2)1.3方案选择 (4)2 硬件介绍 (6)3 仿真及结果 (7)4 测量结果 (8)5 实验心得与体会 (9)谢辞 (11)参考文献 (12)引言课程设计是理论联系实际的重要实践教学环节,是对学生进行的一次综合性专业设计训练。
有源一阶低通滤波器XSC1通带截止频率:假设R R 3=,,C C 1=H f RCπ1=2 通带电压放大倍数:f up R A R 1=1+有源二阶压控低通滤波器Rf R1品质因数:upQ A 1=3-,0.5≤Q ≤100,一般选取Q =1附近的值通带截止频率:假设R R R 32==,C C C 12==,H f RCπ1=2 通带电压放大倍数:f up R A R 1=1+有源二阶压控高通滤波器Rf R1通带电压放大倍数:f up R A R 1=1+通带截止频率:假设R R R 32==,C C C 12==,L f RCπ1=2 品质因数:upQ A 1=3-有源二阶压控带通滤波器Rf R110k Ω通带电压放大倍数:uf up ufA A A =3-。
f up R A R 1=1+应小于3,否则电路不能稳定工作。
通带中心频率:假设R R R R 234=2=2=2,C C C 12==,通带中心频率f RCπ01=2通带宽度:()H L uf BW f f A f 0=-=3-,()L uf f f A 0⎤=-3-⎦2,()H uf ff A 0⎤=+3-⎦2有源二阶压控带阻滤波器Rf R1f uf R A R 1=1+应小于2,否则电路不能稳定工作阻带宽度:()H L uf f BW f f A f Q 00=-=22-=,其中()uf Q A 1=22-,()L uf f A f 0⎤=-2-⎦,()H uf A f 0阻带中心频率:假设,C C C C 1232=2==2R R R R 342==2=,阻带中心频率f RCπ01=2 f ⎤=+2-⎦。
椭圆形的低通滤波器推导一、AR7400低通滤波器原理图AR7400中5-阶的椭圆形的低通滤波器,由元件C75,C70,L14,C79,L16,C76,C80,L17,C71,L15,和C77组成。
二、单端线上的椭圆低通滤波器1.归一化椭圆低通滤波器模型特性:通带内有起伏,阻带内也有起伏:2.5-阶椭圆低通滤波器的归一化模型:归一化低通滤波器截止频率为(1/2∏)Hz,特征阻抗1Ω;3.利用归一化模型设计低通滤波器步骤:4.频率和阻抗变换计算公式:5.设计一个截止频率为68MHz,阻抗为50Ω的低通滤波器:5阶归一化低通滤波器截止频率为(1/2∏)Hz,特征阻抗1Ω;6.对归一化低通滤波器滤波器进行频率变换:5阶低通滤波器截止频率为68MHz,特征阻抗1Ω;7.对以上滤波器进行阻抗变换:5阶低通滤波器截止频率为68MHz,特征阻抗50Ω;8.对5阶低通滤波器截止频率为68MHz,特征阻抗50Ω仿真;f req, MHzd B (S (1,2))5阶低通滤波器截止频率为68MHz ,特征阻抗50Ω仿真图形仿真结果:通带内有两个起伏点,阻带内有两个陷波点,通带截止频率68MHz ,插损小于1.2dB, 阻带内带外抑制≥23 dB (at87~125MHz ), ≥60 dB(at125~860MHz );9. 对AR7400单端线滤波器的仿真;当滤波器中的容值和电感值变化时,如下图,并对其进行仿真,AR7400滤波器的一部分m1m2m3m4m5204060801001201401601800200-45-40-35-30-25-20-15-10-5-500freq, MHzd B (S (1,2))m1m2m3m4m5Reverse Transmission, dBfreq=dB(S(1,2))=-0.98350.00MHz freq=dB(S(1,2))=-1.35080.00MHz freq=dB(S(1,2))=-26.424100.0MHz freq=dB(S(1,2))=-17.464Peak200.0MHz freq=dB(S(1,2))=-1.46160.00MHz仿真结果:通带内有两个起伏点,阻带内有两个陷波点,通带截止频率80MHz ,插损小于1.35dB, 阻带内带外抑制≥17dB (at90~~860MHz ); 说明:电容变小截止频率变大,带外抑制变小;三、差分线上的椭圆低通滤波器与单端走线的比较差分信号与传统的一根信号线一根地线(即单端信号)相比,其优点是: a 、抗干扰能力强。
近代微波技术课程报告姓名王翩学号M*********院系电子信息工程专业电磁场与微波技术类别硕士指导老师马洪考试日期2011年7月8日微带线低通滤波器设计设计参数要求设计特征阻抗为50Ω的低通滤波器,其截止频率为f 1=2.5GHz(3dB 衰减),在f 2=5GHz 处要求衰减大于30dB ,要求有详细设计步骤,并且用分布参数元件实现。
滤波器选型选择巴特沃兹型滤波器,其衰减特性表示为221()10lg[1(/)]n A f f f ε=+其中n 为滤波器阶数,这里取1ε=。
2()30A f ≥代入上式解的n ≥4.98,取n=5,即选取5阶巴特沃兹滤波器。
5阶归一化巴特沃兹低通滤波器(截止频率1/(2)πHz ,特征阻抗1Ω)有如下两种实现方式。
第一种是第一个元件是串联电感,第二种是第一个元件是并联电容,以下简称电感型和电容型。
图1 第一个元件是串联电感的5阶归一化巴特沃兹LPF图2 第一个元件是并联电容的5阶归一化巴特沃兹LPF使用集总参数实现巴特沃兹型LPF设待求滤波器截止频率(1f )与基准滤波器截止频率(0f )的比值为M ,则有1010 2.5 1.57101/(2)f GHz M f Hzπ===⨯ 设计截止频率为1f 的滤波器,要经过频率变换,将基准滤波器中各元件值除以M 。
滤波器特征阻抗变换是通过先求出带设计滤波器阻抗与基准滤波器特征阻抗的比值K ,再用K 去乘基准滤波器中的所有电感元件值和用这个K 去除基准滤波器中所有电容元件值来实现的。
公式如下:50501K ===待设计滤波器的特征阻抗基准滤波器的特征阻抗通过上述两步变换可以得到实际的元件值计算公式:K/M NEW OLD L L =⨯ C /()NEW OLD C KM =下面以以上公式推导出待求滤波器各元件取值。
表一:电感型滤波器各元件值H1 C1 H2 C2 H3 基准滤波器 0.61803H1.61803F2H1.61803F0.61803H待求滤波器1.96723nH2.06013pF 6.36618nH 2.06013pF 1.96723nH表二:电容型滤波器各元件值C1 H1 C2 H2 C3 基准滤波器 0.61803F 1.61803H 2F 1.61803H 0.61803F 待求滤波器0.78690 pF5.15035nH2.54648 pF5.15035nH0.78690 pF图3 电感型5阶巴特沃兹LPFm1m2freq, GHzd B (S (2,1))m1freq=dB(S(2,1))=-3.0102.500GHz freq=dB(S(2,1))=-30.1075.000GHz图4(a) 电感型衰减特性曲线频率(GHz)幅值(d B )图4(b) Matlab 编程得到的衰减特性12345678910-400-300-200-100-500freq, GHzp h图4(c) ADS 仿真相频特性-450-400-350-300-250-200-150-100-50频率(GHz)相位(度)图4(d) Matlab得到的相频特性图5 电容型5阶巴特沃兹LPFfreq, GHzdB(S(2,1))m1m2m1freq=dB(S(2,1))=-3.0102.500GHzm2freq=dB(S(2,1))=-30.1075.000GHz图6(a) 电容型衰减特性曲线频率(GHz)幅值(d B )图6(b) Matlab 编程得到的衰减特性曲线12345678910-400-300-200-100-500freq, GHzp h图6(c) ADS 仿真电容型LPF 相频特性频率(GHz)相位(度)图6(d) Matlab 得到的电容型LPF 相频特性通过图4和图6使用ADS 软件和Matlab 仿真结果可以看出,在2.5GHz 处衰减为3dB ,在5GHz 处衰减大于30dB ,而且通过相频特性曲线可以看出两种LPF 都具有很好的线性相频特性曲线。