第11讲 散点图、相关系数讲解
- 格式:ppt
- 大小:1.40 MB
- 文档页数:45

散点图:直观判断变量相关性的步骤与注意事项使用散点图判断两个变量之间的相关关系是一种直观且有效的方法。
以下是具体步骤和注意事项:步骤1.收集数据:2.首先,确保你有两个变量的数据集。
这些数据集应该是一一对应的,即每个观测值在两个变量上都有对应的取值。
3.绘制散点图:4.使用统计软件(如Excel、SPSS、R、Python等)将两个变量的数据绘制成散点图。
在散点图中,通常一个变量作为横坐标(X轴),另一个变量作为纵坐标(Y轴)。
5.观察散点分布:6.仔细观察散点图中点的分布模式。
点的分布模式会给出两个变量之间关系的直观印象。
7.识别趋势:o正相关:如果随着一个变量的增加,另一个变量也呈现增加的趋势,那么这两个变量之间存在正相关关系。
在散点图中,这通常表现为点集沿斜向上方的方向分布。
o负相关:如果随着一个变量的增加,另一个变量呈现减少的趋势,那么这两个变量之间存在负相关关系。
在散点图中,这通常表现为点集沿斜向下方的方向分布。
o无相关:如果点的分布没有明显的上升或下降趋势,而是呈现随机分布的状态,那么这两个变量之间可能不存在明显的线性相关关系。
但请注意,这并不意味着它们之间不存在其他类型的关系(如非线性关系)。
8.评估紧密程度:9.除了方向外,还可以观察点集的紧密程度来评估相关性的强弱。
如果点集紧密地围绕在某条直线(或曲线)周围,那么相关性可能较强;如果点集分散较开,那么相关性可能较弱。
10.注意异常值:11.检查是否有异常值(即与其他点显著不同的点)影响对关系的判断。
有时,异常值可能是由测量错误或数据录入错误引起的,应该进行核查和处理。
注意事项●散点图只能揭示两个变量之间的关联程度,并不能确定因果关系。
●即使两个变量之间存在显著的相关性,也不意味着一个变量是导致另一个变量变化的原因。
●相关性可以是线性的,也可以是非线性的。
散点图可以帮助识别线性关系,但对于非线性关系的识别可能需要更复杂的分析工具(如回归分析中的多项式模型)。

散点图
1.散点图
【知识点的知识】
1.散点图的概念:
在考虑两个量的关系时,为了对变量之间的关系有一个大致的了解,人们常将变量所对应的点描出来,这些点就组成了变量之间的一个图,通常称这种图为变量之间的散点图.
2.曲线拟合的概念:
从散点图可以看出如果变量之间存在着某种关系,这些点会有一个集中的大致趋势,这种趋势通常可以用一条光滑的曲线来近似,这种近似的过程称为曲线拟合.
3.正相关和负相关:
(1)正相关:对于相关关系的两个变量,如果一个变量的值由小变大时,另一个变量的值也由小变大,这种相关称为正相关,正相关时散点图的点散布在从左下角到右上角的区域内.
(2)负相关:如果一个变量的值由小变大时,另一个变量的值由大变小,这种相关称为负相关,负相关时散点图的点散布在从左上角到右下角的区域.
3、注意:画散点图的关键是以成对的一组数据,分别为此点的横、纵坐标,在平面直角坐标系中把其找出来,其横纵坐标的单位长度的选取可以不同,应考虑数据分布的特征,散点图只是形象的描述点的分布,如果点的分布大致呈一种集中趋势,则两个变量可以初步判断具有相关关系,如图中数据大致分布在一条直线附近,则表示的关系是线性相关,如果两个变量统计数据的散点图呈现如下图所示的情况,则两个变量之间不具备相关关系,例如学生的身高和学生的英语成绩就没有相关关系.
4、散点图又称散点分布图,是以一个变量为横坐标,另一变量为纵坐标,利用散点(坐标点)的分布形态反映变量统计关系的一种图形.特点是能直观表现出影响因素和预测对象之间的总体关系趋势.优点是能通过直观醒目的图形方式反映变量间关系的变化形态,以便决定用何种数学表达方式来模拟变量之间的关系.散点图不仅可传递变量间关系类型的信息,也能反映变量间关系的明确程度.
1/ 1。



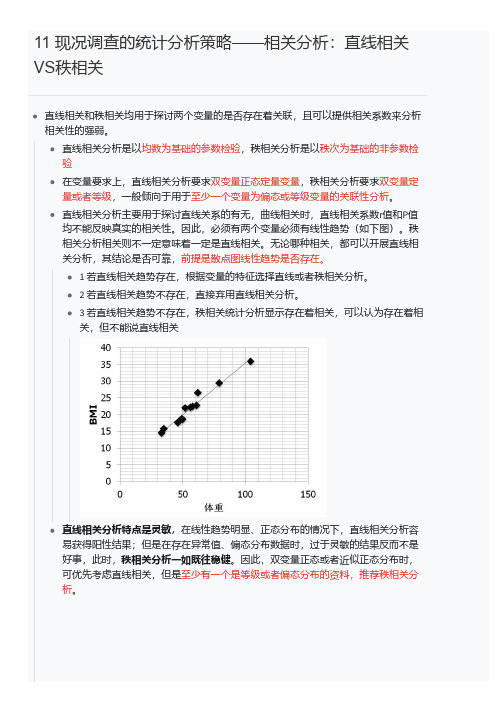
11 现况调查的统计分析策略——相关分析:直线相关VS秩相关直线相关和秩相关均用于探讨两个变量的是否存在着关联,且可以提供相关系数来分析相关性的强弱。
直线相关分析是以均数为基础的参数检验,秩相关分析是以秩次为基础的非参数检验在变量要求上,直线相关分析要求双变量正态定量变量,秩相关分析要求双变量定量或者等级,一般倾向于用于至少一个变量为偏态或等级变量的关联性分析。
直线相关分析主要用于探讨直线关系的有无,曲线相关时,直线相关系数r值和P值均不能反映真实的相关性。
因此,必须有两个变量必须有线性趋势(如下图)。
秩相关分析相关则不一定意味着一定是直线相关。
无论哪种相关,都可以开展直线相关分析,其结论是否可靠,前提是散点图线性趋势是否存在。
1 若直线相关趋势存在,根据变量的特征选择直线或者秩相关分析。
2 若直线相关趋势不存在,直接弃用直线相关分析。
3 若直线相关趋势不存在,秩相关统计分析显示存在着相关,可以认为存在着相关,但不能说直线相关直线相关分析特点是灵敏,在线性趋势明显、正态分布的情况下,直线相关分析容易获得阳性结果;但是在存在异常值、偏态分布数据时,过于灵敏的结果反而不是好事,此时,秩相关分析一如既往稳健。
因此,双变量正态或者近似正态分布时,可优先考虑直线相关,但是至少有一个是等级或者偏态分布的资料,推荐秩相关分析。
相关分析的内容相关分析内容包括计算相关性程度、判断相关性的有无。
计算相关性程度一般便是计算相关系数。
相关系数分为总体相关系数ρ和样本相关系数r。
总体相关系数ρ:若ρ≠0, 称变量存在着相关;若ρ=0, 则简称两变量不相关。
样本相关系数r:往往用来代替总体相关系数总体相关系数是关于总体人群的两个变量相关性,也是研究所想知道的指标。
但统计分析能够计算的,只能是样本相关系数r值,而用r来代替总体反映两个变量的相关性程度。
r的取值范围为|r|≤1,绝对值大小表示两变量之间直线联系的密切程度。
当r为负值时,表示当一个变量的取值增大时,另一个变量的取值减小,即呈相反的变化方向,称为负相关;当r为正值时,表示两个变量的变化方向一致,称为正相关。
散布图与相关性分析散布图是一种常用的数据可视化工具,用于展示两个变量之间的关系。
相关性分析则是通过计算相关系数来衡量两个变量之间的相关程度。
本文将介绍散布图的绘制方法以及相关性分析的原理和应用。
一、散布图的绘制方法散布图通常用于展示两个连续变量之间的关系,其中一个变量作为自变量,另一个变量作为因变量。
绘制散布图的步骤如下:1. 收集数据:首先需要收集两个变量的数据,确保数据的准确性和完整性。
2. 绘制坐标轴:在纸上或计算机软件中绘制坐标轴,横轴表示自变量,纵轴表示因变量。
3. 绘制数据点:根据收集到的数据,在坐标轴上绘制数据点。
每个数据点的横坐标对应自变量的值,纵坐标对应因变量的值。
4. 添加标签:为了更好地理解散布图,可以为坐标轴和数据点添加标签。
标签可以包括变量名称、单位等信息。
5. 绘制趋势线:有时候,我们希望通过趋势线来描述两个变量之间的关系。
趋势线可以是线性的、非线性的或者是其他形式的。
二、相关性分析的原理和应用相关性分析是用来衡量两个变量之间相关程度的统计方法。
常用的相关系数有皮尔逊相关系数、斯皮尔曼相关系数和判定系数等。
1. 皮尔逊相关系数:用于衡量两个连续变量之间的线性相关程度。
取值范围为-1到1,其中-1表示完全负相关,1表示完全正相关,0表示无相关。
2. 斯皮尔曼相关系数:用于衡量两个变量之间的单调关系,不要求变量呈线性关系。
取值范围也是-1到1,含义与皮尔逊相关系数相似。
3. 判定系数:用于衡量自变量对因变量的解释程度。
取值范围为0到1,越接近1表示自变量对因变量的解释程度越高。
相关性分析可以帮助我们了解两个变量之间的关系,从而进行预测和决策。
例如,在市场营销中,我们可以通过相关性分析来确定广告投放和销售额之间的关系,从而优化广告策略;在医学研究中,我们可以通过相关性分析来研究疾病和风险因素之间的关系,从而制定预防措施。
三、散布图与相关性分析的应用案例为了更好地理解散布图和相关性分析的应用,下面以一个实际案例进行说明。