用四心法画椭圆

板书演示
通过课堂教 学使学生掌 握用四心圆
法作椭圆
-
演示
O1
作图步骤： 1、 画出长、 短轴 AB、 CD,连接 AC， C 为圆心， 以 长半轴与短半轴之差为半径画圆弧交 AC 于 E 点。 2、做 AE 中垂线与长、短轴交于 O3、O1 点，并 作出其对称点 O4、O2。 3、分别以 O1、O2 为圆心，O1C 为半径画大弧； 以 O3、O4 为圆心，O3A 为半径画小弧（大小弧 的切点 K 在相应的连心线上） ，即得椭圆。
沭阳中专集体备课教案
组别 人员 教学 目标 教学 重点 教学 难点 课时 安排 高中机械组 课题 高中机械老师
熟练掌握已知长短轴用四心圆法画椭圆的方法 熟练掌握已知长短轴用四心圆法画椭圆的方法 熟练掌握已知长短轴用四心圆法画椭圆的方法 1.11 已知长短轴用四心圆法画椭圆
课型
新授课
1 课时 教学环节及主要内容
学生示范、课堂讲解
通过课堂练 习了解学生 掌握情况
再次明确本 节课程的重 归纳本节课所学的内容。 要 知 识 要 点。
二、课堂练习
练习册习题
教学 步骤 一、 导 入
教学内容
大家想一想我们常见的机械中，有哪些零件或者 设备外形是椭圆形？
师生活动 课堂提问
设计意图
从生活常识 引出新课，引 起注意、激发 求知欲。
二、 一、已知长、短轴用四心圆法作椭圆 新 课内 【作图方法讲解】 容
O2
C K E A K O3
做好课堂笔记
￣
0 O4 D K
K B
口述作图过程 PPT 显示
二、课堂练习 1、用四心圆法作长轴为 100，短轴为 50 的 椭圆 三、 总 结 【小结】 （在学生讨论的基础上，归纳小结） 本节课已知长短轴用四心法画椭圆的方法， 希望课后及时巩固所学内容。 板 书 设 计 课 后 作 业 教 学 反 思

椭圆的画法常用的椭圆近似画法为同心圆法和四心圆法。

图1-20是由长短轴作椭圆的一种画法：以O为圆心长轴半径OA和短轴半径OC为半径分别作圆。

由O作若干射线与两圆相交，再由各交点分别作长、短轴的平行线，即可相应的求出椭圆上的各点。

最后用曲线板将这些点连成椭圆。

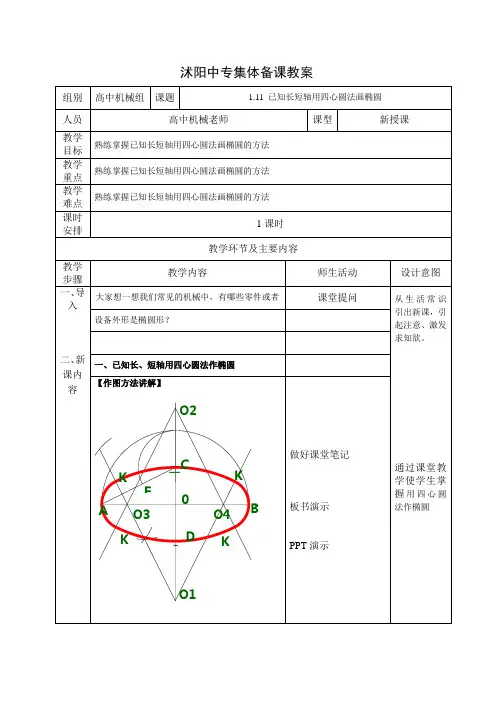
图1-21是用四段圆弧连接起来的图形近似代替椭圆的方法。

如果已知椭圆的长、短轴AB、CD，则其近似画法的步骤如下：(1)连AC，以O为圆心，OA为半径画弧交CD延长线于E，再以C为圆心，CE为半径画弧交AC于E1；(2)作AE1线段的中垂线分别交长、短轴于O1、O2，并作O1、O2的对称点O3、O4，即求出四段圆弧的圆心。

分别以O1、O2、O3、O4为圆心，O1A、O2C、O3B、O3D为半径作弧画成近似椭圆，切点为K、N、N1、K1。

椭圆是一种常见的非圆曲线，一般根据其长轴及短轴绘制。

一、手工绘图时椭圆的画法在一般绘图中，如对椭圆作图精度要求不高时，常用四心扁圆法，也称四心法。

四心法是一种近似画法。

作图步骤：1、作出椭圆的中心线，并分别定出长轴AB、短轴CD，连AC，从C点截取CF=OA-OC，并作线段AF 的垂直平分线，交长轴于O1和短轴的延长线于O2，同时取相应的对称点O3和O4，则O1、O2、O3、O4分别为椭圆上四段圆弧的圆心。

2、连接O1O2、O2O3、O3O4、O4O1为四条连心线；以O2、O4为圆心，O2C（或O4D）为半径画弧12(或34)。

3、以O1、O3为圆心，O1A（或O3B）为半径画弧41（或23），即完成作图。

用曲线板光滑地连接诸点，即得所求的椭圆。
你用鸡蛋比着画应该可以吧。
有同心圆法，四心点法和相似菱形法，同心圆法比较简单。就是按照长短轴画两个圆，无数条直线通过圆心，其实就是若干条，然后大圆交点作垂线和小圆交电作平行线相交，就像个比较宽的直角三角形，交点直角的顶点就是椭圆上的点，然后用曲线板顺次连接，要是画多点就可以找到准确的用圆规画的半径 。
椭圆画法
一、四心近似法
已知相互垂直且平分的椭圆长轴和短轴,则椭圆的近似画法(四心近似法)步骤如下所示:
第一步：
画出长轴AB和短轴CD，连接AC；
第二步：
在AC上截取CF，使其等于AO与CO之差CE；
第三步：
作AF的垂直平分线，使其分别交AO和OD（或其延长线）于O1和O2点。以O为对称中心，找出O1的对称点O3及O2的对称点O4，此O1、O2、O3、O4各点即为所求的四圆心。通过O2和O1、O2和O3、O4和O3各点，分别作连线；
很简单。
现在桌面固定好两个点。在把一根细绳的两端系在两个点上，用铅笔把绳等紧，移动铅笔，其走过的痕迹就是一个椭圆。
高中课讲过用一根毛线，长度要求线的两端在十字的水平两端，将线的中间用笔撑直正好在十字的上端点。将两端固定，之后用笔撑着线画就好了。
一、四心近似法
已知相互垂直且平分的椭圆长轴和短轴,则椭圆的近似画法(四心近似法)步骤如下所示:
第四步：（双击恢复）
分别以O2和O4为圆心，O2C（或O4D）为半径画两弧。再分别以O1和O3为圆心，O1A（或O3B）为半径画两弧，使所画四弧的接点分别位于O2O1、O2O3、O4O1和O4O3的延长线上，即得所求的椭圆。
有同心圆法，四心点法和相似菱形法，同心圆法比较简单。就是按照长短轴画两个圆，无数条直线通过圆心，其实就是若干条，然后大圆交点作垂线和小圆交电作平行线相交，就像个比较宽的直角三角形，交点直角的顶点就是椭圆上的点，然后用曲线板顺次连接，要是画多点就可以找到准确的用圆规画的半径 。

第六节 斜度和锥度 一、斜度 图2-16 斜度的画法 2斜度的画法 图2-16a所示斜度为1∶6，其作图方法如图2-16b所示。
第六节 斜度和锥度 一、斜度 图2-17 斜度的标注 3斜度的标注 斜度的符号如图2-17a所示。符号的方向应与斜度的方向一致。 标注斜度时，可按图2-17b、c、d所示的方法标注。
第六节 斜度和锥度 二、锥度 图2-19 锥度的画法 2锥度的画法 图2-19a所示物体的右部是一个锥度为1∶3的圆锥台，其作图方法如图2-19b所示。
锥度的画法和标注
55
25
2
18
14
1:3
3个单位
1个单位
3锥度的标注
在图样上应采用图2-20a所示的图形符号表示圆锥，该符号应配置在基准线上(图2-20b)。表示圆锥的图形符号和锥度应靠近圆锥轮廓标注，基准线应通过指引线与圆锥的轮廓素线相连。基准线应与圆锥的轴线平行，图形符号的方向应与圆锥方向相一致。 锥度在图样上的标注如图2-20c、d、e所示(图中的C为锥度)。 当所标注的锥度是标准圆锥系列之一(尤其是莫氏锥度或米制锥度)时，可用标准系列号和相应的标记表示(图2-20f)。
第五节 椭圆的画法 一、理论画法
01
02
同心圆法作椭圆
D
C
B
A
O
第五节 椭圆的画法 二、近似画法
已知椭圆长轴AB和短轴CD，用四心圆法作椭圆的步骤如下： (1) 画出相互垂直且平分的长轴AB与短轴CD； (2) 连接AC，并在AC上取CE=OA-OC,如图2-14a所示； (3) 作AE的中垂线，与长、短轴分别交于O1、O2，再作对称点O3、O4，如图2-14b所示； (4) 以O1、O2、O3、O4各点为圆心，O1A、O2C、O3B、O4D为半径，分别画弧，即得近似椭圆，如图2-14c所示。

【最新整理，下载后即可编辑】
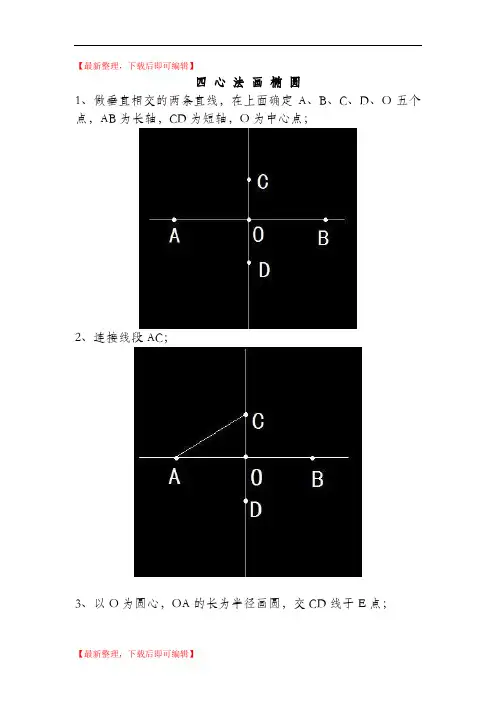
四心法画椭圆
1、做垂直相交的两条直线，在上面确定A、B、C、D、O五个点，AB为长轴，CD为短轴，O为中心点；
2、连接线段AC；
3、以O为圆心，OA的长为半径画圆，交CD线于E点；
4、以C为圆心，CE的长为半径画圆，交AC线于F点；
5、以A为圆心，AF的长为半径画圆；
6、以F为圆心，AF的长为半径画圆，两圆弧相交两点G、H；
7、连接GH，交AB轴于O
1点，交CD轴于O
2
点；
8．以O为圆心，OO
1的长为半径画圆，交OB于O
3
点；
9、以O为圆心，OO
2的长为半径画圆，交OB于O
4
点；
10、以O1为圆心，O
1
A的长为半径画圆；
11、以O
3为圆心，O
3
B的长为半径画圆；
12、以O2为圆心，O
2
C的长为半径画圆；
13、以O
4为圆心，O
4
D的长为半径画圆。

标准椭圆形封头快速近似画法日常生活中，大部分压力容器通常都是由筒体及封头组成。

在设计过程中选择最多的封头是标准椭圆形封头(JB1154-73)。

这种椭圆封头的长半轴长度是短半轴长度的两倍。

在绘制椭圆封头时，一般采用四心法进行作图，见图1。

四心法具体作法是：连接AC ，在线段AC 上取点E ，使CE =OA -OC 。

作AE 的中垂线交短轴和长轴于O 1、O 2。

在长轴AB 上取点O 3，使3OO =2OO 。

以O 2为圆心，AO 2为半径画圆弧AM 。

以O 1为圆心，C O 1为半径画圆弧MN 。

再以O 3为圆心，B O 3为半径画圆弧NB 。

这就是采用四心法作椭圆的过程。

找出圆心O 1、O 2和O 3三点的具体位置是画椭圆形封头的关键。

然后用这种单纯几何作图来绘制标准椭圆形封头很费时间，在椭圆形封头画好后，要擦去辅助线，使得图面不够清晰，并且在确定点O 1的具体位置时，由于直线O 2O 1与直线OO 1的夹角较小，故有时点O 1会出现0.5毫米左右的误差，结果使得椭圆在M 、N 两点处连接不够圆滑。

如何克服上述的不足之处，同时又能迅速准确的画出标准椭圆形封头呢？标准椭圆形封头的曲面高度为其公称直径Dg 的41。

抓住这一特点，就可利用数学关系式找出圆弧线中心点O 1、O 2和O 3的具体位置。

若椭圆形封头的公称直径Dg=2R,则1OO =1.3090R ，3OO =2OO =0.6545R ，r =0.3455R ，R 球=1.8090R ，见图2.按这些尺寸就可以迅速准确的确定O 1、O 2和O 3的具体位置，从而画出椭圆形封头。

上述尺寸是在四心法画椭圆的基础上，按图1进行如下推导而得出的。

在△AOC 中，已知Dg=2R ，CO =0.5R ，AO =R ，则：AC =22CO AO + =22)5.0(R R +=R 25AD =21[AC -CP ] =21[AC -(AO -CO )]=21[R 25-(R-0.5R)] =R 415− CD =AC -AD =R 25-R 415−=R 415+在△AO 2D 与△ACO 中∠DAO 2=∠OAC ，∠ADO 2=∠AOC=90° ∴△AO 2D~△ACO ∴ACAO 2=AOAD把AC =R 25，AD =R 415−，AO =R 代入上式得：2AO =R R R 41-525×=R 855−≈0.3455R同时可得：2OO = AO -2AO = R-0.3455R = 0.6545R 在△O 1CD 与△ACO 中∠O 1CD=∠ACO ，∠CDO 1=∠AOC=90° ∴△O 1CD~△ACO ∴ACC O 1=COCD把AC =R 25，CD =R 415+，CO =0.5R 代入上式得：C O 1=RR R 5.041525+×=R 455+≈1.8090R=C O 1-CO =1.8090R-0.5R=1.3090R。

实用标准文案
四 心 法 画 椭 圆
1、做垂直相交的两条直线，在上面确定 A、B、C、D、O 五个点，AB 为长轴，CD 为短轴，O 为中心点；
2、连接线段 AC；
精彩文档
实用标准文案
3、以 O 为圆心，OA 的长为半径画圆，交 CD 线于 E 点；
4、以 C 为圆心，CE 的长为半径画圆，交 AC 线于 F 点；
精彩文档
实用标准文案
5、以 A 为圆心，AF 的长为半径画圆；
6、以 F 为圆心，AF 的长为半径画圆，两圆弧相交两点 G、H；
精彩文档
实用标准文案
7、连接 GH，交 AB 轴于 O1 点，交 CD 轴于 O2 点；
8．以 O 为圆心，OO1 的长为半径画圆，交 OB 于 O3 点；
精彩文档
实用标准文案
9、以 O 为圆心，OO2 的长为半径画圆，交 OB 于 O4 点；
10、以 O1 为圆心，O1A 的长为半径画圆；源自精彩文档实用标准文案
11、以 O3 为圆心，O3B 的长为半径画圆；
12、以 O2 为圆心，O2C 的长为半径画圆；
精彩文档
实用标准文案
13、以 O4 为圆心，O4D 的长为半径画圆。
精彩文档

图2-17 斜度的标注
第六节 斜度和锥度
二、锥度
1 锥度是指正圆锥体底圆直径与锥高之比。如果是圆
锥台，则为上、下底圆直径之差与圆锥台高度之比，
如图2-18所示。锥度=2tan α=D/L=（D-d）/l 锥度在图样上也以1∶n的简化形式表示。
图2-18 锥度
第六节 斜度和锥度
二、锥度
2
图2-19a所示物体的右部是一个锥度为1∶3的圆锥台，其作图方 法如图2-19b所示。
图2-13 用同心圆法画椭圆
同心圆法作椭圆
C
A
OBຫໍສະໝຸດ D椭圆的画法 二、近似画法
已知椭圆长轴AB和短轴CD，用四心圆法作 椭圆的步骤如下：
(1) 画出相互垂直且平分的长轴AB与短 轴CD；
(2) 连接AC，并在AC上取CE=OA-OC,如图 2-14a所示；
(3) 作AE的中垂线，与长、短轴分别交 于O1、O2，再作对称点O3、O4，如图2-14b所 示；
斜度=tan α=CA/AB=H/L 在图2-15b中，斜度=（H-h）/L 通常在图样中把比值化成1∶n的形式。
图2-15 斜度
第六节 斜度和锥度
一、斜度
2
图2-16a所示斜度为1∶6，其作图方法如图2-16b所示。
图2-16 斜度的画法
第六节 斜度和锥度
一、斜度
3
斜度的符号如图2-17a所示。符号的方向应与斜度的方向一致。 标注斜度时，可按图2-17b、c、d所示的方法标注。
椭圆的画法
一、理论画法
已知椭圆长轴AB和短轴CD，用同心圆法作椭圆的步 骤如下：
(1) 以长轴AB和短轴CD为直径画两同心圆，然后 过圆心作一系列直线与两圆相交，如图2-13a所示；

四心椭圆法大小圆心计算公式摘要：一、四心椭圆法简介二、大小圆心计算公式推导三、公式应用与实际案例四、总结与展望正文：四心椭圆法是一种在平面上绘制椭圆的方法，它通过四个圆心来确定椭圆的大小和形状。

这种方法不仅适用于纸上作图，还可以应用于计算机图形学等领域。

本文将详细介绍四心椭圆法中大小圆心的计算公式，并通过实际案例来说明其应用。

首先，我们需要了解四心椭圆法的基本原理。

如图1 所示，四心椭圆法包括四个圆心O1、O2、O3、O4，分别位于椭圆的长轴、短轴的端点和两个焦点。

我们可以通过计算这四个圆心的坐标来确定椭圆的大小和形状。

图1 四心椭圆法示意图接下来，我们来推导大小圆心的计算公式。

假设椭圆的长轴为2a，短轴为2b，焦距为2c。

根据椭圆的定义，我们有以下关系式：a^2 = b^2 + c^2（1）又因为四心椭圆法中，O1、O2 分别位于长轴的端点，O3、O4 分别位于短轴的端点和焦点，因此有：O1O2 = a（2）O3O4 = b（3）O1O3 = O2O4 = c（4）根据勾股定理，我们可以得到：O1O2^2 = O1O3^2 + O3O2^2即：a^2 = c^2 + (b/2)^2将式（1）代入，可得：b^2 = a^2 - c^2 = (b/2)^2 + c^2解得：b = 2√(a^2 - c^2) （5）同理，可以得到：a = 2√(b^2 + c^2) （6）通过公式（5）和（6），我们可以计算出椭圆的长轴和短轴。

接下来，我们可以利用公式（2）和（3）计算出O1 和O3 的坐标。

以O1 为例，设其坐标为(x1, y1)，则有：x1 = a * cos(θ)y1 = b * sin(θ)其中，θ为O1O3 的连线与水平方向的夹角。

同理，可以计算出O3 的坐标。

最后，根据O1、O2、O3 的坐标，我们可以计算出椭圆的面积和周长。

椭圆的面积公式为：S = πab周长公式为：L = 2π(a + b)通过以上步骤，我们就可以利用四心椭圆法计算出椭圆的大小和形状。

四个中心点绘制椭圆的方法当我们在CAD中遇到四个点让我们绘制出椭圆形，我们能怎么绘制呢？我们看看下图的绘制步骤是否能关心大家。

1、做垂直相交的两条直线，在上面确定A、B、C、D、O五个点，AB为长轴，CD为短轴，O为中心点；2、连接线段AC；3、以O为圆心，OA的长为半径画圆，交CD线于E点；4、以C为圆心，CE的长为半径画圆，交AC线于F点；5、以A为圆心，AF的长为半径画圆；6、以F为圆心，AF的长为半径画圆，两圆弧相交两点G、H；7、连接GH，交AB轴于O1点，交CD轴于O2点；8．以O为圆心，OO1的长为半径画圆，交OB于O3点；9、以O为圆心，OO2的长为半径画圆，交OB于O4点；10、以O1为圆心，O1A的长为半径画圆；以O3为圆心，O3B的长为半径画圆；11、以O2为圆心，O2C的长为半径画圆；12、以O4为圆心，O4D的长为半径画圆。

推举阅读：CAD绘制圆弧的时候先得劣弧推举阅读：CAD培训当我们在CAD中遇到四个点让我们绘制出椭圆形，我们能怎么绘制呢？我们看看下图的绘制步骤是否能关心大家。

1、做垂直相交的两条直线，在上面确定A、B、C、D、O五个点，AB为长轴，CD为短轴，O为中心点；2、连接线段AC；3、以O为圆心，OA的长为半径画圆，交CD线于E点；4、以C为圆心，CE的长为半径画圆，交AC线于F点；5、以A为圆心，AF的长为半径画圆；6、以F为圆心，AF的长为半径画圆，两圆弧相交两点G、H；7、连接GH，交AB轴于O1点，交CD轴于O2点；8．以O为圆心，OO1的长为半径画圆，交OB于O3点；9、以O为圆心，OO2的长为半径画圆，交OB于O4点；10、以O1为圆心，O1A的长为半径画圆；以O3为圆心，O3B的长为半径画圆；11、以O2为圆心，O2C的长为半径画圆；12、以O4为圆心，O4D的长为半径画圆。

推举阅读：CAD绘制圆弧的时候先得劣弧推举阅读：CAD培训— 21 —。