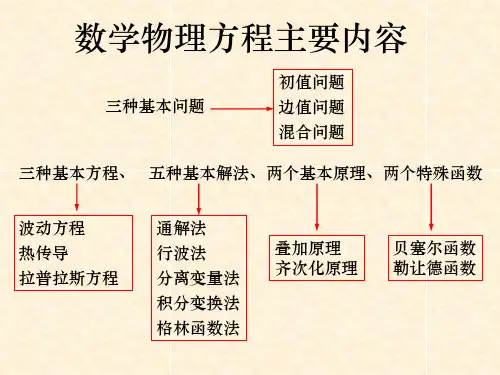
数学物理方程 第一章 定解问题

§1.2 什么是定解问题1. 定解问题定解问题是根据已知物理规律求解特定物理过程的数学条件，它由泛定方程和定解条件两个部分组成，泛定方程也称为数学物理方程。

2. 泛定方程泛定方程是待解物理过程所遵循的物理规律的数学表达式，具体表现为某物理量关于时间和空间变量的偏微分方程，同一类物理过程遵循相同的物理规律，因此泛定方程反映一类物理过程的共性。

方程中物理量对时间变量的偏微分项反映物理过程的因果关联。

方程中物理量对空间变量的偏微分项反映物理过程的内部作用，或内在关联。

例1. 质点运动状态的演化问题在质点动力学问题中常求质点的运动轨迹，一旦求出运动轨迹，则一切与质点运动有关的物理量（如动能、动量、角动量等）都可求出。

质点的运动状态是由质点的位矢和动量完全确定，求质点运动轨迹的方法就是求解质点的运动状态随时间演变的过程，即由前一时刻的位矢和动量推算出下一时刻位矢和动量，从物理上看前后二时刻质点的运动状态的联系为dt t p m t r dt t r t r dt t r )(1)()()()(K K K K K +=+=+， dt t F t p dt t p t p dt t p )()()()()(K K K K K +=+=+ 因此，只要知道质点的受力情况就能由前一时刻的运动状态求出下一时刻的运动状态，这样的推演过程就是求解常微分方程F t r m K K =)(满足初始条件“0000)(,)(v t r r t r K K K K ==”的解。

§1.3 定解条件。

一、初始条件初始条件描述特定物理过程的起因，就t 这个自变数而言，如果泛定方程中物理量u 对t 最高阶偏导数是n 阶偏导数n n tu ∂∂，则要确定具体的定解问题，需要n 个初始条件。

例1：均匀细杆的导热问题满足的泛定方程为02=−xx t u a u ，则要确定具体的导热问题的解只需一个初始条件：)(0x u t ϕ==，即要已知初始温度分布。

第1章 数学物理方程的定解问题§1.1 数学物理方程的一般概念本节讨论：①数学物理方程的基本概念，②三类基本方程的数学表示，③一些简单解法▲数学物理方程的任务与特点 数学物理方程（亦称数理方程）在数学上为二阶偏微分方程。

它的任务有两个方面：①寻找数学定解问题的求解方法，给出解的表达式和计算方法；②通过理论分析得出问题的通解或某些特解的一般性质。

数学物理方程有如下特点：①它紧密地、直接地联系物理学、力学与工程技术中的许多问题。

②它广泛地运用数学物理中许多的技术成果。

如：数学中的复变函数、积分变换、常微分方程、泛函分析、广义函数等等，物理学中的力学、电学、磁学、热力学、原子物理学、振动与波、空气动力学等等。

⒈ 一些基本概念数学物理方程是物理过程中的一些偏微分方程。

由于物理过程是十分复杂的，故它们的数学表达式也是十分广泛的。

本书不能将众多的数学物理方程一一讨论，仅讨论一些常用的二阶线性微分方程。

一般而言，二阶线性偏微分方程可写为2,11nn ij i i j i i j i u u Lu a b cu f x x x ==∂∂=++=∂∂∂∑∑ （1.1.1） 式中：自变量),,(1n x x x ⋅⋅⋅=，系数ij a 、i b 、c 为x 的函数或为常数，并且ji ij a a =。

由于式中关于未知函数u 的导数最高为二阶导数，故方程称为二阶微分方程；同样，由于x 为n 维向量，方程也称为n 维方程；由于方程中对u 的各阶偏导数为线性的，故称为线性方程，否则就称为非线性方程。

若系数ij a 、i b 、c 均为常数，则称为常系数方程，否则称为变系数方程；若0≡f ，则称为齐次方程，反之称为非齐次方程。

▲方程的数学形式 在所有的自变量i x 中，时间变量t 常常被使用，由于它的独特性，人们常常直接用t 表示而不置于i x 之中，关于t 的导数式为：22u u L u a b t t t∂∂=+∂∂ (1.1.2) 故上述方程可改写为：f Lu u L t += (1.1.3)上述方程习惯上也称为n 维方程。

第一章． 波动方程§1 方程的导出。

定解条件1．细杆（或弹簧）受某种外界原因而产生纵向振动，以u(x,t)表示静止时在x 点处的点在时刻t 离开原来位置的偏移，假设振动过程发生的张力服从虎克定律，试证明),(t x u 满足方程()⎪⎭⎫⎝⎛∂∂∂∂=⎪⎭⎫ ⎝⎛∂∂∂∂x u E x t u x t ρ其中ρ为杆的密度，E 为杨氏模量。

证：在杆上任取一段，其中两端于静止时的坐标分别为 x 与+x x ∆。

现在计算这段杆在时刻t 的相对伸长。

在时刻t 这段杆两端的坐标分别为：),();,(t x x u x x t x u x ∆++∆++其相对伸长等于 ),()],([)],([t x x u xxt x u x t x x u x x x ∆+=∆∆-+-∆++∆+θ令0→∆x ，取极限得在点x 的相对伸长为x u ),(t x 。

由虎克定律，张力),(t x T 等于),()(),(t x u x E t x T x =其中)(x E 是在点x 的杨氏模量。

设杆的横截面面积为),(x S 则作用在杆段),(x x x ∆+两端的力分别为x u x S x E )()(x u x x S x x E t x )()();,(∆+∆+).,(t x x ∆+于是得运动方程tt u x x s x ⋅∆⋅)()(ρx ESu t x =),(x x x x x ESu x x |)(|)(-∆+∆+利用微分中值定理，消去x ∆，再令0→∆x 得tt u x s x )()(ρx∂∂=x ESu () 若=)(x s 常量，则得22)(tu x ∂∂ρ=))((x u x E x ∂∂∂∂即得所证。

2．在杆纵向振动时，假设(1)端点固定，(2)端点自由，(3)端点固定在弹性支承上，试分别导出这三种情况下所对应的边界条件。

解：(1)杆的两端被固定在l x x ==,0两点则相应的边界条件为 .0),(,0),0(==t l u t u(2)若l x =为自由端，则杆在l x =的张力x ux E t l T ∂∂=)(),(|lx =等于零，因此相应的边界条件为x u∂∂|lx ==0 同理，若0=x 为自由端，则相应的边界条件为xu∂∂∣00==x (3)若l x =端固定在弹性支承上，而弹性支承固定于某点，且该点离开原来位置的偏移由函数)(t v 给出，则在l x =端支承的伸长为)(),(t v t l u -。