变分法简介(简单_明了_易懂)
- 格式:doc
- 大小:592.51 KB
- 文档页数:12


§1 变分法简介作为数学的一个分支,变分法的诞生,是现实世界许多现象不断探索的结果,人们可以追寻到这样一个轨迹:约翰·伯努利(Johann Bernoulli ,1667-1748)1696年向全欧洲数学家挑战,提出一个难题:“设在垂直平面内有任意两点,一个质点受地心引力的作用,自较高点下滑至较低点,不计摩擦,问沿着什么曲线下滑,时间最短?”这就是著名的“最速降线”问题(The Brachistochrone Problem )。
它的难处在于和普通的极大极小值求法不同,它是要求出一个未知函数(曲线),来满足所给的条件。
这问题的新颖和别出心裁引起了很大兴趣,罗比塔(Guillaume Francois Antonie de l'Hospital 1661-1704)、雅可比·伯努利(Jacob Bernoulli 1654-1705)、莱布尼茨(Gottfried Wilhelm Leibniz,1646-1716)和牛顿(Isaac Newton1642—1727)都得到了解答。
约翰的解法比较漂亮,而雅可布的解法虽然麻烦与费劲,却更为一般化。
后来欧拉(Euler Lonhard ,1707~1783)和拉格朗日(Lagrange, Joseph Louis ,1736-1813)发明了这一类问题的普遍解法,从而确立了数学的一个新分支——变分学。
有趣的是,在1690年约翰·伯努利的哥哥雅可比·伯努利曾提出著名的悬链线问题 (The Hanging Chain Problem)向数学界征求答案,即,固定项链的两端,在重力场中让它自然垂下,问项链的曲线方程是什么。
在大自然中,除了悬垂的项链外,我們还可以观察到吊桥上方的悬垂钢索,挂着水珠的蜘蛛网,以及两根电线杆之间所架设的电线,这些都是悬链线(catenary )。
伽利略(Galileo, 1564~1643)比贝努利更早注意到悬链线,他猜测悬链线是抛物线,从外表看的确象,但实际上不是。
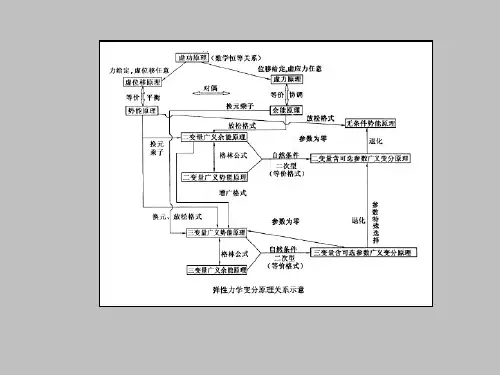



第一章 变分原理与变分法1.1 关于变分原理与变分法(物质世界存在的基本守恒法则)一、 大自然总是以可能最好的方式安排一切,似乎存在着各种安排原理:昼/夜,日/月,阴/阳,静止/运动 等矛盾/统一的协调体; 对静止事物:平衡体的最小能量原理,对称/相似原理;对运动事物:能量守恒,动量(矩)守恒,熵增原理等。
变分原理是自然界静止(相对稳定状态)事物中的一个普遍适应的数学定律,获称最小作用原理。
Examples :① 光线最短路径传播;② 光线入射角等于反射角,光线在反射中也是光传播最短路径(Heron );③CB AC EB AE +>+Summary : 实际上光的传播遵循最小能量原理;在静力学中的稳定平衡本质上是势能最小的原理。
二、变分法是自然界变分原理的数学规划方法(求解约束方程系统极值的数学方法),是计算泛函驻值的数学理论数学上的泛函定义定义:数学空间(集合)上的元素(定义域)与一个实数域间(值域)间的(映射)关系特征描述法:{ J :R x R D X ∈=→⊂r J )(|}Examples :① 矩阵范数:线性算子(矩阵)空间 数域‖A ‖1 = ∑=ni ij ja 1max ;∑=∞=nj ij ia A 1max;21)(1122∑∑===n j ni ij a A② 函数的积分: 函数空间数域 D ⊂=⎰n ba n f dxx f J )(Note : 泛函的自变量是集合中的元素(定义域);值域是实数域。
Discussion :① 判定下列那些是泛函:)(max x f f b x a <<=;x y x f ∂∂),(; 3x+5y=2; ⎰+∞∞-=-)()()(00x f dx x f x x δ ② 试举另一泛函例子。
物理问题中的泛函举例① 弹性地基梁的系统势能i. 梁的弯曲应变能: ⎰=∏l b dx dxw d EJ 0222)(21ii. 弹性地基贮存的能量: dx kw l f ⎰=∏0221 iii. 外力位能: ⎰-=∏l l qwdx 0iv. 系统总的势能:000;})({221222021===-+=∏⎰dxdww x dx qw kw dxw d EJ l泛函的提法:有一种梁的挠度函数(与载荷无关),就会有一个对应的系统势能。


变分法基础老大中变分法是数学和物理学中一种重要的数值计算方法,它在许多领域中都有广泛的应用。
本文将介绍变分法的背景和重要性。
变分法源于数学中的变分计算问题,最早起源于的变分问题。
它是一种求函数最值的方法,旨在寻找函数的极值点或稳定点。
变分法的发展历程经过了数学家们的不断研究和推导,逐渐形成了现代变分法的基础理论。
在物理学中,变分法广泛应用于解决各种力学和场的问题。
通过将物理问题转化为最值问题,可以用变分法来求解微分方程和泛函方程,从而获得物理系统的稳定解、极值解或最优解。
变分法在力学、电磁学、量子力学等领域起到了重要的作用。
在工程学中,变分法常用于优化设计问题和界面问题的求解。
通过对设计参数进行变分,可求解出具有最优性能的工程结构或系统。
变分法的应用可以降低系统的能耗、提高系统的效率,并优化系统与环境的交互效果。
总之,变分法作为一种重要的数值计算方法,在数学、物理学和工程学中都有着广泛的应用和重要的意义。
通过变分法的运用,可以获得优化问题的解析解或近似解,为各个领域的研究和实践提供有力的支持和指导。
泛函泛函是一个函数的集合,其中每个函数都将一个输入映射到一个输出。
在变分法中,我们将研究泛函的性质和优化问题。
变分变分是指对函数的微小变化。
在变分法中,我们将通过对函数进行变分来研究泛函的性质和优化问题。
变分法公式变分法公式是一种用于求解泛函优化问题的数学工具。
它涉及将变分应用于泛函,并通过求解变分问题来得到泛函的极值。
变分法公式可以表示为:对于给定的泛函J[y],寻找函数y 使得J[y]取极值应用变分运算符,通过对函数y 进行变分,得到变分问题求解变分问题,得到泛函J[y]的极值函数y变分法是一种数学方法,广泛应用于不同领域,包括物理学和工程学。
下面列举了一些变分法在这些领域中的应用示例:物理学量子力学:变分法可以用于求解量子系统的基态能量和波函数形式。
经典力学:变分法可以用于求解约束系统的最小作用量路径。

变分法基本引理变分法是数学中一种重要的数学工具,广泛应用于物理学、工程学、经济学等领域。
其基本引理为变分法的核心思想,是变分法的基础和出发点。
本文将围绕变分法基本引理展开讨论,介绍其基本概念、原理和应用。
一、引言变分法是数学中研究变量函数的极值问题的一种方法。
其基本思想是通过将极值问题转化为一个函数的极值问题,从而求解原问题。
变分法的基本引理是变分法的基础,为后续的推导和应用提供了重要的理论支持。
二、变分法基本引理的概念变分法基本引理是对于函数的变分的一种数学表述。
它指出,如果函数在某一点处取得极值,那么在该点处的变分为零。
换言之,如果一个函数在某一点处的变分不为零,那么该点不是函数的极值点。
三、变分法基本引理的原理变分法基本引理可以通过泛函导数的概念来理解。
泛函导数是对函数的变分的一种推广,它表示函数在某一点处的变分相对于该点处的微小变动的比率。
根据变分法基本引理,如果一个函数在某一点处的泛函导数为零,那么该点是函数的极值点。
四、变分法基本引理的应用变分法基本引理在实际问题中有着广泛的应用。
以经济学为例,我们可以将经济系统的效用函数看作一个泛函,通过变分法求解该泛函的极值,得到最优的经济决策。
类似地,变分法在物理学中的应用也十分广泛,例如用于求解最短路径、最小作用量和最小曲面等问题。
五、变分法基本引理的思考虽然变分法基本引理在理论和应用上都具有重要的意义,但在实际问题中的应用也面临一定的挑战。
首先,变分法需要对变分进行严格的数学推导,这对于一些复杂的问题来说是一项困难的任务。
其次,变分法在求解极值问题时并不一定能得到全局最优解,而可能仅能得到局部最优解。
六、结论变分法基本引理是变分法的核心思想,是变分法的基础和出发点。
通过对变分法基本引理的理论分析和应用示例的介绍,我们可以看到变分法在实际问题中的重要性和应用价值。
在今后的研究和应用中,我们应进一步深化对变分法的理解,不断拓展其应用领域,为解决复杂问题提供更有效的数学工具。


变分运算法则范文首先,我们来看一下变分运算法则的定义。
变分运算法则是一种基于极限思想的求导法则,用于求函数的变分导数。
对于给定的函数y=f(x),其变分导数可以表示为δy/δx,其中δ表示微小的变化量。
变分导数可用以下公式进行计算:δy/δx = lim[δy/δh]其中h为函数f的参数的微小变化量。
这个公式表示了当参数h变化时,函数f的变化率。
变分运算法则在数学的不同领域中都有应用。
在变分法中,变分运算法则用于求解变分问题,如最小值或最大值。
在物理学中,变分运算法则用于求解作用量原理问题,如哈密顿原理和拉格朗日原理。
在控制理论中,变分运算法则用于求解最优控制问题,如最小时间问题和最小能耗问题。
接下来,我们将介绍一些具体的应用例子。
第一个例子是求解最小值问题。
假设我们要求函数y=f(x)在给定区间[a,b]上的最小值。
可以通过变分运算法则构建一个变分函数J(f) =∫[a,b] (f'^2 - f^2) dx,其中f'表示函数f的导数。
然后,求解变分运算法则δJ/δf = 0的方程,可以得到函数f的最小值。
第二个例子是求解哈密顿原理问题。
哈密顿原理是物理学中的一种基本原理,用于描述系统的动力学行为。
通过使用变分运算法则,可以求解出满足哈密顿原理的运动方程。
这个问题在经典力学和量子力学中都有广泛的应用。
第三个例子是求解最优控制问题。
最优控制问题是在给定约束条件下,选择最佳控制策略来优化系统性能的问题。
通过使用变分运算法则,可以求解出满足系统动力学方程和约束条件的最优控制策略。
这个问题在控制理论和工程领域中都有重要的应用。
除了以上三个例子,变分运算法则在其他领域也有广泛的应用。
例如,在经济学中,变分运算法则用于求解最优经济政策问题;在计算机科学中,变分运算法则用于求解图像处理和机器学习问题。
总之,变分运算法则在数学和科学的各个领域都有重要的应用。
综上所述,变分运算法则是微积分中的重要工具,可用于求解最小值问题、哈密顿原理问题和最优控制问题等。
变分法的原理和应用1. 变分法的原理简述变分法是数学分析中一种重要的方法,它主要用于求解泛函极值问题。
泛函是一类函数,其自变量是函数而非常数或向量。
变分法将泛函问题转化为一个变分问题,通过寻找泛函对应的变分函数,使得泛函在该函数上取得极值。
变分法的原理基于变分运算和极值原理。
变分运算是对函数进行微小变化的一种数学操作,以求出极值条件。
极值原理是基于变分运算,通过变分函数使得泛函在该函数上取得极值。
2. 变分法的应用领域变分法具有广泛的应用领域,主要包括:2.1 物理学中的应用变分法在物理学中有许多应用,尤其在研究物理系统的最小作用量原理中起到重要作用。
例如,光的传播可以通过费马原理来描述,通过对路径进行变分运算求得光线的轨迹。
变分法还可以用于研究量子力学中的马克思方程和薛定谔方程,以及经典力学中的拉格朗日方程和哈密顿方程。
2.2 工程学中的应用在工程学中,变分法广泛应用于结构力学、流体力学、热传导等领域。
例如,在结构力学中,变分法可以用于计算结构的位移和应力分布,以及优化设计。
在流体力学中,变分法可以用于求解流体的速度和压力分布,以及优化流体系统的设计。
在热传导中,变分法可以用于求解热传导方程的稳态和非稳态解。
2.3 经济学中的应用变分法在经济学中的应用也比较广泛,主要用于优化问题的求解。
经济学中的很多问题可以转化为泛函极值问题,例如最大化效用函数、最小化成本函数等。
变分法可以通过求解泛函的极值,得到经济系统的最优决策。
2.4 其他领域的应用除了物理学、工程学和经济学外,变分法还在其他领域得到了广泛应用。
例如,在计算机图形学中,变分法可以用于图像变形和图像分割等问题的求解。
在机器学习中,变分法可以用于求解概率图模型的参数估计。
在数学建模中,变分法可以用于求解偏微分方程的边界值问题。
3. 变分法的基本步骤变分法的求解过程通常包括以下几个步骤:3.1 高斯法首先,利用高斯法将泛函问题转化为极值问题。
§1 变分法简介作为数学的一个分支,变分法的诞生,是现实世界许多现象不断探索的结果,人们可以追寻到这样一个轨迹:约翰·伯努利(Johann Bernoulli ,1667-1748)1696年向全欧洲数学家挑战,提出一个难题:“设在垂直平面内有任意两点,一个质点受地心引力的作用,自较高点下滑至较低点,不计摩擦,问沿着什么曲线下滑,时间最短?”这就是著名的“最速降线”问题(The Brachistochrone Problem )。
它的难处在于和普通的极大极小值求法不同,它是要求出一个未知函数(曲线),来满足所给的条件。
这问题的新颖和别出心裁引起了很大兴趣,罗比塔(Guillaume Francois Antonie de l'Hospital 1661-1704)、雅可比·伯努利(Jacob Bernoulli 1654-1705)、莱布尼茨(Gottfried Wilhelm Leibniz,1646-1716)和牛顿(Isaac Newton1642—1727)都得到了解答。
约翰的解法比较漂亮,而雅可布的解法虽然麻烦与费劲,却更为一般化。
后来欧拉(Euler Lonhard ,1707~1783)和拉格朗日(Lagrange, Joseph Louis ,1736-1813)发明了这一类问题的普遍解法,从而确立了数学的一个新分支——变分学。
有趣的是,在1690年约翰·伯努利的哥哥雅可比·伯努利曾提出著名的悬链线问题 (The Hanging Chain Problem)向数学界征求答案,即,固定项链的两端,在重力场中让它自然垂下,问项链的曲线方程是什么。
在大自然中,除了悬垂的项链外,我們还可以观察到吊桥上方的悬垂钢索,挂着水珠的蜘蛛网,以及两根电线杆之间所架设的电线,这些都是悬链线(catenary )。
伽利略(Galileo, 1564~1643)比贝努利更早注意到悬链线,他猜测悬链线是抛物线,从外表看的确象,但实际上不是。
变分法综述1.变分法1.1.变分法起源变分法是17世纪末发展起来的一门数学分支,主要是古典变分法,它理论完整,在力学、光学、物理学、摩擦学、经济学、宇航理论、信息论和自动控制论等诸多方面有广泛应用。
20世纪中叶发展起来的有限元法,其数学基础之一就是变分法。
[1]变分法是处理泛函的数学领域,和处理函数的普通微积分相对。
譬如,这样的泛函可以通过未知函数的积分和它的导数来构造。
变分法最终寻求的是极值函数:它们使得泛函取得极大或极小值。
有些曲线上的经典问题采用这种形式表达:一个例子是最速降线,在重力作用下一个粒子沿着该路径可以在最短时间从点A 到达不直接在它底下的一点B 。
在所有从A 到B 的曲线中必须极小化代表下降时间的表达式。
变分法的关键定理是欧拉-拉格朗日方程。
它对应于泛函的临界点。
在寻找函数的极大和极小值时,在一个解附近的微小变化的分析给出一阶的一个近似。
它不能分辨是找到了最大值或者最小值(或者都不是)。
变分法在理论物理中非常重要:在拉格朗日力学中,以及在最小作用量原理在量子力学的应用中。
变分法提供了有限元方法的数学基础,它是求解边界值问题的强力工具。
它们也在材料学中研究材料平衡中大量使用。
而在纯数学中的例子有,黎曼在调和函数中使用狄力克雷原理。
最优控制的理论是变分法的一个推广。
[2]同样的材料可以出现在不同的标题中,例如希尔伯特空间技术,摩尔斯理论,或者辛几何。
变分一词用于所有极值泛函问题。
微分几何中的测地线的研究是很显然的变分性质的领域。
极小曲面(肥皂泡)上也有很多研究工作,称为Plateau 问题。
1.2变分问题类型固定边界的变分问题,可动边界的变分问题,条件极值变分问题和参数形式的变分问题。
[3](1)古典变分问题举例 例1:最速降线或捷线问题(Brachistorone or curve of Steepest descent )问题。
这是历史上出的第一个变分法问题,1696年约翰·伯努利提出的。