当前位置：文档之家 › 弹性力学_第三章 应变

弹性力学_第三章 应变

  • 格式：ppt
  • 大小：893.00 KB
  • 文档页数：66

下载文档原格式

  / 66

合集下载

第三章应变理论课件

第三章应变理论课件


Venant）1797年生于法国，
1886年逝世。1825年毕业于
巴黎桥梁公路学校，后从事
工程设计工作，1837年回该
校任教，1868年当选为法国
科学院院士。在弹性力学、
塑性力学、流体力学等方面
做出了贡献。他的力作用的
局部思想被称为“圣维南原 理”。
圣维南
（A.J.Saint-Venant）
§3-5 变形协调方程
§3-3 转动张量
如图4设过点 从物体中任意取出
一微元线段 。若令点 的坐标
为
，则点 的坐标为
变形后， 变成 的位移为
。令点 的位移为
于是
图4
, 则点
§3-3 转动张量
§3-3 转动张量
其中
若令
则
表示位移矢量 的旋度，
则分别表示物体
内微元体绕相应的坐标轴的旋转分量，而
则代
表微元体的刚性转角。
§3-3 转动张量
应变协调方程的物理意义： ➢ 物体变形后每一单元体都发生形状改变，如变形不满
足一定的关系，变形后的单元体将不能重新组合成连 续体，其间将产生缝隙或出现相互嵌入现象。 ➢ 为使变形后的物体保持连续体，应变分量必须满足一 定的关系。 注：应变协调方程是变形连续的必要和充分条件！
例题
例1. 设物体变形时产生的应变分量为
在略去二阶及更高阶的微量以后简化为 线段 的正应变是
（3）
§3-2 小应变张量（几何方程）
由于位移是微小的， 方向的位移所引起的线段 的伸缩，是更高一阶微小的，略去不计。同样线段
的正应变是 （4）
求出线段 与 之间的直角改变，也就是剪应 变 ，用位移分量来表示。
§3-2 小应变张量（几何方程）
弹性力学有限元第三章

弹性力学有限元第三章


y
v v dy y
u B''
u dy y
B'
B
dy
v P
xy
P' u
dx
o
A'
v dx
yx
x
A''
v A
u u dx x
x
x
u x
y
v y
z
w z
xy
yx
v x
u y
yz
zy
w y
v
z
zx
xz
w x
u z
第三章 空间问题的基本理论
与几何方程等价的是变形连续性方程（也称相容方程 或协调方程），在空间问题里表示为
在S上
xzl yzm zn Z
在混合边界问题中，某些边界条件是位移边界条件， 而另一些边界条件是应力边界条件。
第三章 空间问题的基本理论
§ 3-5 物体内任一点的应力状态
已知物体在任一点P的六个应力分量 x, y,z ,xy yx, yz zy ,zx xz ， 试求经过P点的任一斜面上的应力。
2G 3
2G
y
y
2G
2G 3
2G
z
z
2G
2G 3 2G
及
x e 2G x
y
e
2G y
z e 2G z
xy G xy
xy
xy
G
yz
yz
G
zx
zx
G
yz G yz
zx G zx
其中 、G — 拉密常数
✓ 各种弹性常数之间的关系
G
应力状态不变量 1 x y z
弹性力学-第三章-应变状态

弹性力学-第三章-应变状态


应变，由于六个应变分量对应三个位移分量，则其求解将相
对复杂。 这个问题以后作专门讨论。
几使何用方张程量给符出号的，应几变何通方常程称可为以表工达程为应：变。ij
1 2
ui,j
uj,i
§3.1 变形11
上式表明应变分量ij 将满足二阶张量的坐 标变换关系，应变张量分量与工程应变分 量的关系可表示为
• 刚性位移可以分解为平动与转动 • 刚性转动——变形位移的一部分，但是不产
生变形。
§3.1 变形13
通过分析弹性体内无限邻近两点的位 置变化，则可得出刚体的转动位移与 纯变形位移之间的关系。
设M点的坐标为（x，y，z）
与M点邻近的
位移（u，v，w）
N点的坐标为（x+dx，y+dy，z+dz）
位移（u+du，v+dv，w+dw）
将几何方程
x
u, x
y
v y
,
z
w z
,
中的第 1，2，4 式：
xy
vu, x y
yz
wv, y z
zx
uw z x
作如下求偏导运算：
2 x
y 2
3u xy 2
2 y
x2
3v x2y
2 xy
xy
2 u
yx
y
v x
3u xy 2
3v x 2y
§3.3 应变协调5
从几何方程中消去位移分量，第一式和第二式分别对y和 x求二阶偏导数
(
x
)l
1 2
xym
1 2
xzn
0
1 2
xyl
(
y
)m
1 2
弹性力学课件第三章应变理论

弹性力学课件第三章应变理论

有限元法的实现需要借助计算机编程，利用有限 元分析软件进行建模、求解和后处理。
有限差分法
01
有限差分法是一种基于离散化的数值分析方法，通过将连续的时间或 空间离散化为有限个差分，建立差分方程进行求解。
02
在弹性力学中，有限差分法常用于求解波动问题和热传导问题等偏微 分方程。
03
有限差分法的优点在于简单直观，易于编程实现，特别适合处理规则 区域的问题。
应变分析在断裂力学中的应用对于评估材料的安全性和可靠性具有重要意义，特别是在 航空航天、石油化工和核能等领域的高强度材料中尤为重要。
流体力学中的应变分析
01
流体力学是研究流体运动规律和流体与固体相互作用的一门学科。 在流体力学中，应变分析是研究流体流动状态和流体机械性能的 基础。
02
应变分析在流体力学中主要关注流体在不同压力、温度和 剪切力等条件下的流动行为。通过测量流体的应变响应， 可以评估流体的流动特性和机械性能，为流体机械的设计 和优化提供依据。
应变理论在处理大变形和塑性变形时存在困难，需要 引入更复杂的模型和理论。
应变理论在处理多相材料和复合材料时，难以准确描 述材料的复杂行为。
应变理论的新发展
发展了高阶应变理论，以更准确地描述材料的复杂 变形行为。
引入了有限变形理论，对应变和应力进行更全面的 描述。
结合数值计算方法，如有限元法，对应变进行数值 模拟和分析。
弹性力学课件第三章应变理论
目
CONTENCT
录
• 应变理论概述 • 应变理论基础 • 应变分析方法 • 应变理论应用 • 应变理论发展前景
01
应变理论概述
应变定义与测量
应变定义
物体在外力作用下发生的形状和尺寸 的相对变化。
弹性力学-空间问题的应变分析 (第三章)

弹性力学-空间问题的应变分析 (第三章)


x y z yz zx xy 0
（ a）
代入几何方 程，有
v w u 0, 0, 0, y z x u w v u w v 0, 0 0, z x x y y z
积分式（a）中前三式，有
2
N l x m y n z mn yz nl zx lm xy
2 2 2
（3-5）
—— 任意方向线应变计算公式 任意点线应变的张量与矩阵表示：
N l 2 x m2 y n2 z mn yz nl zx lm xy
u0、v0、w0 分别为沿三个坐标轴方向的刚体位移。
对于平面情形，有
u u0 z y v v0 z x
3. 体积应变
设有一微小正平行六面体，棱长：x、y、z ， 变形前体积：V0
z
x y z
z
x
变形后的边长和体积分别为：
x x x, y y y, z z z;
f 3 ( x, y) i jx ky lxy
（c） 将以上三式代回式（c），得
将上式中的第二、第三式分别对z、 y 求偏导，有：
2 f ( y, z ) 0, 2 f1 ( y, z ) 0 2 1 y z
k f l hx 0 c j d l y 0 g b h d z 0
y
x
y
V (x x x) (y y y) (z z z ) xyz (1 x )(1 y )(1 z )
体积应变（相对体积改变） ：
V V0 xyz (1 x )(1 y )(1 z ) xyz e V0 xyz x y z x y y z z x x y z
弹性力学-第三章 应变分析

弹性力学-第三章 应变分析


(3.9)
α xy
% dr2
% dr1
dr2
α yx
dr1
x
第三章 应变分析 §3-3
应变张量的进一步解释
由式(3.12)得 由式(3.12)得dr1和dr2间直角的减小量为 (3.12)
∆ϕ = 22ε ij nm j j = 2ε 12 = 2ε xy ∆ϕ = ε ij ni i m
上式表示剪应变是角度变化的一半 图中: 图中:
% dr 2 = dr 2 + 2dr ⋅ G ⋅ dr = (1 + 2n ⋅ G ⋅ n)dr 2
第三章 应变分析 §3-2
变形状态和应变张量
只讨论小变形问题,忽略高阶项 只讨论小变形问题 忽略高阶项 式(3.6) 为 其中
∇u ⋅ u∇
(3.7)
% dr 2 = (1 + 2n ⋅ ε ⋅ n)dr 2
ε x 1 γ ε ij = 2 yx 1 γ zx 2
εy
1 γ zy 2
对称张量 张量的剪切应变分量 ≠ 实际的剪切应变
第三章 应变分析 §3-3
应变张量的进一步解释
应变与位移的关系（几何方程） 点的位移是u(x+dx，y)、 应变与位移的关系（几何方程） A点的位移是 点的位移是 ， 、 v(x+dx，y)， ， ，
分别为Y 分别为Y和Z方向的正应变 如图, 如图, 设n为x轴向的单位基矢量即n=e1 轴向的单位基矢量即n=e n1 = 1, n2 = 0, n3 = 0 设m为y轴向的单位基矢量即m=e2 轴向的单位基矢量即m=e O m1 = 0, m2 = 1, m3 = 0
y
ε nn = εijni⋅ ε ⋅ n11 =ε ijxni n j ε = n nj = ε = ε
弹性力学3.

弹性力学3.


求应变分量
解：由于 n=0,任意方向 en e xl2 e ym2 xylm
45
x
e0
0°(l,m)=(1,0) , 45°(l,m)=(0.707,0.707), 90°(l,m)=(0,1)

e 45
则 e 0 e x 2.7 10 4
e90 e y 1105
e 45
1 2
e
x
1 2
e y' e xl22 e ym22 e zn22 xyl2m2 yzm2n2 zxn2l2
e z' e xl32 e ym32 e zn32 xyl3m3 yzm3n3 zxn3l3
代入(1)(2)展开得
x'y' 2 e xl1l2 e ym1m2 e zn1n2 xy (l1m2 l2m1) yz (n1m2 n2m1) zx (l1n2 l2n1)同理
2.主应变的确定 由对应替换关系和应力状态方程。可对应替换得
应变张量的第一不变量 第二不变量 第三不变量
主应变特征方程
J1
J2 J3
ex ey ez
e xe y e ze y
e
xe
ye
z
1 4
e xe z xy yz zx
1
4
2 yz
e x
2 yz
2 zx
e
2 xy
y
2 zx
e
z
数的几何方程不相矛盾；2) 变形 后各单元体能重新组合成连续体， 无缝隙或嵌入现象；3) 单连通域 弹性体, 可以通过几何方程求得单 值连续的位移分量；等应变分量
必须满足的关系。
3.位移边界条件
若边界处已知位移值
u, v, w则可写出
弹性力学_3-应变分析

弹性力学_3-应变分析


相对位移张量反映了一点相对位移的总体情况， 相对位移张量反映了一点相对位移的总体情况，既包含 了因刚体位移产生的相对位移， 了因刚体位移产生的相对位移，又包含了因变形位移产生的 相对位移； 相对位移； 相对位移张量一般为非对称张量。 相对位移张量一般为非对称张量。
二. 转动张量
设 PA = ds , PA1 = ds1 1 若为刚体位移， 若为刚体位移，则 ds = ds1
z A
r u′ r u
A1
(ds)2 = (dx1)2 + (dx2 )2 + (dx3 )2 = dxi dxi (ds1)2 = (dxi +δui )(dxi +δui ) ≈ dxi dxi + 2δuidxi
∴ δui dxi = 0 ⇒ dxui, j dxj = 0 i
展开
x O
P
P1 y
1. 体积应变 由正交三线元可构成一微元体， 由正交三线元可构成一微元体， 考察变形前后微元体体积的变化。 考察变形前后微元体体积的变化。 变形前微元体体积 变形后微元体边长
x P z
t dz
dy s
r
O
dx
y
1 1 ∂w ∂v ε23 = ε32 = γ yz = + 2 2 ∂y ∂z
∂w ε33 = εz = ∂z
应变张量分量与工程应变的原始定义完全相同， 应变张量分量与工程应变的原始定义完全相同， 工程切应变是角应变分量的2 但工程切应变是角应变分量的2倍，故一点应变状态可 由应变张量描述 几何方程可表示为
∂u3 ∂u1 ∂u2 dx1dx1 + dx2dx2 + dx3dx3 ∂x1 ∂x2 ∂x3 ∂u3 ∂u1 ∂u1 ∂u2 ∂u2 ∂u3 +( + )dx1dx2 + ( + )dx2dx3 + ( + )dx3dx1 = 0 ∂x2 ∂x1 ∂x3 ∂x2 ∂x1 ∂x3
弹性力学 复习资料(全) 同济大学

弹性力学 复习资料(全) 同济大学


第五章
线性弹性本构关系
不考虑热效应，克定律。 1、应变能密度和本构关系： ★格林公式 ij
W ，其中 W 是应变能，指外力在准静态过程中所做的功全部转化为由 ij
于变形而储存在弹性体内的能量。 2、广义胡克定律： ij Eijkl kl ，其中 Eijkl 为一个四阶张量，称为弹性系数或弹性模量张量。 4、各向同性弹性体：材料沿所有方向的弹性性质都是相同的，在数学上，即应力应变关系 的分量形式与坐标系无关。 令 C12 , C11 C12 / 2 ，称为 Lame（拉梅）系数
第八章 平面问题的极坐标解答
ui ui , 在S（位移边界）上 u
3、叠加原理：基本方程和边界条件都是线性的，叠加原理成立。对于大变形问题、材料非 线性问题和边界条件非线性的小变形问题，叠加原理不成立。 4、解的存在性和唯一性：逆解法和半逆解法。 5、★位移解法：以位移作为基本未知函数，在基本方程中消去应变张量和应力张量，可导 出仅用位移表示的方程组。 ,i 2ui fi 0 Lame Navier方程：
u v 1 u v ， y ， xy x y 2 y x
1 x x 1 y E1 1 物理方程： y y 1 x E1 1 1 xy xy E1
4
同济大学 弹性力学复习资料
1150899 陈力畅
第七章 平面问题的直角坐标解答
1、平面应变问题： u u x, y ，v v x, y ，w 0 等截面柱形物体；柱体所受的体积力和侧面所受的面力都平行于 Oxy 平面，且它们的分 布沿 z 方向不变。 几何方程： x
第六章
弹性力学-第三章 应力张量 应变张量-1

弹性力学-第三章 应力张量 应变张量-1


上述方程为
的齐次线性方程组， 且常数项都为
零。因为：
，故
不能同时为零，
所以方程组的系数行列式应为零，即
将行列式展开，得到求解主应力 的三次方程，称为 应力张量 的特征方程。
式中
设特征方程的三个根为 展开后有
比较上两式，有
，则 （特征方程）
对一个给定的应力状态，其主应力的大小和方向是确定的，
球形张量应力（静水应力）作用下，物体只产生各向 相同的线应变而无剪应变。对应物体的体积改变，而形状 不变。
应力偏量代表各面正应力中偏离静水应力的量，是正应力 之和为零的应力状态。该应力状态下，物体的体积不改变 而形状改变。
静水压力实验研究表明，在均匀受力情况下，即使应力达到 很大值，材料也不产生塑性变形。 故：应力球形张量不产生材料的塑性变形； 应力偏量是产生塑性变形的真正原因。
对应于经过主轴之一，而平分其他两主轴夹角（与主平面成45°）的 平面，
设
，最大剪应力为：
（2）两主应力相等，设 由第二式，得
方程的解为
表示通过oz轴的平面，该组平面上，剪应力为零。
表示任一个与圆锥面相切的微分面。在该组 面上剪应力取最大值。
（3）三个主应力相等
空间任一方向都为主方向，即任一平面都是主平面， 剪应力均为零。
应力偏量也是一种应力状态，同样存在着不变量。
用
表示。
式中：
问：是否存在一特定的斜截面，其上应力矢量T与截 面法线同向。即T为该截面上的正应力 ，
而剪应力为零。
设斜截面法线方向余弦为： 应力矢量T在坐标轴上的投影为：
由斜面应力(Cauchy)公式
故 或 将上式展开
当斜面法线方向满足上述方程时，该斜面上只有正应 力，没有剪应力，称该平面为主平面；主平面上的正 应力称为主应力；主应力方向（即主平面法线方向） 称为主方向。
第3章 弹性力学基本知识

第3章 弹性力学基本知识

平面ABC上的全应力SN为：
2 2 2 S N X N YN Z N
( X l XY m ZX n) 2 ( XY l Y m ZY n)2 ( XZ l YZ m Z n)2
同理，ΣY=0, ΣZ=0，整理，得
Hale Waihona Puke ： X N X l XY m ZX n YN XY l Y m ZY n Z l m n XZ YZ Z N
物理方程是描述应力和应变关系的方程。对各 向同性的均匀体用广义虎克定律描述。如(3-13):
xy 2(1 ) 1 xy xy x E [ x ( y z )] G E yz 2(1 ) 1 yz y [ y ( x z )] yz E G E 1 zx 2(1 ) z [ z ( x y )] zx zx G E E 这里 E 是弹性模量( modulus of elasticity)或杨氏模量，μ 是泊松比，and G 是剪切模量(shear modulus )or 刚度模量 (modulus of rigidity). 它们有如下关系:
3.2 弹性力学的几个基本概念
3.2.1 外力和内力
1．外力
外力：作用于物体的外力，通常分为表面力（面力）和体积 力。
（1）面力：指分布在物体表面上的外力，如压力容器所受 的内压，物体和物体相互之间的接触压力等。一般地，面力 是位置坐标的函数，即物体表面各点所受的面力是不同的。 （2）体积力：指分布在物体体积内的外力，通常与物体的 质量成正比、且是各质点位置的函数，如重力，惯性力等。
平面ABC上的全应力SN为：

弹性力学第三章：应变分析


y
x
正应变
微元体棱边的相对伸长度
棱边夹角之间的变化
x y z
剪应变
z
将平行六面体 分别投影到3 个坐标面上
M A o m x a
B
y
b
z
M点在Ox轴的位移分量为
u ( x, y, z )
M点在Oy轴的位移分量为 M A o
v ( x, y , z )
B y A点和B点相应的位移分别为
u ( x dx, y, z )
2 2 z ' xl32 y m3 z n3 xyl3m3 yz m3n3 zxn3l3 3 T 3
x ' y ' 2 xl1l2 2 y m1m2 2 z n1n2 xy (l1m2 m1l2 )
dy u m’
a’ a
u x
同理
v m
o
dx
x
v y y
w z z
u
u dy y
y b
b’’
1 tan 1
v v dx v x u dx dx x
u u dx x
b’
2
dy u m’
a’’ m
o
a’
a dx
x
顺次轮换 x, y, z 和
u , v, w
可得其他两个切应变分量
yz
w v y z
xz
u w z x
当 xy , yz , zx 大于零， 表示角度缩小， 反之则表示角度扩大 综上所述。可以得到以下6个关系式
u w v x , yz x y z v u w y , zx y z x w w u z , xy z x y

弹性力学徐芝纶第三章详解


在数学上，x'，y'，z' 必为x，y，
z的单值连续函数
y
x
位移函数具有三阶连续导数
二、应变
对于微分单元体的变形，将分 为两个部分讨论。
一是微分单元体棱边的伸长和缩短 正应变 二是棱边之间夹角的变化 （剪）切应变
符号规定： 伸长为正，缩短为负 直角变小为正，直角变大为负
正应力 剪应力
正应变 剪应变
v x
u y
xy
v x
u y
yz
w y
v z
zx
u z
w x
上式为剪应变的几何方程
x
u x
y
v y
z
w z
xy
v x
u y
yz
w y
v z
zx
u z
w x
这六式为几何方程（柯西方程）
四、转角方程
x
w y
v z
y
u z
w x
z
v x
u y
3－3 一点应变状态、应变张量
一、应变张量
与应力张量相同，应变张量也是二阶对称张量
则，a点的位移为：
u u dx x
v v dx x
b点的位移为：
u u dy y
v v dy y
x
M
' a' 'Ma Ma
(dx
u dx) x
dx
dx
u x
(dy v dy) dy
y
M 'b''Mb Mb
y dy
v y
同理：
x
u x
y
v y
z
w z

弹性力学 第三章应变状态理论


w
w
1 2
xz
dx
1 2
yz
dy
z
dz
1 2
y
dx
1 2
xdy
§3-2 相对位移张量 转动分量
0
u u
v
v
1 2
z
w
w
1 2
y
1 2
z
0
1 2
x
1 2
y
dx
1 2
x
dy
dz
0
x
1 2
xy
1 2
xz
dx
1 2
xy
y
1 2
yz
dy
1 2
xz
1 2
yz
dz
x
u x
y
v y
z
w z
yz
w y
v z
zx
u z
w x
xy
v x
u y
1 2
yz
yz
,
1 2
zx
zx ,
1 2
xy
xy
ij
1 2
(ui,
j
u j,i )
§3-2 相对位移张量 转动分量
相对位移张量：
u u u
x
y
z
v v v
x
y
z
w w w
x y z
转动矢量：
u(x dx, y, z) u u dx
a:
x
v(x dx, y, z) v v dx x
u(x, y dy, z) u u dy
b:
y
b a
v(x, y dy, z) v v dy

第三章力学位移和应变分析


x， y，z
称为转动分 量
p, q, r代表此微分体的刚性转角
故六个应变分量和三个转动分量可以使物体内某点变 形的几何形象表示完全。
二、物体内无限邻近两点位置的变化
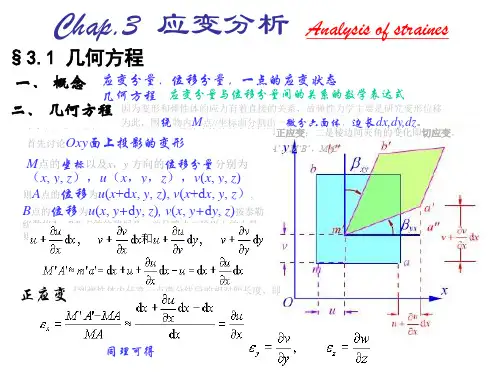
设物体内无限邻近的两点A和B,它们的坐标分别为：
A （x,y,z） B(x+dx,y+dy,z+dz)
变形后，它们到A’和B’ 若A点的位移矢量用u(x,y,z),v (x,y,z), w(x,y,z)表示 则B点的位移矢量用u’,v’,w’表示
说明：
u
P
B
dx A
u u dx x v v dx x
v
dy y

A B

v v dy y
（1） 反映任一点的位移与该点应变间的
u u dy y
关系，是弹性力学的基本方程之一。
当 u、v 已知，则 x , y , xy 可完全确定；反之，已知 x , y , ， xy （ 2） 不能确定u、v。 （∵积分需要确定积分常数，由边界条件决定。）
tan yx
tan xy
v v dx v x v yx dx x
u u dy u y u dy y
xy
1 v u r ( ) 2 x y
r是对角线MQ绕z轴转动的角度。
yx xy , 则r为正号，表示沿逆时针转动；
1 1 1 1 u =u+ x dx xy dy xz dz z dy y dz 2 2 2 2 1 1 1 1 v= v xy dx + y dy yz dz x dz z dx 2 2 2 2 1 1 1 1 w =w zx dx yz dy + z dz y dx x dy 2 2 2 2

材料力学 第三章 应变理论


ij 称为柯西应变张量或小应变张量
其实体表示形式为 1 u u 2
是二阶对称张量，只有六个独立分量。
§3-1 位移和变形
在笛卡尔坐标系中，其常用形式为
11
u1 x1
u x
x ,12
21
1 2
u1 x2
u2 x1
1 u
2
y
v x
xy
yx
22
u2 x2
v y
i
ji
ui x j
j
1
i
ui x j
j
i
可由位移梯度分量 ui 和线元正应变 计算任意方向线元
变形后的方向余弦。x j
考虑两线元间的夹角变化
t cos , t t 2 t 1 1
t
1 t t 2 t
§3-2 小应变张量（几何方程）
若变形前两线元互相垂直，即 t 0
u j xi
ei ej
E 1 u u u u 2
➢ 按照欧拉描述还可以定义描述大变形的阿尔曼西（Almansi,E)
应变张量，即
dS2 dS02 2eijdxidxj
eij
1 2
ui xj
u j xi
um xi
um xj
它也是二阶对称张量
由此可见：物体无变形（线元长度不变，仅作刚体运动） 的充分必要条件是应变张量处处为零。
令 为变形后线元间直角的减小量，则由上式可得
cos
2
cos , t
2 t 2ij it j 2t
通常定义两正交线元间的直角减小量为工程剪应变 t ，即
t 2t 2 t 2ijit j
若 , t 为坐标轴方向的单位矢量，例如 i 1, t j 1(i j)

弹性力学第3章—应变

A
B
B′
O
y
x
研究物体的变形规律，只需要研究物体内各点 的相对位置变动情况，也即研究变形位移
u = u( x, y , z )
张量形式
位移函数
v = v ( x, y , z ) w = w( x , y , z )
ui = ui ( xj )
i = 1, 2, 3
j = 1, 2,3
3.1 变形与应变的概念
( (
) ( ) (
) )
O
′ , y0 ′) P0′( x0
= S + ( u − u0 )
P0 ( x0 , y0 )
x
u、 u0分别为线段起点、终点的位移，所以 其中 S 为原线段，
δ S = S′ − S = u − u0
上式写成张量分量形式，得到线段矢量分量的变化量
δSi = ui − u0i
因此，互相垂直的两个矢量变形 后夹角的改变量为
y
δ S2 x
α = 2ε12
γ xy = 2ε12
同理可得
δ S2 y
该改变量即为剪应变
′ S2
S2
γ zx = 2ε 31
O
S1
δ S1x
δ S1 y
γ yz = 2ε 23
ϕ
S1′
x
3.1 变形与应变的概念
应变张量的物理意义:
汇总
三维问题时应变张量（分量）的物理意义为
3.3 主应变、应变偏量及其不变量
主应变与主方向：
3 2 ′ε n ′ε n − I 3 ′ =0 εn − I1 − I2
上述方程的三个实根即为主应变 ε1 , ε 2 , ε 3 ，进一步可以求 得主方向，以及剪应变的三个极值。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
该应变状态只有体积 等向膨胀或收缩，而 没有形状畸变
x m xy xz eij yx y m yz zy z m zx 应变偏张量
该应变状态只有形状 畸变而没有体积改变。
应变张量分解和应变偏量不变量
1 2
xy y 1 2 zy
1 2 1 2
xz yz z
主应变和应变张量不变量
考虑一个法线为N的斜平面，方向余弦（l1=l，l2=m，l3=n） 斜平面上应变向量qN的三个分量： qNi=ij lj
q N 1 11 12 q N 2 21 22 q N 3 31 32
弹性力学
第三章 应变
§3-1 变形与应变概念 §3-2 变形连续条件 §3-3 应变增量和应变速率张量 §3-4 应力应变分析的相似性与差异性
§3-1 变形与应变概念
弹性体在受外力以后，还将发生变形。物体的 变形状态，一般有两种方式来描述： 1、给出各点的位移；2、给出各体素的变形。 弹性体内任一点的位移，用此位移在x、y、z 三个坐标轴上的投影u、v、w来表示。以沿坐标轴 正方向为正，沿坐标轴负方向为负。这三个投影称 为位移分量。一般情况下，弹性体受力以后，各点 的位移并不是定值，而是坐标的函数。
w u x z
该式表明了一点处的 位移分量和应变分量 所应满足的关系，称 为几何方程，也称为 柯西(Cauchy)关系。
几何方程是用位移导数表示应变，应变描述一点的变 形，但还不足以完全描述弹性单元体的位移变化，因为没 有考虑单元体位置的改变，即单元体的刚体位移。
应变张量
应变分量 x 、 y 、 z 、 xy 、 yz 、 zx 满足张量的性 质，构成一个二阶应变张量。 以 xi 记 x，y，z ; 以 ui 记 u，v，w

§3-1 变形与应变概念
刚体位移：物体内部各点位置变化，但仍保持初始状态相对 位置不变（即其体内任意两点之间距保持不变）。
刚体位移包括平行移动和转动位移
§3-1 变形与应变概念
变形位移：位移不仅使得位置改变，而且改变了物体内部各 个点的相对位置。即物体的形状发生改变。 变形位移包括形状改变和体积改变。
x
A dx 0
图 2-5
v u xy x y
应变分量与位移分量的关系
以上是考察了体素在XOY一个平面内的变形情况
u x x
v y y
v u xy x y
同样方法来考察体素在XOZ和YOZ平面内的变形情况，可得：
该方程一定存在三个根，设为1， 2， 3称为该点主应变:
( 1 )( 2 )( 3 ) 0
主应变和应变张量不变量
再次展开关于 的一元三次方程：
3 (1 2 3 ) 2 (1 2 2 3 31 ) 1 2 3 0
主应变和应变张量不变量
q Ni li

ij
ij l j 0

主方向方程有非零解的条件是其系数行列式必为零。
ij ij 0
展开得关于 的一元三次方程：
主应变特征方程
2 2 2 3 ( x y z ) 2 [ x y y z z x ( xy yz zx )] 2 2 2 x y z 2 xy yz zx x yz y zx z xy 0
3 J1 2 J2 J3 0
在一定的应变状态下，物体内任一点的主应变不会随坐标系 的改变而改变，因而，特征方程中的系数 J1，J2，J3 必为常 数，称为应变不变量。
主应变和应变张量不变量
第一应变不变量
J1 x y z 1 2 3 kk
r
r
N
P(x,y,z)
变形的度量——应变

正（线）应变——线素的相对伸长或缩短
dx dx x dx dy dy y dy dz dz z dz
正应变以伸长时为正，缩短时为负， 与正应力的正负号规定相对应。
变形的度量——应变
剪（切）应变
τ
α
τ
物体内一点 P(x，y，z)的两垂直方向 M 和 N 方向之间的角度变化量，称之为 M 和 N 方向
§3-1 变形与应变概念
刚体平移 刚体位移 *物体内各点之间不产生相对位移 刚体转动 位移 线变形 变形位移 角变形 *物体内各点之间产生相对位移
§3-1 变形与应变概念

由于外部因素 —— 载荷或温度变化 位移 —— 物体内部各点空间位置发生变化 位移形式 刚体位移：物体内部各点位置变化，但仍保持初始状态相对 位置不变。 变形位移：位移不仅使得位置改变，而且改变了物体内部各 个点的相对位置。
应变张量分解和应变偏量不变量
用主应变表示应变偏量：
ex eij 0 0
0 ey 0
0 e1 0 0 ez 0
0 e2 0
0 0 e3
y
yz
z
zx
yx
zy
xz
变形的度量——应变
正（线）应变 σx dx σx u
x
dx
x
u +du
du x dx
物体内一点 P（x,y,z）在 N (l , m, n) 方向上的线应变 r N lim r 0 r r ：变形前在P点处沿 N 方向所取 的微线段 r ：变形后Δr的增量
v v dx x
应变分量与位移分量的关系
由于变形是微小的，所以上式 可将比单位值小得多的 u x 略去，得
v x
v dx x
y
u v v dy y u dy y
C'
D" D '
D C
dy
u
A'

B'
v
v
B"
B
u u dx x
同理，Y向线素AD的转角： u y 因此，剪应变为：
线应变
角应变
③、是一个有单位，无量纲的物理量。 ④、表征某点两坐标轴正方向所夹直角减 少的角应变取正，反之取负。
应变分量与位移分量的关系
ABCD
y
u v v dy y u dy y
ABCD，求线素
A点在X方向的位移分量为u， B点在X方向的位移： u u u u dx x 线素AB的正应变为： u (u dx) u u x x dx x 同理，AD的正应变为： v (v dy ) v v y y dy y
§3-1 变形与应变概念
位移
｛
刚性位移：反映物体整体位置的变动
变形位移：反映物体的形状和尺寸发生变化
研究物体在外力作用下的变形规律，只需研究物体内各点 的相对位置变动情况，即研究变形位移。
◆ 位移函数应是位置坐标的单值连续函数。 ◆ 位移分量函数不能直接表明物体各点处材料变形
的剧烈程度，还需要研究物体内各点的相对位移。
xy yx

2

yz zy

2

zx xz

2

变形的度量——应变
①、涉及受力物体内某一点； ②、涉及该点的某一方向； ③、是一个无量纲的物理量； ④、表征某点某方向伸长变形的线应变取 正，反之取负； ①、涉及受力物体内某一点； ②、涉及过该点的某两相垂直方向；
应变张量分解和应变偏量不变量
1 1 定义平均应变： m ( x y z ) (1 2 3 ) 3 3
应变张量分解：
ij m ij eij
0
m m ij 0 0
m
0
0 0 m
应变球张量
变形的度量——应变
外力作用下，物体各点发生位移，但是某点位移的大 小并不能确定该处应力的大小，它与物体的整体约束有关。
应变反映局部各点相对位置的变化，与应力直接相关，变
形体力学中弹性力学对这种关系作了最为简化的假设，在 各向同性线弹性的条件下，弹性常数只有两个。 1、正应变 2、切应变
x
xy
γ =α +β
β
直角改变量
N
的切应变。
MN
间角度的变化量 则 xy ：变形后 x、y 两垂直方向间夹角的 变化量。
1 2 为变形后 M 、 N 两垂直方向
2
1
M
P( x, y, z)
变形的度量——应变

剪（切）应变——两正交线素夹角的减少
，
，
剪应变以直角变 小时为正，变大 时为负，与剪应 力的正负号规定 相对应。
第二应变不变量
体积应变
2 2 2 J2 x y y z z x xy yz zx 1 1 2 2 3 31 ii kk ik ki
2
第三应变不变量
2 2 2 J3 x y z 2 xy yz zx x yz y zx z xy 1 2 3 ij
1 1 ui u j ij ( ) ( ui , j u j ,i ) 2 2 x j xi
x ij yx zx
xy y zy
xz x 1 yz 2 yx 1 zx z 2
13 l1 23 l2 l 33 3
如果应变矢量 qN 正在平面法线N 方向上，则在这一方向上剪 应变为零，则该法线方向即为主方向（或应变主轴）。其含义 为：在这些方向上，运动前是彼此垂直的，其运动后仍保持垂 直，相应的应变称为主应变 。 剪应变为零的方向就是应变主轴方向；主轴方向的应变就是主应变