弹性力学第3章(徐芝纶第五版)
- 格式:ppt
- 大小:927.00 KB
- 文档页数:40

(完整版)徐芝纶弹性力学主要内容及知识点1.弹性力学是研究弹性体由于受到外力作用、边界约束或温度改变等原因而引起的应力、形变和位移。
2外力分为体积力和面积力。
体力是分布在物体体积内的力,重力和惯性力。
体积分量,以沿坐标轴正方向为正,沿坐标轴负方向为负。
面力是分布在物体表面上的力,面力分量以沿坐标轴正方向为正,沿坐标轴负方向为负。
3内力,即物体本身不同部分之间相互作用的力。
3弹性力学中的基本假定:连续性,完全弹性,均匀性,各向同性,小变形假定。
凡是符合连续性、完全弹性、均匀性、各向同性等假定的物体称之为理想弹性体。
连续性,假定整个物体的体积被组成这个物体的介质所填满,不留下任何空隙。
完全弹性,指的是物体能完全恢复原形而没有任何剩余形变。
均匀性,整个物体时统一材料组成。
各向同性,物体的弹性在所有各个方向都相同。
4求解弹性力学问题,即在边界条件上,根据平衡微分方程、几何方程、物理方程求解应力分量、形变分量和位移分量。
弹性力学、材料力学、结构力学的研究对象分别是弹性体,杆状构件和杆件系统。
解释在物体内同一点,不同截面上的应力是不同的。
应力的符号不同:在弹性力学和材料力学中,正应力规定一样,拉为正,压为负。
切应力:弹性力学中,正面沿坐标轴正方向为正,沿负方向为负。
负面上沿坐标轴负方向为正,沿正方向为负。
材料力学中,所在的研究对象上任一点弯矩转向顺时针为正,逆时针为负。
5.形变:所谓形变,就是形状的改变。
包括线应变(各各线段每单位长度的伸缩,即单位伸缩和相对伸缩,伸长时为正,收缩时为负);切应变(各线段直接直角的改变,用弧度表示,以直角变小时为正,变大为负)6试述弹性力学平面应力问题与平面应变问题的主要特征及区别:平面应力问题:几何形状,等厚度薄板。
外力约束,平行于板面且不沿厚度变化。
平面应变问题:几何形状,横断面不沿长度变化,均匀分布。
外力约束,平行于横截面并不沿长度变化。
7.主应力:设经过P点的某一斜面上的切应力等于0,则该斜面上的正应力称为P点的一个主应力;应力主向:该斜面的法线方向称为该斜面的一个应力主向。







弹性力学徐芝纶课后习题及答案弹性力学是固体力学的重要分支,对于工程技术领域有着广泛的应用。
徐芝纶先生所著的弹性力学教材备受推崇,其中的课后习题更是帮助学习者巩固知识、深化理解的重要途径。
接下来,让我们一起深入探讨一下其中的一些典型习题及答案。
首先,我们来看一道关于平面应力问题的习题。
题目给出了一个矩形薄板,在其边界上受到特定的载荷分布,要求求解板内的应力分布。
对于这类问题,我们首先需要根据已知条件,确定边界条件。
在这个例子中,矩形板的四条边上可能分别有均布力、集中力或者固定约束等。
然后,我们运用弹性力学中的平衡方程、几何方程和物理方程来建立求解方程。
平衡方程描述了物体内部的力的平衡关系;几何方程则将位移与应变联系起来;物理方程则反映了应力与应变之间的关系。
通过联立这些方程,并结合边界条件,我们可以使用数学方法(如傅里叶级数展开、分离变量法等)进行求解。
经过一系列的计算和推导,我们得到板内的应力表达式。
需要注意的是,在计算过程中,要仔细处理各项的系数和积分,确保计算的准确性。
再来看一道关于应变能的习题。
已知物体的应力状态,要求计算其应变能密度。
应变能密度的计算需要先根据应力求出应变,然后利用应力应变的关系计算应变能密度。
这道题主要考察对基本概念和公式的熟练掌握程度。
在求解过程中,要清晰地记住各种应力和应变的分量关系,以及它们在不同坐标系下的转换。
同时,对于复杂的应力状态,要善于运用矩阵运算来简化计算。
还有一道关于厚壁圆筒的习题。
题目给出了圆筒的内外半径、材料属性和承受的内压外压,要求求解圆筒内的应力分布。
对于这种轴对称问题,我们可以利用拉梅方程来求解。
首先确定圆筒的边界条件,即内表面和外表面的压力。
然后代入拉梅方程进行求解。
在计算中,要注意公式中各项的物理意义和单位的统一。
并且要理解厚壁圆筒在不同半径处应力的变化规律。
下面我们来探讨一下答案的重要性以及如何正确使用答案。
答案是对习题的一种验证和参考,但不能完全依赖答案。
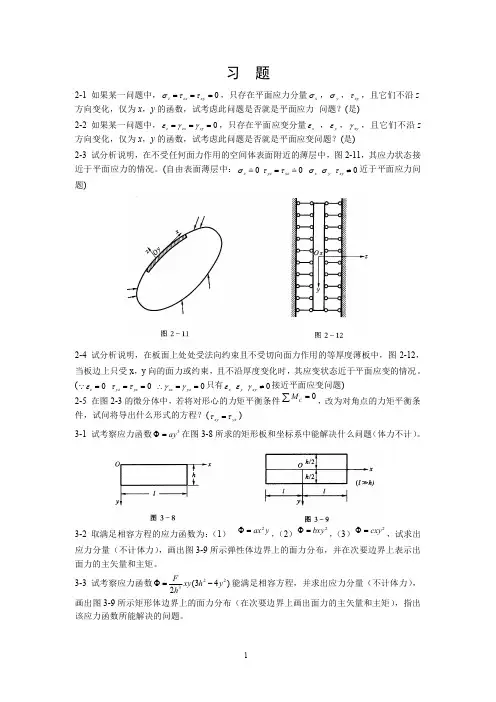


第三章1、解:由题意可知:简支梁所受体力为F g ρ=,所以0,x y f f g ρ==应力函数为:232325432()()2106x A BAy By Cy D x Ey Fy Gy y y Hy Ky Φ=++++++--++从而得应力分量:()2232223222262(62)22622(32)(32)x x y y xy x f x Ay B x Ey F Ay By Hy Ky f y Ay By Cy D gyxx Ay By C Ey Fy G σσρτ∂Φ=-=+++--++∂∂Φ=-=+++-∂=-++-++ (a )考虑对称性,,x y σσ为x 的偶函数,xy τ为x 的奇函数。
于是得:0E F G ===。
下面考虑上下两边的边界条件:22()0,()0y hxy h y y στ=±=±==,代入(a ),得: 3208422h h h hA B C D g ρ+++-= 3208422h h h hA B C D g ρ-+-++= 23()04h x A hB C -++=即2304h A hB C ++=23()04h x A hB C --+=即2304h A hB C -+=以上四式联立得:223,0,,22g g gA B C D h h ρρρ=-===- 代入(a ),并注意0E F G ===得:2322322264+6223226+2x y xy g g x y y Hy K h h g g gy y gy h h g g xy xh ρρσρρρσρρρτ=-++=-+--= (b )现在考虑左右两个边的边界条件,由于对称性,只需考虑一边,例如右边,也就是x l =,用多项式求解,只能要求x σ在这部分边界上合成为平衡力系,也就是要求:2-2()0,h h x x l dy σ==⎰2-2()0h h x x l ydy σ==⎰。
第一章第二章习题答案2-1解:已知 0,0,===-==y x xy y x f f q τσσ1)⎪⎪⎩⎪⎪⎨⎧+∂∂+∂∂+∂∂+∂∂y xy y x yxx f x yf yx τστσ23()()⎩⎨⎧=+=+s xy y s yx x l m m l σστστσ 有:t lq t x -=;代入(*4理、几何方程得:(E x u x ==∂∂ε1(1E y v y ==∂∂ε0==∂∂+∂∂xy yux v γ ()()⇒=+∴0dyy df dx x dg 类似于教材题2-3,可求出 ()()wx v x g wy u y f +=-=00,001;1v wx qy Ev u wy qx Eu ++--=+---=∴υυ从v u ,表达式可见,位移分量是坐标的单值函数,满足位移单值条件。
综合1)~4),。
q xy y x 为问题的正确解答0,=-==τσσ2-2x =σxy τ注意:y x ,代入均满足。
2)验证相容方程:0)(2=+∇y x σσ 亦满足。
3)验证应力边界条件: i) 主要边界:()0,2=±=hy yxy τσ 满足ii) 次要边界:()()()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧===⎰⎰⎰-=-=-=222222320)1(0h h lx xy h h l x x h h l x x Pdy ydy dy τσσ (1)、(2)满足,(3)式左=⎰-===⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-223332212*41*618218hh P h I P h h I P dy y h I P 右 结论:所列xy y x τσσ,,满足平衡方程、相容方程;在主要边界上严格满足应力边界条件,次要边界近似满足应力边界条件,又为单连体,故在圣维南原理的前提下为问题的正确解。
2-3、证明:1)由,,yVf xV fy x∂∂-=∂∂-=则平衡微分方程为: ()()⎪⎪⎩⎪⎪⎨⎧=∂τ∂+∂-σ∂=∂τ∂+∂-σ∂⇒⎪⎪⎩⎪⎪⎨⎧=∂∂-∂τ∂+∂σ∂=∂∂-∂τ∂+∂σ∂0x y V 0yx V 0y V x y 0x V y x yx y xyx yx y xy x (*) 类似于题2-10的推证过程,(*)式的通解为:y x x V yV 2xy 22y 22x ∂∂ϕ∂-=τ∂ϕ∂=-σ∂ϕ∂=-σ;;即: yx V xV y2xy 22y 22x ∂∂ϕ∂-=τ+∂ϕ∂=σ+∂ϕ∂=σ;;2) 对于平面应力问题,相容方程为:()()⎪⎪⎭⎫⎝⎛∂∂+∂∂+-=+∇y f x f y x y x υσσ12即:2222 2-4、x, y n l σσ2==2l应力主向成∴l()2121σσσ+=n 得证。
弹性力学徐芝纶课后习题及答案弹性力学是固体力学的重要分支,对于工程技术领域有着广泛的应用。
徐芝纶先生所著的弹性力学教材备受推崇,而课后习题则是巩固知识、加深理解的重要环节。
下面我们将对部分典型的课后习题及其答案进行详细的探讨。
首先,来看一道关于平面应力问题的习题。
题目给出了一个矩形薄板,在其边界上受到特定的力和约束条件,要求计算板内的应力分布。
对于这道题,我们首先需要根据已知条件确定边界条件。
假设矩形薄板的长为 a,宽为 b,在 x 方向上受到均匀分布的拉力 T,在 y 方向上受到均匀分布的压力 P,并且在四个边上有相应的位移约束。
根据弹性力学的基本方程,我们可以列出平衡方程、几何方程和物理方程。
通过联立这些方程,并结合边界条件,采用适当的求解方法,如应力函数法,逐步推导出应力的表达式。
经过一系列的计算和推导,最终得到板内的应力分布为:在 x 方向上的应力σx = T / b P y / b,在 y 方向上的应力σy = P,剪应力τxy = 0。
接下来,再看一道关于应变能的习题。
题目要求计算一个受扭转的圆柱体的应变能。
对于这道题,我们首先要了解圆柱体扭转时的应力和应变分布情况。
根据弹性力学的理论,圆柱体扭转时,横截面上只有剪应力存在,且剪应力沿半径方向呈线性分布。
然后,通过积分计算出单位体积的应变能,再乘以圆柱体的体积,即可得到整个圆柱体的应变能。
经过计算,圆柱体的应变能表达式为:U =π G L (R^4 r^4) / 8,其中 G 为剪切模量,L 为圆柱体的长度,R 为圆柱体的外半径,r 为圆柱体的内半径。
下面是一道关于应力集中的习题。
题目给出了一个带有圆孔的平板,在板的边缘受到拉伸载荷,要求分析孔边的应力集中现象。
对于这类问题,我们需要运用圣维南原理和应力集中系数的概念。
首先,根据平板的受力情况,计算出无孔时的均匀应力。
然后,通过弹性力学的理论分析,得出孔边的应力分布表达式。
经过计算,发现孔边的应力显著增大,最大应力出现在孔边的某些位置。