材料力学_陈振中_习题第十四章压杆稳定
- 格式:doc
- 大小:142.00 KB
- 文档页数:4



第 九 章 压 杆 稳 定 【2 】一.选择题1.一幻想平均直杆受轴向压力P=P Q 时处于直线均衡状况.在其受到一渺小横向干扰力后产生渺小曲折变形,若此时解除干扰力,则压杆<A ).A.曲折变形消掉,恢复直线外形; B.曲折变形削减,不能恢复直线外形; C.微弯状况不变;D.曲折变形持续增大.2.一修长压杆当轴向力P=P Q 时产生掉稳而处于微弯均衡状况,此时若解除压力P,则压杆的微弯变形<C )A.完整消掉 B.有所缓和 C.保持不变 D.持续增大3.压杆属于修长杆,中长杆照样短粗杆,是依据压杆的<D )来断定的.A.长度B.横截面尺寸C.临界应力D.柔度 4.压杆的柔度分散地反应了压杆的< A )对临界应力的影响.A .长度,束缚前提,截面尺寸和外形; B.材料,长度和束缚前提;C.材料,束缚前提,截面尺寸和外形;D.材料,长度,截面尺寸和外形; 5.图示四根压杆的材料与横截面均雷同, 试断定哪一根最轻易掉稳.答案:< a )6.两头铰支的圆截面压杆,长1m ,直径50mm .其柔度为 ( C >A.60;B.66.7; C .80; D.507.在横截面积等其它前提均雷同的前提下,压杆采用图<D )所示截面外形,其稳固性最好.8.修长压杆的<A ),则其临界应力σ越大.A.弹性模量E 越大或柔度λ越小;B.弹性模量E 越大或柔度λ越大;C.弹性模量E 越小或柔度λ越大;D.弹性模量E 越小或柔度λ越小; 9.欧拉公式实用的前提是,压杆的柔度<C )A.λ≤PEπσ B.λ≤sEπσC .λ≥λ≥10.在材料雷同的前提下,跟着柔度的增大<C )A.修长杆的临界应力是减小的,中长杆不是;B.中长杆的临界应力是减小的,修长杆不是;C.修长杆和中长杆的临界应力均是减小的;D.修长杆和中长杆的临界应力均不是减小的; 11.两根材料和柔度都雷同的压杆<A )A. 临界应力必定相等,临界压力不必定相等;B. 临界应力不必定相等,临界压力必定相等;C. 临界应力和临界压力必定相等;D. 临界应力和临界压力不必定相等;12.鄙人列有关压杆临界应力σe 的结论中,<D )是准确的.A.修长杆的σe 值与杆的材料无关;B.中长杆的σe 值与杆的柔度无关;C.中长杆的σe 值与杆的材料无关;D.粗短杆的σe 值与杆的柔度无关; 13.修长杆推却轴向压力P 的感化,其临界压力与<C )无关.A.杆的材质B.杆的长度C.杆推却压力的大小D.杆的横截面外形和尺寸二.盘算题1. 有一长l =300 mm,截面宽b =6 mm.高h =10 mm 的压杆.两头铰接,压杆材料为Q235钢,E =200 GPa,试盘算压杆的临界应力和临界力.解:<1)求惯性半径i对于矩形截面,假如掉稳必在刚度较小的平面内产生,故应求最小惯性半径mm732.1126121123minmin ===⨯==b bhhb AI i<2)求柔度λλ=μl /i ,μ=1,故λ=1×300/1.732=519>λp =100 <3)用欧拉公式盘算临界应力()MPa8.652.1731020ππ24222cr =⨯==λσE<4)盘算临界力F cr =σcr ×A =65.8×6×10=3948 N=3.95 kN2.一根两头铰支钢杆,所受最大压力KN P 8.47=.其直径mm d 45=,长度mm l 703=.钢材的E =210GPa,pσ=280MPa,2.432=λ.盘算临界压力的公式有:(a> 欧拉公式;(b>直线公式cr σ=461-2.568λ(MPa>.试 <1)断定此压杆的类型;<2)求此杆的临界压力;解:<1) 1=μ8621==PE σπλ5.624===d lilμμλ因为12λλλ<<,是中柔度杆. <2)cr σ=461-2.568λMPaKNA P cr cr 478==σ3.活塞杆<可算作是一端固定.一端自由),用硅钢制成,其直径d=40mm ,外伸部分的最大长度l =1m ,弹性模量E=210Gpa,1001=λ.试<1)断定此压杆的类型;<2)肯定活塞杆的临界载荷. 解:算作是一端固定.一端自由.此时2=μ,而,所以,.故属于大柔度杆-用大柔度杆临界应力公式盘算.4.托架如图所示,在横杆端点D 处受到P=30kN 的力感化.已知斜撑杆AB 两头柱形束缚<柱形较销钉垂直于托架平面),为空心圆截面,外径D=50mm .内径d=36mm ,材料为A3钢,E=210GPa.pσ=200MPa.s σ=235MPa.a=304MPa.b=1.12MPa .若稳固安全系数n w =2,试校杆AB 的稳固性.1.5m0.5mC ABD第第第第30o解 运用均衡前提可有∑=0A M ,107N 5.05.11040230sin 5.123=⨯⨯⨯==P NBDkN2cm 837.32=A ,4cm 144=y I ,cm 04.2=y i ,4cm 1910=x Icm 64.7=x iA3钢的4.99=P λ,1.57=S λ压杆BA 的柔度Sx x i lλμλ<=⨯==7.220764.030cos 5.11Pyy i lλμλ<=⨯==9.820209.030cos 5.11 因x λ.yλ均小于P λ,所以应该用经验公式盘算临界载荷()[]N109.8212.130400329.0)(6⨯⨯-⨯=-==y cr cr b a A A P λσ695=kN压杆的工作安全系数55.6107695=>==st n nBA 压杆的工作安全系数小于划定的稳固安全系数,故可以安全工作.5. 如图所示的构造中,梁AB 为No.14通俗热轧工字钢,CD 为圆截面直杆,其直径为d =20mm,二者材料均为Q235钢.构造受力如图所示,A.C.D 三处均为球铰束缚.若已知pF=25kN,1l =1.25m,2l =0.55m,s σ=235MPa.强度安全因数s n =1.45,稳固安全因数st []n =1.8.试校核此构造是否安全.解:在给定的构造中共有两个构件:梁AB ,推却拉伸与曲折的组合感化,属于强度问题;杆CD ,推却紧缩荷载,属稳固问题.现分离校核如下.(1> 大梁AB 的强度校核.大梁AB 在截面C 处的弯矩最大,该处横截面为安全截面,其上的弯矩和轴力分离为3max p 1(sin 30)(25100.5) 1.25M F l ==⨯⨯⨯°315.6310(N m)15.63(kN m)=⨯⋅=⋅3N p cos302510cos30F F ==⨯⨯°°321.6510(N)21.65(kN)=⨯= 由型钢表查得14号通俗热轧工字钢的333222102cm 10210mm 21.5cm 21.510mm z W A ==⨯==⨯由此得到33max N max 392415.631021.6510102101021.51010z M F W A σ--⨯⨯=+=+⨯⨯⨯⨯6163.210(Pa)163.2(MPa)=⨯= Q235钢的许用应力为s s 235[]162(MPa)1.45n σσ===max σ略大于[]σ,但max([])100%[]0.7%5%σσσ-⨯=<,工程上仍以为是安全的.(2> 校核压杆CD 的稳固性.由均衡方程求得压杆CD 的轴向压力为 N p p 2sin 3025(kN)CD F F F ===°因为是圆截面杆,故惯性半径为 5(mm)4I di A ===又因为两头为球铰束缚 1.0μ=,所以p 31.00.55110101510liμλλ-⨯===>=⨯这表明,压杆CD 为修长杆,故需采用式(9-7>盘算其临界应力,有222932Pcrcr 2220610(2010)41104Ed F A σλ-πππ⨯⨯π⨯⨯==⨯=⨯352.810(N)52.8(kN)=⨯=于是,压杆的工作安全因数为 cr Pcr w st w N 52.8 2.11[] 1.825CD F n n F σσ====>=这一成果解释,压杆的稳固性是安全的.上述两项盘算成果表明,全部构造的强度和稳固性都是安全的.6.一强度等级为TC13的圆松木,长6m,中径为300mm,其强度许用应力为10MPa.现将圆木用来当作起重机用的扒杆,试盘算圆木所能推却的允许压力值.解:在图示平面内,若扒杆在轴向压力的感化下掉稳,则杆的轴线将弯成半个正弦波,长度系数可取为1μ=.于是,其柔度为168010.34liμλ⨯===⨯依据80λ=,求得木压杆的稳固因数为22110.39880116565ϕλ===⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭从而可得圆木所能推却的允许压力为62[][]0.398(1010)(0.3)281.34F A ϕσπ==⨯⨯⨯⨯=(kN>假如扒杆的上端在垂直于纸面的偏向并无任何束缚,则杆在垂直于纸面的平面内掉稳时,只能视为下端固定而上端自由,即2μ=.于是有2616010.34liμλ⨯===⨯求得22280028000.109160ϕλ===62[][]0.109(1010)(0.3)774F A ϕσπ==⨯⨯⨯⨯=(kN>显然,圆木作为扒杆运用时,所能推却的允许压力应为77 kN,而不是281.3 kN.7. 如图所示,一端固定另一端自由的修长压杆,其杆长l = 2m,截面外形为矩形,b = 20 mm.h = 45 mm,材料的弹性模量 E = 200GPa .试盘算该压杆的临界力.若把截面改为 b = h =30 mm,而保持长度不变,则该压杆的临界力又为多大?解:<一).当b=20mm.h=45mm 时 <1)盘算压杆的柔度22000692.82012liμλ⨯===>123cλ=(所所以大柔度杆,可运用欧拉公式>(2>盘算截面的惯性矩由前述可知,该压杆必在xy 平面内掉稳,故盘算惯性矩4433100.312204512mm hb I y ⨯=⨯==<3)盘算临界力μ = 2,是以临界力为()()kN N l EI Fcr 70.337012210310200289222==⨯⨯⨯⨯⨯==-πμπ<二).当截面改为b = h = 30mm 时 <1)盘算压杆的柔度22000461.93012liμλ⨯===>123cλ=(所所以大柔度杆,可运用欧拉公式>(2>盘算截面的惯性矩44431075.6123012mm bh I I z y ⨯====代入欧拉公式,可得()()Nl EI F cr 8330221075.610200289222=⨯⨯⨯⨯⨯==-πμπ从以上两种情形剖析,其横截面面积相等,支承前提也雷同,但是,盘算得到的临界力后者大于前者.可见在材料用量雷同的前提下,选择适当的截面情势可以进步修长压杆的临界力.8. 图所示为两头铰支的圆形截面受压杆,用Q235钢制成,材料的弹性模量E=200Gpa,屈从点应力σs =240MPa,123c λ=,直径d=40mm,试分离盘算下面二种情形下压杆的临界力:<1)杆长l =1.5m;<2)杆长l =0.5m. 解:<1)盘算杆长l =1.2m 时的临界力 两头铰支是以 μ=1惯性半径42406410444d I d i mm d Aππ=====柔度:1150015010liμλ⨯===>123c λ=(所所以大柔度杆,可运用欧拉公式>225223.1421087.64150cr aE MP πσλ⨯⨯===2233.144087.64110.081011044cr cr cr d F A N KNπσσ⨯==⨯=⨯=⨯≈<2)盘算杆长l =0.5m 时的临界力μ=1,i =10mm柔度:15005010liμλ⨯===<123c λ=压杆为中粗杆,其临界力为222400.006822400.0068250222.95cr aMP σλ=-=-⨯=2233.1440222.95280.021028044cr cr cr d F A N kNπσσ⨯==⨯=⨯=⨯≈感激土木0906班王锦涛.刘元章同窗!声名:所有材料为本人收集整顿,仅限小我进修运用,勿做贸易用处. 声名:所有材料为本人收集整顿,仅限小我进修运用,勿做贸易用处.。

第十四章 压 杆 稳 定14.1某型柴油机的挺杆长度l =25.7cm,圆形横截面的直径d =8mm,钢材的E=210Gpa,MPa p 240=σ。
挺杆所受最大压力kN P 76.1=。
规定的稳定安全系数5~2=st n 。
试校核挺杆的稳定性。
解:计算柔度,挺杆两端可认为较支,μ=1, 1294/008.0257.01===⨯il μλ而 9.926922102401021014.31===⨯⨯⨯pE σπλ 1λλ用欧拉公式计算临界压力,校核稳定性。
kN P L EI lj 30.62644)5108(14.39222)257.01(1021014.3)(===⨯⨯⨯⨯-⨯⨯μπ 58.376.130.6===PP lj n 在2~5之间,安全。
14.4图中所示为某型飞机起落架中承受压力的斜撑杆。
杆为空心圆管,外径D=52mm ,内径d =44mm,l =950mm.材料为30CrMnS i N i 2A, 试求斜撑杆的临界压力lj P 和临界应力lj σ。
(原图见教材P173.)(GPa E MPa MPa p b 210,1200,1600===σσ)解:斜撑两端按铰支座处理,5.419.55017.0044.0052.06921012001021014.31017.095.0122412241=======+=+=⨯⨯⨯⨯pE ilmd D i σπμλλ1λλ ,可用拉欧公式计算2)044.0052.0(1040164)044.0052.0(14.3)95.01(1021014.3)(/6654012243449222mMN kN P AP lj l EI lj lj ====⨯==-⨯-⨯⨯⨯πσμπ14.5三根圆截面压杆,直径均为d=160mm,材料为A3钢,E=200Gpa,MPa s 240=σ.两端均为铰支,长度分别为l 1l 2和l 3,且m l l l 532321===。

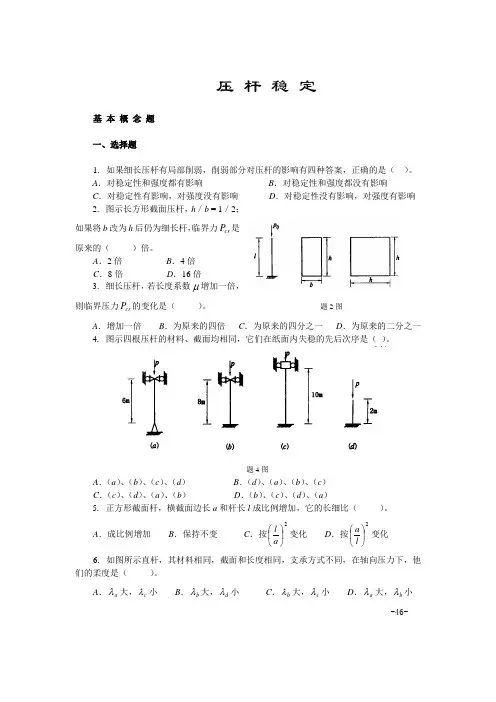
压 杆 稳 定基 本 概 念 题一、选择题1. 如果细长压杆有局部削弱,削弱部分对压杆的影响有四种答案,正确的是( )。
A .对稳定性和强度都有影响 B .对稳定性和强度都没有影响C .对稳定性有影响,对强度没有影响D .对稳定性没有影响,对强度有影响 2. 图示长方形截面压杆,h /b = 1/2;如果将b 改为h 后仍为细长杆,临界力cr P 是原来的( )倍。
A .2倍B .4倍C .8倍D .16倍 3. 细长压杆,若长度系数μ增加一倍,则临界压力cr P 的变化是( )。
题2图A .增加一倍B .为原来的四倍C .为原来的四分之一D .为原来的二分之一4. 图示四根压杆的材料、截面均相同,它们在纸面内失稳的先后次序是( )。
题4图A .(a )、(b )、(c )、(d )B .(d )、(a )、(b )、(c )C .(c )、(d )、(a )、(b )D .(b )、(c )、(d )、(a )5. 正方形截面杆,横截面边长a 和杆长l 成比例增加,它的长细比( )。
A .成比例增加B .保持不变C .按2⎪⎭⎫ ⎝⎛a l 变化D .按2⎪⎭⎫⎝⎛l a 变化6. 如图所示直杆,其材料相同,截面和长度相同,支承方式不同,在轴向压力下,他们的柔度是( )。
A .a λ大,c λ小B .b λ大,d λ小C .b λ大,c λ小D .a λ大,b λ小 -46-7. 若压杆在两个方向上的约束情况不同,且y μ>z μ。
那么该压杆的合理截面应满足的条件是( )。
A .z y I I =B .y I <z IC .y I >z ID .y z λλ=题6图8. 两压杆为管状薄壁容器式的细长杆,管两端封闭,且为铰支承。
(a )杆无内压,(b ) 杆有内压,其它条件相同。
则两杆临界应力的关系是( )。
A .()()b cr a cr σσ=B .()a cr σ>()b cr σC .()a cr σ<()b cr σD .无法比较9. 两根细长杆,直径、约束均相同,但材料不同,且212E E =,则两杆临界应力的关系是( )。




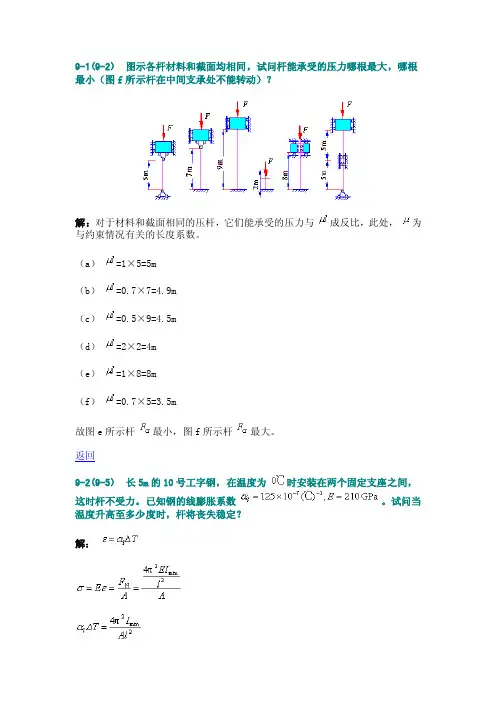
9-1(9-2)图示各杆材料和截面均相同,试问杆能承受的压力哪根最大,哪根最小(图f所示杆在中间支承处不能转动)?解:对于材料和截面相同的压杆,它们能承受的压力与成反比,此处,为与约束情况有关的长度系数。
(a)=1×5=5m(b)=0.7×7=4.9m(c)=0.5×9=4.5m(d)=2×2=4m(e)=1×8=8m(f)=0.7×5=3.5m故图e所示杆最小,图f所示杆最大。
返回9-2(9-5) 长5m的10号工字钢,在温度为时安装在两个固定支座之间,这时杆不受力。
已知钢的线膨胀系数。
试问当温度升高至多少度时,杆将丧失稳定?解:返回9-3(9-6) 两根直径为d的立柱,上、下端分别与强劲的顶、底块刚性连接,如图所示。
试根据杆端的约束条件,分析在总压力F作用下,立柱可能产生的几种失稳形态下的挠曲线形状,分别写出对应的总压力F之临界值的算式(按细长杆考虑),确定最小临界力的算式。
解:在总压力F作用下,立柱微弯时可能有下列三种情况:(a)每根立柱作为两端固定的压杆分别失稳:(b)两根立柱一起作为下端固定而上端自由的体系在自身平面内失稳失稳时整体在面内弯曲,则1,2两杆组成一组合截面。
(c)两根立柱一起作为下端固定而上端自由的体系在面外失稳故面外失稳时最小=。
返回9-4(9-7)图示结构ABCD由三根直径均为d的圆截面钢杆组成,在点B铰支,而在点A和点C固定,D为铰接点,。
若结构由于杆件在平面ABCD内弹性失稳而丧失承载能力,试确定作用于结点D处的荷载F的临界值。
解:杆DB为两端铰支,杆DA及DC为一端铰支一端固定,选取。
此结构为超静定结构,当杆DB失稳时结构仍能继续承载,直到杆AD及DC也失稳时整个结构才丧失承载能力,故返回9-5(9-9) 下端固定、上端铰支、长m的压杆,由两根10号槽钢焊接而成,如图所示,并符合钢结构设计规范中实腹式b类截面中心受压杆的要求。
第十四章 压 杆 稳 定
14.1某型柴油机的挺杆长度l =25.7cm,圆形横截面的直径d =8mm,钢材的E=210Gpa,MPa p 240=σ。
挺杆所受最大压力kN P 76.1=。
规定的稳定安全系数
5~2=st n 。
试校核挺杆的稳定性。
解:计算柔度,挺杆两端可认为较支,μ=1, 1294
/008.0257.01==
=⨯i
l μλ
而 9.926
9
22102401021014.31==
=
⨯⨯⨯p
E σπλ 1λλ
用欧拉公式计算临界压力,校核稳定性。
kN P L EI lj 30.62
644
)5108(14.3922
2
)
257.01(1021014.3)(==
=
⨯⨯
⨯⨯-⨯⨯μπ 58
.376.130
.6===
P
P lj n 在2~5之间,安全。
14.4图中所示为某型飞机起落架中承受压力的斜撑杆。
杆为空心圆管,外径D=52mm ,内径d =44mm,l =950mm.材料为30CrMnS i N i 2A, 试求斜撑杆的临界压力lj P 和临界应力
lj σ。
(原图见教材P173.)(GPa E MPa MPa p b 210,1200,1600===σσ)
解:斜撑两端按铰支座处理,
5
.419
.55017.0044.0052.06
921012001021014.31017.095.01224
1224
1
==
=
====+=
+=
⨯⨯⨯⨯p
E i
l
m
d D i σπμλλ
1λλ ,可用拉欧公式计算
2
)044.0052.0(1040164
)
044.0052.0(14.3)
95.01(1021014.3)(/665401224
3
4
49
222m
MN kN P A
P lj l EI lj lj ==
=
=⨯=
=
-⨯-⨯⨯⨯π
σμπ
14.5三根圆截面压杆,直径均为d=160mm,材料为A3钢,E=200Gpa,MPa s 240=σ.两端均为铰支,长度分别为l 1l 2和l 3,且m l l l 532321===。
试求各杆的临界压力lj P 。
解:对于A3钢 1.57,10012
.1240
3042===≈--b a s σλλ 分别计算三杆的柔度
3
.31)3(5.62)2(125)1(4
/16.025.114/16.05.214/16.05
13
32
21
1==
=
======⨯⨯⨯i l i l i l μμμλλλ
杆1 kN P l EI lj 254064
16
.014.3)51(1020014.3)()1(4
2
9
22
12=⨯=
=
⨯⨯⨯⨯μπ 杆2 kN A b a P lj 470016.010)5.6212.1304()(2414
.36)2(=⨯⨯⨯⨯-=-=λ 杆3 kN A P s lj 482016.010*******.36)3(=⨯⨯⨯==σ
14.10在图示铰接杆系ABC 中,AB 和BC 皆为细长压杆,且截面相同,材料一样。
若因在ABC 平面内失稳而破坏,并规定2
0πθ<
<,试确定P 为最大值时的θ角。
解:设AB 、BC 杆的压力分别N 1,N 2
θθsin ,cos 21P N P N ==或12,P tg N N ==θ设AB 杆长为l 1,则BC 杆长θtg l l 12=β
ππ2
122
21
2
21,tg P l EI lj l EI lj lj P P =
==
只有当N 1和 N 2都达到临界压时,P 才最大,把上两式代入
)
(2
1
2121
21
2βθβ
θβ
c t g tg ctg tg tg P P N N lj lj -=∴==
=
=
14.13蒸气机车的连杆如图所示,截面为工字形,材料为A3钢。
连杆所受最大轴向压力为465kN.连杆在摆动平面(xy 平面)内发生弯曲时,两端可认为铰支;而在与摆动平面垂直的xz 平面内发生弯曲时,两端可认为是固定支座。
试确定其工作安全系数。
(原图见教材P176.)
解:先计算横截面的几何性质
4
612014
.0085.012
096.0)085.014.0(4
512085
.0082.012
14.0096.02
31007.41078.11047.6082.0085.0096.0140.03
3
3
3
m I m I m A y z -⨯⨯--⨯⨯-⨯=+=
⨯=-=
⨯=⨯-⨯=
在xy 平面内失稳
在xy 平面内失稳 和λ2很接近,已属强度问题,不用再算。
14.15某厂自制的简易起重机如图所示,其压杆BD 为20号槽钢,材料为A3钢,起重
机的最大是P=40kN.若规定的稳定安全系数为5=ωn ,试校核BD 杆的稳定性。
解:对A 点取矩计算DB 杆中的压力N
kN N N 107,2405.130sin =⨯=⨯︒
27.315201047.6102356.610.590525.04651520
3612
.1235
3040525.010.3110
47.61078.135====⨯⨯⨯====<======--⨯⨯⨯--P P s lj i l z A I z lj z z
n kN A P m
i σλλμ8
.61,02512.0251.010
.35.0=====⨯y i l y y
y m A
I i μλ
查槽钢表得m i m A y 0209.0,1083.3224=⨯=-, DB 杆长m l 73.1866
.05.1==
为柔度为
1008.820209
.073.11<==
⨯λ
用中等柔度杆的公式计算临界应力
5
48.6693102111083.32/2118.8212.130412.130********
4
2
>===
=⨯⨯⨯===⨯-=-=-P
P lj lj lj lj n kN A P m
MN σλσ
安全.
14.16 10号工字梁的C 端固定,A 端铰支于空心钢管AB 上。
钢管的内径和外径分别30mm 和40mm ,B 端亦为铰支。
梁及钢管同为A3钢。
当重为300N 的重物落于梁的A 端时,试校核AB 杆的稳定性。
规定稳定安全系数5.2=ωn 。
解:先把重量300N 静止放在A 处,计算AB 杆中承受的压力及A 处的垂位移。
AC 梁 查表得4
8
10245m I -⨯=
N m EI
l /1084.15
10245102003338
93
3-⨯⨯⨯⨯⨯==
-
AB 杆
N
m m A EA
L /1082.11050.5)03.004.0(8
1024510200224
2244
9
-⨯⨯⨯-⨯==
⨯=-=-π
设AB 杆受到压力N ,由A 处垂直位移, 可得如下关系式
EA
NL EI
l N =
-3
)300( 或
N N 8
5
1082.1)300(1084.1--⨯=-⨯
算出 N N N 3007.299≈=
A 处垂直位移 m l 68
1046.510
82.1300--⨯=⨯⨯=∆
代入垂直下落撞击的动载系数公式 5.6111116
1046.501
.022=++=+
+=-⨯⨯∆j
h d K AB 杆受的动压力为 kN P K P j d d 5.183005.61=⨯== 再计算AB 杆的临界压力
160
0125.003.004.00125
.021224
1224
1
===+=
+=
⨯λm
d D i
用欧拉公式计算
5
.229.23.42)03.004.0(5
.183.42446414.3)21(1020014.32
9
2<==
=
=-⨯=⨯⨯⨯P
P lj lj
n kN
P
不安全。
1.5m
0.5m。