当前位置：文档之家 › 绝对值三角不等式 课件

绝对值三角不等式 课件

  • 格式：ppt
  • 大小：4.19 MB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

绝对值三角不等式 课件

绝对值三角不等式 课件

证明:∵m 等于|a|,|b|和 1 中最大的一个,|x|>m,
|| > ≥ ||
|| > ||,




||
||
>

≥
||
∴
⇒
∴ + 2 ≤
+ 2 = +
2




||
|| > |b|.
|| > ≥ 1
||
2
|| ||
<
+ 2 =2.故原不等式成立.
2
||
||
∴-4≤y≤4.
∴yma x=4,y min =-4.
迁移与应用
如果关于 x 的不等式|x-3|+|x-4|<a 的解集为空集,求参数 a
的取值范围.
解:只要 a 不大于|x-3|+|x-4|的最小值,则|x-3|+|x-4|<a 的解集
为空集,而|x-3|+|x-4|=|x-3|+|4-x|≥|x-3+4-x|=1,
=|(x-a)(x+a-1)|
=|x-a||x+a-1|
<|x+a-1|
=|Байду номын сангаас-a+2a-1|
≤|x-a|+|2a-1|
<1+|2a|+1
=2(|a|+1),
∴|f(x)-f(a)|<2(|a|+1).
迁移与应用
已知 f(x)=x2 -2x+7,且|x-m|<3,求证:|f(x)-f(m)|<6|m|+15.

绝对值三角不等式 课件

绝对值三角不等式 课件

2．绝对值三角不等式 定理 1：如果 a，b 是实数，则|a＋b|≤|a|＋|b|，当且仅当 ___a_b_≥__0___时，等号成立． 推论 1：如果 a，b 是实数，那么|a|－|b|≤|a－b|≤|a|＋|b|. 推论 2：如果 a，b 是实数，那么|a|－|b|≤|a＋b|≤|a|＋|b|. 定理 2：如果 a，b，c 是实数，那么|a－c|≤|a－b|＋|b－c|，当 且仅当___(a_－__b_)_(_b_－__c_)≥__0____时，等号成立．
利用绝对值三角不等式证明不等式 已知 f(x)＝x2－2x＋7，且|x－m|＜3，求证：|f(x)－f(m)| ＜6|m|＋15.
【证明】 |f(x)－f(m)|＝|(x－m)(x＋m－2)| ＝|x－m|·|x＋m－2|＜3|x＋m－2| ≤3(|x|＋|m|＋2)． 又|x－m|＜3， 所以－3＋m＜x＜3＋m. 所以 3(|x|＋|m|＋2)＜3(3＋|m|＋|m|＋2) ＝6|m|＋15. 所以|f(x)－f(m)|＜6|m|＋15.
利用绝对值三角不等式求函数的最值 (1)求函数 f(x)＝|x－1|＋|x＋1|的最小值； (2)求函数 f(x)＝|x－1|－|x＋1|的值域． 【解】 (1)因为|x－1|＋|x＋1|＝|1－x|＋|x＋1|≥|1－x＋x＋1| ＝2，当且仅当(1－x)(1＋x)≥0， 即－1≤x≤1 时取等号， 所以当－1≤x≤1 时，函数 f(x)＝|x－1|＋|x＋1|取得最小值 2.
(2)当 a＝0 时，f(x)＝x； 当－1≤x≤1 时，f(x)的最大值为 f(1)＝1， 不满足题设条件，所以 a≠0. 又 f(1)＝a＋1－a＝1，f(－1)＝a－1－a＝－1， 故 f(±1)均不是最大值． 所以 f(x)的最大值187应在其对称轴上顶点位置取得， 所以 a＜0.

2.1绝对值三角不等式课件

2.1绝对值三角不等式课件

(3)如果ab=0,则a=0或b=0 易得: |a+b|=|a|+|b|
综上所述,可得:
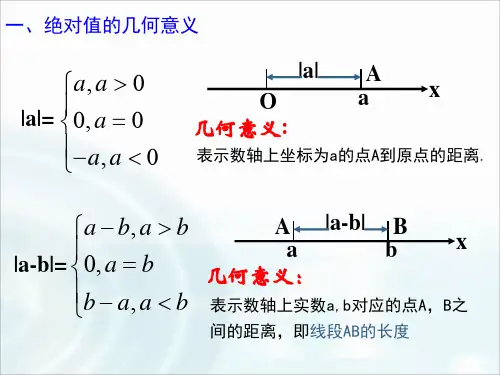
定理1: 如果a,b是实数, 则 |a+b||a|+|b|, 当且仅当ab0时,等号成立.
如果把定理1中的实数a,b分别换为向量 a, b,能得
出什么结果?
定理1的几何意义
在不等式|a+b||a|+|b|中, 绝对值三角不等式
当且仅当(a-b)(b-c)0时,等号成立.
定理2的几何意义
在数轴上,a,b,c所对应的点分别为A,B,C,
AB C x a• b• c•
A
CB x
• •a
•c
•
b
B
AC x
b• •
a• •c
(1)当点B在点A,C之时, |a-c|=|a-b|+|b-c|
(2)当点B在点A,C之外时, |a-c|<|a-b|+|b-c|
思考题：
S(x)=2(|x-10|+|x-20|)，xk 1,k 10
若函数s(x)能取到最小值20，求k的范围。
作业
P20: 1,2,3,4,
谢谢聆听
THANK YOU FOR YOUR
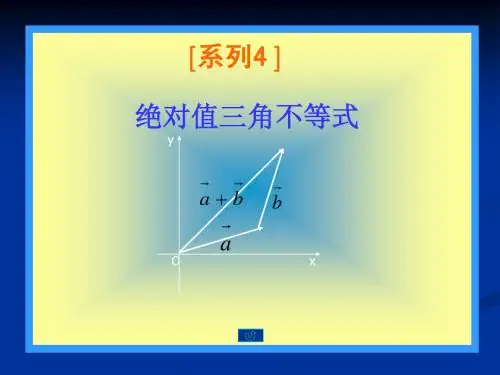
用向量 a、b 分别替换实数a,b,
y
当向量 a b 不共线时,则由向量加法的 a b
三角形法则,
b
向量 a、b、a+b 构成三角形,
ax
O
故可得向量形式的不等式:
|a+b|<|a|+|b|
当向量a b 共线呢?
故该定理的几何意义为:
三角形的两边之和大于第三边.
定理1: 如果a,b是实数, 则 |a+b||a|+|b|, 当且仅当ab0时,等号成立.

绝对值三角不等式 课件

绝对值三角不等式 课件
分析：将2x＋3y－2a－3b写成2(x－a)＋3(y－b)的 形式后利用定理1和不等式性质证明．
证明：|2x＋3y－2a－3b|＝|2(x－a)＋3(y－b)| ≤|2(x－a)|＋|3(y－b)| ＝2|x－a|＋3|y－b|
＜2×4ε＋3×6ε＝ε.
某段铁路线上依次有A、B、C三站，AB＝5 km，BC＝3 km.在列车运行时刻表上，规定列车8时整从A 站出发，8时07分到达B站并停车1分钟，8时12分到达C 站．在实际运行中，假设列车从A站正点发车在B站停留1分 钟，并在行驶时以同一速度v km/h正点发车，在B站停留1 分钟，并在行驶时以同一速度v km/h匀速行驶．列车从A站 到达某站的时间与时刻表上相应时间之差的绝对值称为列 车在该站的运行误差．
绝对值三角不等式
1．解在绝对值符号内含有未知数的不等式(也称绝对 值不等式)，关键在于去掉绝对值符号，化成普通的不等 式．主要的依据是绝对值的意义．
在数轴上，一个点到原点的距离称为这个点所表示的 数的绝对值．
x，如果x＞0 即|x|＝0，如果x＝0 .
－x，如果x＜0
练习1：求下列各数的绝对值：
(1)3 (2)－8 (3)0
①当 0＜v≤3700时，(*)式变形为30v0－7＋48v0－11≤2， 解得 39≤v≤3700； ②当3700＜v≤41810时，(*)式变形为
300 480
解得 39≤v≤3700； ②当3700＜v≤41810时，(*)式变形为 7－3v00＋4v80－11≤2， 解得3700＜v≤41810； ③当 v＞41810时，(*)式变形为 7－3v00＋11－4v80≤2， 解得41810＜v≤1495.
若|a－b|＞c，|b－c|＜a，求证：c＜a. 证明：由|a－b|＞c，及|b－c|＜a得 c－a＜|a－b|－|b－c|≤|(a－b)＋(b－c)| ＝|a－c|＝|c－a|. 由c－a＜|c－a|知c－a＜0，故c＜a.

绝对值三角不等式ppt课件

绝对值三角不等式ppt课件
1、绝对值三角不等式
复习回顾：
实数 a 的绝对值的意义:
a (a 0) ⑴ a 0 (a 0) ;（定义）
，a (a 0)
注：绝对值的几何意义:
a
⑴ a 表示实数 a 在数轴上对应的点与原点的距离;
O
A
(2) a b 表示数轴上的实数 源自 对应的点 A 与实数 b 对应的点 B 之间的距离.如图:
应用一： 证明不等式成立
定理2 如果a、b、c是实数,
-
-------那么|a-c|≤|a-b|+|b-c|
-------当且仅当(a-b)(b-c) ≥0时,等号成立.
证明：由绝对值三角不 等式
a b b c (a b) (b c) a c
ab bc ac
当且仅当(a b)(b c) 0时等号成立
ab a b (当且仅当ab 0时等号成立 )
② a b与a b之间有什么关系？
oa b
ba o
b
oa
ao
b
当a 0,b 0时，a b a b
当a 0,b 0时，a b a b 当a 0,b 0时，a b a b 当a 0,b 0时，a b a b
当a b 0时，a b a b
a b ab (当且仅当ab 0时等号成立) ab a b (当且仅当ab 0时等号成立 )
绝对值三角不等式：
a b ab a b
绝对值三角不等式： 若 a, b 是实数，则 a b a b a b
如果把 a, b 换为向量 a, b ，根据向量加法的三 角形法则,易知 a b ≤ a b .(同向时取等号)
解：由绝对值三角不等 式
x 3 x 9 (x 3) (x 9) 6 求 当且仅当(x 3)(x 9) 0

绝对值三角不等式课件

绝对值三角不等式课件

【防范措施】 正确求参数的取值范围 应用绝对值三角不等式求参数的取值范围是重点考查题型 ,解 答本题的关键是,正确应用绝对值三角不等式求出最值,再根 据题意,求出参数的取值范围,如本例关键是对条件关于x的不 等式|x-3|+|x-4|>a的解集不是R的正确理解.
【类题试解】若不等式|x-1|+|x+3|≥a恒成立，则a的取值范 围是______. 【解析】因为a≤|x-1|+|x+3|恒成立，故a小于等于 |x-1|+|x+3|中的最小值， 又|x-1|+|x+3|=|1-x|+|x+3|≥|1-x+x+3|=4, 故a≤4,即a的取值范围是(-≦,4］. 答案：(-≦,4］
2.函数y=|x－1|+|x－5|的最小值为______,此时x的取值范围 是_____. 【解析】|x－1|+|x－5|=|x－1|+|5－x| ≥|x－1+5－x|=4， 当且仅当(x－1)(5－x)≥0, 即1≤x≤5时等号成立. 答案：4 ［1,5］
类型 三
含绝对值不等式的证明
【典型例题】
(x－4)(x－ 3) 0， 当且仅当 3|， | x－4 || x－
即x≤3时, f(x)取最大值1.
【变式训练】1.若不等式｜x-a｜+｜x-2｜≥1对任意的实数x均成立， 则实数a的取值范围是_____.
2.函数y=|x－1|+|x－5|的最小值为______,此时x的取值范围是_____.
【变式训练】若不等式｜x-a｜+｜x-2｜≥1对任意的实数x均 成立，则实数a的取值范围是_____. 【解析】|x-a|+|x-2|≥1恒成立， 绝对值不等式的几何意义：数轴上 x到a与x到2的距离之和的 最小值为1. 当a=1或a=3时，对任意的x距离和的最小值为1，所以当a≤1 或a≥3时该不等式恒成立, a∈(-≦,1］∪［3,+≦). 答案：(-≦,1］∪［3,+≦)

5.2绝对值三角不等式A 课件(人教A版选修4-5)

5.2绝对值三角不等式A 课件(人教A版选修4-5)

70
60
s x = 2 x-10 + x-20
50
40
30
20
10
-60
-40
-20
10
20
40
60
80
100
-10
-20
-30
x
向量形式的不等式
a b a b
当且仅当
a
与
b 同向 时，等号成立。
由于定理1与三角形之间的这种联系，我们称其中的不等 式为绝对值三角不等式。
知识推广
如果将定理1中的实数a , b改为复数 不等式仍成立吗？
z1, z2
，
z1 z2 z1 z2
练习
1、如果a, b, c是实数，证明
例2
两个施工队分别被安排在公路沿线的两个地点施工， 这两个地点分别位于公路路牌的第10km和第20km 处。现要在公路沿线建两个施工队的共同临时生活区， 每个施工队每天在生活区和施工地点之间往返一次。 要使两个施工队每天往返的路程之和最小，生活区应 该建于何处？
分析：如果生活区建于公路路牌的第xkm处，两个施工队每天往返的路程
a, b ，
能得出什么结果？你能解释它的几何意义吗？
迁移类比
当向量
a b a b
当向量
a, b
不共线时，
y
ab
O
同向：a b a b 反向： a b a b
a, b
共线时，
a
b
（定理1的变形）
4、推论：
a c a b bc
a , b, c R
a b a b a b a b c a b c （定理1的推广）

绝对值三角不等式 课件

绝对值三角不等式 课件

1．将文字语言“m等于|a|，|b|,1中最大的一个”转化为 符号语言“m≥|a|，m≥|b|，m≥1”是证明本题的关键．
2．运用绝对值不等式的性质证明不等式时，要注意放 缩的方向和“尺度”，切忌放缩过度．
1．本题求解的关键在于|a|－|b|≤|a－b|与|a|＋|b|≥|a＋b| 的理解和应用．
2．解决此类问题应从两个方向看推出关系来进行求 解．
条件不变，试求： (1)||a|a|－ －b|b|||＜1成立的充要条件； (2)|a|a|＋ ＋b|b||＞1成立的充要条件． 【解】 (1)因为ab＜0⇔||a|－|b||＜|a－b|⇔|a|a|－ －b|b||＜1，
含绝对值不等式的证明
设m等于|a|，|b|和1中最大的一个，当|x|>m时， 求证：|ax＋xb2|<2.
【思路探究】 不管|a|，|b|,1的大小，总有m≥|a|， m≥|b|，m≥1，然后利用绝对值不等式的性质证明．
【自主解答】 依题意m≥|a|，m≥|b|，m≥1， 又|x|>m， ∴|x|>|a|，|x|>|b|，|x|>1，从而|x|2>|b|. 因此|ax＋xb2|≤|ax|＋|xb2| ＝||ax||＋||xb2||<||xx||＋||xx|22|＝2， 即|ax＋xb2|<2.
2．你能给出定理2的几何解释吗？
【提示】 在数轴上，a，b，c的对应的点分别为A， B，C.当点B在点A，C之间时，|a－c|＝|a－b|＋|b－c|；当点B 不在点A，C之间时，|a－c|<|a－b|＋|b－c|.
绝对值不等式的理解与应用
已知a，b∈R，则有 (1)|a|a|－ －b|b||≤1成立的充要条件是________； (2)|a|a|＋ ＋b|b||≥1成立的充要条件是________． 【思路探究】 利用绝对值三角不等式定理分别求解．

绝对值三角不等式课件

绝对值三角不等式课件

与其他数学知识的结合
绝对值三角不等式与函数
绝对值三角不等式可以应用于函数的性质和图像分析，例如判断函数的单调性、求函数 的极值等。
绝对值三角不等式与数列
在数列的项间关系和求和问题中，绝对值三角不等式可以用来处理带有绝对值的项，简 化计算过程。
在实际生活中的应用
交通规划
在交通路线的规划中，绝对值三 角不等式可以用于计算最短路径 ，优化交通网络。
答案与解析
答案
$(1,0)$ 或 $(0,1)$ 或 $( - 1, - 1)$ 或 $(1, - 1)$
VS
解析
根据绝对值的性质，将不等式转化为 $2a = 2(a + 1)$，解得 $a = -1$，再代入原 式得到 $(b, a) = (0, -1)$ 或 $(1, -1)$。
THANKS
在数列求和中的应用
总结词
绝对值三角不等式可以用于简化数列求和的过程，特别是对于一 些项之间存在一定关系的数列。
详细描述
通过利用绝对值三角不等式，可以将数列中的绝对值项进行放缩， 从而将数列求和问题转化为更容易处理的形式。
举例
例如，对于数列 { a_n }，其中 a_n = |a_(n-1) - a_(n-2)|，可以利 用绝对值三角不等式得出其求和结果。
03
绝对值三角不等式的应用
在不等式证明中的应用
总结词
绝对值三角不等式是证明不等式 的重要工具之一，它可以用于简
化不等式的证明过程。
详细描述
绝对值三角不等式可以用来证明 一些复杂的不等式，通过将不等 式中的绝对值项进行放缩，将其 转化为更容易处理的形式，从而
简化证明过程。
举例
例如，要证明 |a+b| ≤ |a| + |b| ，可以利用绝对值三角不等式直

绝对值三角不等式及其应用ppt课件

绝对值三角不等式及其应用ppt课件
当且仅当(a-b)(b-c)≥0时，等号成立。
7
绝对值三角不等式的应用
8
例1 已知ε> 0,|x - a|<ε,|y - b|<ε,
求 证: |2x + 3y - 2a - 3b|< 5ε
证明： |2x+3y-2a-3b|=|(2x-2a)+(3y-3b)| =|2(x-a)+3(y-b)|≤|2(x-a)|+|3(y-b)| =2|x-a|+3|y-b|<2ε +3ε=5ε.
14
（1）证明 ∵M≥|f（-1）|=|1-a+b|，
M≥|f（1）|=|1+a+b|，
2M≥|1-a+b|+|1+a+b|
≥|（1-a+b）+（1+a+b）|=2|1+b|，
∴M≥|1+b|.
（2）证明 依题意，M≥|f（-1）|，
M≥|f（0）|，M≥|f（1）|，
又f（-1）=|1-a+b|，
所以 |2x+3y-2a-3b|<5ε.
9
例2:两个施工队分别被安排在公路沿线的两个地点 施工,这两个地点分别位于公路路牌的第10km和 第20km处.现要在公路沿线建两个施工队的共同 临时生活区,每个施工队每天在生活区和施工地点 之间往返一次,要使两个施工队每天往返的路程 之和最小,生活区应该建于何处?
S(x)=2(|x-10|+|x-20|)
S 60
S(x)=2(|x-10|+|x-20|)
|x-10|+|x-20|=|x-10|+|20-x| 40
|(x-10)+(20-x)|=10

绝对值三角不等式 课件

绝对值三角不等式 课件

[例2] (1)求函数y＝|x－3|－|x＋1|的最大值和最小值． (2)设a∈R，函数f(x)＝ax2＋x－a(－1≤x≤1)． 若|a|≤1，求|f(x)|的最大值． [思路点拨] 利用绝对值三角不等式或函数思想方法可 求解．
[解] (1)法一：||x－3|－|x＋1|| ≤|(x－3)－(x＋1)|＝4， ∴－4≤|x－3|－|x＋1|≤4. ∴ymax＝4，ymin＝－4.
4．求函数f(x)＝|x－1|＋|x＋1|的最小值． 解：∵|x－1|＋|x＋1|＝|1－x|＋|x＋1|≥ |1－x＋x＋1|＝2， 当且仅当(1－x)(1＋x)≥0， 即－1≤x≤1时取等号． ∴当－1≤x≤1时，函数f(x)＝|x－1|＋|x＋1| 取得最小值2.
5．若对任意实数，不等式|x＋1|－|x－2|>a恒成立，求a的 取值范围． 解：a<|x＋1|－|x－2|对任意实数恒成立， ∴a<[|x＋1|－|x－2|]min. ∵||x＋1|－|x－2||≤|(x＋1)－(x－2)|＝3， ∴－3≤|x＋1|－|x－2|≤3. ∴[|x＋1|－|x－2|]min＝－3. ∴a<－3.即a的取值范围为(－∞，－3)．
绝对值三角不等式
绝对值三角不等式 (1)定理1：如果a，b是实数，则|a＋b|≤|a|＋|b|，当且仅 当 ab≥0 时，等号成立． 几何解释：用向量a，b分别替换a，b. ①当a与b不共线时，有|a＋b|<|a|＋|b|，其几何意义为： 三角形的两边之和大于第三边 ． ②若a，b共线，当a与b 同向时，|a＋b|＝|a|＋|b|，当a与b 反向 时，|a＋b|<|a|＋|b|. 由于定理1与三角形之间的这种联系，故称此不等式为绝 对值三角不等式． ③定理1的推广：如果a，b是实数，则||a|－|b||≤|a±b| ≤|a|＋|b|.

1.5绝对值的三角不等式1课件人教新课标B版

1.5绝对值的三角不等式1课件人教新课标B版
解析:|x-y|=|(x-a)+(a-y)|≤|x-a|+|y-a|<h+k.
答案:C
2
)
3
4
5
1
2
3
4
5
2已知h>0,a,b∈R,命题甲:|a-b|<2h;命题乙:|a-1|<h,且|b-1|<h,则甲
是乙的(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分又不必要条件
解析:显然a与b的距离可以很近,满足|a-b|<2h,但此时a,b与1的距离
同.
(4)根据定理及推论易得:||a|-|b||≤|a±b|≤|a|+|b|.
【做一做1-1】 已知实数a,b满足ab<0,则有 (
A.|a-b|<|a|+|b|
B.|a+b|>|a|-|b|
C.|a+b|<|a-b|
D.|a-b|<||a|-|b||
解析:∵ab<0,∴a,b异号,
∴|a-b|>|a+b|成立.
答案:C
)
【做一做1-2】 若|a-c|<b,则下列不等式不成立的是 (
)
A.|a|<|b|+|c| B.|c|<|a|+|b|
C.b>||c|-|a|| D.b<|a|-|c|
解析:由|a-c|<b,可知b>0,∴b=|b|.
∵|a|-|c|≤|a-c|,
∴|a|-|c|<b,则|a|<b+|c|=|b|+|c|,
答案:D
2.定理2(三个实数的绝对值的三角不等式)

绝对值三角不等式课件

绝对值三角不等式课件
题中也有着重要的应用。例如，在求函数的最 小值或最大值时，可以利用绝对值三角不等式对函数进行放缩，从而得到函数的 最值。
在应用绝对值三角不等式求函数最值时，需要注意处理函数定义域内的特殊情况 ，以及根据函数的性质选择合适的放缩方法。
在数列求和中的应用
总结词
绝对值总是非负的，即对于任何实数x，都有|x| ≥ 0。
详细描述
绝对值表示一个数值不考虑正负的大小，因此无论x是正数、负数还是零，其绝 对值都是非负的。这是绝对值的基本性质之一，也是理解绝对值三角不等式的基 础。
绝对值的传递性
总结词
如果a ≥ b且b ≥ c，那么a ≥ c。
详细描述
绝对值的传递性是指，如果一个数a大于或等于另一个数b，而这个数b又大于或等于数c，那么这个数a必然大于 或等于数c。这个性质在数学中非常重要，也是绝对值三角不等式推导的基础。
绝对值三角不等式在数列求和问题中也有着重要的应用。例 如，在求解数列的项的和或前n项和时，可以利用绝对值三角 不等式对数列进行放缩，从而得到数列的和的上下界。
在应用绝对值三角不等式求数列和时，需要注意处理数列的 项的正负交替出现的情况，以及根据数列的性质选择合适的 放缩方法。
05
绝对值三角不等式的变式
绝对值三角不等式的几何意义
几何解释
绝对值三角不等式表示在数轴上 任意两点A和B的距离之和，等于 它们到原点O的距离之和，即 |OA|+|OB|=|AB|。
应用举例
在解决实际问题时，如测量、定 位、计算距离等问题，可以利用 绝对值三角不等式来求解。
02
绝对值三角不等式的性质
Chapter
绝对值的非负性
绝对值的可加性
总结词
对于任意实数a和b，有|a + b| ≤ |a| + |b|。

数学课件：1.4 绝对值的三角不等式

数学课件：1.4 绝对值的三角不等式
∴-4≤y≤4.∴ymax=4,ymin=-4.
题型一 题型二 题型三
反思对于含有两个绝对值以上的代数式,通常利用分段讨论的方 法转化为分段函数,进而利用分段函数的性质解决相应的问题.利 用含绝对值不等式的性质定理进行“放缩”,有时也能产生比较好的 效果,但这需要准确地处理“数”的差或和,以达到所需要的结果.
故选项A成立. 同理,由|c|-|a|≤|a-c|,得|c|-|a|<b,
∴|c|<|a|+b=|a|+|b|.故选项B成立.
而由选项A成立,得|c|-|a|>-|b|,由选项B成立,得|c|-|a|<|b|,
∴-|b|<|c|-|a|<|b|,
即||c|-|a||<|b|=b.故选项C成立. 由选项A成立知选项D不成立,故选D. 答案:D
题型一 题型二 题型三
利用绝对值的三角不等式求函数的最值
【例2】 求函数y=|x-3|-|x+1|的最大值和最小值. 分析:若把x-3,x+1看作两个实数,则所给的代数式符合两个数绝 对值的差的形式,因而可以联想到两个数和(差)的绝对值与两个数 绝对值的和(差)之间的关系,进而可转化求解.另一种思路是:含有 这种绝对值函数式表示的是分段函数,所以也可以视为是分段函数 求最值.
12345
5已知|x-a|<1,求证:|a|-1<|x|<|a|+1.
证明:∵|x-a|=|a-x|,根据绝对值不等式定理可得||x|-|a||≤|x-a|, ∴|x|-|a|≤|x-a|<1或|a|-|x|≤|x-a|<1, ∴|x|<|a|+1或|a|-1<|x|. ∴|a|-1<|x|<|a|+1.

5.2绝对值三角不等式 课件(人教A版选修4-5)

5.2绝对值三角不等式 课件(人教A版选修4-5)

a<0,b<0 a+b x a O b |a+b|=|a|+|b|
x
a<0,b>0 a+b x a O b |a+b|<|a|+|b|
易得: |a+b|=|a|+|b|
(3)如果ab=0,则a=0或b=0
综上所述,可得:
定理1: 如果a,b是实数,则 |a+b||a|+|b| 当且仅当ab0时,等号成立. 如果把定理1中的实数a,b分别换 为向量
同学们能再探究一下|a|-|b|与|a+b|, |a|+|b|与 |a-b|, |a|-|b|与|a-b|等之间的关系? 如: 如果a,b是实数,则 |a|-|b||a-b||a|+|b| 再如: 如果a,b,c是实数,则 |a-c||a-b|+|b-c|
当且仅当(a-b)(b-c)0时,等号成立.
类比不等式基本性质的得出过程，同学们认为
可以怎样提出关于绝对值不等式性质的猜想？
从“运算”的角度考察绝对值不等式。 如：对于实数a,b，可以考察|a|, |b|, |a+b|, |a-b|, |a|+|b|, |a|-|b| 等之间的关系。
用恰当的方法在数轴上把|a|, |b|, |a+b|表示出来，
S(x)=2(|x-10|+|x-20|) |x-10|+|x-20|=|x-10|+|20-x| |(x-10)+(20-x)|=10 当且仅当(x-10)(20-x)0时 取等号. 又解不等式:
S 60 40 20
S(x)=2(|x-10|+|x-20|)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例 2 设 ε＞0，|x－a|＜ε4 ，|y－b|＜ε6 .
求证：|2x＋3y－2a－3b|＜ε. 分析：将 2x＋3y－2a－3b 写成 2(x－a)＋3(y－b)的形式后利用
定理 1 和不等式性质证明．
证明：|2x＋3y－2a－3b|＝|2(x－a)＋3(y－b)|≤ |2(x－a)|＋|3(y－b)|＝2|x－a|＋3|y－b|＜ 2×ε4 ＋3×ε6 ＝ε.
证明：|xy－ab|＝|xy－bx＋bx－ab| ＝|x(y－b)＋b(x－a)|≤|x(y－b)|＋|b(x－a)| ≤|x||y－b|＋|b||x－a| <A·2ε＋A·2ε＝Aε. 所以有|xy－ab|<Aε.
2．已知函数f(x)＝x2－x＋13，|x－a|<1，求证： |f(x)－f(a)|<2(|a|＋1)．
例 3 设 m 等于|a|、|b|和 1 中最大的一个．当|x|>m a b
时，求证：x＋x2<2.
分析：本题的关键是对题设条件的理解和运用，|a|、 |b|和 1 这三个数中哪一个最大．如果两两比较大小，将 十分复杂，我们可得到一个重要的信息：m≥|a|，m≥|b|， m≥1.
证明：∵m 等于|a|，|b|和 1 中最大的一个，|x|>m，
总之，恒有|a|＋|b|≤16. 而a＝8，b＝－8时， 满足|a＋b＋1|＝1，|a＋2b＋4|＝4，且|a|＋|b|＝16. 因此|a|＋|b|的最大值为16.
3．求函数y＝|x－3|－|x＋1|的最大值和最小值．
分析：若把x－3，x＋1看作两个实数，则所给的代数 式符合两个数绝对值的差的形式，因而可以联想到两个数 和(差)的绝对值与两个数绝对值的和(差)之间的关系，进而 可转化求解，另一思维是：含有这种绝对值函数式表示的 是分段函数，所以也可以视为是分段函数求最值．
解析：方法一 ∵||x－3|－|x＋1||≤|(x－3)－(x＋1)|＝ 4，
∴－4≤|x－3|－|x＋1|≤4.
∴ymax＝4，ymin＝－4.
方法二 把函数看作分段函数．1
4，x<－1， y＝|x－3|－|x＋1|＝2－2x，－1≤x≤3，
－4，x>3.
∴－4≤y≤4，∴ymax＝4，ymin＝－4. 点评：对于含有两个以上绝对值的代数式，通常利用分 段讨论的方法转化为分段函数，进而利用分段函数的性质解 决相应问题．利用含绝对值不等式的性质定理进行“放缩”， 有时也能产生比较好的效果，但这需要准确地处理“数”的 差或和，以达到所0.
3
8
0
2．证明一个含有绝对值的不等式成立，除了要应用一般不等式
的基本性质之外，经常还要用到关于绝对值的和、差、积、商的性质：
(1)|a|＋|b|≥|a＋b|；
(2)|a|－|b|≤|a＋b|；
(3)|a|·|b|＝|a·b|；
(4)||ab||＝ab(b≠0)．
思考2 说出下列不等式等号成立的条件：
(1)|a|＋|b|≥|a＋b|； (2)|a|－|b|≤|a＋b|； (3)|a－c|≤|a－b|＋|b－c|.
(1)等号成立的条件是：ab≥0； (2)等号成立的条件是：ab≤0且a≥b. (3)等号成立的条件是：(a－b)(b－c)≥0
3．含有绝对值的不等式的证明中，常常利用|a|≥a， |a|≥－a及绝对值的和的性质．
绝对值三角不等式
1．研究在绝对值符号内含有未知数的不等式(也 称绝对值不等式)，关键在于去掉绝对值符号，化成普 通的不等式．主要的依据是绝对值的意义．
在数轴上，一个点到原点的距离称为这个点所表 示的数的绝对值．
即|x|＝ x0，，xx＞＝00，， －x，x＜0.
思考1 求下列各数的绝对值：
(1)3；
∴||xx||>>mm≥ ≥||ba||， ， |x|>m≥1
|x|>|a|， ⇒ |x|2>|b|.
a b a b |a| |b| |x| |x|2 ∴x＋x2≤x＋x2＝|x|＋|x|2<|x|＋|x|2＝2，
故原不等式成立．
1．设 A、ε>0，|x－a|<ε2 ，|y－b|<ε2 ，|b|≤A，|x|≤A，求 证：|xy－ab|<Aε.
证明：|f(x)－f(a)|＝|x2－x＋13－(a2－a＋13)| ＝|x2－a2－x＋a|＝|(x－a)(x＋a－1)| ＝|x－a||x＋a－1|<|x＋a－1| ＝|x－a＋2a－1|≤|x－a|＋|2a－1| <1＋|2a|＋1＝2(|a|＋1)． ∴|f(x)－f(a)|<2(|a|＋1)．
题型二 利用绝对值三角不等式求最值
例2 设a，b∈R且|a＋b＋1|≤1，|a＋2b＋4|≤4， 求|a|＋|b|的最大值．
解析：|a＋b|＝|(a＋b＋1)－1|≤|a＋b＋1|＋|－1|≤1
＋1＝2，
|a－b|＝|3(a＋b＋1)－2(a＋2b＋4)＋5|≤3|a＋b＋1|＋ 2|a＋2b＋4|＋5≤3×1＋2×4＋5＝16. ①当ab≥0时，|a|＋|b|＝|a＋b|≤2； ②当ab<0时，则a(－b)>0， |a|＋|b|＝|a|＋|－b|＝|a＋(－b)|≤16.
思考3 当|a|>a时，a∈(_－___∞_,_0_)_；当|a|>－a时， a∈(0，＋∞)．
题型一 利用绝对值三角不等式证明不等式
例1 若|a－b|＞c，|b－c|＜a，求证：c＜a. 证明：由|a－b|＞c及|b－c|＜a得 c－a＜|a－b|－|b－c|≤|(a－b)＋(b－c)|＝ |a－c|＝|c－a|. 由c－a＜|c－a|知c－a＜0，故c＜a.