2016百校联考四

河南省百校联盟2016届高三第四次教学质量监测理 科 数 学第Ⅰ卷一、选择题：本大题共12小题，每小题5分,在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合A ＝{x ｜2x －5x ＋4＞0}，集合B ＝{x ｜y ＝lg （x －2）}，则（CR A ）∩B ＝ A ．（2，4] B ．[2，4] C ．[4，＋∞） D ．（2，＋∞）2．复数z ＝－1，z 为z 的共轭复数．则zz＝A ．1B ．－1iC ．12D ．－123．设命题p ：n ∃∈N ﹡，2n≤2n ＋1，则p ⌝是A ．n ∃∈N ﹡，2n ＞2n ＋1B ．n ∀∈N ﹡，2n＞2n ＋1 C ．n ∃∈N ﹡，2n＝2n ＋1 D ．n ∀∈N ﹡，2n≥2n ＋1 4．若角α的终边在直线y ＝－3x 上，则cos2α＝ A ．45 B ．－45 C ．45± D ．35± 5．若双曲线C ：22221y x a b－＝（a ＞0，b ＞0）的渐近线与圆22(2)x y ＋－＝1相切，则双曲线C 的离心率是A ．2BC D6．一空间几何体的三视图如图所示，则该几何体的表面积是A ．24π＋B ．20π＋C ．24π＋D ．20π＋7．已知△ABC 中，AB ＝10，AC ＝6，BC ＝8，点M 为AB 边上任意一点，则CM uuu r ·CA uu r ＋CM uuu r ·CB uu r的取值范围是A ．[0，100]B ．[36，64]C ．（36，100）D ．[6，10]8．执行如图所示的程序框图，则输出的S 值为 A ．－1008 B ．1008 C ．－2016 D ．20169．将函数f （x ＋cos2x 的图象向右平移m （m ＞0）个单位，所得的函数y ＝g （x ）的图象关于直线x ＝2π对称，当m 取最小值时，f （x ）－g （x ）的最大值是A ．2B ．C ．3D ．10．已知平面区域Ω＝{（x ，y ）｜0≤x ≤1，0≤y ≤12}，曲线C ：y ＝3132x x ＋＋，点A 为区域Ω内任意一点，则点A 落在曲线C 下方的概率是 A ．ln3－ln2 B ．2ln3－2ln2 C ．2ln2－ln3 D ．4ln2－2ln311．如图所示，点E ，F 分别为棱长为的正方体ABCD －A 1B 1C 1D 1的棱AB ，C 1D 1的中点，点P 在EF 上，过点P 作直线l ，使得l ⊥EF ，且l ∥平面ACD 1，直线l 与正方体 的表面相交于M ，N 两点，当点P 由点E 运动到点F 时， 记EP ＝x ，△EMN 的面积为f （x ），则y ＝f （x ）的图象是12．不等式2()aa b e－≥m －2(3)a b －＋对任意实数a ，b 恒成立，则实数m 的最大值是 A ．92BC ．2 D第Ⅱ卷本卷包括必考题和选考题两部分。

理科数学 第Ⅰ卷一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}{}2|21,,|0x A y y x R B x x x ==-∈=->，则AB =（ ）A ．()1,-+∞B ．()1,1-C ．()1,0-D ．()0,12.若复数z 的共轭复数为z ，且满足121zi i=-+，其中i 为虚数单位，则复数z 的模为（ ）A ．1B ．3C ．43.下列满足“()(),0x R f x f x ∀∈+-=且()0f x '≤”的函数是（ ） A ．()xf x xe =- B ．()sin f x x x =+ C ．()()()lg 1,0lg 1,0x x f x x x +≥⎧⎪=⎨-<⎪⎩D ．()2f x x x =4.已知n S 是等差数列{}n a 的前n 项和，3618S S +=，则5S =（ ） A ．14 B ．10 C ．9 D ．55.从1，2，3，4，5，6这六个数字中任取3个数，组成无重复数字的三位数，则十位数字比个位数字和百位数字都大的概率为（ ）A ．16 B ．14 C ．13 D ．126.已知O 为坐标原点，F 为抛物线24y x =的焦点，直线():1l y m x =-与抛物线交于,A B 两点，点A 在第一象限，若3FA FB =，则m 的值为（ ）A ．3B ．3D ．137.如果执行如图所示的程序框图，那么输出的a =（ ）A ．2B ．12C ．-1D ．以上都不正确 8.在正方体1111ABCD A BC D -中，E 为线段1B C 的中点，若三棱锥1E ADD -的外接球的体积为36π，则正方体的棱长为（ ）A ．2B ．．．49.已知()211cos sin cos 222f x x x x x =-++，则下列结论错误的是（ ） A ．()f x 在区间0,6π⎛⎫⎪⎝⎭上单调递增 B ．()f x 的一个对称中心为,012π⎛⎫-⎪⎝⎭C ．当0,3x π⎡⎤∈⎢⎥⎣⎦时，()f x 的值域为⎡⎣ D ．先将函数()f x 的图象的纵坐标不变，横坐标缩短为原来的12倍，再向左平移8π个单位后得到函数2cos 46y x π⎛⎫=+ ⎪⎝⎭的图象 10.如图所示为某几何体的三视图，其体积为48π，则该几何体的表面积为（ ）A ．24πB ．36πC ．60πD ．78π11.已知双曲线()2222:10,0x y C a b a b-=>>的左，右焦点分别为12,,O F F 为坐标原点，P 是双曲线在第一象限上的点，MO OP =，直线2PF 交双曲线C 于另一点N ，若122PF PF =，且02120MF N ∠=，则双曲线C 的离心率为（ ）AB12.已知不等式()()ln 122x a x b +-+≤-恒成立，则32b a -+的最小值为（ ） A ．12e - B ．12e - C ．1e - D ．12e- 第Ⅱ卷二、填空题（本大题共4小题，每题5分，满分20分，将答案填在答题纸上） 13.向量()()1,21a b a b a b ==+-=-，则向量a 与b 的夹角为___________． 14.已知()()5x y x y -+的展开式中24x y 的系数为m ，则211m x dx x ⎛⎫+= ⎪⎝⎭⎰__________．15.若点()2,2Q a b a b +-在不等式组10450210x y x y x y ++≥⎧⎪+-≤⎨⎪-+≥⎩表示的平面区域内，则22z a b =+的最大值为__________．16.已知三角形ABC中，6,4,AB BC D ==为BC 的中点，当AD 最小时，三角形ABC 的面积为_____________．三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17.（本小题满分12分）已知等比数列{}n a 的前n 项和为11,3n S a =，公比11332270,,,2q S a S a S a >+++成等差数列． （1）求n a ； （2）设()12131,log n n n n n nb c b b b a ++==-，求数列{}n c 的前n 项和n T ．18.（本小题满分12分）随着手机的发展，“微信”越来越成为人们交流的一种方式，某机构对“使用微信交流”的态度进行调查，随机抽取 了50人，他们年龄的频数分布及对“使用微信交流”赞成人数如下表：（1）若以“年龄45岁为分界点”，由以上统计数据完成下面22⨯列联表，判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关：（2）若从年龄在[)[)55,6565,75，的被调查人中各随机选取两人进行追踪调查，记选中的4人中赞成“使用微信交流”人数为ξ，求随机变量ξ的分布列及数学期望。

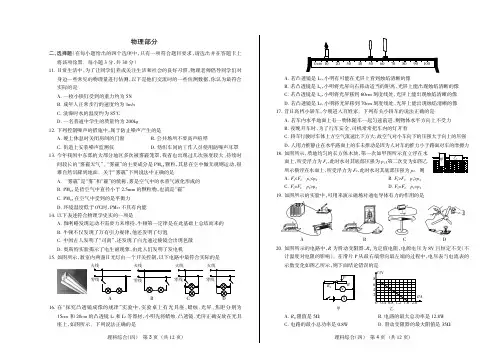
二、选择题（在每小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑。

每小题3分，共30分）11.日常生活中，为了让同学们养成关注生活和社会的良好习惯，物理老师倡导同学们对身边一些常见的物理量进行估测，以下是他们交流时的一些估测数据，你认为最符合实际的是A .一枚小铁钉受到的重力约为5NB .成年人正常步行的速度约为1m/sC .洗澡时水的温度约为85℃D .一名普通中学生的质量约为200kg 12.下列控制噪声的措施中，属于防止噪声产生的是A .晚上休息时关闭房间的门窗B .公共场所不要高声喧哗C .街道上安装噪声监测仪D .纺织车间的工作人员使用防噪声耳罩13.今年我国中东部的大部分地区多次被雾霾笼罩，我省也出现过几次强度较大、持续时间较长的“雾霾天气”。

“雾霾”的主要成分是PM 2.5颗粒，其悬在空中做无规则运动，很难自然沉降到地面。

关于“雾霾”下列说法中正确的是A .“雾霾”是“雾”和“霾”的统称，雾是空气中的水蒸气液化形成的B .PM 2.5是指空气中直径小于2.5mm 的颗粒物，也就是“霾”C .PM 2.5在空气中受到的是平衡力D .环境温度低于0℃时，PM 2.5不具有内能14.以下表述符合物理学史实的一项是A .伽利略发现运动不需要力来维持，牛顿第一定律是在此基础上总结而来的B .牛顿不仅发现了万有引力规律，他还发明了灯泡C .中国古人发明了“司南”，还发现了白光通过棱镜会出现色散D.奥斯特实验揭示了电生磁现象，由此人们发明了发电机15.如图所示，教室内两盏日光灯由一个开关控制，以下电路中最符合实际的是B16.在“探究凸透镜成像的规律”实验中，实验桌上有光具座、蜡烛、光屏、焦距分别为15cm 和20cm 的凸透镜L 1和L 2等器材，小明先将蜡烛、凸透镜、光屏正确安放在光具座上，如图所示。

下列说法正确的是A .若1，小明有可能在光屏上看到烛焰清晰的像B .若凸透镜是L 1，小明将光屏向右移动适当的距离，光屏上能出现烛焰清晰的像C .若凸透镜是L 2，小明将光屏移到60cm 刻度线处，光屏上能出现烛焰清晰的像D .若凸透镜是L 2，小明将光屏移到70cm 刻度线处，光屏上能出现烛焰清晰的像17.昔日高档小轿车，今朝进入百姓家。

百校联盟2016年江苏省高考《考试大纲》调研卷理科数学（第四模拟）一、填空题：共14题1．设全集U=[-2,2],若集合A满足∁U A=[1,2),则A=.【答案】[-2,1)∪{2}【解析】本题主要考查考生对补集的理解,考查考生对基础知识的掌握情况.在数轴上分别作出全集U与∁U A,根据补集的概念可得A=[-2,1)∪{2}.2．在复平面内,复数z=+i2 016(i为虚数单位)对应的点位于第象限.【答案】一【解析】本题考查复数的基本运算,结合i4=1,对式子进行化简,从而判断z对应的点所在的象限.∵z=+1=+1=+,∴z对应的点所在的象限是第一象限.3．某校有甲、乙、丙3个高三文科班,其中甲班有47人,乙班有51人,丙班有49人.现分析3个班的某一次数学考试成绩,计算得甲班的平均成绩是90分,乙班的平均成绩是90分,丙班的平均成绩是87分,则该校这3个高三文科班的数学平均成绩是分.【答案】89【解析】本题考查统计中的平均数,考查考生的运算求解能力.由题意知,3个高三文科班的数学平均成绩=89.4．已知向量a=(2,-1),2b=(-4,6),则(a-b)·(a+b)=.【答案】-8【解析】本题主要考查平面向量的坐标运算、数量积等知识,考查考生对基础知识的掌握情况.解法一因为向量a=(2,-1),2b=(-4,6),所以b=(-2,3),a+b=(0,2),a-b=(4,-4),所以(a-b)·(a+b)=(4,-4)·(0,2)=0-8=-8.解法二因为向量a=(2,-1),2b=(-4,6),所以a2=5,b=(-2,3),b2=13,所以(a-b)·(a+b)=a2-b2=5-13=-8.5．已知等比数列{a n}的各项都是正数,且,,a2成等差数列,则=.【答案】9【解析】本题考查等差数列与等比数列的基础知识,意在考查考生的运算求解能力.破解此题的关键是活用等差数列的性质、等比数列的通项公式和性质.设等比数列{a n}的公比为q(q>0),因为,,a2成等差数列,所以+a2,所以q2=3+2q,所以q=3或q=-1(舍去),所以=9.6．已知△ABC的内角A,B,C所对的边分别为a,b,c,且2b=a+c,若sin B=,cos B=,则b的值为.【答案】4【解析】本题考查余弦定理、同角三角函数的关系等知识的综合运用.∵2b=a+c,sin B=,cos B=,sin2B+cos2B=1,∴ac=15,∴b2=a2+c2-2ac cos B=(a+c)2-48=4b2-48,得b=4.7．从1,2,3,4,5这五个数字中随机取出三个数字,则剩下两个数字都是奇数的概率是.【答案】【解析】本题主要考查古典概型的概率计算公式.解题的关键是正确列出总的基本事件及所求事件包含的基本事件.通解由题意知,从1,2,3,4,5这五个数字中随机取出三个数字的情况有(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),(1,4,5),(2,3,4),(2,3,5),(2,4,5),(3,4,5),共10种,其中剩下两个数字都是奇数的情况有(1,2,4),(2,3,4),(2,4,5),共3种,故所求概率为.优解由题意知,事件“从1,2,3,4,5这五个数字中随机取出三个数字,剩下两个数字都是奇数”的概率与事件“从1,2,3,4,5这五个数字中随机取出两个数字,这两个数字都是奇数”的概率相等,又从1,2,3,4,5这五个数字中随机取出两个数字的情况(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),共10种,其中抽取的两个数字都是奇数的情况有(1,3),(1,5),(3,5),共3种,故所求概率为.8．已知函数f(x)=A sin(ωx+φ)(A>0,ω>0,-<φ<0)的图象的一个最高点为(,),其图象的相邻两个对称中心之间的距离为,则φ=.【答案】-【解析】本题考查三角函数的图象与性质等基础知识,考查考生的运算求解能力.因为函数f(x)的图象的相邻两个对称中心之间的距离为,故函数的最小正周期为T=π,所以ω==2,因为函数f(x)的图象的最高点为(,),所以2×+φ=2kπ+(k∈Z),φ=2kπ-(k∈Z),因为-<φ<0,所以φ=-.9．定义[x]为不超过x的最大整数,例如[1.3]=1.执行如图所示的算法流程图,当输入x的值为4.7时,则输出y的值为.【答案】10.2【解析】本题考查算法流程图的基础知识,考查考生分析问题、解决问题的能力.求解时注意准确判断条件是否满足,决定程序执行的方向.由输入的x为4.7,执行第一个条件判断框后,执行否方向,而4.7-[4.7]=0.7,即4.7-[4.7]不等于0,因而仍执行否方向,得到y=7+([4.7-3]+1)×1.6=10.2,故输出y的值为10.2.10．已知正三棱锥P-ABC的体积为,底面边长为2,则侧棱PA的长为.【答案】2【解析】本题考查空间几何体的体积,一方面要牢记空间几何体的体积公式,另一方面要掌握常见几何体中的基本数量关系.设底面正三角形ABC的中心为O,又底面边长为2,故OA=,由V P-ABC=PO·S△ABC,得PO××22,PO=,所以PA==2.11．已知周期为4的函数f(x)=,则方程3f(x)=x的根的个数为.【答案】3【解析】本题考查分段函数、方程的根等知识.先画出函数f(x)一个周期的图象,再向左、向右扩展,数形结合可得出两个函数图象的交点个数,从而得解.作出函数y=f(x)的图象及直线y=如图所示,则两个图象的交点个数为3,即方程的根的个数为 3.12．在平面直角坐标系中,不等式组 (a为常数)表示的平面区域的面积为4,则x2+y的最小值为.【答案】-【解析】本题考查不等式组表示的平面区域等知识.要注意z=x2+y不是一次型函数,而是二次型函数,故不一定在可行域的边界点处取得最值.由题意作出可行域如图中阴影部分所示,因为平面区域的面积为4,易得A(2,2),B(2,-2),把A,B,O三个边界点的坐标分别代入x2+y,得在这三点处的最小值为0. 令x2+y=0,即y=-x2,y'=-2x,当抛物线y=-x2平移到与直线y=-x相切时,y'=-2x=-1,得x=,即切点P(,-),代入x2+y,得x2+y=-=-,所以x2+y的最小值为-.13．已知双曲线-=1的左、右焦点分别为F1、F2,过点F1作圆x2+y2=a2的一条切线分别交双曲线的左、右两支于B、C两点,与双曲线的渐近线在第二象限内交于点D,且|CD|=|CF2|,则双曲线的离心率为.【答案】【解析】本题主要考查双曲线的定义、几何性质,直线与圆、双曲线的位置关系等知识,考查考生分析问题、解决问题的能力.由双曲线的定义可知,-=2a,又,所以=2a.因为点F1的坐标为(-c,0),直线DF1与圆x2+y2=a2相切,且圆的半径为a,所以直线DF1的方程为y=(x+c),又直线OD的方程为y=-x,联立得点D的坐标为(-,),所以(-+c)2+()2=4a2,得,所以双曲线的离心率为.14．若关于x的不等式(ax-1)(ln x+ax)≥0在(0,+∞)上恒成立,则实数a的取值范围是.【答案】(-∞,-]∪{e}【解析】本题主要考查函数的图象与性质,考查考生的转化与化归能力、运算求解能力和分类讨论思想.(ax-1)(ln x+ax)≥0⇔(a-)(a+)≥0⇔或.设函数f(x)=,g(x)=-,在同一平面直角坐标系内画出它们的图象如图所示,由图象可得实数a的取值范围是(-∞,-]∪{e}.二、解答题：共12题15．已知锐角α满足cos(α+)=.(1)求sin 2α的值;(2)求tan(α-)的值.【答案】(1)因为cos(α+)=,所以cosα-sinα=>0,所以1-sin 2α=,解得sin 2α=.(2)因为sin 2α==2sinαcosα=,即有7tan2α-50tanα+7=0,解得tanα=或tanα=7. 因为cosα-sinα>0,所以0<tanα<1,所以tanα=.则tan(α-)=.【解析】本题主要考查三角函数的运算.解答本题时要注意利用和差角公式与二倍角公式,以及同角三角函数的关系式进行求解.【备注】三角作为高考考查的重点内容,每年必考,其考查的重点是同角三角函数的关系式,三角函数的诱导公式,正弦函数、余弦函数、正切函数的图象与性质,两角和(差)的正弦、余弦及正切公式,二倍角公式,其中两角和(差)的正弦、余弦及正切公式是高考中8个C级考点之一,在复习的过程中要重视公式的逆向应用和变形应用.16．如图,在四棱锥P-ABCD中,AD∥BC,平面APD⊥平面ABCD,且PA=PD,BC=CD=AD,E,F分别为AD,PD的中点.(1)求证:CF∥平面PAB;(2)求证:平面PEC⊥平面PB D.【答案】(1)解法一连接EF,在△APD中,E,F分别为AD,PD的中点,所以EF∥PA,在四边形ABCD中,BC∥AD,又BC=AD,且AE=ED,所以BC AE,四边形BCEA为平行四边形,所以EC∥AB.又EF∩EC=E,PA∩AB=A,所以平面EFC∥平面PAB, 又FC⊂平面EFC,所以CF∥平面PAB.解法二如图,取PA的中点M,连接MF,MB.在△PAD中,PM=MA,PF=FD,所以MF∥AD,且MF=AD. 由已知,BC∥AD,且BC=AD,所以MF∥BC,且MF=BC,所以四边形BCFM为平行四边形,所以FC∥BM, 又FC⊄平面PAB,BM⊂平面PAB,所以CF∥平面PAB.(2)连接BE,在△PAD中,PA=PD,AE=ED,所以PE⊥AD.又平面APD⊥平面ABCD,平面APD∩平面ABCD=AD,所以PE⊥平面ABCD,故PE⊥BD. 在四边形ABCD中,BC∥DE,且BC=DE,所以四边形BCDE为平行四边形.又BC=CD,所以四边形BCDE为菱形,BD⊥CE, 又PE∩EC=E,所以BD⊥平面PEC,又BD⊂平面PBD,所以平面PEC⊥平面PBD.【解析】本题考查几何体的结构特征以及空间中线面平行与面面垂直的证明等,考查考生的空间想象能力以及逻辑推理能力等.(1)可以构造过CF与平面PAB平行的平面;也可以在平面PAB内找出与CF平行的直线;(2)首先由面面垂直,得到PE⊥BD,再分析四棱锥底面的性质,证明BD⊥CE,即可证得BD⊥平面PEC,最后利用面面垂直的判定定理证得结果.【备注】空间中线面位置关系的证明一般都是从平面图形中的线线垂直、平行入手的,所以要注意几何体的结构特征以及平面图形中的基本运算,熟练把握空间中的平行与垂直关系的互化是解决此类问题的关键.17．如图是一个半圆形广场的平面示意图.已知AB为直径,且AB=200 m,O为圆心,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥A B.设∠AOC=x rad(rad为弧度单位).(1)现在准备对半圆形广场进行绿化,在△OCD内栽花,其余部分植树,求植树面积S(x)的最小值;(2)如果从A经过C到D建造一条观光路线,其中A到C是圆弧,C到D是线段C D.设观光路线总长为f(x),求观光路线总长f(x)的最大值.【答案】(1)设半圆形广场的半径为R,由题意知S△OCD=R2sin(π-2x)=5 000sin 2x, 因为C 为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB,所以0<x<.所以植树面积S(x)=S半圆-S△OCD=πR2-5 000sin 2x=5 000(π-sin 2x). 因为0<x<,所以当x=时,S(x)min=5 000(π-1).(2)由题意知,=x×100=100x,CD=200cos x,所以f(x)=100x+200cos x,x∈(0,), 则f'(x)=100(1-2sin x).令f'(x)=0,得x=,则f'(x),f(x)随x的变化情况为所以函数f(x)在x=处取得极大值,这个极大值就是最大值,所以观光路线总长的最大值为f()=100(+)m.【解析】本题是应用性问题,第(1)问先建立植树面积S(x)的函数解析式,再利用三角函数求最值;第(2)问建立观光路线总长f(x)的函数解析式,利用导数求函数的最值.【备注】高考中应用题涉及的数学模型有函数模型、不等式模型、三角模型等,解题时要认真审题,抓住关键词,将实际问题抽象为数学问题,从各种关系中找出最关键的数量关系,将这些关系用有关的量、数字及符号表示出来,从而建立数学模型,运用所学的知识解决问题.18．已知椭圆C:+=1(0<b<4)的左、右顶点分别为A、B,M为椭圆C上异于A、B的任意一点,A关于M的对称点为P.(1)若M的横坐标为,且点P在椭圆的右准线上,求b的值;(2)若以PM为直径的圆恰好经过坐标原点O,求b的取值范围.【答案】(1)∵M是AP的中点,x M=,x A=-2,∴x P=3.∵P在椭圆的右准线上,∴=3,解得b=.(2)设点P的坐标为(x0,y0),点M的坐标为(x1,y1),∵P关于M的对称点为A,∴=x1,=y1,即x0=2x1+2,y0=2y1.∵以PM为直径的圆恰好经过坐标原点O,∴OM⊥OP,∴·=0,即x0x1+y0y1=0,∴(2x1+2)x1+2=0,即=--x1. 又点M在椭圆+=1(0<b<4)上,∴+=1,即b=,∴b=4×=4(1+)=4[1+]=4[1+],∵-2<x1<2,∴2<x1+4<6,∴4≤x1+4+<8,∴≤,即∈(-∞,],∴b∈(-∞,4(1+)],即b∈(-∞,2-].又0<b<4,∴b∈(0,2-].【解析】本题考查直线、圆、椭圆等知识,考查椭圆中基本量的运算、圆的性质等.解题时,(1)由题意建立基本量之间的关系,即可求出b的值;(2)运用基本不等式求出b的取值范围.【备注】解析几何解答题可能涉及圆、椭圆,但更多是直线与椭圆的位置关系的研究,主要考查“设而不求”的思想,往往需要将题目所给的几何关系用代数式进行表达,最终用代数运算解决几何问题.主要类型有:定点(定值)问题、取值范围(最值)问题、存在性问题等.通常以三角形、平行四边形、垂直关系、对称关系等为载体,有时可以借助初中平面几何知识进行转化,一般步骤都是联立方程,写出判别式,然后用代数式刻画几何关系.19．已知函数f(x)=,g(x)=ax-a.(1)若函数g(x)的图象与f(x)的图象相切,求a的值及切点坐标;(2)若m,n∈(0,1],且m>n,求证:≥e m-n.【答案】(1)设函数f(x)的图象与g(x)的图象相切于M(t,),由f'(x)=,则f'(t)==a,且=at-a,消去a得,(2t-1)ln t-t+1=0.设h(t)=(2t-1)ln t-t+1,则h'(t)=2ln t+-1=2ln t-+1.设φ(t)=2ln t-+1,则φ'(t)=+>0,所以φ(t)=2ln t-+1单调递增,即h'(t)=2ln t-+1单调递增,又h'(1)=0,所以当t∈(0,1)时,h'(t)<0,h(t)单调递减,当t∈(1,+∞)时,h'(t)>0,h(t)单调递增,所以h(t)的最小值为h(1)=0,所以(2t-1)ln t-t+1=0仅有一解t=1,此时a==1,切点为M(1,0).(2)要证≥e m-n,即证ln()≥m-n,即证-≥m-n,即证-m≥-n. 设p(x)=-x,因为m,n∈(0,1],m>n,所以只要证p(x)为(0,1]上的增函数即可. 因为p'(x)=-1=,又x∈(0,1],所以p'(x)≥0,所以p(x)为(0,1]上的增函数,从而得证.【解析】本题考查利用导数研究曲线的切线、不等式的证明,考查化归与转化思想.【备注】对于函数与导数的考查,在高考题中多以对数、指数形式出现,而且属于压轴题,对考生能力的要求很高,意在提高区分度.题目可能是从含有参数的函数的单调性、极值、最值、曲线的交点等进行设计,解题时由于对参数的讨论比较复杂,因而有提升的价值,也可能是从切线等角度入手,看似简单,但如果对数学思想方法不能做到运用自如,则很难达到预期效果.因此,在复习过程中对于常规函数的性质及图象要力争做到了如指掌.20．已知数列{a n},{b n}满足b n=a n+1-a n,其中n=1,2,3,….(1)若a1=1,b n=n,求数列{a n}的通项公式;(2)若b n+1b n-1=b n(n≥2),且b1=1,b2=2.(i)记c n=a6n-1,求证:数列{c n}为等差数列;(ii)若数列{}中任意一项的值均未在该数列中重复出现无数次,求a1应满足的条件.【答案】(1)当n≥2时,有a n=a1+(a2-a1)+(a3-a2)+…+(a n-a n-1)=a1+b1+b2+…+b n-1=1+-+1. 又a1=1也满足上式,所以数列{a n}的通项公式为a n=-+1.(2)(i)因为对任意的n∈N*,有b n+6==b n,所以c n+1-c n=a6n+5-a6n-1=b6n-1+b6n+b6n+1+b6n+2+b6n+3+b6n+4=1+2+2+1++=7(n≥1),所以数列{c n}为等差数列.(ii)设d m=a6m+i(m≥0,i为常数且i∈{1,2,3,4,5,6}),所以d m+1-d m=a6m+6+i-a6m+i=b6m+i+b6m+i+1+b6m+i+2+b6m+i+3+b6m+i+4+b6m+i+5=7(m≥0),所以数列{a6m+i}均是以7为公差的等差数列.设f k=+,当a i=时,对任意的n=6k+i(k≥0,i为{1,2,3,4,5,6}中的一个常数),有,此时由已知条件可推得a1=,,,-,-,.当a i≠时,f k+1-f k=-=(a i-)[-]=(a i-)·,①若a i>,则对任意的k∈N,有f k+1<f k,所以数列{}为单调递减数列;②若a i<,则对任意的k∈N,有f k+1>f k,所以数列{}为单调递增数列.综上,设集合B={}∪{}∪{}∪{-}∪{-}∪{}={,,,-,-},则当a1∈B时,数列{}中必有某数重复出现无数次;当a1∉B时,{} (i=1,2,3,4,5,6)均为单调数列,任意一个数在每个数列中最多出现一次,所以数列{}中任意一项的值均未在该数列中重复出现无数次.【解析】本题考查数列的基本运算及其通项公式的求解等,考查考生基本的计算能力、分类讨论思想.【备注】数列求和要注意通项公式的特征,灵活选用相应的方法,其中裂项相消法与错位相减法是高考命题的热点,应熟练掌握求解的基本步骤.21．如图,在☉O的直径AB的延长线上任取一点C,过点C作直线CE与☉O交于点D、E,记点E关于直径AB的对称点为F,连接DF,交AB于G.若CB=AB,求的值.【答案】连接OE、OF,易知∠EDG=∠EOF,又点E、F关于直径AB对称,所以,得∠EOA=∠EOF, 所以∠EDG=∠EOA,又∠EOG+∠EOA=π,所以∠EOG+∠EDG=π,故E、D、G、O四点共圆. 故CE·CD=CO·CG,又CE·CD=CA·CB,所以CA·CB=CO·CG,又CB=AB,所以CO=AB,CA=AB,故.【解析】本题主要考查四点共圆的判定、圆的割线定理等,属于中档题.先证∠EDG=∠EOA,再证E、D、G、O四点共圆,在两个圆中分别由割线定理可得CE·CD=CO·CG,CE·CD=CA·CB,进而可得CA·CB=CO·CG,再由CB=AB可得的值.22．已知二阶矩阵M的属于特征值λ=3的一个特征向量为e1=,且M对应的变换将点(-1,2)变换成(9,15),求矩阵M.【答案】设M=,则=3,故 ,故解得a=-1,b=4,c=-3,d=6,故M=.【解析】本题考查矩阵的特征值与特征向量、矩阵的变换.23．已知两条曲线的极坐标方程分别为ρ=1与ρ=2cos(θ+),它们相交于A,B两点,求线段AB的长.【答案】以极点为原点,极轴为x轴的非负半轴建立平面直角坐标系,则由ρ=1得,x2+y2=1, ∵ρ=2cos(θ+)=cosθ-sinθ,∴ρ2=ρcosθ-ρsinθ,∴x2+y2-x+y=0,由,得A(1,0),B(-,-)或A(-,-),B(1,0).∴|AB|=.【解析】本题考查极坐标方程与直角坐标方程的互化.先联立方程求出两个交点的坐标,再由两点间的距离公式求出线段AB的长.24．已知函数f(x)=|x-1|+|x-2|.若不等式|a+b|+|a-b|≥|a|f(x)(a≠0,a,b∈R)恒成立,求实数x的取值范围.【答案】由|a+b|+|a-b|≥|a|f(x),且a≠0,得≥f(x) .又≥=2,则2≥f(x), 解不等式|x-1|+|x-2|≤2,得≤x≤,即实数x的取值范围为[,].【解析】本题主要考查绝对值不等式的性质及绝对值不等式的求解,考查考生分析问题、解决问题的能力.25．某学习小组由3名男生和3名女生组成,现从中选取参加学校座谈会的代表,规则是每次选取1人,依次选取,每人被选取的机会均等.(1)若要求只选取2名代表,求选出的2名代表都是男生或都是女生的概率;(2)若选取过程中只要有女生入选,选取即结束,记所选取的代表的人数为X,求X的分布列和数学期望EX.【答案】(1)记“选出的2名代表都是男生或都是女生”为事件A,则P(A)=.(2)由题意知,X=1,2,3,4.P(X=1)=,P(X=2)=,P(X=3)=,P(X=4)=.所以X的分布列为EX=1×+2×+3×+4×.【解析】离散型随机变量的分布列与数学期望是高中概率与统计的核心内容,为高考考查的重点,备考中要牢牢抓住该部分,通过各类练习,熟练掌握其解法.本题中要特别注意第(2)问中“只要有女生入选,选取即结束”,理解其含义,正确计算X取各个值的概率.26．已知平面内有n(n≥2,n∈N*)条直线,其中任意两条不平行,任意三条不共点,设这n条直线将平面分成f(n)个区域,如f(2)=4,f(3)=7.(1)试猜想f(n)的表达式,并用数学归纳法加以证明;(2)请用类比的方法,写出n个平面将空间最多分成多少个部分.(不要求证明)(注:12+22+32+…+n2=).【答案】(1)通过画图可求出f(4)=11,f(5)=16,观察发现:f(3)=f(2)+3,f(4)=f(3)+4,f(5)=f(4)+5. 猜想f(n)-f(n-1)=n,进而用累加法求得f(n)-f(2)=n+(n-1)+…+3,所以f(n)=+1. 下面用数学归纳法证明.①当n=2时,f(2)=4显然成立;②假设当n=k(k≥2,k∈N*)时成立,即f(k)=+1,则当n=k+1时,因为第k+1条直线与前面的k 条直线都不平行,而且也不交于同一点(因为任意三条直线不共点),所以第k+1条直线与其他k条直线有k个交点,这k个交点将第k+1条直线分成k+1段,其中每一段都将所在区域一分为二,所以增加了k+1个区域,所以f(k+1)=f(k)+k+1,由归纳假设得,f(k+1)=f(k)+k+1=+k+1+1=+1=+1,即当n=k+1时也成立.综合①②,得f(n)=+1对任意的n(n≥2,n∈N*)均成立.所以f(n)=+1(n≥2,n∈N*).(2)设这n个平面将空间最多分成g(n)个部分,当这n个平面任意两个不平行,任意三个不共线(即交线不重合)时才能最多,用类比法得g(n+1)=g(n)+f(n),从而求得g(n)=4+f(2)+…+f(n-1)=.【解析】本题考查推理与证明.第(1)问通过归纳推理得到结论,再利用数学归纳法给出证明;第(2)问运用类比推理写出结果.。

2016届高三年级第三次四校联考理科综合试题命题：临汾一中忻州一中长治二中康杰中学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共300分，考试时间150分钟第Ⅰ卷（选择题共126分）可能用到的相对原子质量H=1 C=12 N=14 O =16 Na=23 S=32 Cu=64 Ba=137一、选择题：(本题共13小题，每小题6分，共78分。

在每小题给出的四个选项中，只有一项是符合题目要求的)1．下列实验中所用材料、试剂与颜色反应的对应关系中，错误的是选项材料试剂实验目的颜色A 动物细胞台盼蓝检测细胞的死活死细胞被染成蓝色，活细胞不着色B 洋葱内表皮细胞甲基绿和吡罗红混合染液观察DNA和RNA在细胞中的分布细胞核被染成绿色，细胞质被染成红色C 洋葱根尖分生区细胞改良苯酚品红染液观察染色体的数目和形态染色体被染成红色D人口腔上皮细胞健那绿染液观察线粒体的形态和分布线粒体为深绿色，细胞质基质为蓝绿色2．把数条5 cm长的马铃薯条分别浸在蒸馏水和不同浓度的蔗糖溶液中,每隔一段时间测量薯条的长度。

右图显示薯条在不同溶液中长度改变的百分率。

下列相关叙述错误的是A．马铃薯条通过渗透吸(失)水改变其长度B．在0.10 M蔗糖溶液中马铃薯细胞发生质壁分离C．马铃薯细胞液浓度相当于0.30 M的蔗糖溶液D．在0.40 M蔗糖溶液中马铃薯细胞失水3．从水体中取得一定水样，首先测定其初始溶氧量。

然后将水样灌入两个相同的瓶子中，一个白瓶完全透光，另一个黑瓶完全不透光，然后放回原来水层。

24小时后取出，分别测量白瓶和黑瓶中的溶氧量。

下列相关叙述错误的是A．如在实验中意外损坏了黑瓶，则总光合量数据无法获得B．如在实验中白瓶意外坠落水底，则短时间内，瓶内生物叶绿体中C3含量会减少C．呼吸量应从黑瓶测定的数据计算得出D．测黑白瓶中的溶氧量时水样量应一致4．果蝇(2N=8)体内的A/a与B/b两对等位基因独立遗传，基因型为AaBb的果蝇体内的某细胞正在发生细胞分裂(无染色体变异)。