上机实验3、单因素与多因素的方差分析

单因素方差分析1.基本理解方差分析：是一种利用实验获取数据并进行分析的统计方法，经常用于研究不同效应对指定实验的影响是否显著。

方差分析用于检验连续型随机变量在三及以上分类数据不同水平上的差异情况。

方差分析包括：单因素方差分析、多元素方差分析、多元方差分析、协方差分析、重复测量方差分析。

在问卷数据中：单因素方差分析使用较多。

单因素方差分析：用于检验单个因素取不同水平是某因变量的均值是否有显著的变化，也可进一步用于因变量均值的多重比较（检验某些水平下的实验结果具体区别于其他水平的显著差异）。

图1检验步骤2.单因素方差分析操作步骤操作步骤第一步：首先将数据导入spss中并进行赋值后，点击分析、比较平均值、单因素ANOVA检验。

图2单因素方差分析第一步操作步骤第二步：进入图中对话框后将需检验的变量放入因变量列表中，在因子中放入分类变量，点击事后比较勾选假定等方差（LSD），不假定等方差（塔姆黑泥T2）点击继续。

图3单因素方差分析事后比较勾选3.当因素方差分析结果后点击线性进入图中下方选项框、勾选描述、方差齐性检验点击继续、确定。

图4单因素方差分析选项勾选然后单因素方差分析的描述、方差齐性、假设检验就出来了。

图5单因素方差分析结果单因素方差分析事后两两比较结果。

图6事后比较结果4.结果整理将首先将描述统计的结果粘贴复制到Excel表格中进行整理，保留均值和标准差及前面的内容，后在后面加入ANOVA表中的F和p值，将整理好的两两比较结果粘贴到表格的最后，最后将整理好的结果粘贴到Word文档中进行整理。

可参考图中结果整理。

（注：一般在看结果时首先看ANOVA表的结果，看显著情况，显著（p<0.05）看方差齐性检验的结果，若方差齐性检验的结果方差齐（p>0.05），然后再看事后比较的结果，方差齐看LSD，方差不齐看塔姆黑泥的结果，同样差异的显著看事后比较每行对应的显著性（若p<0.05，代表比较的对象显著。

单因素方差分析和多因素方差分析简单实例
单因素方差分析与多因素方差分析（即分析方差分析，简称 ANOVA）是统计学中常用
的一种方法。

它可以用来评估相关变量之间的差异程度，以确定这些变量对数据集的影响
程度。

本文将对两种方法进行简单介绍，并通过一个实例来帮助大家更好地理解。

1、单因素方差分析
单因素方差分析是统计学中最常见的研究方法之一，可以用来评估一个单独变量的影响。

在这种情况下，我们分别将多个样本分为两组或以上，每组有不同的自变量。

然后使
用单因素处方差分析检验来检验这些样本组之间的均值的差异，从而得出该自变量对样本
组之间的均值的影响大小。

举个例子，假设我们有一个取自不同地区的样本，想要测试该样本收入水平是否受某
个城市所在地区影响，那么我们可以把这些样本分为两组：一组是属于某个城市所在地区，另一组是其他地区，然后使用单因素方法分析测试这两组样本收入水平是否显著不同。

拿前面的例子来说，我们在检验受某个城市影响的收入水平的时候如果只用单因素分
析可能不太准确，因为受某个城市影响的收入水平还可能受到一些其他因素的影响，比如
年龄、阶层等，这时就可以使用多因素方差分析来进行检验和确定不同因素的影响程度。

所以，单因素方差分析和多因素方差分析都是用来评估变量之间差异程度的统计方法，但并不能确定变量之间的关联性和互动作用。

至于哪一个方法更适合于某种特定情况，需
要结合实际情况，根据具体分析需求而定。

方差分析
单因素方差分析
目的：在不同水平的控制变量下，观察目标是否存在显著的差异
本次数据选用R中胆固醇(cholesterol)的数据
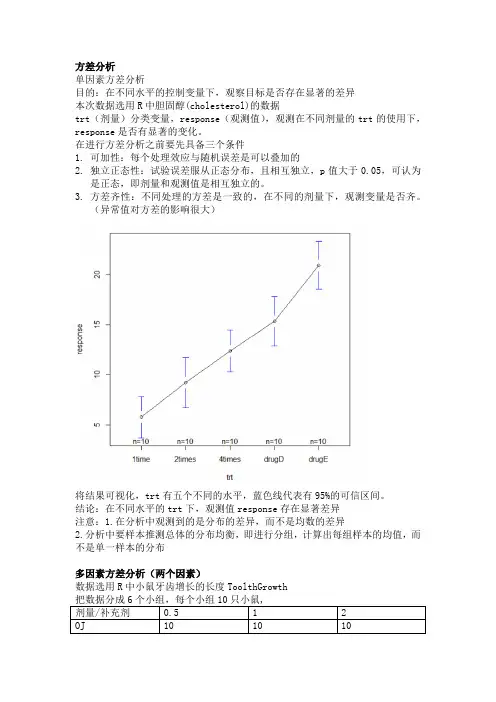
trt（剂量）分类变量，response（观测值），观测在不同剂量的trt的使用下，response是否有显著的变化。

在进行方差分析之前要先具备三个条件
1.可加性：每个处理效应与随机误差是可以叠加的
2.独立正态性：试验误差服从正态分布，且相互独立，p值大于0.05，可认为
是正态，即剂量和观测值是相互独立的。

3.方差齐性：不同处理的方差是一致的，在不同的剂量下，观测变量是否齐。

（异常值对方差的影响很大）
将结果可视化，trt有五个不同的水平，蓝色线代表有95%的可信区间。

结论：在不同水平的trt下，观测值response存在显著差异
注意：1.在分析中观测到的是分布的差异，而不是均数的差异
2.分析中要样本推测总体的分布均衡，即进行分组，计算出每组样本的均值，而不是单一样本的分布
VC 10 10 10
如图为均值分布图，两个因素补充剂（supp）和剂量（dose）作用下，小鼠牙齿。

t检验可以解决单样本、两个样本时的均值比较问题，但是对于两个以上样本，就不能用t检验了，而要使用方差分析。

t检验是借助t分布，方差分析是借助F分布，基于变异分解的思想进行。

在算法上，由于线性模型的引入，在SPSS中，方差分析在比较均值、一般线性模型菜单中都可以做。

在适用条件上，方差分析和两独立样本t检验一样，也分别是独立性、正态性、方差齐性。

方差检验的原假设是：
n个样本均值相同或n个样本来自同一个总体或自变量对因变量没有影响
由于是两组以上样本进行分析，那么方差分析除了要说明多个样本均值是否有差异之外，还需要进一步说明到底是哪些样本存在差异，因此需要多重比较。

一、分析—比较均值—单因素ANOVA
二、分析—一般线性模型—单变量
在一般线性模型菜单中，也可以做方差分析，并且根据线性模型的思想所做出的方差分析更加具体细致。

以上是单因素方差分析，但是实际工作中经常会碰到两个以上因素对于因变量产生影响，和单因素方差最大不同是，两个以上因素要考虑它们之间的交互作用，因此更加复杂。

SPSS上机实验报告（6）学生姓名学号成绩上机实验题目考勤上机表现实验时间一、实验目的：1．熟悉并掌握单因素、双因素方差分析，univarate协方差分析的SPSS操作，其他较简单的方差分析问题，多元方差分析，重复测量的方差分析的具体操作。

2、对分析的结果能给出统计学的解释二、实验内容：1、熟悉方差分析菜单界面，掌握方差分析的操作。

2、对得到的结果进行解释。

3、掌握不同实验设计所使用的统计方法。

4、实际应用1）p151的三个实例，根据提示作相应的方差分析2）P153（5、6、7、8）题建立数据文件，进行方差分析三、实验要求：1、根据上机报告模板详细书写上机报告2、作业发到邮箱*****************四第七题第1步分析：需要研究不同包装和不同摆放位置对销量的影响。

这是一个多因素(双因素)方差分析问题。

第2步数据组织：如上表的变量名组织成4列数据。

第3步变量设置：按“分析|一般线性模型| 单变量”的步骤打开单变量对话框。

并将“销量”变量移入因变量框中，将“casing”和“摆放位置”移入固定因子中，如下图：第4步选择建立多因素方差分析的模型种类：打开“模型”对话框，本例用默认的全因子模型。

第5步以图形方式展示交互效果：设置方式如下图第6步设置方差齐性检验：由于方差分析要求不同casing数据方差相等，故应进行方差齐性检验，单击“选项”按钮，选中“方差齐性检验”，显著性水平设为默认值0.05。

75步设置控制变量的多重比较分析：单击“两两比较”按钮，如下图，在其中选出需要进行比较分析的控制变量，这里选“casing”，再选择一种方差相等时的检验模型，如LSD。

第8步对控制变量各个水平上的观察变量的差异进行对比检验：选择“对比”对话框，对两种因素均进行对比分析，用“简单”方法，并以最后一个水平的观察变量均值为标准。

五、程序运行结果:第七题运行结果UNIANOVA主体间因子值标签N包装1 A1 92 A2 93 A3 9摆放位置1 B1 92 B2 93 B3 9误差方差等同性的 Levene 检验a因变量: 销量F df1 df2 Sig..754 8 18 .646检验零假设，即在所有组中因变量的误差方差均相等。

方差分析公式单因素与多因素方差分析的关键公式方差分析是一种统计方法，用于比较不同因素对变量的影响是否显著。

通过方差分析，我们可以确定不同因素之间是否存在统计学差异，并进一步研究这些差异的来源。

在方差分析中，单因素与多因素方差分析是两种常见的方法。

本文将介绍这两种方差分析中的关键公式。

一、单因素方差分析公式在单因素方差分析中，我们只考虑一个因素对变量的影响。

假设我们有k个水平（或组），每个水平下有n个观测值。

那么总观测值的个数为N=k*n。

在进行单因素方差分析之前，我们需要计算以下几个统计量：1. 总平方和（SST）：表示所有观测值与整体均值之间的差异的总和。

计算公式为：SST = Σ(Σ(x_ij - X¯)^2)其中，x_ij表示第i组的第j个观测值，X¯表示所有观测值的均值。

2. 组间平方和（SSB）：表示各组均值与整体均值之间的差异的总和。

计算公式为：SSB = Σ(n_i * (X¯_i - X¯)^2)其中，n_i表示第i组的观测值个数，X¯_i表示第i组的均值。

3. 组内平方和（SSW）：表示每组内个体与组内均值之间的差异的总和。

计算公式为：SSW = Σ(Σ(x_ij - X¯_i)^2)其中，x_ij表示第i组的第j个观测值，X¯_i表示第i组的均值。

根据以上统计量，我们可以计算方差分析的F值，来判断组间差异是否显著。

F值的计算公式为：F = (SSB / (k-1)) / (SSW / (N - k))其中，k表示组数，N表示总观测值的个数。

二、多因素方差分析公式在多因素方差分析中，我们考虑两个或两个以上的因素对变量的影响。

假设我们有r个因素，每个因素有k个水平（或组）。

那么总观测值的个数为N = k^r。

在进行多因素方差分析之前，我们需要计算以下几个统计量：1. 总平方和（SST）：表示所有观测值与整体均值之间的差异的总和。

单因素方差分析与多因素方差分析在统计学中，方差分析是一种常用的统计方法，用于比较多个样本或组之间是否存在显著性差异。

它分为单因素方差分析和多因素方差分析两种类型。

本文将对这两种分析方法进行详细讲解，并探讨其应用场景及步骤。

一、单因素方差分析单因素方差分析适用于只有一个自变量（或称因素）的情况。

它的目的是通过比较组间的差异，确定各组之间是否存在显著性差异。

以下是进行单因素方差分析的步骤：1. 设定假设：在进行方差分析之前，首先需要设定空假设和备择假设。

空假设（H0）通常假设各组的总体均值相等，备择假设（Ha）则假设至少有一组的总体均值与其他组不同。

2. 收集数据：收集与研究对象相关的数据，确保样本的选择具有代表性，并满足方差分析的基本要求。

3. 计算平方和：根据收集到的数据，计算总平方和（SST），组内平方和（SSW）和组间平方和（SSB）。

总平方和表示总体误差的方差，组内平方和表示各组内部误差的方差，组间平方和表示不同组之间的差异。

4. 计算均方：根据平方和计算均方，即总均方（MST），组内均方（MSW）和组间均方（MSB）。

均方是指平方和除以自由度。

5. 计算F值：通过计算方差比（F值）来检验组间差异的显著性。

F值越大，说明组间差异越显著。

6. 进行假设检验：基于计算的F值和设定的显著性水平，进行假设检验。

如果计算得到的F值大于临界值，则拒绝空假设，认为组间存在显著差异。

7. 进行事后比较：如果拒绝了空假设，需要进一步进行事后比较，确定具体哪些组之间存在显著差异。

一般常用的事后比较方法有Tukey、LSD等。

二、多因素方差分析多因素方差分析适用于有两个以上自变量的情况。

它能够同时考察多个自变量对因变量的影响，并进一步分析这些自变量之间的交互效应。

以下是进行多因素方差分析的步骤：1. 设定假设：与单因素方差分析一样，需要设定空假设和备择假设。

2. 收集数据：收集与研究对象相关的数据，确保样本的选择具有代表性，并满足方差分析的基本要求。

第八章 方差分析与回归分析第一节 单因素试验的方差分析在科学试验、生产实践和社会生活中，影响一个事件的因素往往很多。

例如，在工业生产中，产品的质量往往受到原材料、设备、技术及员工素质等因素的影响；又如，在工作中，影响个人收入的因素也是多方面的，除了学历、专业、工作时间、性别等方面外，还受到个人能力、经历及机遇等偶然因素的影响. 虽然在这众多因素中，每一个因素的改变都可能影响最终的结果，但有些因素影响较大，有些因素影响较小. 故在实际问题中，就有必要找出对事件最终结果有显著影响的那些因素. 方差分析就是根据试验的结果进行分析，通过建立数学模型，鉴别各个因素影响效应的一种有效方法.分布图示★ 引言★ 基本概念 ★ 例1★ 例2★ 假设前提 ★ 方差分析的任务★ 偏差平方和及其分解 ★ E S 和A S 的统计特性 ★ 检验方法★ 例3★ 例4★ 习题8-1内容要点一、基本概念在方差分析中，我们将要考察的对象的某种特征称为试验指标. 影响试验指标的条件称为因素. 因素可分为两类，一类是人们可以控制的（如上例的原材料、设备、学历、专业等因素）；另一类人们无法控制的（如上例中员工素质与机遇等因素）.今后，我们所讨论的因素都是指可控制因素。

因素所处的状态，称为该因素的水平. 如果在一项试验中只有一个因素在改变，则称为单因素试验；如果多于一个因素在改变，则称为多因素试验. 为方便起见，今后用大写字母,,,C B A 等表示因素，用大写字母加下标表示该因素的水平，如 ,,21A A 等.二、假设前提设单因素A 具有r 个水平，分别记为,,,,21r A A A 在每个水平),,2,1(r i A i 下，要考察的指标可以看成一个总体，故有r 个总体，并假设:(1) 每个总体均服从正态分布; (2) 每个总体的方差相同;(3) 从每个总体中抽取的样本相互独立.那么，要比较各个总体的均值是否一致，就是要检验各个总体的均值是否相等，设第i 个总体的均值为i μ，则假设检验为 .:210r H μμμ=== 备择假设为 .,,,:211不全相等r H μμμ 通常备择假设可以不写.在水平),,2,1(r i A i =下，进行i n 次独立试验，得到试验数据为,,,,21i in i i X X X 记数据的总个数为n =.1∑=ri i n由假设有 ~ij X ),(2σμi N （i μ和2σ未知），即有-ij X i μ~),,0(2σN 故-ij X i μ可视为随机误差.记-ij X i μ=ij ε，从而得到如下数学模型:⎩⎨⎧==+=未知和相互独立各个2i 2, ),,0(~,,2,1,,,2,1,σμεσεεμij ij iij i ij N n j r i X （1） 方差分析的任务:1) 检验该模型中r 个总体),(2σμi N ),,2,1(r i =的均值是否相等; 2) 作出未知参数r μμμ,,,21 , 2σ的估计.为了更仔细地描述数据，常在方差分析中引入总平均和效应的概念. 称各均值的加权平均,11∑==ri ii n nμμ为总平均. 其中n =.1∑=ri i n 再引入,μμδ-=i i ,,,2,1r i =i δ表示在水平i A 下总体的均值i μ与总平均μ的差异，称其为因子A 的第i 个水平i A 的效应.易见，效应间有如下关系式：,0)(11=-=∑∑==ri iir i ii n n μμδ利用上述记号，前述数学模型可改写为⎪⎪⎩⎪⎪⎨⎧===++=∑=未知和相互独立各个2i 21,),,0(~0,,2,1,,,2,1,σμεσεδεδμij ijr i i i r ij i ij N n n j r i X （2） 而前述检验假设则等价于:.,,,:.:211210不全为零r r H H δδδδδδ ===三、偏差平方和及其分解为了使造成各ij X 之间的差异的大小能定量表示出来，我们先引入:记在水平i A 下数据和记为: ∑==in j ij i X X 1.，其样本均值为.i X =,11∑=in j ij iXn 因素A 下的所有水平的样本总均值为X =∑∑==ri n j ij iX n111=∑=ri i Xr 1.1,为了通过分析对比产生样本ij X , r i ,,2,1 =，k j ,,2,1 =之间差异性的原因，从而确定因素A 的影响是否显著，我们引入偏差平方和来度量各个体间的差异程度:=T S ∑∑==-ri n j ij iX X 112)( （3）T S 能反映全部试验数据之间的差异，又称为总偏差平方和.如果0H 成立，则r 个总体间无显著差异，也就是说因素A 对指标没有显著影响，所有的ij X 可以认为来自同一个总体),(2σμN ，各个ij X 间的差异只是由随机因素引起的。

单因素方差分析实例[例6-8]在1990 年秋对“亚运会期间收看电视的时间”调查结果如下表所示。

问：收看电视的时间比平日减少了（第一组）、与平日无增减（第二组）、比平日增加了（第三组）的三组居民在“对亚运会的总态度得分”上有没有显著的差异？即要检验从“态度”上看，这三组居民的样本是取自同一总体还是取自不同的总体在SPSS 中进行方差分析的步骤如下：（1）定义“居民对亚运会的总态度得分”变量为X（数值型），定义组类变量为G（数值型），G=1、2、3 表示第一组、第二组、第三组。

然后录入相应数据，如图6-66所示图6-66 方差分析数据格式（2）选择[Analyze]=>[Compare Means]=>[One-Way ANOVA...]，打开[One-Way ANOVA]主对话框（如图6-67所示）。

从主对话框左侧的变量列表中选定X，单击按钮使之进入[Dependent List]框，再选定变量G，单击按钮使之进入[Factor]框。

单击[OK]按钮完成。

图6-67 方差分析对话框（3）分析结果如下：因此，收看电视时间不同的三个组其对亚运会的态度是属于三个不同的总体。

多因素方差分析[例6-11]从由五名操作者操作的三台机器每小时产量中分别各抽取1 个不同时段的产量，观测到的产量如表6-31所示。

试进行产量是否依赖于机器类型和操作者的方差分析。

SPSS 的操作步骤为：（1）定义“操作者的产量”变量为X（数值型），定义机器因素变量为G1（数值型）、操作者因素变量为G2（数值型），G1=1、2、3 分别表示第一、二、三台机器，G2=1、2、3、4、5 分别表示第1、2、3、4、5 位操作者。

录入相应数据，如图6-68所示。

图6-68 双因素方差分析数据格式（2）选择[Analyze]=>[General Linear Model]=>[Univariate...]，打开[Univariate]主对话框（如图6-69所示）。

单因素及双因素方差分析及检验的原理及统计应用一、本文概述本文将全面探讨单因素及双因素方差分析及检验的原理及其在统计中的应用。

方差分析是一种在多个样本均数间进行比较的统计方法，其基本原理是通过分析不同来源的变异对总变异的贡献大小，从而确定可控因素对研究结果的影响。

单因素方差分析适用于只有一个独立变量影响研究结果的情况，而双因素方差分析则适用于存在两个独立变量的情况。

这两种方法在科学研究、经济分析、医学实验等众多领域具有广泛的应用价值。

本文将首先介绍单因素及双因素方差分析的基本概念和原理，包括方差分析的前提假设、模型的构建以及检验的步骤。

随后，通过实例演示如何进行单因素及双因素方差分析，并解释分析结果的意义。

本文还将讨论方差分析的局限性，以及在实际应用中需要注意的问题。

通过本文的学习，读者将能够掌握单因素及双因素方差分析及检验的基本原理和方法，了解其在不同领域的统计应用，提高数据分析和处理的能力。

本文还将为研究者提供有益的参考，帮助他们在实践中更好地运用方差分析解决实际问题。

二、单因素方差分析（One-Way ANOVA）单因素方差分析（One-Way ANOVA）是一种统计方法，用于比较三个或更多独立组之间的均值差异。

这种方法的前提假设是各组间的方差相等，且数据服从正态分布。

在进行单因素方差分析时，首先需要对数据进行正态性和方差齐性的检验。

如果数据满足这些前提条件，那么可以进行单因素方差分析。

该分析的基本思想是，如果各组之间的均值没有显著差异，那么各组内的变异应该主要来自随机误差。

如果有显著差异，那么各组间的变异将大于组内的变异。

单因素方差分析通过计算F统计量来检验各组均值是否相等。

F 统计量是组间均方误差与组内均方误差的比值。

如果F统计量的值大于某个显著性水平（如05）下的临界值，那么我们可以拒绝零假设，认为各组间的均值存在显著差异。

单因素方差分析在许多领域都有广泛的应用，如医学、生物学、社会科学等。