单因素方差分析的计算步骤

单因素方差分析公式研究单因素方差分析的公式单因素方差分析公式研究在统计学中，单因素方差分析是用于比较两个或多个组之间差异的一种方法。

它可以帮助我们确定因素对观测值的影响程度，并判断这种影响是否具有统计学上的显著性。

本文将对单因素方差分析的公式进行研究和解析，以帮助读者更好地理解和应用该方法。

一、方差的概念和计算公式方差是描述数据分散程度的统计量，用于衡量观测值与其均值之间的偏离程度。

对于一个样本数据集，方差的计算公式如下：\[S^2 = \frac{\sum{(X_i - \bar{X})^2}}{n-1}\]其中，\(S^2\)表示样本方差，\(\sum{(X_i - \bar{X})^2}\)表示所有观测值与均值之差的平方和，\(n\)表示样本容量。

二、单因素方差分析的公式在单因素方差分析中，我们将观测值按照某个因素分成两个或多个组，并比较这些组之间的差异。

单因素方差分析的计算公式如下：\[F = \frac{SSB}{SSW}\]其中，\(F\)表示方差分析的统计量，\(SSB\)表示组间平方和，\(SSW\)表示组内平方和。

三、组间平方和的计算方法组间平方和是一种衡量不同组之间差异的统计量，它的计算方法如下：\[SSB = \sum{\frac{T_i^2}{n_i}} - \frac{T^2}{N}\]其中，\(T_i\)表示第\(i\)组的总和，\(n_i\)表示第\(i\)组的样本容量，\(T\)表示所有观测值的总和，\(N\)表示总样本容量。

四、组内平方和的计算方法组内平方和是一种衡量同一组内观测值之间差异的统计量，它的计算方法如下：\[SSW = \sum{(X_{ij} - \bar{X_i})^2}\]其中，\(X_{ij}\)表示第\(i\)组的第\(j\)个观测值，\(\bar{X_i}\)表示第\(i\)组的均值。

五、方差分析的统计显著性检验通过计算得到方差分析的统计量\(F\)后，需要进行显著性检验来判断因素对观测值的影响是否具有统计学上的显著性。

单因素方差分析的计算步骤Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】一、 单因素方差分析的计算步骤假定实验或观察中只有一个因素（因子）A ,且A 有m 个水平，分别记为,,,21m A A A 在每一种水平下，做n 次实验，在每一次试验后可得一实验值，记做ij x 表示在第j 个水平下的第i 个试验值()m j n i ,2,1;,2,1==。

结果如下表：m A A A ,,21看成是m 个正态总体，而()m j n i x ij ,2,1;,2,1==看成是取自第j 总体的第i 个样品，因此，可设()m j n i a N x j ij ,2,1;,2,1,,~2==σ。

可以认为j j j a εεμ,+=是因素A 的第j 个水平j A 所引起的差异。

因此检验因素A 的各水平之间是否有显着的差异，就相当于检验：μ====m a a a H 210:或者 具体的分析检验步骤是：（一）计算水平均值令j x 表示第j 种水平的样本均值，式中，ij x 是第j 种水平下的第i 个观察值，j n 表示第j 种水平的观察值次数（二）计算离差平方和在单因素方差分析中，离差平方和有三个，它们分别是总离差平方和，组内离差平方和以及组间平方和。

首先，总离差平方和，用SST 代表，则，其中,n x x ij ∑∑=它反映了离差平方和的总体情况。

其次，组内离差平方和，用SSE 表示，其计算公式为：其中j x 反映的是水平内部或组内观察值的离散状况，即反映了随机因素带来的影响。

最后，组间平方和，用SSA 表示，SSA 的计算公式为：用各组均值减去总均值的离差的平方，乘以各组观察值个数，然后加总，即得到SSA 。

可以看出，它所表现的是组间差异。

其中既包括随机因素，也包括系统因素。

根据证明，SSA SSE SST ,,之间存在着一定的联系，这种联系表现在： 因为：在各组同为正态分布，等方差的条件下，等式右边最后一项为零，故有，即 SSA SSE SST +=（三）计算平均平方用离差平方和除以各自自由度即可得到平均平方。

一、 单因素方差分析的计算步骤假定实验或观察中只有一个因素（因子）A ,且A 有m 个水平，分别记为,,,21m A A A 在每一种水平下，做n 次实验，在每一次试验后可得一实验值，记做ij x 表示在第j 个水平下的第i 个试验值()m j n i ,2,1;,2,1==。

结果如下表3.1： 表3.1 单因素方差分析数据结构表为了考察因素A 对实验结果是否有显著性影响，我们把因素A 的m 个水平m A A A ,,21看成是m 个正态总体，而()m j n i x ij ,2,1;,2,1==看成是取自第j 总体的第i 个样品，因此，可设()m j n i a N x j ij ,2,1;,2,1,,~2==σ。

可以认为j j j a εεμ,+=是因素A 的第j 个水平j A 所引起的差异。

因此检验因素A 的各水平之间是否有显著的差异，就相当于检验：μ====m a a a H 210:或者 0:210====m H εεε具体的分析检验步骤是： （一） 计算水平均值令j x 表示第j 种水平的样本均值，jn i ijj n xx j∑==1式中，ij x 是第j 种水平下的第i 个观察值，j n 表示第j 种水平的观察值次数 （二）计算离差平方和在单因素方差分析中，离差平方和有三个，它们分别是总离差平方和，组内离差平方和以及组间平方和。

首先，总离差平方和，用SST 代表，则，2)(∑∑-=x x SST ij其中,nxx ij∑∑=它反映了离差平方和的总体情况。

其次，组内离差平方和，用SSE 表示，其计算公式为：()∑∑⎥⎦⎤⎢⎣⎡-=j i j ij x x SSE 2其中j x 反映的是水平内部或组内观察值的离散状况，即反映了随机因素带来的影响。

最后，组间平方和，用SSA 表示，SSA 的计算公式为：()()22∑∑∑-=-=x x n x x SSA j j j用各组均值减去总均值的离差的平方，乘以各组观察值个数，然后加总，即得到SSA 。

1、划分变异原因总变异=处理间变异＋区组间变异＋误差变异2、列出试验结果并初步计算，求处理和T,区组和T ，和总和T。

3、分解并计算各项平方和、自由度（1）求平方和n （区组）=4k （处理）=6矫正数39609.37501257.631099.3855.46102.79(2)求各项自由度235使用说明：①使用前请详细阅读文档为娱乐学习之用，处理及区组均为10个，作中的蓝字为使用者填入，其他如工作表、格式及果给予重视，如为“不能反映处理间效应”或“一、单因素随机化完全区组设计的方差分析2=nkT C =k 2i i=11n A SS C T ∙==∑－==∑=C SS T B －n 1j 2j .k 1=--=SS SS SS SS B A T e ==1-nk T f =-=1f k A =-=1n f B --=)1)(1(n k f e n n 2ij i=1j=1x T SS C ==∑∑－3155、进行F检验64（2）求F值32.092.70（3）查F表（4）检验由表中F值和F临界值相比较得知：①否定H01，差异极显著2②接受H02，区组间差异不显著1结论：该项试验结果能极显著反映处理间的效应。

已知k=65种 ， n=41.30893 3.16 4.351.3089 4.14 5.69②4 3.25 4.461.3089 4.25 5.84③5 3.31 4.551.3089 4.33 5.95④6 3.36 4.611.3089 4.40 6.03⑤0#VALUE!#VALUE! 1.3089#VALUE!#VALUE!⑥二、邓肯（Duncan）多重极差法（LSR法），a有2、3……等(1)求LSR（1）H 01：α1=α2=…=αH 02；β1=β2=…=β=1-nk T f =-=1f k A =-=1n f B =--=)1)(1(n k f e ==22/e A A S S F 22e /=B B F S S =X S =0#VALUE!#VALUE! 1.3089#VALUE!#VALUE!⑦0#VALUE!#VALUE! 1.3089#VALUE!#VALUE!⑧细阅读统计学有关资料，按照相关要求进行完善，同时建议按照统计学示例进行验算；②本之用，处理及区组均为10个，作者不承担由使用该文档而产生的法律责任，如不赞同，请删除；③文者填入，其他如工作表、格式及公式等内容请勿非专业改动或删除；④在输入数据后请对方差分析结为“不能反映处理间效应”或“不能接受”，多重比较已无意义，请核对原始数据。

方差分析公式单因素方差分析多因素方差分析的计算公式方差分析公式计算单因素和多因素方差分析的方法是统计学中常用的数据分析技术。

方差分析可以用来比较两个或多个组之间的均值是否存在显著差异。

在本文中，将介绍单因素方差分析和多因素方差分析的计算公式和步骤。

一、单因素方差分析的计算公式单因素方差分析适用于只有一个自变量（因素）的情况下比较多个组的均值是否存在差异。

在进行单因素方差分析时，需要计算以下几个统计量。

1. 总平方和（SST）：总平方和表示各组数据与整体均值之间的偏差总和。

其计算公式如下：SST = Σ(xi - x)²其中，xi为每个观察值，x为所有观察值的均值。

2. 组内平方和（SSW）：组内平方和表示各组数据与各组均值之间的偏差总和。

其计算公式如下：SSW = Σ(xi - x i)²其中，xi为每个观察值，x i为各组观察值的均值。

3. 组间平方和（SSB）：组间平方和表示各组均值与整体均值之间的偏差总和。

其计算公式如下：SSB = Σ(ni * (x i - x)²)其中，ni为每个组的观察次数，x i为各组观察值的均值，x为所有观察值的均值。

4. 平均平方和（MSW和MSB）：平均平方和表示各组之间的平均差异程度。

其计算公式如下：MSW = SSW / (n - k)MSB = SSB / (k - 1)其中，n为总观察次数，k为组的个数。

5. F统计量：F统计量用于检验组间均值是否存在显著差异。

其计算公式如下：F = MSB / MSW二、多因素方差分析的计算公式多因素方差分析适用于两个或更多个自变量（因素）的情况下比较多个组的均值是否存在差异，并确定各因素之间的交互影响。

在进行多因素方差分析时，需要计算以下几个统计量。

1. 总平方和（SST）：总平方和的计算方式与单因素方差分析相同。

2. 组内平方和（SSW）：组内平方和的计算方式与单因素方差分析相同。

单因素方差分析范文单因素方差分析（One-way Analysis of Variance，简称ANOVA）是统计学中一种常用的方法，用于比较三个或三个以上的组的均值是否存在显著差异。

本篇文章将从原理、假设、步骤和应用等方面进行介绍。

一、原理二、假设在进行单因素方差分析时，需要假设组间均值是否存在显著差异。

具体的假设如下：H0：各组均值相等（即组间均值差异不显著）H1：至少有两组均值不相等（即组间均值差异显著）三、步骤进行单因素方差分析的步骤如下：1.根据研究目的和问题选择合适的统计方法；2.收集数据，涉及到多个组的测量值；3. 计算总平方和（SS_total），表示总变异性大小；4. 计算组间平方和（SS_between），表示组间变异性大小；5. 计算组内平方和（SS_within），表示组内变异性大小；6. 根据以上计算结果，计算组间均方（MS_between）和组内均方（MS_within）；7. 计算F值，即F=MS_between/MS_within；8.根据设定的显著性水平（通常为0.05），查表或计算得到临界值；9.比较计算得到的F值与临界值，判断是否达到显著性水平。

四、应用1.医学研究：比较不同药物对疾病治疗效果的影响；2.教育研究：比较不同教学方法对学生学习成绩的影响；3.市场调查：比较不同广告对产品销量的影响；4.农业实验：比较不同施肥方式对作物产量的影响。

五、总结单因素方差分析是一种常用的统计方法，通过比较三个或三个以上组的均值差异来判断各组之间是否存在显著差异。

它的优点是可以同时比较多个组均值的差异，从而提高实验效率和减少误判，应用广泛且实用。

因此，研究者在进行多组均值比较时，可以选择单因素方差分析方法进行分析。

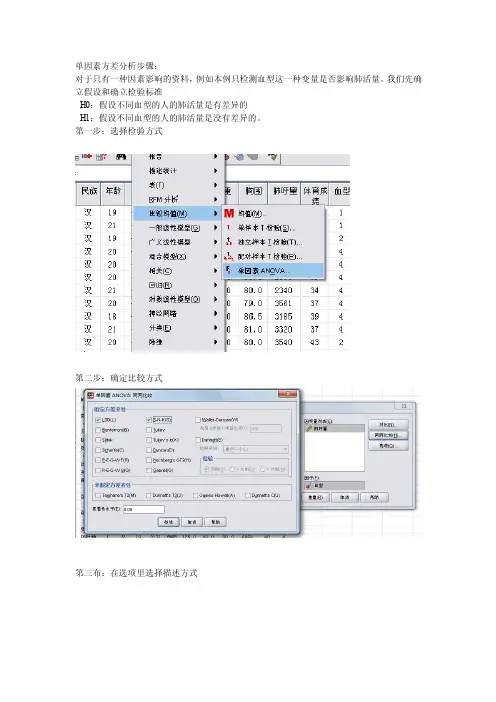
单因素方差分析步骤：对于只有一种因素影响的资料，例如本例只检测血型这一种变量是否影响肺活量。

我们先确立假设和确立检验标准H0：假设不同血型的人的肺活量是有差异的H1：假设不同血型的人的肺活量是没有差异的。

第一步：选择检验方式第二步：确定比较方式第三布：在选项里选择描述方式第四步：得出结果：由本图可知，p》0.05，可知肺活量的总体方差无差异，方差齐则可做方差分析再有下图可知：p= 0.789是大与0.05的，所以不是小概率事件，不拒绝H0，所以认为不同血型的人的肺活量是没有差异的。

随机区组设计资料的方差分析2.如果对四种饲料对猪体重增加量有无差异进行分析，则可将猪随机分组，本例中以a代表分组，b代表饲料，x代表体重增加量如图：对于这种资料分析，应选用单变量方差分析，主要是影响因素是多样的，主要描述的是体重增加量。

那么我们首先应1、确定假设：对于处理组：H0，假设三种处理方式体重增加量是相等的H1，假设三种处理方式体重增加量是不等的。

对于区组：H0，假设三组之间体重增加量是相等的H1，假设三组之间体重增加量是不等的。

2、确立检验标准a=0.053、计算统计量F F1=MS处理/MS误差F2=MS区组/MS误差4、确定p值，做出推断结论。

第一步：选择分析方式第二步：选择确立因变量，本题描述的是体重增加量，故选用x，确立区间，处理措施。

如图：第三步：确定模型，本题为确定区组a与处理措施b的交互作用，因此选用a，b交互模式。

如图：如需作图比较分组a 与处理措施b 的交互作用对体重影响有无差异可添加对比组，如图：确定观察均值的两两比较，主要针对与各分组的均值比较，及各处理方式的均值比较：在选项里设定输出，描述统计及方差齐性检验，显示分组及处理方式的均值。

最后得出结果：有本图可知F＜3，p＞0.05，可知各组间方差齐，可做方差检验。

如下图所示，可知p≥0.05，统计无差异，所以可知，三种处理方式对体重增加是无差异的。

单因素⽅差分析（one-wayANOVA）单因素⽅差分析（⼀）单因素⽅差分析概念是⽤来研究⼀个控制变量的不同⽔平是否对观测变量产⽣了显著影响。

这⾥，由于仅研究单个因素对观测变量的影响，因此称为单因素⽅差分析。

例如，分析不同施肥量是否给农作物产量带来显著影响，考察地区差异是否影响妇⼥的⽣育率，研究学历对⼯资收⼊的影响等。

这些问题都可以通过单因素⽅差分析得到答案。

（⼆）单因素⽅差分析步骤第⼀步是明确观测变量和控制变量。

例如，上述问题中的观测变量分别是农作物产量、妇⼥⽣育率、⼯资收⼊；控制变量分别为施肥量、地区、学历。

第⼆步是剖析观测变量的⽅差。

⽅差分析认为：观测变量值的变动会受控制变量和随机变量两⽅⾯的影响。

据此，单因素⽅差分析将观测变量总的离差平⽅和分解为组间离差平⽅和和组内离差平⽅和两部分，⽤数学形式表述为：SST=SSA+SSE。

第三步是通过⽐较观测变量总离差平⽅和各部分所占的⽐例，推断控制变量是否给观测变量带来了显著影响。

（三）单因素⽅差分析原理总结在观测变量总离差平⽅和中，如果组间离差平⽅和所占⽐例较⼤，则说明观测变量的变动主要是由控制变量引起的，可以主要由控制变量来解释，控制变量给观测变量带来了显著影响；反之，如果组间离差平⽅和所占⽐例⼩，则说明观测变量的变动不是主要由控制变量引起的，不可以主要由控制变量来解释，控制变量的不同⽔平没有给观测变量带来显著影响，观测变量值的变动是由随机变量因素引起的。

（四）单因素⽅差分析基本步骤1、提出原假设：H0——⽆差异；H1——有显著差异2、选择检验统计量：⽅差分析采⽤的检验统计量是F统计量，即F值检验。

3、计算检验统计量的观测值和概率P值：该步骤的⽬的就是计算检验统计量的观测值和相应的概率P值。

4、给定显著性⽔平，并作出决策（五）单因素⽅差分析的进⼀步分析在完成上述单因素⽅差分析的基本分析后，可得到关于控制变量是否对观测变量造成显著影响的结论，接下来还应做其他⼏个重要分析，主要包括⽅差齐性检验、多重⽐较检验。

单因素方差分析公式总结单因素方差分析是统计学中常用的一种分析方法，用于比较两个或多个样本均值之间的差异是否显著。

在进行单因素方差分析时，我们需要计算一系列的统计指标和公式，以便更好地理解和解释研究结果。

下面是单因素方差分析中常用的公式总结。

一、总平方和 (Total Sum of Squares, SST)总平方和是用来衡量所有观测值与总均值之间的离散程度，其计算公式为：SST = Σ(xi - x)^2其中，xi代表每个观测值，x代表总均值，Σ代表求和。

二、处理组平方和 (Between-group Sum of Squares, SSB)处理组平方和用来衡量不同处理组之间的均值差异，其计算公式为：SSB = Σ(nk * (xk - x)^2)其中，nk表示每个处理组的样本量，xk代表每个处理组的均值，x代表总均值，Σ代表求和。

三、误差平方和 (Error Sum of Squares, SSE)误差平方和是用来衡量同一处理组内观测值与处理组均值之间的离散程度，其计算公式为：SSE = Σ((xi - xk)^2)其中，xi代表每个观测值，xk代表每个处理组的均值，Σ代表求和。

四、总均方 (Mean Square Total, MST)总均方用来衡量所有观测值与总均值之间的离散程度，其计算公式为：MST = SST / (N - 1)其中，SST代表总平方和，N代表总观测值个数。

五、处理组均方 (Mean Square Between, MSB)处理组均方用来衡量不同处理组之间的均值差异，其计算公式为：MSB = SSB / (k - 1)其中，SSB代表处理组平方和，k代表处理组的个数。

六、误差均方 (Mean Square Error, MSE)误差均方用来衡量同一处理组内观测值与处理组均值之间的离散程度，其计算公式为：MSE = SSE / (N - k)其中，SSE代表误差平方和，N代表总观测值个数，k代表处理组的个数。

单因素方差分析方法首先在单因素试验结果的基础上，求出总方差V 、组内方差vw、组间方差vB。

总方差 v=()2ijx x -∑组内方差 v w =()2ij x x i-∑ 组间方差 v B=b ()2ix x -∑从公式可以看出，总方差衡量的是所有观测值xij对总均值x 的偏离程度，反映了抽样随机误差的大小，组内方差衡量的是所有观测值xij对组均值x 的偏离程度，而组间方差则衡量的是组均值x i对总均值x 的偏离程度，反映系统的误差。

在此基础上，还可以得到组间均方差和组内均方差： 组间均方差2Bs ∧=1B-a v组内均方差 2ws∧=aab vw-在方差相等的假定下，要检验n 个总体的均值是否相等，须首先给定原假设和备择假设。

原假设 H：均值相等即μ1=μ2=…=μn备择假设H 1：均值不完全不相等则可以应用F 统计量进行方差检验：F=)()(b ab a vv w--1B =22∧∧ss WB该统计量服从分子自由度a-1，分母自由度为ab-a 的F 分布。

给定显著性水平a ，如果根据样本计算出的F 统计量的值小于等于临界值)(a ab 1a F --，α，则说明原假设H不成立，总体均值不完全相等，差异并非仅由随机因素引起。

下面通过举例说明如何在Excel 中实现单因素方差分析。

例1：单因素方差分析某化肥生产商需要检验三种新产品的效果，在同一地区选取3块同样大小的农田进行试验，甲农田中使用甲化肥，在乙农田使用乙化肥，在丙地使用丙化肥，得到6次试验的结果如表2所示，试在0.05的显著性水平下分析甲乙丙化肥的肥效是否存在差异。

表2 三块农田的产量甲 50 46 49 52 48 48 乙 49 50 47 47 46 49 丙515049465050要检验三种化肥的肥效是否存在显著差异，等同于检验三者产量的均值是否相等：给定原假设H：三者产量均值相等；备择假设H 1：三者的产量均不相等，对于影响产量的因素仅化肥种类一项，因此可以采用单因素方差分析进行多总体样本均值检验。

spss教程：单因素方差分析用来测试某一个控制变量的不同水平是否给观察变量造成显著差异和变动。

方差分析前提：不同水平下，各总体均值服从方差相同的正态分布。

所以方差分析就是研究不同水平下各个总体的均值是否有显著的差异。

统计推断方法是计算F统计量，进行F检验，总的变异平方和 SST，控制变量引起的离差SSA（Between Group离差平方和），另一部分随机变量引起的SSE（组内Within Group离差平方和），SST=SSA+SSE。

方法/步骤1.计算检验统计量的观察值和概率P_值：Spss自动计算F统计值，如果相伴概率P小于显著性水平a，拒绝零假设，认为控制变量不同水平下各总体均值有显著差异，反之，则相反，即没有差异。

2.方差齐性检验：控制变量不同水平下各观察变量总体方差是否相等进行分析。

采用方差同质性检验方法（Homogeneity of variance），原假设“各水平下观察变量总体的方差无显著差异，思路同spss两独立样本t检验中的方差分析”。

图中相伴概率0.515大于显著性水平0.05，故认为总体方差相等。

趋势检验：趋势检验可以分析随着控制变量水平的变化，观测变量值变化的总体趋势是怎样的，线性变化，二次、三次等多项式。

趋势检验可以帮助人们从另一个角度把握控制变量不同水平对观察变量总体作用的程度。

图中线性相伴概率为0小于显著性水平0.05，故不符合线性关系。

3.多重比较检验：单因素方差分析只能够判断控制变量是否对观察变量产生了显著影响，多重比较检验可以进一步确定控制变量的不同水平对观察变量的影响程度如何，那个水平显著，哪个不显著。

常用LSD、S-N-K方法。

LSD方法检测灵敏度是最高的，但也容易导致第一类错误（弃真）增大，观察图中结果，在LSD项中，报纸与广播没有显著差异，但在别的方法中，广告只与宣传有显著差异。

4.相似性子集：由图可知，划分的子集结果是一样的。

通常在相似性子集划分时多采用S-N-K方法的结论。

单因素方差分析的计算步骤步骤1：制定假设首先，我们需要明确研究的问题以及相应的假设。

通常，单因素方差分析的研究问题是判断不同组之间均值是否存在显著差异，即研究问题可以被表述为"不同组的均值是否相等"。

根据问题，我们可以制定空假设和备择假设。

空假设通常是"不同组的均值相等"，而备择假设通常是"不同组的均值不相等"。

步骤2：收集数据在进行单因素方差分析之前，我们需要收集相关数据。

收集数据的过程可能涉及实验设计、随机采样等方法。

数据的收集应该遵循一定的数据收集原则，以保证数据的真实性和可靠性。

步骤3：计算平均值第一步是计算每个组的平均值。

对于每个组，将其所有观测值相加，然后除以观测值的总数，即可得到该组的平均值。

计算每个组的平均值是了解数据分布和比较不同组均值的重要步骤。

步骤4：计算组内平方和接下来，我们需要计算组内平方和。

组内平方和表示每个组内各个观测值与该组平均值之差的平方的总和。

具体计算方法如下：-对于每个观测值，将其与该组的平均值相减，然后将结果平方。

-对于每个组，将每个观测值得到的平方差加起来，即得到该组的组内平方和。

-最后，将所有组的组内平方和相加，得到总的组内平方和。

步骤5：计算组间平方和接下来，我们需要计算组间平方和。

组间平方和表示不同组平均值之间的差异的平方的总和。

具体计算方法如下：-对于每个组，将其平均值与总体平均值相减，然后将结果平方。

-对于每个组，将每个计算得到的平方差相加，即得到该组的组间平方和。

-最后，将所有组的组间平方和相加，得到总的组间平方和。

步骤6：计算均方接下来，我们需要计算组内均方和组间均方。

组内均方是组内平方和除以自由度（总观测值数减去组数）得到的结果，而组间均方是组间平方和除以自由度（组数减去1）得到的结果。

步骤7：计算F值计算F值是判断组间均方和组内均方之间差异是否显著的重要步骤。

F值是组间均方除以组内均方计算得到的结果。

spss教程：单因素方差分析用来测试某一个控制变量的不同水平是否给观察变量造成显著差异和变动。

方差分析前提：不同水平下，各总体均值服从方差相同的正态分布。

所以方差分析就是研究不同水平下各个总体的均值是否有显著的差异。

统计推断方法是计算F统计量，进行F检验，总的变异平方和 SST，控制变量引起的离差SSA（Between Group离差平方和），另一部分随机变量引起的SSE（组内Within Group离差平方和），SST=SSA+SSE。

方法/步骤1.计算检验统计量的观察值和概率P_值：Spss自动计算F统计值，如果相伴概率P小于显著性水平a，拒绝零假设，认为控制变量不同水平下各总体均值有显著差异，反之，则相反，即没有差异。

2.方差齐性检验：控制变量不同水平下各观察变量总体方差是否相等进行分析。

采用方差同质性检验方法（Homogeneity of variance），原假设“各水平下观察变量总体的方差无显著差异，思路同spss两独立样本t检验中的方差分析”。

图中相伴概率0.515大于显著性水平0.05，故认为总体方差相等。

趋势检验：趋势检验可以分析随着控制变量水平的变化，观测变量值变化的总体趋势是怎样的，线性变化，二次、三次等多项式。

趋势检验可以帮助人们从另一个角度把握控制变量不同水平对观察变量总体作用的程度。

图中线性相伴概率为0小于显著性水平0.05，故不符合线性关系。

3.多重比较检验：单因素方差分析只能够判断控制变量是否对观察变量产生了显著影响，多重比较检验可以进一步确定控制变量的不同水平对观察变量的影响程度如何，那个水平显著，哪个不显著。

常用LSD、S-N-K方法。

LSD方法检测灵敏度是最高的，但也容易导致第一类错误（弃真）增大，观察图中结果，在LSD项中，报纸与广播没有显著差异，但在别的方法中，广告只与宣传有显著差异。

4. 相似性子集：由图可知，划分的子集结果是一样的。

通常在相似性子集划分时多采用S-N-K 方法的结论。

单因素方差分析公式的详解整理在统计学中，方差可以用来衡量一组数据的离散程度。

而单因素方差分析是一种常用的统计方法，用于比较不同组之间均值是否存在显著差异。

本文将详细介绍单因素方差分析的公式和其计算步骤。

一、方差分析的基本假设在进行单因素方差分析之前，我们需要明确一些基本假设。

首先，我们假设各组数据满足正态分布，并且方差相等。

其次，我们假设各组之间是相互独立的。

最后，我们需要定义显著性水平，即确定拒绝原假设的临界值。

二、总体方差的计算总体方差（Total Variance）用来衡量所有数据点与总体均值之间的离散程度。

它可以通过计算每个数据点与总体均值之间的差的平方和来得到。

若有n个观测值，总体方差的计算公式如下：\[SS_{Total} = \sum_{i=1}^{n} (X_i - \overline{X})^2\]其中，\(X_i\) 表示第i个观测值，\(\overline{X}\) 表示总体均值。

三、组内方差的计算组内方差（Within-Group Variance）用来衡量同一组内数据点与组内均值之间的离散程度。

它可以通过计算每个数据点与组内均值之间的差的平方和来得到。

若第i组有m个观测值，组内方差的计算公式如下：\[SS_{Within} = \sum_{j=1}^{m} (X_{ij} - \overline{X}_i)^2\]其中，\(X_{ij}\) 表示第i组的第j个观测值，\(\overline{X}_i\) 表示第i组的均值。

四、组间方差的计算组间方差（Between-Group Variance）用来衡量不同组之间数据点与组间均值之间的离散程度。

它可以通过计算每个组的均值与总体均值之间的差的平方和来得到。

若有k组数据，组间方差的计算公式如下：\[SS_{Between} = \sum_{i=1}^{k} m_i (\overline{X}_i -\overline{X})^2\]其中，\(m_i\) 表示第i组的观测值个数，\(\overline{X}_i\) 表示第i组的均值，\(\overline{X}\) 表示总体均值。

方差分析公式单因素与多因素方差分析的关键公式方差分析是一种统计方法，用于比较不同因素对变量的影响是否显著。

通过方差分析，我们可以确定不同因素之间是否存在统计学差异，并进一步研究这些差异的来源。

在方差分析中，单因素与多因素方差分析是两种常见的方法。

本文将介绍这两种方差分析中的关键公式。

一、单因素方差分析公式在单因素方差分析中，我们只考虑一个因素对变量的影响。

假设我们有k个水平（或组），每个水平下有n个观测值。

那么总观测值的个数为N=k*n。

在进行单因素方差分析之前，我们需要计算以下几个统计量：1. 总平方和（SST）：表示所有观测值与整体均值之间的差异的总和。

计算公式为：SST = Σ(Σ(x_ij - X¯)^2)其中，x_ij表示第i组的第j个观测值，X¯表示所有观测值的均值。

2. 组间平方和（SSB）：表示各组均值与整体均值之间的差异的总和。

计算公式为：SSB = Σ(n_i * (X¯_i - X¯)^2)其中，n_i表示第i组的观测值个数，X¯_i表示第i组的均值。

3. 组内平方和（SSW）：表示每组内个体与组内均值之间的差异的总和。

计算公式为：SSW = Σ(Σ(x_ij - X¯_i)^2)其中，x_ij表示第i组的第j个观测值，X¯_i表示第i组的均值。

根据以上统计量，我们可以计算方差分析的F值，来判断组间差异是否显著。

F值的计算公式为：F = (SSB / (k-1)) / (SSW / (N - k))其中，k表示组数，N表示总观测值的个数。

二、多因素方差分析公式在多因素方差分析中，我们考虑两个或两个以上的因素对变量的影响。

假设我们有r个因素，每个因素有k个水平（或组）。

那么总观测值的个数为N = k^r。

在进行多因素方差分析之前，我们需要计算以下几个统计量：1. 总平方和（SST）：表示所有观测值与整体均值之间的差异的总和。

方差分析中的重要公式概览与详解方差分析是一种用于比较两个或多个样本均值是否存在差异的统计方法。

在实际应用中，方差分析通常需要借助一些重要的公式来计算和解释结果。

本文将从公式的角度来概览与详解方差分析中的重要公式。

一、单因素方差分析的公式在单因素方差分析中，我们有一个自变量（或因素）和一个因变量（或结果变量），我们希望比较不同水平的自变量对因变量的影响是否存在显著差异。

以下是单因素方差分析中的重要公式：1. 总平方和（Total Sum of Squares，SST）：总平方和表示因变量的总变异程度。

计算公式如下：SST = ∑(Xi - Xavg)^2其中，Xi表示每个观测值，Xavg表示所有观测值的平均值。

2. 组内平方和（Within-group Sum of Squares，SSW）：组内平方和表示各组内的变异程度。

计算公式如下：SSW = ∑(Xij - Xig)^2其中，Xij表示第i组中第j个观测值，Xig表示第i组中所有观测值的平均值。

3. 组间平方和（Between-group Sum of Squares，SSB）：SSB = SST - SSW4. 平均平方（Mean Square，MSW和MSB）：平均平方是组内和组间平方和除以自由度（df）得到的。

计算公式如下：MSW = SSW / dfWMSB = SSB / dfB其中，dfW表示组内自由度，即总观测数减去组数；dfB表示组间自由度，即组数减去1。

5. F统计量（F-statistic）：F统计量用于判断因变量在不同水平的自变量上是否存在显著差异。

计算公式如下：F = MSB / MSW其中，MSB为组间均方，MSW为组内均方。

二、多因素方差分析的公式在多因素方差分析中，我们有两个或两个以上的自变量，我们希望研究这些自变量对因变量的影响是否存在显著差异。

以下是多因素方差分析中的重要公式：1. 总平方和（Total Sum of Squares，SST）：SST = ∑(Xi - Xavg)^2其中，Xi表示每个观测值，Xavg表示所有观测值的平均值。

单因素方差分析检验单因素方差分析（One-Way ANOVA）是一种常用的统计方法，用于比较两个或多个组之间的平均值是否存在差异。

它是一种非参数方法，不需要对数据做任何假设，适用于测量数据。

在本文中，我们将详细介绍单因素方差分析的原理、步骤以及如何进行结果解读。

1.原理：-零假设（H0）：各组的均值相等，即总体均值相等。

-备择假设（H1）：至少有两组的均值不相等，即总体均值不相等。

2.步骤：-收集数据：收集每个组的样本数据，并确保数据满足方差分析的基本假设。

-计算总平均值：计算所有样本数据的平均值，并计算每个组的平均值。

-计算组内和组间的变异：计算组内的变异，即每个组内个体与该组的平均值之差的平方和。

同时计算组间的变异，即所有组的平均值与总平均值之差的平方和。

- 计算均方：将组内变异和组间变异除以自由度，得到组内均方（Mean Square Within，MSW）和组间均方（Mean Square Between，MSB）。

-计算计算统计量F：计算计算统计量F，即组间均方与组内均方的比值。

-比较P值：通过查找F分布表，得到计算统计量F对应的P值。

-结果解读：如果P值小于显著性水平（通常为0.05），则拒绝零假设，接受备择假设，认为至少有两组的均值不相等。

3.结果解读：通过单因素方差分析得到的结果通常包括以下几个方面：-F值：表示组间变异相对于组内变异的大小。

F值越大，说明组间的差异越大。

-P值：表示观察到的F值对应的概率。

P值越小，说明组间差异的显著性越高。

-自由度：组间自由度为组数减1，组内自由度为总样本量减去组数。

-均方：组间均方与组内均方用于计算计算统计量F。

如果P值小于显著性水平（通常为0.05），则可以拒绝零假设，接受备择假设，认为至少有两组的均值存在差异。

否则，在统计学意义上无法得出两个或多个组均值之间的差异。

总之，单因素方差分析是一种比较两个或多个组平均值差异的非参数统计方法。

它可以帮助我们了解不同组之间的差异性，从而做出更准确的决策。