下载文档原格式
minitab实验之试验设计Minitab 实验之试验设计实验目的：本实验主要引导学生利用Minitab 统计软件进行试验设计分析，包括全因子设计、部分因子设计、响应曲面设计、混料设计、田口设计以及响应优化，并能够对结果做出解释。
实验仪器：Minitab 软件、计算机实验原理：“全因子试验设计”（full factorial design）的定义是：所有因子的所有水平的所有组合都至少要进行一次试验的设计。
由于包含了所有的组合，全因子试验所需试验的总次数会比较多，但它的优点是可以估计出所有的主效应和所有的各阶交互效应。
所以在因子个数不太多，而且确实需要考察较多的交互作用时，常常选用全因子设计。
一般情况下，当因子水平超过 2 时，由于试验次数随着因子个数的增长而呈现指数速度增长，因而通常只作 2 水平的全因子试验。
进行 2 水平全因子设计时，全因子试验的总试验次数将随着因子个数的增加而急剧增加，例如，6 个因子就需要 64 次试验。
但是仔细分析所获得的结果可以看出，建立的 6 因子回归方程包括下列一些项：常数项、主效应项有 6 项、二阶交互作用项 15 项、三阶交互项 20 项，…，6 阶交互项1 项，除了常数项、主效应项和二阶交互项以外，共有42 项是 3 阶以及 3 阶以上的交互作用项，而这些项实际上已无具体的意义了。
部分因子试验就是在这种思想下诞生的，它可以使用在因子个数较多，但只需要分析各因子和 2 阶交互效应是否显著，并不需要考虑高阶的交互效应，这使得试验次数大大减少。
在实际工作中，常常要研究响应变量 Y 是如何依赖于自变量，进而能找到自变量的设置使得响应变量得到最佳值（望大、望小或望目）。
如果自变量的个数较少（通常不超过3 个），则响应曲面方法（response surface methodology， RSM）是最好的方法之一，本方法特别适合于响应变量望大或望小的情形。
通常的做法是：先用 2 水平因子试验的数据，拟合一个线性回归方程（可以包含交叉乘积项），如果发现有弯曲的趋势，则希望拟合一个含二次项的回归方程。
Minitab做实验设计（DOE）（田口法）（3因子3水平）编著：鲁仁山2007.12.271．双击桌面上的Minitab图标。
2．这是打开后的界面。
3.如上所示，将资料输入表中。
4. 数据输入完毕，打开Stat菜单，点选DOE Taguchi Create Taguchi Design…5. 这是弹出的界面。
6.根据水平的数量点选相应的水平设计，根据因子的数量点选相应的数字，然后按下Designs…按钮。
7.在弹出的界面上点选相应的正交方案，本例点选L9，然后按OK确认。
8. 这是弹出的界面，之前的灰色按钮（未激活）的已全部激活，按下Factors按钮。
9. 这是弹出的界面。
10．如图所示，将资料输入弹出的界面，然后按OK确认。
11.按下Options按钮，这是弹出的界面。
12. 如图所示，钩选Store design in worksheet，然后按OK确认。
13.这是弹出的实验设计组合排列表。
14.将根据实验组合进行实验得到的实验数据作为响应填入表中。
15. 打开Stat菜单，点选DOE Taguchi Analyze Taguchi Design…16. 这是弹出的界面。
17.在Response data are in处填入响应所在的栏位号，然后按下Graphs…18. 这是弹出的界面。
19.根据需要，如图所示点选相应的项目，按OK确认，然后按下Analysis。
20. 这是弹出的界面。
21. 根据需要，如图所示点选相应的项目，按OK确认，然后按下Terms。
22. 这是弹出的界面。
23. 如图所示点选相应的项目，按OK确认，然后按下已激活的Analysis Graphs。
24. 这是弹出的界面。
25. 如图所示点选相应的项目，按OK确认，然后按下Options。
26. 如图所示点选相应的项目，按OK确认，然后按下Storage。
27. 这是弹出的界面。
28. 如图所示点选相应的项目，按全部OK确认。
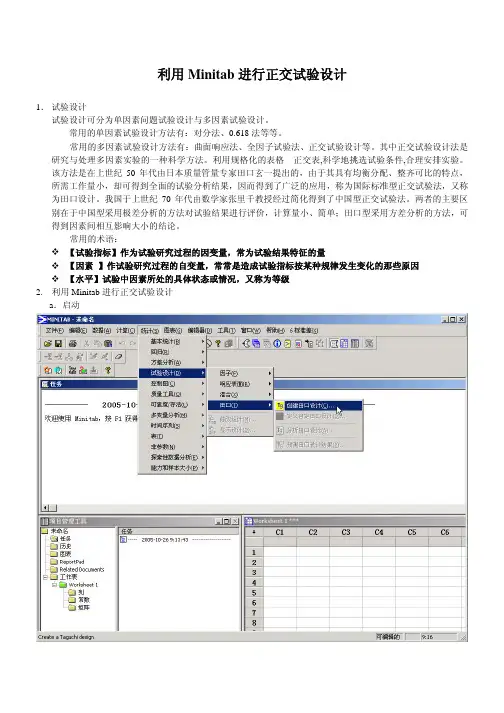
利用Minitab进行正交试验设计1．试验设计试验设计可分为单因素问题试验设计与多因素试验设计。
常用的单因素试验设计方法有：对分法、0.618法等等。
常用的多因素试验设计方法有：曲面响应法、全因子试验法、正交试验设计等。
其中正交试验设计法是研究与处理多因素实验的一种科学方法。
利用规格化的表格—正交表,科学地挑选试验条件,合理安排实验。
该方法是在上世纪50年代由日本质量管量专家田口玄一提出的，由于其具有均衡分配、整齐可比的特点，所需工作量小，却可得到全面的试验分析结果，因而得到了广泛的应用，称为国际标准型正交试验法，又称为田口设计。
我国于上世纪70年代由数学家张里千教授经过简化得到了中国型正交试验法。
两者的主要区别在于中国型采用极差分析的方法对试验结果进行评价，计算量小、简单；田口型采用方差分析的方法，可得到因素间相互影响大小的结论。
常用的术语：【试验指标】作为试验研究过程的因变量，常为试验结果特征的量【因素】作试验研究过程的自变量，常常是造成试验指标按某种规律发生变化的那些原因【水平】试验中因素所处的具体状态或情况，又称为等级2. 利用Minitab进行正交试验设计a．启动b．创建正交设计表在这里选择3－Level Design，在因素数量上选择4 factors。
选择正交设计试验表，选Design：选择L9_3_4正交表设计：进行因素设计，选择Factor。
对因素名称和水平值进行设定，也可以不进行设定。
在options选项中选择将设计保存于工作表。
点击ok，在工作表区生成所需正交表。
在新的一列加入试验指标－试验结果。
并将试验结果的数据输入。
对试验结果进行分析，选择Analyze Taguchi Design。
出现分析设计对话框。
点击“选择”所要评价的试验指标。
设定分析的“选项”，这里选“望大”。
点击“确定”进行分析，在任务窗口出现均值和信噪比的分析结果，从结果可以看出磨制时间对指标的影响最大。
食品科学研究中实验设计的案例分析——正交设计优选白芨多糖包合丹皮酚最佳工艺以及包合物的鉴定[1]摘要：本实验采用用minitab软件设计L9(34)正交试验优选白芨多糖包合丹皮酚的最佳工艺，结果显示：以丹皮酚和白芨多糖的物料比、反应时间和反应温度为考察指标，得到优化工艺为：物料比1:6、反应时间4h、温度30℃，包封率可达29.38%，收得率74.29%。
关键词：正交设计 minitab1 正交试验因素水平的确定选择丹皮酚与白芨多糖的A物料比(W/W)、B反应时间(h)、C包合温度(℃)三个对试验结果影响较大的因素为考察对象，每个因素各取三个水平(表1)。
采用L9(34)正交试验表进行正交试验。
以所得包合物的收得率和药物包封率为考察指标，确定最佳工艺。
表一正交试验因素水平表水平因素A物料比（w/w）B反应时间（h）C反应温度（℃）1 1：2 2 302 1：43 403 1：64 502 正交试验设计步骤：1 选择统计—＞DOE—＞田口—＞创建田口设计。
2 得出田口设计窗口，在这个窗口中我们可以设计正交试验，本试验选择3水平4因素，其中一个因素作为误差列。
3 点击显示可用设计，进入如下图的窗口，选择L9 2-44 点击“设计”选项，选择L9 3**4，这样我们就得到了L9(34)5 点击“因子”选项，得到如下图窗口，可以对其名称进行设计，如“A”改为“A物料比”6 设计完成，得到如下图的正交试验表7 导入数据（包封率和收得率）8 点击“DOE”—＞“田口”—＞“分析田口设计”，得到下图9 在响应数据位于栏中选择“包封率”10 在“项”选项中，选中A B C的内容，注意不要选中误差列，按下图进行设计。
11 点击确定，可得出下列的分析数据。
（再按上述8-11，对收得率进行分析，可得出另外一个分析数据）12 点击“统计”—＞“方差分析”—＞“一般线性模型”13 在“响应”栏中选择“包封率”,在“模型”栏中选择A B C D14 点击确定，得出方差分析数据，如下图。
Minitab实现有交互作用的正交实验的设计与结果分析一、本文概述Overview of this article正交实验设计是一种在多个因素中找出最优组合的高效实验设计方法。
通过正交表，我们可以合理安排实验，使得每个因素在每个水平下都能被充分考察，同时减少实验次数，提高实验效率。
在实际应用中，我们经常遇到有交互作用的因素，即两个或多个因素同时作用时，它们的效果会发生变化。
因此，在正交实验设计中考虑交互作用至关重要。
Orthogonal experimental design is an efficient experimental design method that finds the optimal combination among multiple factors. Through orthogonal tables, we can arrange experiments reasonably so that each factor can be fully examined at each level, while reducing the number of experiments and improving experimental efficiency. In practical applications, we often encounter interactive factors, that is, when two or more factors act simultaneously, theireffects will change. Therefore, considering interaction is crucial in orthogonal experimental design.本文将详细介绍如何在Minitab中实现有交互作用的正交实验设计，并对实验结果进行分析。
食品科学研究中实验设计的案例分析
——正交设计优选白芨多糖包合丹皮酚最佳工艺以及包合物的鉴定[1]
摘要：本实验采用用minitab软件设计L9(34)正交试验优选白芨多糖包合丹皮酚的最佳工艺，结果显示：以丹皮酚和白芨多糖的物料比、反应时间和反应温度为考察指标，得到优化工艺为：物料比1:6、反应时间4h、温度30℃，包封率可达29.38%，收得率74.29%。
关键词：正交设计 minitab
1 正交试验因素水平的确定
选择丹皮酚与白芨多糖的A物料比(W/W)、B反应时间(h)、C包合温度(℃)三个对试验结果影响较大的因素为考察对象，每个因素各取三个水平(表1)。
采用L9(34)正交试验表进行正交试验。
以所得包合物的收得率和药物包封率为考察指标，确定最佳工艺。
表一正交试验因素水平表
水平
因素
A物料比（w/w）B反应时间（h）C反应温度（℃）
1 1：
2 2 30
2 1：4
3 40
3 1：6
4 50
2 正交试验设计步骤：
1 选择统计—＞DOE—＞田口—＞创建田口设计。
2 得出田口设计窗口，在这个窗口中我们可以设计正交试验，本试验选择3水平4因素，其中一个因素作为误差列。
3 点击显示可用设计，进入如下图的窗口，选择L9 2-4
4 点击“设计”选项，选择L9 3**4，这样我们就得到了L9(34)
5 点击“因子”选项，得到如下图窗口，可以对其名称进行设计，如“A”改为“A物料比”
6 设计完成，得到如下图的正交试验表
7 导入数据（包封率和收得率）
8 点击“DOE”—＞“田口”—＞“分析田口设计”，得到下图
9 在响应数据位于栏中选择“包封率”
10 在“项”选项中，选中A B C的内容，注意不要选中误差列，按下图进行设计。
11 点击确定，可得出下列的分析数据。
（再按上述8-11，对收得率进行分析，可得出另外一个分析数据）
12 点击“统计”—＞“方差分析”—＞“一般线性模型”
13 在“响应”栏中选择“包封率”,在“模型”栏中选择A B C D
14 点击确定，得出方差分析数据，如下图。
15 重复上述动作，对收得率进行方差分析
2结果与分析
2.1原论文案例白芨多糖包合丹皮酚正交试验数据分析
白芨多糖包合丹皮酚的L9(34)正交试验结果见表2。
经SPSS15.0软件分析结果表明，以包封率为指标，投料比因素的极差最大，表明投料比的影响最大，各因素对包封率的影响程度依次为A(投料比)＞C(温度)＞B(时间)，且A因素对包封率的影响达到了显著性差异(p＜0.05)( 表3) 。
由此分析，此包合反应条件的最佳组合为A3B3C1。
以收得率为指标，投料比因素的极差也最大，投料比的影响最大，各因素对收得率的影响
依次为A＞C＞B。
最佳组合为A3B3C3。
综合考虑包封率和收得率两个指标，投料比对包封率的影响显著(p＜0.05)，对收得率的影响较大，投料比和时间选择一致的A3和B3。
从节约能源又不太影响结果的角度考虑，温度选择30℃。
所以最佳组合应为A3B3C1，即投料比1:6、包合时间4h、温度30℃、在此条件，包封率达29.39%，收得率74.29%。
按照选取的白芨多糖包合丹皮酚的优化工艺条件(A3B3C1)制备3批样品，结果白芨多糖包合丹皮酚：收得率的均值为74.37%，包封率均值为30.12%均明显优于正交试验的其他组，可以验证正交试验的结果。
2.2本人对白芨多糖包合丹皮酚正交试验数据分析
表2 正交试验直观分析图
序列号A物料比B反应时
间
C反应温
度D误差包封率%
收得
率 %
1 1 1 1 1 8.54 54.67
2 1 2 2 2 4.6
3 50.67
3 1 3 3 3 4.3
4 58
4 2 1 2 3 20.36 70
5 2 2 3 1 15.81 69.6
6 2 3 1 2 27.65 70.4
7 3 1 3 2 17.85 78
8 3 2 1 3 29.39 74.29
9 3 3 2 1 21.01 73.71
包封率% k1=5.837 15.583 21.86 k2=21.273 16.61 15.333 k3=22.750 17.667 12.667 R=16.913 2.083 9.193
收得率% k1=54.45 67.56 66.45
k2=70.00 64.85 64.79
k3=75.33 67.37 68.37
R=20.89 2.7 3.74
表3.1 以包封率为指标的方差分析
来源自由度误差平方和
SS
调整后的
SS
调整后的均方
MS F P
A物料比 2 526.53 526.53 263.27 41.33 0.024 * B反应时
间 2 6.51 6.51 3.26 0.51 0.662
C反应温
度 2 134.23 134.23 67.11 10.54 0.087
误差 2 12.74 12.74 6.37
合计8 680.01
S = 2.52375 R-Sq = 98.13% R-Sq（调整） = 92.51%
表3.2 以收得率为指标的方差分析
来源自由度误差平方和
SS
调整后的
SS
调整后的均方
MS F P
物料比 2 706.6 706.6 353.3 211.05 0.005 ** 反应时间 2 13.68 13.68 6.84 4.08 0.197
反应温度 2 21.07 21.07 10.53 6.29 0.137
误差 2 3.35 3.35 1.67
合计8 744.7
S = 1.29384 R-Sq = 99.55% R-Sq（调整） = 98.20%
白芨多糖包合丹皮酚的L9(34)正交试验结果见表2。
经minitab15.0软件分析结果表明，以包封率为指标，投料比因素的极差最大，表明投料比的影响最大，各因素对包封率的影响程度依次为A(投料比)＞C(反应温度)＞B(反应时间)，且A因素对包封率的影响达到了显著性差异(p＜0.05)。
由此分析，此包合反应条件的最佳组合为A3C1B3。
以收得率为指标，投料比因素的极差也最大，投料比的影响最大，各因素对收得率的影响依次为A＞C＞B，最佳组合为A3C3B1，原论文案例出现的错误是包合物收得率对B反应时间的k1和k3求法有误，两者结果正好相反，由此得出的最佳组合是有误的，经校正后的结果是最佳组合是A3C3B1。
综合考虑包封率和收得率两个指标，投料比对包封率的影响显著(p＜0.05)，对收得率的影响极显著，投料比选择A3,根据包封率和收得率的方差分析可知，只有投料比呈显著关系，反应时间和反应温度都不呈显著关系。
从节约能源又不太影响结果的角度考虑，温度选择30℃。
故选择的组合为A3B2C1即投料比1:6、反应时间4h、温度30℃、在此条件，包封率达29.39%，收得率74.29%。
参考文献
[1] 王如平,吴婷,张卫明等.正交设计优选白芨多糖包合丹皮酚最佳工艺以及包合物的鉴定[J].食品科学,2008,29(12):259-263.。
