2扩展式博弈与标准式博弈

1博弈的分类博弈模型一般分为合作博弈( cooperative game )和非合作博弈( non- cooperativegame),如图。

合作博弈是以单个参与者的可能行动集合为基本元素，而非合作博弈是以参与人群的可能联合行动集合为基本元素( Martin and Ariel Rub in stein ，2000, P2),也就是说，在合作博弈中，博弈中所有参与者都独立行动，不存在有约束力的合作、联合或联盟的关系，而在非合作博弈中，在一些参与者之间存在着有约束力的合作、联合或联盟的关系，并因为这种关系影响到博弈的结局。

合作博弈强调的是团体理性( collectiverati on ality )、效率、公正和公平；非合作博弈强调的是个人理性、个人最优决策，其结果可能是有效率的，也可能是低效率或无效率的(张维迎，1996，P5)。

20世纪50年代，合作博弈的研究达到鼎盛期，同时开始出现对非合作博弈的研究，此后，博弈论的研究主流逐步转向在非合作博弈领域。

有些人认为非合作博弈模型比合作博弈更“基本”，但有些人认为两者不相上下(Martin and Ariel Rubinstein ，2000，P2)。

合作博弈，有时也叫做联盟博弈( coalitional game )，一般根据有无转移支付而分为两类：可转移支付联盟博弈( coalitio nal game with tran sferable payoff )和不可转移支付联盟博弈(coalitional game with non-transferable payoff )。

可转移支付也叫有旁支付(side payment )，可转移支付联盟博弈假设博弈中各参与者都用相同的尺度来衡量他们的赢得，且各联盟的赢得可以按任意方式在联盟成员中分摊；否则，就是不可转移支付联盟博弈。

可转移支付合作博弈合作博弈不可转移支付合作博、非合作博弈非合作博弈的分类主要从两个角度进行划分。

博弈论策略的扩展式和战略式表述下载温馨提示:该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by theeditor.I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!博弈论策略的扩展式与战略式表述：深度解析博弈论，作为经济学、社会学、心理学等领域的核心理论工具，主要研究决策者在相互影响的环境下如何做出选择。

博弈论的发展历程虽然早在18世纪初以前便开始了对具有策略依存特点的决策问题的零星研究，但博弈论真正的发展还是在20世纪。

20世纪初期是博弈论的萌芽阶段，其研究对象主要是从竞赛与游戏中引申出来的严格竞争博弈，即二人零和博弈。

这类博弈中不存在合作或联合行为，对弈两方的利益严格对立，一方所得必意味着存在另一方的等量损失。

这符合下棋等二人室内游戏的情形，但应用在经济与政治上，则大多数情况并不合适。

此时，关于二人零和博弈理论有丰硕的研究成果，尤其是提出了博弈扩展型策略、混合策略等重要概念，为日后研究对象范围的拓展与研究的深化奠定了基础。

这一阶段最重要的成就是泽梅罗定理（1913）与冯·诺伊曼的最小最大定理（1928），后者为二人零和博弈提供了解法，同时对博弈论的发展产生了重大影响，例如非合作几人博弈中的基本概念——纳什均衡就是最小最大定理的延伸与推广。

1944年，美国数学家冯·诺伊曼（Von Neumann）和摩根斯坦（Morgensien）合著的《博弈论与经济行为》一书的出版，标志着系统的博弈理论的初步形成。

该巨著汇集了当时博弈论的研究成果，将其框架首次完整而清晰地表述出来，使其作为一门学科获得了应有的地位。

同时身为经济学家的摩根斯顿首先清楚而全面地确认，经济行为者在决策时应考虑到经济学上的利益冲突性质。

该书详尽地讨论了二人零和博弈，并对合作博弈作了深入探讨，开辟了一些新的研究领域。

更重要的是将博弈论加以空前广泛的应用，尤其是在经济学上，由于博弈论数学上的严整性与经济学应用上的广泛性，一些经济学家将该巨著的出版视为数理经济学确立的里程碑。

接下来的一段时期对合作博弈的研究有了长足进步。

按豪尔绍尼（1966）的观点，如果一博弈中意愿表示——协议、承诺、威胁——具有完全的约束力并可强制执行，则该博弈是合作的。

如意愿表示不可强制执行，则为非合作博弈。

非合作博弈随后发展起来，纳什、泽尔滕和豪尔绍尼因此而获奖，但当时注意力主要集中在合作博弈上。

博弈论的extensive form博弈论是研究具有相互冲突和合作元素的情境下的决策制定的数学理论。

在博弈论中，一个游戏（博弈）可以被表示为扩展式（extensive form）或标准式（normal form）。

扩展式博弈也被称为树形结构，它详细地描述了游戏的所有可能的决策过程和时间顺序。

在扩展式博弈中，每个玩家根据游戏的历史（从根节点到当前决策点的路径）做出选择。

这种表示方法允许捕捉到玩家之间的行动顺序和信息传递，非常适合描述具有时间序列和信息不完全的动态决策过程。

扩展式博弈的主要组成部分包括：1. 历史（History）：历史是一个有序集合，表示从博弈的开始到当前决策点所采取的行动序列。

在扩展式博弈的树形结构中，历史从根节点开始，每个节点代表一个决策点，节点之间的路径代表了行动的历史。

2. 玩家函数（Player Function）：玩家函数P(h) 定义了在历史h 之后做出决策的玩家。

在扩展式博弈中，玩家函数确保了在每一个决策点，只有一个玩家负责做出选择。

3. 纯策略（Pure Strategy）：纯策略是玩家在每个决策点上可能采取的行动集合。

一个玩家在扩展式博弈中的纯策略可以被表示为一个函数，该函数将历史映射到一个具体的选择上。

4. 博弈长度（Length of the Game）：博弈长度l(G) 是指从根节点到叶节点的最长路径长度，它代表了博弈的持续时间。

扩展式博弈的优点在于它能够精确地描述玩家之间的决策顺序和信息结构，但它也有可能变得非常复杂，尤其是在参与者数量多或者决策序列长的情况下。

尽管如此，扩展式博弈是分析具有时序特征和信息不完全的决策问题的有力工具，特别是在经济学、政治学、心理学和人工智能等领域。

第2章扩展式博弈与标准式博弈标准式：博弈过程以数字矩阵表示，矩阵两侧为参与者的不同的战略选择扩展式：博弈过程以树形图表示，树形图的每一树枝节代表了一种战略选择不确定事件：可能发生也可能不发生的事件相机战略：仅在不确定事件发生时才会采取的战略。

在扩展式博弈中，只要博弈的一方在不知情的情况下决策，或者同时决策，我们就将其所有的选择都列在从一个节点出发的分支中，以此表示信息的不充分（标准式：博弈过程以数字矩阵表示，矩阵两侧为参与者的不同的战略选择，往往用于表达静态博弈表达动态博弈）第3章占优战略与社会两难占优战略：无论其他参与人选择什么战略，参与人的某一种战略均是最优的。

占优战略均衡：如果博弈中的每位参与者都有占优战略，并且也实施其占优战略，我们就可以获得一个占优战略均衡。

合作解：不管是通过协议还是其他形式的强制手段，只要博弈中的参与者能够保证自己履行协调后的战略，那么他们选择的战略及其收益就被称作合作解非合作解：占优战略均衡是一种非合作解，也就是说每位参与者都独立行动，而不是一起协商其战略。

在非合作解中，每位参与者都会根据对方的战略选择自己的最优战略假定所有人都这样做那么每一位参方的战略选择自己的最优战略，假定所有人都这样做，那么每位参与者所选的战略就都是针对他人最优战略的最优反应。

（参与者在行动选择时无法达成约束性的协议的解集。

）社会两难：社会两难是一种存在占优战略均衡的博弈，并且参与者采用这种均衡的战略收益比采用非均衡战略的收益要差。

（当一个博弈存在占优战略时，人们就会理所当然地选择该战略而不是另一个。

囚徒困境与垃圾处理博弈非常相似这些博弈都属于社会两难理博弈非常相似，这些博弈都属于社会两难。

）第4章纳什均衡纳什均衡：给定你的策略，我的策略是最好的策略；给定我的策略，你的策略也是最好的策略，即双方在给定的战略上不愿意改变自己的策略。

纳什均衡战略：如果有两个战略（或者更一般的，有多个战略，每个战略都对应着一个参与者），并且每个战略都是另一个战略（或者其他参与者的战略）的最优反应，我们就称这一战略组合为纳什均衡战略。

博弈论知识总结博弈论概述：1、博弈论概念：博弈论：就是研究决策主体的行为发生直接相互作用时的决策以及这种决策的均衡问题。

博弈论研究的假设：1、决策主体是理性的，最大化自己的收益。

2、完全理性是共同知识3、每个参与人被假定为可以对所处环境以及其他参与者的行为形成正确的信念与预期2、和博弈有关的变量：博弈参与人：博弈中选择行动以最大化自己受益的决策主体。

行动：参与人的决策选择战略：参与人的行动规则，即事件与决策主体行动之间的映射，也是参与人行动的规则。

信息：参与人在博弈中的知识，尤其是其他决策主体的战略、收益、类型（不完全信息）等的信息。

完全信息：每个参与人对其他参与人的支付函数有准确的了解；完美信息：在博弈过程的任何时点每个参与人都能观察并记忆之前各局中人所选择的行动，否则为不完美信息。

不完全信息：参与人没有完全掌握其他参与人的特征、战略空间及支付函数等信息，即存在着有关其他参与人的不确定性因素。

支付：决策主体在博弈中的收益。

在博弈中支付是所有决策主题所选择的行动的函数。

从经济学的角度讲，博弈是决策主体之间的相互作用，因此和传统个人决策存在着区别：3、博弈论与传统决策的区别：1、传统微观经济学的个人决策就是在给定市场价格、消费者收入条件下，最大化自己效用，研究工具是无差异曲线。

可表示为：maxU(P,I)，其中P为市场价格，I为消费者可支配收入。

2、其他消费者对个人的综合影响表示为一个参数——市场价格，所以在市场价格既定下，消费者效用只依赖于自己的收入和偏好，不用考虑其他消费者的影响。

但是在博弈论理个人效用函数还依赖于其他决策者的选择和效用函数。

4、博弈的表示形式：战略式博弈和扩展式博弈战略式博弈：是博弈问题的一种规范性描述，有时亦称标准式博弈。

战略式博弈是一种假设每个参与人仅选择一次行动或战略，并且参与人同时进行选择的决策模型，因此，从本质上来讲战略式博弈是一种静态模型，一般适用于描述不需要考虑博弈进程的完全信息静态博弈问题。

博弈模型扩展式-回复什么是博弈模型扩展式？博弈模型扩展式是指在传统的博弈模型基础上，通过增加相关规则、参与者或策略等因素，对博弈模型进行扩展和延伸的一种理论框架。

扩展式的博弈模型可以更好地描述现实世界中的复杂决策场景，使得博弈论在经济学、管理学、政治学等领域的应用更为广泛。

一、基础的博弈模型在介绍博弈模型扩展式之前，我们先简要回顾一下基础的博弈模型。

基础的博弈模型主要由参与者、策略和收益函数构成。

参与者根据收益函数和其他参与者的策略来选择自己的策略，并且最终根据收益函数来分配收益。

传统的博弈模型包括纳什均衡、博弈矩阵和博弈树等。

但是这些模型在描述现实中一些复杂情况时存在局限性。

二、增加的参与者在博弈模型中，我们可以通过增加参与者的数量来扩展博弈模型。

通常，博弈模型中的参与者被视为独立决策实体，他们根据自己的利益来选择策略。

然而，在现实生活中，存在许多博弈模型中没有考虑到的共同利益或合作关系。

因此，将更多的参与者纳入博弈模型可以更好地反映出现实情况中的决策情景。

例如，在环境保护领域的博弈中，传统模型只考虑了公司在追求利润最大化的同时对环境的影响。

然而，在现实中，政府和非政府组织等参与者对环境保护同样关注。

因此，我们可以通过增加政府和非政府组织等参与者，构建一个多参与者博弈模型，以更好地分析环境保护政策的制定和实施。

三、引入动态策略除了增加参与者，我们还可以通过引入动态策略来扩展博弈模型。

在传统的博弈模型中，参与者只能在某个时刻选择自己的策略，并且这个选择是一次性的，不可更改的。

然而，在现实生活中，很多决策是连续的，参与者可以根据其他参与者的策略变化来调整自己的策略。

例如，在股市投资中，投资者的决策往往是连续的，他们会根据市场走势和其他投资者的行为来调整自己的投资策略。

因此，我们可以通过引入动态策略，构建一个连续时间博弈模型，以更好地分析股市中的投资决策。

四、考虑不完全信息博弈模型扩展式还可以考虑参与者之间的信息不对称问题。

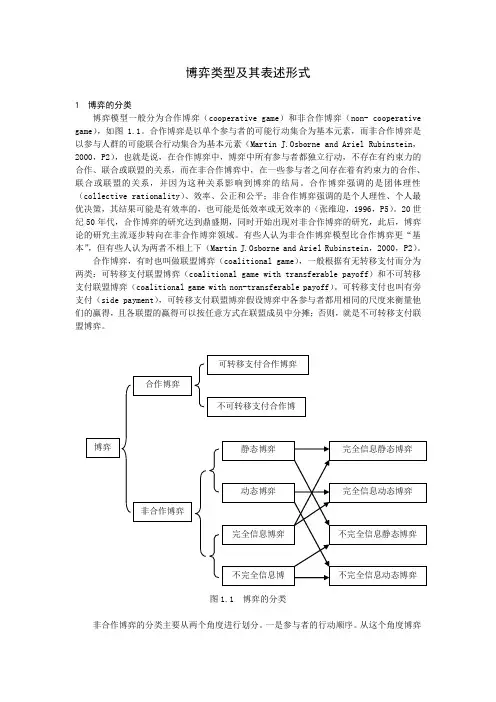
博弈类型及其表述形式1 博弈的分类博弈模型一般分为合作博弈（cooperative game ）和非合作博弈（non- cooperative game ），如图1.1。

合作博弈是以单个参与者的可能行动集合为基本元素，而非合作博弈是以参与人群的可能联合行动集合为基本元素（Martin J.Osborne and Ariel Rubinstein ，2000，P2），也就是说，在合作博弈中，博弈中所有参与者都独立行动，不存在有约束力的合作、联合或联盟的关系，而在非合作博弈中，在一些参与者之间存在着有约束力的合作、联合或联盟的关系，并因为这种关系影响到博弈的结局。

合作博弈强调的是团体理性（collective rationality ）、效率、公正和公平；非合作博弈强调的是个人理性、个人最优决策，其结果可能是有效率的，也可能是低效率或无效率的（张维迎，1996，P5）。

20世纪50年代，合作博弈的研究达到鼎盛期，同时开始出现对非合作博弈的研究，此后，博弈论的研究主流逐步转向在非合作博弈领域。

有些人认为非合作博弈模型比合作博弈更“基本”，但有些人认为两者不相上下（Martin J.Osborne and Ariel Rubinstein ，2000，P2）。

合作博弈，有时也叫做联盟博弈（coalitional game ），一般根据有无转移支付而分为两类：可转移支付联盟博弈（coalitional game with transferable payoff ）和不可转移支付联盟博弈（coalitional game with non-transferable payoff ）。

可转移支付也叫有旁支付（side payment ），可转移支付联盟博弈假设博弈中各参与者都用相同的尺度来衡量他们的赢得，且各联盟的赢得可以按任意方式在联盟成员中分摊；否则，就是不可转移支付联盟博弈。

图1.1 博弈的分类非合作博弈的分类主要从两个角度进行划分。

博弈论的总结|博弈论总结博弈论学习的个人总结刘艳丽第一局部：根本情况视频耶鲁公开课《博弈论》1----5讲，人人影视参考资料：耶鲁校园网《博弈论--战略分析^p 入门》，美，罗杰A麦凯恩，原毅军译，机械工业出版社，2022，42元《策略博弈》，阿维纳什迪克西特，蒲勇健译，中国人民大学出版社，第二版，2022，65元班级：工商，人力08级学生课时：8节我的时间投入：视频26个小时；书籍，25小时；上网时间，无法统计。

第二局部：知识层面一、The five lessons：五个根本的结论1、Don"t play a strictly dominated strategy2、Rational choices can lead to bad outes3、You can"t get what you want4、Put yourself in other people"s shoes5、Yale students are evil二、Game 2: "pick a number."数字游戏Without showing your neighbor what you"re doing, put in the box below a whole number between 1 and a 100 [whole number between 1 and 100--integer.] We will calculate the average number chosen in the class. The winner in this game is the person whose number is closest to two-thirds times the average in the class.三、The Prisoners" Dilemma：some exles囚徒困境A joint projectPrice petitionA mon resourceGlobal warming and carbon emissionsmunication，contracts，treaties betweencountries，regulation，education cannot work Solutions OF The Prisoners" Dilemma： changing payoffs.改变收益构造四、The ingredients of a game：博弈的根本构造Players：i 、jStrategies："si" to be a particular strategy of Player iSi" to be the set of alternatives."s" to mean a particular play of the gamePayoffs："U" for utile, to be Player i"s payoff.the way up to Player N"s choices.profileS-i" to mean a strategy choice for everybody except person "i."Assume that everybody knows the possible strategies everyone else could choose and everyone knows everyone else"s payoffs五、如何寻找博弈平衡解1、成绩案例-----求解方法，如存在最优策略，那么选择最优。

引言博弈论简史。

博弈论是数字的分支，它实际上产生于1940年至1950年之间，并由约翰•冯纽曼所创立。

尽管起初该理论的大部分数学问题都专注于室内游戏，但其后又逐渐顾及人们之间战略互动的其他重要形式。

例如，约翰•纳什发展出一种解的概念，由此预测宏观经济学领域的行为，他因为这一贡献而获得诺贝尔奖。

博弈论也被理解为决策理论，因为与概率论关注机会相比较，博弈论更关注人们所作出的构成其追求结果的战略的一部分的决策。

为了简便起见，我们将只提博弈论，虽然从任何一点来讲它都可以替代决策理论。

博弈论涉及若干种数字科学的应用，包括概率、代数、微积分甚至几何。

博弈论应用已经拓展到法律、军事行动、经济、社会变革、政治理论等领域，并且应用到婚姻法这样一个很小的方面。

博弈论中的数学问题是复杂的，然而其基本原理并非如此。

在这个简要的概述中，我们将致力于讨论这些原理。

定义（A）什么是博弈［1］？1）必须有两个或者两个以上的参与人，他们在战略上相互关联。

所谓战略关联，意味着双方参与人之间的关系必须包括构成一个博弈的下述条件。

2）规则。

必须有参与人严格遵守的规则。

3）收益。

在通常的博弈理论中，收益实际上称为效用（效益），但收益是一个更易理解的概念。

作为博弈或者博弈的一部分（称为结）的结果，必须存在一个收益。

我们在此不用报酬一词，因为一个收益可能不是一个报酬，但可能只是简单比令人厌恶的结局稍强一些。

例如，一个罪犯承认一项较小的罪行不是争取某项报酬，而是更轻的处罚。

4）每方参与人必须拥有有用的与决策有关的战略。

假如参与人受制于机会或全无选择，就没有博弈可言。

事实上，参与人都有选择的余地和确定不同行动的旨趣，这些促成了博弈。

（B）博弈的解的概念。

这是博弈论的中心主题，这意味着博弈必有其解，至少在不同的结上是如此。

即便无限重复博弈也有一个解。

例证：标准式博弈：参与人A和参与人B打一局抽签牌。

就一局牌而言，每位参与人将要作出若干决策（比方说，是否下赌、加注或出牌，赌多少，是否取另一张牌，余局是不是停止比继续下去更好，等等）。

mathematical 计算博弈过程概述及解释说明1. 引言1.1 概述在现代社会中，决策和博弈过程无处不在。

无论是在政治、经济还是商业领域，我们都需要进行各种决策，并且这些决策的结果受到各种因素的影响。

数学计算博弈理论提供了一种分析和解释这些决策过程的方法，使我们能够更好地理解和预测各种博弈情境下的可能结果。

1.2 文章结构本文将从以下几个方面对数学计算博弈过程进行概述和解释说明。

首先，在第二部分“数学计算博弈过程概述”中，将介绍博弈理论的基本背景和概念。

然后，在第三部分“解释说明数学计算博弈过程的基本要点”中，将详细讨论博弈过程中涉及到的策略、收益以及纳什均衡等关键要素。

接下来，在第四部分“示例及实际应用案例分析”中，将通过具体案例来展示这些理论知识在实际问题中的应用。

最后，在第五部分“结论与未来研究方向展望”中，将总结文章的主要内容，并对数学计算博弈的未来发展方向进行展望。

1.3 目的本文旨在通过对数学计算博弈过程的概述和解释说明，帮助读者更加深入地了解和理解博弈理论及其应用。

同时，本文还将提供一些实例和案例分析，以便读者能够更好地将这些理论知识应用到实际问题中。

最后，本文还将探讨数学计算博弈未来的研究方向，为相关研究者提供新的思路和视角。

通过阅读本文，读者将能够拓宽自己对于数学计算博弈过程的认识，并用于解决实际问题。

2. 数学计算博弈过程概述:2.1 博弈理论简介:博弈理论是研究决策制定者在相互依赖的环境中进行决策的分析工具。

它提供了一种框架，用于研究多方参与、相互影响以及利益冲突的情境中的最优决策。

博弈理论主要关注个体或团体之间的互动，并通过模型化、分析和解释不同参与者的选择行为来揭示最佳策略。

2.2 基本概念和术语:在数学计算博弈中，存在一些基本概念和术语需要了解。

首先，需要明确博弈参与者（玩家）的角色和数量。

通常将玩家抽象为不同实体，他们根据各自目标和偏好进行选择。

其次，策略是玩家在特定情境下可选择的行动方式。

博弈类型及其表述形式1 博弈的分类博弈模型一般分为合作博弈（cooperative game ）和非合作博弈（non- cooperative game ），如图 1.1。

合作博弈是以单个参与者的可能行动集合为基本元素，而非合作博弈是以参与人群的可能联合行动集合为基本元素（Martin J.Osborne and Ariel Rubinstein ，2000，P2），也就是说，在合作博弈中，博弈中所有参与者都独立行动，不存在有约束力的合作、联合或联盟的关系，而在非合作博弈中，在一些参与者之间存在着有约束力的合作、联合或联盟的关系，并因为这种关系影响到博弈的结局。

合作博弈强调的是团体理性（collective rationality ）、效率、公正和公平；非合作博弈强调的是个人理性、个人最优决策，其结果可能是有效率的，也可能是低效率或无效率的（张维迎，1996，P5）。

20世纪50年代，合作博弈的研究达到鼎盛期，同时开始出现对非合作博弈的研究，此后，博弈论的研究主流逐步转向在非合作博弈领域。

有些人认为非合作博弈模型比合作博弈更“基本”，但有些人认为两者不相上下（Martin J.Osborne and Ariel Rubinstein ，2000，P2）。

合作博弈，有时也叫做联盟博弈（coalitional game ），一般根据有无转移支付而分为两类：可转移支付联盟博弈（coalitional game with transferable payoff ）和不可转移支付联盟博弈（coalitional game with non-transferable payoff ）。

可转移支付也叫有旁支付（side payment ），可转移支付联盟博弈假设博弈中各参与者都用相同的尺度来衡量他们的赢得，且各联盟的赢得可以按任意方式在联盟成员中分摊；否则，就是不可转移支付联盟博弈。

图1.1 博弈的分类非合作博弈的分类主要从两个角度进行划分。

平狄克《微观经济学》（第7版）第13章博弈论和竞争策略复习笔记跨考网独家整理最全经济学考研真题，经济学考研课后习题解析资料库，您可以在这里查阅历年经济学考研真题，经济学考研课后习题，经济学考研参考书等内容，更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验，从前辈中获得的经验对初学者来说是宝贵的财富，这或许能帮你少走弯路，躲开一些陷阱。

以下内容为跨考网独家整理，如您还需更多考研资料，可选择经济学一对一在线咨询进行咨询。

1．博弈和策略性决策博弈论又称对策论，是描述、分析多人对策行为的理论，由棋奕、桥牌、战争中借用而来，在经济学中应用广泛，如用来表现寡头间相互依存的竞争特点便有其突出的优越性。

现代经济博弈理论始于1944年冯·诺依曼和奥斯卡·莫根施特恩的《博弈论与经济行为》一书。

（1）非合作和合作博弈博弈可以分为合作博弈和非合作博弈。

如果各博弈方可以谈定能使它们设计联合策略的有约束力的合同，博弈就是合作的。

如果不可能谈判并执行有约束力的合同，博弈就是非合作的。

合作博弈的一个例子是关于一个行业中的两个厂商谈判开发一种新技术的联合投资（假设其中任何一个厂商都没有能独自成功的足够知识）。

如果两个厂商能够签订一份分配联合投资利润的有约束力的合同，则使双方都获益的合作的结果就是可能的。

非合作博弈的一个例子就是两竞争的厂商相互考虑到对方的可能的行为，并独立确定价格或广告策略以夺取市场份额的情况。

在这两类博弈中，策略设计的最重要的方面就是理解你的对手的处境，并（如果你的对手是理性的）正确推导出其对你的行为会作出的反应。

（2）二者差别合作和非合作博弈之间的基本差别在于签订合同的可能性。

在合作博弈中有约束力的合同是可能存在的，而在非合作博弈中它们是不可能存在的。

2．占优策略有些策略在竞争者作某些选择时很可能是成功的，但如果他们作另外的选择就会失败。

而其他一些策略却不管竞争者选择什么都会成功。

占优策略——不管对手做什么——对博弈方都是最优的策略。