博弈论测试题四

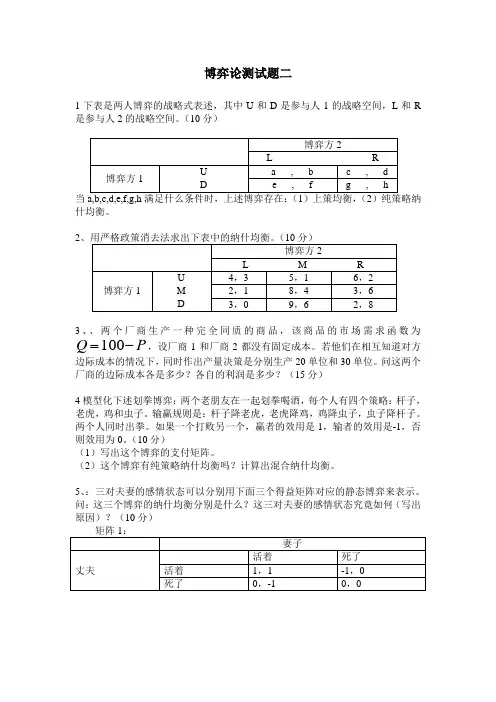
博弈论测试题二1下表是两人博弈的战略式表述，其中是参与人2的战略空间。

（10分）U 和D 是参与人1的战略空间，L 和R当a,b,c,d,e,f,g,h 满足什么条件时，上述博弈存在：（1）上策均衡，（2）纯策略纳 什均衡。

2、用严格政策消去法求出下表中的纳什均衡。

（10分）3、、两个厂商生产一种完全同质的商品，该商品的市场需求函数为 Q = 100- P ，设厂商1和厂商2都没有固定成本。

若他们在相互知道对方 边际成本的情况下，同时作出产量决策是分别生产 20单位和30单位。

问这两个 厂商的边际成本各是多少？各自的利润是多少？ （ 15分）4模型化下述划拳博弈：两个老朋友在一起划拳喝酒，每个人有四个策略：杆子, 老虎，鸡和虫子。

输赢规则是：杆子降老虎，老虎降鸡，鸡降虫子，虫子降杆子。

两个人同时出拳。

如果一个打败另一个，赢者的效用是 1,输者的效用是-1,否则效用为0。

（ 10分） （1） 写出这个博弈的支付矩阵。

（2） 这个博弈有纯策略纳什均衡吗？计算出混合纳什均衡。

5、:三对夫妻的感情状态可以分别用下面三个得益矩阵对应的静态博弈来表示。

问：这三个博弈的纳什均衡分别是什么？这三对夫妻的感情状态究竟如何（写出 原因）？（ 10分）矩阵1：矩阵2:矩阵3:6企业甲和企业乙都是彩电制造商，都可以选择生产低档产品或高档产品，每个企业在四种不同的情况下的利润如以下得益矩阵所示。

如果企业甲先于企业乙进行产品选择并投入生产，即企业乙在决定产品时已经知道企业甲的选择，而且这一点双方都清楚。

（10分）（1）用扩展型表示这一博弈。

（2）这一博弈的子博弈完美纳什均衡是什么?7、下面的博弈可以解释为两个寡头企业的价格竞争博弈，其中P是企业1的价格，q是企业2的价格。

企业1的利润函数是二i二（p-aq+c）2+q二2二（q-b）2+p求解（1）两个企业同时决策时的（纯战略）纳什均衡；（2）企业（1）先决策时的子博弈完美纳什均衡；（3）企业（2）先决策时的子博弈完美纳什均衡；本题（15分）8、案例分析（20分）2008年伊始，新加坡航空公司、新加坡淡马锡控股公司与中国国有企业中国东方航空公司轰轰烈烈”的股权交易（东新恋），被中国东方航空公司自己的股东否决了。

博弈数学测试题及答案一、选择题（每题2分，共20分）1. 以下哪个不是博弈论中的基本概念？A. 纳什均衡B. 混合策略C. 马尔可夫链D. 纯策略答案：C2. 在零和博弈中，以下哪个说法是正确的？A. 参与者的收益总和为零B. 参与者的损失总和为零C. 参与者的总收益为零D. 参与者的总损失为零答案：A3. 以下哪个不是博弈论中的策略类型？A. 纯策略B. 混合策略C. 静态策略D. 动态策略答案：D4. 博弈论中的“囚徒困境”主要说明了什么？A. 合作总是最优选择B. 个体理性可能导致集体非理性C. 集体理性总是最优选择D. 个体非理性可能导致集体理性答案：B5. 在博弈论中，以下哪个不是纳什均衡的特点？A. 每个参与者都选择了自己的最优策略B. 每个参与者的策略都是对其他参与者策略的最佳响应C. 参与者可以通过改变策略来获得更好的结果D. 所有参与者都达到了自己可能的最大收益答案：C6. 以下哪个是博弈论中的合作博弈？A. 囚徒困境B. 石头剪刀布C. 公共品博弈D. 零和博弈答案：C7. 在博弈论中，哪个术语描述了参与者在没有沟通的情况下做出决策？A. 沟通博弈B. 非合作博弈C. 同时博弈D. 顺序博弈答案：C8. 以下哪个不是博弈论中的结果类型？A. 帕累托效率B. 纳什均衡C. 社会福利最大化D. 个人最优答案：D9. 在博弈论中，以下哪个不是博弈的分类？A. 完全信息博弈B. 不完全信息博弈C. 静态博弈D. 动态博弈答案：C10. 以下哪个是博弈论中的“重复博弈”？A. 参与者只进行一次决策B. 参与者进行多次决策C. 参与者在博弈中没有记忆D. 参与者在博弈中不能交流答案：B二、填空题（每空1分，共10分）1. 博弈论是由数学家______提出的。

答案：约翰·冯·诺伊曼2. 博弈论中的“纳什均衡”是由______命名的。

答案：约翰·纳什3. 在博弈论中，如果参与者的策略选择是相互独立的，这种博弈被称为______博弈。

南开大学智慧树知到“经济学”《初级博弈论》网课测试题答案（图片大小可自由调整）第1卷一.综合考核(共15题)1.当静态贝叶斯博弈中博弈方的一个策略组合是贝叶斯纳什均衡时，意味着不会有任何一个博弈方想要改变自己策略中的哪怕只是一种类型下的一个行动。

()A.正确B.错误2.有限理性意味着所有博弈方都不会采用完全理性博弈的均衡策略。

()A.正确B.错误3.乙向甲索要1000元，并且威胁甲如果不给就与他同归于尽。

当然甲不一定会相信乙的威胁。

请用扩展形表示该博弈，并找出纯策略纳什均衡和子博弈完美纳什均衡。

4.若对一个博弈运用严格下策反复消去法后，如果该博弈的策略组合中只有惟一一个幸存下来，这个策略组合就是该博弈的结果。

()A.正确B.错误5.不允许存在有约束力协议的博弈称为非合作博弈。

()A.错误B.正确6.教育程度在劳动力市场招聘员工时受到重视的理由是，经济学已经证明教育对于提高劳动力素质有不可替代的作用。

()A.正确B.错误7.囚徒的困境博弈中的(坦白，坦白)不是一个上策均衡。

()A.错误B.正确8.追求集体利益最大化称为“集体理性”。

()A.正确B.错误9.因为零和博弈中博弈方之间的关系都是竞争性的、对立的，因此零和博弈就是非合作博弈。

()A.正确B.错误10.无限次重复博弈均衡解的得益一定优于原博弈均衡解的得益。

()A.错误B.正确11.因为上策均衡反映了所有博弈方的绝对偏好，因此非常稳定，根据上策均衡可以对博弈结果作出最肯定的预测。

()A.错误B.正确12.静态贝叶斯博弈与完全信息博弈之间在策略和策略空间相同。

()A.正确B.错误13.古玩市场的交易中买卖双方的后悔都来自于自己对古玩价值判断的失误，若预先对价值的判断是正确的，那么交易者肯定不会后悔。

()A.正确B.错误14.不完美信息动态博弈的基本特征之一是博弈方之间在信息方面是不对称的。

()A.正确B.错误15.因为零和博弈中博弈方之间的关系都是竞争性的、对立的，因此零和博弈就是非合作博弈。

石头剪刀布博弈论答案“石头、剪子、布”（或者“老虎、鸡、杠子”）是一个很多人都玩过的游戏，如果我们两个人一起来玩这个游戏，赌注是人民币100元，并且事先我就告诉你：我接下去会出“石头”！请问：你会出什么？其实，我这里真正要问的是：你接下去要出的内容和我事先告诉你要出“石头”是否有关？请进一步分析，“言语”是否能够在利益对立的博弈中起作用？为什么？从课后许多同学的测试结果看，对方出剪子的比例往往是最小的，而出石头的比例是最大的，请构建相应的博弈模型，以便解释该现象。

如果您是那个说要出“石头”的人，请问你实际上会出什么？为什么？从后续的高级版游戏结果看（当赔率是1：2：5时），出石头总是输的，出剪子总是赢的，为什么会这样呢？原因何在？以上的游戏结果还对你有哪些方面的启发？请对游戏结果发表你的思考与分析。

<br />1. “石头、剪子、布”（或者“老虎、鸡、杠子”）是一个很多人都玩过的游戏，如果我们两个人一起来玩这个游戏，赌注是人民币100元，并且事先我就告诉你：我接下去会出“石头”！请问：你会出什么？其实，我这里真正要问的是：你接下去要出的内容和我事先告诉你要出“石头”是否有关？我会出剪子。

我认为我接下去要出的内容和老师事先告诉我要出“石头”有关。

2. 请进一步分析，“言语”是否能够在利益对立的博弈中起作用？为什么？“言语”可以在利益对立的博弈中起作用，但是起作用是有一定要求的。

下面那我来阐述原因。

首先我们要清楚这是一个利益对立的博弈，因此作为具有理性的博弈双方，对自己的游戏（Game）策略保密无疑是双方实现利益最大化的最保险的一项举措。

因此，当双方都缄默时，此时进行的博弈就是一个完全理论上的双方进行猜拳的最简单的模型，每一个人出石头、剪刀、布的概率都分别是1/3，而胜出的概率也是双方各1/3（考虑到平局的情况，当然这具体还要看关于赌注的游戏的规则）。

然而，正像我刚才所说，双方对策略保密是实现利益最大化的最保险举措，而并不一定是最优举措。

博弈问题总结（基础篇）博弈问题总结（基础篇）前⾔最近做的博弈问题的题⽐较多，所以我就汇总了⼀下博弈问题的⼏种题型，⽅便之后的做题博弈论定义博弈论就是指有若⼲个⼈进⾏⼀些对弈，并且默认每个⼈都是最聪明的，不会失误，都可以找到当前的最优解，然后来寻找有没有哪个⼈有必胜/必败的的策略。

A、尼姆博弈为什么叫尼姆博弈呢？因为这是尼姆（英⽂名：Nimm Game）发明的数学游戏。

博弈模型有n堆各若⼲个物品，两个⼈轮流从某⼀堆取任意多的物品，规定每次⾄少取⼀个，多者不限，最后取光者得胜。

分析我们先考虑简单的情况1、n=1这时先⼿必胜，因为他只需要把唯⼀的这⼀堆⽯⼦取⾛就可以了2、n=2若a[1]=a[2]，先⼿必败，因为⽆论先⼿在哪⼀堆⽯⼦中取⾛⼏个，后⼿总能在另⼀堆⽯⼦中取⾛相同的个数若a[1]!=a[2]，我们假设a[1]>a[2]，此时先⼿必胜，因为先⼿可以在第⼀堆⽯⼦中取⾛a[1]-a[2]个，这时两堆⽯⼦的个数相同，下⼀次⽆论后⼿取⾛多少个，先⼿都可以在另⼀堆取⾛同样多个，因此先⼿必胜若a[1]<a[2]，同上，先⼿必胜3、要是n=3或者更⼤呢？我们显然不能像上⾯⼀样去枚举每种情况，所以我们要得出⼀个更为⼀般的结论我们设总共有n堆⽯⼦，每⼀堆⽯⼦的个数分别为a[1]、a[2]、a[3]……a[n]若a[1] ^ a[2] ^ a[3] ^ …… ^ a[n] =0先⼿必败，反之先⼿必胜下⾯是证明如果异或和的最⾼位为i，那么必定有⼀堆⽯⼦的第 i 位为1我们设这⼀堆⽯⼦的个数为k，其它所有⽯⼦的异或和为m，总异或和为x则必定有k ^ m=x，我们把这⼀堆⽯⼦变成k^x（k ^ x） ^ m=0这时，所有⽯⼦的异或和都变成了0举个例⼦:11001 ^ 11100=00101，则有（11001 ^ 00101）^ 11100=0如果当前所有数字的异或和为0，那么下⼀次⽆论你怎么取⽯⼦，异或和⼀定不会为0这样我们可以得出结论：如果先⼿异或和不为0，可以⼀步让后⼿的情况为异或和为0；如果先⼿异或和为0，那么后⼿异或和就不为0这样，我们不断进⾏游戏，最终⼀定会达到所有的数都为0的情况，⽽最后⾯对这种情况的⼀定会输所以我们可以得出结论：若a[1] ^ a[2] ^ a[3] ^ …… ^ a[n] =0先⼿必败，反之先⼿必胜例题洛⾕P2197模板题（好裸的板⼦）题意甲，⼄两个⼈玩 Nim 取⽯⼦游戏。

哪国人养鱼（Zebra Puzzle）1. 一条街上有五座不同颜色的房子，每座房子住着不同国籍的人，每个人抽不同的烟，喝不同的饮料，养不同的宠物。

2. 英国人住在红房子里。

3. 西班牙人养狗。

4. 住在绿房子里的人喝咖啡。

5. 乌克兰人喝茶。

6. 绿房子就在乳白色房子的右边。

7. 抽流金岁月（烟名）的人养蜗牛。

8. 抽薄荷烟的住在黄房子里。

9. 住在中间的房子里的人喝牛奶。

10. 挪威人住在第一座房子里。

11. 抽契斯特菲尔德（烟名）的人住在养狐狸的人旁边。

12. 抽薄荷烟的人住在养马的人旁边。

13. 抽好彩（烟名）的人喝橙汁。

14. 日本人抽百乐门（烟名）。

15. 挪威人住在蓝房子隔壁。

那么，谁喝水？谁养斑马？这个谜题已知的最早出处是1962 年12 月17 日的《生活》（Life）杂志国际版上。

1963 年3 月25 日，杂志公布了答案和世界各地数百个解决者的名单。

这个谜题有无数的变种，其中一个就是网络上流传更广的“哪国人养鱼”。

人怕出名猪怕壮，这个叙述繁琐的谜题竟莫名其妙地归功于了20 世纪最聪明的大脑——爱因斯坦。

此题乃“爱因斯坦年幼时所编”的说法广为流传，于是这个谜题也经常被叫做“爱因斯坦谜题”（Einstein…s Puzzle）。

但也有人说，作者其实是路易斯·卡罗尔（Lewis Carroll）。

好吧，我们不要管这些追星族了，因为现在没有任何证据证明作者是他们中的任何一个。

况且，谜题里的香烟品牌在爱因斯坦小时候还没有出现呢。

海盗分金谜题（Pirate Puzzle）这是个流传很广的谜题，包含了诸如海盗、金钱、民主之类的流行元素。

故事是这样的：有五个理性的海盗A、B、C、D、E，他们得到了100 个金币，要进行分赃。

海盗世界等级分明，这五个海盗的排名如下：A > B > C > D > E。

分赃制度也很民主：首先由等级最高的海盗提出一个分配方案，然后所有海盗（包括提议人）投票表决是否接受。

博弈论测试题二1下表是两人博弈的战略式表述，其中U 和D 是参与人1的战略空间，L 和R 是参与人2的战略空间。

（10分）当什均衡。

23、、两个厂商生产一种完全同质的商品，该商品的市场需求函数为P Q -=100，设厂商1和厂商2都没有固定成本。

若他们在相互知道对方边际成本的情况下，同时作出产量决策是分别生产20单位和30单位。

问这两个厂商的边际成本各是多少？各自的利润是多少？（15分）4模型化下述划拳博弈：两个老朋友在一起划拳喝酒，每个人有四个策略：杆子，老虎，鸡和虫子。

输赢规则是：杆子降老虎，老虎降鸡，鸡降虫子，虫子降杆子。

两个人同时出拳。

如果一个打败另一个，赢者的效用是1，输者的效用是-1，否则效用为0。

（10分）（1）写出这个博弈的支付矩阵。

（2）这个博弈有纯策略纳什均衡吗？计算出混合纳什均衡。

5、：三对夫妻的感情状态可以分别用下面三个得益矩阵对应的静态博弈来表示。

问：这三个博弈的纳什均衡分别是什么？这三对夫妻的感情状态究竟如何（写出原因）？（10分）6、企业甲和企业乙都是彩电制造商，都可以选择生产低档产品或高档产品，每个企业在四种不同的情况下的利润如以下得益矩阵所示。

如果企业甲先于企业乙进行产品选择并投入生产，即企业乙在决定产品时已经知道企业甲的选择，而且（2）这一博弈的子博弈完美纳什均衡是什么？7、下面的博弈可以解释为两个寡头企业的价格竞争博弈，其中P是企业1的价格，q是企业2的价格。

企业1的利润函数是π1=-（p-aq+c）2+qπ2=-（q-b）2+p求解（1）两个企业同时决策时的（纯战略）纳什均衡；（2）企业（1）先决策时的子博弈完美纳什均衡；（3）企业（2）先决策时的子博弈完美纳什均衡；本题（15分）8、案例分析（20分）2008年伊始，新加坡航空公司、新加坡淡马锡控股公司与中国国有企业中国东方航空公司“轰轰烈烈”的股权交易（东新恋），被中国东方航空公司自己的股东否决了。

随后，另一家中国国有企业，中国国际航空公司突然表示，有意竞购“老对手”中国东方航空公司的股份。

“帽子问题”及其衍生问题作者：司志本张琪来源：《中学数学杂志(高中版)》2017年第04期“帽子问题”是大家比较熟悉的一道思维训练题.如果你阅读一些有关博弈论的书籍，那么你就会发现，博弈论中一些比较经典的问题与“帽子问题”是非常相似的，我们可以把这些问题视为“帽子问题”的衍生问题.经常思考一些这样的问题，对于训练我们的思维是十分有益的.例1 帽子问题.这是一个游戏，A、B、C三个人围坐在一起，主持人备有3顶红帽子和2顶白帽子.将其中的3顶帽子分别戴在这三个人的头上.每个人都能看见其他两个人头上的帽子，但看不见自己头上戴的帽子，并且也不知道剩余的2顶帽子的颜色.主持人首先问A：“你戴的是什么颜色的帽子？” A回答说：“不知道.” 接着，主持人又问B同样的问题，B想了想之后，也回答说：“不知道.”主持人最后问C，C回答说：“在听了A、B的回答之后，我知道我戴的帽子是什么颜色了.” 请问C戴的是什么颜色的帽子？分析首先，不可能有两个人同时戴白帽子.例如，假设A 、B戴的都是白帽子，那么C不需要听取A、B的答案，就能够判断出自己戴的是红帽子；其次，不可能只有一个人戴白帽子.事实上，假如A戴的是白帽子，那么对于C来说，他看到的情况是：A戴白帽子，B戴红帽子，因为不可能有2人都戴白帽子，所以，C由此可以判断，自己戴的一定是红帽子.上述的“帽子问题”也经常以下面的形式出现：C、B、A三个人从前到后站成一列，主持人备有3顶红帽子，2顶白帽子，将其中的3顶帽子分别戴在这三个人的头上，他们都只能看见站在自己前面那些人的帽子.主持人首先问排在最后面的A：“你戴的是什么颜色的帽子？”A回答说：“不知道.” 接着，主持人又问B同样的问题，B也回答说：“不知道.”主持人最后问C. C回答说：“在听了A、B的回答之后，我知道我戴的帽子是什么颜色了.” 请问C戴的是什么颜色的帽子？分析站在最后边的A不知道自己所戴帽子的颜色，说明他前面的B和C所戴的帽子不都是白色的，否则，A就能够判断出自己戴的是红帽子了；此时，如果排在第一位的C戴的是白帽子，那么排在第二位的B根据A的回答，就可以判断自己戴的不是白帽子，而是红帽子；现在B也不知道自己帽子的颜色，这就说明C戴的不是白帽子.所以，C戴的帽子一定是红色的.“帽子问题”中的人数还可以增加.例如4个人的情况就是下面的问题：有A、B、C、D四个人围坐在一起，主持人准备了4顶红帽子，3顶白帽子.将其中的4顶帽子分别给这四个人戴在头上.他们每个人都能看到别人的帽子，但看不到自己头上帽子的颜色.主持人对他们四个人说：“你们中间至少一个人戴的是红色帽子，你们知道自己头上帽子的颜色吗？”四个人都说不知道.主持人连续问了三次同样的问题，他们都说不知道.当主持人问到第四遍时，四个人同时回答说：知道了.请问，这四个人所戴帽子是什么颜色的？分析如果A、B、C、D这四个人中只有一个人的帽子是红色的，不妨假设A的帽子是红色的，那么A看见另外三个人的帽子都是白色的，此时，主持人第一次提问时，A就能判断出自己的帽子是红色的.主持人第一次提问时，四个人都回答说不知道自己帽子的颜色，这说明不止A一个人的帽子是红色的；如果只有两个人的帽子是红色的，不妨假设A和B的帽子是红色的，那么A和B两个人会看见一个人戴红帽子，两个人戴白帽子，进而判断出自己戴的是红帽子，在主持人第二次提问时，A和B就会给出答案.因此不可能只有两人戴红帽子；如果只有三个人的帽子是红色的，不妨假设A、B、C的帽子是红色的，那么A、B、C中任意两个人会看见两个人戴红帽子，一个人戴白帽子，由前面分析可知，不可能只有一个或两个人戴红帽子，所以，A、B、C可以判断出自己戴的是红帽子.主持人前三次提问时，四个人都说不知道.到这时，这四个人已经判断出他们的帽子都是红色的了，所以，当主持人第四次提问时，四个人同时回答说：知道了.他们四个人所戴的帽子都是红色的.例2 脏脸问题.“脏脸问题”是许多博弈论书上都提到的一个问题，最简单的情况是这样的：一个房间里有三个人，三个人的脸都是脏的，他们都知道别人的脸是脏的，却不知道自己的脸是脏的.这时主持人走进来对他们说：“你们中间至少有一个人的脸是脏的.”这三个人听完之后，互相看看，没有任何反应；主持人见他们这样，又继续提醒道：“你们知道吗？”这时三个人又相互打量起来；当主持人第三次提醒时，他们突然都意识到自己的脸是脏的.三个人的脸一下子都红了.分析如果三个人中只有一个人是脏脸，那么脏脸人看见另外两个人的脸都是干净的，此时，主持人第一次提醒时，脏脸人就会意识到自己的脸是脏的，他就会感到脸红.主持人第一次提醒后，三个人谁都没有脸红，这说明，不止一个人脸脏；如果只有两个人脸脏，那么脏脸的两个人会看见一张干净脸和一张脏脸，进而意识到自己的脸是脏的，当主持人第二次提醒时，这两个人就会脸红.因为主持人第二次提醒时，没有人脸红，这说明不只两个人的脸脏，所以，当主持人第三次提醒时，三个人的脸都红了.三个人的脸都是脏的.例3 病狗问题.大家都知道微软公司的面试是与众不同的，他们面试题大体上可以分为四类：第一类，快速估算题，测试你的快速反应能力；第二类，开放性思维题，考验你的逻辑推理能力；第三类，基础数学题，考核你的数学基础是否扎实；第四类，智力测试题，看你能否创造性地思考.下面的“病狗问题”就是微软公司的一道招聘试题：一个大院子里住了50户人家，每家都养了一条狗，有一天他们接到通知说院子里有狗生病了，并要求所有主人在发现自己家狗生病的当天就要把狗枪杀掉.然而所有主人和他们的狗都不能够离开自己的房子，主人与主人之间也不能通过任何方式进行沟通，他们能做的只是通过窗户观察别人家的狗是否生病，从而判断自己的狗是否有病.第一天没有枪声，第二天还是没有枪声，第三天传出一阵枪声.问有多少条病狗被枪杀.分析如果只有1条狗是病狗，那么第一天这条病狗的主人发现另外的49条狗都是正常的，从而判断自己的狗是病狗.因此，第一天主人就应该把自己的狗给杀死.第一天没有枪声，说明至少有2条病狗.如果只有2条病狗，那么第二天这2条病狗的主人只能看到1条病狗和48条没病的狗.因为病狗多于1条，所以，2条病狗的主人可以判断自己的狗是病狗，第二天应该把自己的狗给杀死.第二天没有枪声，说明至少有3条病狗.如果有4条或4条以上的病狗，那么每个主人至少能够看到3条病狗.由于病狗的数量是不是3条无法确定，每个人也无法判定自己的狗是不是病狗，所以第三天就不会有枪声.第三天传出枪声，说明只有3条病狗.。