第4章 梁的内力liu1
- 格式:ppt
- 大小:4.54 MB
- 文档页数:79
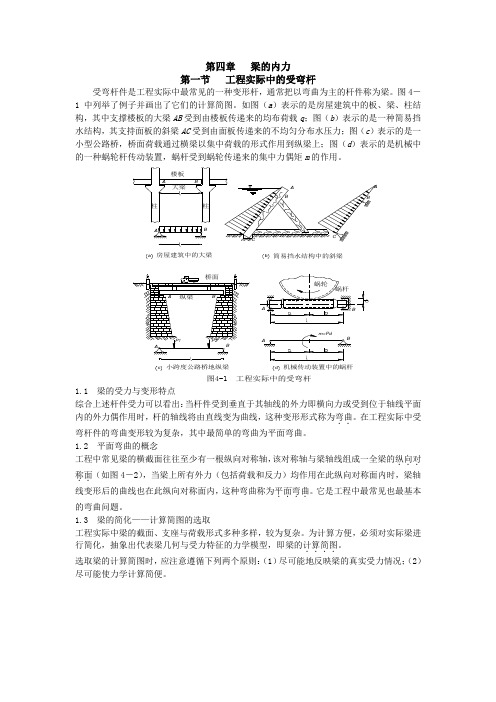
第四章 梁的内力第一节 工程实际中的受弯杆受弯杆件是工程实际中最常见的一种变形杆,通常把以弯曲为主的杆件称为梁。
图4-1中列举了例子并画出了它们的计算简图。
如图(a )表示的是房屋建筑中的板、梁、柱结构,其中支撑楼板的大梁AB 受到由楼板传递来的均布荷载q ;图(b )表示的是一种简易挡水结构,其支持面板的斜梁AC 受到由面板传递来的不均匀分布水压力;图(c )表示的是一小型公路桥,桥面荷载通过横梁以集中荷载的形式作用到纵梁上;图(d )表示的是机械中的一种蜗轮杆传动装置,蜗杆受到蜗轮传递来的集中力偶矩m 的作用。
a房屋建筑中的大梁b简易挡水结构中的斜梁c 小跨度公路桥地纵梁d 机械传动装置中的蜗杆图4-1 工程实际中的受弯杆1.1 梁的受力与变形特点 综合上述杆件受力可以看出:当杆件受到垂直于其轴线的外力即横向力或受到位于轴线平面内的外力偶作用时,杆的轴线将由直线变为曲线,这种变形形式称为弯曲..。
在工程实际中受弯杆件的弯曲变形较为复杂,其中最简单的弯曲为平面弯曲。
1.2 平面弯曲的概念工程中常见梁的横截面往往至少有一根纵向对称轴,该对称轴与梁轴线组成一全梁的纵向对...称面..(如图4-2),当梁上所有外力(包括荷载和反力)均作用在此纵向对称面内时,梁轴线变形后的曲线也在此纵向对称面内,这种弯曲称为平面弯曲....。
它是工程中最常见也最基本的弯曲问题。
1.3 梁的简化——计算简图的选取工程实际中梁的截面、支座与荷载形式多种多样,较为复杂。
为计算方便,必须对实际梁进行简化,抽象出代表梁几何与受力特征的力学模型,即梁的计算简图....。
选取梁的计算简图时,应注意遵循下列两个原则:(1)尽可能地反映梁的真实受力情况;(2)尽可能使力学计算简便。
图4-2 梁的平面弯曲一般从梁本身、支座及荷载等三方面进行简化:(1)梁本身简化——以轴线代替梁,梁的长度称为跨度;(2)荷载简化——将荷载简化为集中力、线分布力或力偶等;(3)支座简化——主要简化为以下三种典型支座:(a)活动铰支座(或辊轴支座),其构造图及支座简图如图4-3(a)所示。





梁的内力分析方法摘要本文归纳总结了计算梁的内力方法以及梁的内力与载荷及结构之间的规律,并以汽车起重机底架大梁为例,对梁的内力求解方法作了分析。
关键词梁;内力;约束;扭转;载荷简化1 截面法用截面法求内力,建立剪力、弯矩方程,根据方程绘剪力、弯矩图是一种基本方法。
2 剪力图和弯矩图一般情况下,梁横截面上的剪力和弯矩随截面位置不同而变化,将剪力和弯矩沿梁轴线的变化情况用图形表示出来,这种图形分别称为剪力图和弯矩图。
画剪力图和弯矩图的基本方法有2种。
2.1 剪力、弯矩方程法若以横坐标x表示横截面在梁轴线上的位置,则各横截面上的剪力和弯矩可以表示为x的函数,即Q=Q(x)M=M(x)上述函数表达式称为梁的剪力方程和弯矩方程。
根据剪力方程和弯矩方程即可画出剪力图和弯矩图。
画剪力图和弯矩图时,首先要建立Q-x和M-x坐标。
然后根据截荷情况分段列出方程。
由截面法和平衡条件可知,在集中力、集中力偶和分布载荷的起止点处,剪力方程和弯矩方程可能发生变化,所以这些点均为剪力方程和弯矩方程的分段点。
分段点截面也称控制截面。
求出分段点处横截面上剪力和弯矩的数值(包括正负号),并将这些数值标在Q-x、M-x坐标中相应位置处。
分段点之间的图形可根据剪力方程和弯矩方程绘出。
最后注明最大的数值位置。
2.2 微分关系法考察承受任意载荷的梁。
从梁上受分布载荷的段内截取微段,观察其受力,作用在微段上的分布载荷可以认为是均布的,并设向上为正。
微段两侧截面上的内力均设为正方向。
若x截面上的内力为Q(x)、M(x),则x+dx截面上的内力为Q(x)+d Q(x)、M(x)+d M(x)。
因为梁整体是平衡的,dx微段也应处于平衡。
根据平衡条件∑y=0和∑mo=0,得到式(1)、(2)和(3)是剪力、弯矩和分布载荷集度q之间的平衡微分关系。
它表明:剪力图上某处的斜率等于梁在该处的分布载荷集度q;弯矩图上某处的斜率等于梁在该处的剪力;弯矩图上某处的斜率变化率等于梁在该处的分布载荷集度q。