(完整版)梁的内力计算

主梁的内力计算主梁的内力计算包括恒载内力计算和活载内力计算。

根据上述梁跨结构纵、横截面的布置，计算活载作用下的梁桥荷载横向分布系数，求出各主梁控制截面（取跨中、四分点、变化点截面及支点截面）的恒载和最大活载内力，然后再进行主梁内力组合。

一、恒载内力计算1、恒载集度⑴预制梁自重（第一期恒载）①．跨中截面段主梁自重（四分点截面至跨中截面，长7.25m ）(1)0.861625.07.25156.165g KN =⨯⨯=②．马蹄抬高与腹板变宽段梁的自重近似计算（长3.7m ） 主梁端部截面面积为A=1.176m 2()(2) 1.17600.8616 3.725.0/294.239g KN =+⨯⨯=③．支点段梁的自重（长3.55m ）(3) 1.1760 3.5525.0=104.37g KN =⨯⨯④．横隔梁的自重 中横隔梁体积为：()30.16 1.590.920.240.72/20.120.12/20.219072m ⨯⨯-⨯-⨯= 端横隔梁体积为：()30.25 1.840.80.20.6/20.353m ⨯⨯-⨯=故半跨内横隔梁重量()(4)20.21907210.3532519.7786g KN =⨯+⨯⨯=⑤．主梁永久作用集度()156.16594.239104.3719.7786/14.9825.00/g KN m KN m I =+++= （2）第二期恒载①翼缘板中间湿接缝集度()50.40.1625.0 1.6/g KN m =⨯⨯=②现浇部分横隔梁一片中横隔梁（现浇部分）体积：30.16 1.590.20.05088m ⨯⨯= 一片端横隔梁（现浇部分）体积：30.250.2 1.840.092m ⨯⨯= 故()()630.0508820.09225.0/29.960.2809/g KN m =⨯+⨯⨯=③桥面铺装层6cm 沥青混凝土铺装：0.0612.52317.25/KN m ⨯⨯=将桥面铺装重量均分给五片主梁，则()717.25/5 3.45/g KN m ==④防撞栏：两侧防撞栏均分给五片主梁，则()87.52/53/g KN m =⨯=⑤主梁二期永久作用集度II 1.60.2809 3.4538.3309/g KN m =+++=2、永久作用效用：下面进行永久作用效用计算（参照图1-4），设c 为计算截面至左侧支座的距离，并令/a c l =。

主梁的内力计算主梁的内力计算包括恒载内力计算和活载内力计算。

根据上述梁跨结构纵、横截面的布置，计算活载作用下的梁桥荷载横向分布系数，求出各主梁控制截面（取跨中、四分点、变化点截面及支点截面）的恒载和最大活载内力，然后再进行主梁内力组合。

一、恒载内力计算1、恒载集度⑴预制梁自重（第一期恒载）①．跨中截面段主梁自重（四分点截面至跨中截面，长7.25m ）(1)0.861625.07.25156.165g KN =⨯⨯=②．马蹄抬高与腹板变宽段梁的自重近似计算（长3.7m ） 主梁端部截面面积为A=1.176m 2()(2) 1.17600.8616 3.725.0/294.239g KN =+⨯⨯=③．支点段梁的自重（长3.55m ）(3) 1.1760 3.5525.0=104.37g KN =⨯⨯④．横隔梁的自重 中横隔梁体积为：()30.16 1.590.920.240.72/20.120.12/20.219072m ⨯⨯-⨯-⨯= 端横隔梁体积为：()30.25 1.840.80.20.6/20.353m ⨯⨯-⨯=故半跨内横隔梁重量()(4)20.21907210.3532519.7786g KN =⨯+⨯⨯=⑤．主梁永久作用集度()156.16594.239104.3719.7786/14.9825.00/g KN m KN m I =+++= （2）第二期恒载①翼缘板中间湿接缝集度()50.40.1625.0 1.6/g KN m =⨯⨯=②现浇部分横隔梁一片中横隔梁（现浇部分）体积：30.16 1.590.20.05088m ⨯⨯= 一片端横隔梁（现浇部分）体积：30.250.2 1.840.092m ⨯⨯= 故()()630.0508820.09225.0/29.960.2809/g KN m =⨯+⨯⨯=③桥面铺装层6cm 沥青混凝土铺装：0.0612.52317.25/KN m ⨯⨯=将桥面铺装重量均分给五片主梁，则()717.25/5 3.45/g KN m ==④防撞栏：两侧防撞栏均分给五片主梁，则()87.52/53/g KN m =⨯=⑤主梁二期永久作用集度II 1.60.2809 3.4538.3309/g KN m =+++=2、永久作用效用：下面进行永久作用效用计算（参照图1-4），设c 为计算截面至左侧支座的距离，并令/a c l =。

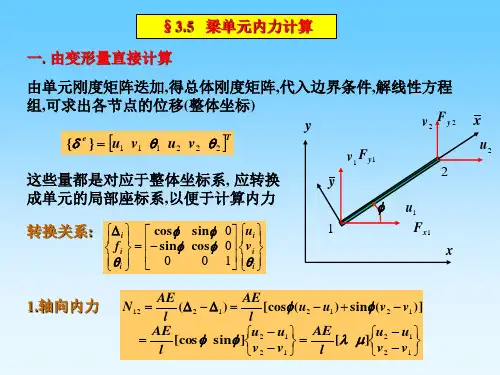
受静载荷梁的内力及变位计算公式1.集中力的作用下的受静载荷梁内力计算公式：(1)弯矩(M)的计算公式：M=F*x其中，M是梁的弯矩，F是集中力，x是集中力作用点到支点的距离。

(2)剪力(V)的计算公式：V=F其中，V是梁的剪力，F是集中力。

2.均布力的作用下的受静载荷梁内力计算公式：(1)弯矩(M)的计算公式：M=w*x^2/2其中，M是梁的弯矩，w是均布力的单位长度的大小，x是梁上的任意一点到支点的距离。

(2)剪力(V)的计算公式：V=w*x其中，V是梁的剪力，w是均布力的单位长度的大小，x是梁上的任意一点到支点的距离。

3.其他外力作用下的受静载荷梁内力计算公式：当存在多个外力作用在梁上时，我们可以将其分解为集中力和均布力的叠加。

然后可以使用前面提到的公式来计算相应的内力。

变位计算公式主要有两种方法，分别是力偏心法和位移法。

4.力偏心法：利用力偏心引起的弯矩和剪力，根据梁的弹性理论和材料的本构关系，可以计算出梁的变位。

其中，弯矩引起的变位可由以下公式计算：δ=M*l^2/(2*E*I)其中，δ是梁的变形，M是梁上弯矩的最大值，l是梁的长度，E是梁的弹性模量，I是梁的截面惯性矩。

剪力引起的变位可由以下公式计算：δ=V*l/(G*A)其中，δ是梁的变形，V是梁上剪力的最大值，l是梁的长度，G是梁的剪切模量，A是梁的截面面积。

5.位移法：利用位移函数法，将梁的各个节点的位移表示为节点位移和激励项的组合，可以通过解线性代数方程组得到梁的节点位移。

其中，节点位移可以用来计算梁的变位。

综上所述，受静载荷梁的内力和变位计算可以通过公式和方法进行求解。

具体的计算公式和方法取决于梁的受力情况和边界条件。

在实际工程中，通常会采用数值分析方法，如有限元法等，来计算受静载荷梁的内力和变位。

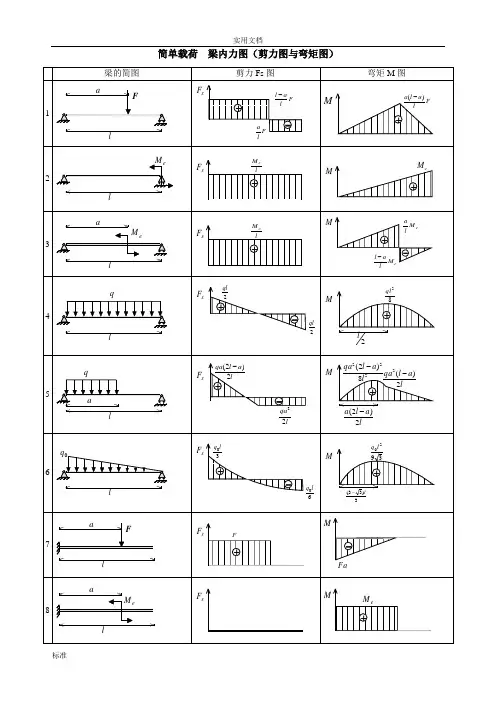
简单载荷梁内力图（剪力图与弯矩图）表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注：力边界条件即剪力图、弯矩图在该约束处的特征。

常用截面几何与力学特征表表2-5标准标准标准标准标准标准标准注：1．I 称为截面对主轴（形心轴）的截面惯性矩（mm 4）。

基本计算公式如下：⎰•=AdA yI 22．W 称为截面抵抗矩（mm 3），它表示截面抵抗弯曲变形能力的大小，基本计算公式如下：maxy I W =3．i 称截面回转半径（mm ），其基本计算公式如下：AIi =4．上列各式中，A 为截面面积（mm 2），y 为截面边缘到主轴（形心轴）的距离（mm ），I 为对主轴（形心轴）的惯性矩。

5．上列各项几何及力学特征，主要用于验算构件截面的承载力和刚度。

实用文档2．单跨梁的内力及变形表（表2-6~表2-10）（1）简支梁的反力、剪力、弯矩、挠度表2-6（2）悬臂梁的反力、剪力、弯矩和挠度表2-7（3）一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8（4）两端固定梁的反力、剪力、弯矩和挠度表2-9（5）外伸梁的反力、剪力、弯矩和挠度表2-103．等截面连续梁的内力及变形表（1）等跨连续梁的弯矩、剪力及挠度系数表（表2-11~表2-14）1）二跨等跨梁的内力和挠度系数表2-11注：1．在均布荷载作用下：M ＝表中系数×ql 2；V ＝表中系数×ql ；EIw 100ql 表中系数4⨯=。

2．在集中荷载作用下：M ＝表中系数×Fl ；V ＝表中系数×F ；EIw 100Fl 表中系数3⨯=。

[例1] 已知二跨等跨梁l ＝5m ，均布荷载q ＝11.76kN/m ，每跨各有一集中荷载F ＝29.4kN ，求中间支座的最大弯矩和剪力。

[解] M B 支＝（－0.125×11.76×52）＋（－0.188×29.4×5）＝（－36.75）＋（-27.64）＝－64.39kN ·m V B 左＝（－0.625×11.76×5）＋（－0.688×29.4）＝（－36.75）＋（－20.23）＝－56.98kN[例2] 已知三跨等跨梁l ＝6m ，均布荷载q ＝11.76kN/m ，求边跨最大跨中弯矩。

受静载荷梁的内力及变位计算公式受静载荷梁的内力及变位计算公式符号意义及正负号规定简图P——集中载荷q——均布载荷R——支座反力，作用方向向上者为正Q——剪力，对邻近截面所产生的力矩沿顺时针方向者为正M——弯矩，使截面上部受压，下部受拉者为正θ——转角，顺时针方向旋转者为正f——挠度，向下变位者为正E——弹性模量I——截面的轴惯性矩a、b、c——见各栏图中所示简图支座反力、支座反力矩区段剪力弯矩挠度转角R B＝PM B＝-PlQ x＝-P M x＝-P xR B＝PM B＝-PbAC Q x＝0M x＝0CB Q x＝-P M x＝-P(x-a)R B＝nPR B＝qlQ x＝-qxR B＝qcM B＝-qcbAC Q x＝0M x＝0CD Q x＝-q(x-d)DB Q x＝-qc M x＝-qc(x-a)ACCBR B＝0M B＝M x＝-MQ x＝0M x＝-M?ω值见表梁分段的比值及ω的函数表；a、b、c——见各栏中所示简图支座反力、支座反力矩区段剪力弯矩挠度转角R A＝R B＝ACCBR A＝R B＝ACCBM x＝Pa(1-ξ)M C＝M max＝R A＝R B＝PAC Qx＝P M x＝PxCD Q x＝0M x＝M max＝PaCDDB若a＞c：当n为奇数：当n为偶数：当n为奇数：当n为偶数：当n为奇数：当n为偶数：当n为奇数：当n为偶数：R A＝R B＝qaAC Q x＝q(a-x)CD Q x＝0R A＝R B＝ACCDCDDBR A＝R B＝qcAC Q x＝qc M x＝qcxCDDE Q x＝0M x＝M max＝qcb当x＝ACACCB若a＞b，M x＝M(1-ξ)M max＝MM0＝M2-M1若M1＞M2：M max＝M1ACM x＝MξM C左＝MαCBM x＝-MζM C右＝-Mβ?ω值见表梁分段的比值及ω的函数表；——见各栏图中所示简图支座反力、支座反力矩区段剪力弯矩挠度转角???ACCB当x＝：AC Q x＝R A M x＝R A xCB Q x＝R A-P M x＝R Ax-P(x-a)Q MCD Qx＝R A-P M x＝R A x-P(x-a)DB Q x＝R A-2P M x＝R A x-P(2x-l)M C＝M max＝R A a当x＝：R B＝qc-R AM B＝R A l-qcbAC Q x＝R A M x＝R A xCD Qx＝R A-q(x-d)DB Qx＝R A-qc M x＝R A x-qc(x-a)当x＝：M max＝当x＝：当x＝：M max＝当x＝：AC当x＝：M max＝当x＝：M A＝M max＝MAC?Q x＝R ACBM C右＝M max＝M+M C左?ω值见表梁分段的比值及ω的函数表；a、b、c——见各栏图中所示简图支座反力、支座反力矩区段剪力弯矩挠度转角AC反弯点在及处R A＝R B＝PAC Qx＝P M x＝Pl(ξ-ωRα)CD Q x＝0AC Q x＝R A M x＝M A+R A xCB Q x＝R A-P M x＝M A+R A x-P(x-a)若当n为奇数：当n为偶数：当n为奇数：当n为偶数：当n为奇数：当n为偶数：当n为奇数：当n为偶数：反弯点在x＝及x＝处R A＝R B＝qaACCD Qx＝0ACCDAC Q x＝R A M x＝M A+R A xR B＝qc＝R ACD Q x＝R A-q(x-d )DB Q x＝R A-qc M x＝M A+R Ax-qc(x-a)当x＝：M max＝当x＝：ACACCDACQ x＝R AM x＝M A+R A xCB Mx＝M A+R A x+M?5．带悬臂的梁简图支座反力、支座反力矩区段剪力弯矩挠度转角R A＝P(1+λ)AC Q x＝-P M x＝-PxRM AB QM(1+当R A＝R B＝PM A＝M B＝-PmAC Q x＝-P M x＝-Px当x＝m+时：AB Q x＝0M x＝-PmACABQ x＝-qxQ x＝R A-qxAC Qx＝-qx当x＝m+时：ABR A＝R B＝qmAC Q x＝-qx当x＝m+时：AB Q x＝0M A＝-PmAC Q x＝-P M x＝-Px：ABMx＝-Px+R A(x-m)ACABQ x＝-qxQ x＝R A-qx当m＝时：M B＝0AC Qx＝-qxAB Q x＝RA-qxM A＝MAC Q x＝0M x＝MAB M x＝-RA(x-m)+M6．双跨、三跨梁OAM O＝M B＝0DE＝AC＝FG＝两支点中间：x＝处：R A＝(q1l1+q2l2)-(R O+R B)OAM O＝M B＝0M O＝M C＝0OAABM O＝M D＝0x＝处：R B＝P1+P2-(R O+R2)M O＝M D＝0 ?。

斜梁的内力图（补充内容）
应用：梁式楼梯、板式楼梯、屋面斜梁及具有斜杆的刚架。

1、两种荷载形式：①水平向均匀荷载：活载（人群、雪载）
②沿杆轴线均布q '：恒载(自重)，
2、水平向均匀荷载q ，斜角α （1）支座反力：考虑整体平衡：)(2/,0↑===ql F F F By Ay Ax
（2）求截面K 的内力方程：取AK 段隔离体，把力沿着N 方向和S 方向分解：
0=∑S
F , ααcos 2cos )(⎪⎭
⎫
⎝⎛-=-=qx ql qx V F A S （l x ≤≤0） 0=∑K M , 222
qx x ql M K -= l x ≤≤0（与相应水平简支梁完全一样） 0=∑N
F ,αsin 2⎪⎭
⎫ ⎝⎛+-=qx ql F N l x ≤≤0 （3）作内力图。

（4）几点说明：①横截面有轴力。

②与等跨简支梁弯矩图相同：（由于竖向支座反力相同，而水平
反力均为零。

）
而F N 图和F Q 图有如下关系：
αsin 0
Q N F F -=
αcos 0Q Q F F =
③若将B 支座换成与梁轴垂直的支座如何（思考：）
3、沿斜向荷载q '：楼梯自重
等效转换：根据同一微段上合力相等原则，换算成水平方向均布荷载：
qdx ds q ='
，αcos ''q dx
ds q q ==
结论：沿杆轴方向均布荷载作用下简支斜梁的内力图等于水平向均布荷载作用
下内力图除以αcos 即可
4、斜梁的区须叠加法
5、例题：
图 3-4e
28
1ql。

第四章梁的内力第一节工程实际中的受弯杆受弯杆件是工程实际中最常见的一种变形杆，通常把以弯曲为主的杆件称为梁。

图 4 —i中列举了例子并画出了它们的计算简图。

如图（a表示的是房屋建筑中的板、梁、柱结构，其中支撑楼板的大梁AB受到由楼板传递来的均布荷载口；图（b）表示的是一种简易挡水结构，其支持面板的斜梁AC受到由面板传递来的不均匀分布水压力；图（c）表示的是- 小型公路桥，桥面荷载通过横梁以集中荷载的形式作用到纵梁上；图（d）表示的是机械中的一种蜗轮杆传动装置，蜗杆受到蜗轮传递来的集中力偶矩m的作用。

1.1 梁的受力与变形特点综合上述杆件受力可以看出：当杆件受到垂直于其轴线的外力即横向力或受到位于轴线平面内的外力偶作用时，杆的轴线将由直线变为曲线，这种变形形式称为弯曲.。

在工程实际中受弯杆件的弯曲变形较为复杂，其中最简单的弯曲为平面弯曲。

1.2 平面弯曲的概念工程中常见梁的横截面往往至少有一根纵向对称轴，该对称轴与梁轴线组成一全梁的纵向对..称面（如图4 —2）,当梁上所有外力（包括荷载和反力）均作用在此纵向对称面内时，梁轴线变形后的曲线也在此纵向对称面内，这种弯曲称为平面弯曲.。

它是工程中最常见也最基本的弯曲问题。

1.3 梁的简化一一计算简图的选取工程实际中梁的截面、支座与荷载形式多种多样，较为复杂。

为计算方便，必须对实际梁进行简化，抽象出代表梁几何与受力特征的力学模型，即梁的计算简图...。

选取梁的计算简图时，应注意遵循下列两个原则：（1）尽可能地反映梁的真实受力情况；（2）尽可能使力学计算简便。

a房屋建筑中的大梁c小跨度公路桥地纵梁图4-1b简易挡水结构中的斜梁图4-2 梁的平面弯曲一般从梁本身、支座及荷载等三方面进行简化：（1） 梁本身简化一一以轴线代替梁，梁的长度称为跨度； （2） 荷载简化一一将荷载简化为集中力、线分布力或力偶等； （3） 支座简化——主要简化为以下三种典型支座：（a ） 活动铰支座（或辊轴支座），其构造图及支座简图如图4— 3 （a ）所示。