当前位置：文档之家 › 概率论与数理统计第六章样本及抽样分布}第二节：样讲义本分布函数直方图

概率论与数理统计第六章样本及抽样分布}第二节：样讲义本分布函数直方图

  • 格式：ppt
  • 大小：370.50 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

概率论与数理统计 第六章 样本及抽样分布

概率论与数理统计 第六章 样本及抽样分布

x0 o.w.
n 1
n5
n 15
15
（2）t-分布（学生分布）
设 X ~ N ( 0 ,1), Y ~ 2 ( n ) 且X、Y为独立随 机变量，则称随机变量
t
X Y /n

X
1 n 2 ( X 12 ...... X n )
为自由度为n的t-分布。记为： t ~ t ( n ) 。
3
§1 随机样本
总体: 研究对象在某项数量指标的全体. 记为X。通常称总体X。 个体: 总体X中的每一个元素（实数）xi。 根据总体所含的个体数分为： 有限总体和无限总体。
4
总体与取样
X1
X
X2 X3 Xn
取样模型
X
X2 X1
X3
X4
X5
河流污染取样
5
总体、样本、统计量
总体 样本 统计量
X1 X2
2 ( n ) 分布:
具有可加性
2 X X 12 ...... X n , X i ~ N (0,1)
3. 4.
t ( n ) 分布:
X ~ N (0,1), Y ~ 2 ( n )
t(n) X Y /n
F ( n1 , n 2 ) 分布: U ~ 2 ( n1 ), V ~ 2 ( n 2 )



F (n1 , n2 )
19
分位点及性质:
定义: Pr[ X z ]

z
(1)标准正态分布分位点

(x)
( x)dx 1 ( x)dx


z
z1
( x)
Pr[ X z ]

概率论与数理统计第2版教学课件第6章

概率论与数理统计第2版教学课件第6章

随机样本与统计量
6.1.2
样本统计量
定义4 (极差) 设X1,X2,…,Xn是来自总体X的样本，则称统计量
R=X(n)-X(1)
为样本的极差。
极差反映了样本观测值的波动幅度。它同方差一样是反映观察值离散程度的数量指标。
(6-8)
6.1
随机样本与统计量
6.1.2
样本统计量
例 从某工厂生产的轴承中随机地抽取10只，测得其重量(以kg计)为
从一个总体X抽取n个个体，由于抽样的独立性与随机性，每个个体都是一个随机变量
Xi(i=1,2,…,n)。这里X1,X2,…,Xn相互独立，并且Xi与X具有相同分布。这样的n个随机变量称为总体X的
一个容量为n的样本。但是在具体抽样后，它们就有了具体的数值
x1,x2,…,xn,
称为样本观察值。
6.1
随机样本与统计量
有钢筋视为一个总体，则这一天生产的每一根钢筋为个体。又如，要检验一批灯泡的质量，这一批灯
泡可看成是一个总体，每一个灯泡则为个体。
在数理统计中，我们往往对表征总体性质的某一个或某n个数量指标感兴趣。如灯泡的使用寿命X
就是灯泡质量的一个重要的数量指标；钢筋的抗拉强度Y1，抗剪切力的大小Y2是表征钢筋质量的两个
一些带有严重破坏性的自然灾害进行必要的估计与预测。如在建造桥梁时，为了防止洪水冲塌桥梁这
类事故发生，设计时就必须事先考虑到在使用期间该河流可能爆发的最高水位；在建造高大建筑物时，
也要考虑到今后若干年内的最大风压、地震的最大震级等。了解这些随机变量的概率分布，就是极值
的分布。
6.2
抽样分布
6.2.2
6.1.1
总体、个体与样本
定义1 设X1,X2,…,Xn是来自总体X的容量为n的样本，若X1,X2,…,Xn相互独立，且每个

概率论与数理统计A第6章-文档资料

概率论与数理统计A第6章-文档资料
1 n 2 S ( X X ) i n 1 i 1
样本标准差
样本k阶原点矩
1 k A Xi k=1,2,… k n i1
样本k阶中心矩
n
它反映了总体k 阶矩的信息
1 k M (X X ) k i ni 1
n
它反映了总体k 阶 中心矩的信息
统计量的观察值
1n x xi; n i1
2
tx 1 ( x ) e t dt , x 0 0
2

来定义.
1 2 2 (1 )就是 , 2 分布 . 由定义 X ~ (1 ), 注 已知 i 2 n 1 n 2 2 2 即 Xi ~ 可加性知 Xi ~ ,2.再由 ,2. i 1 2 2
x 是一个样本的观察值 , 则 g ( x ,x , x ) 也是统 n 1 2 n
几个常见统计量
它反映了 1 n 样本平均值 总体均值 X Xi n i 1 的信息 n 1 2 2 样本方差 S (X X ) i n 1i 1 它反映了总体 方差的信息
1 n 2 2 X n X i n 1 i 1
这就是矩估计法的理论 根据 .
经验分布函数
设 X ,X , ,X 是总体 F 的一个样本， s ( x )x 1 2 n
表示 x ,x , ,x 中不大于 x 的随机变量的 . 1 2 n
定义 经验分布函数为
1 F (x ) s (x ) x n n 例设总体 F 具有一个样本值 1 ， 1 ， 2 ，则经验分布函
顺序统计量
极差: 最直接也是最简单的方法，即最大值－最小 值（也就是极差）来评价一组数据的离散度。

概率统计第六章 样本及抽样分布

概率统计第六章 样本及抽样分布

第六章数理统计的基本概念数理统计与概率论是两个有密切联系的姊妹学科（基础 应用）．概率论研究的是在知道随机变量分布的情况下求事件的概率．但对具体问题，如何判断某随机变量服从某种分布呢？诚然，我们可以根据经验判断出随机变量的分布，但参数又是什么呢？这些问题概率论回答不了，由数理统计来回答．数理统计是通过数据来回答这些问题的．这些数据带有随机性（不同于会计中的数据），根据数据得出的结论难免会出错，我们希望所犯错误越少越好，而这就需要使用概率论的语言来表述．数据不是从天上掉下来的，要获得数据，首先要进行观察或实验，收集整理数据，然后进行推断，这就是数理统计要研究的内容．即数理统计学是收集、分析数据，并根据数据进行推断的科学和艺术（强调它的艺术性是为着重说明统计方法需要灵活使用，很依赖于人的判断乃至灵感．强调这一点很有好处，它提醒人们不要以教条式的态度来看待数理统计方法，以为只要记住一些公式和方法，碰到什么问题套上去就行）．数理统计课程着重于统计推断。

所谓统计推断，就是由样本来推断总体，或者由部分推断总体．统计估计和假设检验是统计推断的基础，以此为基础发展了许多实用的统计方法：回归分析、方差分析、时间序列分析及其他多元统计分析方法等．第一节样本与统计量一总体与个体1．总体（Population）和个体（Individual）1）【定义】把研究“对象”的全体称为总体．用X、Y、Z等表示总体．组成总体的每个元素称为个体．例如：全国英语四级考试刚刚结束，阅卷评分尚需一段时间，有关部门急于了解这次考试成绩的分布状况（应试的400万考生）；另外，想了解全国大学生的身体状况；想了解用新工艺生产的一批灯泡寿命等等。

这里的“应试的考生”，“全国的大学生”“这批灯泡”等，就构成了各自的总体。

2）总体X的分布函数称为总体分布函数。

当X为离散型随机变量时，称X的概率函数为总体概率函数。

当X为连续型随机变量时，称X的密度函数为总体密度函数。

东华大学《概率论与数理统计》课件 第6章样本与抽样分布

东华大学《概率论与数理统计》课件 第6章样本与抽样分布

X
的
n
一
个
样
本的
观察
值
,
则g( x1 , x2 , xn )是统计量g( X1 , X 2 , X n )的观察值.
例1 设总体X 服从两点分布b(1, p) ，其中p 是未知参数，
X1,
,
X
是
5
来自X的简
单
随机样本.试指出
X1
X
，
2
max
1 i 5
X
i
,
X5 2 p,
( X5 X1)2
哪些是统计量,哪些不是统计量，为什么？
从国产轿车中抽5辆进行耗 油量试验
样本容量为5 抽到哪5辆是随机的
对总体X在相同条件下，进行n次重复、独立观察，其结果依次记 为 X1,X2,…,Xn.这样得到的随机变量X1,X2,…,Xn.是来自总体的一个简单 随机样本，其特点是：
1. 代表性：X1,X2,…,Xn中每一个与所考察的总体X有相同的分布. 2. 独立性：X1,X2,…,Xn相互独立.
k同分布,
E(
X
k i
)
k
k 1, 2, , n 再由辛钦大数定律可得上述结论.
再由依概率收敛性质知，可将上述性质推广为
g( A1 , A2 , , Ak ) P g(1, 2 , , k )
其中g为连续函数.
矩估计法的理论依据
2. 经验分布函数
设X1, X2,
,
X
是
n
总
体
F的
一
个Hale Waihona Puke 本，用S(
x
则称变量
t X Yn
所服从的分布为自由度为 n的 t 分布.

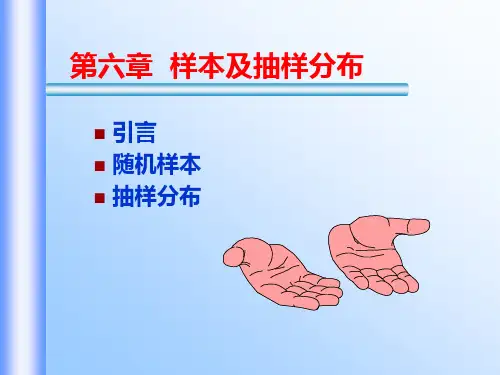
概率论与数理统计-第六章

概率论与数理统计-第六章
大街上随机抽取200人，进行调查。记录了
这200人的年龄数据。
总体：北京市民的年龄 随机变量：年龄X
个体：张三28岁；李四5岁；
样本：{ 28；5；14；56；23；2；39；…；69} 样本容量：200
抽样：随机抽取200人进行调查的过程
6
例2：为了确定工厂生产的电池电量分布情况，在
产品中随机抽取500个，测量其电量。记录了
x
0
F n1 , n2
F分布的分位数
x
F分布的上α分位点
对于给定的 , 0 1, 称满足条件
F n1 , n2
f x; n1 , n2 dx 的点F n1 , n2
为F n1 , n2 分布的上 分位数。F n1 , n2 的值可查F 分布表
17
不易计算！
18
抽样分布 —— 任意统计量 Q = g (X1, X2, …, Xn ) 的分布函数 抽样分布的计算： 多维随机变量（独立、同分布）的函数的分布 函数的计算问题。
得到统计量 Q 的抽样分布，就可以用来解决
关于总体 X 的统计推断问题。
19
关于随机变量独立性的两个定理
解：(1)作变换 Yi
显然Y1 , Y2 ,
2 n i 1
Xi
, Yn相互独立，且Yi N 0,1 i 1, 2,
Xi

i 1, 2,
,n
,n
于是 (

) Yi 2 2 n
2 i 1
28
n
(2)
2 ( X X ) X1 X 2 ~ N (0, 2 2 ), 1 2 2 ~ 2 (1) 2

概率论与数理统计第六章样本与抽样分布精品PPT课件

概率论与数理统计第六章样本与抽样分布精品PPT课件

100.9 99.6 103.1 98.1 99.2 101.4 100.4 99.1 100.2 97.5 99.7
99.8 102.9 98.2 96.0 101.5 100.3 96.9 101.2 98.1 99.4 100.6
102.7 97.7 95.8 99.0 100.2 97.8 99.5 100.2 97.4 101.8 102.1
第六章 样本与抽样分布
• 本章主要内容
§1 总体与个体 §2 直方图与经验分布函数 §3 统计量及其分布
2021年1月20日星期三
1
§6.1 总体与个体
一.总体与个体
1.定义1：一个统计问题总有它明确的研究对象.
研究对象的全体称为总体(母体)， 总体中每个成员称为个体.
总体
…
研究某批灯泡的质量
2021年1月20日星期三
从国产轿车中抽5辆 进行耗油量试验
样本容量为5
2021年1月20日星期三
9
§6.1 总体与个体
样本是随机变量.
抽到哪5辆是随机的
容量为n的样本可以看作n维随机变量.
但是，一旦取定一组样本，得到的是 n个具体的数 (x1,x2,…,xn)，称为样本的一 次观察值，简称样本值 .
2021年1月20日星期三
某批 灯泡的寿命
鉴于此，常用随机变量的记号
或用其分布函数表示总体. 如 说总体X或总体F(x) .
2021年1月20日星期三
7
§6.1 总体与个体
类似地，在研究某地区中学生的营养状 况时，若关心的数量指标是身高和体重，我 们用X和Y分别表示身高和体重，那么此总体 就可用二维随机变量(X,Y)或其联合分布函数 F(x,y)来表示.

概率论与数理统计第六章

概率论与数理统计第六章
今后，我们称X的分布函数和数字特征分别为总体 的分布函数和数字特征，并不再区分总体与相应的 随机变量X。 对总体的称呼: 总体，总体X与总体F。
例6.3（例6.l续）在例6.l中，若农户年收入以万元 计, 假定N户中收入X为以下几种取值:
0.5, 0.8, l, 1.2和1.5。 取这些值的农户个数分别为：n1, n2, n3, n4, n5, (这里n1+n2+n3+n4+n5=N)。
,
0, x x(1)
Fn
(
x)
k
/
n,
x(k ) x x(k1)
1,
x x(n)
对不同的样本值, 得到的 经验分布函数不同。但 当样本容量较大时, 经验 分布函数Fn(x)是总体分 布函数F(x)的良好近似。
统计量的分布称为抽样分布。数理统 计中常用到来自正态总体的三个分布：
2—分布、 t —分布和F—分布。
而在数理统计中的随机变量，它的分布是未知的 ，或者不完全知道，人们通过对所研究的随机变 量进行重复、独立的观察，得到许多观察值，对 这些数据进行分析，从而对随机变量的分布作出 种种判断。
现实世界中存在着形形色色的数据，分析这些数据 需要多种多样的方法。 因此,数理统计中的方法和支持这些方法的相应理 论是相当丰富的，概括起来可以归纳成两大类: 参数估计──根据数据，用一些方法对分布的未知 参数进行估计。 假设检验──根据数据，用一些方法对分布的未知 参数进行检验。 它们构成了统计推断的两种基本形式。这两种推断 渗透到了数理统计的每个分支。
n i 1
X
2 i
nX
2
)
它反映了总体 方差的信息
样本标准差 S S2 ,

北京理工大学《概率论与数理统计》课件-第6章样本及抽样分布-2

北京理工大学《概率论与数理统计》课件-第6章样本及抽样分布-2
17
注:
（1）统计量是不含未知参数的样本的函数。
（2）统计量是随机变量的函数，故统计量 是随机变量。
例1
设 X1 ,…,Xn 为来自总体 X ~ N(μ,σ2) 的一个样本， 其中μ,σ2未知，问下列随机变量中哪些是统计量
1 n
Xn n i1 Xi
1
n
n i 1
Xi
S 2
1 n1
n i 1
对标准正态密度函数( x)有
sup pn( x) ( x) 0.0041
x
45
t分布的性质 定理2.5: 如果Z～N(0,1) , ~ 2(n), 且Z与 相互独立，则有
Z ~ t(n)
n
46
正态总体的抽样分布（2）
定理 2.6 如果X1,X2,…,Xn是来自正态总体 N (, 2 )
)
(E(
Xi
))2
1
Var(
X
2 i
)
E
(
X
4 i
)
[
E
(
X
2 i
)]2
3
1
2,
i 1, 2,
n
n
n
所以 E( ) E(
X
2 i
)
E
(
X
2 i
)
n.
i 1
i 1
n
n
Var( ) Var(
X
2 i
)
Var(
X
2 i
)
2n.
i 1
i 1
36
证明：(2)设X1, X2, , Xnm是来自总体N (0,1)的样本
样本是联系二者的桥梁
总体分布决定了样本取值的概率规律，也 就是样本取到样本值的规律，因而可以由样本 值去推断总体。

概率论与数理统计PPT课件(共8章)第六章 数理统计的基本概念

概率论与数理统计PPT课件(共8章)第六章 数理统计的基本概念

代表性
每个样本Xi(i=1,2,…,n)与 总体X具有相同的分布
独立性
各个样本X1,X2,…,Xn的取 值互不影响，即X1,X2,…,Xn是 相互独立的随机变量．
6.1.3 样本的联合分布
若 X1 ，X2 ， ，Xn 为总体 X 的一个样本， X 的分布函数为 F(x) ，则 X1 ，X2 ， ，Xn
n
n
xi
n xi
p i1 (1 p) i1 ，
概
率
论
与
数 理
6.2
统
计
统计量与抽样分布
6.2.1 统计量
定义 6.2 不含任何未知参数的样本 X1 ，X2 ， ，Xn 的连续函数 g(X1 ，X2 ， ，Xn )
称为统计量．
下面列出一些常用的统计量．
（1）样本均值
X
1 n
n i1
Xi
（2）样本方差
概
率
论
与
数
理 统 计
数理统计的基本概念
第六章
概
率
论
与
数
理 统
壹 总体与样本
计
贰 统计量与抽样分布
目录
概
率
论
与
数 理
6.1
统
计
总体与样本
总体与个体
6.1.1 总体
在数理统计中，通常把研究对象的全体称为总体，把构 成总体的每个研究对象称为个体．
总体分布
为了便于数学上的处理，我们将总体定义为随机变量， 记作．随机变量的分布称为总体分布.
N
(1
，12
)
与
N
(2
，
2 2
)
的样本，且这两个样本相互独立．设

概率论与数理统计—第六章样本及抽样分布

概率论与数理统计—第六章样本及抽样分布

)n X +=2)i X -，S 2()iX X -21(,2N μ22(,4N μ212()22x e μ--⋅如果用X 的测试值x 估计μ1，用Y 的测试值y 估计μ2，从上面的图形可以看出，当可靠性（概率）取相同值（如90%）时，y 比x 更“接近”它的待估计量.当要求两个“接近"相同时，y 比x 的可靠性更高。

能够得到这些有价值的结论,应归功于我们知道了X 和Y 的分布.综上所述，我们需要知道统计量g （X 1，X 2，…,X n ）的分布。

那么，g (X 1，X 2，…，X n )服从什么分布呢？不同的g 会有不同的结果.下面给出几种常见的分布，这些分布在统计推断中起着重要的作用。

（一）2χ分布(2χdistribution ）设n X X X ,,,21 为相互独立的随机变量，它们都服从标准正态)1,0(N 分布，则随机变量221ni i X χ==∑ 服从自由度为n 的2χ分布，记作22()n χχ．)(2n χ分布的密度函数为122/210()2(/2)00n yn y e y f y n y --⎧>⎪=Γ⎨⎪≤⎩其中 )(αΓ称为伽马函数，定义为10(),0x x e dx ααα∞--Γ=>⎰。

下图描绘了)(2n χ分布密度函数在n = 1，4，10，20时的图形。

μ10.16μ20.082χ分布具有可加性:如果2211()n χχ、2222()n χχ，则 2221212()n n χχχ++2χ分布期望和方差：设22~()n χχ,则2()E n χ=,2()2D n χ=。

2χ分布分位点 对于给定的α( 0 〈 α < 1），称满足条件222(){()()}()ααn n n f y dy αχχχ+∞>==⎰P的数2()αn χ为2()n χ分布的上分位点。

教材后附表的2χ分布表给出分位点2()αn χ，可通过查表得到.如20.99(17) 6.408χ=，20.90(17)10.085χ=，20.05(17)27.587χ=等等。

概率论与数理统计基本概念及抽样分布PPT课件

概率论与数理统计基本概念及抽样分布PPT课件

~
2 (n1 ),
2 2
~
2 (n2 ), 且它们相互独立，
则
2 1
2 2
~
2 (n1
n2 )
《概率统计》
返回
下页
结束
4. 2分布的百分位点
对给定的α（0＜α＜1）
（1）称满足
P{ 2
2
(n)}
，即
f ( y)dy
x2 ( n)
的点为 2分布的上100α百分位点。
f(y)
（2）称满足
注：在研究中，往往关心每个个体的一个(或几个)数量指标和 该数量指标在总体中的分布情况. 这时，每个个体具有的数量 指标的全体就是总体.
或，总体：研究对象的某项数量指标的值的全体.
《概率统计》
某批 灯泡的 寿命
该批灯泡寿命的 全体就是总体
返回
下页
结束
为推断总体分布及各种特征，按一定规则从总体中抽取若 干个体进行观察试验，以获得有关总体的信息，这一抽取过程 为 “抽样”.
( x)
（1）称满足条件 P{X＞Xα} =α，
α
即
( x)dx
X
的点Xα为N(0，1)分布的上100α百分位点.
X1－α
0
由于 P{X X } 1 记 －Xα= X1－α
（2）称满足条件 P {| X | X }
2
2
的点 X 为N(0，1)分布的双侧100α百分位点.
X
2
则
E(X )
E(1 n
n i 1
Xi)
1 n
n i 1
E(Xi )
1 n
n
D(X ) D(1 n
n i1
Xi)

概率第6章 样本及抽样分布PPT课件

概率第6章 样本及抽样分布PPT课件

Xi
i 1, 2,
,n
显然Y1,Y2, ,Yn相互独立，且Yi N 0,1 i 1, 2,
于是
2
n i 1
(
X
i
)2
n
Yi 2
i 1
2
n
(2)
X1
X2
~
N
(0,
2
2
),
(
X1 X
2 2
2
)2
~
2 (1)
2X3
X4
X5
~
N(0, 6
2 ), (2X3
X4
6 2
X 5 )2
~
[说明]：后面提到的样本均指简单随机样本，由概率论知，若总体X 具有概率密度f(x)，
则样本（X1,X2,…,Xn）具有联合密度函数：
n
fn x1, x2, xn f xi
i1
3
统计量：样本的不含任何未知参数的函数。
常用统计量：设（X1,X2,…,Xn）为取自总体X的样本
1.
样本均值
定理6.4：t n分布的概率密度为：f t, n
n1 2
n
n 2
1
t2 n
n1 2
,
t
对给定的 ,
0
1, 称满足条件
t n
f
t, n dt
的点t
n
为t n分布的上分位数。t分布的上分位数可查t分布表
f (x)
n 10
f x
t1 (n) t (n)
n4
n 1
3 2 1 0 1 2 3
Y1 g1 X1, , X n1 ,Y2 g2 X n11, , X n2 , ,Yk gk X , n1 nk11 , X n

概率论第六章样本及其抽样分布

概率论第六章样本及其抽样分布
定义 若样本函数 gX1, X 2, , X n 中不含有任何未知 量，则称这类样本函数为统计量。
24
例 设 X1, X 2 , , X n 是来自总体 N ( , 2 )
的随机样本,其中 已知, 未知,
则( )不是统计量
n
[1]
1 n
Xi
i1
n
n
[2]
1 n
(Xi )2
[3]
1 n
(Xi X)2
为了讨论正态总体下的抽样分布，先引入由正态 分布导出的统计中的三个重要分布，即
2分布，t 分布，F分布。
掌握三大分布的4点：
1、构成形式； 2、密度函数的大致图像；
本节大家要理解的基本概念主要有:
1. 总体
4.简单随机样本
2. 总体分布 3. 样本
5. 样本的二重性 6. 样本的分布
9
1. 总体与个体
(population and individual)
在统计学中,将研究问题所涉及的对象全 体称为总体,而把总体中的每个成员称为个体.
例如: 我们想要研究一家工厂某种产品的次品率.
i1
i1
n
[4]
1 n
(
X
i μ σ
)
2
[5] X12 X22 σ2
i1
[6] 2X1X2...Xn
25
数理统计中最常用的统计量及其观测值有：
1 样本均值 观测值记为 2 样本方差
X
1 n
n i 1
Xi
(1)
x
1 n
n i 1
xi
(2)
S 2 1 n n 1 i1
Xi X
2
1 n 1
Xi X

概率论与数理统计讲义第六章 样本与抽样分布

概率论与数理统计讲义第六章 样本与抽样分布

第六章样本与抽样分布§6.1 数理统计的基本概念一．数理统计研究的对象例：有一批灯泡，要从使用寿命这个数量指标来看其质量,设寿命用X表示。

(1)若规定寿命低于1000小时的产品为次品。

此问题是求P(X 1000)=F(10000),求F(x)? (2)从平均寿命、使用时数长短差异来看其质量，即求E(x)?、D(x)?。

要解决二个问题1．试验设计抽样方法。

2．数据处理或统计推断。

方法具有“从局部推断总体”的特点。

二.总体（母体）和个体1.所研究对象的全体称为总体，把组成总体的每一个对象成员（基本单元）称为个体。

说明：(1)对总体我们关心的是研究对象的某一项或某几项数量指标(或属性指标)以及他们在整体中的分布。

所以总体是个体的数量指标的全体。

(2)为研究方便将总体与一个R.V X对应(等同)。

a.总体中不同的数量指标的全体，即是R.V.X的全部取值。

b.R.V X的分布即是总体的分布情况。

例：一批产品是100个灯泡，经测试其寿命是：1000小时1100小时1200小时20个30个50个X 1000 1100 1200P 20/100 30/10050/100(设X表示灯泡的寿命)可知R.V.X的分布律，就是总体寿命的分布，反之亦然。

常称总体X，若R.VX～F(x)，有时也用F(x)表示一个总体。

(3)我们对每一个研究对象可能要观测两个或多个数量指标，则可用多维随机向量（X,Y,Z, …）去描述总体。

2.总体的分类有限总体无限总体三．简单随机样本.1.定义6.1 ：从总体中抽得的一部分个体组成的集合称为子样（样本），取得的个体叫样品，样本中样品的个数称为样本容量（也叫样本量）。

每个样品的测试值叫观察值。

取得子样的过程叫抽样。

样本的双重含义：(1)随机性：用(X1，X2,……X n) n维随机向量表示。

X i表示第i个被抽到的个体，是随机变量。

（i=1,2,…n）(2)确定性：(x1,x2,……x n)表示n个实数，即是每个样品Xi观测值x i(i=1,2,…n)。

第6章抽样分布

第6章抽样分布

* * Xm 的分布已知，故可求出 X 函数的分布，设 m
所以 n! 1 m 1 nm hm ( y ) f ( x)[1 F ( x)] [ F ( x)] (n m)!(m 1)! f ( x) n! y m 1 (1 y ) n m , (n m)!(m 1)! 0 y 1, m 1 ~ n
所以
X 的特征函数为
2 2 t / n iat / n x t exp 2
n
t 2 2 exp iat 2 n
可见 X ~ N ( a,
2
n
) 分布。
（二）样本均值的极限分布 定理：设 X1, X2，…，Xn来自一般总体X,且E(X)=a,
若总体X为连续型随机变量，其密度函数为f (x),则(X1,X2,…，Xn) 的联合密度函数为
§6－2 样本分布
一、频率直方图
二、样本分布函数
如果我们从随机变量X的总体中抽取了一个样本，把样本的n个值
* * * x1，x2，…， xn加以排队 x1 ，并把它看成是某个离散 x2 xn 随
1 n 2 S (Xi X ) n i 1 2 2
_

1 n S* (Xi X ) n 1 i 1
2
2 2 2、设X ~ N ( a1 , 1 ), Y ~ N ( a2 , 2 ), X 1 , X 2 ,..., X n1 及Y1 , Y2 ,..., Yn 2 分别为
—
t 1 式中 ( ) 是 X 的特征函数。 n nn n 1 证： X X i 1 X i ，且 1 X , 1 X ,, 1 X 相互独立 1 2 n n i 1 i 1 n
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

其中和式
xi
是对小于或等于
x
x
的一切
x(i)
的频率
fi
求和,
则称 Fn(x)为样本分布函数,经验分布函数。
2. 样本分布函数Fn(x)具有下列性质：
(1) 0 ≤ Fn(x) ≤1 (2) Fn(x)是非减函数
(3 )F n 0 , F n 1
(4) Fn(x)在每个观测值 x(i)处是右连续的, 点 x(i)是 Fn(x)的跳跃间断点， Fn(x)在该点的跃度就等于频率fi
并以各子区间为底, 以 fi /(ti - ti-1)为高作小矩形,
各个小矩形的面积 ∆Si 就等于样本观测值落在该子区间内的频率,
即:
S ititi 1 ti fiti 1fi,l
i1 ,2, ,l.
l
所有小矩形的面积的和: Si fi 1.
i1
i1
这样作出的所有小矩形就构成了直方图。
写出零件质量的频率分布表并作直方图。
解: 因为样本观测中最小值为 237, 最大值为 265, 所以我们把数据的分布区间确定为: (236.5, 266.5)
并把这个区间等分为 10个子区间:
(236.5, 239.5), (239.5, 242.5), …, (263.5, 266.5)
数理统计
由此得到零件质量的频率分布表：
因为样本容量 n充分大时, 随机变量 X的取值落在 各个子区间 (ti-1 - ti)内的频率近似等于其概率, 即:
f i P t i 1 X t i,i 1 ,2 , ,l
所以直方图大致地描述了总体X的概率分布。
例2: 测量100个某种机械零件的质量, 得到样本观测值如下(单位:g):
246 251 259 254 246 253 237 252 250 251 249 244 249 244 243 246 256 247 252 252 250 247 255 249 247 252 252 242 245 240 260 263 254 240 255 250 256 246 249 253 246 255 244 245 257 252 250 249 255 248 258 242 252 259 249 244 251 250 241 253 250 265 247 249 253 247 248 251 251 249 246 250 252 256 245 254 258 248 255 251 249 252 254 246 250 251 247 253 252 255 254 247 252 257 258 247 252 264 248 244
观测值 x 1
频数
n1
频率
f1
x 2
…
n2
…
f2
…
数理统计
x l
总计
nl
nபைடு நூலகம்
fl
1
其中 x1x2 xl
fi
ni n
i1,2,
,l
l n
l
ni n
i1
l
fi 1
i1
1. 定义: 设函数:
0,
x x1
Fn
x
fi , xi x xi1
xi x
1,
x xl
数理统计
i1,2, ,l1
理 论基础．
例 1:设 总 体 F 具 有 一 个 样 本 值 1， 1， 2，数理统计
则 经 验 分 布 函 数 F 3(x)的 观 察 值 为 :
0, 若x 1
F3 ( x)
2 3
,
若1
x
2
1, 若 x 2
二、直方图(histogram)
作样本的频率直方图(简称直方图), 步骤如下：
太多则由于频率的随机摆动而使分布显得杂乱,
太少则难于显示分布的特征。
此外, 为了方便起见, 分点 ti 应比样本观测值 xi多取一位小数.
3. 把所有样本观测值逐个分到各子区间内,
并计算样本观测值落在各子区间内的频数 ni及频率:
fi
ni ,i
n
1,2,
,l.
数理统计
4. 在 Ox轴上截取各子区间,
数理统计
样本分布函数Fn(x)的图形
数理统计
对于任意的实数 x总体分布函数 F(x)是事件X ≤ x 的概率； 样本分布函数 Fn(x)是事件 X ≤ x发生的频率． 根据伯努利大数定理可知, 当 n→∞时, 对于任意的正数 ε, 有:
ln i m PF nxF x1
格利文科(Glivenko) 进一步证明了, 当n→∞时， 样本分布函数 Fn(x)与总体分布函数 F(x)之间存在着更密切的 近似关系的结论. 这些结论就是我们在数理统计中可以依据样本来推断总体的
数理统计
1. 找出样本观测值 x1, x2, …, xn中的最小值与最大值, 分别记作 x1* 与 xn*, 即: x1* =min(x1, x2, …, xn), xn* =max(x1, x2, …, xn)
2. 适当选取略小于 x1*的数 a与略大于 xn*的数 b, 并用分点: a=t0 < t1 < t2 < … < tl-1 < tl=b
数理统计
总计
100
1.00
直方图如图所示:
THANK YOU
精品
概率论与数理统计第六章样本 及抽样分布}第二节：样本分布
函数直方图
一、样本分布函数(sample distribution function) 数理统计
我们把总体的分布函数 F(x)=P(X ≤ x) 称为总体分布函数. 从总体中抽取容量为 n 的样本得到 n 个样本观测值, 若样本容量 n 较大,则相同的观测值可能重复出现若干次, 为此,应当把这些观测值整理,并写出下面的样本频率分布表：
把区间 (a, b)分成 l个子区间:
(a, t1), (t1, t2), …, (ti-1, ti), …, (tl-1, b) 第 i个子区间的长度为: ti ti ti 1 ,(i 1 ,2 , ,l)
各子区间的长度可以相等, 也可以不等;
若使各子区间的长度相等,
则有:
ti
b
l
a
子区间的个数一般取为 8至 15个,