经验分布函数与直方图共43页

经验分布和分布函数在统计学中，经验分布和分布函数是两个重要的概念。

经验分布是指根据一组观测数据得到的概率分布函数的估计，而分布函数则是用于描述一个随机变量的概率分布的函数。

经验分布是通过对观测数据进行统计分析来估计真实概率分布的方法之一。

在实际应用中，我们通常无法获得全部的数据，而只能通过抽样得到一部分数据。

因此，我们需要通过对抽样数据进行分析来得到总体的概率分布。

经验分布的计算方法很简单，只需要统计抽样数据中每个取值出现的频率即可。

然后将这些频率按照大小顺序累加，就得到了经验分布。

经验分布是对真实分布的一种估计，它可以用来描述抽样数据的分布特征。

分布函数是用来描述一个随机变量的概率分布的函数。

它定义为随机变量小于等于某个特定值的概率。

分布函数通常用大写字母F表示，其数学表达式为F(x) = P(X ≤ x)，其中X表示随机变量，x表示一个实数。

分布函数是概率论中最基本的概念之一，它能够完整地描述一个随机变量的概率分布。

分布函数具有以下性质：1) F(x)是一个非减函数；2) F(x)的取值范围在0到1之间；3) F(x)在x趋于负无穷时趋于0，x趋于正无穷时趋于1。

经验分布和分布函数在统计学中有着广泛的应用。

它们可以用来描述随机变量的分布特征，从而对随机变量进行概率推断和统计推断。

例如，在假设检验中，我们可以通过计算经验分布和分布函数来判断某个假设的可行性。

另外，在参数估计中，我们也可以利用经验分布和分布函数来估计未知参数的值。

此外，经验分布和分布函数还可以用来进行模型拟合和预测，从而对未来的观测数据进行预测和分析。

经验分布和分布函数是统计学中两个重要的概念。

它们可以用来描述随机变量的分布特征，进行参数估计和假设检验。

在实际应用中，我们可以通过对观测数据进行统计分析来计算经验分布和分布函数，从而对随机变量的概率分布进行估计和推断。

经验分布和分布函数的应用范围广泛，对于统计学的研究和实践都具有重要的意义。

求 F ( u, v ) ．对于任意 u, v ，有
PX (1) u, X ( n ) v Pu X 1 v,, u X n v Pu X 1 v Pu X n v [ F ( v ) F ( u)]n , 若u v， 0 , 若u v ； F ( u, v ) PX (1 ) u, X ( n ) v PX ( n ) v PX (1 ) u, X ( n ) v [ F (v )]n [ F (v ) F ( u )]n , 若u v， n ， 若 u v． [ F (v )]
1.3 顺序统计量
§1.3
顺序统计量、经验分布函数和直方图
一、顺序统计量 另一类常见的统计量是顺序统计量. 定义 1 设 X 1 , X 2 ,, X n 是取自总体 X 的样本, X ( i ) 称为 该样本的第 i 个顺序统计量，它的取值是将样本观测值由小 到大排列后得到的第 i 个观测值。x(1) x( 2 ) x( n ) ，X ( i ) 的值是 x ( i ) 。其中 X (1) minX 1 , X 2 ,, X n 称为该样本的最小顺 序统计量，称 X ( n ) maxX 1 , X 2 ,, X n 为该样本的最大顺序统 计量。 我们知道， 在一个样本中， X 1 , X 2 ,, X n 是独立同分布的， 而次序统计量 X (1) , X ( 2) ,, X ( n) 则既不独立，分布也不相同， 看下例。
假设总体 X 在区间[0,2]上服从均匀分布； Fn ( x )
是总体 X 的经验分布函数， 基于来自 X 的容量为 n 的简单随 机样本，求 Fn ( x ) 的概率分布，数学期望和方差． 解 总体 X 的分布函数为

河北 8362
浙江 14655
山西 5460
安徽 5221
内蒙古 6463
福建 12362
辽宁 12041
江西 5221
吉林 7640
山东 10465
黑龙江 9349
河南 5924
湖北 湖南 广东 广西 海南 重庆 四川 贵州 7813 6054 13730 4668 7135 5654 5250 2895
P
fn (x)
p(x)
1
2
E fn (x)
p(x)2
2 2
E fn (x) Efn (x)2 Efn (x) p(x)2
(1)
由于Rn(a,b)~B(n,pk)，其中
pk P
X [tk , tk 1)
tk1 p( y)dy Kh
tk
所以当n
时，E
fn (x)
Efn (x)2
用事件{X<x)发生的频率作为其估计即可。这就引出了下面 所谓经验分布函数的概念。
一、经验分布函数 设X1,…,Xn是抽自总体X的一个样本，观察值为x1,…,xn， 次序观测值x(1)≤ …≤x(n)，则总体X的经验分布函数定义为
Fn
(x)
样本中小于x的观测值的个数 n
，x
R.
即
0,
Fn
(x)
k
0.032258 0.00000516
频率直方图如下图所示：
初步判断数据是来自什么样的总体？ 这个例子中数据量相对来说比较少，一般情况下数据量最好大于100， 分组的个数根据数据量来确定，一般介于[n/10,n/5]之间，最多不能 超过20组。
定理6.2.2 密度函数p(x)在点x[t0,tm)处连续，样本容量为n，且

条形图与直方图的异同：
相同点：都能呈现 各组数据的多少和 差距
不同点：
1.条形图各矩形间 有空隙，直方图各 矩形间无空隙.
2.条形图表示分类 数据，直方图表示 连续数据的分组数 据.
用表格整理数据
身高 149 151 153 154 155 156 157 158 159 160 161
人数 1 1 3 3 2 5 5 8 7 4 2
要挑出身高相差不多的40名同学参加比赛，我们 该怎样挑选呢？
学习目标
了解组距、组数的概念 画直方图的步骤 学会对数据进行合理的分组处理,通过学习用简单频
数分布直方图描述数据的方法,进一步体会统计图表 在描述数据中的作用. 会画简单的频数分布直方图,并利用频数分布直方图 解释数据中蕴含的信息。
（不含合1计64 cm）的学生中选队员．
63
4、绘制频数分布直方图
频数 （学生人数）
横轴表示身高 纵轴表示频数
身高/cm
4、绘制频数分布直方图
频数 （学生人数）
20
横轴表示身高 纵轴表示频数ຫໍສະໝຸດ 151050
149 152 155 158 161 164 167 170 173
身高/cm
4、绘制频数分布直方图
学生人数
60
理得到如图所示的频数分布 50
直方图，请回答下列问题： 40
（1）此次抽样调查 的样本容量是_____
30
28
20 15
10 10 5
0
28 14
0~35 36~47 48~59 60~71 72~83 84~95 96~107 108~120
分数
2003年中考结束后，某市从参加中考的12000名学生中抽

某班一次数学测表 验2成0.1绩.2的频数分布表
组别
划记
唱票
画列频频率数分分布布直表方的图一的般一步般骤步:骤
(1) 计算最大值与最小值的差(极
差).极差: 95-53=42（分） (2) 决定组距与组数.
极差/组距=42/10=4.2 数据分成5组.
(3) 决定分点.
49.5~59.5, 59.5~69.5, …89.5~99.5
频数（人）
的频数分布直方图
频数分布直方图如图。请
根据这个直方图回答下面 的问题：
8
（1）参加测试的总人 6
数是多少？ 15人
4
（2）自左至右最后
一组的频数、频率是 2
多少？ 3，0.2
（3）数据分布是，组距 0
是多少 25次
62 87 112 137 跳绳次数
根据以下两个频数分布表，分别画出频数分布直方图
10 9
同学较少，不及格的 学生数最少．
5 2
54.5 64.5 74.5 84.5 94.5
为了使图形清晰美观， 频数分布直方图的横轴 上可只标出组中值，不 标出组界.
（分）
某班一次数学测验成绩的频数分布直方图 频数（人） 14 9 10
议一议:
频数分布直方图和一般条 形统计图有和区别?
5 2
（分）
67.5~72.5
70
2
72.5~77.5
75
4
77.5~82.5
80
9
82.5~87.5
85
组别(℃) 组中值(℃) 频数
16别(环) 组中值(环) 频数
5.5～6.5
6
6
() ()
19.5～22.5

（ξ1,ξ2,..,ξn), 则（ξ1,ξ2,…,ξn)的联合分布函
数为： F ( x1 , x2 ,L , xn )
= P { ξ1 < x1 , ξ 2 < x2 , ..., ξ n < xn }
= P { ξ1 < x1}P{ ξ 2 < x2 } ⋅ ... ⋅ P{ ξ n < xn }
（2）χ2 分布（Chi-square distribution）
χ 2 ～χ 2 (n)
{ } p分位点：χ p2 (n ) 满足P
χ
2
<
χ
2 p
(n)
=p
p53（9 347）表 4
χ
2 0.95
(9
)
=
16.91（9
p540)
表p 4 χ2 分布分位数表
n
p
8
9
0 ．90 13．362 14．684
又如：α = 0.1，uα = u0.1 = ? (表中没有)
u0.1 = −u1−0.1 = −u0.9 = −1.282
对称性(symmetricy)：
0.1
uα = −u1−α
α = 0.1
u0.1
u1− 0.1
习题或附表中α通常是指分位点之外的概率（面积）
单侧分位点：α放在分位点u1−α的一侧 双侧分位点: α分割放在正负对称的
2 +L +
)
m
1
9
二. t 分布 (t distribution)
Definition: 若ξ～N(0,1), η～χ2(n)且相互独立,
则有
t=
ξ η
～ t (n )

2.在水平射线上，适当分配条形的位置，确定直条 的宽度和间隔。
3.在与水平射线垂直的射线上，根据数据的大小情 况，确定单位长度的多少，再照根据大小，画出长 短不同的直条并注名数量
条形图直方图的区别
1：条形图各矩形间有空隙， 直方图各矩形间无空隙
2.直方图的横轴数据是连续 的小组的位置是固定的
而条形图不是
全班 40人 呦
D小沈 6
频数： 每个小组内数据的个数 频率﹦ 频数÷总数
某班一次数学测验成绩如下：
63，84，91，53，69，81，61，69，91，78，75，81，80， 67，76，81，79，94，61，69，89，70，70，87，81，86， 90，88，85，67，71，82，87，75，87，95，53，65，74， 77．
你认为原因是什么？
2
15 25 35 45 55 65 75 年龄 （岁）
心系 灾区
去年6月份以后我国南方强降雨范围继续扩大， 雨量增强，部分县市区降雨量达100毫米以上， 造成严重洪涝灾害。
（1）降雨量在100毫米以上的有几个县市？36 （2）最需要救助的县市有几个？ 4个
频 数
20 16 12 8 4
1、 计算最大值与最小值. 在上面的数据中:最小值是149，最大值是172。 它们的差是23.说明身高总的变化范围是23.
2、决定组距和组数. 把所有数据分成若干组,每个小组的两个端点之间的
19 男 164 83 89 优
20 女 161 75 77 良
21 男 162 86 97 优
22 男 164 91 91 优
23 女 163 87 82 优
24 男 154 82 88 优
25 男 172 68 70 中

直方图是为了把表中的结果直观地表示出来，它
们是频数分布的“数”与“形”的两种不同形式，
互相补充．
（来自《点拨》）
知2－练
1 某学校八年级共有你n名男生. 现测量他们的身高 (单位：cm. 结果精确到1 cm)，依据数据绘制的 频数分布直方图如图所示(为了避免有些数据落 在分组的界限上，对作为分点的数保留一位小数).
的学生为正常，试求身高正常的学生的百分比．
知2－讲
导引知：先识确点定最大值与最小值的差为180－140＝40(cm)，故可
将数据按组距为5进行分组，可分40÷5＝8(组)． 解：(1)计算这组数据的最大值与最小值的差为180－140＝
40(cm)． 确定组数与组距，将数据按组距为5进行分组，可分 为40÷5＝8(组)，即每个小组的范围分别是140≤x＜ 145，145≤x＜150，150≤x＜155，155≤x＜160，160≤ x＜165，165≤x＜170，170≤x＜175，175≤x≤180. 其中x为学生身高．
C．8组
D．10组
导引：因为这组数据的最大值是187，最小值是140，最 大值与最小值的差是47，且 47 7 5 ，所以应 66 分为8组. 答案：C
总结
知1－讲
确定组数的方法：若最大值与最小值的差除 以组距所得的商是整数，则这个商即为组数；若 最大值与最小值的差除以组距所得的商是小数， 则这个商的整数部分＋1即为组数．
知2－讲
知2－讲
例2 某中学部分同学参加全国初中数学竞赛，取得了优异的成
绩，指导老师统计了所有参赛同学的成绩(成绩都是整数， 试题满分120分)，并且绘制了如图所示的频数分布直方图 (每组中含最低分数，但不含最高分数)，请回答： (1)该中学参加本次数学竞

4
（5）Weibull分布
f
(x)


1


x
c 1
exp
x
c
,

0,
x
x0
(1.17)
EX (1 1)， DX 2 {( 2 1) (1 1)}2
c
c
c
背景：由瑞典物理学家Wallodi Weibull于1939年引
100
C 80
u
m
u
l
a t
60
i
v
e
P e 40 r c e n t
20
0
60
65
70
75
80
85
x
Normal Curve:
Mu=73.66, Sigma=3.9401
2020/1/12
图1.6 n=100 蛋白含量的经验分布函数Fn (x)及拟合 F(x)
11
（3）作正态分布QQ图
85
图
80
密度
f (x)
1
2
exp
(x )2 2 2

EX , DX 2
（2）对数正态分布
（1.13）

f
(x)


1
2 (x


)
. exp


(log(x ) 2 2


)2
,

0,
x
（1.14）
x0
背景：如一变量可看成许多独立因子之和，近似正 态分布.如股票投资长益可看成每天收益率的乘积.
s 3.94 61.5

实验过程：
1、经验分布函数的作图n=4。
1在Excel中产生一个服从均匀分布U(1,6)的样本容量n=4的随机样本。在单元格A2中输入产生均匀分布U(1,6)的随机数命令“=1+5*RAND()”，再将其拖放填充至A5,就可在单元格区域A2:A5中产生4个样本观测值x1,x2,x3,x4,每按一次F9键，这些随机数就会发生变化，这为我们进行动态显示带来方便。接着我们把样本观测值x1,x2,x3,x4从小到大排序，在单元格B2：B5中分别使用命令“=SMALL($A$2:$A$5,1)”(k=1,2,3,4)得到顺序样本观测值。
实验二经验分布函数图形的绘制与演示
实验序号：2日期：2014年5月29日
班级
数学学院2012级F班
学号
124080Leabharlann 45姓名王信实验名称
经验分布函数图形的绘制与演示
问题的背景和目的：
设X1,X2,…,Xn是取自总体X的随机样本，Fn(x)是总体X的经验分布函数，当n→∞时由格列汶科定理知
该定理说明Fn(x)在整个实数轴上一概率1均匀收敛于F(x)。当样本容量n充分大时，经验分布函数Fn(x)可以作为总体分布函数F(x)的一个良好的近似，这是数理统计学中以样本推断总体的理论依据。
2在单元格C2内输入起始值0，单击【编辑】/【填充】/【系列】，在出现的对话框输入相应选项（如图1所示），就可在单元格区域C2：C702中顺序产生0,0.01,0.02,…,7共703个自变量x的取值序列。
图1
3在D2单元格内输入公式“=IF(C2<$B$2,0,IF(C2<$B$3,1/4,IF(C2<$B$4,2/4,IF(C2<$B$5,3/4,1))))”，再利用拖放填充功能将D2单元格内的计算公式复制到整个单元格区域D2:D702,就自动计算出所有Fn(x)的取值。

10% 10% 10% 11% 11% 11% 11% 11% 11% 11% 11% 11% 11% 11% 11% 12% 12% 12% 12% 12% 12% 12% 14% 15% 15% 15% 15% 14% 14%
13% 13% 13% 13% 13% 14% 14% 15% 15% 15% 15% 15% 15% 16% 16% 16% 16% 16% 16% 16% 16% 17% 16% 17% 25% 30% 15% 18% 16%
1.4 直方图应用
当直方图的形状呈正常型时，即工序在此时刻处于稳定状态时，还需要进 一步讲直方图同规格界限（即公差）进行比较，以分析判断工序满足公差 要求的程度。
1.5 直方图实例
5% 6% 6% 6% 6% 7% 7% 7% 7% 7% 8% 8% 8% 8% 8% 9% 9% 9% 9% 9% 10% 10% 14% 14% 14% 15% 16% 16% 16% 18%
直方图(Histogram)又称质量分布图。是一种统计报告图，由一系列高 度不等的纵向条纹或线段表示数据分布的情况。 一般用横轴表示数据类 型，纵轴表示分布情况。
1.2 直方图绘制
收集数据（n≥50）
确定数据极差R 确定组数 确定组距
数据N 组数K
50-100 6-10
组距=极差R/组数
100-250 7-12
250以上 10-20
确定组界 画图
第一组下组界 = 最小值－测定值最小位數／２ 第一组上组界 = 第一组下组界 + 组距 第一组上组界 = 第一组下组界 + 组距 第二组上组界 = 第二组下组界 + 组距
1.2 直方图绘制（EXCEL）
1.2 直方图绘制（SPSS）

直方图与经验分布函数总体X 分布未知samplepopulation直方图（Histogram）总体X 的sample ：12,,,n X X X ":()pdf f x 具体步骤：①Sample 观测值12,,,nX X X "min{,1,X X i n =="max{1,,}X X i n =="(1){,}i (){,n i[a,b]m 个小区间（m<n ）小区间长度可以不等，设分点为②将[,]分成个小区间,小区间长度可以不等设分点为算数率n bt t t a m =<<<="10③ 计算频数j n 及频率1,,jj f j m n==" ④ 作图：],[1t t −为底边,j f 为高作长方形,面积为f (m 个长方形之和为1)j j jt Δj 用直方图对应的分布函数()jn jf x t Φ=Δ1(,]j j x t t −∈1,,j m ="⎧引进“随机变量”11(,]1,2,,0i j j j x t t i n otherwise ξ−⎪∈⎪⎪==⎨⎪⎪"⎪⎩11{(,]}{1}(1)xxj j j p P x t t P p p ξ−−=∈⇐==−由SLLN（kolmogorov）有1n SLLNjj i i n f E pn ξξ===∑→1j n =jt 11{(,]}()j j j t P x t t f x dx −−=∈=∫()n →∞{lim }1P ==n ⇒→∞{j n f p →∞f 近似代替以)(x f 为曲边的曲边梯形的面积。

j 若∞→n ，j t Δ较小时，可用j f x =Φx x t t jn t Δ)(，近似代替()f ,1(,]j j −∈Example 1:原始数据data=[16,25,19,20,25,33,24,23,20,24,25,17,15,21,22,26,15,23,22,24,20,14,16,11,14,28,18,13,27,31,25,24,16,19,23,26,17,14,30,21,18,16,18,19,2022192218262613211311192318242813112515171820,22,19,22,18,26,26,13,21,13,11,19,23,18,24,28,13,11,25,15,17,18,22,16,13,12,13,11,9,15,18,21,15,12,17,13,14,12,16,10,8,23,18,11,16,28,13,21,22,12,8,15,21,18,16,16,19,28,19,12,14,19,28,28,28,13,21,28,191115182418162819151322141624202818182814132819,11,15,18,24,18,16,28,19,15,13,22,14,16,24,20,28,18,18,28,14,13,28,29,24,28,14,18,18,18,8,21,16,24,32,16,28,19,15,18,18,10,12,16,26,18,19,33,8,11,18,27,23,11,22,22,13,28,14,22,18,26,18,16,32,27,25,24,17,17,283816202832192318281524282916171918]28,38,16,20,28,32,19,23,18,28,15,24,28,29,16,17,19,18]数字特征计算：mean(data) median(data) std(data) var(data) skewness(data) kurtosis(data)195650185000592723513140343125599计算结果19.5650 18.5000 5.9272 35.1314 0.3431 2.5599histfit(data,13)35150经验分布函数(Experience DistributedFunction)经验分布函数(Experience Distributed Function)总体X 的分布函数F 未知，Sample 12,,,()()n n X X X F x F x ⇒⇒"构造（)(x F n ）方法：12,,,nX X X "(1)(2)()n X X X ≤≤≤"(1)0x X ⎧≤⎪()()(1)()n k k k F x X x X +⎪⎪⎪⎪=<≤⎨⎪1,2,,1k n =−"()1n n x X ⎪⎪⎪>⎪⎩仿真试验固定,()n X F x ：表示事件{}X x <在n 次试验中出现的频率，1(){}n i F x x X =−∞落在（，）中的个数n 类似可证：{lim )()}1nP F x F x ==（ n →∞Theorem(Glivenko-Cantelli)：对任意给定的自然数n ，设12,,,n X X X " 是取自总体X 分布函数)(x F 的一个样本观测值，)(x F n 为其经验 分布函数，记)()({sup x F x F D nx n −=∞<<∞− 则{lim 0}1n n P D →∞==经验分布函数（数据如前例）程序：[h,stats]=cdfplot(data)[h,stats]cdfplot(data) 程序运行结果：Empirical CDF Empirical CDF统计量及分布统计量（St ti ti Sample X X X "，构造statistics ,poplation 统计量（Statistics）Sample 的函数不含参数的函数p 12,,,n ,p p12(,,,)n T T X X X ="Example 7、Sample,statistics：180952809.52i X X n==∑1154.28S ==∑结论：平均（X ），悬殊（S ）不大Popalatrion X 的SampleX X X "，则常用的Statistics 1X X = (Mean) p p 12,,,n ①i n∑样本均值()1② S =∑ 样本方差（Sample Variance ） ③ 2S S =样本标准差（Standard Variance ）④ 11nkk i i A X n ==∑ 样本k 阶原点矩（Moment ）1nkB =−样本⑤1()k i i X X n =∑k 阶中心矩二维两总体X Y 总体的Sample X Y X Y X Y "则有：(,)p 1122(,),(,),,(,)n n ① 121()(ni i S X X Y Y =−− 样本协方差（Covariance ）1i n =∑S ②Y x S S 12ˆ=ρ 样本相关系数（Correlation Clefficient ）Histogram nn f ii =0x X ⎧⎪≤⎪Experience (1)(1)()()n k k k F x X x X n −⎪⎪⎪⎪=<≤⎨⎪ ()1n x X ⎪⎪⎪>⎪⎪⎩Ordered statistics :Sample X X X"p 12,,,n(1)(2)(1)(2)(),,,n n X X X X X X ≤≤≤⇒"" ()()()()()()1!(1))!()!x F k n k n F x u u du −−⎧⎪⎪=−⎪()(1)0()((1)!(()1(1())k x n x k n k F x F x ⎪−−⎪⎪⎪=−−⎨⎪∫()()(())n n x F x F x ⎪⎪⎪=⎪⎪⎪⎩():'k X k th ordered statistic⇐(1):min X imum ordered statistici d d t ti ti⇐():max n X imum ordered statisticn ()()11!(,)[()][()()][1()](1!(1)!(1)!()!1!i j i j i n j x x f x y F x F y F x F y p i j i n j −−−−=−−−−−−⎧()()2(1)[()()]()()(,)0i n n x x n n F y F x p x p y x y f x y otherwise −⎪−−<⎪⎪=⎨⎪⎪⎪⎩ 11212!()()(,,)n nn n f x f x x x x f x x x ⎧⎪<<<⎪⎪=⎨⎪"""0otherwise⎪⎪⎩X ⎧⎪⎪1()2*()(1)221[]2n n n M X X ++⎪⎪=⎨⎪+⎪⎪⎪⎪⎩ *()(1)n D X X =−反例：..2(,)~i i di X N μσ⇒2111,(),ni X X X μ−∑是1i n σ=Sample二重性Statistic二重性抽样分布2χ分布..22(01)~i i dn=∑"Definition ：1()1,,(0,1)~nin i X X N Y Xχ=⇒Theorem1.1（2χ分布addition ）：k 个相互独立的r.v. 12,,,k Y Y Y "且2~()j j Y n χ，1,,j k ="Then ： 211~()nnj j j j Y Y n χ===∑∑..i i dProof ：2=k 推出：If ：112121,,,,,,(0,1)~n nnn X X X X X N ++""Then⎪⎪⎫∑∑=+=211122121,n j jn n i jX Y X Y 同分布与同分布与 ⎪⎪⎭⎬∑∑==+121112221n i n j jn j X X Y Y 相互独立与相互独立与又⇓同分布与∑∑∑+===+=++=2112112112221n n j j n i n j j n j X X X Y Y YTheorem1.22~==Theorem1.2X χ⇒① n X n EX 2var ②：的pdf X Where10()0xxe dx ααα∞−−Γ=>∫⎧122210n x n x e x n −−⎪⎪>⎪⎪⎪⎪=()2(20f x otherwise Γ⎨⎪⎪⎪⎪⎪⎪⎩Proof ：① ..(0,1)~i i dnii X N X X ⇒∑与同分布1i =且22n nn∑且：111var iii i i i EX E X EXX n=======∑∑（）n EX X E X X X ni iiini i∑∑∑===−===1224212])(([var var(var ））时，X t xty y 22121122−−=−②1=n dt e t dye x P x F 022}{)(∫=∫=<=ππn x −−⎧⎪12212101()2()x e x f x ⎪>⎪⎪⎪⎪=Γ⎨ 20otherwise ⎪⎪⎪⎪⎪⎪⎩设：22~(1),~(1),Y n Z Y Z χχ−且与相互独立Then ：同分布与Z Y Y +（2χ分布的可加性）11222221102211()()()()11n yy x x Y n f x f y f x y dy ye x y en −−+∞−−−−−∞=−=⋅−−∫∫2(2()22ΓΓ11112221x n −−−−−12()12()2n eyx y dyn −=−Γ∫1x n n 1111222221(1)112n exzz dzn −−−−−=−−ΓΓ∫()(221221n x x e −−=22(2n n ΓB函数duu uB q p 1111−−−=Beta函数q p 0)(),(∫Beta与Gamma关系)()()(),(),(q P q p P q B q p B +ΓΓΓ==t 分布与F 分布Definition设 2~(0,1)~X N Y n X 与Y 相互独立 则(,)()χ~X=()T t n2⎧211()2x X n x f x π−−−⎪⎪⎪=⎪⎪⎪⎪⎧⎪1221()2n n x −−+Γ=22210()2(2n Y y e y n f y ⎪⎪⎨>⎪⎪⎪⎪⎪=⎪⎨Γ⎪⎪⎪⎪⎪()(1)()2T f x n n n π⇒+Γ00x ⎪⎪⎪≤⎪⎪⎩⎪⎩Definition ：If 21~()X n χ，22~()Y n χ X 与Y 相互独立, themX 112~(,)n T F n n Y =2ndf为类似可得 ),(21n n F 的pdf 为：⎧1121212122212()20n n n n n n n x n x +⎪+⎪Γ⎪⎪⎪⋅>⎪=12212()()()()220f x n n n x n elsewhere⎨⎪ΓΓ+⎪⎪⎪⎪⎪⎪⎩性质：①),(~1),(~1221n n F n n F F ⇒F②),1(~)(~2n F XY n t X =⇒③1,n n F =),()(12121n n F αα−分位数（quantile）.:RV X CDF F X,,给定(){}:()F x P X x CDF F x =<⇒给定的值，要确定X 取什么值？ Definition ：设X 的,(){}01CDF F X F X P X X ααααα=<=<<为满足 则称αX 为F 的α分为数（点）若X 有pdf )(x f ，则分为数αX 表示αX 以左的一块阴影面积为α。

面积表示每一组频数的 长方形组成的统计图。
某班一次数学测验成绩的频数直方图
频数
14
10 9
5 2
为了使图形清晰 美观，频数分布 直方图的横轴上 可只标出组中值， 不标出边界值.
54.5 64.5 74.5 84.5 94.5
（分）
画频数分布直方图的一般步骤:
(1)计算极差(最大值与最小值的差) (2) 确定组距和组数；
(4)列频数表.
75 ， 87 ， 95 ， 53 ， 65 ， 74 ， 7975．
某班一次数学测表验2成0.1绩.2 的频数分布表
组别 (分)
划记
某班一次数学表测2验0.1成.2 绩的频数分布表 (5) 频数直方图.
组别
由若干个宽等于组距，
划组记中值 54.5 64.5 74.5 84.5 94.5
(3)自左至右最后一 频 组的两个边界值分别 数 是多少？该组的频数、 人
()
频率分别是多少?
8
边界值分别是124.5次，
6
149.5次
4
频数是3
2
七年级若干名学生每分跳绳次数 的频数分布直方图
6
4
2
3
频率是0.2
0
62 87 112 137
跳绳次数(次)
2.请观察右图,并回答下面的问题:各种矿泉水PH的频数分布直方图
元之间的家庭约占55% 175----375元
看图回
答
4. 下图是有关“碟片播放时间”的调查统
计图，仔细观察，你在图中找到了哪些信息，
请与你的同伴交流。
估计样本的平均数
57.75分
404张0张碟碟片片播播放放时时间间的的统统计计图图

F ( x1, x2, x3, x4 ) F ( x1 )F ( x2 )F ( x3 )F ( x4 )
4 i1
(1
e 2xi
)
0,
xi 0, i 1,2,3,4 其它
6.1.2 样本与抽样
【例6.2】已知总体X的分布为P{X = i} = 1/4，
i = 0,1,2,3,抽取n=36的简单随机样本X1,X2,...,X36, 36
36
E(Y ) E( X i ) 36E( X ) 54, i 1
36
5
D(Y ) D( i1 X i ) 36D( X ) 36 4 45
又因为n
=
36较大，依中心极限定理，Y
36
X近i 似
服从正态分布 N(54,45) ，所以
i 1
P{50.4
Y
64.8}
P 50.4
54
Y
54
64.8
例如，在质量检验中，随机抽出n件产品，测 得的数据x1，x2，...，xn，就称它们是样本观测 值．
在抽样前，不知道样本观测值究竟取何值，应 该把它们看作为随机变量，记作X1，X2，...，Xn， 称其为容量为n的样本.
（在不会混淆的情况下，有时我们也将观测数据 x1，x2，...，xn称为样本，如“质量控制问题”中 的30个数据，也可以说成是一个容量为30的样 本）．
【数理统计简史】
社会统计学派始于19世纪末，首创人物是德国 的克尼斯（K. G. A. Knies），他认为统计学是一 个社会科学，是研究社会现象变动原因和规律性 的实质性科学．各国专家学者在社会经济统计指 标的设定与计算、指数的编制、统计调查的组织 和实施、经济社会发展评价和预测等方面取得了 一系列的重要成果．德国统计学家恩格尔 （C.L.E.Engel，1821-1896）提出的“恩格尔”系 数，美国经济学家库兹涅茨和英国经济学家斯通 等人研究的国民收入和国内生产总值的核算方法 等，都是伟大的贡献．

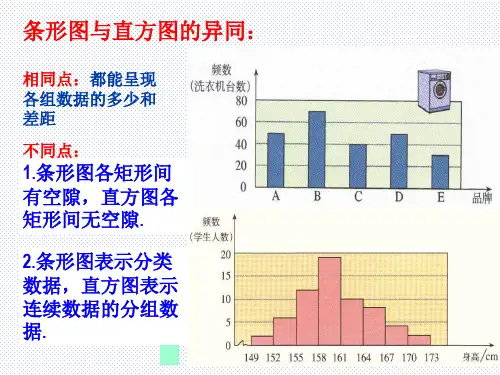
§6.2直方图和箱线图在数理统计中，我们常常用图形来直观地显示观察到的数据，以便对总体X的分布有一个直观、粗略的了解。

四川大学徐小湛本节讲以下图形：直方图箱线图（自学）经验分布函数及其图形直方图（频率直方图）Histogram百度传课我们通过一个例子来说明直方图的作法。

25 19 39 72 49 58 65 75 68 66 61 78 51 60 45 74 73 77 29 16 90 12 64 61 40 57 40 46 81 51 52 58 73 70 87 33 49 61 83 41 52 46 38 77 63 75 61 45 51 62 51 59 66 68 97 53 54 70 54 54 38 50 83 50最低分和最高分分别是 12 和 97例1 设有64个学生的考试成绩如下：四川大学 徐小湛25 19 39 72 49 58 65 75 68 66 61 78 51 60 45百74度73传7课7显得杂乱无章29 16 90 12 64 61 40 57 40 46 81 51 52 58 73 70 87 33 49 61 83 41 52 46 38 77 63 75 61 45 51 62 51 59 66 68 97 53 54 70 54 54 38 50 83 50 四川大学 徐小湛 用Excel 作出数据的条形图(柱形图)(Bar Chart)四川大学用Excel将成绩排序：121619252933383839404041454546 464949505051515151525253545454 575858596061616161626364656666 68687070727373747575777778818383 87 90 97百度传课12161925 29 33 38 38 39 40 40 41 45454646 49 49 50 50 51 51 51 51 52525354 54 54 57 58 58 59 60 61 61616162 63 64 65 66 66 68 68 70 70727373 74 75 75 77 77 78 81 83 83 87 90 97下面来分析各分数段得分的人数和频率将分数分成9段将区间(9.5, 99.5) 等分成9个子区间每个区间长(99.5-9.5)/9=1083 87 90 97百度传课分 组 频数 f i9.5~19.5 3 19.5~29.5 2 29.5~39.5 4 39.5~49.5 9 49.5~59.5 16 59.5~69.5 13 69.5~79.5 11 79.5~89.5 4 89.5~99.5212 16 19 25 29 33 38 38 39 40 40 41 45 45 46 46 49 49 50 50 51 51 51 51 52 52 53 54 54 54 57 58 58 59 60 61 61 61 61 62 63 64 65 66 66 68 68 70 70 72 73 73 74 75 75 77 77 78 81 83 将区间(9.5, 99.5) 等分成 9 个子区间每个区间长 1032 4911频数直方图161342百度传课四川大学徐小湛9.5 19.5 29.5 39.5 49.5 59.5 69.5 79.5 89.5 99.5百度传课分组频数fi 频率fi/649.5~19.530.0469 19.5~29.520.0313 29.5~39.540.0625 39.5~49.590.1406 49.5~59.5160.2500 59.5~69.5130.2031 69.5~79.5110.1719 79.5~89.540.0625 89.5~99.520.0313四川大学徐小湛9.5 19.5 29.5 39.5 49.5 59.5 69.5 79.5 89.5 99.50.04690.03130.06250.14060.25000.20310.1719频率直方图0.0313矩形面积之和64 ( f i 9∑ i =1 64 i i =19⨯10) = 10 ∑ f 64 = 10 ⨯ 64 = 10 0.0625不满足规范性百度传课四川大学徐小湛分组频数fi 频率fi/64矩形高f i /64/109.5~19.530.04690.0047 19.5~29.520.03130.0031 29.5~39.540.06250.0063 39.5~49.590.14060.0141 49.5~59.5160.25000.0250 59.5~69.5130.20310.0203 69.5~79.5110.17190.0172 79.5~89.540.06250.0063 89.5~99.520.03130.00310.00470.0031 0.00630.01410.02500.02030.01720.00630.0031矩形面积之和9 fii=164⨯10∑ 964 if( ⨯10) = 1 ∑i =1164=⨯64 =1百度传课满足规范性频率直方图Frequencyhistogram四川大学徐小湛9.5 19.5 29.5 39.5 49.5 59.5 69.5 79.5 89.5 99.59.5 19.5 29.5 39.5 49.5 59.5 69.5 79.5 89.5 99.5 这几个直方图的形状是一样的，区别只是纵坐标的刻度不一样。

3/11/2021
〖定义〗 设总体X的 n个独立观测值为x1,x2,…,xn, 将它们从小到大
排序后为x1*,x2 *,…,xn *, 令
0,
Fn
(
x)
k n
,
1,
x x1*
x
* k
x
x* k 1
xn* x
称Fn(x)为总体X 的经验分布函数. （也称为样本分布函数）
① 0 Fn( x) 1 ② 单调不减； ③ 处处右连续.
n
P( X xi )
i 1
8
3/11/2021
例1 已知总体X ~（）分布，写出样本 (X1, X2,…, Xn)的分布律。
析：
X的分布律 P{ X k} k e ,
k!
可以写成 P{ X x} x e ,
x!
k 0,1,2, x 0,1,2,
样本 (X1, X2,…, Xn)的分布律
5
3/11/2021
❖3、样本
➢从总体X中随机抽取n个个体X1,X2,Xn所组成的一个个体 组（X1,X2,,Xn），称为总体X的一个样本，个体的数目n
称为样本容量。
➢ 通过试验对样本(X1,X2,,Xn)进行观测，得到的n个确定的 实验数据(x1,x2,,xn)，称为样本(X1,X2,,Xn)的一个观察值，
(X1 ,X2,…Xn1), (Y1 ,Y2,…Yn2)分别为取自总体X,Y的样本,则
3/11/2021
1> 当12= 22时
(X Y ) ( 1 2)
S
11 n1 n2
~
t(n1 n2 2)
其中S 2
(n1
1)S12 (n2 1)S22 n1 n2 2

经验分布和分布函数
经验分布指的是从样本中获得的分布函数，它反映了样本数据的实际情况。

当样本量足够大时，经验分布可以逼近真实分布。

经验分布可以用来研究随机变量的各种性质，比如均值、方差、偏度和峰度等。

分布函数是随机变量取值的概率分布描述，它可以用来计算随机变量落在某个区间内的概率。

分布函数的形式可以是累积分布函数或密度函数。

累积分布函数指的是随机变量小于等于某个值的概率，密度函数指的是随机变量取某个值的概率密度。

分布函数可以用来描述随机变量的位置、形状和分散程度等特征。

经验分布和分布函数在统计学中应用广泛。

它们可以用来研究随机变量的分布特征、评估随机变量的性质和进行假设检验等。

此外，它们还可以用来建立数学模型、优化决策和进行数据分析等。

- 1 -。