经验分布函数与直方图

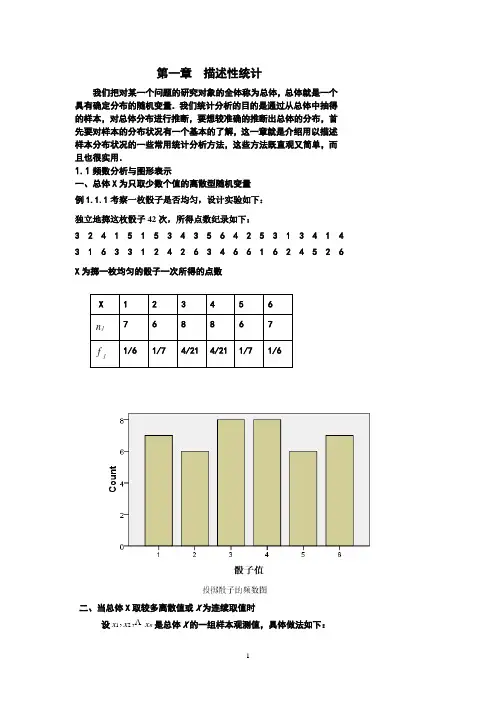
第一章 描述性统计我们把对某一个问题的研究对象的全体称为总体，总体就是一个具有确定分布的随机变量．我们统计分析的目的是通过从总体中抽得的样本，对总体分布进行推断，要想较准确的推断出总体的分布，首先要对样本的分布状况有一个基本的了解，这一章就是介绍用以描述样本分布状况的一些常用统计分析方法，这些方法既直观又简单，而且也很实用．1.1频数分析与图形表示一、总体X 为只取少数个值的离散型随机变量 例1.1.1考察一枚骰子是否均匀，设计实验如下： 独立地掷这枚骰子42次，所得点数纪录如下：3 24 15 1 5 3 4 3 56 4 2 5 3 1 3 4 1 4 3 1 6 3 3 1 2 4 2 6 3 4 6 6 1 6 2 4 5 2 6 X 为掷一枚均匀的骰子一次所得的点数二、当总体X 取较多离散值或X 为连续取值时设x x x n ,,21是总体X 的一组样本观测值，具体做法如下：1求出x )1(和x n )(，取a 略小于x )1(,b 略大于x n )(；2将区间[a ，b]分成m 个小区间（m ＜n ）,小区间长度可以不等，分点分别为a =t t t m <<< 10=b注意：使每个小区间中都要有一定量的观测值，且观测值不在分点上。

划分区间个数的确定：区间过少：分布信息混杂，丢失信息． 区间过多：出现很多空区间．区间划分个数m 依赖于样本总数n ，理论上有如下两个公式可参考： Moore(1986) ： m ≈C n 5/2，C = 1～3； Sturges(1928) ： m ≈1+3.322（lg n ）；3用n j 表示落在小区间（t j 1-,t j ]中观测值的个数（频数）并计算频率f j =nn j （j=1,2,…,m ）；4在直角坐标系x-o-y 的x 轴上标出t t t m ,,,10 ，分别以（t j 1-,t j ]为底边，以n j 为高作矩形，即得频数条形图。

数理统计例举王晓谦wxqmath@南京师范大学主要内容随机变量及其分布经验分布函数和频率直方图参数估计假设检验相关分析与回归分析简介MATLAB例题例1能量供应问题（二项分布）例2 放射性（泊松）例3正态分布例4指数分布例5 多元随机变量例6经验分布函数例7超市问题（指数分布）例8区间估计例9 拟合检验1例10拟合检验2 例11概率纸检验法例12道德（独立性检验）例13肠癌例14J 效应随机变量及其分布例1、能量供应问题（二项分布）假定有10n =个工人间歇性地使用电力，估计所需要的总负荷。

首先我们要知道，或者是假定，每个工人彼此独立工作，而每一时刻每个工人都以相同的概率p 需要一个单位的电力。

那么，同时使用电力的人数就是一个随机变量，它服从所谓的二项分布。

用X 表示这个随机变量，记做(,)X B n p ，且有()(1),k k n k n P X k C p p -==-0,1,,k n =这是非常重要的一类概率分布。

其中E(X)＝np ， D(X)=np(1-p)。

其次，要根据经验来估计出，p 值是多少？例如，一个工人在一个小时里有12分钟在使用电力，那么应该有120.260p ==。

最后，利用公式我们求出随机变量X 的概率分布表如下：为直观计，我们给出如下概率分布图：目录 Back Next可以看出，{6}1{6}0.000864P X P X >=-≤=，也就是说，如果供应6个单位的电力，则超负荷工作的概率只有0.000864，即每11147200.000864≈≈分钟小时中，才可能有一分钟电力不够用。

还可以算出，八个或八个以上工人同时使用电力的概率就更小了，比上面概率的111还要小。

问题：二项分布是一个重要的用来计数的分布。

什么样的随机变量会服从二项分布？进行n次独立观测，在每次观测中所关心的事件出现的概率都是p，那么在这n次观测中事件A出现的总次数是一个服从二项分布B（n，p）。

数理统计知识小结------缪晓丹 20114041056第五章 统计量及其分布§5.1总体与样本一、 总体与样本在一个统计问题中，把研究对象的全体称为总体，构成总体的每个成员称为个体。

对于实际问题，总体中的个体是一些实在的人或物。

这样，抛开实际背景，总体就是一堆数，这堆数中有大有小，有的出现机会多，有的出现机会小，因此用一个概率分布去描述和归纳总体是合适的，从这个意义上说：总体就是一个分布，而其数量指标就是服从这个分布的随机变量。

例5.1.1考察某厂的产品质量，将其产品分为合格品和不合格品，并以0记合格品，以1记不格品，若以p 表示不合格品率，则各总体可用一个二点分布表示：不同的p 反映了总体间的差异。

在有些问题中，我们对每一研究对象可能要观测两个或更多个指标，此时可用多维随机向量及其联合分布来描述总体。

这种总体称为多维总体。

若总体中的个体数是有限的，此总体称为有限总体；否则称为无限总体。

实际中总体中的个体数大多是有限的，当个体数充分大时，将有限总体看作无限总体是一种合理抽象。

二、样本与简单随机样本 1、样本为了了解总体的分布，从总体中随机地抽取n 个个体，记其指标值为 n x x x ,,,21 , 则n x x x ,,,21 称为总体的一个样本，n 称为样本容量或简称为样本量，样本中的个体称为样品。

当30 n 时，称n x x x ,,,21 为大样本，否则为小样本。

首先指出，样本具有所谓的二重性：一方面，由于样本是从总体中随机抽取的，抽取前无法预知它们的数值，因此样本是随机变量，用大写字母 n X X X ,,,21 表示；另一方面，样本在抽取以后经观测就有确定的观测值，因此样本又是一组数值，此时用小写字母n x x x ,,,21 表示。

简单起见，无论是样本还是其观测值，本书中均用n x x x ,,,21 表示，从上下文我们能加以区别。

每个样本观测值都能测到一个具体的数值，则称该样本为完全样本，若样本观测值没有具体的数值，只有一个范围，则称这样的样本为分组样本。

用R也能做精算—actuar包学习笔记（一）李皞（中国人民大学统计学院风险管理与精算）本文是对R中精算学专用包actuar使用的一个简单教程。

actuar项目开始于2005年，在2006年2月首次提供公开下载，其目的就是将一些常用的精算功能引入R系统。

actuar是一个集成化的精算函数系统，虽然其他R包中的很多函数可以供精算师使用，但是为了达到某个目的而寻找某个包的某个函数是一个费时费力的过程，因此，actuar将精算建模中常用的函数汇集到一个包中，方便了人们的使用。

目前，该包提供的函数主要涉及风险理论，损失分布和信度理论，特别是为非寿险研究提供了很多方便的工具。

如题所示，本文是我在学习actuar包过程中的学习笔记，主要涉及这个包中一些函数的使用方法和细节，对一些方法的结论也有稍许探讨，因此能简略的地方简略，而讨论的地方可能讲的会比较详细。

文章主要是针对R语言的初学者，因此每种函数或数据的结构进行了尽可能直白的描述，以便于理解，如有描述不清或者错漏之处，敬请各位指正。

闲话少提，下面就正式开始咯！1 数据描述本节介绍描述数据的基本方法，数据类型主要分为分组数据和非分组数据。

对于非分组数据的描述方法大家会比较熟悉，无论是数量上，还是图形上的，比如均值、方差、直方图、柱形图还有核密度估计等。

因此下文的某些部分只介绍如何处理分组数据。

1.1 构造分组数据对象分组数据是精算研究中经常见到的数据类型，虽然原始的损失数据比分组数据包含有更多的信息，但是某些情况下受条件所限，只能获得某个损失所在的范围。

与此同时，将数据分组也是处理原始数据的基本方法，通过将数据分到不同的组中，我们可以看到各组中数据的相对频数，有助于对数据形成直观的印象（比如我们对连续变量绘制直方图）；而且在生存函数的估计中，数据量经常成千上万，一种处理方法是选定合适的时间或损失额度间隔，对数据进行分组，然后再使用分组数据进行生存函数的估计，这样可以有效减小计算量。

第4章数据汇总这一章，我们介绍数据的描述和汇总方法•这些方法大部分以图形的方式展示数据，也可以用其揭示数据结构•在不使用随机模型的情况下，这些方法可以达到描述性分析的目的•如果考虑随机模型，那获得的数据％,X2,…,X n，在一些情形下将它们视为独立同分布的n个随机变量X i,X2, ,X n的实现.我们首先讨论经验累积分布函数等，这些方法可以用于展示数据值的分布。

接着，我们讨论直方图和相关的图形，它们扮演着随机变量的概率密度的角色，从另一角度展示数据值的分布•我们还将介绍数据的简单汇总，比如用以代表数据中心的样本均值、中位数等，用以量化数据分散程度的样本标准差等，这些统计量比直方图等图形提供了更加浓缩的汇总信息•接着将介绍箱线图，它通过一种简单的图形方式将中心值、散度和分布形状等信息汇总起来•最后介绍散点图，用以揭示变量相关性的信息.§ 4.1基于累积分布函数的方法经验累积分布函数设x1,x2/，x!是一组数据，经验累积分布函数(empirical cumulative distributen function,ecdf)定义为1F n(X)= —#{X 兰X}n显然F n(x)是阶梯形的右连续的函数例 4.1 （见P261）如果要进一步讨论经验累积分布函数的统计性质，那必须置于随机模型下去讨论.数据x1,x2/ ,x n视为简单随机样本X1,X2/ ,X n的实现, 它们公共的分布函数为F(x)( —般假定F(x)是连续型分布).样本X i,X2,…,X n的经验累积分布函数定义为1F n(x) #{X i 沁}n对于任意给定的实数x , F n(x)是一个随机变量，并且n F n(x) ~B(n,F(x)),从而1E(F n(x)) E(V n(x)) =F(x),nVar(F n(x))二Var(V n(x)) = F(x)(1-F(x)).n n可见,F n(x)是F(x)的无偏估计,且n「:时Var(F n(x)) > 0,从而知F n(x) 是F(x)的相合估计.关于F n(x)还有更强的结论：定理(格里汶科)对于任意的自然数n,设X i,X2,…，X n是来自总体分布函数F(x)的一个样本，F n(x)为其经验分布函数，记D n = sup |F n(X)-F(x)|，则有x ■■■：::P(lim D n=0) =1n )：:该定理表明，经验分布函数F n(x)会一致地强收敛于总体分布函数F(x). 这也说明用经验分布函数F n(x)推断总体分布函数F(x)，用样本各阶矩(即F n(x)的矩)去推断总体的矩等是合理的，是有理论依据的 .生存函数随机变量T的生存函数定义为S(t)=P(T t)设随机变量T的分布函数为F(t)，那么生存函数S(t)=1-F(t)，两者给出的信息是等价的•在应用中，对于寿命数据(一般是非负的)，通常分析生存函数而不是分布函数•若样本的经验分布函数为&(t)，那么经验生存 函数为S n (t)=1-F n (t)例 4.2(见 P262)生存函数与危险函数有联系.危险函数定义为其中f(t),F(t)分别为T 的密度函数和分布函数也即为了看清危险函数的统计意义，我们考查元件在使用了 t 时间还未失效 的条件下，在接下来的时间段(t,r .］内失效的条件概率P(t :::T I ：|t t)假设密度f(t)在t 处连续，那么有F(t ：)- F(t)丄 f(t) 1-F(t)S(t) 因此h(tp P(t ：：T -^ A l T t)或P(t T <t -qT t)MtTm 。