特殊值法巧解数列题示例

特殊值法解数学题编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（特殊值法解数学题）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为特殊值法解数学题的全部内容。

用特殊值法解题湖北省公安县斑竹当中学雷学池特殊值法是用满足条件的特殊值（式)代入题目去验证、计算，从而得到正确结论的一种方法．特殊值法在解题中有下列应用．1．解选择题:例1 若a＞b＞c＞0，m＞n＞0．（m、n为数），则下列各式中成立的是［］A．a m b n＞b n c m＞c n a m B．a m b n＞c n a m＞b n c mC．c n a m＞a m b n＞b n c m D．b n c m＞c n a m＞a m b n解∵a＞b＞c＞0．m＞n＞0（m、n为整数）取特殊值，a=3,b=2，c=1，m=2，n=1得a mb n=32×21=18b nc m=21×12=2c n a m=11×32＝9∴a m b n＞c n a m＞b n c m故选B．2．确定多项式的系数例2已知当x是任何实数时,x2—2x+5＝a（x+1）2＋b（x＋1)＋c都成立，求a、b、c的值．解用特殊值法．当x=-1时，原式为8=c①当x=0时，原式为5=a＋b＋c②当x=1时,原式为4=4a+2b＋c③由①、②、③可知a=1，b=—4,c=8．3．判断命题的真假例3 判断命题“式子a2＋（a＋1）2＋a2(a＋1）2=（a2＋a—1)2是恒等式”的真假．解取特殊值,当a=1时，原式左边为9,右边为1，因为9≠1,故原命题是假命题．4．解证定值问题例4 若a、b为定值，且无论k取何值时，关于x的一次方程由①、②可得a=3，b=-2．练习用特殊值法解下列各题:2．命题“式子x3＋9=（x＋2)3-6（x＋2）2+12（x+2）是恒等式”是真命题，对吗？值，求a、b应满足的关系式．并求出这个定值．4．已知 a＋ b＋c≠ 0，求证：不论a、b、c取何实数时，三答案2．取x=0，左边为9，右边为8，9≠8．故不对．式得质证明．巧取特殊值解选择题山东省茌平县傅平镇中学初三·一班鲁傅我在解某些选择题时，采用了取特殊值法,使问题简捷,迅速地获得解决,如下面几例．例1 已知a、b、c都是实数，且a＞b＞c,那么下列式子中正确的是［］（98年全国初中数学联赛)解：∵a＞b＞c,∴可取a=1，b=0，c=-1代入各选择支,只有a+b=1＞b＋c=-1成立．故选（B）．例2 设a、b、c是不全相等的任意实数，若x=a2—bc，y=b2—ca，z=c2—ab，则x、y、z［ ]A．都不小于0B．都不大于0C．至少有一个小于0D．至少有一个大于0（94年全国初中数学联赛题）解：若令a=0，b=1，c=-1，则x=y=z=1，故可排除（B)、（C）；再令a=0,b=c=1,则x=-1，y=z=1,又可排除（A）．故选（D）．（94年全国初中数学联赛题)则[］A．M＜Q＜P＜N B．M＜P＜Q＜NC．Q＜N＜P＜M D．N＜Q＜P＜M(第六届全国部分省市初中数学通讯赛试题)解：∵ x＜y＜0，∴可取x=-2，y=-1并代入上式，则例5 如果a、b均为有理数，且b＜0,则a、a—b，a＋b的大小关系是[ ]A．a＜a+b＜a—b B．a＜a-b＜a+bC．a＋b＜a＜a—b D．a-b＜a＋b＜a（95年“希望杯”全国数学邀请赛初一试题）解：∵a、b均为有理数，且b＜0，∴可取a=1,b=—1并代入上式,得a—b＝1—（—1）＝2,a＋b=1＋（—1)=0．∵0＜1＜2，∴a+b＜a＜a-b．故选（C）．例6二次函数y=ax2＋bx＋c的图象经过点（-2，1)和（2,3），且与y 轴的交点为P,若P点的纵坐标是小于1的正数，则a的取值范围是[］（94年山东省初中数学竞赛题）。

1.已知y x ,为正实数，且4142=++y x xy ，则y x +的最小值为.解法一：消元因为⎪⎭⎫⎝⎛∈+-=241,04241x x x y ，所以()8644944492449424241≥-+++=++-=+++-+=+-+=+x x x x x x x x x x y x 当且仅当5,3==y x 时，等号成立。

解法二：因式分解因为4142=++y x xy ，所以()()9424=++y x ，()()()()86242624=-++≥-+++=+y x y x y x 当且仅当5,3==y x 时，等号成立。

解法三：判别式法设0,>=+t t y x ，则x t y -=代入条件得，()()4142=-++-x t x x t x ，化简得,()041422=-+-+-t x t x ,方程有根的必要条件是0≥∆，()0016-12164-16222≥+=+-=∆t t t t 解得8≥t ，经检验，8=t 时，5,3==y x 可以取得。

2.若将函数()⎪⎭⎫⎝⎛+=32sin πx x f 的图象沿x 轴向右平移()0>ϕϕ个单位后所得的图象与()x f 的图象关于x 轴对称，则ϕ的最小值为.解法一：图象法实线是原函数()⎪⎭⎫⎝⎛+=32sin πx x f ，虚线是新图象，很明显，当实线向右至少平移半个周期2π即可.解法二：特殊值法由图可知，要使得新图象()⎪⎭⎫⎝⎛-+=ϕπ232sin x x g 与原图象()⎪⎭⎫ ⎝⎛+=32sin πx x f 关于x 轴对称，只要原图象的最高点对应新图象的最低点。

于是取原图象()⎪⎭⎫ ⎝⎛+=32sin πx x f 在12π=x 处取得1，此时-112=⎪⎭⎫⎝⎛πg ，即12cos 22sin 12-==⎪⎭⎫⎝⎛-=⎪⎭⎫⎝⎛ϕϕππg ，Z k k ∈+=,22ππϕ，Z k k ∈+=,2ππϕ，所以ϕ的最小正值为2π.解法三：函数对称关系若()()x g x f -=，则函数()x f 与()x g 关于x 轴对称.新图象()⎪⎭⎫ ⎝⎛-+=ϕπ232sin x x g 与原图象()⎪⎭⎫ ⎝⎛+=32sin πx x f 关于x 轴对称，所以⎪⎭⎫ ⎝⎛-+=⎪⎭⎫ ⎝⎛+ϕππ232sin -32sin x x ，即⎭⎬⎫⎩⎨⎧⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+32-2sin 32sin πϕπx x 只要Z k k ∈+=,22ππϕ即可，所以ϕ的最小值正值为2π.3.在ABC ∆中，BC =+，若ABC ∆的面积的最大值为2，则边BC 的长为.解法一：建系，研究动顶点A 的轨迹建立如图坐标系，设a BC =，()y x A a C a B ,,0,2,0,2⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-，=+，所以2226a y a x =+⎪⎭⎫ ⎝⎛-，即当顶点位于最远离x 轴位置时，此时高为a ，2212max ==a S ，所以2=a 。

特殊值法解题技巧广东省和平县下车中学 刘玉燕特殊值法解题,可以绕开复杂的推理、运算,准确、快捷地得出答案。

在讲究解题速度的考试时使用能收到事半功倍的效果。

特殊值法解题的要点是: 1.在取值范围内取特殊值； 2.为使运算简便,一般所取的值应是绝对值较小的整数；3.将所取的值代入题中,通过运算、比较,得出答案。

下面常见的考试题用特殊值法来解，真是妙不可言。

一、填空题例 1. 已知点11(,)A x y ，22(,)B x y 在函数234yx x的图象上，若21330,22x x 则1y ，2y 具有的大小关系为______________分析：因为抛物线234yx x的对称轴是32x，由21330,22x x 易知A ，B 两点在抛物线对称轴的两侧，要确定1y ，2y 大小关系，通常要先把A ，B 点转移到对称轴的同一侧,再根据12,x x 的大小关系确定1y ，2y 大小关系.而若在取值范围内取12,x x 的特殊值，代入234yx x求出1y ，2y ，再比较，就很容易。

解: 21330,22x x 取213,1,x x 此时133310,22y213146, 2233344,64,y 故12y y例2．（1）若1a ，则21,,,a a a a从小到大排列为______________。

（2） 若01a ，则21,,,a a a a从小到大排列为______________。

分析：上题若用不等式的性质来解，容易造成混乱。

取特殊值后就很清晰。

解：（1）1,a 取2,a 则2112,,42aa a211224,2aaa a（2）01,a 取12a，则2111,2,.24a a a211112,.242aa aa二、选择题例 3已知一次函数(2)1y a x 的图象不经过第三象限，则化简296a a 的结果是（ ）（A ） 1 （B ） 1 （ C ）25a( D) 52a 分析：||a ，再由0,0,0a a a 确定结果。

专题突破时间的犁,在勤奋者的额头,开出无数条智慧之渠. 谚语破解数列题7招湖南 龙志明数列是高中数学的重要内容,是进一步学习高等数学的基础,在每年高考中都占有一定比重.下面对求解数列题的一些常用方法进行归纳,提炼出7种常用途径,供参考.1 活用数列的概念数列的概念是求解数列问题的基础,灵活运用数列的概念,往往简捷明了,出奇制胜.例1 设{a n }是公差为-2的等差数列,如果a 1+a 4+a 7+ +a 97=50,那么a 3+a 6+a 9+ +a 99等于( ).A -182;B -78;C -148;D -82若以条件求出a 1,再求和,则运算较为繁琐.注意到2个和式中的项数相等,且均是等差数列.(a 3+a 6+a 9+ +a 99)-(a 1+a 4+a 7+ +a 97)=(a 3-a 1)+(a 6-a 4)+(a 9-a 7)+ +(a 99-a 97)=66d =-132.所以a 3+a 6+a 9+ +a 99=-82,选D.例2 有4个数,其中前3个数成等差数列,后3个数成等比数列,并且第1个数与第4个数的和是16,第2个数与第3个数的和是12,求这4个数.从等差、等比数列的概念入手,设前3个数为a -d,a,a +d,则第4个数为(a +d)2a.由a -d +(a +d)2a=16,2a +d =12,解得a =4,d =4;或a =9,d =-6.所以4个数为0,4,8,16或15,9,3,1.活用等差、等比数列的概念,沟通了有关元素间的内在联系,且使运算得以简化.2 巧用数列的性质数列的性质是对概念内涵的揭示与显化,是求解数列问题的有力武器.例3 在各项均为正数的等比数列{a n }中,若a 5a 6=9,则log 3a 1+log 3a 2+ +lo g 3a 10=( ).A 12;B 10;C 8;D 2+log 35;等比数列{a n }中,若m +n =p +q,则有a m a n =a p a q .所以a 1a 10=a 2a 9= =a 5a 6=9,a 1a 2a 3 a 10=(a 5a 6)5=95.所以log 3a 1+lo g 3a 2+ +log 3a 10=log 395=10,选B .3 运用整体思想从整体上考虑问题,往往能够避免局部运算的困扰,使问题得以迅速求解.例4 等差数列{a n }的前m 项和为30,前2m项和为100,则其前3m 项和为( ).A 130;B 170;C 210;D260这里无需求出a 1、d ,然后再求S 3m .从整体上考虑,因为{a n }是等差数列,所以S m 、S 2m -S m 、S 3m -S 2m 也成等差数列,所以S m +S 3m -S 2m =2(S 2m -S m ),即30+(S 3m -100)=2(100-30),S 3m =210.选C.例5 是否存在常数a,b,c.使得等式1 22+2 32+ +n (n +1)2=n(n +1)(an 2+bn +c)对一切自然数n 都成立?证明你的结论.左式= nk =1k (k +1)2= nk =1(k 3+2k 2+k )=n 2(n +1)24+n(n +1)(2n +1)3+n(n +1)2=n(n +1)12(3n 2+11n +10).这样,问题转化为上式与n(n +1)12(an 2+bn +c)对一切自然数n 恒等.所以a =3,b =11,c =10.放眼全局,从整体考虑问题,通过研究问题的整体形式、整体结构,达到简捷解决问题的目的.4 运用函数思想数列是一种特殊的函数.运用函数的思想处理数列问题,往往能把握问题的本质,使求解过程简捷明快.例6 已知数列{b n }是等差数列,b 1=1,且b 1+b 2+ +b 10=145.(1)求数列{b n }的通项b n ;(2)设数列{a n }的通项a n =log a 1+1b n(a >0,a 1),记S n 是数列{a n }的前n 项和,试比较S n 与13log a b n +1的大小,并证明你的结论.12专题突破取之有度,用之有节,则常足.警言由10 1+10 92d =145,得d =3.所以b n =1+(n -1) 3=3n -2.a n =log a 1+13n -2=log a 3n -13n -2.S n =a 1+a 2+ +a n =log a 21+lo g a 54+lo g a 87+ +lo g a 3n -13n -2=lo g a2 5 8 (3n -1)1 4 7 (3n -2),因13log a b n +1=log a 33n +1,所以S n -13log a b n +1=lo g a 2 5 8 (3n -1)1 4 7 (3n -2)33n +1.记f (n )=2 5 8 (3n -1)1 4 7 (3n -2) 33n +1,则f (n +1)f (n)=(3n +2) 33n +1(3n +1)33n +4令3n +1=t 3t 3+3t 2+3t +1t 3+3t 2>1.所以f (n +1)>f (n),即f (n)是单调递增的,所以f (n) f (1)=234>1,即2 5 8 (3n -1)>33n +1.当a >1时,S n >13log a b n +1;当0<a <1时,S n <13log a b n +1.借助于函数的单调性,巧妙解决了比较大小的问题.将数列看成某一函数,应多考虑这一函数的有关性质.5 运用方程的思想把握数列各基本量之间的关系,运用方程的思想建立已知与未知的关系,把问题的求解转化为对方程的解析、处理来进行.例7 设{a n }是由正数组成的等比数列,S n 是其前n 项和.是否存在常数c >0,使得lg (S n -c)+lg (S n +2-c)2=lg (S n +1-c)成立?并证明你的结论.要使lg (S n -c)+lg (S n +2-c)2=lg (S n +1-c)成立,则有(S n -c)(S n +2-c)=(S n +1-c)2,S n -c >0.(1)(2)若q =1,则(S n -c)(S n +2-c)-(S n +1-c)2=(na 1-c)[(n +2)a 1-c]-[(n +1)a 1-c]2=-a 21<0,不满足(1),故不存在常数c >0使结论成立.若q 1,则由(S n -c)(S n +2-c)-(S n +1-c)2=a 1(1-q n )1-q -ca 1(1-q n +2)1-q-c -a 1(1-q n +1)1-q-c2=-a 1q n [a 1-c(1-q)]=0,得a 1-c(1-q)=0,所以c =a 1.因为c >0,a 1>0,所以0<q <1,S n -c =a 1(1-q n )1-q -a11-q =-a 1q n1-q<0,不满足(2).故不存在常数c >0,使结论成立.综上所述,使结论成立的正数c 不存在.运用方程思想,将存在性问题转化为方程(组)的解是否存在的探索,使问题得以巧妙转化.6 运用数形结合思想从直观性角度研究数列问题,可使问题变得形象生动,易于求解.例8 在等差数列中,a 1>0,且S 20=0,那么当n = 时,S n 最大.我们知道,S n =na 1+n(n -1)2d =d 2n 2+a 1-d2n是关于n 的二次式,且不含常数项.又由a 1>0,S 20=0知该等差数列是递减的,则d <0.因此S n 的图象(一些点)在开口向下的抛物线上.该抛物线过点(0,0)和点(20,0),由其对称性,易见n =10时,S n 取最大值.7 运用转化思想想方设法将非常规问题化为我们熟悉的数列问题来求解的方法即为化归法.一般将数列问题尽可能转化中等差数列或等比数列问题来求解.例9 在数列{a n }中,a 1=1,a n +1=a n1+na n,求a n .原式可化为1a n +1-1a n =n,得1a n +1-1a n为等差数列,所以1a 2-1a 1=1,1a 3-1a 2=2,1a 4-1a 3=3, ,1a n -1a n -1=n -1.将这n -1个式子两边同时相加得1a n -1a 1=1+2+ +(n -1),所以a n =2n 2-n +2.例10 已知数列{a n }满足a 1=15,且当n>1,n N *时,有a n -1a n =2a n -1+11-2a n.求a n 当n 2时,由a n -1a n =2a n -1+11-2a n,得a n -1-a n -4a n -1a n =0.两边同除以a n a n -1得,1a n -1a n -1=4,即1a n -1a n -1=4,对n >1且n N *成立,所以1a n是以首项为5,公13专题突破才能的火花,常常在勤奋的磨石上迸发. 威廉 李卜克内西差为4的等差数列.1a n =1a 1+(n -1)d =4n +1,所以,a n =14n +1.本题借助1a n为等差数列得到了{a n }的通项公式,是典型的化归法.常用的化归还有取对数化归,待定系数化归等,一般化归为等比数列或等差数列的问题,是高考中的常见方法.例11 已知数列{a n }满足a 1=1,且a n +1=3a n+2,求a n .设a n +1+t =3(a n +t ),则a n +1=3a n +2t,t =1,a n +1+1=3(a n +1).所以{a n +1}为等比数列,a n +1=(a 1+1) 3n -1=2 3n -1,a n =23n -1-1.求递推式形如a n +1=p a n +q (p 、q 为常数)的数列通项,可用待定系数法构造新数列a n +1+qp -1=p a n +qp -1来求得,这也是近年高考考得很多的一种题型.链接练习1.数列{a n }中,a 1=1,对于所有的n 2,n N 都有a 1 a 2 a 3 a n =n 2,则a 3+a 5等于( ).A 6116;B 259;C 2516; D31152.根据市场调查结果,预测某种家用商品从年初开始的n 个月内累积的需求量S n (万件)近似地满足关系式S n =n 90(21n -n 2-5)(n =1,2, ,12),按此预测,在本年度内,需求量超过1.5万件的月份是( ).A 5、6月;B 6、7月;C 7、8月;D 8、9月3.若数列{a n }前8项的值各异,且a n +8=a n ,对任意的n N *都成立,则下列数列中,能取遍数列{a n }前8项值的数列是( ).A {a 2k +1};B {a 3k +1};C {a 4k +1};D {a 6k +1}4.设a n =-n 2+10n +11,则数列{a n }从首项到第( )项的和最大.A 10;B 11;C 10或11;D 125.已知方程(x 2-2x +m)(x 2-2x +n)=0的4个根组成一个首项为14的等差数列,则|m -n |等于( ).A 1;B 34;C 12;D386.设{a n }是由正数组成的等比数列,公比q =2,且a 1 a 2 a 3 a 30=230,那么a 3 a 6 a 9 a 30等于( ).A 210;B 220;C 216;D 2157.等差数列{a n }的前n 项和记为S n ,若a 2+a 4+a 15的值是一个确定的常数,则数列{S n }中也为常数的项是( ).A S 7;B S 8;C S 13;D S 158.等差数列{a n }是递增数列,前n 项和为S n ,且a 1,a 3,a 9成等比数列,S 5=a 25.求数列{a n }的通项公式.链接练习参考答案1.A .解:令n =2、3、4、5,分别求出a 3=94,a 5=2516,所以a 3+a 5=6116.2.C .解:由S n 解出a n =130(-n 2+15n -9),再解不等式130(-n 2+15n -9)>1.5,得6<n <9.3.B .解:由已知得数列以8为周期,当k 分别取1,2,3,4,5,6,7,8时,a 3k +1分别与数列中的第4项,第7项,第2项,第5项,第8项,第3项,第6项,第1项相等,故{a 3k +1}能取遍前8项.4.C .解:a n =-n 2+10n +11是关于n 的二项函数,它是抛物线f (x )=-x 2+10x +11上的一些离散的点,从图象可看出前10项都是正数,第11项是0,所以前10项或前11项的和最大.另解:由-n 2+10n +11 0得-1 n 11,又n N *,所以0<n 11.所以前10项为正,第11项为0.5.C .解:设4个根分别为x 1、x 2、x 3、x 4,则x 1+x 2=2,x 3+x 4=2,由等差数列的性质,当m +n =p +q 时,a m +a n =a p +a q .设x 1为第1项,x 2必为第4项,可得数列为14,34,54,74,所以m =716,n =1516.所以|m -n |=12.6.B .解:由等比数列的定义,a 1 a 2 a 3=a 3q3,故a 1 a 2 a 3 a 30=a 3 a 6 a 9 a 30q 103.又q =2,故a 3 a 6 a 9 a 30=220.7.C .解:设a 2+a 4+a 15=p (常数),所以3a 1+18d =p ,即a 7=13p .所以S 13=13 (a 1+a 13)2=13a 7=133p.8.解:设数列{a n }公差为d(d >0),所以a 1,a 3,a 9成等比数列,所以a 23=a 1a 9.即(a 1+2d)2=a 1(a 1+8d),得d 2=a 1d,因为d 0,所以a 1=d 因为S 5=a 25,所以5a 1+5 42 d =(a 1+4d)2.由 得:a 1=35,d =35,所以a n =35+(n -1) 35=35n.(作者单位:湖南省岳阳市岳化一中)14。

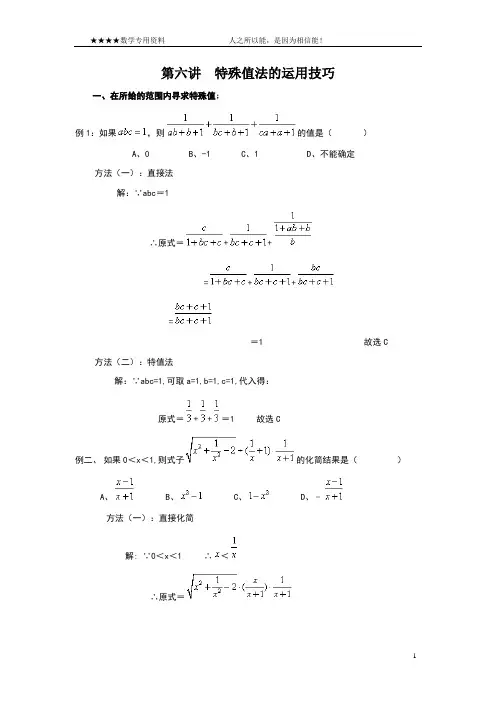
第六讲特殊值法的运用技巧一、在所给的范围内寻求特殊值；例1：如果，则的值是（）A、0B、-1C、1D、不能确定方法（一）：直接法解：∵abc＝1∴原式＝++=++=＝1故选C 方法（二）：特值法解：∵abc=1,可取a=1,b=1,c=1,代入得：原式＝++＝1故选C例二、如果0＜x＜1,则式子的化简结果是（）A、 B、 C、 D、﹣方法（一）：直接化简解: ∵0＜x＜1∴＜∴原式＝===＝＝﹣方法（二）：特值法解：∵0＜x＜1，可取＝∴原式＝××＝，∵﹣＝﹣＝×＝∴选D。

例2：若a＜﹣1,则3－的最后结果是（）A、3-aB、3+aC、-3-aD、a-3方法（一）：直接法解：∵解：∵a＜﹣1，＜﹣1，∴a-3＜0∴原式=3-=3-（-）=3+a方法（二）：特值法解：∵a＜﹣1，可以取a=-4，代入计算：原式=-1，又3+a=-1，∴选B。

二、在隐含的范围内寻求特殊值；例：如果x、y、z是不全相等的实数，且，，则以下结论正确的是（）A、a、b、c都不小于0B、a、b、c都不大于0C、a、b、c至少一个小于0D、a、b、c至少一个大于0分析：此题若直接解比较繁杂，可采用特值法，较为简便，由x、y、z是不全相等的实数，可分为两种情况：①x、y、z都不相等；②x、y、z中有两个相等；当x、y、z都不相等时，可取x=1,y=0,z=-1,则a=1，b=1，c=1，可排除B和C；当x、y、z中有两个相等时，可以取x=0,y=z=1,则a=-1,b=1,c=1，可排除A 综合以上情况，所以选D。

三、在选择的结论范围内寻求特殊值例1、如果方程有两个不相等的实数根，则q的取值范围是（）A、q≤0B、q＜C、0≤q＜D、q≥方法（一）：直接法解：∵∴y≥0,则y≥q∴q≥0或q＜0∴∵△=1-4q＞0即q＜当q＜0时，方程无根，∴0≤q＜方法（二）：特值法在A、B范围内取q＝-6，代入方程化简为，此时方程有一负根，可排除A、B。

第 83 炼 特殊值法解决二项式展开系数问题一、基础知识：1、含变量的恒等式：是指无论变量在已知范围内取何值，均可使等式成立。

所以通常可对 变量赋予特殊值得到一些特殊的等式或性质2、二项式展开式与原二项式呈恒等关系，所以可通过对变量赋特殊值得到有关系数（或二 项式系数）的等式3、常用赋值举例：（1）设ab n C n0an Cn 1a n 1b C n 2a n2b 2L C n ran r br L C n nb n，①令 a b 1 ，可得： 2nC n 0C n 1L C n n②令 a1,b1，可得：0 C n 0C 1nC n 2C n 3Ln1nC；，即：CnCn2nnL C n nC 1nC n 3LCn n 1(C n (假设n 为偶数），再结合①可得：C 0C 2nnLC n nC 1nC n 3 Ln1C n2n 1（2）设fx 2x 1 na 0a 1x a 2x 2Ln a nx n① 令 x 1，则有：a 0 a 1 a 2L a n2 n1 1 nf1，即展开式系数和② 令 x 0， 则有： a 0 20n1 n f0，即常数项③ 令 x1 ，设 n 为偶数，则有：a 0 aa 2a 3 La n1 2 1 n f1a 0 a 2 L a n a 1 a 3 L a n 1f1即偶次项系数和与奇次项系数和的差由①③即可求出 a 0a 2 La n 和 a 1 a 3 L a n 1 的值二、典型例题：例 1：已知 3x 1 8 a 02a 1x a 2xL a 8x 8 ，则 a 1 a 3a 5 a 7 的值为 __________思路：观察发现展开式中奇数项对应的 x 指数幂为奇数，所以考虑令 x 1,x 1 ，则偶数 项相同，奇数项相反，两式相减即可得到 a 1 a 3 a 5 a 7 的值解：令 x 1 可得： 28 a 0 a 1 L a 8 ①令 x 1 可得：4 a o a 〔 a 2 L a 8答案:求式子特点可令x 2，得到a oa 1 Lan o ,只需再求出a o 即可。

数学考试技巧附案例习题解题技巧-特殊值法在数学研究中，“从特殊到一般”是重要的思想方法。

数学竞赛题，由于其难度，多少有些研究的性质。

于是对许多竞赛题目，“特殊值法”显得至关重要。

3.1 什么是“特殊值法”特殊值法，又称“和谐法”，就是对题目中所给的表达式，代入特殊值，寻找其规律。

特殊值，就是易于计算、求解的值。

对代数问题，往往是中值（平均值）、边值（最大最小）。

当自变量取特殊值时，函数值往往位于极值点（区间上的最大、最小值）。

对其它问题，就是规模较小，简单的，或具有特殊性质的代入值。

3.2 特殊值法的理论依据若函数f(x)为凸函数，由琴生不等式（导数法证明），有f(a1x1+a2x2+...+a n x n)≤a1 f(x1)+a2 f(x2)+...+a n f(x n). 即：对n个不同变量，他们和的函数与函数的和具有不等关系。

同样，对其他运算，也有类似的不等式存在。

特殊值法的证明，通用方法是导数法。

以3个变量的函数f(x,y,z)为例，设x+y+z=k为常数，x≥y≥z.其中x≥k/3, z≤k/3.先固定x，调整y,z, 即函数f(y,z).又y+z=k-x为常数，则有z=k-x-y,三元函数变为一元函数f(z). 求f(z)含z单项的导数f’(z),可得当z=(k-x)/2时，f’(z)=0; z<(k-x)/2时，f’(z)<0; z>(k-x)/2时，f’(z)>0. 即应用单调性可得，对0<z<k/3, y=z 时f(z)最大。

此时y=z=(k-x)/2. 这次调整使y,z相等。

同理，固定z, 可得x=y. 由此，x=y=z. 这是一种逐步调整的策略。

对于多元函数的情形，可类似的证明。

（详细推导步骤见单墫《利用导数证明不等式》，《中等数学》2006年第2期）由此，我们知道特殊值法的适用范围：当不等式的“一项”为单峰函数（中间值最大或最小）时，可使用特殊值法，此时最值取在均值处，而边值处为另一个最值。

巧用特殊值法巧用特殊值法，提高解题效率（一）所谓特殊值法，就是对题目中出现的字母取具体的数值，代入有关代数式进行计算，快速求出代数式的值的一种方法。

这种方法在解有关问题时，它有独到之处，对付一类选择、填空题有一定特效。

例1、（2009年衡阳市）已知33-=-y x ，则y x 35+-的值是（）A ．0B ．2C ．5D ．8 解法一：33,535(3)5(3)8x y x y x y -=-∴-+=--=--=，∴选D 。

解法二：33,33,535(33)38x y x y x y y y -=-∴=-∴-+=--+=，∴选D 。

解法三：33,x y -=-设0,x =则得1y =，则5350318x y -+=-+?=，∴选D 。

比较上述三种解题方法，第一种方法用的是整体值思想，第二种方法用的是消元、转化的思想，解法三用的是特殊值方法，显然，第三种方法比较快速、准确。

本题已知条件是一个不定方程33-=-y x ，符合条件的实数对,x y 有无数个，对于x 、y 取符合条件的特殊数值，代入代数式计算，很快就能得出本题的答案。

要注意这种方法主要用于字母的值可以变化但要求的代数式的值是定值选择题或填空题，不要求写出解题过程，只选择正确答案或直接写出结果的问题。

特殊值的选取，一是要符合条件，二是要使计算简单。

有时还要多取几个不同的数值进行计算、验证。

练习1：（2009年枣庄市）若m +n =3，则222426m mn n ++-的值为（）Ａ．12 Ｂ．6Ｃ．3 Ｄ．0 （提示：对m 取特殊值）练习2：（2008安徽芜湖）已知113,x y -=则代数式21422x xy y x y y --=-- 。

（提示：对x 取特殊值）例2、（2009年牡丹江）若01x <<则x ，1x，2x 的大小关系是（） A ．21x x x << B ．21x x x << C ．21x x x << D ．21x x x<< 本题是确定代数式值大小的问题，用推理方法当然可以得出答案为C 。

用特殊值法解题
特值法解题技巧
特值法就是通过设题中某个未知量为特殊值，从而通过简单的运算，得出最终答案的
一种方法。

这个特殊值应该满足的条件：首先，无论这个量的值是多少，对最终结果所要
求的量的值没有影响;其次，这个量应该要跟最终结果所要求的量有相对紧密的联系;最后，这个量在整个题干中给出的等量关系是一个不可或缺的量。

特值法在化解应用题时以其直观的思维和方便快捷的解题过程颇受社会各界学生亲睐，在本文中融合真题对“特值法”展开全面了解，以便各位学生能够快速精确地利用特值法
化解比例有关问题。

一、特值法
题目中没牵涉某个具体内容量的大小，并且这个量大小并不影响最终结果的时候，我
们可以利用特值法，进而精简排序。

这里告诫学生一定必须特别注意，特值法可以根据题
目的实际须要，挑选出最有助于快速排序的任何数值。

二、适用题型
特值法广为应用于工程问题、行程问题、价格问题、浓度问题等。

符合下列特点之一的可用特值法：
特点一、题目中发生比例关系，没或者很少牵涉至具体内容实值;
特点二、题目中出现不变量或相同量，进行多次不同的分配。

大招一：当只有一个条件时，特殊值，令每一项为x 。

1．（2012•洛阳模拟）设等差数列{}n a 前n 项和为n S ，若972S =，则249(a a a ++=)A ．12B ．18C ．24D ．362．（2014•河北模拟）在等差数列{}n a 中，912162a a =+，则数列{}n a 的前11项和11(S = )A ．24B ．48C ．66D ．1323．（2016•全国模拟）在等差数列{}n a 中，91226a a =+，则数列{}n a 的前11项和11(S = )A ．24B ．48C ．66D ．1324．（2014秋•梧州期末）已知数列{}n a 是等差数列，且1472a a a π++=，则35tan()a a +的值为( )A ．3B ．CD ．3−5．（2018•商洛模拟）等差数列{}n a 中，18153120a a a ++=，则9102a a −的值为()A ．20B ．22C ．24D ．8−6．（2012•安徽）公比为2的等比数列{}n a 的各项都是正数，且31116a a =，则5(a =)A ．4B ．2C ．1D ．8大招二：21(21)n n S n a −=− 不仅仅是奇数哦 12n n S na +=7．（2008•天津）若等差数列{}n a 的前5项和525S =，且23a =，则7(a = )A ．12B ．13C ．14D ．158．（2017•新课标Ⅰ）记n S 为等差数列{}n a 的前n 项和．若4524a a +=，648S =，则{}n a 的公差为( )A ．1B ．2C ．4D ．89．（2012•吉林模拟）已知等差数列{}n a 的前n 项和为n S ，若1m >，且21110m m m a a a −++−−=，2139m S −=，则m 等于( )A ．39B ．20C ．19D ．10大招三：等差数列n S n 是以2d为公差的等差数列 10．（2013•南开区一模）已知n S 为等差数列{}n a 的前n 项和，728S =，1166S =，则9S 的值为( )A ．47B ．45C ．38D ．5411．（2017秋•秦州区校级月考）已知等差数列{}n a 的前n 项和是n S ，39S =，636S =，则公差d 为( )A ．6B ．2−C ．9D ．212．（2016•静宁县一模）设等差数列{}n a 的前n 项和为n S ，若12288S =，9162S =，则6(S = )A ．18B ．36C ．54D ．72大招四：选项分析法（前两项就足够）13．（2015•遵义校级二模）在数列{}n a 中，若11a =，212a =，*12211()n n n n N a a a ++=+∈，则该数列的通项公式为( ) A ．1n a n=B ．21n a n =+ C ．22n a n =+ D ．3n a n=14．（2015•安徽二模）设数列{}n a 的前n 项和为n S ，若2*2()n S n n n N =+∈，则12231111(n n a a a a a a +++⋯+= ) A ．11321n −+B ．11323n −+C ．11643n −+ D ．11646n −+15．（2012•大纲版）已知数列{}n a 的前n 项和为n S ，11a =，12n n S a +=，则当1n >时，(n S = )A ．13()2n −B ．12n −C ．12()3n −D ．111(1)32n −−16．（2017秋•兴庆区校级期中）已知数列{}n a 的前n 项和为n S ，11a =，12n n S a +=，则(n a = )A ．12n −B ．13()2n −C ．12()3n −D ．21,113(),222n n n −=⎧⎪⎨⎪⎩17．（2016•广东模拟）设n S 为数列{}n a 的前n 项的和，且*3(1)()2n n S a n N =−∈，则(n a = )A ．3(32)n n −B ．32n n +C ．3nD ．132n −18．（2011•云南模拟）在等差数列{}n a 中，24a =，612a =，那么数列1{}2nn a +的前n 项和等于( )A ．222nn +−B ．112nn ++C ．12nn +D ．1(1)2n n n +−大招五：选项分析法之年份题19．（2014•和平区三模）已知数列{}n a 的前n 项和为n S ，首项123a =−，且满足12(2)n n nS a n S ++=．则2014S 等于( ) A ．20122013−B ．20132014−C ．20142015−D ．20152016−20．（2015•船营区校级二模）数列{}n a 满足11a =，且对于任意的*n N ∈都有11n n a a a n +=++，则122014111a a a ++⋯+等于( ) A ．40262015B ．40282015C ．20132014D ．2014201521．（2016•益阳模拟）若数列{}n a 满足11a =，且对于任意的*n N ∈都有11n n a a n +=++，则122016111a a a ++⋯+等于( ) A ．40302016 B ．20152016C ．40322017D ．2016201722．（2017•大观区校级三模）数列{}n a 满足11a =，且对于任意的*n N ∈都有11n n a a a n +=++，则122017111a a a ++⋯+等于( ) A ．20162017B ．40322017C ．20172018D ．40342018大招六：和比与项比，五秒出答案23．（2016•中山市二模）两个等差数列的前n 项和之比为51021n n +−，则它们的第7项之比为( )A ．45:13B ．3:1C ．80:27D ．2:124．（2013秋•浦东新区校级月考）两个等差数列，它们前n 项和之比为5321n n +−，则两个数列的第9项之比是( )A ．53B ．85C ．83D ．7425．（2015•黄冈模拟）设n S ，n T 分别是等差数列{}n a ，{}n b 的前n 项和，若*()21n n S nn N T n =∈+，则56(a b = ) A ．513B ．919C ．1123D ．923大招七：n S 、2n n S S −、32n n S S −，等差依旧是等差，等比依旧是等比26．（2018春•东湖区校级期中）设等比数列{}n a 的前n 项和为n S ，若363S S =，则69(S S = ) A ．2B ．83C ．37D ．327．（2007•陕西）各项均为正数的等比数列{}n a 的前n 项和为n S ，若102S =，3014S =，则40S 等于( )A ．80B ．30C ．26D ．1628．（2016•太原一模）各项均为正数的等比数列{}n a 的前n 项和为n S ，若2n S =，314n S =，则4n S 等于( )A ．80B ．30C ．26D ．1629．（2017春•芜湖期末）设等比数列{}n a 的前n 项和为n S ，若105:1:2S S =，则51015105(S S S S S ++=− )A ．72 B ．72−C ．92D ．92−二．填空题（共7小题）30．（2013•广东）在等差数列{}n a 中，已知3810a a +=，则573a a += ． 31．（2014秋•中山市校级月考）等比数列{}n a 的各项均为正数，且1516a a =，则2122232425log log log log log a a a a a ++++= ．32．（2017•葫芦岛模拟）已知等差数列{}n a 的前n 项和为n S ，且满足32132S S −=，则数列{}n a 的公差是 ．大招八：等差数列通项为一次函数33．等差数列{}n a 中，p a q =，q a p =．(p ，q N ∈，且)p q ≠则p q a +=．34．等差数列{}n a 和{}n b 的前n 项和分别为n S 和n T ，若对一切正整数n 都有3221n n T n S n −=+，则1111ab =．35．（2013春•中江县校级月考）等差数列{}n a 、{}n b 的前n 项和分别为n S 、n T ，若3123n n S n T n −=+，则611a b = ． 36．（2010•江苏模拟）等差数列前m 项和是30，前2m 项和是100，则它的前3m 项和是 ．大招九：等差数列和为二次函数，最值可秒37．（2009秋•沈北新区校级月考）已知等差数列{}n a ，129a =，1020S S =， （1）问这个数列的前多少项的和最大？（2）并求最大值．38．（2016春•宜春校级月考）已知等差数列{}n a 中，129a =，1020S S =， （1）问这个数列的前多少项和最大？并求此最大值．（2）求数列{||}n a 的前n 项和n T 公式．39．等差数列{}n a 的首项10a >，设其前n 项和为n S ，且512S S =，则当n 为何值时，n S 有最大值？。

数列通项公式的多种妙解方式经典题型一：观察法经典题型二：叠加法经典题型三：叠乘法经典题型四：待定系数法经典题型五：同除以指数经典题型六：取倒数法经典题型七：取对数法经典题型八：已知通项公式a n 与前n 项的和S n 关系求通项问题经典题型九：周期数列经典题型十：前n 项积型经典题型十一：“和”型求通项经典题型十二：正负相间讨论、奇偶讨论型经典题型十三：因式分解型求通项经典题型十四：其他几类特殊数列求通项经典题型十五：双数列问题经典题型十六：通过递推关系求通项(2022·全国·高考真题)记S n 为数列a n 的前n 项和，已知a 1=1,S n a n 是公差为13的等差数列．(1)求a n 的通项公式；(2)证明：1a 1+1a 2+⋯+1a n<2．【解析】(1)∵a 1=1，∴S 1=a 1=1,∴S 1a 1=1,又∵S n a n 是公差为13的等差数列，∴S n a n =1+13n -1 =n +23,∴S n =n +2 a n 3,∴当n ≥2时，S n -1=n +1 a n -13，∴a n =S n -S n -1=n +2 a n 3-n +1 a n -13,整理得：n -1 a n =n +1 a n -1,即a n a n -1=n +1n -1,∴a n =a 1×a 2a 1×a 3a 2×⋯×a n -1a n -2×a n a n -1=1×31×42×⋯×n n -2×n +1n -1=n n +1 2，显然对于n =1也成立，∴a n 的通项公式a n =n n +1 2；(2)1a n =2n n +1 =21n -1n +1 , ∴1a 1+1a 2+⋯+1a n=21-12 +12-13 +⋯1n -1n +1 =21-1n+1<2(2022·全国·高考真题(理))记S n为数列a n的前n项和．已知2S nn+n=2a n+1．(1)证明：a n是等差数列；(2)若a4,a7,a9成等比数列，求S n的最小值．【解析】(1)因为2S nn+n=2a n+1，即2S n+n2=2na n+n①，当n≥2时，2S n-1+n-12=2n-1a n-1+n-1②，①-②得，2S n+n2-2S n-1-n-12=2na n+n-2n-1a n-1-n-1，即2a n+2n-1= 2na n-2n-1a n-1+1，即2n-1a n-2n-1a n-1=2n-1，所以a n-a n-1=1，n≥2且n∈N*，所以a n是以1为公差的等差数列．(2)由(1)可得a4=a1+3，a7=a1+6，a9=a1+8，又a4，a7，a9成等比数列，所以a72=a4⋅a9，即a1+62=a1+3⋅a1+8，解得a1=-12，所以a n=n-13，所以S n=-12n+nn-12=12n2-252n=12n-2522-6258，所以，当n=12或n=13时S n min=-78．类型Ⅰ观察法：已知数列前若干项，求该数列的通项时，一般对所给的项观察分析，寻找规律，从而根据规律写出此数列的一个通项．类型Ⅱ公式法：若已知数列的前项和与a n的关系，求数列a n的通项a n可用公式a n=S1,(n=1)S n-S n-1,(n≥2)构造两式作差求解．用此公式时要注意结论有两种可能，一种是“一分为二”，即分段式；另一种是“合二为一”，即a1和a n合为一个表达，(要先分n=1和n≥2两种情况分别进行运算，然后验证能否统一)．类型Ⅲ累加法：形如a n+1=a n+f(n)型的递推数列(其中f(n)是关于n的函数)可构造：a n-a n-1=f(n-1)a n-1-a n-2=f(n-2)...a2-a1=f(1)将上述m2个式子两边分别相加，可得：a n=f(n-1)+f(n-2)+...f(2)+f(1)+a1,(n≥2)①若f(n)是关于n的一次函数，累加后可转化为等差数列求和；②若f(n)是关于n的指数函数，累加后可转化为等比数列求和；③若f(n)是关于n的二次函数，累加后可分组求和；④若f(n)是关于n的分式函数，累加后可裂项求和．类型Ⅳ累乘法：形如a n +1=a n ⋅f (n )a n +1a n=f (n )型的递推数列(其中f (n )是关于n 的函数)可构造：a n a n -1=f (n -1)a n -1a n -2=f (n -2)...a 2a 1=f (1)将上述m 2个式子两边分别相乘，可得：a n =f (n -1)⋅f (n -2)⋅...⋅f (2)f (1)a 1,(n ≥2)有时若不能直接用，可变形成这种形式，然后用这种方法求解．类型Ⅴ构造数列法：(一)形如a n +1=pa n +q (其中p ,q 均为常数且p ≠0)型的递推式：(1)若p =1时，数列{a n }为等差数列；(2)若q =0时，数列{a n }为等比数列；(3)若p ≠1且q ≠0时，数列{a n }为线性递推数列，其通项可通过待定系数法构造等比数列来求．方法有如下两种： 法一：设a n +1+λ=p (a n +λ)，展开移项整理得a n +1=pa n +(p -1)λ，与题设a n +1=pa n +q 比较系数(待定系数法)得λ=q p -1,(p ≠0)⇒a n +1+q p -1=p a n +q p -1 ⇒a n +q p -1=p a n -1+qp -1 ，即a n +q p -1 构成以a 1+qp -1为首项，以p 为公比的等比数列．再利用等比数列的通项公式求出a n +qp -1 的通项整理可得a n .法二：由a n +1=pa n +q 得a n =pa n -1+q (n ≥2)两式相减并整理得a n +1-a na n -a n -1=p ,即a n +1-a n 构成以a 2-a 1为首项，以p 为公比的等比数列．求出a n +1-a n 的通项再转化为类型Ⅲ(累加法)便可求出a n .(二)形如a n +1=pa n +f (n )(p ≠1)型的递推式：(1)当f (n )为一次函数类型(即等差数列)时：法一：设a n +An +B =p a n -1+A (n -1)+B ，通过待定系数法确定A 、B 的值，转化成以a 1+A +B 为首项，以A m n =n ！n -m !为公比的等比数列a n +An +B ，再利用等比数列的通项公式求出a n +An +B 的通项整理可得a n .法二：当f (n )的公差为d 时，由递推式得：a n +1=pa n +f (n )，a n =pa n -1+f (n -1)两式相减得：a n +1-a n =p (a n -a n -1)+d ，令b n =a n +1-a n 得：b n =pb n -1+d 转化为类型Ⅴ㈠求出 b n ，再用类型Ⅲ(累加法)便可求出a n .(2)当f (n )为指数函数类型(即等比数列)时：法一：设a n +λf (n )=p a n -1+λf (n -1) ，通过待定系数法确定λ的值，转化成以a 1+λf (1)为首项，以A m n =n ！n -m !为公比的等比数列a n +λf (n ) ，再利用等比数列的通项公式求出a n +λf (n ) 的通项整理可得a n .法二：当f (n )的公比为q 时，由递推式得：a n +1=pa n +f (n )--①，a n =pa n -1+f (n -1)，两边同时乘以q 得a n q =pqa n -1+qf (n -1)--②，由①②两式相减得a n +1-a n q =p (a n -qa n -1)，即a n +1-qa na n -qa n -1=p ，在转化为类型Ⅴ㈠便可求出a n .法三：递推公式为a n +1=pa n +q n (其中p ，q 均为常数)或a n +1=pa n +rq n (其中p ，q ， r 均为常数)时，要先在原递推公式两边同时除以q n +1，得：a n +1q n +1=p q ⋅a n q n +1q ，引入辅助数列b n (其中b n=a n q n)，得：b n +1=p q b n +1q 再应用类型Ⅴ㈠的方法解决．(3)当f (n )为任意数列时，可用通法：在a n +1=pa n +f (n )两边同时除以p n +1可得到a n +1p n +1=a n p n +f (n )p n +1，令an p n =b n ，则b n +1=b n +f (n )pn +1，在转化为类型Ⅲ(累加法)，求出b n 之后得a n =p n b n ．类型Ⅵ对数变换法：形如a n +1=pa q (p >0,a n >0)型的递推式：在原递推式a n +1=pa q 两边取对数得lg a n +1=q lg a n +lg p ，令b n =lg a n 得：b n +1=qb n +lg p ，化归为a n +1=pa n +q 型，求出b n 之后得a n =10b n.(注意：底数不一定要取10，可根据题意选择)．类型Ⅶ倒数变换法：形如a n -1-a n =pa n -1a n (p 为常数且p ≠0)的递推式：两边同除于a n -1a n ，转化为1a n =1a n -1+p 形式，化归为a n +1=pa n +q 型求出1a n的表达式，再求a n ；还有形如a n +1=ma n pa n +q 的递推式，也可采用取倒数方法转化成1a n +1=m q 1a n +mp形式，化归为a n +1=pa n +q 型求出1a n的表达式，再求a n ．类型Ⅷ形如a n +2=pa n +1+qa n 型的递推式：用待定系数法，化为特殊数列{a n -a n -1}的形式求解．方法为：设a n +2-ka n +1=h (a n +1-ka n )，比较系数得h +k =p ,-hk =q ，可解得h 、k ，于是{a n +1-ka n }是公比为h 的等比数列，这样就化归为a n +1=pa n +q 型．总之，求数列通项公式可根据数列特点采用以上不同方法求解，对不能转化为以上方法求解的数列，可用归纳、猜想、证明方法求出数列通项公式a n .(1)若数列{a n }的前n 项和为S n ，通项公式为a n ，则a n =S 1，n =1S n -S n -1，n ≥2，n ∈N ∗注意：根据S n 求a n 时，不要忽视对n =1的验证．(2)在数列{a n }中，若a n 最大，则a n ≥a n -1a n ≥a n +1 ，若a n 最小，则a n≤a n -1a n ≤a n +1 .经典题型一：观察法1.(2022·全国·高三专题练习)数列a n 的前4项为：12,15,18,111，则它的一个通项公式是( )A.12n -1B.12n +1C.13n -1D.13n +1【答案】C【解析】将12,15,18,111可以写成13×1-1,13×2-1,13×3-1,13×4-1，所以a n 的通项公式为13n -1；故选:C2.(2022·全国·高三专题练习(文))如图所示是一个类似杨辉三角的递推式，则第n 行的首尾两个数均为( )A.2nB.2n -1C.2n +2D.2n +1【答案】B【解析】依题意，每一行第一个数依次排成一列为：1，3，5，7，9，⋯，它们成等差数列，通项为2n -1，所以第n 行的首尾两个数均为2n -1.故选：B3.(2022·全国·高三专题练习)“一朵雪花”是2022年北京冬奥会开幕式贯穿始终的一个设计理念，每片“雪花”均以中国结为基础造型构造而成，每一朵雪花都闪耀着奥运精神，理论上，一片雪花的周长可以无限长，围成雪花的曲线称作“雪花曲线”，又称“科赫曲线”，是瑞典数学家科赫在1901年研究的一种分形曲线，如图是“雪花曲线”的一种形成过程：从一个正三角形开始，把每条边分成三等份，然后以各边的中间一段为底边分划向外作正三角形，再去掉底边，反复进行这一过程.若第一个正三角形(图①)的边长为1，则第5个图形的周长为___________.【答案】25627【解析】由题意知下一个图形的边长是上一个图形边长的13，边数是上一个图形的4倍，则周长之间的关系为b n =13⋅4⋅b n -1=43b n -1，所以{b n }是公比为q =43的等比数列，而首项b 1=3，所以b n =3⋅43n -1，当n =5时，“雪花”状多边形的周长为b 5=25627.故答案为：25627经典题型二：叠加法4.(2022·全国·高三专题练习)在数列{a n }中，已知a 1=1p ，a n +1=a n na n +1，p >0,n ∈N *.若p =1，求数列{a n }的通项公式.【解析】由题意，a n +1=a n na n +1 ，得：1a n +1-1a n=n ，运用累加法：1a 2-1a 1+1a 3-1a 2+⋯+1a n -1a n -1=1+2+⋯+n -1=n n -1 2，n ≥2∴1a n -1a 1=n n -1 2，即1a n =n n -1 2+p ，n ≥2 ，当p =1时，a n =2n 2-n +2，n ≥2 ，当n =1时，a n =1成立，所以a n =2n 2-n +25.(2022·全国·高三专题练习)已知数列a n 满足a n +1n +1-a n n =1n n +1n ∈N *，且a 1=1，求数列a n 的通项公式；【解析】因为a n +1n +1-a n n =1n n +1=1n -1n +1，所以a n n -a n -1n -1=1n -1-1n n ≥2 ，a n -1n -1-a n -2n -2=1n -2-1n -1，⋯a 22-a 11=1-12，所以累加可得a n n -a 1=1-1nn ≥2 ．又a 1=1，所以a n n =2n -1n，所以a n =2n -1n ≥2 ．经检验，a 1=1，也符合上式，所以a n =2n -1．6.(2022·全国·高三专题练习)已知数列a n 中，a 1=1中，a n +1=a n +n (n ∈N *)中，则a 4=________，a n =________.【答案】 7n 2-n +22【解析】依题意，n ∈N *，n ≥2，a n -a n -1=n -1，而a 1=1，则a n =a 1+(a 2-a 1)+(a 3-a 2)+⋯+(a n -a n -1)=1+1+2+⋯+(n -1)=1+1+n -12⋅n -1 =n 2-n +22，而a 1=1满足上式，所以a n =n 2-n +22，a 4=42-4+22=7.故答案为：7；n 2-n +22经典题型三：叠乘法7.(2022·全国·高三专题练习)在数列a n 中，a n +1=nn +2a n (n ∈N *)，且a 1=4，则数列a n 的通项公式a n =________.【答案】8n n +1【解析】由a n +1=n n +2a n ，得a n +1a n =nn +2，则a 2a 1=13，a 3a 2=24，a 4a 3=35，⋮a n a n -1=n -1n +1n ≥2 ，累乘得a n a 1=13×24×35×⋯×n -3n -1×n -2n ×n -1n +1=2n n +1，所以a n =8n n +1.故答案为：8n n +1 .8.(2022·全国·高三专题练习)设a n 是首项为1的正项数列，且(n +2)a n +12-na n 2+2a n +1a n =0(n ∈N *)，求通项公式a n =___________【答案】2n (n +1)【解析】由(n +2)a n +12-na n 2+2a n +1a n =0(n ∈N *)，得[(n +2)a n +1-na n ](a n +1+a n )=0，∵a n >0，∴a n +1+a n >0，∴(n +2)a n +1-na n =0 ，∴a n +1a n =nn +2，∴a n =a 1⋅a 2a 1⋅a 3a 2⋅a 4a 3⋅⋅⋅⋅⋅a n a n -1=1×13×24×35×⋅⋅⋅×n -2n ×n -1n +1=2n (n +1)(n ≥2)，又a 1=1满足上式，∴a n =2n (n +1).故答案为：2n (n +1).9.(2022·全国·高三专题练习)数列a n 满足：a 1=23，2n +2-1 a n +1=2n +1-2 a n n ∈N * ，则a n 的通项公式为_____________.【答案】a n =2n2n -1 2n +1-1【解析】由2n +2-1 a n +1=2n +1-2 a n 得，a n +1a n =2n +1-22n +2-1=2⋅2n -12n +2-1，则a n a n -1⋅a n -1a n -2⋅a n -2a n -3⋅⋅⋅a 2a 1=2⋅2n -1-12n +1-1⋅2⋅2n -2-12n -1⋅2⋅2n -3-12n -1-1⋅⋅⋅2⋅21-123-1=2n -1⋅32n +1-1 2n -1，即a n a 1=3⋅2n -12n -1 2n +1-1 ，又a 1=23，所以a n =2n 2n -1 2n +1-1.故答案为：a n =2n2n -1 2n +1-1.经典题型四：待定系数法10.(多选题)(2022·广东惠州·高三阶段练习)数列a n 的首项为1，且a n +1=2a n +1，S n 是数列a n 的前n 项和，则下列结论正确的是( )A.a 3=7 B.数列a n +1 是等比数列C.a n =2n -1 D.S n =2n +1-n -1【答案】AB【解析】∵a n +1=2a n +1，可得a n +1+1=2a n +1 ，又a 1+1=2∴数列a n +1 是以2为首项，2为公比的等比数列，故B 正确；则a n +1=2n ，∴a n =2n -1，故C 错误；则a 3=7，故A 正确；∴S n =21-2n1-2-n =2n +1-n -2，故D 错误.故选：AB .11.(2022·河南安阳·三模(文))已知数列a n 满足a n +1=2a n +12，且前8项和为506，则a 1=___________.【答案】32【解析】由题意得：∵a n +1=2a n +12∴a n +1+12=2a n +12 ，即a n +1+12a n +12=2∴数列a n +12 是以a 1+12为首项，2为公比的等比数列，记数列a n +12 的前n 项和为T n T 8=a 1+12 (1-28)1-2=a 1+12+a 2+12+a 3+12+⋯+a 8+12=(a 1+a 2+a 3+⋯a 8)+12×8=506+4=510解得：a 1=32故答案为：3212.(2022·河北衡水·高三阶段练习)已知数列a n 的前n 项和为S n ，且满足2S n +n =3a n ，n ∈N *．(1)求数列a n 的通项公式；(2)若b n =a 2n ，求数列b n 的前10项和T 10．【解析】(1)当n =1时，2S 1+1=3a 1，即2a 1+1=3a 1，解得a 1=1；当n ≥2时，∵2S n +n =3a n ，∴2S n -1+n -1=3a n -1，两式作差得2a n +1=3a n -3a n -1，即a n =3a n -1+1,a n +12=3a n -1+12，∴a n +12a n -1+12=3，又a 1+12=32，∴数列a n +12 是以32为首项，3为公比的等比数列，∴a n +12=32×3n -1=3n 2，a n =3n 2-12=123n -1 .(2)∵b n =a 2n ，则T 10=b 1+b 2+b 3+⋯+b 10=a 2+a 4+⋯+a 20=1232-1 +34-1 +⋯+320-1=1232+34+⋯+320 -10=12321-910 1-9-10 =911-8916．13.(2022·全国·高三专题练习)设数列a n 满足a 1=2，a n -2a n -1=2-n n ∈N * ．(1)求证：a n -n 为等比数列，并求a n 的通项公式；(2)若b n =a n -n ⋅n ，求数列b n 的前n 项和T n ．【解析】(1)因为a 1=2，a n -2a n -1=2-n n ∈N * ，所以a n =2a n -1+2-n ，即a n -n =2a n -1-n -1又a 1-1=2-1=1，所以a n -n 是以1为首项，2为公比的等比数列，所以a n -n =1×2n -1，所以a n =2n -1+n (2)由(1)可得b n =a n -n ⋅n =n ×2n -1，所以T n =1×20+2×21+3×22+⋯+n ×2n -1①，所以2T n =1×21+2×22+3×23+⋯+n ×2n ②，①-②得-T n =1+1×21+1×22+1×23+⋯+1×2n -1-n ×2n即-T n =1-2n1-2-n ×2n ，所以T n =n -1 ×2n +1；14.(2022·全国·高三专题练习)在数列a n 中，a 1=5，且a n +1=2a n -1n ∈N * .(1)证明：a n -1 为等比数列，并求a n 的通项公式；(2)令b n =(-1)n ⋅a n ，求数列b n 的前n 项和S n .【解析】(1)因为a n +1=2a n -1，所以a n +1-1=2a n -1 ，又a 1-1=4，所以a n +1-1a n -1=2，所以a n -1 是以4为首项，2为公比的等比数列.故a n -1=4×2n -1，即a n =2n +1+1.(2)由(1)得b n =(-1)n⋅2n +1+1 ，则b n =2n +1+1,n =2k ,k ∈N *-2n +1+1 ,n =2k -1,k ∈N* ，①当n =2k ,k ∈N *时，S n =-22-1 +23+1 -24+1 +⋯+-2n -1 +2n +1+1 =-22+23-24+25+⋯-2n +2n +1=22+24+⋯+2n =432n -1 ;②当n =2k -1,k ∈N *时，S n =S n +1-b n +1=432n +1-1 -2n +2+1 =-2n +2+73，综上所述，S n =432n -1 ,n =2k ,k ∈N*-2n +2+73,n =2k -1,k ∈N *经典题型五：同除以指数15.(2022·广东·模拟预测)已知数列a n 中，a 1=5且a n =2a n -1+2n -1n ≥2,n ∈N ∗ ，b n =a n -1n +1(1)求证：数列b n 是等比数列；(2)从条件①n +b n ，②n ⋅b n 中任选一个，补充到下面的问题中并给出解答．求数列______的前n 项和T n ．注：如果选择多个条件分别解答，按第一个解答计分．【解析】(1)因为a 1=5且a n =2a n -1+2n -1n ≥2,n ∈N ∗ ，所以当n ≥2时，a n -1=2a n -1-1 +2n ，所以a n -12n =a n -1-12n -1+1，即a n -12n -a n -1-12n -1=1所以a n -12n 是以a 1-12=2为首项，1为公差的等差数列，所以a n -12n =2+n -1 ×1=n +1，所以a n =n +1 2n+1，b n =a n -1n +1=n +1 2n+1-1n +1=2n因为b 1=a 1-11+1=2，n ≥2时，b n b n -1=2n 2n -1=2所以数列b n 是以2为首项，2为公比的等比数列．(2)选①：因为b n =2n ，所以n +b n =n +2n ，则T n =(1+2)+2+22 +3+23 +⋅⋅⋅+n +2n=1+2+3+⋅⋅⋅+n +2+22+23+⋅⋅⋅+2n=12n n +1 +21-2n 1-2=n 22+n2+2n +1-2选②：因为b n =2n ，所以nb n =n ⋅2n，则T n =1×21+2×22+⋅⋅⋅+n ×2n (i )2T n =1×22+2×23+⋅⋅⋅+n ×2n +1(ii )(i )-(ii )得-T n =1×21+22+23+⋅⋅⋅+2n -n ×2n +1T n =n ×2n +1-21-2n 1-2=n ×2n +1-2n +1+2=n -1 2n +1+216.(2022·全国·高三专题练习)已知数列a n 满足a 1=1，a n +1=2a n +3n ，求数列a n 的通项公式.【解析】由a n +1=2a n +3n 两边同除以3n +1得a n +13n +1=23⋅a n 3n +13，令b n =a n 3n ，则b n +1=23b n +13，设b n +1+λ=23(b n +λ)，解得λ=-1，b n +1-1=23(b n -1)，而b 1-1=-23，∴数列{b n -1}是以-23为首项，23为公比的等比数列，b n -1=-23 n ，得a n =3n -2n17.(2022·全国·高三专题练习)在数列a n 中，a 1=1，S n +1=4a n +2，则a 2019的值为( )A.757×22020B.757×22019C.757×22018D.无法确定【答案】A【解析】∵a 1=1，S n +1=4a n +2，∴S 2=a 1+a 2=4a 1+2，解得a 2=5.∵S n +1=4a n +2，∴S n +2=4a n +1+2，两式相减得，a n +2=4a n +1-4a n ，∴a n +2-2a n +1=2a n +1-2a n ，∴a n +1-2a n 是以a 2-2a 1=3为首项，2为公比的等比数列，∴a n +1-2a n =3×2n -1，两边同除以2n +1，则a n +12n +1-a n 2n=34，∴a n 2n 是以34为公差，a 121=12为首项的等差数列，∴a n 2n =12+n -1 ×34=3n -14，∴a n =3n -14×2n =3n -1 ×2n -2，∴a 2019=3×2019-1 ×22017=757×22020.故选：A .经典题型六：取倒数法18.(2022·全国·高三竞赛)数列a n 满足a 1=p ，a n +1=a 2n +2a n ．则通项a n =______．【答案】p +1 2n -1-1【解析】∵a n =a 2n -1+2a n -1，∴a n +1=a n -1+1 2=a n -2+1 22=⋯=a 1+1 2n -1=p +1 2n -1．即a n =p +1 2n -1-1．故答案为p +1 2n -1-119.(2022·全国·高三专题练习)已知数列a n 满足a 1=12，且a n +1=a n 3a n +1，则数列a n =__________【答案】13n -1【解析】由a n +1=a n 3a n +1两边取倒数可得1a n +1=1a n +3，即1a n +1-1a n=3所以数列1a n 是等差数列，且首项为2，公差为3，所以1a n=3n -1，所以a n =13n -1；故答案为：13n -120.(2022·全国·高三专题练习)数列a n 满足a n +1=a n 1+2a nn ∈N ∗，a 1=1，则下列结论错误的是( )A.2a 10=1a 3+1a 17B.21an是等比数列C.2n -1 a n =1D.3a 5a 17=a 49【答案】D 【解析】由a n +1=a n 1+2a n ，且a 1=1，则a 2=a 12a 1+1>0，a 3=a 21+2a 2>0，⋯，以此类推可知，对任意的n ∈N ∗，a n >0，所以，1a n +1=1+2a n a n =1a n +2，所以1a n +1-1a n =2，且1a 1=1，所以，数列1a n 是等差数列，且该数列的首项为1，公差为2，所以，1a n =1+2n -1 =2n -1，则2n -1 a n =1，其中n ∈N ∗，C 对；21a n +121a n=21an +1-1a n=22=4，所以，数列21an是等比数列，B 对；由等差中项的性质可得2a 10=1a 3+1a 17，A 对；由上可知a n =12n -1，则3a 5a 17=3×12×5-1×12×17-1=199，a 49=12×49-1=197，所以，3a 5a 17≠a 49，D 错.故选：D .21.(2022·全国·高三专题练习)已知数列a n 满足a 1=1，a n +1=a n 4a n +1，(n ∈N *)，则满足a n >137的n 的最大取值为( )A.7 B.8C.9D.10【答案】C【解析】因为a n +1=a n 4a n +1，所以1a n +1=4+1a n ，所以1a n +1-1a n =4，又1a 1=1，数列1a n是以1为首项，4为公差的等差数列．所以1a n =1+4(n -1)=4n -3，所以a n =14n -3，由a n >137，即14n -3>137，即0<4n -3<37，解得34<n <10，因为n 为正整数，所以n 的最大值为9；故选：C 经典题型七：取对数法22.(2022·湖南·长郡中学高三阶段练习)若在数列的每相邻两项之间插入此两项的积，形成新的数列，再把所得数列按照同样的方法不断构造出新的数列.现对数列1，2进行构造，第一次得到数列1，2，2；第二次得到数列1，2，2，4，2；依次构造，第n n ∈N * 次得到的数列的所有项的积记为a n ，令b n =log 2a n ，则b 3=___________，b n =___________.【答案】 143n +12【解析】设第n 次构造后得到的数列为1，x 1，x 2，⋯，x k ，2.则a n =2x 1x 2⋯x k ，则第n +1次构造后得到的数列为1，x 1，x 1，x 1x 2，x 2，⋯，x k -1x k ，x k ，2x k ，2.则a n +1=4x 1x 2⋯x k 3=4×a n 2 3=12a 3n ，∴b n +1=log 2a n +1=log 212a 3n=-1+3b n ，∴b n +1-12=3b n -12 ，又∵b 1=log 222=2，∴数列b n -12 是以32为首项，3为公比的等比数列，∴b n -12=32×3n -1=3n 2，b n =3n +12，b 3=14.故答案为：14；3n +1223.(2022·全国·高三专题练习(文))英国著名物理学家牛顿用“作切线”的方法求函数零点时，给出的“牛顿数列”在航空航天中应用广泛，若数列x n 满足x n +1=x n -f x nf x n，则称数列x n 为牛顿数列．如果函数f x =2x 2-8，数列x n 为牛顿数列，设a n =ln x n +2x n -2，且a 1=1，x n >2．数列a n 的前n 项和为S n ，则S n =______．【答案】2n -1【解析】∵f x =2x 2-8，∴f x =4x ，又∵x n +1=x n -f x n f x n=x n -2x n 2-84x n =x n 2+42x n ，∴x n +1+2=x n +2 22x n ，x n +1-2=x n -222x n，∴x n +1-2x n +1-2=x n +2x n -2 2，又x n >2∴ln x n +1+2x n +1-2=ln x n +2x n -2 2=2ln x n +2x n -2 ，又a n =ln x n +2x n -2，且a 1=1，所以a n +1=2a n ，∴数列a n 是首项为1，公比为2的等比数列，∴a n 的前n 项和为S n ，则S n =1×1-2n1-2=2n -1.故答案为：2n -1.经典题型八：已知通项公式a n 与前n 项的和S n 关系求通项问题24.(2022·江苏南通·高三开学考试)从条件①2S n =n +1 a n ，②a 2n +a n =2S n ,a n >0，③S n +S n -1=a n n ≥2 ，中任选一个，补充到下面问题中，并给出解答.已知数列a n 的前n 项和为S n ,a 1=1，___________.(1)求a n 的通项公式；(2)设b n =a n +1+12n +1，记数列b n 的前n 项和为T n ，是否存在正整数n 使得T n >83.【解析】(1)若选择①，因为2S n =n +1 a n ,n ∈N *，所以2S n -1=na n -1,n ≥2，两式相减得2a n =n +1 a n -na n -1，整理得n -1 a n =na n -1,n ≥2,即a n n =a n -1n -1,n ≥2，所以a n n 为常数列，而a n n =a 11=1，所以a n =n ；若选择②，因为a 2n +a n =2S n n ∈N *，所以a 2n -1+a n -1=2S n -1n ≥2 ，两式相减a 2n -a 2n -1+a n -a n -1=2S n -2S n -1=2a n n ≥2 ，得a n -a n -1 a n +a n -1 =a n +a n -1n ≥2 ，因为a n >0,∴a n +a n -1>0,∴a n -a n -1=1n ≥2 ，所以a n 是等差数列，所以a n =1+n -1 ×1=n ；若选择③，由S n +S n -1=a n n ≥2 变形得，S n +S n -1=S n -S n -1，所以S n +S n -1=S n +S n -1 S n -S n -1 ，由题意知S n >0，所以S n -S n -1=1，所以S n 为等差数列，又S 1=a 1=1，所以S n =n ,S n =n 2,∴a n =S n -S n -1=2n -1n ≥2 ，又n =1时，a 1=1也满足上式，所以a n =2n -1；(2)若选择①或②，b n =n +1+12n +1=n +22n +1，所以T n =3×12 2+4×12 3+5×12 4+⋯+n +2 ×12n +1,所以12T n =3×12 3+4×12 4+5×12 5+⋯+n +2 ×12n +2，两式相减得12T n =3×12 2+12 3+12 4+⋯+12 n +1-n +2 ×12n +2=34+181-12n -1 1-12-n +2 ×12 n +2=1-n +42n +2，则T n =2-n +42n +1，故要使得T n >83，即2-n +42n +1>83，整理得，n +42n +1<-23，当n ∈N *时，n +42n +1>0，所以不存在n ∈N *，使得T n >83.若选择③，依题意，b n =a n +1+12n +1=n +12n，所以T n =2×12+3×12 2+4×12 3+⋯+n +1 ×12n，故12T n =2×12 2+3×12 3+4×12 4+⋯+n +1 ×12 n +1，两式相减得：12T n =1+12 2+12 3+⋯+12 n -n +1 ×12 n +1=1+141-12n -1 1-12-n +1 ×12 n +1=32-n +32n +1，则T n =3-n +32n ，令T n =3-n +32n >83，则n +32n <13，即2n -3n -9>0，令c n =2n -3n -9，则c 1=-10<0，当n ≥2时，c n +1-c n =2n +1-3n +1 -9-2n -3n -9 =2n -3>0，又c 4<0,c 5>0，故c 2<c 3<c 4<0<c 5<c 6⋯，综上，使得T n >83成立的最小正整数n 的值为5.25.(2022·河南省上蔡第一高级中学高三阶段练习(文))记各项均为正数的等比数列a n 的前n 项和是S n ，已S n =a n +43a n +1-4n ∈N * .(1)求a n 的通项公式；(2)求数列na n 的前n 项和T n .【解析】(1)设等比数列a n 的公比为q .因为S n =a n +43a n +1-4n ∈N * ，所以当n =1时，a 1=a 1+43a 2-4，解得a 2=3；当n =2时，a 1+a 2=a 2+43a 3-4，则a 1=43a 3-4.因为a n 是等比数列，所以a 1a 3=a 22，即43a 3-4 a 3=9，整理得4a 23-12a 3-27=0，解得a 3=-32(舍去)或a 3=92.所以q =a 3a 2=32,a 1=a 2q=2，所以a n =2×32n -1.(2)由(1)得na n =2n ×32 n -1，所以T n =2×1+2×32+3×32 2+⋯+n -1 × 32 n -2+n ×32 n -1①则32T n =2×1×32+2×32 2+3×32 3+⋯+ n -1 ×32 n -1+n ×32 n ②①-②得-T n 2=2×1+32+32 2+323+⋯+ 32 n -1 -2n ×32 n=2×1-32 n1-32-2n ×32 n =-4+4-2n ×32 n ,所以T n =4n -8 ×32n+8.26.(2022·全国·高三专题练习)设数列{a n }的前n 项和为S n ，a n +1=-S n S n +1n ∈N * ，a 1=1. 求证：数列1S n是等差数列.【解析】∵-S n S n +1=a n +1=S n +1-S n ，S 1=1≠0，则S n ≠0，所以-1=S n +1-S nS n S n +1，有1S n +1-1S n=1，所以数列1S n 是以1为首项，1为公差的等差数列.经典题型九：周期数列27.(2022·上海中学高二期末)数列{x n }满足x n +1=x n -x n -1,n ≥2,n ∈N *,x 1=a ,x 2=b ，则x 2019=_________.【答案】b -a .【解析】由题干中递推公式，可得：x 1=a ，x 2=b ，x 3=x 2-x 1=b -a ，x 4=x 3-x 2=b -a -b =-a ，x 5=x 4-x 3=-a -(b -a )=-b ，x 6=x 5-x 4=-b -(-a )=a -b ，x 7=x 6-x 5=a -b -(-b )=a ，x 8=x 7-x 6=a -(a -b )=b ，x 9=x 8-x 7=b -a ，⋯∴数列{x n }是以6为最小正周期的周期数列．∵2019÷6=336⋯3，∴x 2019=x 3=b -a ．故答案为b -a .28.(2022·全国·高三专题练习)数列{a n }满足a 1=2，a 2=11-a 1，若对于大于2的正整数n ，a n =11-a n -1，则a 102=__________.【答案】12【解析】由题意知：a 2=11-2=-1,a 3=11--1 =12,a 4=11-12=2,a 5=11-2=-1，故{a n }是周期为3的周期数列，则a 102=a 3×34=a 3=12.故答案为：12.29.(2022·河南·模拟预测(文))设数列a n 满足a n +1=1+a n 1-a n ,且a 1=12，则a 2022=( )A.-2 B.-13C.12D.3【答案】D【解析】由题意可得：a 2=1+a 11-a 1=1+121-12=3，a 3=1+a 21-a 2=1+31-3=-2，a 4=1+a 31-a 3=1+-2 1--2 =-13，a 5=1+a 41-a 4=1-131+13=12=a 1，据此可得数列a n 是周期为4的周期数列，则a 2022=a 505×4+2=a 2=3.故选：D30.(2022·全国·高三专题练习)设数列a n 的通项公式为a n =-1 n 2n -1 ⋅cos n π2+1n ∈N * ，其前n 项和为S n ，则S 120=( )A.-60 B.-120C.180D.240【答案】D【解析】当n =4k -3，k ∈N *时，cos n π2=0，a 4k -3=1；当n =4k -2，k ∈N *时，cosn π2=-1，a 4k -2=2×4k -2 -1 ×-1 +1=-8k +6；当n =4k -1，k ∈N *时，cos n π2=0，a 4k -1=1；当n =4k ，k ∈N *时，cos n π2=1，a 4k =2×4k -1+1=8k .∴a 4k -3+a 4k -2+a 4k -1+a 4k =1+-8k +6 +1+8k =8，∴S 120=1204×8=240.故选：D 经典题型十：前n 项积型31.(2022·全国·高三专题练习)设数列a n 的前n 项积为T n ，且T n =2-2a n n ∈N * .(1)求证数列1T n 是等差数列；(2)设b n =1-a n 1-a n +1 ，求数列b n 的前n 项和S n .【解析】(1)因为数列a n 的前n 项积为T n ，且T n =2-2a n n ∈N * ，∴当n =1时，T 1=a 1=2-2a 1，则a 1=23，1T 1=32.当n ≥2时，T n =2-2T n T n -1⇒1=2T n -2T n -1，∴1T n -1T n -1=12，所以1T n 是以1T 1=32为首项，12为公差的等差数列；(2)由(1)知数列1T n =n +22，则由T n =2-2a n 得a n =n +1n +2，所以b n =1n +2 n +3=1n +2-1n +3，所以S n =13-14 +14-15 +⋯+1n +2-1n +3 =13-1n +3=n 3n +9.32.(2022·全国·高三专题练习)记T n 为数列a n 的前n 项积，已知1T n +3a n=3，则T 10=( )A.163B.154C.133D.114【答案】C 【解析】n =1,T 1=43,T n =a 1a 2a 3⋯a n ,则a n =T n T n -1(n ≥2)，代入1T n +3a n =3，化简得：T n -T n -1=13，则T n =n +33,T 10=133.故选:C .33.(2022·全国·高三专题练习)记S n 为数列a n 的前n 项和，b n 为数列S n 的前n 项积，已知2S n +b n =2，则a 9=___________.【答案】1110【解析】因为b n =S 1∙S 2∙⋯S n ，所以b 1=S 1=a 1，b n -1=S 1∙S 2∙⋯S n -1(n ≥2)，S n =b nb n -1(n ≥2), 又因为2S n +b n =2，当n =1时，得 a 1=23，所以b 1=S 1=a 1=23， 当n ≥2时， 2×b nb n -1+b n =2，即2b n =2b n -1+1，所以2b n 是等差数列，首项为2b 1=3，公差d =1， 所以2b n=3+(n -1)×1=n +2，所以b n =2n +2，满足 b 1=23，故b n =2n +2，即S 1∙S 2∙⋯S n =2n +2，所以S 1∙S 2∙⋯S n -1=2n +1(n ≥2)，两式相除得：S n =n +1n +2，所以S n -1=nn +1(n ≥2)，所以a n =S n -S n -1=n +1n +2-n n +1=1(n +1)(n +2)，所以a 9=111×10=1110.故答案为：1110.经典题型十一：“和”型求通项34.(2022·山西·太原市外国语学校高三开学考试)在数列a n 中，a 1=1，且n ≥2，a 1+12a 2+13a 3+⋯+1n -1a n -1=a n .(1)求a n 的通项公式；(2)若b n =1a n a n +1，且数列b n 的前项n 和为S n ，证明：S n <3.【解析】(1)因为n ≥2,a 1+12a 2+13a 3+⋯+1n -1a n -1=a n ，所以当n ≥3,a 1+12a 2+13a 3+⋯+1n -2a n -2=a n -1，两式相减，得1n -1a n -1=a n -a n -1，即nn -1a n -1=a n ，当n =2时，a 2=a 1=1，所以当n ≥3时，a n a n -1=nn -1，所以当n ≥3时，a n =a n a n -1×a n -1a n -2×⋯×a 3a 2×a 2=n n -1×n -1n -2×⋯×32×1=n2，当n =2时，上式成立；当n =1时，上式不成立，所以a n =1,n =1n2,n ≥2.(2)证明：由(1)知b n =1,n =14n (n +1),n ≥2当n ≥2时，b n =4n (n +1)=41n -1n +1 ，所以当n =1，S 1=1<3；当n ≥2时，S n =1+412-13 +413-14 +⋯+41n -1n +1=1+412-13+13-14+⋯+1n -1n +1 =1+412-1n +1 =3-4n +1<3.综上，S n <3.35.(2022·全国·高三专题练习)数列a n 满足a 1∈Z ，a n +1+a n =2n +3，且其前n 项和为S n .若S 13=a m ，则正整数m =( )A.99 B.103C.107D.198【答案】B【解析】由a n +1+a n =2n +3得a n +1-(n +1)-1=-a n -n -1 ，∴a n-n-1为等比数列，∴a n-n-1=(-1)n-1a1-2，∴a n=(-1)n-1a1-2+n+1，a m=(-1)m-1a1-2+m+1，∴S13=a1+a2+a3+⋯+a12+a13=a1+2×(2+4+⋯+12)+3×6=a1+102，①m为奇数时，a1-2+m+1=a1+102，m=103；②m为偶数时，-a1-2+m+1=a1+102，m=2a1+99，∵a1∈Z，m=2a1+99只能为奇数，∴m为偶数时，无解，综上所述，m=103.故选：B.36.(2022·黑龙江·哈师大附中高三阶段练习(理))已知数列a n的前n项和为S n，若S n+1+S n=2n2n∈N*，且a1≠0，a10=28，则a1的值为A.-8B.6C.-5D.4【答案】C【解析】对于S n+1+S n=2n2，当n=1时有S2+S1=2，即a2-2=-2a1∵S n+1+S n=2n2，∴S n+S n-1=2(n-1)2，(n≥2)两式相减得：a n+1+a n=4n-2a n+1-2n=-a n-2(n-1)，(n≥2)由a1≠0可得a2-2=-2a1≠0,∴a n+1-2na n-2(n-1)=-1(n≥2)即a n-2(n-1)从第二项起是等比数列，所以a n-2(n-1)=a2-2(-1)n-2，即a n=a2-2(-1)n-2+2(n-1)，则a10=a2-2+18=28，故a2=12，由a2-2=-2a1可得a1=-5，故选C.经典题型十二：正负相间讨论、奇偶讨论型37.(2022·河南·高二阶段练习(文))数列a n满足a1=1,a n+a n+1=3n n∈N*，则a2018=__________ _.【答案】3026【解析】∵a n+a n+1=3n，∴a n+1+a n+2=3n+1，得a n+2-a n=3，∵a1=1,a n+a n+1=3n n∈N*，∴a1+ a2=3⇒a2=2，所以a n的偶数项构成等差数列，首项为2，公差为3，∴a2018=a2+1008×3=2+3024= 3026.故答案为：302638.(2022·全国·高三专题练习)已知数列a n中，a1=1，a2=2，a n+2=-1n+1a n+2，则a18a19=( )A.3B.113C.213D.219【答案】D【解析】当n为奇数时，a n+2-a n=2，即数列a n中的奇数项依次构成首项为1，公差为2的等差数列，所以，a19=1+10-1×2=19，当n为偶数时，a n+2+a n=2，则a n+4+a n+2=2，两式相减得a n+4-a n=0，所以，a18=a4×4+2=a2=2，故a18a19=219，故选：D.39.(2022·广东·高三开学考试)已知数列a n满足a1=3，a2=2，a n+2=a n-1,n=2k-1 3a n,n=2k .(1)求数列a n的通项公式；(2)求数列a n的前2n项的和S2n.【解析】(1)当n为奇数时，a n+2-a n=-1，所以所有奇数项构成以a1=3为首项，公差为-1的等差数列，所以a n=3+(n-1)⋅-12=7-n2，当n为偶数时，a n+2=3a n，所以所有偶数项构成以a2=2为首项，公比为3的等比数列，所以a n=2×(3)n-2=2×3n-22，所以a n=7-n2,n=2k-1 2×3n-22,n=2k ；(2)S2n=a1+a2+⋯+a2n=a1+a3+a5+⋯+a2n-1+a2+a4+⋯+a2n=3n+(-1)⋅n(n-1)2+21-3n1-3=(7-n)n2+3n-1=-12n2+72n+3n-1.40.数列{a n}满足a n+2+(-1)n+1a n=3n-1，前16项和为540，则a2= ．【解析】解：因为数列{a n}满足a n+2+(-1)n+1a n=3n-1，当n为奇数时，a n+2+a n=3n-1，所以a3+a1=2，a7+a5=14，a11+a9=26，a15+a13=38，则a1+a3+a5+a7+a9+a11+a13+a15=80，当n为偶数时，a n+2-a n=3n-1，所以a4-a2=5，a6-a4=11，a8-a6=17，a10-a8=23，a12-a10=29，a14-a12=35，a16-a14=41，故a4=5+a2，a6=16+a2，a8=33+a2，a10=56+a2，a12=85+a2，a14=120+a2，a16=161+a2，因为前16项和为540，所以a2+a4+a6+a8+a10+a12+a14+a16=540-80=460，所以8a2+476=460，解得a2=-2．故答案为：-2．41.(2022•夏津县校级开学)数列{a n}满足a n+2+(-1)n a n=3n-1，前16项和为508，则a1= ．【解析】解：由a n+2+(-1)n a n=3n-1，当n为奇数时，有a n+2-a n=3n-1，可得a n-a n-2=3(n-2)-1，⋯a3-a1=3⋅1-1，累加可得a n-a1=3[1+3+⋯+(n-2)]-n-12=(n-1)(3n-5)4；当n为偶数时，a n+2+a n=3n-1，可得a4+a2=5，a8+a6=17，a12+a10=29，a16+a14=41．可得a2+a4+⋯+a16=92．∴a 1+a 3+⋯+a 15=416．∴8a 1+14(0+8+40+96+176+280+408+560)=416，∴8a 1=24，即a 1=3．故答案为：3．经典题型十三：因式分解型求通项42.(2022秋•安徽月考)已知正项数列{a n }满足：a 1=a ，a 2n +1-4a 2n +a n +1-2a n =0，n ∈N *．(Ⅰ)判断数列{a n }是否是等比数列，并说明理由；(Ⅱ)若a =2，设a n =b n -n ．n ∈N *，求数列{b n }的前n 项和S n ．【解析】解：(Ⅰ)∵a 2n +1-4a 2n +a n +1-2a n =0，∴(a n +1-2a n )(a n +1+2a n +1)=0，又∵数列{a n }为正项数列，∴a n +1=2a n ，∴①当a =0时，数列{a n }不是等比数列；②当a ≠0时，an +1a n=2，此时数列{a n }是首项为a ，公比为2的等比数列．(Ⅱ)由(Ⅰ)可知：a n =2n ，∴b n =2n +n ，∴S n =(21+22+⋯+2n)+(1+2+⋯+n )=2(1-2n )1-2+n (1+n )2=2n +1-2+n (n +1)2．43.(2022•怀化模拟)已知正项数列{a n }满足a 1=1，2a 2n -a n -1a n -6a 2n -1=0(n ≥2,n ∈N *)设b n =log 2a n ．(1)求b 1，b 2b 3；(2)判断数列{b n }是否为等差数列，并说明理由；(3){b n }的通项公式，并求其前n 项和为S n ．【解析】解：(1)a 1=1，2a 2n -a n -1a n -6a 2n -1=0，a n >0，可得(2a n +3a n -1)(a n -2a n -1)=0，则a n =2a n -1，数列{a n }为首项为1，公比为2的等比数列，可得a n =2n -1；b n =log 2a n =n -1，b 1=0，b 2b 3=1×2=2；(2)数列{b n }为等差数列，理由：b n +1-b n =n -(n -1)=1，则数列{b n }为首项为0，公差为1的等差数列；(3)b n =log 2a n =log 22n -1=n -1，前n 项和为S n =12n (0+n -1)=n 2-n2．44.(2022秋•仓山区校级月考)已知正项数列{a n }满足a 1=2且(n +1)a 2n +a n a n +1-na 2n +1=0(n ∈N *)(Ⅰ)证明数列{a n }为等差数列；(Ⅱ)若记b n =4a n a n +1，求数列{b n }的前n 项和S n ．【解析】(I )证明：由(n +1)a 2n +a n a n +1-na 2n +1=0(n ∈N *)，变形得：(a n +a n +1)[(n +1)a n -na n +1]=0，由于{a n }为正项数列，∴a n +1a n =n +1n，利用累乘法得：a n =2n (n ∈N *)从而得知：数列{a n }是以2为首项，以2为公差的等差数列．(Ⅱ)解：由(Ⅰ)知：b n=42n∙2(n+1)=1n(n+1)=1n-1n+1，从而S n=b1+b2+⋯+b n=1-1 2+12-13+13-15+⋯+1n-1-1n+1=1-1n+1=n n+1．经典题型十四：其他几类特殊数列求通项45.(2022·全国·高三专题练习)在数列{a n}中，已知各项都为正数的数列{a n}满足5a n+2+4a n+1-a n=0.(1)证明数列{a n+a n+1}为等比数列；(2)若a1=15，a2=125，求{a n}的通项公式.【解析】(1)各项都为正数的数列{a n}满足5a n+2+4a n+1-a n=0，得a n+1+a n+2=15(a n+1+a n)，即a n+1+a n+2 a n+a n+1=15所以数列{a n+a n+1}是公比为15的等比数列；(2)因为a1=15，a2=125，所以a1+a2=625，由(1)知数列{a n+a n+1}是首项为625，公比为15的等比数列，所以a n+a n+1=625×15n-1，于是a n+1-15n+1=-an-15 n=(-1)n a1-15，又因为a1-15=0，所以a n-15 n=0，即a n=15 n.46.(2022·湖北·天门市教育科学研究院模拟预测)已知数列a n满足a1=1,a2=6，且a n+1=4a n-4a n-1, n≥2,n∈N*.(1)证明数列a n+1-2a n是等比数列，并求数列a n的通项公式；(2)求数列a n的前n项和S n.【解析】(1)因为a n+1=4a n-4a n-1,n≥2,n∈N*所以a n+1-2a n=2a n-4a n-1=2(a n-2a n-1)又因为a2-2a1=4所以a n+1-2a n是以4为首项，2为公比的等比数列.所以a n+1-2a n=4×2n-1=2n+1变形得a n+12n+1-a n2n=1所以a n2n是以a12=12为首项，1为公差的等差数列所以a n2n=12+n-1=n-12，所以a n=(2n-1)2n-1(2)因为T n=1×20+3×21+5×22+⋅⋅⋅+(2n-1)2n-1⋯①所以2T n=1×21+3×22+5×23+⋅⋅⋅+(2n-1)2n⋯②①-②得：-T n=1+22+23+⋅⋅⋅+2n-1-(2n-1)2n=1+22(1-2n-1)1-2-(2n-1)2n所以T n=(2n-1)2n-2n+1+3=(2n-3)2n+347.(2022·内蒙古·赤峰红旗中学松山分校模拟预测(理))设数列{a n}的前n项和为S n，满足2S n=a2n+1a n n∈N*，则下列说法正确的是( )A.a2021⋅a2022<1B.a2021⋅a2022>1C.a2022<-22022D.a2022>22022【答案】A【解析】因为数列{a n}的前n项和为S n，满足2S n=a2n+1a n n∈N*，。

2016国家公务员考试行测答题技巧：特殊值法巧解数学运算题数学运算是2016国家公务员考试行测考试中的重点题型，其关键是用最优的解题方法快速解答。

华图教育为了考生可以迅速理清思路、简化解题过程，向大家介绍特殊值法，以下就是《2016国家公务员考试行测答题技巧：特殊值法巧解数学运算题》的全部内容，希望可以帮助各位考生更好的备考2016国家公务员考试。

(一)定义特殊值法，就是在题目所给的范围内取一个恰当的特殊值直接代入，将复杂的问题简单化的方法。

特殊值法必须选取满足题干的特殊数、特殊点、特殊函数、特殊数列或特殊图形代替一般的情况，并由此计算出结果，从而快速解题。

(二)适用范围特殊值法常应用于和差倍比问题、行程问题、工程问题、浓度问题、利润问题、几何问题等。

其中，在工程问题、浓度问题相关的比例问题时，一般将特殊值设为1;在涉及多个比例的问题时，有时为了将数值整数化，可以设特殊值为总量的最小公倍数。

(三)解题原则在运用特殊值法时，要注意：1.确定这个特殊值不影响所求结果;2.数据不要太繁琐，应便于快速、准确计算，可尽量使计算结果为整数;3.结合其他方法灵活使用。

2016国家公务员考试行测答题技巧：特殊值法巧解数学运算题(2)一个人从家到公司，当他走到路程一半的时候，速度下降了10%，问：他走完全程所用时间的前半段和后半段所走的路程比是：A.10∶9B.21∶19C.11∶9D.22∶18【例题2】一项工程计划用20天完成，实际只用了16天就完成了，则工作效率提高的百分率是：A.20%B.25%C.50%D.60%2016国家公务员考试行测答题技巧：特殊值法巧解数学运算题(3)两个相同的瓶子装满某种化学溶液，一个瓶子中溶质与水的体积比是3∶1，另一个瓶子中溶质与水的体积比是4∶1，若把两瓶化学溶液混合，则混合后的溶质和水的体积之比是：A.31∶9B.7∶2C.31∶40D.20∶11以上就是文章的全部内容，希望各位考生可以学以致用，在2016国家公务员考试中获得优秀成绩!相关备考入口：2016年国考行测技巧|2016年国考申论备考|2016年国考申论热点历年国考真题True|必备2016年国考图书| 2016年国家公务员招考信息汇总。

基础知识1．斐波那契数列莱昂纳多斐波那契（1175－1250）出生于意大利比萨市，是一名闻名于欧洲的数学家，其主要的著作有《算盘书》、《实用几何》和《四艺经》等。

在1202年斐波那契提出了一个非常著名的数列，即：假设一对兔子每隔一个月生一对一雌一雄的小兔子，每对小兔子在两个月以后也开始生一对一雌一雄的小兔子，每月一次，如此下去。

年初时兔房里放一对大兔子，问一年以后，兔房内共有多少对兔子？这就是非常著名的斐波那契数列问题。

其实这个问题的解决并不是很困难，可以用表示第个月初时免房里的免子的对数，则有，第个月初时，免房内的免子可以分为两部分：一部分是第个月初就已经在免房内的免子，共有对；另一部分是第个月初时新出生的小免子，共有对，于是有。

现在就有了这个问题：这个数列的通项公式如何去求？为了解决这个问题，我们先来看一种求递归数列通项公式的求法——特征根法。

特征根法：设二阶常系数线性齐次递推式为（），其特征方程为，其根为特征根。

（1）若特征方程有两个不相等的实根，则其通项公式为（），其中A、B由初始值确定；（2）若特征方程有两个相等的实根，则其通项公式为（），其中A、B由初始值确定。

（这个问题的证明我们将在后面的讲解中给出）因此对于斐波那契数列，对应的特征方程为，其特征根为：，所以可设其通项公式为，利用初始条件得，解得所以。

这个数列就是著名的斐波那契数列的通项公式。

斐波那契数列有许多生要有趣的性质，如：它的通项公式是以无理数的形式给出的，但用它计算出的每一项却都是整数。

斐波那契数列在数学竞赛的组合数学与数论中有较为广泛地应用。

为了方便大家学习这一数列，我们给出以下性质：（请同学们自己证明）（1）斐波那契数列的前项和；（2）；（3）（）；（4）（）；（5）（）；2．分群数列将给定的一个数列{}：按照一定的规则依顺序用括号将它分组，则可以得到以组为单位的序列。

如在上述数列中，我们将作为第一组，将作为第二组，将作为第三组，……依次类推，第组有个元素，即可得到以组为单位的序列：（），（），（），……我们通常称此数列为分群数列。