新版弹性地基梁计算实际及算例教材

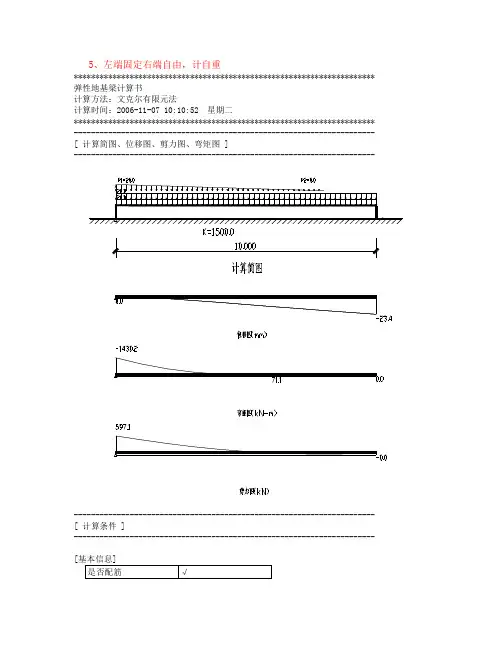
5、左端固定右端自由，计自重********************************************************************** 弹性地基梁计算书计算方法：文克尔有限元法计算时间：2006-11-07 10:10:52 星期二********************************************************************** ---------------------------------------------------------------------- [ 计算简图、位移图、剪力图、弯矩图 ]-------------------------------------------------------------------------------------------------------------------------------------------- [ 计算条件 ]---------------------------------------------------------------------- [[[各跨信息]No. L Ix B H A γ u K E Ri Rj1 10.000 427.083 4.100 0.500 2.050 25.00 0.20 1500.020000.0 固定自由注：L ----跨长，单位：mIx ----截面惯性矩，单位：m4/10000B ----截面底部宽度，单位：mH ----截面高度，单位：mA ----截面面积，单位：m2γ ----材料容重，单位：kN/m3u ----材料泊松比K ----基床系数，单位：kN/m3E ----弹性模量，单位：MPaRi ----梁左端约束Rj ----梁右端约束[第注：P1、P2 ----对集中力单位：kN----对分布荷载单位：kN/m----------------------------------------------------------------------[ 各单元计算结果 ]----------------------------------------------------------------------单元号 Xi Xj Qi Qj Mi Mj Di Dj1 0.00 1.00 597.09 458.90 -1430.24 -902.92 0.0 -0.72 1.00 2.00 458.89 332.23 -902.91 -508.58 -0.7 -2.53 2.00 3.00 332.23 222.19 -508.57 -232.90 -2.5 -4.94 3.00 4.00 222.18 131.44 -232.89 -57.76 -4.9 -7.65 4.00 5.00 131.43 61.02 -57.76 36.76 -7.6 -10.46 5.00 6.00 61.02 11.02 36.76 71.10 -10.4 -13.17 6.00 7.00 11.02 -18.95 71.10 65.49 -13.1 -15.88 7.00 8.00 -18.95 -29.39 65.49 39.71 -15.8 -18.39 8.00 9.00 -29.39 -22.43 39.71 12.50 -18.3 -20.810 9.00 10.00 -22.43 -0.00 12.50 0.00 -20.8 -23.4 注：1.Xi----单元i端坐标(m)2.Xj----单元j端坐标(m)3.Qi----单元i端剪力(kN)4.Qj----单元j端剪力(kN)5.Mi----单元i端弯矩(kN-m)6.Mj----单元j端弯矩(kN-m)7.Di----单元i端位移(mm)8.Dj----单元j端位移(mm)----------------------------------------------------------------------[ 各跨计算结果 ]----------------------------------------------------------------------注：下面的“中”是指梁的几何中点，不一定是弯矩最大点跨号： 1 左中右弯矩(kN-m)：-1430.24 36.76 0.00剪力(kN)： 597.09 61.02 -0.00位移(mm)： 0.00 -10.38 -23.36上部纵筋(mm2)： 12226.7 4100.0 4100.0下部纵筋(mm2)： 4100.0 4100.0 4100.0箍筋(mm2)： 595.1 595.1 595.1截面验算：满足满足满足注：1. 输出的内力值不包括“结构重要性系数γ0”。

1、楼面活载qk=2.0kn/㎡，恒荷载gk=3.765kn/㎡主梁尺寸为200mm x 550mm板厚为125mm荷载设计值：q=1.4x2=2.8kn/㎡g+q/2=4.518+1.4=5.918kn/㎡g=1.2x3.765=4.518kn/㎡g+q=2.8+4.518=7.318kn/㎡2、计算跨度内跨：l0=l c，边跨：l0=l c+200/2结构平面布置如图：共分为12种区格板（包含阳台板）A区格板计算跨度：l01=1.5-0.2=1.3m l02=3.5-0.2=3.3m跨中弯矩m=(g+q)l201/24=7.318x1.3x1.3/24=0.515kn·m支座弯矩M1=-(g+q)l201/12=-7.318x1.3x1.3/12=-1.03kn·mM2=-(g+q)l201/12=-7.318x1.3x1.3/12=-1.03kn·m环境类别一级，C30混凝土，板的最小保护层厚度C=15mm，假定纵向钢筋直径为6mm，板厚125mm，则截面有效高度h0=125-15-6/2=107mm，板宽b=1000mm。

α1=1.0，f c=14.3kn/m㎡；f y=360 kn/m㎡。

跨中正弯矩配筋计算：αs=M/（α1f c bh2）=0.515/（1x14.3x1x0.1072）=0.031§=1-1−2α=0.0315As= §bh0α1f c/f y=0.0315x1000x107x14.3/360=133.9mm2I区格板计算跨度：l01=1.2-0.1=0.9m l02=3.1-0.1=3.0m跨中弯矩m=(g+q)l201/24=8.018x0.92/24=0.27kn·m支座弯矩M1=-(g+q)l201/12=-8.018x0.92/12=-0.54kn·mM2=-(g+q)l201/12=-8.018x0.92/12=-0.54kn·m跨中正弯矩配筋计算：αs=M/（α1f c bh2）=0.27/（1x14.3x1x0.1072）=0.016§=1-1−2α=0.016As= §bh0α1f c/f y=0.016x1000x107x14.3/360=68.0mm2K区格板计算跨度：l01=1.5-0.1=1.4m l02=5-0.1=4.9m跨中弯矩m=(g+q)l201/24=7.318x1.4x1.4/24=0.6kn·m支座弯矩M1=-(g+q)l201/12=-7.318x1.4x1.4/12=-1.20kn·mM2=-(g+q)l201/12=-7.318x1.4x1.4/12=-1.20kn·m跨中正弯矩配筋计算：αs=M/（α1f c bh2）=0.6/（1x14.3x1x0.1072）=0.037§=1-1−2α=0.038As= §bh0α1f c/f y=0.038x1000x107x14.3/360=161.51mm2L区格板计算跨度：l01=1.5-0.1=1.4m l02=3.5-0.1=3.4m跨中弯矩m=(g+q)l201/24=7.318x1.4x1.4/24=0.6kn·m支座弯矩M1=-(g+q)l201/12=-7.318x1.4x1.4/12=-1.20kn·mM2=-(g+q)l201/12=-7.318x1.4x1.4/12=-1.20kn·m跨中正弯矩配筋计算：αs=M/（α1f c bh2）=0.6/（1x14.3x1x0.1072）=0.037§=1-1−2α=0.038As= §bh0α1f c/f y=0.038x1000x107x14.3/360=161.51mm2G区格板计算跨度：l01=4.6m l02=5.1m跨中弯矩M1=（0.0291+0.2x0.0224）x（g+q/2）l201+（0.0456+0.2x0.0358）ql201/2=8.05kn•mM2=（0.0224+0.2x0.0291）x（g+q/2）l201+（0.0358+0.2x0.0456）ql201/2=6.81kn•m支座弯矩M1`=M1``=-0.0776(g+q)l201=-12.02kn•mM2``=M2``=-0.0716(g+q)l201=-11.08kn•m配筋计算截面有效高度：由于是双向配筋，两个方向的截面有效高度不同。

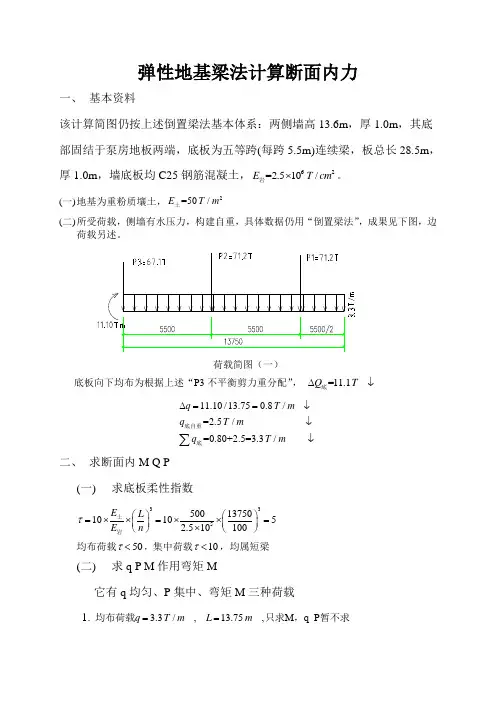
弹性地基梁法计算断面内力一、 基本资料该计算简图仍按上述倒置梁法基本体系：两侧墙高13.6m ，厚1.0m ，其底部固结于泵房地板两端，底板为五等跨(每跨5.5m)连续梁，板总长28.5m ，厚1.0m ，墙底板均C25钢筋混凝土，62=2.510/E T cm ⨯岩。

(一) 地基为重粉质壤土，2=50/E T m 土(二) 所受荷载，侧墙有水压力，构建自重，具体数据仍用“倒置梁法”，成果见下图，边荷载另述。

荷载简图（一）底板向下均布为根据上述“P3不平衡剪力重分配”， =11.1Q T∆↓底11.10/13.750.8/=2.5/=0.80+2.5=3.3/q T m q T mqT m∆==↓↓↓∑底自重底二、 求断面内M Q P (一)求底板柔性指数33550013750101052.510100E L E n τ⎛⎫⎛⎫=⨯⨯=⨯⨯= ⎪ ⎪⨯⎝⎭⎝⎭土岩 均布荷载50τ<，集中荷载10τ<，均属短梁(二) 求q P M 作用弯矩M它有q 均匀、P 集中、弯矩M 三种荷载1. 3.3/,13.75,M q P q T m L m ==均布荷载只求，暂不求220.010.01 3.313.75 6.24q M MqL M M T m ==⨯⨯=⋅，M 查表2. 集中荷载11171.2, 2.75/13.750.2,0.010.0171.213.759.8P Ta M MPL M M T m =====⨯⨯=⋅22271.2,8.25/13.750.6,7.8P P Ta M M Tm ====3367.1,13.75/13.751,0.010.0167.113.759.23P Ta M MPL M M T m =====⨯⨯=⋅3. 98.3,13.75/13.75 1.0,0.010.01M m M T m a M MM M T m =-⋅====-⋅弯矩4. 弯矩M 叠加5. 绘M 图（二）弯矩图（二）(三) 边荷载影响泵房两侧自排涵不同：东侧涵总宽8.2m ，顶底高程差16.578.97.67m ∇-=，填土涵上高程22.00m ∇，其为安装间顶高程38.00m ∇，安装重24/T m 。

第3章 弹性地基梁的计算计算基础梁常用的三种假设： (1)地基反力按直线分布的假定； (2)文克尔假定；(3)地基为弹性半无限体(或弹性半无限平面)的假定。

3.1按文克尔假定计算基础梁的基本方程1. 弹性地基梁的挠度曲线微分方程根据文克尔假定，地基反力用下式表达。

Ky =σ (3-1) 式中，σ－任一点的地基反力（kN/m 2）y －相应点的地基沉陷量（m ）K －弹性压缩系数（kN/m 3）梁的角变，位移、弯矩、剪力及荷载的正方向均如图中所示。

推导出基础梁的挠度曲线微分方程。

图3-1从弹性地基梁中取出微段，根据平衡条件∑y =0，得 (dQ Q +)－Q +dx x q )(－dx σ＝0 化简后变为)(x q dx dQ-=σ (3-2) 再根据∑M =0，得M －(M +dM )+(dQ Q +)dx +2)(2)()(22dx dx x q σ-=0 整理并略去二阶微量，则得dx dM Q =(3-3) 由式(3-2)和式(3-3)，知)(22x q dx Md dx dQ -==σ (3-4)若不计剪力对梁挠度的影响，则由材料力学中得dx dy =θdx d EJM θ-== 22dx y d EJ - (3-5)33dx y d EJ dx dM Q -== 将式(3-5)代人式(3-4)，并应用式(3-1)，则得)(44x q Ky dx yd EJ +-= (3-6) 令 α＝44EJ K（3-7） 代入式(3-6)，得)(444444x q K y dx y d αα=+ (3-8)式中α叫做梁的弹性标值。

式(3-8)就是弹性地基梁的挠度曲线微分方程。

为了便于计算，在上式中用变数x α代替变数x ，二者有如下的关系：)()()(x d dy dxx d x d dy dx dy αααα== (3-9) 将上式代入式(3-9)，则得)(44)(44x q K y x d y d αα=+ (3-10)2. 挠度曲线微分方程的齐次解解的一般形式为：x x sh C x x sh C x x ch C x x ch C y ααααααααsin cos sin cos 4321+++= （3-11） 在上式中引用了2x x e e x sh ααα--=， 2xx e e x ch ααα-+=3.2按文克尔假定计算短梁1. 初参数和双曲线三角函数的引用图示一等截面基础梁，设左端有位移0y ，角变0θ、弯矩0M 和剪力0Q ，它们的正方向如图中所示。